A two-stage robust generation expansion planning framework for regional integrated energy systems with carbon growth constraints

After proposing the carbon peaking and carbon neutrality target, China further proposed a series of specific carbon emission growth limit sub-targets. How to decarbonize the energy system to ensure the realization of the carbon growth limit sub-targets is a meaningful topic. At present, generation expansion planning of renewable energy in integrated energy systems has been well studied. However, few of the existing studies consider specific carbon emission growth targets. To address this research gap, a two-stage robust generation expansion planning framework for regional integrated energy systems with carbon growth constraints is proposed in this paper, which takes into account multiple uncertainties. In this framework, the objective function is to minimize the total operation cost and wind turbine investment cost. The first stage is the decision-making level of the wind turbine capacity configuration scheme. The second stage is the optimal economic dispatching in the worst-case scenario, which is a bi-level problem of max-min form. Thus, the two-stage robust optimization framework constitutes a problem of min-max-min form, which is pretty hard to solve directly with a commercial solver. Therefore, a nested column-and-constraint generation algorithm is adopted and nested iterations are performed to solve the complex problem. Finally, case studies are carried out on a regional electric-gas integrated energy system. The MATLAB/YALMIP simulation platform with the Gurobi solver is used to verify the effectiveness and superiority of the proposed framework. Compared with other four cases, 5,000 Monte Carlo scheduling tests demonstrate that the proposed framework can ensure the system carbon emission to be controlled within a certain limit even in the worst scenario. Due to the consideration of multiple uncertainties, the proposed framework planning results are both robust and economical for investment. This study can provide theoretical support for the actual regional integrated energy system to achieve a certain carbon growth target.

1 Introduction

Low carbon is the common theme of development in the world today. After the Paris Agreement was put forward, countries around the world have attached great importance to carbon reduction (Höhne et al., 2021; Liu Y. et al., 2022). Since China announced the carbon peak and carbon neutrality goals, it has concreted the macro-strategic goals into various regional development indicators (Zhang et al., 2021; Sun et al., 2022). The energy system is a key area of carbon emissions in a region (Huang et al., 2020). Therefore, it is of great practical significance to study the low-carbon optimization of regional integrated energy systems (Xie et al., 2022).

Renewable energy power generation is an essential path to decarbonizing the regional integrated energy system. Therefore, renewable energy generation expansion planning has attracted the attention of many scholars. A group of scholars focused on power generation expansion planning for different objects (Toloo et al., 2022) considered both centralized and distributed solar, wind, hydro, geothermal and biomass power generation expansion plans (Fang et al., 2021) studied the joint planning of renewable energy generation and energy storage batteries in renewable energy integrated microgrids (Gonzalez-Romero et al., 2020) presented a review of the state-of-the-art on the coordination of generation and transmission expansion planning (Zhang et al., 2020) conducted a coordination planning study of wind farms, energy storage, and transmission network.

On the other hand, many scholars have studied the power generation expansion planning of renewable energy considering different factors or scenarios, and proposed various new models. The continuous penetration of renewable energy has an impact on the optimization model construction (Deng and Lv, 2020) screened out 34 studies of power system planning considering increasing variable renewable energy, and then the models of which were further deconstructed and compared. A new hierarchical modeling framework that integrates two multi-period and multi-regional generation expansion planning models was studied in (Lyrio de Oliveira et al., 2022). While the objective function of most power generation expansion research is the total cost, (Li et al., 2020) focused on increasing the utilization of renewable energy and reducing the renewable energy curtailment., and proposed a new objective function to maximize the accommodation of renewable energy during the planning horizon (Jabarnejad, 2021) integrated dynamic-line rating and transmission switching into the renewable sources generation-expansion planning problem.

Two factors, the uncertainties and carbon emissions, are usually considered in the planning problems of integrated energy systems. The uncertainty is an unavoidable consideration when studying power generation expansion planning (Yang et al., 2022) summarized various uncertainty modeling methods and discussed the application of uncertainty modeling in power system planning and operation. For the integrated energy system, the uncertainties of renewable energy and energy demand are usually considered (Fang et al., 2021) considered the uncertainties of wind power and solar power in the planning of renewable energy generation and storage batteries in a renewable energy integrated microgrid (Shen et al., 2020) considered the uncertainties of load and wind power output at the same time when they studied the power generation expansion planning of the energy system (Ahmadi et al., 2020) proposed a dynamic, robust generation-transmission expansion planning in the presence of wind farms under long-term and short-term uncertainties of wind power (Lei et al., 2020) proposed a multi-objective stochastic planning method based on the multi-dimensional correlation scenario generation method for the regional integrated energy system integrated renewable energy considering the uncertainties of renewable energies and loads of multiple energy types. The above studies have fully considered various uncertainties of sources and loads of various energy types. However, under the current turbulent international situation and the swaying global economy, the impact of natural gas price uncertainty on the regional integrated energy system has not been paid enough attention in the power generation expansion planning.

The power generation expansion planning considering the carbon emissions has been well researched. In the context of low-carbon development, some power generation expansion planning studies have considered carbon trading. A two-layer low-carbon expansion generation planning model considering carbon trading and carbon capture technology was established in (Mi et al., 2021). An innovative carbon emission trading scheme was formulated and applied to the co-planning of distributed renewable energy generation units, energy storage systems, and capacitor banks in (Melgar-Dominguez et al., 2020). (Liu J. et al., 2022) established a multi-flexibility resource planning model with a ladder-type carbon trading. The power generation expansion planning considering carbon trading can effectively promote the allocation of renewable energy power generation and mitigate system carbon emissions but cannot limit the amount of the total carbon emissions. Although there are few studies of expansion planning considering the carbon emission constraints (LU; Zhigang et al., 2022), a certain macro-target of carbon emissions isn’t considered in the regional development planning.

All in all, the existing research on power generation expansion planning in the regional integrated energy system has been well studied, but there is still a lack of integrating the actual regional carbon emission control targets and the uncertainty of natural gas price into the planning. To fill the research gap, this paper mainly makes the following contributions.

(1) Based on regional macro development goals, e.g., GDP (Gross Domestic Product) growth rate, energy consumption per unit of GDP, and carbon emission per unit of GDP, a regional integrated energy system carbon growth constraint model is constructed.

(2) In the power generation expansion planning of the regional integrated energy system, this paper considers multiple uncertainties in the process of robust optimization. In addition to the conventional wind power output and load uncertainties, the impact of natural gas price uncertainty on regional integrated energy system planning is also considered in light of the international situation. The influence mechanism of the three kinds of uncertainties on planning results is also briefly analyzed.

(3) A two-stage robust generation expansion planning framework for regional integrated energy systems with carbon growth constraints is proposed to obtain the wind power capacity that ensures the system meets carbon growth targets even in the worst-case scenarios. Based on the nested column-and-constraint generation (C&CG) algorithm, the proposed framework can be transformed into several mixed integer quadratic programming models that can be solved by commercial solvers.

The remainder of the paper is organized as follows: Section 2 describes the multiple uncertainty modeling and the proposed carbon growth constraints modeling. In Section 3, the proposed robust generation expansion planning framework and solution procedure are constructed. In Section 4, case studies are demonstrated. Section 5 concludes the work.

2 Methodology

2.1 Uncertainty modeling

Robust optimization does not require the probability distribution of uncertain parameters to be given in advance, but describes the fluctuation of parameters through a certain bounded set, which is called an uncertain set. As long as the value of the parameter is within the range of the uncertain set, the solution of the robust optimization model must be feasible. Commonly used uncertain sets include box uncertain sets, polyhedral uncertain sets, ellipsoid uncertain sets, and N-k uncertain sets (Zhu et al., 2017). The first three sets are suitable for continuous uncertain parameters such as bus injected power and electricity price, and the third set is suitable for discrete uncertain parameters such as fault states.

2.1.1 Uncertainty modeling of power system

Common uncertainties in power system include uncertainty of injected power, uncertainty of electricity price, uncertainty of power load and uncertainty of N-k fault (Zhu et al., 2017). This study mainly focuses on the uncertainty of wind power and power load. Since the optimization results of the box uncertainty set are too conservative, polyhedral uncertainty sets are adopted to model uncertainties of wind power and power load. The polyhedral uncertainty set of power load are shown as Eq. 1.

$\begin{array}{c}{u}^L=\left\{{\stackrel{\sim }{P}}_{i,t}^L|{\stackrel{\sim }{P}}_{i,t}^L=P_{i,t}^L+∆P_{i,t}^L{\stackrel{\sim }{g}}_{i,t}^L,{\displaystyle \sum }_{t=1}^T\left|{\stackrel{\sim }{g}}_{i,t}^L\right|\le {\Gamma }^L,{\stackrel{\sim }{g}}_{i,t}^L\in \left[-\mathrm{1,1}\right],i\in {\Omega }^L\right\}\end{array}(1)$

where $u^L$ denotes the uncertainty set of power load, ${\stackrel{\sim }{P}}_{i,t}^L$, $P_{i,t}^L$ and $∆P_{i,t}^L$ represent the uncertain power load, forecast power load value, and power load deviation, respectively; ${\stackrel{\sim }{g}}_{i,t}^L$ represents an uncertain variable between −1 and 1; $T$ is the period of the optimization; ${\mathrm{\Gamma }}^L$ represents the budget value to limit the uncertainty of power loads; ${\mathrm{\Omega }}^L$ denotes the set of power loads.

To better characterize the fluctuation of wind power, the relative value of wind power deviation is used to generate the base uncertainty set, which is a special polyhedron uncertainty set. The base uncertainty set of wind power are shown as Eq. 2.

$\begin{array}{c}{u}^W=\left\{{\stackrel{\sim }{P}}_{i,t}^W|0\le {\stackrel{\sim }{P}}_{i,t}^W\le {\mathrm{P}}_{N,i}^{WT},{\displaystyle \sum }_{t=1}^T\left|\frac{{\stackrel{\sim }{P}}_{i,t}^W-{\widehat{P}}_i^W}{{\widehat{P}}_i^W}\right|\le {\Gamma }^W,i\in {\Omega }^W\right\}\end{array}(2)$

where $u^W$ denotes the uncertainty set of wind power, ${\stackrel{\sim }{P}}_{i,t}^W$ represents the uncertain wind power; ${\mathrm{P}}_{N,i}^{WT}$ and ${\widehat{P}}_i^W$ represent the rated capacity and expectation value of wind power output, respectively; ${\mathrm{\Gamma }}^W$ represents the budget value to limit the uncertainty of wind power; ${\mathrm{\Omega }}^W$ denotes the set of wind turbines.

2.1.2 Uncertainty modeling of the gas system

Since natural gas can be compressed, the uncertainty of natural gas load can be mitigated by sufficient storage capacity in the transmission pipeline (Guo et al., 2020; Yi et al., 2022). Therefore, the gas load uncertainty can usually not be considered in the research. However, as stated in the Section 1, the gas price will even increase several times in a short period of time because there are many uncertain factors affecting it, and its uncertainty is strong. Therefore, this study mainly focuses on the uncertainty of gas price and a polyhedral uncertainty set are adopted to model uncertainties of gas price. The polyhedral uncertainty set of gas price are shown as Eq. 3.

$\begin{array}{c}{u}^{gp}=\left\{{\stackrel{\sim }{c}}_{i,t}^{gp}|{\stackrel{\sim }{c}}_{i,t}^{gp}=c_{i,t}^{gp}\left(1+{\stackrel{\sim }{g}}_{i,t}^{gp}\right),{\displaystyle \sum }_{t=1}^T\left|{\stackrel{\sim }{g}}_{i,t}^{gp}\right|\le {\Gamma }^{gp},{\stackrel{\sim }{g}}_{i,t}^{gp}\in \left[-\mathrm{0.5,1.2}\right],i\in {\Omega }^S\right\}\end{array}(3)$

where $u^{gp}$ denotes the uncertainty set of gas price, ${\stackrel{\sim }{c}}_{i,t}^{gp}$ and $c_{i,t}^{gp}$ represent the uncertain gas price, and base gas price, respectively; ${\stackrel{\sim }{g}}_{i,t}^{gp}$ represents an uncertain variable between −0.5 and 1.2; ${\mathrm{\Gamma }}^{gp}$ represents the budget value to limit the uncertainty of the gas price; ${\mathrm{\Omega }}^S$ denotes the set of gas sources.

2.2 Carbon growth constraint modeling

A regional integrated energy system plan should be incorporated into the regional macro development plan. After putting forward the goal of achieving peak carbon neutrality, the Chinese government further put forward the target of reducing carbon emission per unit of GDP, reducing energy consumption per unit of GDP. Considering these macroscopic development goals, a specific constraint for regional integrated energy system planning can be proposed. The following takes China’s 14th Five-Year Plan as an example to illustrate the modeling of carbon growth constraints.

The reduction target of carbon emission per unit GDP during the 14th Five-Year Plan period can be expressed as Eq. 4.

$\begin{array}{c}\frac{C_{2025}}{G_{2025}}=\frac{C_{2021}}{G_{2021}}\left(1-{\alpha }^{crb}\right)\end{array}(4)$

where $C_{2021}$ and $C_{2025}$ represent the total regional carbon emissions in 2021 and 2025, respectively. $G_{2021}$ and $G_{2025}$ represent the region’s GDP in 2021 and 2025, respectively. ${\alpha }^{crb}$ represents the reduction rate of carbon emissions per unit of GDP in the region during the 14th Five-Year Plan period.

The target of reducing energy consumption per unit of GDP during the 14th Five-Year Plan period can be expressed as Eq. 5.

$\begin{array}{c}\frac{E_{2025}}{G_{2025}}=\frac{E_{2021}}{G_{2021}}\left(1-{\beta }^{erg}\right)\end{array}(5)$

where $E_{2021}$ and $E_{2025}$ represent the total regional energy consumption in 2021 and 2025, respectively. ${\beta }^{erg}$ represents the reduction rate of regional energy consumption per unit of GDP during the 14th Five-Year Plan period.

The GDP growth target during the 14th Five-Year Plan period can be expressed as Eq. 6.

$\begin{array}{c}{G}_{2025}=G_{2021}{\left(1+{\gamma }^{GDP}\right)}^{N_{year}}\end{array}(6)$

where ${\gamma }^{GDP}$ represents the average annual GDP growth rate of the region during the 14th Five-Year Plan period. $N_{year}$ represents the number of years in the 14th Five-Year Plan period, i.e., 5.

According to Eqs 4, 6, the average annual carbon emission growth rate ${\eta }^{crb}$, i.e., the carbon growth constraint, is Eq. 7.

$\begin{array}{c}{\eta }^{crb}=\left(1+{\gamma }^{GDP}\right){\left(1-{\alpha }^{crb}\right)}^{1/N_{year}}-1\end{array}(7)$

According to Eqs 5, 6, the annual growth rate of energy consumption ${\eta }^{erg}$ is Eq. 8.

$\begin{array}{c}{\eta }^{erg}=\left(1+{\gamma }^{GDP}\right){\left(1-{\beta }^{erg}\right)}^{1/N_{year}}-1\end{array}(8)$

3 The proposed robust generation expansion planning framework and solution procedure

Planning problems that consider uncertainty can usually be solved by fuzzy optimization, stochastic optimization, or robust optimization. Compared with fuzzy optimization and stochastic optimization, robust optimization does not require artificially given membership function or probability distribution function of uncertain parameters, and can strictly guarantee the feasibility of the solution (Du et al., 2022). Achieving carbon reduction targets is a daunting and important task, and this study aims to explore how power generation expansion planning can be done under various uncertainties to achieve carbon reduction targets. Therefore, a robust generation expansion planning framework are proposed in this paper.

3.1 The proposed two-stage robust planning framework

According to the number of decision-making stages, robust optimization can be divided into static robust optimization and two-stage robust optimization. Static robust optimization, also known as single-stage robust optimization, is characterized by making decisions before the specific realization of uncertain parameters is known, so the results are usually too conservative and inconsistent with the actual situation. Because the decision of the two-stage robust optimization is carried out in stages, the conservativeness of the model is weaker than that of the static robust optimization model (Zhu et al., 2017). Therefore, two-stage robust optimization are adopted in this study to solve the generation expansion planning considering the carbon emission growth limits. The schematic diagram of proposed two-stage robust generation expansion planning framework is shown as Figure 1.

FIGURE 1

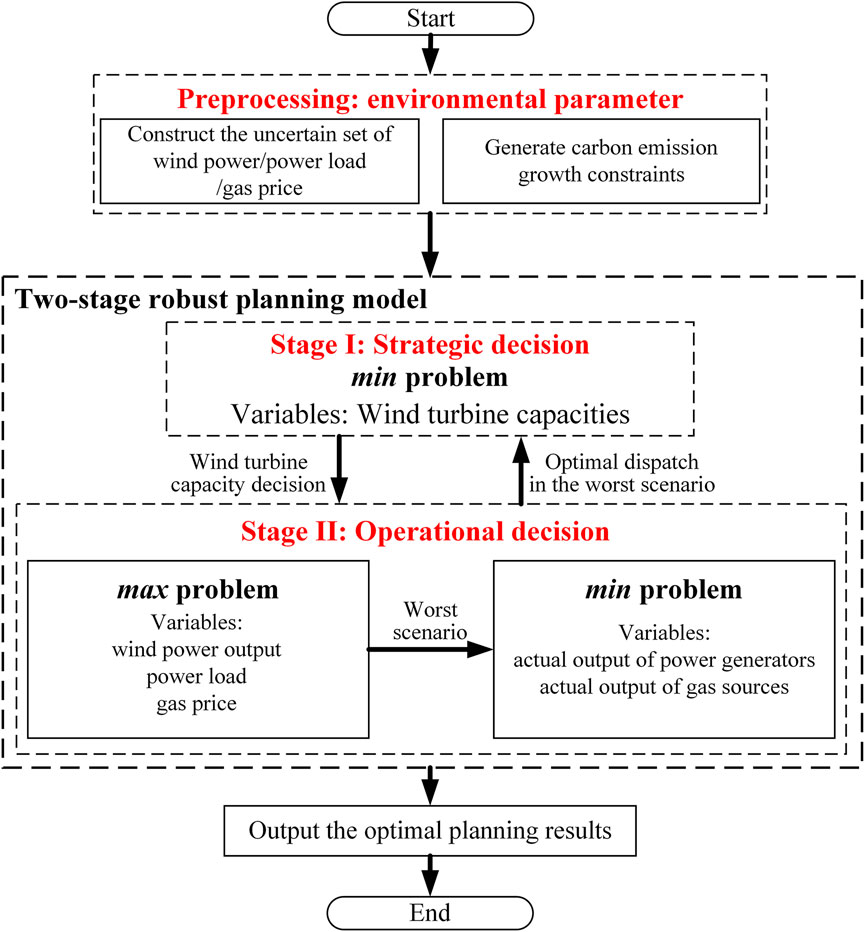
FIGURE 1. The schematic diagram of the proposed two-stage robust generation expansion planning framework.

3.1.1 Objective function

The two-stage robust optimization model is adopted to handle the uncertainties of wind power, power loads, and gas prices. The objective function of stage I consists of wind turbine investment costs and its strategic decision variables are the capacities of wind turbines. Stage II is to carry out the economic dispatch in the worst scenario of the whole uncertain set under the situation of the first-stage decision. Its operational decision variables are the actual outputs of power generators and gas sources. The objective function of stage II consists of the energy supply costs of the electric-gas integrated energy system. The complete formulation of the objective function in the proposed two-stage robust optimization model is shown as Eq. 9.

$\begin{array}{c}\min \left({\displaystyle \sum }_{w\in {\Omega }^W}{c}^{WI}{P}_{N,w}^{WT}+maxmin\left({\displaystyle \sum }_{t=1}^T\left({\displaystyle \sum }_{i\in {\Omega }^W\cup {\Omega }^C}{c}^G{P}_{g,t}^G+{\displaystyle \sum }_{j\in {\Omega }^S}{\stackrel{\sim }{c}}_{i,t}^{gp}{F}_{g,t}^S\right)\right)\right)\end{array}(9)$

where $c^{WI}$ and $c^G$ are cost coefficients of wind turbine investment and power generation, respectively; $P_{N,w}^{WT}$ represents the rated capacities of wind turbines; $P_{g,t}^G$ and $F_{g,t}^S$ denotes the actual generator output and gas flow of gas sources; ${\mathrm{\Omega }}^C$ represents the set of coal-fired generators.

3.1.2 Constraints

Since carbon emissions in the power system are closely related to active power flow, the DC power flow modeling is adopted in this paper. Constraints Eqs 10–16 represent the power system operational constraints. Constraint Eq. 17 represents the wind turbine capacity constraint. Constraints of uncertain sets of power load, wind power and gas price are shown in Eqs 1–3.

$\begin{array}{c}{\underset{¯}{P}}_i^G\le P_{i,t}^G\le {\overline{\mathrm{P}}}_i^{G}i\in {\complement }_{{\Omega }^G}{\Omega }^W\end{array}(10)$

$\begin{array}{c}0\le P_{i,t}^G\le {\stackrel{\sim }{P}}_{i,t}^{W}i\in {\Omega }^W\end{array}(11)$

$\begin{array}{c}{P}_{ij,t}=\frac{{\theta }_{ij,t}}{x_{ij}}\end{array}(12)$

$\begin{array}{c}{\underset{¯}{P}}_{ij}{\le P}_{ij,t}\le {\overline{P}}_{ij}\end{array}(13)$

$\begin{array}{c}{P}_{i,t}^G={\displaystyle \sum }_{j\in {\Omega }_i}{P}_{ij,t}+{\stackrel{\sim }{P}}_{i,t}^L\end{array}(14)$

$\begin{array}{c}{\underset{¯}{\theta }}_{ij}\le {\theta }_{ij,t}\le {\overline{\theta }}_{ij}\end{array}(15)$

$\begin{array}{c}{\theta }_{ref,t}=0\end{array}(16)$

$\begin{array}{c}0\le {\mathrm{P}}_{N,i}^{WT}\le {\overline{\mathrm{P}}}_N^{WT}\end{array}(17)$

where $P_{i,t}^G$ represents the actual outputs of power generators; ${\overline{P}}_i^G$ and ${\underset{¯}{P}}_i^G$ represent the upper and lower limits of power generation; $P_{ij,t}$, ${\theta }_{ij,t}$ and $x_{ij}$ represent the power flow, phase angle difference, and reactance of branch $i-j$; ${\overline{P}}_{ij}$ and ${\underset{¯}{P}}_{ij}$ represent the upper and lower limits of branch transmission; ${\overline{\theta }}_{ij}$ and ${\underset{¯}{\theta }}_{ij}$ represent the upper and lower limits of branch phase angle difference; ${\theta }_{ref,t}$ is the phase angle of the slack bus; ${\overline{\mathrm{P}}}_N^{WT}$ represents the maximum value of wind turbine capacity; ${\mathrm{\Omega }}^G$ is the set of power generators; ${\mathrm{\Omega }}_i$ represents the set of buses adjacent to bus $i$.

The steady-state modeling of gas system based on the Weymouth function (De Wolf and Smeers, 2000) is adopted in this paper. Constraints Eqs 18–22 represent the gas system operational constraints. Constraints Eqs 23, 24 represent operational constraints of coupling units. Constraints Eq. 25 denotes the carbon emission growth constraints.

$\begin{array}{c}{\underset{¯}{F}}_m^S\le F_{m,t}^S\le {\overline{F}}_m^{S}m\in {\Omega }^S\end{array}(18)$

$\begin{array}{c}{F}_{mn,t}\left|F_{mn,t}\right|=k_{mn}\left({\pi }_{m,t}^2{-\pi }_{n,t}^2\right)\end{array}(19)$

$\begin{array}{c}{\underset{¯}{F}}_{mn}\le F_{mn,t}\le {\overline{F}}_{mn}\end{array}(20)$

$\begin{array}{c}{F}_{m,t}^S+F_{m,t}^{P2G}={\displaystyle \sum }_{n\in {\mathrm{\Omega }}_m}{F}_{mn}+F_{m,t}^L+F_{m,t}^{GFU}\end{array}(21)$

$\begin{array}{c}{\underset{¯}{\pi }}_m\le {\pi }_{m,t}\le {\overline{\pi }}_m\end{array}(22)$

$\begin{array}{c}{P}_{i,t}^G={\eta }^{GFU}{F}_{m,t}^{GFU}i\in {\Omega }^{GF}\end{array}(23)$

$\begin{array}{c}{F}_{m,t}^{P2G}={\eta }^{P2G}{P}_{i,t}^{P2G}m\in {\Omega }^{P2G}\end{array}(24)$

$\begin{array}{c}{CE}^{total}\le \left(1+{\eta }^{crb}\right){CE}^{initial}\end{array}(25)$

where $F_{m,t}^S$, ${\underset{\_}{F}}_m^S$ and ${\overline{F}}_m^S$ represent the mass flow rate of gas sources and their upper and lower limits; $F_{mn,t}$, ${\underset{\_}{F}}_{mn}$ and ${\overline{F}}_{mn}$ represent the mass flow rate of pipeline $m-n$ and its upper and lower limits; $k_{mn}$ is a constant determined by the pipeline parameters and environmental parameters; ${\pi }_{m,t}$, ${\underset{\_}{\pi }}_m$ and ${\overline{\pi }}_m$ represent the gas pressure of node $m$ and its upper and lower limits; $F_{m,t}^{P2G}$, $F_{m,t}^L$ and $F_{m,t}^{GFU}$ represent the mass flow rates of the power-to-gas unit, gas demand, and gas-fired unit; ${\eta }^{GFU}$ and ${\eta }^{P2G}$ represent the energy conversion efficiencies of the gas-fired power generator and power-to-gas unit; ${\mathrm{\Omega }}^{GF}$ and ${\mathrm{\Omega }}^{P2G}$ represent the set of gas-fired generators and set of power-to-gas units; ${\mathrm{\Omega }}_m$ represents the set of nodes adjacent to node $m$. ${CE}^{total}$ and ${CE}^{initial}$ represent the total carbon emission of the regional integrated energy system after expansion planning and before the growth of energy demand.

3.2 Solution procedure based on the nested C&CG algorithm

Even the easiest two-stage robust optimization (TRO), composed of three levels, can be an NP-hard problem. To overcome the computational burden, the Benders-dual cutting plane algorithm and column-and-constraint generation algorithm are commonly used to solve the two-stage robust optimization. Compared to the Benders-dual cutting plane algorithm, the C&CG algorithm performs an order of magnitude faster and therefore is commonly used to solve the TRO (Zeng and Zhao, 2013). Specifically in this study, the Weymouth function in constraints Eq. 19 is quadratic and can be piecewise linearized by introducing 0–1 variables. Since stage II in the proposed planning framework is a bi-level mixed integer programming problem that cannot be solved by the traditional C&CG algorithm, a nested C&CG algorithm proposed in (Long and Bo, 2012) was adopted to the TRO with integer variables in the second stage. According to the nested C&CG algorithm, the proposed TRO problem is divided into the master problem (MP) and the subproblem (SP) which is divided into the master problem of SP (MP_S) and the subproblem of SP (SP_S). Specifically, MP_S is a single-level max problem converted from a bi-level max-min problem by KKT conditions and given values of binary variables ${\mathit{Z}}^{v*}$. To improve readability, the proposed planning model in Section 3.1 is divided into MP, MP_S, and SP_S in matrix form. The MP, MP_S, and SP_S are shown as Eqs 26–28.

$\begin{array}{c}\begin{array}{c}\left(\mathbf{M}\mathbf{P}\right)\underset{\mathit{X}}{\min }{\mathit{a}}^T\mathit{X}+\eta \\ s.t.\begin{array}{c}\begin{array}{c}\mathit{A}\mathit{X}\le d\\ \eta {\ge \mathit{b}}^T{\mathit{Y}}^r\end{array}\\ \begin{array}{c}{\mathit{B}}_{\mathbf{1}}\mathit{X}+{\mathit{C}}_{\mathbf{1}}{\mathit{Y}}^r+{\mathit{D}}_{\mathbf{1}}{\mathit{Z}}^r+{\mathit{E}}_{\mathbf{1}}{\mathit{u}}^{\mathit{r}*}\le \mathit{e}\\ {\mathit{B}}_{\mathbf{2}}\mathit{X}+{\mathit{C}}_{\mathbf{2}}{\mathit{Y}}^r+{\mathit{D}}_{\mathbf{2}}{\mathit{Z}}^r+{\mathit{E}}_{\mathbf{2}}{\mathit{u}}^{\mathit{r}*}=\mathit{f}\end{array}\end{array}\end{array}\end{array}(26)$

$\begin{array}{c}\begin{array}{c}\left({\mathbf{M}\mathbf{P}}_{\mathbf{S}}\right)\underset{\mathit{u}}{\max }\tau \\ s.t.\begin{array}{c}\begin{array}{c}\begin{array}{c}\tau \le {\mathit{b}}^T{\mathit{Y}}^v\\ {\mathit{B}}_{\mathbf{1}}{\mathit{X}}^{*}+{\mathit{C}}_{\mathbf{1}}{\mathit{Y}}^{\mathit{v}}+{\mathit{D}}_{\mathbf{1}}{\mathit{Z}}^{v*}+{\mathit{E}}_{\mathbf{1}}{\mathit{u}}^{\mathit{v}}\le \mathit{e}\end{array}\\ \begin{array}{c}{\mathit{B}}_{\mathbf{2}}{\mathit{X}}^{*}+{\mathit{C}}_{\mathbf{2}}{\mathit{Y}}^v+{\mathit{D}}_{\mathbf{2}}{\mathit{Z}}^{v*}+{\mathit{E}}_{\mathbf{2}}{\mathit{u}}^{\mathit{v}}=\mathit{f}\\ \mathit{b}+{\mathit{C}}_{\mathbf{1}}^T{\mathit{\pi }}^{\mathit{v}}+{\mathit{E}}_{\mathbf{1}}^T{\mathit{\pi }}^{\mathit{v}}+{\mathit{C}}_{\mathbf{2}}^T{\mathit{\mu }}^{\mathit{v}}+{\mathit{E}}_{\mathbf{2}}^T{\mathit{\mu }}^{\mathit{v}}=\mathbf{0}\end{array}\end{array}\\ \begin{array}{c}{\mathit{\pi }}^{\mathit{v}}\left({\mathit{B}}_{\mathbf{1}}{\mathit{X}}^{*}+{\mathit{C}}_{\mathbf{1}}{\mathit{Y}}^{\mathit{v}}+{\mathit{D}}_{\mathbf{1}}{\mathit{Z}}^{v*}+{\mathit{E}}_{\mathbf{1}}{\mathit{u}}^{\mathit{v}}-\mathit{e}\right)=\mathbf{0}\\ {\mathit{\pi }}^{\mathit{v}}\ge 0\end{array}\end{array}\end{array}\end{array}(27)$

$\begin{array}{c}\begin{array}{c}\left({\mathbf{S}\mathbf{P}}_{\mathbf{S}}\right)\underset{\mathit{Y},\mathit{Z}}{\min }{\mathit{b}}^T{\mathit{Y}}^v\\ s.t.\begin{array}{c}{\mathit{B}}_{\mathbf{1}}{\mathit{X}}^{*}+{\mathit{C}}_{\mathbf{1}}{\mathit{Y}}^{\mathit{v}}+{\mathit{D}}_{\mathbf{1}}{\mathit{Z}}^v+{\mathit{E}}_{\mathbf{1}}{\mathit{u}}^{\mathit{v}*}\le \mathit{e}\\ {\mathit{B}}_{\mathbf{2}}{\mathit{X}}^{*}+{\mathit{C}}_{\mathbf{2}}{\mathit{Y}}^v+{\mathit{D}}_{\mathbf{2}}{\mathit{Z}}^v+{\mathit{E}}_{\mathbf{2}}{\mathit{u}}^{\mathit{v}*}=\mathit{f}\end{array}\end{array}\end{array}(28)$

where $\mathit{a}$ and $\mathit{b}$ are the coefficient matrixes of objective functions in stage I and stage II, respectively; $\mathit{X}$ represents the decision variables of stage I, i.e., the capacities of wind turbines; ${\mathit{Y}}^r$ represents the decision variables of stage II in the $r$ cycle, i.e., the actual outputs of the power generators, gas sources, and coupling units; ${\mathit{Z}}^r$ represents the binary variables introduced by the segment linearization of the Weymouth function in the gas system; ${\mathit{u}}^{\mathit{r}}$ represents the uncertain variables, i.e., the power load, wind power output, and gas price, and the marker * indicate that this value is given by the previous step in the algorithm; ${\mathit{B}}_{\mathbf{1}},{\mathit{C}}_{\mathbf{1}},{\mathit{D}}_{\mathbf{1}},{\mathit{E}}_{\mathbf{1}}$ and ${\mathit{B}}_{\mathbf{2}},{\mathit{C}}_{\mathbf{2}},{\mathit{D}}_{\mathbf{2}},{\mathit{E}}_{\mathbf{2}}$ represent the coefficient matrixes of inequality constraints and equality constraints, respectively; $\mathit{e}$ and $\mathit{f}$ represent the matrixes of constants in inequality constraints and equality constraints, respectively; ${\mathit{\pi }}^{\mathit{v}}$ and ${\mathit{\mu }}^{\mathit{v}}$ represent the matrixes of dual variables; $r$ and $v$ reresent the number of outer loops and inner loops, respectively. The detailed process of solving Algorithm 1 is as follows:

Algorithm 1. The nested C and CG algorithm.

Outer loop: Solve the MP

Step 1: Set the loop index, upper bound, and lower bound of the outer loop, and artificially give an initial scenario of uncertain sets: $r=1,{UB}^{out}=+\infty ,{LB}^{out}=+\infty ,{\mathit{u}}^{\mathit{r}*}={\mathit{u}}^{\mathbf{0}}$.

Step 2: Solve the MP and obtain the optimal wind turbine capacities ${\mathit{X}}^{\mathit{r}*}$ = X, and update the lower bound of the outer loop ${LB}^{out}=\mathit{max}\left\{{LB}^{out},{\mathit{a}}^T{\mathit{X}}^{*}+\eta \right\}$.

Step 3: Jump to the inner loop, solve the SP and obtain the worst scenario of the uncertain set ${\mathit{u}}^{\mathit{r}*}$.

Step 4: Determine whether it is convergent. 1) If $1-{LB}^{out}/{UB}^{out}<\epsilon$ ($\epsilon$ is the convergence threshold), output the final planning result ${\mathit{X}}^{*}$ = ${\mathit{X}}^{\mathit{r}*}$ and terminate the loop. 2) If $1-{LB}^{out}/{UB}^{out}\ge \epsilon$, set $r=r+1$, jump to Step 2 in outer loop and add the following constraints to MP.

$\begin{array}{l}\left\{\begin{array}{l}\eta {\ge \mathit{b}}^T{\mathit{Y}}^r\\ \begin{array}{l}{\mathit{B}}_{\mathbf{1}}\mathit{X}+{\mathit{C}}_{\mathbf{1}}{\mathit{Y}}^r+{\mathit{D}}_{\mathbf{1}}{\mathit{Z}}^r+{\mathit{E}}_{\mathbf{1}}{\mathit{u}}^{\mathit{r}*}\le \mathit{e}\\ {\mathit{B}}_{\mathbf{2}}\mathit{X}+{\mathit{C}}_{\mathbf{2}}{\mathit{Y}}^r+{\mathit{D}}_{\mathbf{2}}{\mathit{Z}}^r+{\mathit{E}}_{\mathbf{2}}{\mathit{u}}^{\mathit{r}*}=\mathit{f}\end{array}\end{array}\right.\end{array}(29)$

Inner loop: Solve the SP

Step 1: Set the loop index, upper bound, and lower bound of the inner loop, and give initial values of binary variables ${\mathit{Z}}^{v*}$ if $v=1$: $v=1,{UB}^{in}=+\infty ,{LB}^{in}=+\infty ,{\mathit{Z}}^{\mathit{v}*}={\mathit{Z}}^{\mathit{r}}$.

Step 2: Solve the MP_S, obtain the current worst scenario of the uncertain set ${\mathit{u}}^{\mathit{v}*}={\mathit{u}}^{\mathit{v}}$ and update the upper bound of the inner loop ${UB}^{in}=\mathit{min}\left\{{UB}^{in},\tau \right\}$.

Step 3: Solve the SP_S, obtain the binary variables ${\mathit{Z}}^{v*}$ and update the lower bound of the inner loop ${LB}^{in}=\mathit{max}\left\{{LB}^{in},{\mathit{b}}^T{\mathit{Y}}^v\right\}$.

Step 4: Determine whether it is convergent. 1) If $1-{LB}^{in}/{UB}^{in}<\epsilon$, terminate the inner loop, return ${\mathit{u}}^{\mathit{r}*}$ = ${\mathit{u}}^{\mathit{v}*}$ and ${UB}^{out}={UB}^{in}$ to the outer loop. 2) If $1-{LB}^{in}/{UB}^{in}\ge \epsilon$, set $v=v+1$ and ${\mathit{Z}}^{v*}={\mathit{Z}}^{v-1*}$, jump to Step 2 in the inner loop, and add the following constraints to MP_S.

$\begin{array}{c}\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}\tau \le {\mathit{b}}^T{\mathit{Y}}^v\\ {\mathit{B}}_{\mathbf{1}}{\mathit{X}}^{*}+{\mathit{C}}_{\mathbf{1}}{\mathit{Y}}^{\mathit{v}}+{\mathit{D}}_{\mathbf{1}}{\mathit{Z}}^{v*}+{\mathit{E}}_{\mathbf{1}}{\mathit{u}}^{\mathit{v}}\le \mathit{e}\end{array}\\ \begin{array}{c}{\mathit{B}}_{\mathbf{2}}{\mathit{X}}^{*}+{\mathit{C}}_{\mathbf{2}}{\mathit{Y}}^v+{\mathit{D}}_{\mathbf{2}}{\mathit{Z}}^{v*}+{\mathit{E}}_{\mathbf{2}}{\mathit{u}}^{\mathit{v}}=\mathit{f}\\ \mathit{b}+{\mathit{C}}_{\mathbf{1}}^T{\mathit{\pi }}^{\mathit{v}}+{\mathit{E}}_{\mathbf{1}}^T{\mathit{\pi }}^{\mathit{v}}+{\mathit{C}}_{\mathbf{2}}^T{\mathit{\mu }}^{\mathit{v}}+{\mathit{E}}_{\mathbf{2}}^T{\mathit{\mu }}^{\mathit{v}}=\mathbf{0}\end{array}\end{array}\\ \begin{array}{c}{\mathit{\pi }}^{\mathit{v}}\left({\mathit{B}}_{\mathbf{1}}{\mathit{X}}^{*}+{\mathit{C}}_{\mathbf{1}}{\mathit{Y}}^{\mathit{v}}+{\mathit{D}}_{\mathbf{1}}{\mathit{Z}}^{v*}+{\mathit{E}}_{\mathbf{1}}{\mathit{u}}^{\mathit{v}}-\mathit{e}\right)=\mathbf{0}\\ {\mathit{\pi }}^{\mathit{v}}\ge 0\end{array}\end{array}\right.\end{array}(30)$

4 Case studies

To verify the validity and superiority of the proposed planning framework, case studies were conducted on a regional integrated energy system formed by the coupling of IEEE 24-bus power system and 7-node natural gas system. All emulators run on a desktop computer with an Intel Core i7-8700 CPU and 32 GB memory. The case models were constructed based on the MATLAB/YALMIP platform and solved by Gurobi solver.

4.1 System parameters

The regional electric-gas integrated energy system adopted in this section is shown in Figure 2 (Zimmerman et al., 2011). The power system consists of five coal-fired units and two gas-fired units, as well as three wind turbines to be planned. The relevant parameters of the generator set are shown in Table 1 (Jamie McIntyre et al., 2011; Zimmerman et al., 2011). The natural gas system consists of two gas sources, five branches and one compressor. The parameters of the gas source are shown in Table 2. The parameters of the natural gas pipeline are shown in Table 3. Compressor ratios in natural gas systems range from 1.1 to 1.5. There are 12 electrical loads and three gas loads in the integrated energy system. The reference values of electrical load and gas load are shown in Table 4 and Table 5. The prediction value of the 24-h power load and gas load is shown in Figure 3. As described in Section 2, the uncertainty of natural gas load can be ignored. The maximum prediction error of power load is 20% (Guo et al., 2020). The uncertainty parameters of electric load, wind power and natural gas prices are shown in Table 6. The electric power system and natural gas system are coupled by two gas turbine units and one power-to-gas (P2G) unit. The installed capacity of the P2G unit is 150 MW. The maximum wind power capacity planned for each node in the system is 500 MW. During the 14th Five-Year Plan period, the carbon emission per unit GDP in this region is targeted to be reduced by 19%, the energy consumption per unit GDP is targeted to be reduced by 14.5%, and the average annual growth rate of GDP is 7%. The fixed investment cost of wind power is 115 USD/(MW∙day).

FIGURE 2

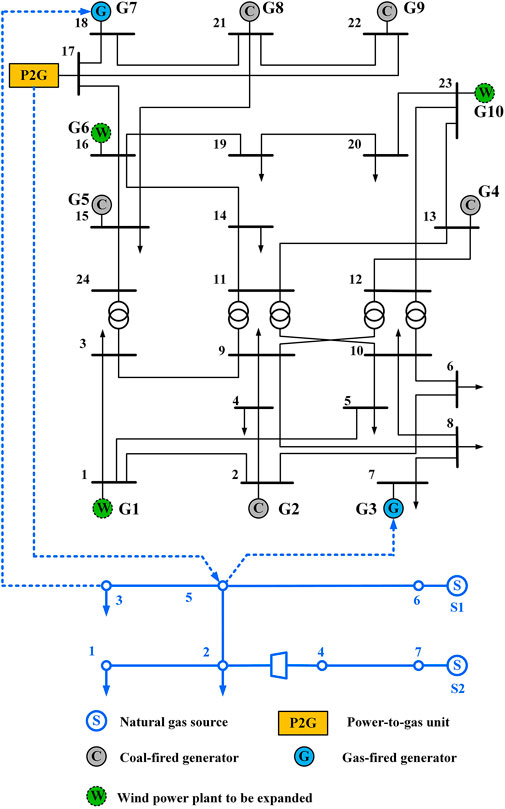
FIGURE 2. Integrated energy system coupled with IEEE 24-bus power system and 7-node natural gas system.

TABLE 1

TABLE 1. Parameters of generators.

TABLE 2

TABLE 2. Natural gas source parameters.

TABLE 3

TABLE 3. Natural gas pipeline parameters.

TABLE 4

TABLE 4. Electrical load reference value before planning.

TABLE 5

TABLE 5. Gas demand reference value before planning.

FIGURE 3

FIGURE 3. Power load and natural gas demand.

TABLE 6

TABLE 6. Parameters of uncertainty.

4.2 Optimized results of the proposed two-stage robust planning framework

The nested C&CG algorithm is used to solve the proposed two-stage robust programming framework. The convergence condition is the percentage deviation between the objective function values of the MP and SP. In the process of solving the model in this paper, the convergence condition is set to 0.8%. Figure 4 illustrates the convergence process for solving the proposed two-stage robust planning framework and the solution time of proposed nsted C&CG algorithm is 1864.2 s.

FIGURE 4

FIGURE 4. The convergence process of the proposed model.

Before adopting the proposed framework, the total carbon emission of the test system is 52,513 tCO₂. According to Eqs 7, 8, the annual energy demand of the test system increases by 3.70% brought by regional economic development, and the growth of carbon emissions should be controlled within 2.58%. It can be seen that after the planning of wind power in the regional integrated energy system, the total carbon emissions of the system should be controlled within 53,868 tCO₂ in any scenario.

Figure 5 shows the wind power planning capacity of the three buses under the proposed planning framework. To verify whether the planning results can ensure carbon emissions meet the requirements, this paper conducts a robust scheduling test on the planning results. The results show that the planning results can indeed make the system meet the carbon growth constraints in the worst scenario, as shown in Figure 5. Therefore, it can be verified that the proposed two-stage robust planning framework can effectively promote wind power configuration. In addition, it can ensure that the carbon emissions of the regional integrated energy system will not exceed the limited target during the dispatch operation even in the worst scenario.

FIGURE 5

FIGURE 5. The planning results of the proposed model and system carbon emissions.

4.3 Effect analysis of carbon emission constraints

The planning framework proposed in this paper embeds carbon growth constraints based on regional macro-development goals. To study the impact of carbon growth constraints on the planning results, the following two cases are set for comparison as shown in Table 7. Case 1 is the planning framework proposed in this paper, and Case 2 is the control group.

TABLE 7

TABLE 7. Carbon constraint effect analysis cases.

The results of wind turbine capacity planned in Case 1 are shown in Figure 5 above. In Case 2, the optimal planning capacity of the wind turbines at the three buses is all 0. Since the carbon growth constraints are not considered in Case 2, while relatively cheap and sufficient thermal power can meet the growing energy demand, wind turbines with fixed investment costs will not be planned. In Case 1, in the two-stage robust optimization, the system will be forced to plan the wind turbines to meet the carbon growth constraints.

To compare the effect of planning results on system carbon emissions in the two cases, this paper conducts 5,000 Monte Carlo simulations on the planning results of Case 1 and Case 2 in the dispatch model with carbon growth constraints and multiple inferior uncertainty sets. The simulation results are shown in Table 8. It is obvious that the planning results of Case 2 can hardly meet the carbon emission growth constraints when dispatching in inferior scenarios. Thus, the necessity of considering carbon growth constraints in the proposed framework is further highlighted.

TABLE 8

TABLE 8. Monte Carlo simulation results.

The wind power planning capacity of Case 1 is obtained under the worst scenario in robust optimization. In order to further study the carbon reduction potential of the system in Case 1, the wind turbine capacity of Case 1 is tested in the system economic dispatch. Figure 6 comparatively presents the carbon emissions of the system under economic dispatch and robust dispatch with the wind turbine capacity of Case 1. It can be seen that the wind power capacity obtained by the proposed planning framework cann’t only enable the system to meet the carbon growth targets in the worst scenario, but also have a huge space for carbon reduction in actual dispatch.

FIGURE 6

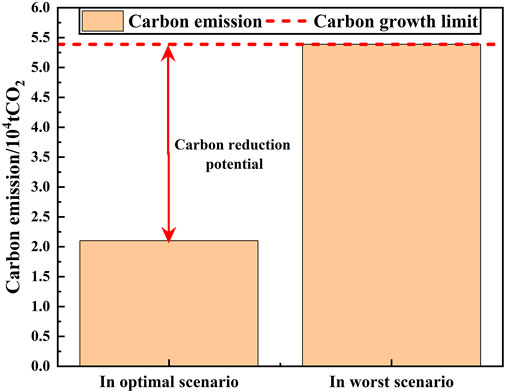
FIGURE 6. System carbon emissions of economic dispatch and robust dispatch with wind turbine capacity of Case 1.

4.4 Robustness analysis

The proposed two-stage robust planning framework takes into account the three uncertainties of power load, wind power and natural gas prices. To test the advantages of the proposed model in terms of robustness, several sets of cases as shown in Table 9 are set up for comparison.

TABLE 9

TABLE 9. Robustness analysis cases.

Figure 7 presents the capacity of wind turbines obtained by two-stage robust optimization of Case 1, Case 3, Case 4, and Case 5. It can be found that the total wind power capacities planned in Case 3 and Case 5 are significantly lower than those in Case 1 and Case 4. Case 3 doesn’t consider the uncertainty of power load, so in the two-stage robust optimization, there will be lower load requirements compared with Case 1, which directly leads to lower wind turbine capacity requirements. Case 5 doesn’t consider the uncertainty of natural gas prices. The optimal operation of coupling equipment depends on the relative price of electricity and natural gas. Therefore, in the robust optimization, Case 1 will generate higher gas prices than Case 5. As a result, the P2G is promoted to operate and consume electric power, as shown in Figure 8, which is equivalent to increasing the power load. Therefore, natural gas price uncertainty and power load uncertainty have similar effects. In addition, it can be noticed that the total capacity of wind turbines in Case 4 is slightly larger than that in Case 1, which is affected by the uncertainty of wind power. Since Case 1 considers the uncertainty of wind power compared with Case 4, Case 1 has a worse wind power scenario in the two-stage robust planning. In this way, considering the fixed investment cost of wind turbines, the equivalent cost of wind power generation in Case 1 is higher than that in Case 4. Therefore, the installed capacity of wind turbines in Case 4 will be irrationally configured as much as possible. Overall, in the two-stage robust optimization, the uncertainties of power load and natural gas price will promote the capacity planning of wind turbines in the regional integrated energy system, while the uncertainty of wind power will inhibit the capacity planning of wind turbines.

FIGURE 7

FIGURE 7. Wind turbine capacity planned in Case1, Case3, Case4, and Case5.

FIGURE 8

FIGURE 8. P2G power consumption under robust dispatch in Case 1 and Case 5.

To demonstrate the superiority of the proposed model, 5,000 times of Monte Carlo robust dispatching simulations are performed on the planned wind turbine capacity of the above four cases. The simulation results are shown in Table 10.

TABLE 10

TABLE 10. Monte Carlo simulation results.

According to the results in Table 10, it can be seen that the planning results of Case 1 and Case 4 have good robustness, while the planning results of Case 3 and Case 5 are less robust. Although the robustness of Case 4 is good, the wind power uncertainty is not considered in the robust optimization, which will lead to irrational configuration of wind turbine capacities and waste of wind turbine investment. The proposed Case 1 considers more comprehensive uncertainties, and the planning results are both robust and economical in investment, which is a better planning scheme.

5 Conclusion

In this paper, a two-stage generation expansion planning framework for a regional integrated energy system is proposed considering carbon emission constraints. The uncertainties of wind power, power load, and natural gas price are also considered in the proposed framework. The nested C&CG algorithm is used to solve the two-stage robust planning model. Based on the IEEE 24-bus power system and 7-node natural gas system integrated energy system, the effectiveness and superiority of the proposed framework are verified. The following conclusions can be obtained through numerical simulation.

(1) The proposed two-stage robust generation expansion planning framework with carbon growth constraints can effectively promote the configuration of wind turbines and ensure that the carbon emissions of the regional integrated energy system will not exceed the defined target even in the worst scenario.

(2) The wind plant planning result of the proposed model is the configuration result in the worst scenario. Therefore, in actual operation, the wind power capacity obtained by the proposed planning framework can not only enable the system to meet the carbon growth targets in the worst scenario but also have a huge space for carbon reduction.

(3) In the two-stage robust optimization, both electricity load uncertainty and natural gas price uncertainty will promote the capacity planning of wind power, while wind power uncertainty will inhibit the capacity planning of wind turbines.

(4) By comparing the model planning results with different uncertainty sets, it can be found that the proposed model has good robustness, and at the same time, it takes into account the economy of wind turbine planning investment.

This article focuses on the wind turbine capacity planning, so the operating cost of P2G isn’t considered. P2G isn’t only a coupling channel for integrating energy systems, but also an effective way to introduce low-carbon natural gas into gas systems. In future studies, the proposed model can further consider the coordinated planning of wind turbines and P2G units.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JN, JF, and HZ conceptualized the study, performed the methodology, and validated the results. JN and JF prepared the original draft. XD contributed to the improvement of the study design. LG and KS reviewed and edited the draft. HZ supervised the study. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

LG was employed by State Grid Corporation of China. KS was employed by State Grid Zhejiang Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadi, S., Mavalizadeh, H., Ghadimi, A. A., Miveh, M. R., and Ahmadi, A. (2020). Dynamic robust generation–transmission expansion planning in the presence of wind farms under long- and short-term uncertainties. IET Generation, Transm. Distribution 14 (23), 5418–5427. doi:10.1049/iet-gtd.2019.1838

CrossRef Full Text | Google Scholar

De Wolf, D., and Smeers, Y. (2000). The gas transmission problem solved by an extension of the simplex algorithm. Manag. Sci. 46 (11), 1454–1465. doi:10.1287/mnsc.46.11.1454.12087

CrossRef Full Text | Google Scholar

Deng, X., and Lv, T. (2020). Power system planning with increasing variable renewable energy: A review of optimization models. J. Clean. Prod. 246, 118962. doi:10.1016/j.jclepro.2019.118962

CrossRef Full Text | Google Scholar

Du, G., Zhao, D., and Liu, X. (2022). Research review on optimal scheduling considering wind power uncertainty. Zhongguo Dianji Gongcheng Xuebao/Proceedings Chin. Soc. Electr. Eng. 1–21.

Google Scholar

Fang, F., Zhu, Z., Jin, S., and Hu, S. (2021). Two-layer game theoretic microgrid capacity optimization considering uncertainty of renewable energy. IEEE Syst. J. 15 (3), 4260–4271. doi:10.1109/jsyst.2020.3008316

CrossRef Full Text | Google Scholar

Gonzalez-Romero, I. C., Wogrin, S., and Gómez, T. (2020). Review on generation and transmission expansion co-planning models under a market environment. IET Generation, Transm. Distribution 14 (6), 931–944. doi:10.1049/iet-gtd.2019.0123

CrossRef Full Text | Google Scholar

Guo, Z., Li, G., and Zhou, M. (2020). Fast and dynamic robust optimization of integrated electricity-gas system operation with carbon trading. Power Syst. Technol. 44 (4), 1220–1228.

Google Scholar

Höhne, N., Gidden, M. J., den Elzen, M., Hans, F., Fyson, C., Geiges, A., et al. (2021). Wave of net zero emission targets opens window to meeting the Paris Agreement. Nat. Clim. Change 11 (10), 820–822. doi:10.1038/s41558-021-01142-2

CrossRef Full Text | Google Scholar

Huang, W., Zhang, N., Cheng, Y., Yang, J., Wang, Y., and Kang, C. (2020). Multienergy networks analytics: Standardized modeling, optimization, and low carbon analysis. Proc. IEEE 108 (9), 1411–1436. doi:10.1109/jproc.2020.2993787

CrossRef Full Text | Google Scholar

Jabarnejad, M. (2021). Linearized generation-expansion planning considering transmission planning, switching, and dynamic-line rating. J. Energy Eng. 147 (4). doi:10.1061/(asce)ey.1943-7897.0000769

CrossRef Full Text | Google Scholar

Jamie McIntyre, B. B., Harvey, S., and Borchardt, S. (2011). Comparison of lifecycle greenhouse gas emissions of various electricity generation sources. World Nuclear Association, London.

Google Scholar

Lei, Y., Wang, D., Jia, H., Chen, J., Li, J., Song, Y., et al. (2020). Multi-objective stochastic expansion planning based on multi-dimensional correlation scenario generation method for regional integrated energy system integrated renewable energy. Appl. Energy 276, 115395. doi:10.1016/j.apenergy.2020.115395

CrossRef Full Text | Google Scholar

Li, Q., Wang, J., Zhang, Y., Fan, Y., Bao, G., and Wang, X. (2020). Multi-Period generation expansion planning for sustainable power systems to maximize the utilization of renewable energy sources. Sustainability 12 (3), 1083. doi:10.3390/su12031083

CrossRef Full Text | Google Scholar

Liu, J., Liu, M., Wang, Z., Yang, J., and Lou, S. (2022a). Multi-flexibility resources planning for power system considering carbon trading. Sustainability 14 (20), 13296. doi:10.3390/su142013296

CrossRef Full Text | Google Scholar

Liu, Y., Du, M., Cui, Q., Lin, J., Liu, Y., Liu, Q., et al. (2022b). Contrasting suitability and ambition in regional carbon mitigation. Nat. Commun. 13 (1), 4077. doi:10.1038/s41467-022-31729-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, Z., and Bo, Z. (2012). An exact algorithm for two-stage robust optimization with mixed integer recourse problems. University of South Florida, Tampa.

Google Scholar

Lyrio de Oliveira, L., de Oliveira Ribeiro, C., and Qadrdan, M. (2022). Analysis of electricity supply and demand intra-annual dynamics in Brazil: A multi-period and multi-regional generation expansion planning model. Int. J. Electr. Power and Energy Syst. 137, 107886. doi:10.1016/j.ijepes.2021.107886

CrossRef Full Text | Google Scholar

Melgar-Dominguez, O. D., Pourakbari-Kasmaei, M., Lehtonen, M., and Sanches Mantovani, J. R. (2020). An economic-environmental asset planning in electric distribution networks considering carbon emission trading and demand response. Electr. Power Syst. Res. 181, 106202. doi:10.1016/j.epsr.2020.106202

CrossRef Full Text | Google Scholar

Mi, Y., Liu, C., Yang, J., Zhang, H., and Wu, Q. (2021). Low-carbon generation expansion planning considering uncertainty of renewable energy at multi-time scales. Glob. Energy Interconnect. 4 (3), 261–272. doi:10.1016/j.gloei.2021.07.005

CrossRef Full Text | Google Scholar

Shen, W., Qiu, J., Meng, K., Chen, X., and Dong, Z. Y. (2020). Low-carbon electricity network transition considering retirement of aging coal generators. IEEE Trans. Power Syst. 35 (6), 4193–4205. doi:10.1109/tpwrs.2020.2995753

CrossRef Full Text | Google Scholar

Sun, L.-L., Cui, H.-J., and Ge, Q.-S. (2022). Will China achieve its 2060 carbon neutral commitment from the provincial perspective? Adv. Clim. Change Res. 13 (2), 169–178. doi:10.1016/j.accre.2022.02.002

CrossRef Full Text | Google Scholar

Toloo, M., Taghizadeh-Yazdi, M., and Mohammadi-Balani, A. (2022). Multi-objective centralization-decentralization trade-off analysis for multi-source renewable electricity generation expansion planning: A case study of Iran. Comput. Industrial Eng. 164, 107870. doi:10.1016/j.cie.2021.107870

CrossRef Full Text | Google Scholar

Xie, B.-C., Lu, L., and Duan, N. (2022). Environmental efficiency assessment of China’s integrated power system under the assumption of semi-disposability. Comput. Industrial Eng. 167, 108023. doi:10.1016/j.cie.2022.108023

CrossRef Full Text | Google Scholar

Yang, C., Sun, W., Han, D., and Yin, X. (2022). Research on power system flexibility considering uncertainties. Front. Energy Res. 10. doi:10.3389/fenrg.2022.967220

CrossRef Full Text | Google Scholar

Yi, W., Bu, Q., Lu, S., Qin, Y., and Li, P. (2022). Distributionally robust optimal dispatching of integrated energy system considering line pack effect of gas network. Electr. Power Autom. Equip. 42 (6), 53.

Google Scholar

Zeng, B., and Zhao, L. (2013). Solving two-stage robust optimization problems using a column-and-constraint generation method. Operations Res. Lett. 41 (5), 457–461. doi:10.1016/j.orl.2013.05.003

CrossRef Full Text | Google Scholar

Zhang, C., Cheng, H., Liu, L., Zhang, H., Zhang, X., and Li, G. (2020). Coordination planning of wind farm, energy storage and transmission network with high-penetration renewable energy. Int. J. Electr. Power and Energy Syst. 120, 105944. doi:10.1016/j.ijepes.2020.105944

CrossRef Full Text | Google Scholar

Zhang, S., Li, M., Wang, C., An, K., Zhou, J., and Cai, B. (2021). Carbon emission trend analysis of China' s provinces and their differentiated peak strategy design. China Popul. Resour. Environ. 31 (9), 45–54.

Google Scholar

Zhigang, L., Liu, Y., Dong, W., Li, Y., He, L., and Guo, X. (2022). Joint transformation planning of solar energy storage in carbon neutral area based on electricity-carbon coupling operation. High. Volt. Technol. 1–16. doi:10.13336/j.1003-6520.hve.20220852

CrossRef Full Text | Google Scholar

Zhu, G., Lin, J., Luo, Z., Dai, S., Qin, L., and Liu, C. (2017). Review of robust optimization for generation scheduling in power systems. Zhongguo Dianji Gongcheng Xuebao/Proceedings Chin. Soc. Electr. Eng. 37 (20), 5881–5892. doi:10.13334/j.0258-8013.pcsee.161950

CrossRef Full Text | Google Scholar

Zimmerman, R. D., Murillo-Sanchez, C. E., and Thomas, R. J. (2011). Matpower: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 26 (1), 12–19. doi:10.1109/tpwrs.2010.2051168

CrossRef Full Text | Google Scholar