Research on electrical load distribution using an improved bacterial foraging algorithm

This paper proposes an improved bacterial foraging algorithm for electrical load distribution to impro-ve power plants’ efficiency and reduce energy consumption costs. In the chemotaxis stage, the adaptive step size is introduced to accelerate the random search speed compared with the traditional algorithm. In the replication stage, a hybrid crisscross operator is proposed to replace the traditional binary replication method in the algorithm to ensure the diversity of the population and improve the efficiency of the algorithm. The adaptive dynamic probability is used instead of the initial fixed probability to improve the global search performance of the algorithm. The mathematical model of electrical load distribution in a natural power plant is established, and the improved bacterial foraging algorithm is used to solve the model. Through comparative analysis of two power plant unit experiments, it is proved that the results of the improved algorithm can reduce 3.671% and 1.06% respectively compared with the particle swarm optimization algorithm, and 7.26% and 1.37% respectively compared with the traditional bacterial foraging algorithm, which can significantly reduce the coal consumption of the power plant.

1 Introduction

The adjustment of electric power and energy structure is a hot topic. Germany proposes to realize the energy structure adjustment in 2035 so that the proportion of renewable energy generation can reach or even exceed half (Kopiske et al., 2017). Although the optimization of the power energy structure in China started late, it is also being optimized and adjusted constantly. With the integration of more and more distributed new energy into the power grid, the stability of the power grid faces many challenges due to the uncertainty brought by power generation methods such as wind photovoltaic power. As the main output method of my country’s power resources, thermal power generation is of great significance to the stable operation of the power grid. The energy consumption problem caused by thermal power generation gradually becomes prominent with the increasing demand for power resources in recent years. Some achievements have been made in reducing the energy consumption of thermal power generation by upgrading traditional industrial equipment (Wu et al., 2019). However, it also faces a bottleneck period. It is essential to reduce energy consumption through electrical load distribution (ELD) among thermal power units. Therefore, optimizing coal consumption can not only improve the competitiveness of thermal power resources but also contribute significantly to the goal of “carbon neutrality” while ensuring the stability of the power production process and reducing the cost of thermal power.

Meta heuristic algorithms, such as [sine cosine algorithm (Aye et al., 2019) (Yildiz et al., 2020), seagull algorithm (Panagant et al., 2020), grasshopper algorithm (Yildiz et al., 2022a; Yildiz et al., 2022b) (Yildiz et al., 2021a; Yildiz et al., 2021b)], are widely used to solve various problems depending on their excellent convergence effects. In recent years, the optimization of heuristic algorithms has also become increasingly mature and improved. The efficiency of heuristic algorithms and their vulnerability to local optima are gradually improving with the optimization process. Ref (Premkumar et al., 2021) proposed a new multi-objective arithmetic optimization algorithm (MOAOA), which uses distance mechanism and elite sorting to optimize and upgrade the single objective arithmetic optimization algorithm, and can be applied to multiple scenarios in reality. Ref (Yildiz et al., 2021a; Yildiz et al., 2021b) proposed a political optimization algorithm (POA), which has better search ability and computational efficiency than other algorithms. In Ref (Yildiz et al., 2021c), an EBO algorithm is proposed. Compared with the slime mold algorithm, marine predator algorithm and other novel algorithms, this algorithm is not only simpler, but also more robust and has better design results. Ref (Yildiz et al., 2022a; Yildiz et al., 2022b) applies the idea of chaotic mapping to HGSO algorithm, which can effectively improve the convergence speed and robustness of the algorithm. In Ref (Yildiz and Erdas 2021), a new hybrid algorithm HTSSA is proposed, which can better jump out of the local optimum. Compared with some new algorithms, this algorithm has more advantages. In Ref (Yildiz et al., 2022c), chaotic map is used to mix Levy flight, which effectively improves the convergence speed of the algorithm. A new algorithm HSSA-NM is proposed in Ref (Yildiz 2020), which can effectively optimize engineering design problems through the hybrid salp swarm algorithm.

Meta heuristic algorithm is widely used in the power field (Chi et al., 2022). Used COOA algorithm to apply to the distribution network with photovoltaic generators. Compared with other algorithms, it proved that this method can not only effectively reduce the active power loss, but also significantly reduce the solution time. In Ref (Nguyen et al., 2022), an IEO algorithm is proposed to select the location and scale of photovoltaic power generation in the distribution network. The algorithm is improved by updating the concentration. Compared with a large number of meta heuristic algorithms, the improved method can effectively reduce the loss. In Ref (Pham et al., 2022), ECSA is used to solve the generation cost of integrated power system. Compared with equilibrium optimizer and marine predator algorithm, this method has the lowest cost. The ELD refers to achieving maximum economic benefits under the conditions of meeting production needs and power constraints from the perspective of an electric power producer. The methods of Unit Commitment (UC) can be divided into four categories: Mixed Integer Linear Programming (MILP), dynamic programming, decomposition method, and heuristic method. In the past, the optimization of thermal power units was usually done by mixed integer linear programming or dynamic programming. However, with the development of swarm intelligence algorithms in recent years, more and more swarm intelligence algorithms have been applied to ELD. (Jianjun et al., 2021) proposed an improved invasive weed algorithm for the non-linear programming model of thermal power units. Traditional swarm intelligence algorithms, represented by particle swarm optimization (PSO), cuckoo algorithm (CS) and genetic algorithm (GA), are widely used in ELD problems because of their stability and simplicity. However, they are all faced with problems such as easy to fall into local optimal solution, slow convergence, high iteration number requirements, and low efficiency, which are also some defects of swarm intelligence algorithms themselves. With the deepening of research, the application of swarm intelligence algorithm in ELD mainly focuses on solving the above problem. (Zou et al., 2019) improves and optimizes the selection, crossover, and mutation of the GA algorithm and applies it to the economic dispatch model of cogeneration. The results show that the improved method can improve the convergence speed and result from accuracy. In (Mahdi et al., 2018), a quantum-inspired particle swarm optimization algorithm is used to improve the robustness and efficiency of ELD processing. (Al-Bahrani and Patra 2018) proposes a multi-gradient PSO, which solves the problem that global particle swarm optimization with inertia weight (GPSO-w) is not efficient in the optimization process of large-scale thermal power units. It is found that the performance of this method is better than several improved PSO algorithms through experimental comparison. The other group of intelligent algorithms is also gradually being developed is applied to the ELD problems. (Hatata and Hafez 2019) is optimized by the ant lion algorithm (ALO) compared with the PSO algorithm and artificial immune system (AIS). The results found that the ALO in dealing with ELD has higher efficiency and convergence precision. In addition, (Kumar et al., 2021) also uses the improved Slap Swarm algorithm to optimize the load problem of large-scale power plants, and the experimental results confirm the high efficiency of its solving process. (Carmen et al., 2021) compares the advantages and disadvantages of various methods used in current UC optimization for the Italian power market application scenarios.

Bacterial Foraging Optimization (BFO) (de et al., 2022), (Chen et al., 2021) and (Farshi and Orujpour 2021) has been an emerging swarm intelligence algorithm in recent years. BFO is a bionic algorithm to simulate the foraging behavior of Escherichia coli. Bacterial foraging algorithms are widely used, such as image segmentation, path planning, power system, parameter optimization and identification. The improvement of bacterial foraging in the existing research mainly focuses on the chemotaxis and dispersion of bacteria, as shown in the reference (Hu et al., 2020), (Chen et al., 2017), (Wang et al., 2019), (Ramaporselvi and Geetha 2021) and (Devi and Srinivasan 2021). The contributions of this paper mainly focus on the improvement of the three key steps of the algorithm. The improvements are aimed at the characteristics of the bacterial foraging algorithm, such as slow convergence speed, low efficiency, and easily falling into local optimum.

(1) The adaptive modified step is used instead of the traditional fixed step to solve the problem of slow solution speed in the chemotaxis stage.

(2) The traditional fitness value ranking dichotomous replication optimization method was improved by using a crisscross algorithm mixture in the process of bacterial replication.

(3) Adaptive dynamic probability is used to replace the traditional fixed dispersal probability to avoid the optimal result elimination problem and ensure the algorithm’s efficiency in the dispersal stage.

Through two case studies and comparison of different algorithms, it is proved that the improved hybrid bacteria foraging algorithm proposed in this paper has better results.

This paper consists of five sections. The first section establishes the mathematical model of ELD. Section 2 describes the improvement of chemotaxis, replication and dispersal of the bacterial foraging algorithm. In Section 3, an improved hybrid bacterial foraging algorithm is used to solve the ELD problem, and the pseudo-code is given. The fourth section is the experimental part, which analyzes the case of 10 units of a medium power plant and 3 units of a small power plant and proves that the improved algorithm can significantly reduce coal consumption. The fifth section is the summary of this paper.

2 Mathematical model of ELD

Coal consumption characteristics and valve-point effect of generating units are taken as objective functions, and unit output and load balance are taken as mathematical models with constraints in the model of ELD.

2.1 Objective function

The characteristic of coal consumption refers to the curve of coal consumption of a thermal power unit changing with the load. It is the critical basis for analyzing energy consumption and load optimization scheduling of a thermal power plant. When a load of a single unit decreases with the generation condition, its coal consumption rate will increase, and the formula is as follows:

$F\left(P_g\left(x\right)\right)=a\left(x\right)+b\left(x\right)\ast P_g\left(x\right)+c\left(x\right)\ast P_g{\left(x\right)}^2(1)$

In Eq. 1, $F\left(P_g\left(x\right)\right)$ represents the coal consumption of the thermal power unit; $a\left(x\right)$, $b\left(x\right)$, $c\left(x\right)$ represents the coal consumption characteristic parameters of the x unit; and $P_g\left(x\right)$ represents the x unit’s power.

The influence of the valve-point effect on UC should be considered in the unit operation process. The leakage of steam causes the valve-point effect at the opening moment of the regulating valve of the steam turbine, which is reflected as the pulsation influence at high load in the coal consumption characteristic curve of the unit. The formula is as follows:

$G\left(P\left(x\right)\right)=\left|d\left(x\right)\ast \sin \left(e\left(x\right)\ast \left(P_{\min }\left(x\right)-P\left(x\right)\right)\right)\right|(2)$

In Eq. 2, $d\left(x\right)$, and $e\left(x\right)$ represent the valve-point coefficient $P_{\min }\left(x\right)$ represents the lowest power value of the x unit.

The mathematical model of the objective function can be expressed as the compound superposition function in summary. In the model, the quadratic function and the sine function of the valve-point effect are set for solving the minimum coal consumption characteristic. It can be expressed as follows:

$\min f\left(P\left(x\right)\right)={\displaystyle \sum }_{x=1}^N\left(F\left(P\left(x\right)\right)+G\left(P\left(x\right)\right)\right)(3)$

2.2 Constraint function

Capacity constraint function is the prerequisite for the standard and safe operation of the thermal power unit. Its formula is as follows:

$P_{\min }\left(x\right)\le P\left(x\right)\le P_{\max }\left(x\right)(4)$

Where $P_{\max }\left(x\right)$ denotes the upper limit of capacity constraint and $P_{\min }\left(x\right)$ the lower limit of capacity constraint. This paper ignores power flow loss and assumes that only thermal power units participate in power generation in the network. Load balance constraint means that the sum of the power of each unit needs to be consistent with the total load, and its formula is as follows:

${\displaystyle \sum }_{x=1}^{N}P\left(x\right)=Load(5)$

In Eq. 5, $Load$ represents the total load of the system.

2.3 Penalty function

The purpose of adding a penalty function is to consider some other constraints or ignored losses, and its formula is as follows:

$h\left(P\left(x\right)\right)=\epsilon \ast \left|{\displaystyle \sum }_{x=1}^{N}P\left(x\right)-Load\right|(6)$

In Eq. 6, $\epsilon$ represents the penalty coefficient which can be fixed or changed to an adaptive value according to the characteristics of the algorithm. Thus, the mathematical model of ELD can be expressed as follows:

$\min F=f\left(P\left(x\right)\right)+h\left(P\left(x\right)\right)(7)$

3 Improved crisscross algorithm mixed bacterial foraging optimization (ICSBFO)

3.1 The improve the chemotactic process with adaptive modification of step size

Chemotaxis is to simulate the motion part of E. coli foraging behavior. The process includes forward and reverses in two parts. E. coli runs along the vector direction with a random vector until the fitness value cannot continue to be smaller. In (Long et al., 2020), the cost function of the A∗ algorithm is used to improve the chemotaxis process to solve the path planning problem under different working conditions effectively. In the process of chemotaxis, the step length C is an essential factor affecting the movement process of E. coli. The step length C of chemotaxis is a fixed value in the traditional BFO algorithm. It will bring some disadvantages. The minor C value can improve the search accuracy, but it will reduce the search efficiency of the algorithm and easy to fall into the local optimal. The larger value of C can improve the search speed of the algorithm, but it will reduce the accuracy of the search results and lead to search misjudgment. Therefore, the value of step size dramatically affects the excellence of the algorithm. Inspired by the fish swarm algorithm, (Yufang and Jianwen 2021) uses an exponential function to modify the step size. Adaptive modified step size is used to replace the traditional fixed value in this paper.

$C\left(x\right)=\exp \left(-{\left(N_c\ast N_{re}\ast N_{ed}-\frac{\tau }{j+\left(k-1\right)\ast N_c\left(l-1\right)\ast N_{re}\ast N_{ed}}\right)}^{\frac{1}{\alpha }}\right)\ast C(8)$

In Eq. 8, $N_c$, $N_{re}$, $N_{ed}$ respectively represent the number of chemotactic restrictions, replication restrictions, and dispersal restrictions in BFO algorithm. $\alpha$ denoted as the step coefficient. j, k and l represent the current times of chemotaxis, replication and dispersion respectively. $\tau$ is a dynamic change. The BFO algorithm can search for optimization with giant steps in the early stage of the search to accelerate the algorithm’s convergence through the adaptive step correction exponential formula. And search for optimization with a small step in the late stage of search to improve the accuracy of the algorithm.

3.2 The replication process of the hybrid crisscross algorithm to optimize

The replication process is a process that simulates biological evolution and survival of the fittest. The E. coli are arranged in ascending order according to the cumulative fitness value. The first half of the high-quality E. coli is copied instead of the second half of the poor E. coli. The total number is unchanged in this process. Although this method reduces the algorithm’s complexity, it also brings some disadvantages. The diversity of the population is greatly decreased to ensure the diversity of the population and ensure that high-quality bacteria individuals are not lost. (Jufeng et al., 2020) used single individual ranking and crossover operations to replace the cumulative health ranking method. In this paper, the Crisscross Algorithm (Xiongmin et al., 2022), (Shaowei et al., 2021) and (Anbo et al., 2022) is a novel population random search algorithm that is proposed to improve the replication process. The Crisscross Algorithm includes two parts, horizontal crisscross, and longitudinal crisscross. Compared with the previous generation, the method achieves the optimal effect through each iteration of the crisscross process. Horizontal crossover is like the crossover process in GA, but it also has a comparison process with the previous generation.

$M{S}_{hc}\left(x,d\right)=r_1\ast X\left(x,d\right)+\left(1-r_1\right)\ast X\left(y,d\right)+c_1\ast \left(X\left(x,d\right)-X\left(y,d\right)\right)(9)$

$M{S}_{hc}\left(y,d\right)=r_1\ast X\left(y,d\right)+\left(1-r_1\right)\ast X\left(x,d\right)+c_1\ast \left(X\left(y,d\right)-X\left(x,d\right)\right)(10)$

The parameters x and y in Eqs. 9, 10 represent individual bacteria, d represents dimension solved by the algorithm, and $r_1{c}_1$ both represent random numbers. The former is between 0 and 1, and the latter is between −1 and 1. This formula represents the offspring of bacteria x and y after horizontal crossing in the d dimension. Longitudinal crossover is similar to the mutation process in a genetic algorithm, and longitudinal crossover is the crossover of different dimensions of the same bacterium. After each crossover, a progeny with different dimensions from the previous generation is produced. The progeny produced each time should be compared with the previous generation to retain the optimal value.

$M{S}_{vc}\left(x,d_1\right)=r\ast X\left(x,d_1\right)+\left(1-r\right)\ast X\left(x,d_2\right)(11)$

According to Eq. 11, bacteria x can produce a progeny by crossing dimensions $d_1{d}_2$. The crisscross algorithm was used to cross-optimize the chemotactic population. Compared with the traditional sequencing and replication method, the optimization and replication process of the crisscross algorithm not only retained high-quality bacterial individuals but also ensured the diversity of the population.

3.3 Adaptive dispersal probability to improve dispersal process

The random dispersal optimization of E. coli individuals was carried out according to a fixed dispersal probability. In this process, certain high-quality individuals were also dispersed to random areas. Although the global search performance of the algorithm was ensured in principle, the fitness value of the algorithm would also deteriorate, which would decrease the efficiency of the algorithm. In this paper, we use the adaptive dispersal probability instead of the traditional fixed value to avoid falling into the local optimum and ensure the global search performance of the algorithm.

$P\left(x\right)=P_{ed}\ast \frac{J_{worst}-J_x}{J_{worst}-J_{best}}(12)$

In Eq. 12, $J_{worst}$ represents the worst fitness value, $J_{best}$ represents the optimal fitness, and $J_x$ is the real-time fitness value of the xth bacterium. The dispersal probability of E. coli was modified adaptively by this fraction. The fitness value of bacteria individuals with good fitness was small, and the dispersal probability was reduced while the dispersal probability of individuals with poor fitness was increased. In this way, the loss of high-quality individuals is avoided and the efficiency and performance of the algorithm are guaranteed.

3.4 Flowchart of ICSBFO

The parameters need to be initialized first in the algorithm. It includes the number of iterations maxgen, the dimension p of the search range, the number of bacteria s, the maximum number of chemotaxis $N_c$, the maximum number of steps of one-way movement in chemotaxis operation $N_s$, the maximum number of replication $N_{re}$, the maximum number of dispersal $N_{ed}$, and the fixed probability of bacterial dispersal $P_{ed}$, the number of attractive factors and the release speed d_attract, ommiga_attract, the number of repellant factors and the release speed h_repellant, ommiga_repellant. Then the population is initialized. The population of this algorithm is generated according to the lower limit of unit load plus the difference between the upper and lower limits of unit load multiplied by a random number. Initialize the population as a high-dimensional array. After the population initialization is completed, the cycle is carried out. The maximum number of dispersals, replication, and chemotaxis, are determined first, and the chemotaxis operation is carried out after the requirements are met. In the chemotaxis process in this paper, $N_c$ is 60; $N_s$ is 4. After determining the adaptive correction step and the repulsive attraction between the bacteria, the fitness value was calculated. The bacteria turn over and then proceed with dynamic steps in the direction of the randomly generated vector until the maximum swimming limit is reached or the fitness value is updated to the optimal value. During this period, the bacterial constraint should be considered, namely the upper and lower limits of the unit output constraint. After the chemotactic process, the fitness value is updated to enter the replication stage. During replication, bacteria are sorted according to their cumulative fitness values, and new populations are formed in ascending order. Replicate 2 times in total. The longitudinal and horizontal crossover operators were used to update the fitness value, retain the perfect result and eliminate the wrong result. Finally, the bacteria were dispersed according to the adaptive dispersal probability when it came to the dispersal stage. The dispersal probability of the perfect result was tiny, while the dispersal probability of the impaired result was extensive. After the dispersal, the bacteria died out, and the new bacteria re-determined the random position. The algorithm ends when the maximum number of dispels reaches 4, and the algorithm iterates 480 times in total. The flow chart of bacterial foraging algorithm is shown in Figure 1.

FIGURE 1

FIGURE 1. Flowchart of ICSBFO.

4 ICSBFO addresses ELD issues

4.1 ELD based on ICSBFO

In the process of solving the ELD problem by ICSBFO, the control variable is the initial population of E. coli, and the dependent variable is the coal consumption of the unit. Use the algorithm to solve Eq. 7, first, it is necessary to tune the relevant parameters of the ICSBFO algorithm in solving the ELD problem. The initial population of E. coli is generated with the upper and lower limits of the power load, and the number of units is set as the solution dimension. Then we need to determine the load and solve the ELD model. The fitness value in the solving process is the objective function proposed above after considering the penalty coefficient. If there is no new load command or percentage load requirement, each unit’s optimal load distribution and optimal coal consumption can be output.

4.2 ICSBFO solves ELD model pseudo code

5 Analysis of two cases

This paper uses the case of 10-unit medium-sized and 3-unit small-scale power plants, respectively, to prove the feasibility of the ICSBFO algorithm. The experimental environment is Windows7, Intel Core i5 quad-core 1.70 GHz processor, 8 GB physical memory, and Matlab 2018a simulation platform. Case 1 Using the ICSBFO, CSO, BFO, and PSO to solve the ELD problem of the 10-unit model, the experimental results show that the ICSBFO algorithm has the smallest coal consumption. Experiments are carried out with different load conditions, and the ICSBFO and BFO algorithms are compared. We find that the lower the load, the more pronounced the optimization effect of ICSBFO. Case 2 Using ICSBFO, BFO, and PSO to solve the ELD problem of the 3-unit model, the experimental results demonstrate that ICSBFO has the best optimization results and point out the limitations of bacterial foraging algorithms when dealing with small-scale unit data.

5.1 Case of 10 units

In Case 1, taking 10 units in a power plant (Basu 2016) as an example, the coal consumption characteristic parameters of the unit and the upper and lower limits of the unit load are shown in the following Table 1:

TABLE 1

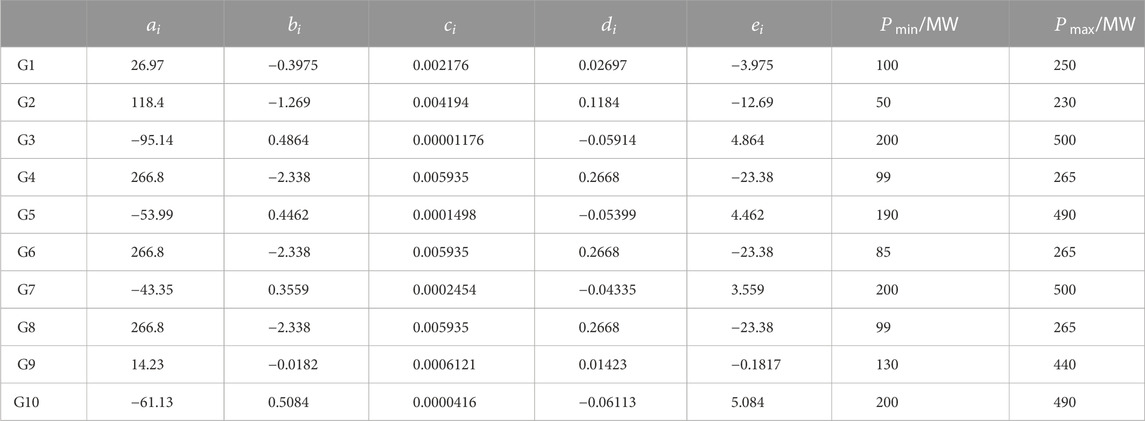
TABLE 1. Coal consumption characteristic parameters of a 10-unit power plant and upper and lower limits of unit load.

In the case of a 10-unit medium-sized power plant, this paper uses the improved crisscross hybrid bacterial foraging algorithm (ICSBFO), the crisscross algorithm (CSO) (Meng et al., 2015), the bacterial foraging algorithm (BFO), and the particle swarm algorithm (PSO) (Hatata and Hafez 2019) to solve the 10-unit load optimization distribution model of a medium-sized power plant. Since different unit parameters and valve point effect parameters greatly influence the results of unit load economic dispatch, this paper uses the methods proposed by them in their respective articles to simulate the unit parameters of the same case. In the process of PSO testing, a mutation strategy is introduced to improve the problem that PSO is easy to fall into the local optimum. Since the test algorithms all contain a random search mechanism, each group is tested 30 times in this experiment, and the experimental results are taken as the average value of the tests. During the test, the population size was 50, the dimension was 10, the load was 2,700 MW, and the total number of iterations of various algorithms is 480.

In the process of dealing with ELD problems, PSO is widely used because of its fast convergence speed, but its disadvantage is poor robustness. CSO shows good convergence efficiency and accuracy in the ELD process due to its independent update iterations in the horizontal and vertical directions, and a simplified algorithm process characterizes it. It can be seen from Figure 2 that the improved bacterial foraging algorithm has faster convergence speed and convergence results than the previous two, which is due to the improvement of the convergence speed by the adaptive correction step size and the mixing in the replication process. Compared with traditional BFO, improvement optimization is more significant. In taking the average value of multiple experiments, we also found that ICSBFO has better robustness and the smallest variance of its optimal coal consumption. Research on the high-quality robustness of ICSBFO is expected to be carried out in the future.

FIGURE 2

FIGURE 2. Convergence curve of unit economic dispatch of case 1.

It can be seen from the above Table 2 that the optimal coal consumption of ICSBFO is the smallest. Compared with the CSO, the coal consumption reduced by the ICSBFO algorithm is 4.6317 $g·k{W}^{-1}·h^{-1}$. The percentage reduction is 0.707%. Compared with the PSO, the coal consumption optimization results are more prominent, decreasing 24.0534 $g·k{W}^{-1}·h^{-1}$. The percentage reduction is 3.671%. Compared with the unimproved traditional BFO algorithm, the effect is more prominent, ICSBFO reduces coal consumption by 47.5621 $g·k{W}^{-1}·h^{-1}$. The percentage reduction is 7.26%. The resulting significant reduction in coal consumption can improve the efficiency of the power plant, reduce the economic cost of the power plant and reduce the pollution to the environment. (From the load distribution of each unit solved by the ICSBFO algorithm, since the upper and lower limits of a load of units 9 and 10 are both high, the outputs of units 9 and 10 are the most, which are 413 and 479 MW respectively.)

TABLE 2

TABLE 2. Load optimization results of units under 2700 MW load with different algorithms.

To test the influence of different loads on the performance and solution quality of the algorithm, this paper uses 90%, 80%, and 70% of the rated load to solve the load optimization distribution model of the 10-unit case of the medium-sized power plant. This experiment compares the ICSBFO and unimproved traditional BFO.

Affected by the valve-point effect, traditional methods often perform poorly in low-load optimization of processing units. For example, in the traditional BFO algorithm, it can be seen from the above Figure 3 that the optimization of coal consumption by BFO in reducing the load is not very obvious. In this process, the coal consumption at 70% load is higher than 80% load, which shows that BFO can no longer effectively optimize the ELD problem at low load. However, ICSBFO can solve the problem of adapting to low-load optimization. As seen from the above Figure 3, as the load rate decreases, the convergence speed of ICSBFO gradually slows down, but the optimization result of ICSBFO is still significantly better than that of BFO. It can be seen from Table 3 that under the condition of 90% load rate, under the load of 2430 MW, the optimized reduction is 66.2689 $g·k{W}^{-1}·h^{-1}$. The percentage reduction is 12.624%. Under the load rate of 80%, the load of 2160MW, the coal consumption is saved by 90.4748 $g·k{W}^{-1}·h^{-1}$.The percentage reduction is 21.183%. Under the load rate of 70% and the load capacity of 1890MW, the optimized amount is 220.1997 $g·k{W}^{-1}·h^{-1}$. The percentage reduction is 65.357%. From the analysis of the load optimization distribution of different units, the ICSBFO algorithm can give full play to the output advantages of different units. In this case, the two units G9 and G10, with higher upper and lower load limits, have the most output under different load ratios. From this, it can also be concluded that ICSBFO has an excellent performance in optimizing the load of 10 units. By comparing different load rates, it can be found that under high load rates, the optimized amount of ICSBFO is small, and as the load rate decreases, the optimized coal consumption gradually increases. The traditional BFO algorithm has a poor unit optimization effect in the case of low load, but ICSBFO still has an excellent optimization effect in the case of low load rate. Therefore, the algorithm is expected to have good application scenarios during the low-peak electricity consumption period in spring and autumn.

FIGURE 3

FIGURE 3. Comparison of ICSBFO and BFO under different load factors in Case 1.

TABLE 3

TABLE 3. Comparison results of ICSBFO and BFO under different loads.

5.2 Case of 3 units

In case 2, taking 3 units of a miniature thermal power plant as an example, the coal consumption characteristic parameters of the units and the upper and lower limits of unit load are shown in the following Table 4:

TABLE 4

TABLE 4. Coal consumption characteristic parameters and upper and lower limits of unit load in a particular 3-unit power plant.

In the case of a small power plant with 3 units, this paper uses ICSBFO, BFO and PSO to solve and compare the load distribution optimization model of the same unit data. In this experiment, each group was tested 30 times, and the average was taken. The population size was 50, the dimension was 3, the load was 900 MW, and the total number of iterations of various algorithms is 480.

This experiment sets the number of units as the solution dimension. The crisscross algorithm used in this paper in the replication process, its horizontal crossover operator is the crossover of dimensions, while the dimension of this experimental case is 3, and the crossover dimension is too small, resulting in The offspring after crossover are highly similar to the previous generation, so the horizontal crossover operator is omitted in this experiment, and only the vertical crossover operator is used to improve the replication process, so as to ensure the diversity of the population. Although the energy consumption coefficients of the three units in this experiment are different, the upper and lower limits of the unit load are the same. It can be seen from Figure 4 that the result of ICSBFO is significantly better than that of PSO and BFO, but the convergence rate will be slightly lower. Under the condition of 900 MW load, the optimal coal consumption of ICSBFO is 975.23 $g·k{W}^{-1}·h^{-1}$, which is 1.37% lower than that of BFO algorithm and 1.06% lower than that of PSO. Combining the low load rate in the 10-unit case and the 3-unit case, it can be concluded that the traditional bacterial foraging algorithm generally performs in processing the optimization data of small-scale units, and the solution time is slightly longer. However, the improved bacterial foraging algorithm can overcome such problems. Given this characteristic, follow-up research will be carried out on the case of large-scale power plant units. In addition, in the future work, we will also study the dynamic ELD problem with multiple constraints, not limited to the valve-point effect constraint.

FIGURE 4

FIGURE 4. Economic dispatch curve of units in case 2.

6 Conclusion

In this paper, we improve the three main steps of bacterial foraging in dealing with slow speed problems in the ELD process. The step size is a key factor affecting the speed of the BFO algorithm. Therefore, in this paper, an improved adaptive correction step size is used to replace the fixed step size in the chemotaxis process to speed up the convergence speed of ICSBFO. Given the excellent hybridization of the CSO algorithm, we propose to use the CSO operator to hybridize the population in the replication process to ensure the diversity of the population; in the dispersal part, the adaptive dynamic dispersal probability is used instead of the fixed probability to solve the problem that the traditional BFO algorithm easily leads to the loss of the optimal solution, and the algorithm efficiency is guaranteed. The mathematical model of the ELD problem is established. By comparing with other algorithms, it is proved that the ICSBFO proposed in this paper has excellent performance, which can significantly reduce coal consumption and improve the economic benefits of the power plant. At the same time, through the case study of small-scale units, it is found that ICSBFO can also solve the problem that BFO is not good at processing the scheduling data of small-scale units. In the follow-up research, we will try to apply ICSBFO to the problems of multi-objective microgrid scheduling optimization and multi-region joint dynamic economic scheduling and add disturbances to the population initialization and dispersal stage of ICSBFO to test the performance of the algorithm.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization and Methodology, YZ; Data curation and Investigation, YL.

Funding

This work is supported by the fund of the education department of Jilin province No. JJKH20210257KJ, the fund of the Science and Technology Development Project of Jilin Province No. 20220203190SF.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

CSO, Crisscross Algorithm; BFO, Bacterial Foraging Algorithm; PSO, Particle Swarm Optimization; ELD, Electrical Load Distribution; ICSBFO, Improved Crisscross Algorithm Mixed Bacterial Foraging Algorithm; EBO, Ecogeography-based Optimization Algorithm; HGSO, Henry Gas, Solubility Optimization Algorithm; HTTSA, Hybrid Taguchi Salp Swarm Algorithm; HSSA-NM, Hybrid Salp Swarm-Nelder-Mead; COOA, Coot Optimization Algorithm; IEO, Improved Equilibrium Optimizer; ECSA, Effective Cuckoo Search Algorithm.

References

Al-Bahrani, L. T., and Patra, J. C. (2018). Multi-gradient PSO algorithm for optimization of multimodal, discontinuous and non-convex fuel cost function of thermal generating units under various power constraints in smart power grid. Energy 147, 1070–1091. doi:10.1016/j.energy.2017.12.052

CrossRef Full Text | Google Scholar

Anbo, M., Cong, Z., Xuancong, X., Weifeng, D., Shiyun, L., De, C., et al. (2022). Decentralized power economic dispatch by distributed crisscross optimization in multi-agent system. Energy 246, 123392. doi:10.1016/j.energy.2022.123392

CrossRef Full Text | Google Scholar

Aye, C. M., Pholdee, N., Yildiz, A. R., Bureerat, S., and Sait, S. M. (2019). Multi-surrogate-assisted metaheuristics for crashworthiness optimisation. Int. J. Veh. Des. 80 (2-4), 223–240. doi:10.1504/ijvd.2019.109866

CrossRef Full Text | Google Scholar

Basu, M. (2016). Quasi-oppositional group search optimization for multi-area dynamic economic dispatch. Int. J. Electr. Power Energy Syst. 78, 356–367. doi:10.1016/j.ijepes.2015.11.120

CrossRef Full Text | Google Scholar

Carmen, F. M., Stefano, P., Mauro, C., and Federico, Q. (2021). A review on unit commitment algorithms for the Italian electricity market. Energies 15 (1), 18. doi:10.3390/en15010018

CrossRef Full Text | Google Scholar

Chen, G., Heng, T., and Ben, N. (2021). Evolutionary state-based novel multi-objective periodic bacterial foraging optimization algorithm for data clustering. Expert Syst. 39 (1). doi:10.1111/exsy.12812

CrossRef Full Text | Google Scholar

Chen, Y.-P., Li, Y., Wang, G., Zheng, Y.-F., Xu, Q., Fan, J.-H., et al. (2017). A novel bacterial foraging optimization algorithm for feature selection. Expert Syst. Appl. 83, 1–17. doi:10.1016/j.eswa.2017.04.019

CrossRef Full Text | Google Scholar

Chi, K. L., Thi, B. N. T., Minh, P. T., and Trung, N. T. (2022). Coot optimization algorithm for optimal placement of photovoltaic generators in distribution systems considering variation of load and solar radiation. Math. Problems Eng. 2022, 1–17. doi:10.1155/2022/2206570

CrossRef Full Text | Google Scholar

de, M. C. H. V., de, V. B. J. L., Germano, L., de, A. G. C. C., and Almeida, C. C. I. d. (2022). Intelligent power distribution restoration based on a multi-objective bacterial foraging optimization algorithm. Energies 15 (4), 1445. doi:10.3390/en15041445

CrossRef Full Text | Google Scholar

Devi, J. A., and Srinivasan, V. P. (2021). A two-fold optimization framework using hybrid B2 algorithm for resource allocation in long-term evolution based cognitive radio networks system. Int. J. Commun. Syst. 35 (3). doi:10.1002/dac.5023

CrossRef Full Text | Google Scholar

Farshi, T. R., and Orujpour, M. (2021). “A multi-modal bacterial foraging optimization algorithm,” in Journal of ambient intelligence and humanized computing. (prepublish).

Google Scholar

Hatata, A. Y., and Hafez, A. A. (2019). Ant lion optimizer versus particle swarm and artificial immune system for economical and eco-friendly power system operation. Int. Trans. Electr. Energy Syst. 29 (4), e2803. doi:10.1002/etep.2803

CrossRef Full Text | Google Scholar

Hu, J., Jin, N., Li, P., and Zhang, H. (2020). An improved bacterial foraging algorithm for multi-modal problems. 中国湖北武汉.

Google Scholar

Jianjun, W., Shuo, Z., Jikun, H., Yan, Z., Li, L., and Taoya, H. (2021). Dispatch optimization of thermal power unit flexibility transformation under the deep peak shaving demand based on invasive weed optimization. J. Clean. Prod. 315, 128047. doi:10.1016/j.jclepro.2021.128047

CrossRef Full Text | Google Scholar

Jufeng, W., Chunfeng, L., and MengChu, Z. (2020). Improved bacterial foraging algorithm for cell formation and product scheduling considering learning and forgetting factors in cellular manufacturing systems. IEEE Syst. J. 14, 3047–3056. doi:10.1109/jsyst.2019.2963222

CrossRef Full Text | Google Scholar

Kopiske, J., Spieker, S., and Tsatsaronis, G. (2017). Value of power plant flexibility in power systems with high shares of variable renewables: A scenario outlook for Germany 2035. Energy 137, 823–833. doi:10.1016/j.energy.2017.04.138

CrossRef Full Text | Google Scholar

Kumar, C. V., and Babu, M. R. (2021). An exhaustive solution of power system unit commitment problem using enhanced binary salp swarm optimization algorithm. J. Electr. Eng. Technol. 17, 395–413. (prepublish). doi:10.1007/s42835-021-00889-0

CrossRef Full Text | Google Scholar

Long, Y., Zuo, Z., Su, Y., Li, J., and Zhang, H. (2020). An A∗-based bacterial foraging optimisation algorithm for global path planning of unmanned surface vehicles. J. Navigation 73, 1247–1262. doi:10.1017/s0373463320000247

CrossRef Full Text | Google Scholar

Mahdi, F. P., Vasant, P., Abdullah-Al-Wadud, M., Watada, J., and Kallimani, V. (2018). A quantum-inspired particle swarm optimization approach for environmental/economic power dispatch problem using cubic criterion function. Int. Trans. Electr. energy Syst. 28 (3), e2497. doi:10.1002/etep.2497

CrossRef Full Text | Google Scholar

Meng, A., Hu, H., Yin, H., Peng, X., and Guo, Z. (2015). Crisscross optimization algorithm for large-scale dynamic economic dispatch problem with valve-point effects. Energy 93, 2175–2190. doi:10.1016/j.energy.2015.10.112

CrossRef Full Text | Google Scholar

Nguyen, T., Trung, N., Thanh, T., and Quan, M. (2022). “An improved equilibrium optimizer for optimal placement of photovoltaic systems in radial distribution power networks,” in Neural computing and applications. (prepublish).

CrossRef Full Text | Google Scholar

Panagant, N., Pholdee, N., Bureerat, S., Yildiz, A. R., and Sait, S. M. (2020). Seagull optimization algorithm for solving real-world design optimization problems. Mater. Test. 62 (6), 640–644. doi:10.3139/120.111529

CrossRef Full Text | Google Scholar

Pham, L., Huu, D., Hoang, N. B., and Trung, T. (2022). “Optimal power flow for an integrated wind-solar-hydro-thermal power system considering uncertainty of wind speed and solar radiation,” in Neural computing and applications. (prepublish).

CrossRef Full Text | Google Scholar

Premkumar, M., Jangir, P., Kumar, B. S., Sowmya, R., Alhelou, H. H., Abualigah, L., et al. (2021). A new arithmetic optimization algorithm for solving real-world multiobjective CEC-2021 constrained optimization problems: Diversity analysis and validations. IEEE ACCESS 9, 84263–84295. doi:10.1109/access.2021.3085529

CrossRef Full Text | Google Scholar

Ramaporselvi, R., and Geetha, G. (2021). Congestion management in deregulated power system using adaptive moth swarm optimization. COMPEL - Int. J. Comput. Math. Electr. Electron. Eng. 41, 334–356. doi:10.1108/compel-06-2021-0198

CrossRef Full Text | Google Scholar

Shaowei, W., Wenlong, T., Bo, O., and Jeng-Shyang, P. (2021). Reversible data hiding method for multi-histogram point selection based on improved crisscross optimization algorithm. Inf. Sci. 549, 13–33. doi:10.1016/j.ins.2020.10.063

CrossRef Full Text | Google Scholar

Wang, Y., Cui, Z., and Li, W. (2019). A novel coupling algorithm based on glowworm swarm optimization and bacterial foraging algorithm for solving multi-objective optimization problems. Algorithms 12 (3), 61. doi:10.3390/a12030061

CrossRef Full Text | Google Scholar

Wu, T., Wei, H., Ge, Z., Yang, L., and Du, X. (2019). Cooling water mass flow optimization for indirect dry cooling system of thermal power unit under variable output load. Int. J. Heat Mass Transf. 133, 1–10. doi:10.1016/j.ijheatmasstransfer.2018.12.097

CrossRef Full Text | Google Scholar

Xiongmin, T., Zhengshuo, L., Xuancong, X., Zhijun, Z., Tianhong, J., Wenrui, F., et al. (2022). Multi-objective economic emission dispatch based on an extended crisscross search optimization algorithm. Energy 244, 122715. doi:10.1016/j.energy.2021.122715

CrossRef Full Text | Google Scholar

Yildiz, A. R., and Erdas, M. U. (2021). A new Hybrid Taguchi-salp swarm optimization algorithm for the robust design of real-world engineering problems. Mater. Test. 63 (2), 157–162. doi:10.1515/mt-2020-0022

CrossRef Full Text | Google Scholar

Yildiz, B. S., Kumar, S., Pholdee, N., Bureerat, S., Sait, S. M., and Yildiz, A. R. (2022c). A new chaotic Levy flight distribution optimization algorithm for solving constrained engineering problems. EXPERT Syst. 39 (8). doi:10.1111/exsy.12992

CrossRef Full Text | Google Scholar

Yildiz, B. S., Patel, V., Pholdee, N., Sait, S. M., Bureerat, S., and Yildiz, A. R. (2021c). Conceptual comparison of the ecogeography-based algorithm, equilibrium algorithm, marine predators algorithm and slime mold algorithm for optimal product design. Mater. Test. 63 (4), 336–340. doi:10.1515/mt-2020-0049

CrossRef Full Text | Google Scholar

Yildiz, B. S., Pholdee, N., Bureerat, S., Erdas, M. U., Yildiz, A. R., and Sait, S. M. (2021a). Comparision of the political optimization algorithm, the Archimedes optimization algorithm and the Levy flight algorithm for design optimization in industry. Mater. Test. 63 (4), 356–359. doi:10.1515/mt-2020-0053

CrossRef Full Text | Google Scholar

Yildiz, B. S., Pholdee, N., Bureerat, S., Yildiz, A. R., and Sait, S. M. (2022a). Enhanced grasshopper optimization algorithm using elite opposition-based learning for solving real-world engineering problems. Eng. Comput. 38 (5), 4207–4219. doi:10.1007/s00366-021-01368-w

CrossRef Full Text | Google Scholar

Yildiz, B. S., Pholdee, N., Bureerat, S., Yildiz, A. R., and Sait, S. M. (2021b). Robust design of a robot gripper mechanism using new hybrid grasshopper optimization algorithm. EXPERT Syst. 38 (3). doi:10.1111/exsy.12666

CrossRef Full Text | Google Scholar

Yildiz, B. S., Pholdee, N., Bureerat, S., Yildiz, A. R., and Sait, S. M. (2020). Sine-cosine optimization algorithm for the conceptual design of automobile components. Mater. Test. 62 (7), 744–748. doi:10.3139/120.111541

CrossRef Full Text | Google Scholar

Yildiz, B. S., Pholdee, N., Panagant, N., Bureerat, S., Yildiz, A. R., and Sait, S. M. (2022b). A novel chaotic Henry gas solubility optimization algorithm for solving real-world engineering problems. Eng. Comput. 38 (2), 871–883. doi:10.1007/s00366-020-01268-5

CrossRef Full Text | Google Scholar

Yildiz, B. S. (2020). Robust design of electric vehicle components using a new hybrid salp swarm algorithm and radial basis function-based approach. Int. J. Veh. Des. 83 (1), 38–53. doi:10.1504/ijvd.2020.10037481

CrossRef Full Text | Google Scholar

Yufang, D., and Jianwen, T. (2021). Knowledge worker scheduling optimization model based on bacterial foraging algorithm. Future Gener. Comput. Syst. 124, 330–337. doi:10.1016/j.future.2021.05.028

CrossRef Full Text | Google Scholar

Zou, D., Li, S., Kong, X., Ouyang, H., and Li, Z. (2019). Solving the combined heat and power economic dispatch problems by an improved genetic algorithm and a new constraint handling strategy. Appl. Energy 237, 646–670. doi:10.1016/j.apenergy.2019.01.056

CrossRef Full Text | Google Scholar

Nomenclature

S The number of bacteria

${\mathit{N}}_{\mathit{c}}$ Maximum number of chemotaxis

${\mathit{N}}_{\mathit{s}}$ $\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{o}\mathrm{n}\mathrm{e}–\mathrm{w}\mathrm{a}\mathrm{y}\mathrm{m}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$

${\mathit{N}}_{\mathit{r}\mathit{e}}$ Number of replication

${\mathit{N}}_{\mathit{e}\mathit{d}}$ $\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{a}\mathrm{l}$

${\mathit{P}}_{\mathit{e}\mathit{d}}$ $\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}\mathrm{o}\mathrm{f}\mathrm{b}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{a}\mathrm{l}$

d_attract, ommiga_attract The number of attractive factors and the release speed

h_repellant, ommiga_repellant The number of repellant factors and the release speed

P Population

C Step size

J Fitness value