
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 27 January 2023
Sec. Energy Storage
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1100456
This article is part of the Research Topic Muti-Energy Integration towards Energy Decarbonization View all 7 articles
Recently, incorporating renewable energy resources (RERs) like wind turbines (WTs) in a distribution network is rapidly increased to meet the load growth. However, distribution networks have been facing many challenges to withstand the intermittent output power of RERs. Battery energy storage (BES) is used with RERs to smoothly inject the output power to the grid by RERs. Therefore, this paper proposes an effective strategy for optimal allocation of WT and BES in RDS to decrease the total system losses. In addition, a modified bald eagle search (BES-optimizer) is proposed to obtain the preferable allocations of WT and BES simultaneously in the radial distribution system (RDS) considering the probabilistic distribution of the WT and load demand. IEEE 69-bus RDS is utilized as a test system. Based on the obtained results, installing WTs with BES gives better results than installing WTs alone in the RDS. However, the proposed algorithm proved its efficiency to obtain the best global results compared with other well-known techniques.
Increasing uncertainty in energy flow in power grids today is due to intermittent production of renewable resources and time-varying load (Ashfaq and Ianakiev, 2018; Ludin et al., 2018; Liu et al., 2019; Peng et al., 2019; Sun et al., 2019). Therefore, power grids are facing a period of change caused by many issues such as reliability (Schienbein and DeSteese, 2002; Islam et al., 2015) and expansion of the power system (Carrano et al., 2007), power quality improvement (Short, 2018), load growth management (Das et al., 2013a; Hossain et al., 2015; Van Der Stelt et al., 2018; Mousavi et al., 2019), penetration of renewable resources (Das and Alam, 2012; Das et al., 2013b; Das et al., 2016; Yan et al., 2017), and minimization of greenhouse gas emission (Mazumder et al., 2014; Nemet et al., 2016). Incorporating battery energy storage (BES) in the distribution system is rapidly increasing to provide many benefits to environmental, technical, and economic issues (Das et al., 2018a; Das et al., 2018b). These provide facilitation to RER (renewable energy resource) integration (Solomon et al., 2014; Zhang et al., 2016; Parra et al., 2017), reduction of greenhouse gas emission (De Sisternes et al., 2016; Lin et al., 2016; Ogunjuyigbe et al., 2016), network expansion (Go et al., 2016; Sardi et al., 2017), power equality enhancement (Wen et al., 2014; Nick et al., 2015), reliability improvement (Awad et al., 2014), and load management (Marini et al., 2015; Parra et al., 2016; Zhang et al., 2017a; Zhang et al., 2017b; Li et al., 2017; Zhu et al., 2018).
Installation of RERs like wind turbines in a distribution system is commonly used due to its clean energy that depends on the natural source and its inertia capable of carrying a load in a transient condition (Bevrani et al., 2010). WTs (wind turbines) are used to convert the kinetic energy that is based on wind velocity into electrical energy. The WT generates power when the wind speed reaches its rated magnitude and stops and starts running when the wind speed exceeds the cut-out and cut-in magnitudes of wind speed, respectively (Abdel-Mawgoud et al., 2021a). Therefore, the output power of WTs is intermittent as they depend on wind speed which is varied during the day. BES has a technology that can produce fast response for discharging and charging power. The main advantages of installing BES in the RDS (radial distribution system) are reducing the electricity cost by charging the electricity at light load as long as its price is low and discharging the electricity at peak load as long as its price is high (Saboori et al., 2015). In addition, BES is utilized to enhance the penetration of RERs in the RDS by smoothing the intermittent output power of RERs (Zhang et al., 2017a; Ahmad et al., 2018; Arani et al., 2019; Gan et al., 2019; Hlal et al., 2019; Murty and Kumar, 2020).
In recent years, many researchers studied the optimal allocation of the WT and BES in the RDS. In Saboori et al., (2015), the optimal placement and sizing of BES in the RDS has been determined to minimize the system annual cost using the particle swarm optimization (PSO) algorithm. In Kalkhambkar et al., (2017), the optimal allocation of BES with PV and WT in the RDS has been determined to decrease the annual energy loss using gray wolf optimizer (GWO). Also, GWO has been applied for obtaining the sizing of BES in the RDS by decreasing the system annual cost (Fathy and Abdelaziz, 2017) and for determining the sizing of the inverter with the WT and electric vehicle by decreasing the system energy loss (Ali et al., 2020). The best sizing and locations of BES with the PV and WT to minimize the line loading, power loss, and voltage deviation in RDS using the artificial bee colony (ABC) algorithm have been presented in Das et al., (2018b). In Abdel-Mawgoud et al., (2021b), the optimal placement and sizing of PV with BES in the RDS has been studied to decrease the system loss using the modified Henry gas solubility optimization algorithm (modified HGSO). The whale optimization algorithm (WOA) has been utilized to determine the sizing of BES in the RDS by decreasing the system losses (Wong et al., 2019) and for determining the optimal allocation of BES with PV by decreasing the system cost (Kasturi and Nayak, 2017). The genetic algorithm (GA) has been applied to obtain the optimal allocation of the WT and BES by minimizing the costs of integrated sources and system losses (Khaki and Das, 2019).The GA has also been utilized to calculate the best sizing of BES and PV in the RDS by minimizing the voltage deviation, system loss, and cost of energy generated (Teng et al., 2012; Chedid and Sawwas, 2019). Recently, creating metaheuristic hybrid algorithms by hybridizing two algorithms is becoming more popular in most recent research works (Blum and Roli, 2008; Ehrgott and Gandibleux, 2008; Duan et al., 2012; Wang et al., 2012; Wang et al., 2013; Wang and Guo, 2013; Wang et al., 2014a; Wang et al., 2016; Elgamal et al., 2020; Abdel-Mawgoud et al., 2021a; Abdel-Mawgoud et al., 2021b). Several hybrid methods are utilized in different optimization problems, such as the ant colony optimization–genetic algorithm (ACO-GA) (Nemati et al., 2009), particle swarm optimization–differential evolution (PSO-DE) algorithm (Niu and Li, 2008), particle swarm optimization–genetic algorithm(PSO-GA) (Shi et al., 2005), particle swarm optimization–ant colony optimization (PSO-ACO) algorithm (Holden and Freitas, 2008), ant colony optimization–differential evolution (ACO-DE) algorithm (Duan et al., 2010), genetic algorithm–differential evolution (GA-DE) algorithm (Lin, 2010), cuckoo search krill herd (CSKH) method (Wang et al., 2016), and biogeography-based krill herd (BBKH) approach (Wang et al., 2014b).
Bald eagle search (BES-optimizer) is an efficient metaheuristic algorithm that mimics the intelligent social behavior or hunting strategy of the bald eagle when it seeks for fish (Alsattar et al., 2020). The hunting behaviors of BES are represented by three stages: (1) selecting the search space to determine the best promising area that contains the greatest number of fishes, (2) searching for a fish (prey) inside the best promising area that is selected before, and (3) starting swooping to determine the best position to hunt. The sine cosine algorithm (SCA) is a metaheuristic algorithm based on cosine and sine functions (Mirjalili, 2016). Also, the SCA has an effective exploration phase to be used in different optimization problems by many researchers (Biswal and Shankar, 2018). This paper proposes a modified BES-optimizer for improving the performance of the original BES-optimizer by avoiding local minima and enhancing its exploration phase. This modified algorithm is utilized to obtain the optimal allocation of the WT and BES in the RDS to minimize the real loss as a single function. The simulation results are obtained by installing the WT alone or simultaneously with the BES in the RDS considering the probabilistic distribution of WT and system load demand. Installing the BES and WT in the RDS enhances the minimum voltage, decreases system loss, improves the power equality, enhances system reliability, increases system capacity, and decreases greenhouse gas emission. The paper´s contributions are outlined as follows:
✓ Proposing the modified BES-optimizer with the aim of improving the performance of the original BES-optimizer.
✓ Applying the original BES-optimizer, the modified version, and the SCA algorithm for determining the best placement and sizing of the WT and BES in the RDS.
✓ The preferable allocation of the WT and BES is utilized to minimize the total power losses of the system.
✓ Determining the placement and sizing of the WT and BES in the RDS considering the generation uncertainty and time-varying load.
✓ The high efficiency of the modified BES-optimizer is confirmed by comparing its results with those obtained by other techniques.
The remainder of the paper is organized as follows. The total system modeling including the commercial load demand, WT, and BES is presented in section two. Next, the problem formulation is presented in Section three. After that, the proposed algorithm is explained in Section four. Subsequently, the obtained results are analyzed and discussed in Section five. Finally, Section six discusses the conclusion of the paper.
This paper studies the preferable allocation of WT alone or with BES in the RDS as two cases to decrease the total active loss as a single objective function. In the first case, installing WTs alone is utilized to inject active power only to the RDS. In the second case, the BES and WT are installed simultaneously to inject active power only by them to the RDS. Also, BES is utilized to be charged from WT during light load and discharges the stored energy to the system at high load, thus helping in enhancing the system reliability. Therefore, BES is modeled to draw the active power from the WT during charging when the load demand is less than 75% of the reference load and deliver active power to the system during discharging when the load demand is more than 75% of the reference load. Also, BES is disconnected from the system when the load level reaches 75 % of the reference system load. The forward–backward method is utilized to calculate the system load flows (Eminoglu and Hocaoglu, 2008). The active and reactive load flows in RDS are calculated by Eqs 1, 2, respectively. The value of bus voltage (d+1) is calculated by Eq. 3. Figure 1shows the system load flows are changed by installing WT alone or with BES, as shown in Eqs 4, 5.
where
The total active power loss during 24 h is used as the objective function as follows:
where
The formulation of the problem is implemented under inequality and equality constraints shown as follows.
The active and reactive load flows are represented as equality constraints, as shown in Eqs 7, 8. Also, the power parlance equations are formulated as equality constraints, as shown in Eqs 9, 10.
These constraints are based on operation system constraints such as branch constraints, WT output constraints, and bus system voltage
1) System Voltage constraints
where
2) WT output constraints
where
3) Branch constraints
where
Figure 2 presents an output of commercial load modeling in per unit through 24 h (Lopez et al., 2004). This model is based on voltage-dependent loads that are represented by Eqs 14, 15 (Khoubseresht and Shayanfar, 2020). Also, this model is applied on the studied system load to become as commercial load curve via the day (Kasturi and Nayak, 2017).
where the real and reactive load voltage exponents are
The generating power of the WT depends on the wind speed, so the uncertainty of wind speed can be modeled using Weibull probability density function (Abdel-Mawgoud et al., 2021a). Therefore, the probability of wind speed can be evaluated using Eq. 16.
where
The output and the average power of the output are evaluated using Eqs 19, 20, respectively.
where
The battery storage system is a storage device that is utilized in a power grid to enhance the system reliability and minimize the intermittent output of renewable resources and the variable load. The BES can be connected to the distribution system via an inverter to convert the DC voltage from BESs to AC voltage, as shown in Figure 1. In this paper, the charging and discharging of the BES is based on the load level, as shown in Figure 3. The BES is charging or discharging when the load level is less or above 75% of the base load. Therefore, the BES can be simulated as the load or the generator during the charging or discharging status.
BES-optimizer is an efficient metaheuristic algorithm that is inspired by the hunting behavior of bald eagles in nature. The hunting behavior of the BES-optimizer begins with selecting space, then searching in the selected space, and finally moving to swooping behavior. In the selecting space behavior stage, bald eagles search for the promising area (search space) that has a greater number of fish or prey. In the searching behavior stage, the bald eagles move in the promising area to search for fish. In the swooping behavior stage, the bald eagles move to the prey predetermined before the second stage. These behaviors can be formulated as follows:
Stage 1: Selecting the search area
Bald eagles search for a new search space
where
Stage 2: Searching in the search space
Bald eagles move in a spiral space in the search space selected before in the first stage to search for fish. Therefore, the new position of bald eagles can be formulated by Eq. 22.
where
Stage 3: Swooping
Bald eagles swing from its best position that is predetermined from the second stage to the fish. The swing behavior is formulated from Eq. 26, as follows:
where
The SCA is based on cosine and sine functions that lead to solutions fluctuating toward or outward the best solution. The implementation of the SCA during the optimization process is based on the exploration phase and exploitation phase. In addition, the SCA starts its optimization process by generating solutions with a high rate of randomness during the exploration phase and then generates solutions with a low rate of randomness during the exploitation phase. There are several parameters in the SCA to make a control balance of exploration and exploitation phases during the optimization process. The updating positions of the SCA are formulated by Eq. 30.
where
The SCA has an efficient exploration phase that depends on generating solutions with a high rate of randomness to explore the best promising area that has many prey. The exploration phase of the BES-optimizer is based on the parameter
Stage 1: Selecting the search area
The second and third stages of the BES-optimizer remain the same as follows.
Stage 2: Searching in the search space
Stage 3: Swooping
The summarized steps of the developed BES-optimizer to obtain the preferable allocation of the WT and BES in the RDS are presented as follows:
Step 1:. Read the system constraints with line and bus data.
Step 2:. Set the parameters of BES-optimizer such as
Step 3:. Generate initial population of among the lower (low) and upper (high) values of the control variable as follows:
where
Step 4:. The obtained solutions of bald eagles are formulated as follows:
Step 5: . Evaluate the fitness of all bald eagles and obtain the best position and best fitness.Step 6:. Updating the positions of bald eagles according to the first stage using the following equation:
Step 7:. Evaluate the fitness of all updating position of bald eagles and obtain the best position that is represented as the best search space or promising area.
Step 8:. Updating the positions of bald eagles according to the second stage using the following equation:
Step 9:. Evaluate the fitness of all updating position of bald eagles and obtain the best position in the promising area to make swooping.
Step 10:. Updating the positions of bald eagles to make swooping and go to the prey or fish according to the third stage using the following equation:
Step 11: . Evaluate the fitness of all the updating position of bald eagles and obtain the best position that is represented as the position of prey or fish.
Step 12:. Repeat Step 6 to 11 when maximum iteration is achieved.
Step 13:. Obtain the best position (locations and sizes of the WT and BES) with the best fitness.
The proposed modified BES-optimizer is validated and utilized to obtain the best allocation of the WT and BES in IEEE 69-bus RDS. This test system has a total load of 3.802 MW and 2.695 MVAr (Sahoo and Prasad, 2006). The branches and buses of this system are 68 and 69, respectively, as shown in Figure 5. The system power flow is evaluated in per unit under the base value of 100 MVA and 12.66 kV. The system constraints and the algorithm parameters are given in Table 1.
In this case, the WT is integrated in the RDS to inject active power only to the grid during the day. Installing one WT decreases the system loss to 1015.892 kW with sizes of 2051.9 kW at bus 61 and total energy of 27073 kWh, as shown in Figure 6. Table 2 shows the optimal sizes of two WTs are 1954.23 kW and 573.8 kW at buses 61 and 17, respectively, leading to a decrease in the real loss to 920.147 kW. Figure 7 shows the energies of two WTs through 24 h are 25784 kWh and 7570.8 kWh at buses 61 and 17, respectively. Table 2 shows installing three WTs achieves superior results than other cases as it reduces the system loss to 902.37 kW. The preferable sizing of three WTs at buses 61, 18, and 11 are 1888.503 kW, 415.586 kW, and 552.257 kW, respectively. Figure 8 shows the energies of three WTs through 24 h at buses 61, 18, and 11 are 24917 kWh, 5483.2 kWh, and 7286.5 kWh, respectively. The total energies of two and three WTs through 24 h are 33354.8 kWh and 37686.7 kWh, respectively. Table 3 shows the proposed algorithm proves its efficiency to obtain better results than SCA, the original BES-Optimizer, and modified Manta ray foraging optimizer.

TABLE 3. Comparison among the modified BES-optimizer, SCA, original BES-optimizer, and modified MRFO used for determining the allocation of the WT alone in the RDS.
In this case, the best allocation of the WT and BES simultaneously in the RDS is determined using the proposed optimizer. Table 4 shows the best sizing of one WT and BES is 2284 kW and 286 kW at bus 61, respectively, which can minimize the system loss to 881.774 kW. Figure 9 and Figure 10 show that one WT has a total energy of 30135 kWh that can charge one BES with an energy of 4290 kW with a charge rate of 286 kW and inject an energy of 25845 kWh to the grid. In addition, the BES can discharge an energy of 1716 kWh to the grid during the day, with a discharge rate of 286 kW. The total energy capacity of one BES during the day is shown in Figure 11. Installing two WTs with the BES can enable injecting a total energy of 26407 kWh and 7580.9 kWh to the grid at buses 61 and 17, respectively. The superior allocation of two WTs with the BES in the RDS is 2188.4 kW and 628.4636 kW for the WT and 274 kW and 79 kW for the BES at buses 61 and 17, respectively. Figure 12 shows the total energy of two WTs is 28873 kWh and 8291.9 kW, which can enable injecting an energy of 24763 kWh and 7106.9 kWh at buses 61 and 17, respectively. The charging and discharging energies of two BESs are 4110 kWh and 1644 kWh at bus 61 and 1185 kWh and 474 kWh at bus 17, respectively, as shown in Figure 13. The total energies from the WT and BES to the grid are 26407 kWh and 7580.9 kWh at buses 61 and 17, respectively. The total energies of two BESs during the day are shown in Figure 14. Integrating three WTs with the BES in the RDS decreases the system loss to 753.5304 kW with sizes of 2093.2 kW, 468.3 kW, and 638.3 kW for WT and 262 kW, 59 kW, and 80 kW for BES at buses 61, 18, and 11, respectively. From Figure 15, it can be observed that the total energies of three WTs are 27618 kWh, 6178.7 kWh, and 8422.2 kWh to inject energies of 2368.8 kWh, 5293.7 kWh, and 7222.2 kWh at buses 61, 18, and 11, respectively. Three BESs can be charged from three WTs during the day with energies of 3930 kWh, 885 kWh, and 1200 kWh to inject energies of 1572 kWh, 354 kWh, and 480 kWh at buses 61, 18 and 11, respectively. Both three WTs and BES can inject total energies of 25260 kWh, 5647.7 kWh, and 7702.2 kWh to the grid at buses 61, 18, and 11, respectively. The charging and discharging power of three BESs during the day are shown in Figure 16. Also, the energy capacity of three BESs during the day is shown in Figure 17. The performance of the modified BES-optimizer is measured by comparing its results with those obtained by the SCA and the original BES-optimizer, as shown in Table 5. From BES modeling, the BES is charging or discharging when the load level is less or above 75% of the base load. Therefore, BESs are charged with a specific power rate from hour 1 to hour 6 and then are discharged from hour 7 to hour 12, as shown in Figure 10; Figure 13; Figure 16. In addition, the total stored energy of BESs decreased 0 at hour 12 when the last discharging power rate is injected into the system at hour 12, which leads to the stored energy to become 0 at hours 13, 14, and 15. Finally, the BES is charged again from hour 16 to hour 24 when the load level is less than 75% of the base load to increase the stored energy of BESs again until it reaches to the maximum value at hour 24, as shown in Figure 11; Figure 14; Figure 17. The statistical results of the BES, SCA, and the modified-BES algorithms with the simulation time by installing three WTs with and without BES in RDS are illustrated in Table 6. BES-optimizer, BES, and SCA algorithms are applied 15 times for installing three WTs alone and with the BES in the RDS to obtain the minimum, STD, maximum, and average values of total system loss as shown in Table 6. Table 6 shows the best results obtained by the BES-optimizer with high simulation time when compared to BES and SCA algorithms.
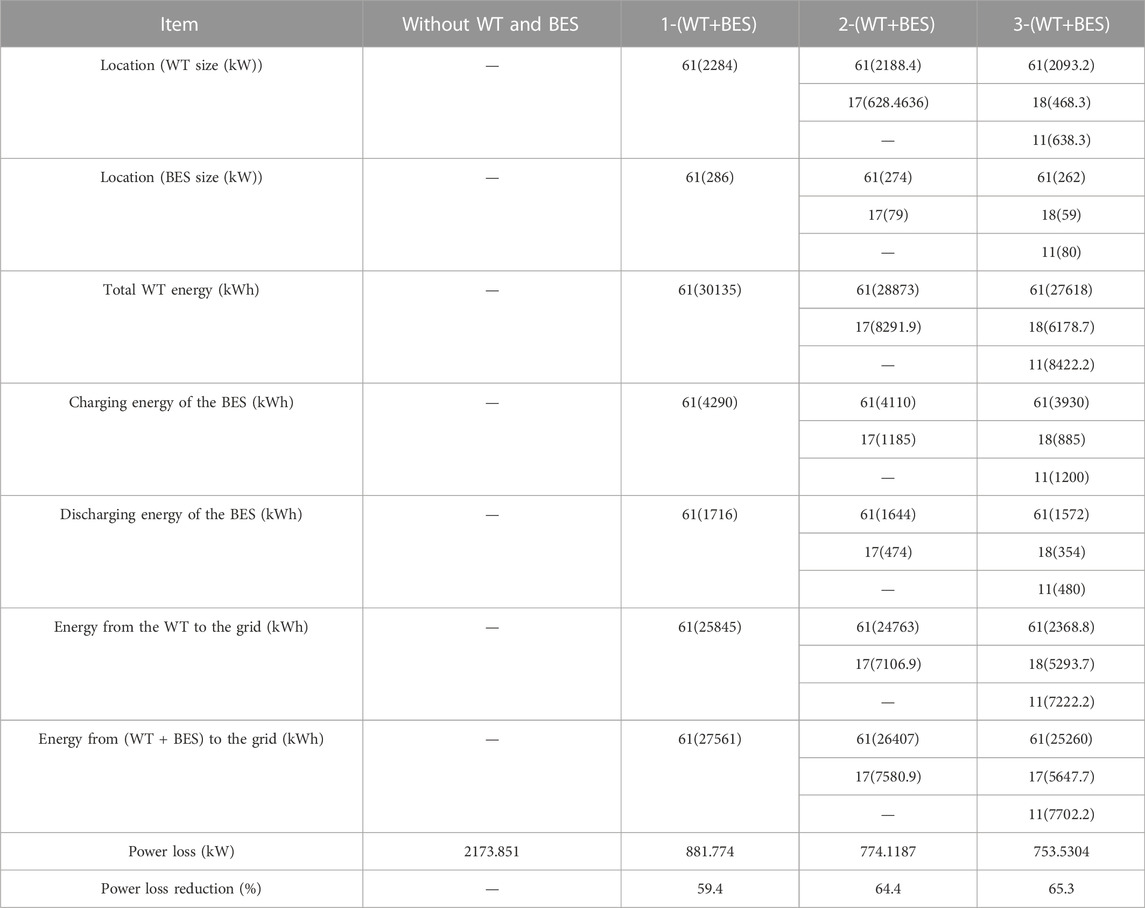
TABLE 4. Results of the optimal allocation of the WT with the BES using the modified BES-optimizer in the RDS.
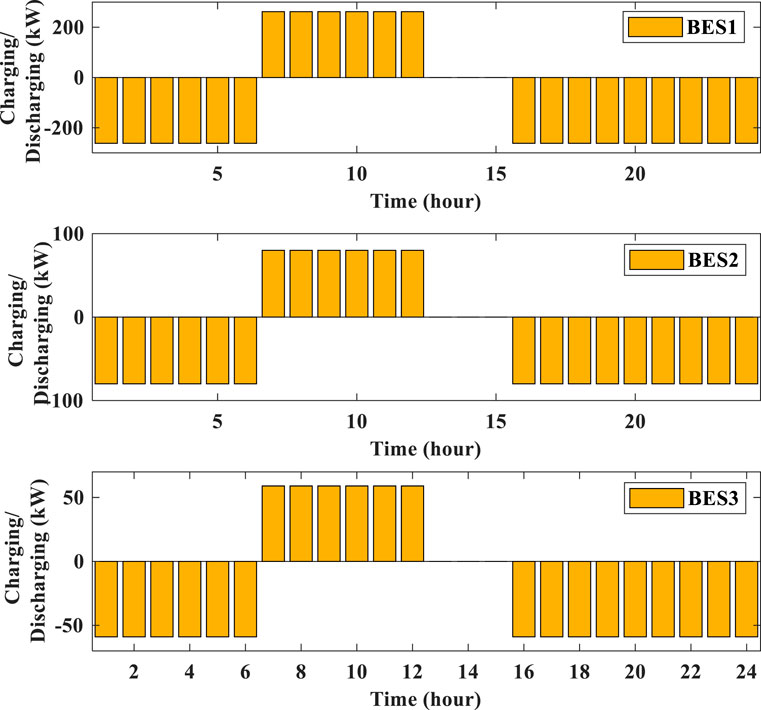
FIGURE 16. Charging and discharging energies of BES1, BES2, and BES3 by installing 3-(WT-BES) in the RDS.
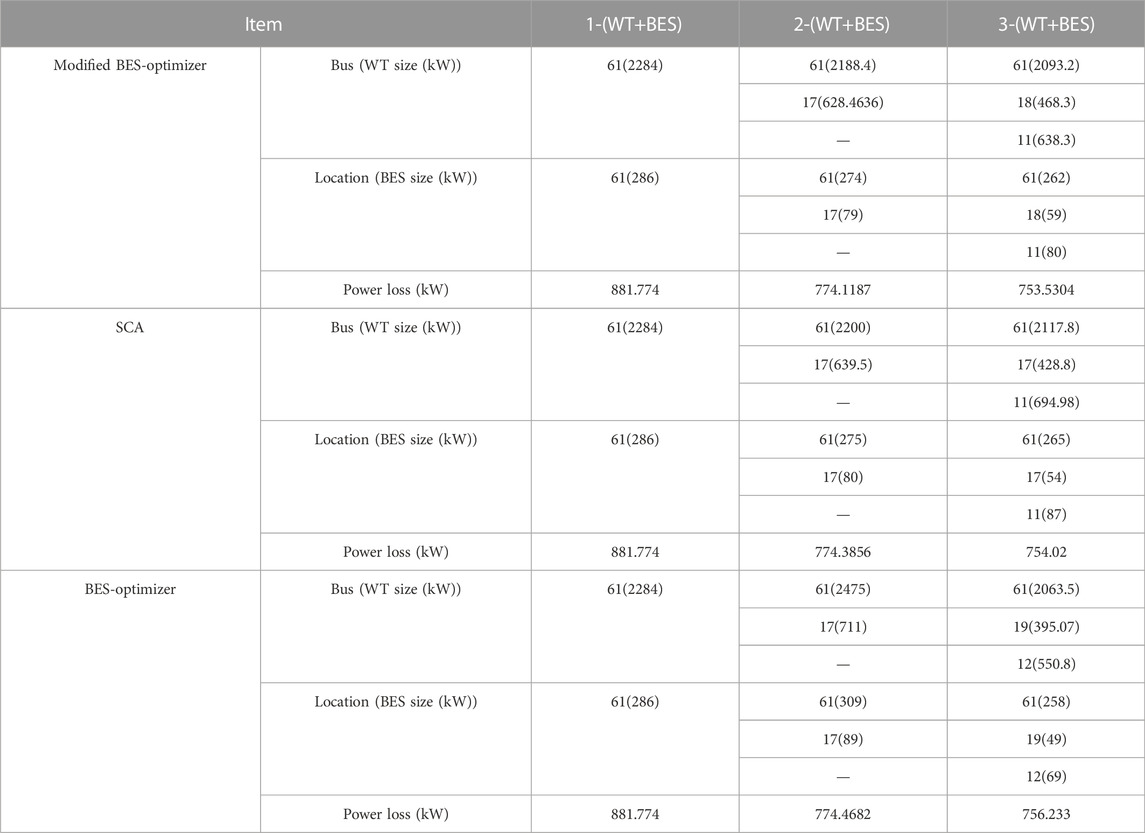
TABLE 5. Comparison among the modified BES-optimizer, SCA, and original BES-optimizer in determining the optimal allocation of the WT with the BES in the RDS.
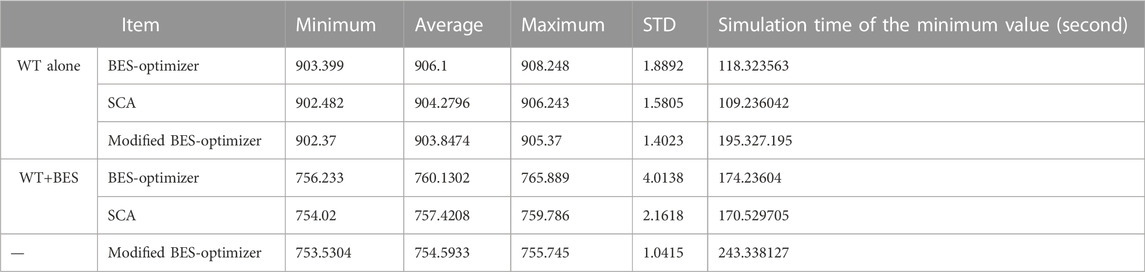
TABLE 6. Statistical results and simulation time of the BES, SCA, and modified-BES algorithms by installing three WTs with and without the BES in the RDS.
In this paper, determining the preferable allocation of the WT alone or simultaneously with the BES in the RDS considering uncertainty of generation and time-varying load has been presented. A modified BES-optimizer has been proposed by inserting the SCA with the original BES-optimizer, with the aim of improving the performance of the original BES. The reduction in total active loss has been presented as a problem formulation, considering system constraints. The results proved that the maximum reduction in the active loss by incorporating one, two, and three WTs alone in RDS are 53.3%, 57.7%, and 58.5%, respectively. However, the maximum reduction in active loss is increased to 59.4%, 64.4%, and 65.3% by integrating one, two, and three WTs with BES, respectively. The performance of the modified BES-optimizer is measured by comparing its results with those obtained by other efficient algorithms such as modified MRFO, SCA, and the original BES-optimizer.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
This project was supported by the Deanship of Scientific Research at Prince Sattam Bin Abdulaziz University under the research project (PSAU-2022/01/19492).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abdel-Mawgoud, H., Ali, A., Kamel, S., Rahmann, C., and Abdel-Moamen, M. (2021). A modified manta ray foraging optimizer for planning inverter-based photovoltaic with battery energy storage system and wind turbine in distribution networks. IEEE Access 9, 91062–91079. doi:10.1109/access.2021.3092145
Abdel-Mawgoud, H., Kamel, S., Khasanov, M., and Khurshaid, T. (2021). A strategy for PV and BESS allocation considering uncertainty based on a modified Henry gas solubility optimizer. Electr. Power Syst. Res. 191, 106886. doi:10.1016/j.epsr.2020.106886
Ahmad, J., Imran, M., Khalid, A., Iqbal, W., Ashraf, S. R., Adnan, M., et al. (2018). Techno economic analysis of a wind-photovoltaic-biomass hybrid renewable energy system for rural electrification: A case study of kallar kahar. Energy 148, 208–234. doi:10.1016/j.energy.2018.01.133
Ali, A., Mahmoud, K., Raisz, D., and Lehtonen, M. (2020). Optimal allocation of inverter-based WTGS complying with their DSTATCOM functionality and PEV requirements. IEEE Trans. Veh. Technol. 69, 4763–4772. doi:10.1109/tvt.2020.2980971
Alsattar, H. A., Zaidan, A., and Zaidan, B. (2020). Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 53, 2237–2264. doi:10.1007/s10462-019-09732-5
Aman, M., Jasmon, G., Bakar, A. H. A., and Mokhlis, H. (2014). A new approach for optimum simultaneous multi-DG distributed generation Units placement and sizing based on maximization of system loadability using HPSO (hybrid particle swarm optimization) algorithm. Energy 66, 202–215. doi:10.1016/j.energy.2013.12.037
Arani, A. K., Gharehpetian, G., and Abedi, M. (2019). Review on energy storage systems control methods in microgrids. Int. J. Electr. power & energy Syst. 107, 745–757. doi:10.1016/j.ijepes.2018.12.040
Ashfaq, A., and Ianakiev, A. (2018). Features of fully integrated renewable energy atlas for Pakistan; wind, solar and cooling. Renew. Sustain. Energy Rev. 97, 14–27. doi:10.1016/j.rser.2018.08.011
Awad, A. S., El-Fouly, T. H., and Salama, M. M. (2014). Optimal ESS allocation and load shedding for improving distribution system reliability. IEEE Trans. Smart Grid 5, 2339–2349. doi:10.1109/tsg.2014.2316197
Bevrani, H., Ghosh, A., and Ledwich, G. (2010). Renewable energy sources and frequency regulation: Survey and new perspectives. IET Renew. Power Gener. 4, 438–457. doi:10.1049/iet-rpg.2009.0049
Biswal, S. R., and Shankar, G. (2018). “Optimal sizing and allocation of capacitors in radial distribution system using sine cosine algorithm,” in 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, December 18–21, 2018, 1–4.
Blum, C., and Roli, A. (2008). “Hybrid metaheuristics: An introduction,” in Hybrid metaheuristics (Germany: Springer), 1–30.
Carrano, E. G., Guimarães, F. G., Takahashi, R. H., Neto, O. M., and Campelo, F. (2007). Electric distribution network expansion under load-evolution uncertainty using an immune system inspired algorithm. IEEE Trans. Power Syst. 22, 851–861. doi:10.1109/tpwrs.2007.894847
Chedid, R., and Sawwas, A. (2019). Optimal placement and sizing of photovoltaics and battery storage in distribution networks. Energy Storage 1, e46. doi:10.1002/est2.46
Das, C., and Alam, M. (2012). “An innovative Energy Neutral Home system for rural areas of Bangladesh,” in 2012 7th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, December 20–22, 2012, 888–891.
Das, C., Ehsan, M., Kader, M., Alam, M., and Shafiullah, G. (2016). A practical biogas based energy neutral home system for rural communities of Bangladesh. J. Renew. Sustain. Energy 8, 023101. doi:10.1063/1.4942783
Das, C., Hossain, S. M., and Hossan, M. (2013). “Introducing speed breaker as a power generation unit for minor needs,” in 2013 International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, May 17–18, 2013, 1–6.
Das, C., Kader, M., and Alam, M. (2013). Design and implementation of a hybrid energy neutral home system for Bangladesh. Int. J. Renew. Energy Resour. 3, 66–72.
Das, C. K., Bass, O., Kothapalli, G., Mahmoud, T. S., and Habibi, D. (2018). Optimal placement of distributed energy storage systems in distribution networks using artificial bee colony algorithm. Appl. energy 232, 212–228. doi:10.1016/j.apenergy.2018.07.100
Das, C. K., Bass, O., Kothapalli, G., Mahmoud, T. S., and Habibi, D. (2018). Overview of energy storage systems in distribution networks: Placement, sizing, operation, and power quality. Renew. Sustain. Energy Rev. 91, 1205–1230. doi:10.1016/j.rser.2018.03.068
De Sisternes, F. J., Jenkins, J. D., and Botterud, A. (2016). The value of energy storage in decarbonizing the electricity sector. Appl. Energy 175, 368–379. doi:10.1016/j.apenergy.2016.05.014
Duan, H., Yu, Y., Zhang, X., and Shao, S. (2010). Three-dimension path planning for UCAV using hybrid meta-heuristic ACO-DE algorithm. Simul. Model. Pract. Theory 18, 1104–1115. doi:10.1016/j.simpat.2009.10.006
Duan, H., Zhao, W., Wang, G., and Feng, X. (2012). Test-sheet composition using analytic hierarchy process and hybrid metaheuristic algorithm TS/BBO. Math. Problems Eng. 2012.
Ehrgott, M., and Gandibleux, X. (2008). “Hybrid metaheuristics for multi-objective combinatorial optimization,” in Hybrid metaheuristics (Germany: Springer), 221–259.
Elgamal, Z. M., Yasin, N. B. M., Tubishat, M., Alswaitti, M., and Mirjalili, S. (2020). An improved harris hawks optimization algorithm with simulated annealing for feature selection in the medical field. IEEE Access 8, 186638–186652. doi:10.1109/access.2020.3029728
Eminoglu, U., and Hocaoglu, M. H. (2008). Distribution systems forward/backward sweep-based power flow algorithms: A review and comparison study. Electr. Power Components Syst. 37, 91–110. doi:10.1080/15325000802322046
Fathy, A., and Abdelaziz, A. Y. (2017). Grey wolf optimizer for optimal sizing and siting of energy storage system in electric distribution network. Electr. Power Components Syst. 45, 601–614. doi:10.1080/15325008.2017.1292567
Gan, W., Ai, X., Fang, J., Yan, M., Yao, W., Zuo, W., et al. (2019). Security constrained co-planning of transmission expansion and energy storage. Appl. energy 239, 383–394. doi:10.1016/j.apenergy.2019.01.192
Go, R. S., Munoz, F. D., and Watson, J.-P. (2016). Assessing the economic value of co-optimized grid-scale energy storage investments in supporting high renewable portfolio standards. Appl. energy 183, 902–913. doi:10.1016/j.apenergy.2016.08.134
Hlal, M. I., Ramachandaramurthya, V. K., Padmanaban, S., Kaboli, H. R., Pouryekta, A., Bin, T. A. R., et al. (2019). NSGA-II and MOPSO based optimization for sizing of hybrid PV/wind/battery energy storage system. Int. J. Power Electron. Drive Syst. 10, 463. doi:10.11591/ijpeds.v10.i1.pp463-478
Holden, N., and Freitas, A. A. (2008). A hybrid PSO/ACO algorithm for discovering classification rules in data mining. J. Artif. Evol. Appl. 2008, 1–11. doi:10.1155/2008/316145
Hossain, S. M., Das, C., Hossan, M. S., and Jarin, S. (2015). Electricity from wasted energy of the moving vehicle using speed breaker. J. Teknol. 73. doi:10.11113/jt.v73.3256
Islam, M., Alam, A. M. S., and Das, C. (2015). “Multi-agent system modeling for managing limited distributed generation of microgrid,” in 2015 2nd International Conference on Electrical Information and Communication Technologies (EICT), Khulna, Bangladesh, December 10–12, 2015, 533–538.
Kalkhambkar, V., Kumar, R., and Bhakar, R. (2017). “Joint optimal sizing and placement of renewable distributed generation and energy storage for energy loss minimization,” in 2017 4th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, January 6–7, 2017, 1–9.
Kasturi, K., and Nayak, M. R. (2017). “Optimal planning of charging station for EVs with PV-BES unit in distribution system using WOA,” in 2017 2nd International Conference on Man and Machine Interfacing (MAMI), Bhubaneswar, India, December 21-23, 2017, 1–6.
Khaki, B., and Das, P. (2019). "Sizing and placement of battery energy storage systems and wind turbines by minimizing costs and system losses," arXiv preprint arXiv:1903.12029.
Khoubseresht, O., and Shayanfar, H. (2020). The role of demand response in optimal sizing and siting of distribution energy resources in distribution network with time-varying load: An analytical approach. Electr. Power Syst. Res. 180, 106100. doi:10.1016/j.epsr.2019.106100
Li, X., Campana, P. E., Li, H., Yan, J., and Zhu, K. (2017). Energy storage systems for refrigerated warehouses. Energy Procedia 143, 94–99. doi:10.1016/j.egypro.2017.12.653
Lin, W.-Y. (2010). A GA–DE hybrid evolutionary algorithm for path synthesis of four-bar linkage. Mech. Mach. Theory 45, 1096–1107. doi:10.1016/j.mechmachtheory.2010.03.011
Lin, Y., Johnson, J. X., and Mathieu, J. L. (2016). Emissions impacts of using energy storage for power system reserves. Appl. energy 168, 444–456. doi:10.1016/j.apenergy.2016.01.061
Liu, J., Yao, W., Wen, J., Fang, J., Jiang, L., He, H., et al. (2019). Impact of power grid strength and PLL parameters on stability of grid-connected DFIG wind farm. IEEE Trans. Sustain. Energy 11, 545–557. doi:10.1109/tste.2019.2897596
Lopez, E., Opazo, H., Garcia, L., and Bastard, P. (2004). Online reconfiguration considering variability demand: Applications to real networks. IEEE Trans. Power Syst. 19, 549–553. doi:10.1109/tpwrs.2003.821447
Ludin, N. A., Mustafa, N. I., Hanafiah, M. M., Ibrahim, M. A., Teridi, M. A. M., Sepeai, S., et al. (2018). Prospects of life cycle assessment of renewable energy from solar photovoltaic technologies: A review. Renew. Sustain. Energy Rev. 96, 11–28. doi:10.1016/j.rser.2018.07.048
Marini, A., Latify, M. A., Ghazizadeh, M. S., and Salemnia, A. (2015). Long-term chronological load modeling in power system studies with energy storage systems. Appl. Energy 156, 436–448. doi:10.1016/j.apenergy.2015.07.047
Mazumder, P., Jamil, M. H., Das, C., and Matin, M. (2014). “Hybrid energy optimization: An ultimate solution to the power crisis of St. Martin Island, Bangladesh,” in 2014 9th International Forum on Strategic Technology (IFOST), Cox’s Bazar, Bangladesh, October 21-23, 2014, 363–368.
Mirjalili, S. (2016). SCA: A sine cosine algorithm for solving optimization problems. Knowledge-based Syst. 96, 120–133. doi:10.1016/j.knosys.2015.12.022
Mousavi, N., Kothapalli, G., Habibi, D., Khiadani, M., and Das, C. K. (2019). An improved mathematical model for a pumped hydro storage system considering electrical, mechanical, and hydraulic losses. Appl. energy 247, 228–236. doi:10.1016/j.apenergy.2019.03.015
Murty, V., and Kumar, A. (2020). Retraction Note: Multi-objective energy management in microgrids with hybrid energy sources and battery energy storage systems. Prot. Control Mod. Power Syst. 5, 11–20. doi:10.1186/s41601-022-00229-y
Nemati, S., Basiri, M. E., Ghasem-Aghaee, N., and Aghdam, M. H. (2009). A novel ACO–GA hybrid algorithm for feature selection in protein function prediction. Expert Syst. Appl. 36, 12086–12094. doi:10.1016/j.eswa.2009.04.023
Nemet, A., Klemeš, J. J., Duić, N., and Yan, J. (2016). Improving sustainability development in energy planning and optimisation, 184. Netherland: Elsevier, 1241–1245.
Nick, M., Cherkaoui, R., and Paolone, M. (2015). Optimal siting and sizing of distributed energy storage systems via alternating direction method of multipliers. Int. J. Electr. Power & Energy Syst. 72, 33–39. doi:10.1016/j.ijepes.2015.02.008
Niu, B., and Li, L. (2008). “A novel PSO-DE-based hybrid algorithm for global optimization,” in International conference on intelligent computing, Shanghai, China, September 15–18, 2008, 156–163.
Ogunjuyigbe, A., Ayodele, T., and Akinola, O. (2016). Optimal allocation and sizing of PV/Wind/Split-diesel/Battery hybrid energy system for minimizing life cycle cost, carbon emission and dump energy of remote residential building. Appl. Energy 171, 153–171. doi:10.1016/j.apenergy.2016.03.051
Parra, D., Norman, S. A., Walker, G. S., and Gillott, M. (2017). Optimum community energy storage for renewable energy and demand load management. Appl. energy 200, 358–369. doi:10.1016/j.apenergy.2017.05.048
Parra, D., Norman, S. A., Walker, G. S., and Gillott, M. (2016). Optimum community energy storage system for demand load shifting. Appl. Energy 174, 130–143. doi:10.1016/j.apenergy.2016.04.082
Peng, X., Yao, W., Yan, C., Wen, J., and Cheng, S. (2019). Two-stage variable proportion coefficient based frequency support of grid-connected DFIG-WTs. IEEE Trans. Power Syst. 35, 962–974. doi:10.1109/tpwrs.2019.2943520
Saboori, H., Hemmati, R., and Jirdehi, M. A. (2015). Reliability improvement in radial electrical distribution network by optimal planning of energy storage systems. Energy 93, 2299–2312. doi:10.1016/j.energy.2015.10.125
Sahoo, N., and Prasad, K. (2006). A fuzzy genetic approach for network reconfiguration to enhance voltage stability in radial distribution systems. Energy Convers. Manag. 47, 3288–3306. doi:10.1016/j.enconman.2006.01.004
Sardi, J., Mithulananthan, N., Gallagher, M., and Hung, D. Q. (2017). Multiple community energy storage planning in distribution networks using a cost-benefit analysis. Appl. energy 190, 453–463. doi:10.1016/j.apenergy.2016.12.144
Schienbein, L. A., and DeSteese, J. G. (2002). Distributed energy resources, power quality and reliability-Background. Richland, WA (United States): Pacific Northwest National Lab.PNNL.
Shi, X., Liang, Y., Lee, H., Lu, C., and Wang, L. (2005). An improved GA and a novel PSO-GA-based hybrid algorithm. Inf. Process. Lett. 93, 255–261. doi:10.1016/j.ipl.2004.11.003
Solomon, A., Kammen, D. M., and Callaway, D. (2014). The role of large-scale energy storage design and dispatch in the power grid: A study of very high grid penetration of variable renewable resources. Appl. Energy 134, 75–89. doi:10.1016/j.apenergy.2014.07.095
Sun, K., Yao, W., Fang, J., Ai, X., Wen, J., and Cheng, S. (2019). Impedance modeling and stability analysis of grid-connected DFIG-based wind farm with a VSC-HVDC. IEEE J. Emerg. Sel. Top. Power Electron. 8, 1375–1390. doi:10.1109/jestpe.2019.2901747
Teng, J.-H., Luan, S.-W., Lee, D.-J., and Huang, Y.-Q. (2012). Optimal charging/discharging scheduling of battery storage systems for distribution systems interconnected with sizeable PV generation systems. IEEE Trans. Power Syst. 28, 1425–1433. doi:10.1109/tpwrs.2012.2230276
Van Der Stelt, S., AlSkaif, T., and van Sark, W. (2018). Techno-economic analysis of household and community energy storage for residential prosumers with smart appliances. Appl. Energy 209, 266–276. doi:10.1016/j.apenergy.2017.10.096
Wang, G.-G., Gandomi, A. H., and Alavi, A. H. (2014). An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model. 38, 2454–2462. doi:10.1016/j.apm.2013.10.052
Wang, G.-G., Gandomi, A. H., Alavi, A. H., and Hao, G.-S. (2014). Hybrid krill herd algorithm with differential evolution for global numerical optimization. Neural Comput. Appl. 25, 297–308. doi:10.1007/s00521-013-1485-9
Wang, G.-G., Gandomi, A. H., Yang, X.-S., and Alavi, A. H. (2016). A new hybrid method based on krill herd and cuckoo search for global optimisation tasks. Int. J. Bio-Inspired Comput. 8, 286–299. doi:10.1504/ijbic.2016.10000414
Wang, G., and Guo, L. (2013). A novel hybrid bat algorithm with harmony search for global numerical optimization. J. Appl. Math. 2013, 1–21. doi:10.1155/2013/696491
Wang, G., Guo, L., Duan, H., Wang, H., Liu, L., and Shao, M. (2012). A hybrid metaheuristic DE/CS algorithm for UCAV three-dimension path planning. Sci. World J. 2012, 1–11. doi:10.1100/2012/583973
Wang, G., Guo, L., Duan, H., Wang, H., Liu, L., and Shao, M. (2013). Hybridizing harmony search with biogeography based optimization for global numerical optimization. J. Comput. Theor. Nanosci. 10, 2312–2322. doi:10.1166/jctn.2013.3207
Wen, S., Lan, H., Fu, Q., David, C. Y., and Zhang, L. (2014). Economic allocation for energy storage system considering wind power distribution. IEEE Trans. power Syst. 30, 644–652. doi:10.1109/tpwrs.2014.2337936
Wong, L. A., Ramachandaramurthy, V. K., Walker, S. L., Taylor, P., and Sanjari, M. J. (2019). Optimal placement and sizing of battery energy storage system for losses reduction using whale optimization algorithm. J. Energy Storage 26, 100892. doi:10.1016/j.est.2019.100892
Yan, J., Sun, F., Choug, S., Desideri, U., Li, H., Campana, P., et al. (2017). Transformative innovations for a sustainable future-Part II.
Zhang, Y., Campana, P. E., Lundblad, A., and Yan, J. (2017). Comparative study of hydrogen storage and battery storage in grid connected photovoltaic system: Storage sizing and rule-based operation. Appl. energy 201, 397–411. doi:10.1016/j.apenergy.2017.03.123
Zhang, Y., Lundblad, A., Campana, P. E., Benavente, F., and Yan, J. (2017). Battery sizing and rule-based operation of grid-connected photovoltaic-battery system: A case study in Sweden. Energy Convers. Manag. 133, 249–263. doi:10.1016/j.enconman.2016.11.060
Zhang, Y., Lundblad, A., Campana, P. E., and Yan, J. (2016). Employing battery storage to increase photovoltaic self-sufficiency in a residential building of Sweden. Energy Procedia 88, 455–461. doi:10.1016/j.egypro.2016.06.025
Zhu, K., Li, X., Campana, P. E., Li, H., and Yan, J. (2018). Techno-economic feasibility of integrating energy storage systems in refrigerated warehouses. Appl. energy 216, 348–357. doi:10.1016/j.apenergy.2018.01.079
ACO-DE Ant colony optimization–differential evolution
BBKH Biogeography-based krill herd
CSKH Cuckoo search krill herd
GA-DE Genetic algorithm–differential evolution
ACO-DE Ant colony optimization–differential evolution
GA Genetic algorithm
ABC Artificial bee colony
GWO Gray wolf optimizer
PSO-ACO Particle swarm optimization–ant colony optimization
GA Genetic algorithm
PSO-GA Particle swarm optimization–genetic algorithm
PSO Particle swarm optimization
PSO-DE Particle swarm optimization-differential evolution
ACO-GA Ant colony optimization–genetic algorithm
Modified HGSO Modified Henry gas solubility optimization
SCA Sine cosine algorithm
BES-Optimizer Bald eagle search optimizer
RDS Radial distribution system
BES Battery energy storage
WT Wind turbine
PV Photovoltaic
NBES Set of BESs in the RDS
NWT Set of WTs in the RDS
NL Set of branches in the RDS
NB Set of buses in the RDS
s Index of BESs
n Index of WTs
L Index of branches in the RDS
b Index of buses in the RDS
QL,d+1, PL,d+1 The reactive and active loads at bus d+1
Xd,d+1, Rd,d+1 The reactance and resistance among buses d and d+1
IN,L The high limiting current of branch (L)
PWT,U, PWT,L The upper and lower values of the WT output power
VN, Vn The maximum and minimum allowable operating bus voltage
Hbest, Hi Represent the best and current position
r1, r2, r3, r4 Represent a random number among [0,1]
R Represents a parameter that equals a value between 0.5 and 2
a Represents a parameter that equals a value between 5 and 10
∝ Represents a number between 1.5 and 2
r Represents a random number among [0,1]
Prated, Dm Rated power and the average velocity of the WT
Dr Rated velocity of the WT
Dco, Dci Cut-off and cut-in velocities of the WT
δs, ρs Standard deviation and mean of the wind velocity
a, w Shape and scale parameters of Weibull function
nQ Reactive load modeling voltage index
nP Active load modeling voltage index
Pdischarge The discharging power rate of the BES
Pcharge The charging power rate of the BES
IL The current in the branch (L)
Psubstation, Qsubstation The injected active and reactive power from substation
PWT, PBES The generated active power of the WT and BES
Vd, Vd+1 The voltage value of bus d and bus d+1
Qd, Pd The reactive power and real power among buses d and d+1
Ploss(z) Represents the power losses at branch z
fob The main objective function
f (D) The Weibull probability density function of the wind speed (D)
Keywords: distribution systems, renewable energy, wind turbine, battery energy storage, uncertainty, optimization
Citation: Kamel S, Abdel-Mawgoud H, Alrashed MM, Nasrat L and Elnaggar MF (2023) Optimal allocation of a wind turbine and battery energy storage systems in distribution networks based on the modified BES-optimizer. Front. Energy Res. 11:1100456. doi: 10.3389/fenrg.2023.1100456
Received: 16 November 2022; Accepted: 05 January 2023;
Published: 27 January 2023.
Edited by:
Lorenzo Ferrari, University of Pisa, ItalyReviewed by:
Yashwant Sawle, Madhav Institute of Technology & Science Gwalior, IndiaCopyright © 2023 Kamel, Abdel-Mawgoud, Alrashed, Nasrat and Elnaggar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohammed M. Alrashed, bW0uYWxyYXNoZWRAcHNhdS5lZHUuc2E=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.