Estimation of biases and uncertainties on PWR nuclide inventories for severe accidents analyses

The work presented in this paper deals with bias and uncertainty quantification on nuclear fuel inventory in a pressurized water reactors core during normal operation. This actinides and fission products inventory is used as input data for radiological releases evaluation in case of a severe accident. The different sources of bias and uncertainty, as well as their impacts for UO₂ and MOX fuel at the assembly and core levels, are discussed. Uncertainty sources include technological uncertainties (e.g. dimensions, irradiation history, temperatures), modeling assumptions, uncertainties related to the resolution methods used in the calculation tools and nuclear data uncertainties. For each source of uncertainty investigated in this paper, an evaluation of the associated biases and uncertainties on nuclide inventory is performed. It is shown that, among the sources of bias and uncertainties studied, spread due to nuclear data as well as the bias and uncertainties due to “infinite lattice approximation” are the most significant ones, for the isotopes of interest.

1 Introduction

Nuclide inventory is an important quantity for the characterization of spent nuclear fuel. Moreover, it contains the amount of fission products (FP) present in the core at the initial time of a hypothetical severe accident leading to core fusion and radiological release. Thus, this inventory is of great importance for the radiological release estimation necessary for severe accident management and emergency response. Therefore, it is crucial to accurately estimate radionuclide inventory, as well as the uncertainties associated with this inventory. Furthermore, it should be stressed that the estimation of uncertainties associated with in-core isotopic inventories is a vast and non-trivial subject [1] [2]. Indeed, the calculations of nuclear fuel depletion under irradiation require complex simulations, which include many sources of bias and uncertainty. The work presented in this paper assesses the impact of the main sources of uncertainty affecting the calculation of isotopic concentrations in pressurized water reactor cores but does not claim to be exhaustive. The notions of bias and uncertainty relating to isotopic inventories are differentiated in several situations.

- technological uncertainties (manufacturing tolerances, moderator and fuel temperatures, etc.) and uncertainties in operational history;

- uncertainties and biases due to the approximations in the model;

- uncertainties related to the unreliability of nuclear data.

The impact of these different sources of bias and uncertainty on the assessment of the nuclide inventory, at the assembly and core levels, is evaluated for two types of fuel mainly used in the French nuclear power plants (UO₂ and MOX). The analysis of the results has been performed on a list of 47 nuclides, usually used at IRSN for the assessment of the radiological consequences of severe accidents, presented in Supplementary Appendix S1. This list of radionuclides has been selected for their contribution to residual power or radiological source term and extracted from reference [3] Table 2. B.3, except ⁵⁸Co, ⁶⁰Co, ⁸⁶Rb, ⁹¹Sr, ¹²⁷Te, ¹²⁹Te, ^131mTe which are negligible contributors to health effects or unavailable in CASMO outputs.

It should be noted that among the sources of uncertainty that may have a significant impact on the core inventory, some of potential sources have not been investigated. These include, for example, the impact of power fluctuations during the irradiation cycle that have a strong impact on the short-lived isotope concentrations. However, the nominal power simulation usually tends to maximize their concentration, so that the approach is considered as conservative in terms of safety. Moreover, concerning nuclear data uncertainties, a very simple approach has been used as a first approximation, instead of a complete uncertainty propagation.

2 Methodology

Time evolution of isotope inventory, particularly fuel composition, is calculated from the Bateman equation (see Eq. 1), in which the variation of the quantity N_i of a nuclide i over a period Δt is a balance between its disappearance and its creation by decay or neutron interaction of some other nuclides j. Solution to the Bateman equation requires the calculation, usually using the Boltzmann (or transport) equation, of the neutron spectrum ϕ(E,t) at each time step, which depends on the medium and its composition. Solving this equation therefore requires the nuclear radioactive decay data λ and the effective cross sections σ for all isotopes and reactions.

$\frac{\mathit{d}{\mathit{N}}_{\mathit{i}}}{\mathit{d}\mathit{t}}=-\left({\mathit{\lambda }}_{\mathit{i}}+〈{\mathit{\sigma }}_{\mathit{i},r}〉\bullet \mathit{\varphi }\right)\bullet {\mathit{N}}_{\mathit{i}}+{\displaystyle \sum }_{\mathit{j}\ne \mathit{i}}\left({\mathit{\lambda }}_{\mathit{j}\to \mathit{i}}+〈{\mathit{\sigma }}_{\mathit{j},\mathit{r}\to \mathit{i}}〉\bullet \mathit{\varphi }\right)\bullet {\mathit{N}}_{\mathit{j}}(1)$

In practice, the fuel depletion is calculated with simulation codes which iterate between a transport calculation to determine the neutron spectrum ϕ(E,t) and the energy-averaged cross sections ⟨σ_k⟩, and a depletion calculation which solves the Bateman equation to determine a new material composition at the next time step. Nevertheless, the transport calculation method, as well as the method used to solve the Bateman equation, may differ depending on the calculation tool.

2.1 Neutronics codes used for the inventory calculations

A short overview of the VESTA and CASMO5 codes as used in the study presented in this paper is described in this section. VESTA and CASMO5 are representative of the two main types of codes for calculating the isotopic concentration of fuel under irradiation and represent the state of the art in neutronics calculation tools. The VESTA code relies on the Monte-Carlo method, whereas the CASMO5 code uses a deterministic approach.

2.1.1 VESTA

VESTA [4] is a computer tool developed at IRSN, which couples a Monte Carlo neutron transport code with a depletion module. In VESTA, the Boltzmann and Bateman equations are coupled and form a closed and complete system of equations that describes the transport of particles as a function of time. It iterates between a Monte Carlo steady state transport calculation and a depletion calculation which solves the Bateman equations using the data (flux, reaction rates) derived by the transport calculation to calculate the isotopic concentrations. VESTA allows therefore the depletion of materials for different geometrical scales, and the calculation of the material isotopic compositions during irradiation at the pin cell level of the assembly.

The last release of the code, VESTA 2.2 [4], uses the MCNP6 [5] code coupled to the PHOENIX depletion module. VESTA 2.2 has been validated [6] [7] [8] for isotopic inventory calculations (for 90 isotopes) from 53 samples of radiochemical measurements and 52 PWR UO₂ assembly decay heat measurements, using the JEFF-3.1 [9], JEFF-3.2 [10], ENDF/B-VII.0 [11] and ENDF/B-VII.1 [12] nuclear data libraries. The validation database contains a wide variety of reactors (PWR, BWR, VVER) and fuel (UO₂, MOX) types with and without burnable absorbers.

2.1.2 CASMO5

CASMO5 [13] is a deterministic code developed by Studsvik Scandpower Inc. Company. It is a multi-group two-dimensional lattice and depletion code based on the Method of Characteristics (MoC) transport calculation. It uses 586 neutron groups for the 1D collision-probability-based pin cell calculations and a few energy groups for the MoC calculation (19 groups for UO₂ fuel and 35 groups for MOX fuel). In particular, the CASMO5 multi-assembly capability (MxN) has been used for color-set and full core calculations. This feature allows 2D full core plane (or a smaller pattern) modeling with the same transport theory methodology (MoC) as the single assembly (SA) calculations. In addition, it also allows for accurate modeling of the radial reflector. The CASMO5 default burnup mesh was used for the calculations¹. For all the SA, color-set and full core calculations presented in this paper, the default options of CASMO5 have been considered, except for the following options which were used and are not part of the default options.

- Consideration of “extended” decay chains for both heavy nuclides and fission products;

- Consideration of the maximum number of isotopes in the output listing.

In addition, to allow consistent comparisons with the VESTA calculation tool, the fourth-order Runge-Kutta-Fehlberg depletion solver has been turned on and the effective Doppler temperature model and the CASMO5 resonance up-scattering model have been turned off. Finally, the MCNP input files used for the VESTA calculations have been generated with a dedicated CASMO option.

All the CASMO5 calculations used in this study have been performed with the ENDF/B-VII.1 library, in the so called “202 neutron data library” of CASMO5 version 3.01.

2.2 Selected isotopes

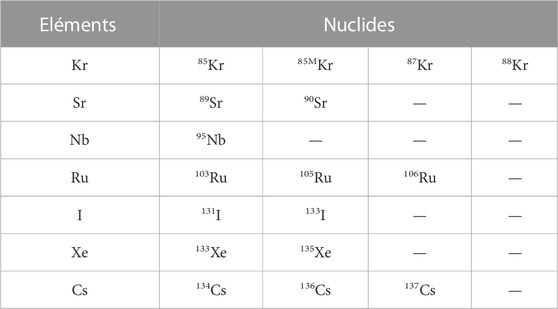
A list of 47 radionuclides of interest, considered in severe accidents studies at IRSN, is presented in Supplementary Appendix S1. These nuclides are selected for their contribution to residual power and to radiological release impact on the installation and the environment (dose, fission product release, etc.). Among those, a sub-list of “main” nuclides (main contributors to radiological impact) was defined (see Table 1) including nuclides of Kr, Sr, Nb, Ru, I, Xe and Cs elements.

TABLE 1

TABLE 1. List of 17 “main” radionuclides for severe accidents analysis.

2.3 Methodology for the biases and uncertainties estimations

As presented above, different bias and uncertainty sources are to be considered in the assessment of reactor core isotopic concentrations. It is therefore complex to estimate these uncertainties and biases simultaneously in a comprehensive study. For this reason, this paper presents separately the different sources which are therefore considered hereafter as independent and uncorrelated.

About uncertainties due to nuclear data, a rigorous evaluation of the impact of nuclear data uncertainties would require appropriate tools (still under development) to propagate these uncertainties through all the calculation chain, from evaluated nuclear data to depleted core inventory computations. Nevertheless, this study considers a wide source of uncertainties in order to establish which uncertainties are sensitive on isotopic inventories for radiological releases estimations in case of a severe accident. This objective leads to the adopt a simplified approach for nuclear data as a first step. With this approach, only a spread of results between available libraries has been evaluated.

Depending on the sources, the uncertainties have been studied with the most suitable calculation code in terms of calculation time or required resources. For example, the simplified approach on nuclear data uses VESTA code with distinct nuclear data libraries, as it can use a large number of continuous energy² nuclear data libraries. Conversely, the estimation of uncertainties and biases associated with the technological uncertainties and the modeling biases, which require the simulation of many configurations, have been studied with CASMO5. Finally, in order to estimate the bias due to the resolution method on calculated isotopic compositions, inter-code comparison has been performed. For clarity reasons, the uncertainties and biases are presented for three different burnup values. At the assembly level, the selected burnup values correspond to the beginning of life (BOL), middle of life (MOL) and end of life (EOL of the assembly, i.e. at about 1, 30 and 59 GWd/t. Similarly, at the core level, the considered burnup values correspond to the beginning (beginning of post-refueling irradiation, noted BOC thereafter), middle (MOC) and end of cycle (before shutdown for refueling, noted EOC thereafter), i.e. approximately 1, 7 and 15 GWd/t depending of the fuel management.

3 Data and modeling

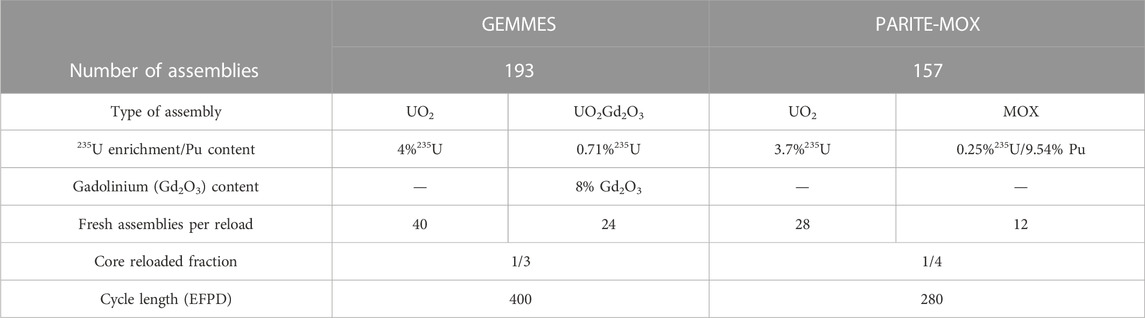
The fuels and fuel patterns modeled for full core calculations are those of the GEMMES and PARITE-MOX fuel management used by EDF (Électricité de France) on the equilibrium cycles ([14-17]). They are respectively applied to 1,300 and 900 MWe PWR (pressurized water reactors). Table 2 shows the main information about these fuel management options. Furthermore, for single assembly and color-set calculations, two fuel types are studied: one UO₂ fuel case enriched to 3.7% ²³⁵U and a MOX NT (MOX “Nouvelle Teneur”) fuel case with a plutonium content of 9.54%. The main characteristics of these fuels are summarized in Table 3, which shows the geometrical characteristics of each type of fuel assembly, including the dimensions of the rods, guide tubes and fuel pellets.

TABLE 2

TABLE 2. General data on GEMMES and PARITE-MOX fuel management.

TABLE 3

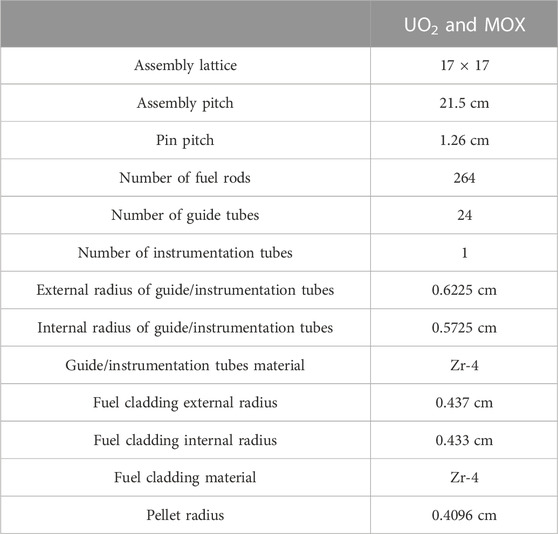
TABLE 3. Geometrical input data for both UO₂ and MOX assemblies extracted from [14].

The VESTA 2.2 assembly modeling of the UO₂ and MOX cases has been carried out in accordance with the experimental validation procedure [6], namely.

- Modeling of a 17 × 17 assembly in an infinite environment;

- Model considered as “2D”, using one axial depletion zone (active length of 1 m);

- Each fuel rod is depleted independently of the others;

- Constant boron concentration (600 ppm for the UOX and MOX cases) during irradiation;

- Constant and homogeneous temperatures:

• 900 K for the fuel;

• 600 K for the moderator and fuel cladding.

- The burnup steps length is 1 GWd/t.

In addition, the number of neutrons simulated in the Monte Carlo calculations is an important input data as it drives the statistical uncertainty of the results. In the context of this paper, the simulated neutron histories are respectively higher than 4×10⁷ for the modeling of one assembly and 9×10⁶ for one-eighth of an assembly. All the continuous energy libraries used by VESTA are processed at IRSN into the ACE format at different temperatures with the GAIA1 [18] nuclear data processing code from IRSN, which relies on NJOY [19].

For comparison purposes, the CASMO5 modeling follows, as far as possible, the VESTA modeling. Nevertheless, for CASMO, the fuel and moderator temperatures correspond to the nominal operating conditions of the reactors, i.e. 873.15 K and 579.15 K respectively. It should be noted that these slight differences between CASMO5 and VESTA 2.2 are not significant to question the validity of the results, especially for the isotopes of interest which are fission products and thus less impacted by neutron thermalization.

4 Uncertainties on nuclide inventories at the assembly level

In this section, for each source of uncertainty and bias previously mentioned, CASMO5 and VESTA 2.2 have been used to compute the isotopic concentrations for the two fuel assembly types described in Section 3, which are considered representative of the French PWR reactors.

In the following, bias and uncertainties below 5% will be considered as not important in view of the radiological context we are considering.

4.1 Statistical uncertainties estimation

The Monte-Carlo method inherently involves statistical uncertainties and for depletion calculations the statistical uncertainties from static calculations are propagated throughout the irradiation of the fuel. In order to evaluate this uncertainty on the nuclide inventories calculated with VESTA code, 50 independent calculations have been performed with different initial random seeds. In this study, the uncertainty retained, ${\sigma }_{Stat}^i$, is the standard deviation of the dispersion for each isotope at each burnup step. It should be noted that this uncertainty depends on the number of simulated neutron histories and on the modeling used in these calculations (geometry, materials...).

The analysis of the standard deviations, obtained from 50 independent VESTA calculations, shows ${\sigma }_{Stat}^i$ values well below 1% for most of the studied isotopes for the two fuel types. The largest standard deviation is of the order of 0.34% and is associated with ²³⁷U and ²³⁸Np at the beginning of irradiation. The results obtained for UO₂ fuel are comparable to the uncertainties of the MOX. In conclusion, the statistical uncertainties associated with the VESTA calculations performed in these studies are not significant and are considered as negligible in the following.

4.2 Spread due to nuclear data libraries

Nuclear data (cross sections, decay data, number of neutrons emitted per fission, etc.) used by the codes are not perfectly known. They depend on experimental measurements and adjustments based on theoretical models and are time-to-time updated following the state of the art. Nuclear data are thus always subject to uncertainty. It is a source of uncertainty that is inherent to the calculation, which cannot be avoided and must be evaluated and controlled as accurately as possible.

In this paper, only a spread of the results due to the use of different nuclear data libraries is presented, based on the comparison of results separately obtained with the VESTA 2.2 code for seven different libraries. The choice of libraries is based on European (JEF, JEFF) and American (ENDF/B) libraries, from the oldest to the most recent: JEF2.2 [20], JEFF-3.1, JEFF-3.2, JEFF-3.3 [21], ENDF/B-VII.0, ENDF/B-VII.1 and ENDF/B-VIII.0 [22]. Note that the most recent nuclear data libraries come with evaluated uncertainties on the data (cross sections, decay data, fission yields, etc.), and correlations listed in covariance matrices for cross sections. A correct estimation of nuclide inventory uncertainties due to nuclear data should propagate all these uncertainties and their correlations through the whole calculation chain. However, this method has not been used because the tools used in this study are not yet mature enough (or at least not without prohibitive computation load) for full core inventory assessment.

The spread is evaluated, for each nuclide, as the maximum value of the concentration differences obtained with the distinct libraries at the considered burnup. While this approach, as a first approximation, should provide a representative order of magnitude of the nuclide inventories uncertainty due to nuclear data for a large part of isotopes, it should be noted that it may be limited when several libraries use identical estimates for the same nuclide, as libraries are never completely uncorrelated. The statistical uncertainty is neglected in this part because it is negligible compared to the deviations obtained with the different nuclear data libraries. Thus, the spread due to the use of various nuclear data libraries (${\Delta }_{ND}^i$) is evaluated, for each isotope i, by comparing the extreme values obtained with the VESTA 2.2 code between the seven libraries, with respect to the mean value, for UO₂ and MOX assemblies and for burnup values ranging from 0 to 59 GWd/t, as:

${\mathit{\Delta }}_{\mathit{N}\mathit{D}}^{\mathit{i}}=\frac{{{\mathit{C}}_{\mathit{max}}^{\mathit{i}}-\mathit{C}}_{\mathit{min}}^{\mathit{i}}}{{\mathit{C}}_{\mathit{m}\mathit{e}\mathit{a}\mathit{n}}^i}(2)$

The maximum deviations obtained between nuclear data libraries, for UO₂ fuel, at 1 GWd/t, 30 and 59 GWd/t are shown on Figure 1, for the list of 47 nuclides presented in Supplementary Appendix S1. The results for MOX fuel are broadly similar for all the isotopes identified as important for severe accidents.

FIGURE 1

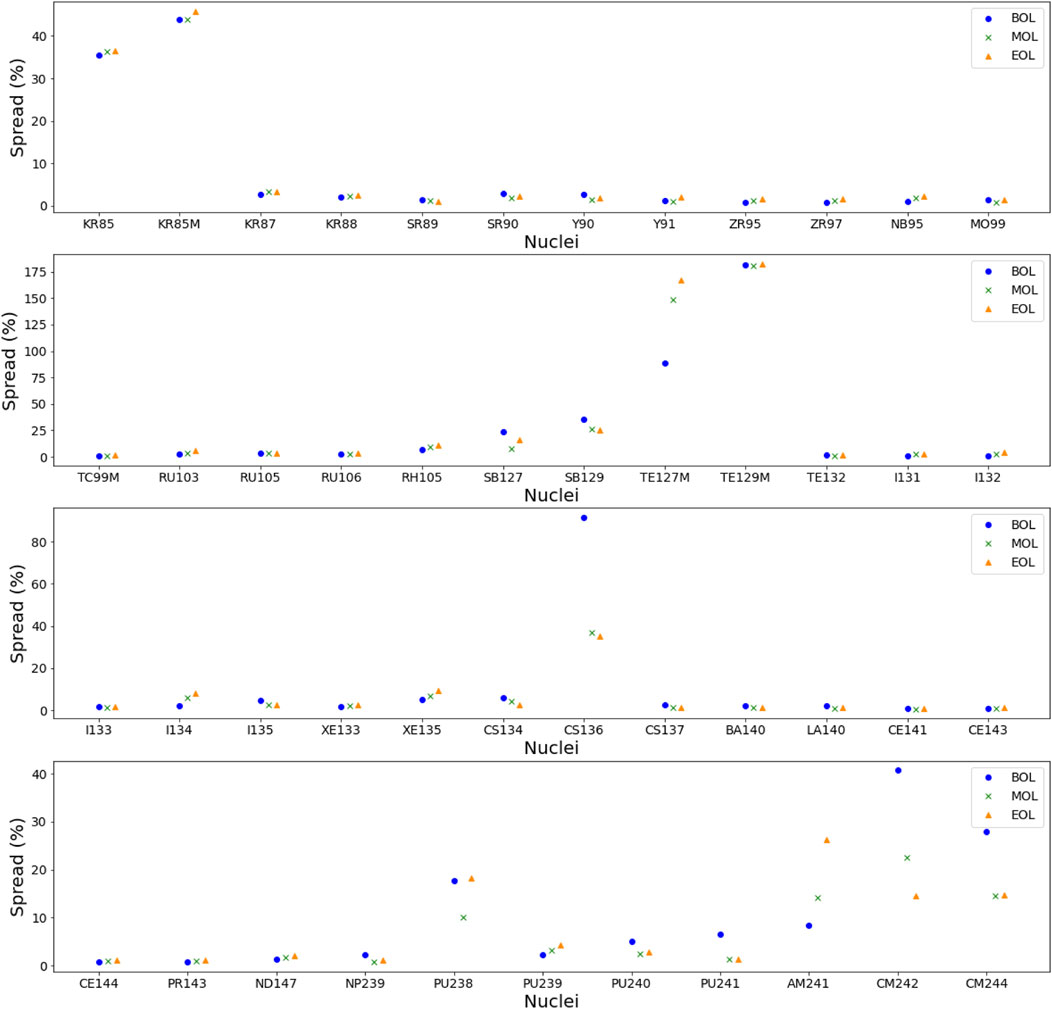
FIGURE 1. Spread on the assembly nuclide inventory due to the use of various nuclear data libraries, for three burnup values, for UO₂ fuel.

Among the 17 nuclides presented in Table 1, the associated deviations are in general relatively small (<5%) and only a few nuclides show larger discrepancies. These are ⁸⁵Kr, ^85MKr and ¹³⁶Cs. For ⁸⁵Kr and ^85MKr, the discrepancy of the order of 40%–50% is explained by lower concentrations calculated with the ENDF/B-VII.1 and ENDF/B-VIII.0 libraries. The isotopes of iodine and xenon show small discrepancies between libraries, less than 5%, except for ¹³⁵Xe which shows some increasing discrepancies with burnup that reach 9% for UO₂ and 5% for MOX, at the end of the irradiation.

It should be noted that, among the 47 nuclides of interest, even if most of them show deviations below 10%, other isotopes show significant deviations. In both cases, about twenty isotopes are impacted and, overall, the isotopes with significant deviations are the same for UO₂ and MOX fuel. It is especially the case of the ¹²⁷Sb, ¹²⁹Sb, ^127MTe, ^129MTe, ²³⁸Pu, ²⁴¹Am, ²⁴²Cm and ²⁴⁴Cm.

However, some isotopes show different deviations depending on the fuel type. ²³⁸Pu, as well as ²⁴²Cm and ²⁴⁴Cm show lower deviations for MOX fuel, due to their higher quantity. But some isotopes show upper deviations for MOX fuel. This is the case of ⁹⁰Y, for which the deviations for MOX fuel can be explained by the cumulative fission yield of ²³⁵U and ²³⁹Pu, of 5% and 2% respectively. As less amount of ⁹⁰Y is produced in MOX fuel, the spread is larger.

It should also be noted that the deviations of a few isotopes are strongly affected by burnup as shown on Figure 1. ¹³⁶Cs, ²⁴²Cm, ²⁴⁴Cm show larger deviations at the beginning of irradiation, due to their very little amount. On the opposite, ^127MTe and ²⁴¹Am show larger deviations at the end of irradiation. The large deviations for ²⁴¹Am at the end of irradiation are not observed for ²⁴¹Pu which shows similar spread between middle and end of irradiation, whereas both ²⁴¹Am and ²⁴¹Pu have similar spreads at the beginning of irradiation. The spread observed for ²⁴¹Am at the end of irradiation can thus be attributed to cross-sections data of ²⁴¹Am.

Among the list of the 17 main isotopes, only four isotopes (⁹⁰Sr, ¹⁰⁶Ru, ¹³⁴Cs and ¹³⁷Cs) are present in the VESTA 2.2 experimental validation, for PWR fuel assemblies [6]. Table 4 presents the maximal deviations between libraries obtained for these isotopes from the VESTA calculations, for UO₂ and MOX fuel respectively, regarding VESTA experimental validation bias. The deviations between libraries are less than 5% for UO₂ fuel and less than 7% for MOX fuel. It appears that the deviations due to libraries are much smaller than the validation biases. Very large measurement uncertainties are actually obtained, for ⁹⁰Sr and ¹⁰⁶Ru. The latter also shows a very wide dispersion of the validation results, depending on the sample and on the measurement. The very large VESTA over- and under-estimations for ¹⁰⁶Ru, reaching 80%, do not seem to be explained by the spread due to nuclear data libraries, which is of 3% maximum.

TABLE 4

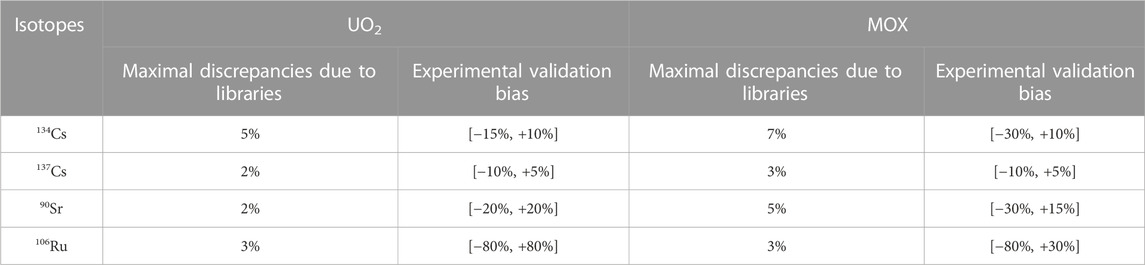
TABLE 4. Maximal nuclear data discrepancies and experimental validation bias for UO₂ (center) and MOX (right) fuel.

It should however be noted that, although the calculations have been carried out with the continuous energy VESTA code, other sources of uncertainty may affect the results. Indeed, certain modeling choices made (infinite lattice approximation, constant and homogeneous boron concentration and temperatures during irradiation, etc.), the lack of precise knowledge of the irradiation history, as well as the technological uncertainties may have a non-negligible impact on the results. The impact of the technological uncertainties is presented in Section 4.4 and the impact of the infinite lattice approximation is presented in Section 5.

To conclude, this uncertainty source is complex to assess and analyze. It can be very variable depending on the isotope. It should be remembered that the method for evaluating this uncertainty source has been carried out, as a first approximation, by comparing results obtained from different libraries, and without considering the uncertainties and correlations associated with the nuclear data present in the covariance matrices. The consideration of a simple maximum discrepancy between libraries may be, depending on the isotope, questionable, as it strongly depends on the sufficient plurality and diversity of the evaluations present in these libraries. In any case, the estimated spread can reach more than 30%, or even 100%, for some isotopes, which is largely significant compared to other uncertainty and bias sources considered in this study.

4.3 Systematical bias due to the resolution method

This section is dedicated to the estimation of the bias introduced by the resolution method used to simulate the neutron transport and the isotopic composition depletion of the fuel during irradiation. Two main types of methods exist for neutronics calculations, the Monte-Carlo and deterministic methods.

- The Monte Carlo method uses a stochastic approach to determine the physical quantities. This method does not require any simplification for the solution of the neutron transport equations, but it does require significant computational resources. This computational cost becomes limiting for the depletion of a complete reactor core. Monte-Carlo calculations are however generally considered as reference calculations. In addition, beyond the fact that the calculation is carried out in exact geometry, nuclear data libraries used in the calculation are continuous in energy and therefore very precise. Nevertheless, as presented previously, this method implies statistical uncertainties, associated with the calculated physical quantities, which are propagated throughout the depletion calculation.

- The deterministic method is based on the numerical resolution of the neutron transport equations, which requires calculation simplifications based on a discretization of space and energy. Deterministic calculations thus implement methods of energy condensation (multi-group approach) and homogenization of the medium, which can lead to biases in the nuclide inventories. However, this approach has the advantage of being fast and of allowing full core depletion calculations. For these reasons, this type of approach is usually used for reactor cores simulations.

The systematic bias related to the resolution method (ε_codeⁱ) used in this study is evaluated, for each isotope i by a deterministic/Monte Carlo comparison of the C_VESTAⁱ and C_CASMOⁱ concentrations calculated respectively with the VESTA 2.2 and the CASMO5 codes. This bias has been determined for UO₂ and MOX assemblies and for burnup ranging from 0 to 59 GWd/t, by Eq. 3.

${\mathit{\epsilon }}_{\mathit{c}\mathit{o}\mathit{d}\mathit{e}}^{\mathit{i}}=\frac{{{\mathit{C}}_{\mathit{C}\mathit{A}\mathit{S}\mathit{M}\mathit{O}}^{\mathit{i}}-\mathit{C}}_{\mathit{V}\mathit{E}\mathit{S}\mathit{T}\mathit{A}}^{\mathit{i}}}{{\mathit{C}}_{\mathit{V}\mathit{E}\mathit{S}\mathit{T}\mathit{A}}^{\mathit{i}}}(3)$

In order to minimize discrepancies due to modeling differences, let us remind that the MCNP inputs used by VESTA were generated automatically from the CASMO5 ones. This approach ensures consistency between the two models. In this section, the ENDF/B-VII.1 library has been used with the two codes. However, it should be noted here that the ENDF/B-VII.1 library from CASMO slightly differs for some isotopes³, from the official continuous energy library used by VESTA. However, the impact of these modified isotopes is not discussed in this paper. Nor is there any discussion of the possible different treatment of nuclear data between the two codes, which could have an impact for some isotopes.

The systematic bias ε_codeⁱ thus integrates all the resolution approximations specific to deterministic methods, among which (non-exhaustive list).

- the energy self-shielding model linked to the multi-group approximation;

- the spatial discretization of the geometry;

- the accuracy of the numerical methods used to solve the Boltzmann equation.

Figure 2 presents the systematic bias due to the resolution method, obtained in this case between ⁴CASMO and VESTA, for the list of 47 nuclides presented in Supplementary Appendix S1 for UO₂ fuel case. In general, the systematic bias ε_codeⁱ is relatively small, less than 5%, with a small dependence on the burnup value. Nevertheless, for about ten isotopes, the bias is more important and can reach up to 50% (⁸⁵Kr and ^85MKr cases). For cases where the bias is more pronounced, a dependence on burnup can be noted. For some fission products (¹³⁶Cs), which can show a large overestimation, and most of actinides (e.g. ²³⁸Pu, ²⁴⁰Pu, ²⁴¹Pu, ²⁴¹Am, ²⁴²Cm), deviations are larger at the beginning of irradiation.

FIGURE 2

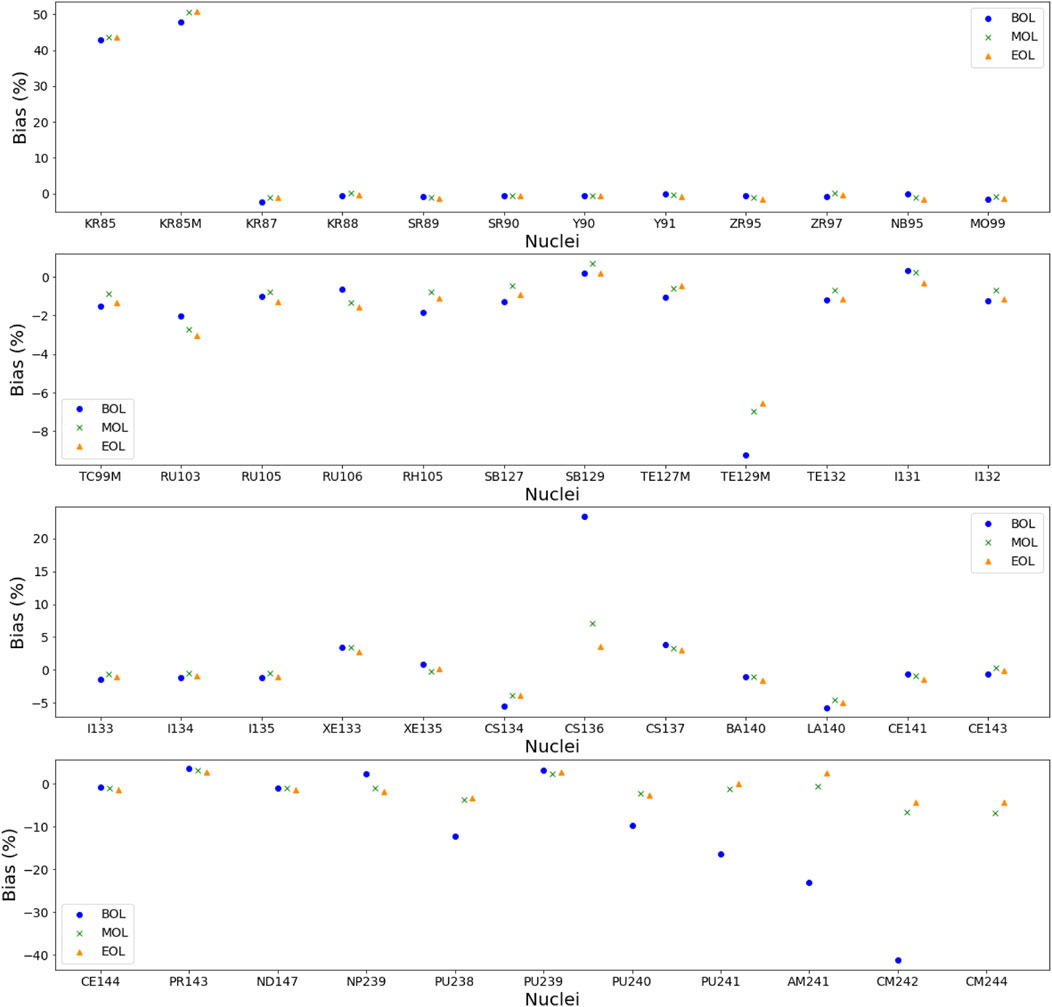
FIGURE 2. Bias due to the resolution method ${\epsilon }_{code}^i$ (between CASMO and VESTA) on the assembly nuclide inventory, for three burnup values, for UO₂ fuel.

Nevertheless, it has been verified that in the CASMO ENDF/B-VII.1 “202 neutron data library” the ^85MKr isotope is taken from TENDL-2012 library, which could explain the large deviations with VESTA. The same conclusions can be drawn for the actinides, knowing that the ²³⁹Pu from the CASMO library is extracted from the JENDL-4.0 evaluation.

For the Iodine and Xenon isotopes, the deviations are very small, less than 5% for all burnups. Finally, no major difference between UO₂ and MOX fuel can be reported.

To conclude, it appears that the choice of the resolution method, in this case when comparing the CASMO results to the VESTA results, for estimating isotopic inventories important for severe accidents has a relatively small impact. Except for a few specific isotopes, the bias introduced by the use of CASMO is less than 5% whatever the type of fuel or burnup.

It should be noted that this bias is totally dependent of the codes used and is not intended to be used as such for a generic deterministic versus Monte-Carlo bias estimation.

4.4 Technological uncertainties and variability of operating conditions

Manufacturing tolerances are associated to each assembly physical data. This may include, for example, the radius and density of the fuel pellets, or their enrichment. These manufacturing uncertainties are likely to impact the isotopic inventory during irradiation. On the other hand, the various operating conditions, linked to the operation of the reactor, can also affect the isotopic inventory results. They mainly concern the moderator and fuel temperatures, which have an influence on the neutronics calculations, especially due to their effects on the density of the materials, but also on the neutron-nucleus reactions, which depend on the temperature. The core power is also a variable that directly influences the fuel burnup. Consequently, the variability of operating conditions generates uncertainties on the evolution of the isotopic inventory during irradiation.

Thus, this section is dedicated to the estimation of the uncertainty, of random origin, introduced by the variability of the technological and operating data used for the modeling of fuel assemblies. The variable data considered in this study are listed in Table 5. This list, although not exhaustive, is extracted from the NEA-SFCOMPO TRG [25] working group recommendations and provides an order of magnitude of the uncertainties associated with the fuel manufacturing tolerances and the measurement processes implemented during reactor core operation.

TABLE 5

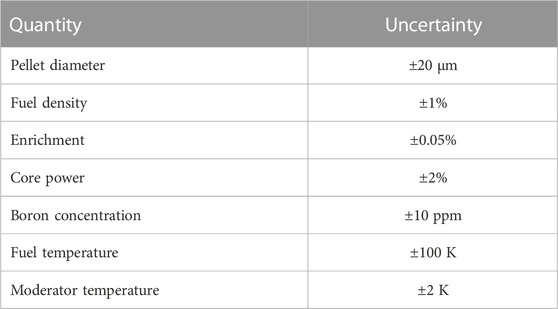
TABLE 5. Technological uncertainties provided in SFCOMPO [25].

The methodology adopted consists of considering these uncertainties as extreme values and carrying out a combinatorial approach by considering the minimum and maximum values of each parameter. These combinations, corresponding to 128 depletion calculations per type of assembly, using CASMO5, allow to estimate the technological uncertainties for each isotope i (σ_Techⁱ) as the dispersion of the distribution of deviations (standard deviations, quantiles, etc.) with respect to the nominal irradiation conditions as:

${\mathbf{\sigma }}_{\mathbf{T}\mathbf{e}\mathbf{c}\mathbf{h}}^{\mathbf{i}}=\sqrt{\frac{\mathbf{1}}{\mathbf{N}}{\displaystyle \sum }_{\mathrm{n}=\mathbf{1}}^{\mathbf{N}}{\left({\mathit{\Delta }}_{\mathbf{n}}^{\mathbf{i}}-\overline{{\mathit{\Delta }}_{\mathbf{n}}}\right)}^{\mathbf{2}}}(4)$

With,

- N the number of calculations per assembly type (128 in this case);

-${∆}_n^i=\left({C_n^i-C}_{nominal}^i\right)/C_{nominal}^i$ the deviation from the composition obtained under nominal operating conditions;

- And $\overline{{∆}_n}$ the average of the deviations (in the particular case of the presented method, $\overline{{∆}_n}=0$ since the variations are assumed symetrical around the nominal evolution conditions).

Figure 3 presents the uncertainty related to the variability of technological and operating data for the list of 47 nuclides in the case of UO₂ fuel. In general, the uncertainty σ_Techⁱ is small, less than 3%, with a particularly strong burnup dependence at the beginning of irradiation for the majority of nuclides. The maximum uncertainty is obtained for the case of ²⁴²Cm with a little more than 5% at the beginning of the irradiation.

FIGURE 3

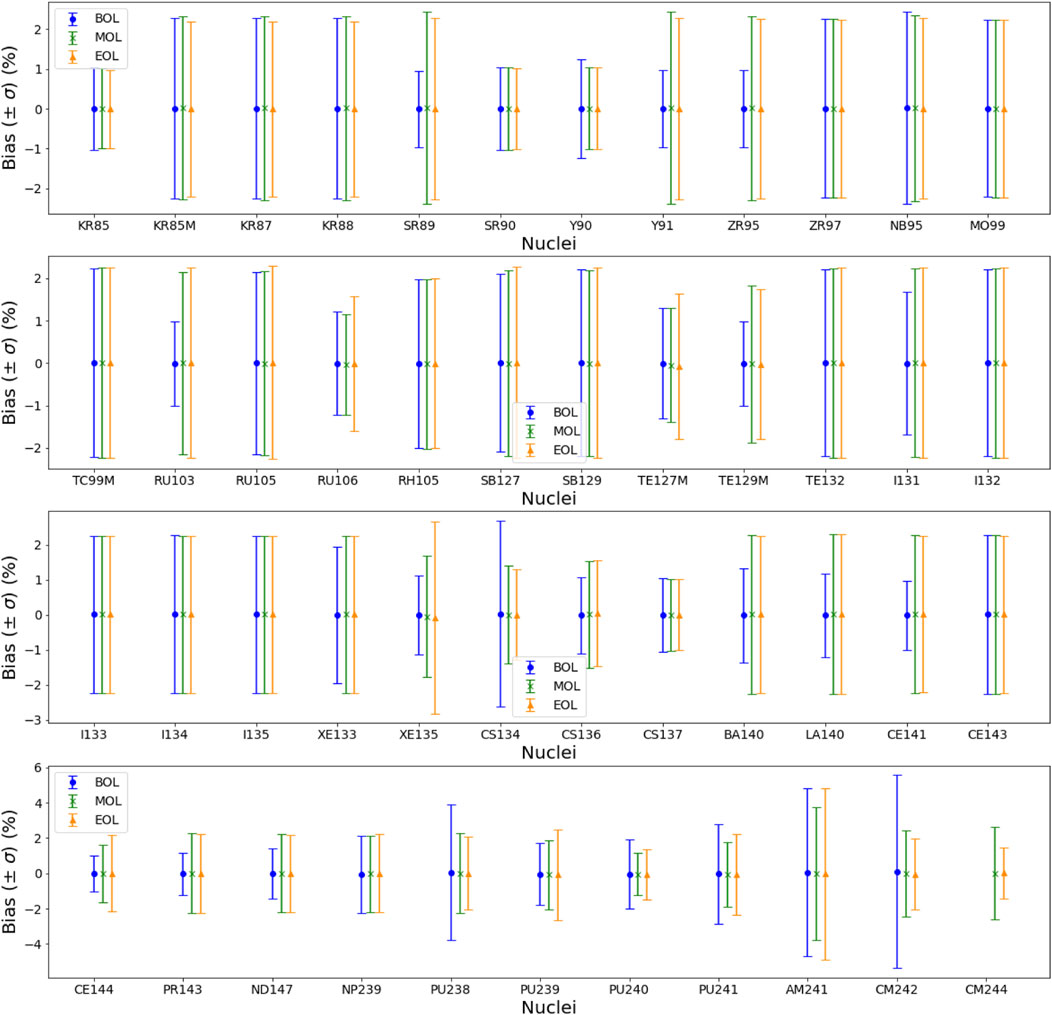
FIGURE 3. Technological uncertainties (average bias and 1σ error bars) on the assembly nuclide inventory, for three burnup values, for UO₂ fuel.

To conclude, it appears that technological uncertainties have very small impact on the estimation of the isotopic inventory of a fuel assembly. Except for a few specific isotopes, the technological uncertainties are less than 3% whatever the burnup or fuel type.

4.5 Biases and uncertainties due to constant boron concentration approximation

Infinite medium lattice simulations are usually performed at constant boron concentration, with an average value of around 600 ppm. In order to quantify the uncertainties related to this approximation, isotopic concentrations have been compared with simulations performed with a boron concentration varying linearly and cyclically between 1,200 and 0 ppm in pseudo-cycles of 15 GWd/t. All the simulations, both constant and variable boron, have been performed with CASMO5.

For both UO₂ and MOX fuel the effect is less than 5% for all isotopes and burnup values. Boron letdown is not a major source of uncertainties in the isotopic inventories of burnt fuels.

5 Biases and uncertainties due to infinite lattice approximation

The simulation of the fuel depletion involves many modeling assumptions to ensure reasonable calculation time with accessible computational resources. One of the main assumptions usually applied is to limit the modeling to a single fuel assembly, repeated ad infinitum in all space directions, assuming that the environment of the studied assembly is identical to itself. This assumption, which implements reflective conditions on the limits of the modeling, is called “infinite lattice approximation” (ILA). Without direct core calculation, the nuclide inventory of the core is thus reconstructed from the nuclide inventories of the reactor core assemblies obtained with single assembly calculations in infinite medium at the desired burnups. This assumption leads to a bias on the nuclide concentrations, as it does not consider surrounding effects (flux, spectrum and burnup gradient). In addition, core reconstruction also requires the knowledge of the distribution of the reactor core assemblies’ burnups.

To account for the non-physical ILA, deterministic lattice transport codes use various leakage corrections to achieve the criticality. There are several models to account for leakage [26], which assume that surrounding assemblies are identical and only adjust the neutron leakage in each energy group to reach criticality. While the use of a leakage model is commonly accepted by the scientific community, there is no clear consensus of using a model or another [27] and whatever the leakage model considered in lattice calculation, the varying compositions of surrounding assemblies also need to be addressed.

Indeed, the neutron flux and energy distribution are affected when the surrounding of the fuel assembly is accounted for. Thus, during fuel depletion, isotopes whose composition exhibits a dependence on the neutron flux are strongly affected by the ILA. Therefore, it is possible to distinguish two categories of nuclides.

- Fission products and actinides that rapidly reach saturation, if the production by fission of the considered isotope balances with its disappearance by radioactive decay and/or neutron capture. The fissions and captures in the fuel are directly related to the neutron flux, to the effective capture and fission cross-sections of the father nuclide, and to the associated fission yields. The contribution of radioactive decay depends on the half-life of the isotope with respect to the time scales considered. The ¹³⁵Xe and ¹⁴⁹Sm are characteristic of this category.

- Fission products and actinides that accumulate or disappear indefinitely: if the absorption cross-section and flux level are low compared to the fission yield or decay rate of the father isotope, then the considered isotope accumulates or disappears in proportion to the cumulative fission rate (rate accumulating the direct production by fission and the indirect production by decay of a short-lived intermediate fission product).

A recent study using the MxN modeling capability of CASMO5 was performed to estimate the biases and uncertainties due to ILA for 2D color-set configurations and 2D full core configurations [28]. Updated results, taking into account a new calculation methodology for 2D color-set configurations are presented here.

5.1 2D color-set configurations

The methodology for the estimation of systematic bias and uncertainty induced by ILA is evaluated by comparing the concentration results of an assembly in an infinite lattice of itself with a selection of different 3 × 3 cluster configurations representative of the fuel environment during the reactor operation. The methodology is described hereafter, using the following terminology.

- the term of bias corresponds to the systematic impact of considering an environment surrounding the assembly compared to a single assembly in infinite lattice, which is the statistical mean of differences and is expressed as:

${\epsilon }_{Env}^i=\frac{1}{N}{\displaystyle \sum }_{n=1}^N\frac{C_n^i-C_{infinite}^i}{C_{infinite}^i}(5)$

- the term uncertainty refers to the variability of possible surrounding assemblies in a fuel core management, which is quantified by the statistical standard deviation of differences and is expressed as:

${\sigma }_{\mathrm{E}\mathrm{n}\mathrm{v}}^{\mathrm{i}}=\sqrt{\frac{1}{\mathrm{N}}{\displaystyle \sum }_{\mathrm{n}=1}^{\mathrm{N}}{\left(\frac{C_n^i-C_{infinite}^i}{C_{infinite}^i}-{\epsilon }_{Env}^i\right)}^2}(6)$

Using this convention, it should be noted that a positive bias means an underestimation for calculations using ILA compared to more precise color-set calculations, whereas a negative bias means an overestimation.

For each type of fuel (UO₂ and MOX), several environment histories has been modeled. Each history assumes that the considered assembly goes through four cycles in the core, with constant burnup variation of 15 GWd/t, from its beginning of life (BOL or burnup 0 GWd/t) to its end of life (EOL or 60 GWd/t). At each refueling, a different environment is considered, with random selection of the type (UO₂ or MOX) and initial burnup (0, 15, 30 or 45 GWd/t) of each of the eight surrounding assemblies. The variability of the environment and the probability of each random selection were chosen to be representative of the configurations encountered in the French PARITE-MOX fuel management, which means fuel type proportions of 2/3 UO₂ and 1/3 MOX, and burnup proportions of 30%, 30%, 30% and 10% for 0, 15, 30 and 45 GWd/t respectively. The initial composition of each surrounding assembly is taken from infinite lattice calculations, whereas the composition of the central assembly is kept at each recycling, which considers its variable environment history. To derive systematic biases and associated uncertainties, a total of 160 environment histories has been modeled (80 for each type of fuel).

It is to be noted that in this study color-set configurations are modeled with mirror boundary conditions (as in single fuel assembly infinite lattice calculations), assuming that fuel assemblies beyond the color-set boundary have a negligible impact on the nuclide inventory of the central fuel assembly for a given burnup. This assumption should be tested in future prospects. Moreover the environment of fuel assemblies close to the core periphery with water and steel reflector assemblies has not been taken into account in this study. Their impact also should be tested in complementary studies.

The mean bias and 1σ uncertainty due to ILA, obtained by this method, for a UO₂ assembly, are presented on Figure 4. The infinite medium approximation introduces a systematic bias on the isotopic concentrations dependent on the considered isotope and the assembly burnup. This bias is less than 5% for most cases except for some fission products (¹³⁵Xe, ¹³⁴Cs) for which it can reach 8%, and for most actinides, mainly at low burnup, for which it can reach 33%. In most cases, this bias between cluster and infinite lattice calculations is either small or positive, meaning an underestimation in usual calculations using the infinite lattice approximation. For some isotopes (like ¹³⁵Xe), this systematic bias increases between the beginning and the end of life, whereas for some others (like ¹³⁴Cs) it decreases, but for the majority it is not significantly dependent on burnup.

FIGURE 4

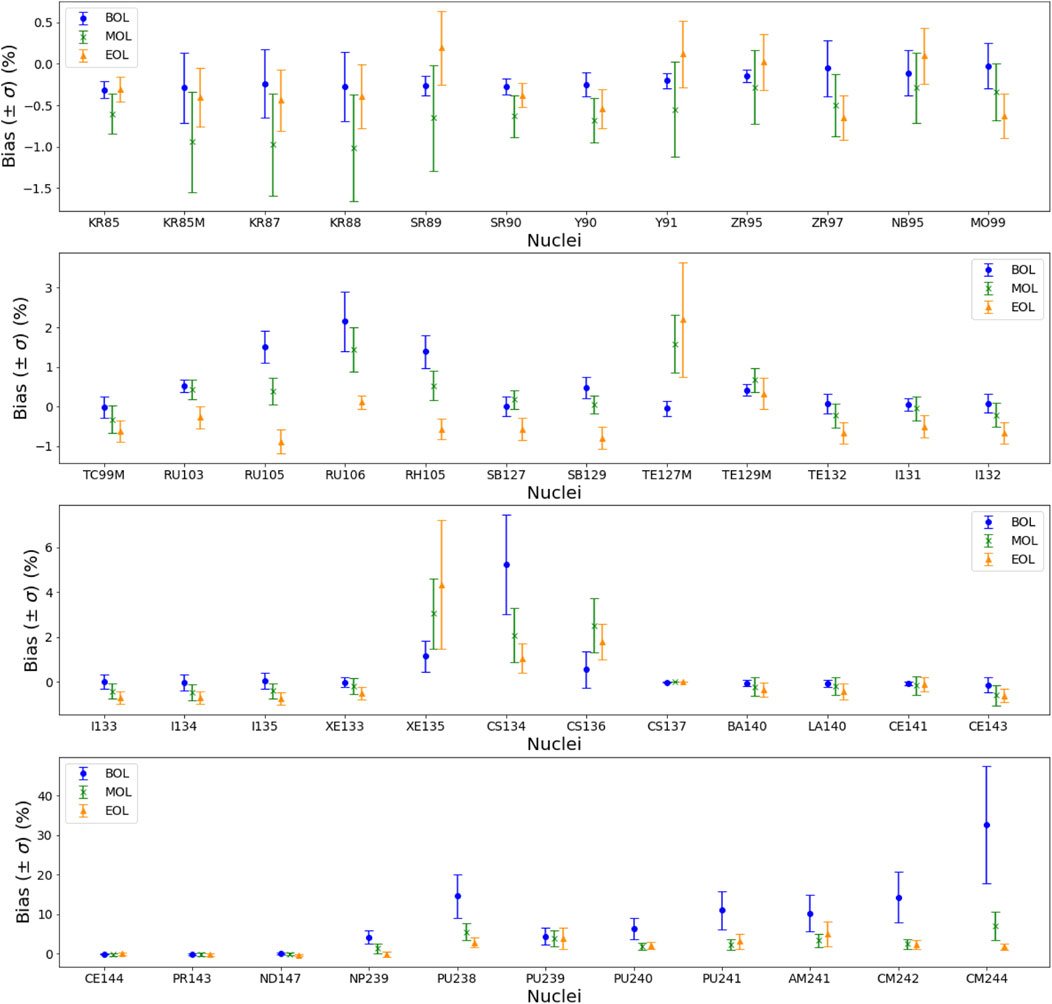
FIGURE 4. Average bias and its uncertainty (1σ) due to ILA on the assembly nuclide inventory, for three burnup values, for UO₂ fuel.

An example of nuclide for which bias and uncertainty due to ILA increase with assembly burnup is given in Figure 5, for ¹³⁵Xe in a UO₂ fuel assembly. The mean value of the bias is presented, together with the minimum and maximum value of the bias. It clearly shows a build-up of differences of ¹³⁵Xe concentrations in the cases of a central UO₂ assembly surrounded by a varying environment (including MOX and irradiated UOX) compared to the infinite lattice UO₂ case. This comes from the harder neutron spectrum in cluster cases causing more neutron capture in ²³⁸U resonances, generating more ²³⁹Pu, for which the fission yield of ¹³⁵I/¹³⁵Xe is higher than for ²³⁵U (+16%).

FIGURE 5

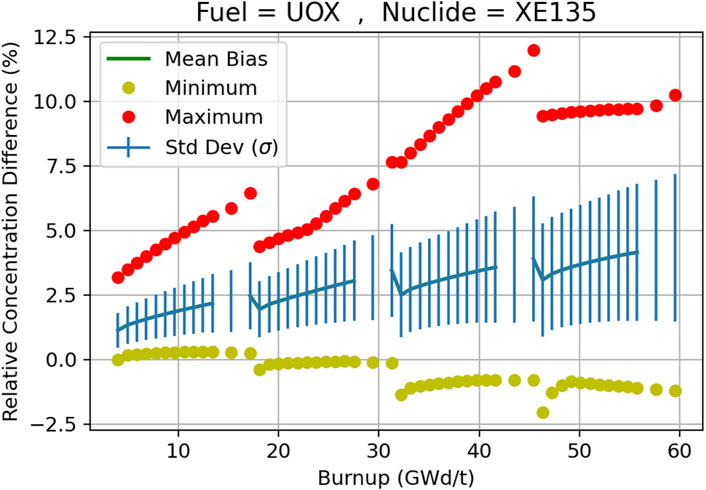
FIGURE 5. Differences on the ¹³⁵Xe concentration, with burnup, between cluster calculations and ILA, for UO₂ assembly.

The mean bias and 1σ uncertainty due to ILA for a MOX assembly is presented on Figure 6. In this case, the infinite medium approximation introduces a systematic bias on the isotopic concentrations less than 5% for most cases except for some actinides (²³⁹Pu, ²⁴⁴Cm). Overall, biases are rather small for a MOX assembly, in most cases they are either small or negative, and as in the case of a UO₂ assembly, for some isotopes, this systematic bias increases between the beginning and the end of life, whereas for others it decreases.

FIGURE 6

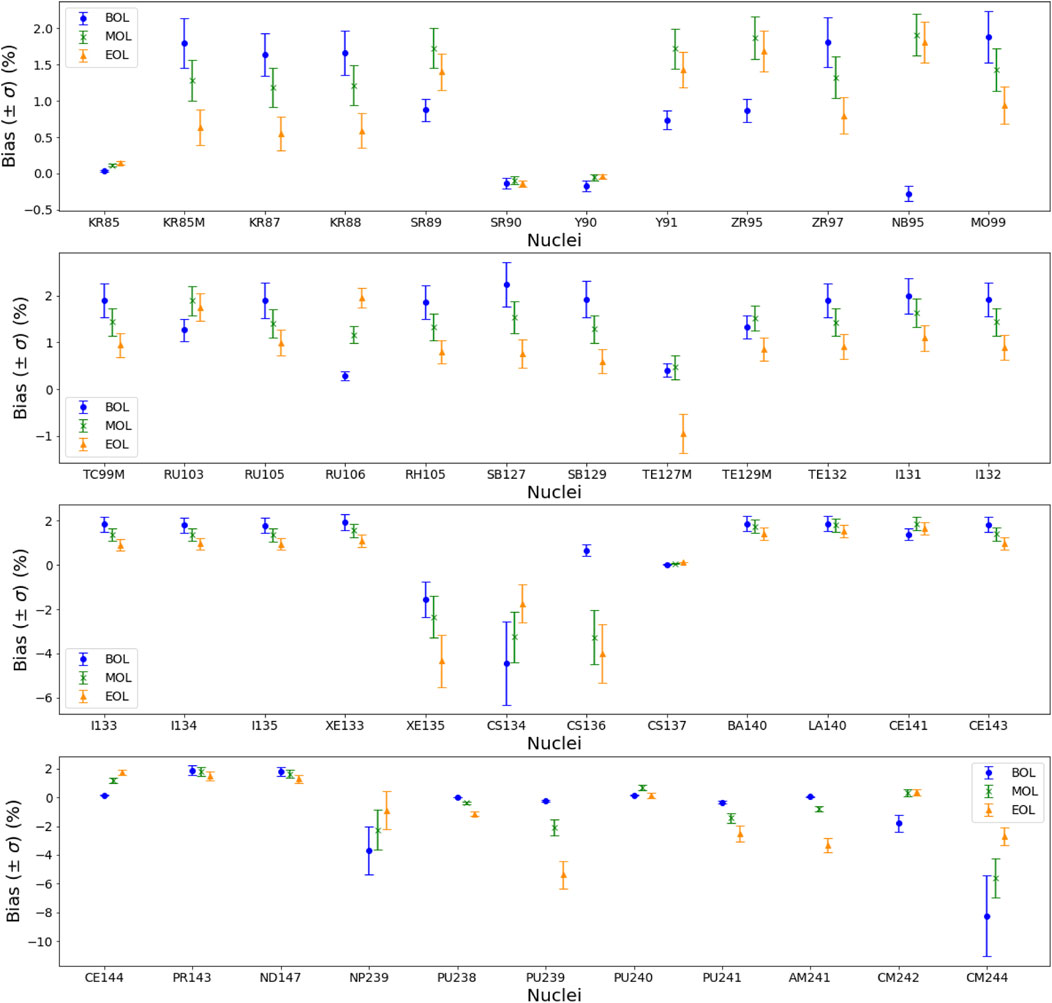
FIGURE 6. Average bias and its uncertainty (1σ) due to ILA on the assembly nuclide inventory, for three burnup values, for MOX fuel.

The combination of both bias and uncertainty is presented in Table 6, for all nuclides for which the combination of bias and uncertainty can exceed ± 5%, either for UO₂ or MOX fuel assemblies. It concerns a dozen of nuclides for UO₂ fuel assemblies, for which a positive bias is obtained (underestimation with ILA), but a bit less nuclides for MOX fuel assemblies for which a negative bias is obtained (overestimation with ILA).

TABLE 6

TABLE 6. Significant maximum discrepancies (bias ± 1σ) due to ILA.

To conclude, while the magnitude of the uncertainty and the average bias introduced by ILA on the concentrations are highly depending on the isotope and the assembly burnup, they are largely correlated to the equilibrium kinetics of the isotope, its capture capability and the flux level in the assembly. The combination of both bias and uncertainty can lead to an underestimation up to 47% for UO₂ fuel assemblies or an overestimation up to 12% for MOX fuel assemblies (²⁴⁴Cm) in the case of infinite lattice calculations, which is significant compared to the other uncertainty and bias sources considered in this paper.

It should be noted that the most significant discrepancies are mainly observed at low burnup, when the nuclides concentrations are still very low, and that some extreme values even higher than the ones quoted here can be observed for specific cases.

5.2 2D full core configurations

The methodology implemented for full core configurations, and described in [28], to estimate the effects of the ILA on fuel compositions consists in comparing the nuclide concentration results obtained with the two following approaches.

- The first method consists, for each fuel pattern, of a reference multi-assembly calculation carried out with CASMO5 MxN modeling capability and initialized with the assemblies’ burnup from EDF fuel patterns. With this approach, all surrounding effects are considered, both those between neighboring assemblies and those between the assemblies and the radial reflector. It should be noted that the compositions of the core assemblies at the beginning of the cycle are derived from an ILA calculation type.

- The second method consists in single assembly calculations in infinite medium for each type of assembly present in the loading pattern. These calculations are performed for the burnups of the assemblies obtained in the reference calculation at BOC, MOC and EOC. Therefore, the average fuel compositions at the core level can be obtained by a reconstruction method from the single assembly calculation inventories.

Finally, the bias due to the ILA on the core nuclide inventory, noted ${\epsilon }_{\mathit{Inf}\to Core}^i,$ expressed as the relative deviation between the reconstructed estimation and the reference calculation, is calculated with Eq. 7. ${C_{\mathit{Inf}}^{i}andC}_{Core}^i$ are respectively the concentration of the isotope i obtained with reconstructed single assembly calculations in infinite medium and direct core calculations.

${\mathit{\epsilon }}_{\mathit{I}\mathit{n}\mathit{f}\to \mathit{C}\mathit{o}\mathit{r}\mathit{e}}^{\mathit{i}}=\frac{{{\mathit{C}}_{\mathit{Inf}}^{\mathit{i}}-C}_{\mathit{C}\mathit{o}\mathit{r}\mathit{e}}^{\mathit{i}}}{{\mathit{C}}_{\mathit{C}\mathit{o}\mathit{r}\mathit{e}}^{\mathit{i}}}(7)$

The results of the bias estimation for the 17 nuclides presented in Table 1 are presented on Figure 7.

FIGURE 7

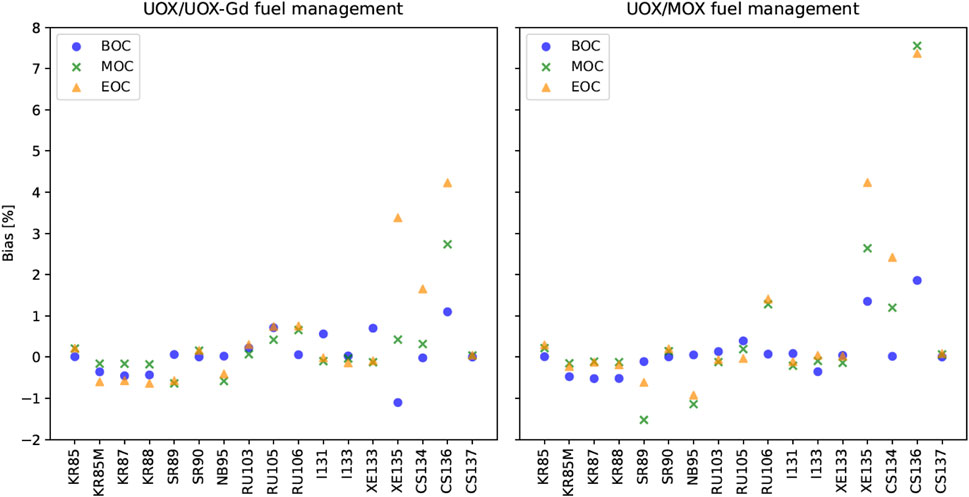
FIGURE 7. ILA bias on the core nuclide inventory, at BOC, MOC and EOC, for both UO₂ (left) and MOX (right) fuel management.

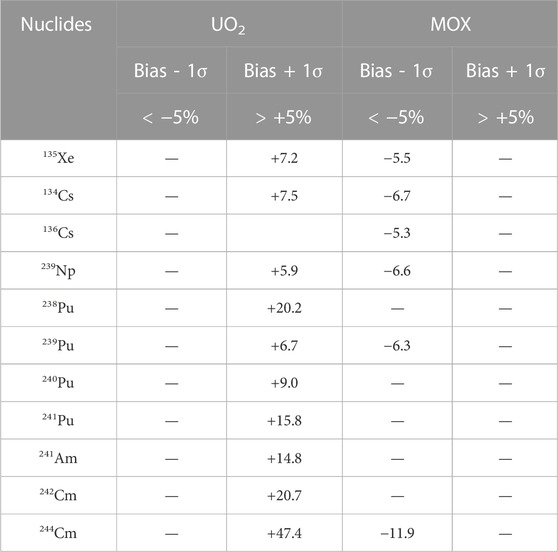
For the majority of isotopes presented on Figure 7, as well as for all the main isotopes for severe accidents calculated by CASMO, the bias due to ILA on the core nuclide inventory is very small, within 1% in order of magnitude, both for GEMMES (UO₂) and PARITE-MOX (MOX) fuel management. However, the biases are slightly larger in the presence of MOX assemblies in the reactor core. In addition, a small increase of the bias can be observed as a function of the burnup cycle for both fuel management, except for some isotopes for which this variation is more pronounced (¹³⁵Xe or ¹³⁶Cs as an example). As one can see on Figure 7, only few isotopes (¹³⁵Xe, ¹³⁴Cs and ¹³⁶Cs) present a bias larger than 2%. Concerning ¹³¹I, ¹³³I and ¹³³Xe, which are particularly important with respect to radiological consequences, the bias is very small (<1% in absolute value) for both fuel management whatever the cycle burnup. Whereas for ¹³⁵Xe, the bias is small at BOC (∼1% in absolute value) but it can reach 3%–4% at EOC. In addition, the bias for the ¹³⁶Cs at EOC can reach more than 4% (UO₂) and 8% (MOX), as observed in Figure 7.

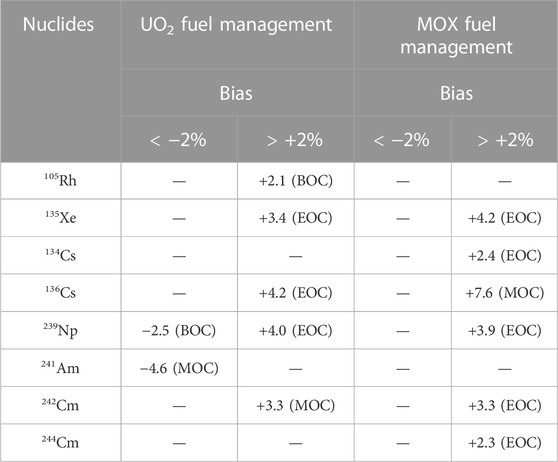
The most significant biases are presented in Table 7, for all nuclides among the 47 of Supplementary Appendix S1, for which the absolute value of the bias exceeds ± 2%, either for UO₂ or MOX fuel management.

TABLE 7

TABLE 7. Maximum significant bias ($\left|bias\right|>2\%$) due to ILA for UO₂ and MOX fuel management.

The main parameters of influence that can explain the observed biases, as explained in [28], are.

- the isotope concentration: significant biases are observed for isotopes with concentrations lower than 10¹⁸ atoms/cm³;

- the relative power of the assemblies: for isotopes highly sensitive to neutron flux, the bias obtained in each assembly of the core is strongly correlated to its relative power;

- the compensation effects between core assemblies: as the bias depends on the assembly being considered (especially on his power level), the combination of the biases of all the core assemblies can induce some compensations.

To illustrate these conclusions, the example of ¹³⁵Xe can be discussed. ¹³⁵Xe has a bias of about 4% at the core level at EOC, whereas when we consider the bias at the scale of each assembly, it varies from +90%, for the least powerful assemblies, to −10% for the most powerful assemblies. The value of the bias is correlated to the power of the assembly and thus to the level of neutron flux “seen” by the assembly. Indeed, in a SA calculation in infinite medium, the fission rate in the assembly is nominal, whereas for an assembly in the core, the fission rate varies spatially according to its position in the core. Nevertheless, the production of ¹³⁵Xe depends directly on this flux level and the disappearance of ¹³⁵Xe by neutron capture is also very strongly dependent on the flux level, given the very large capture cross section of this isotope for a thermal neutron. The combination of these effects leads to a core bias that remains limited for this isotope.

Finally, at the core level, the order of magnitude of the bias introduced by the ILA is limited and smaller than at the assembly level. The average core bias for the 47 nuclides considered in this paper is within 1% with a 2% standard deviation and the maximum variations are within −5% and 10% depending on the fuel management being considered. These limited biases are mainly due to the compensation effects between core assemblies, that can be correlated to the relative power of the assemblies, for some isotopes highly sensitive to neutron flux. In particular, the bias for these isotopes are much smaller because of these compensations.

This study highlights the fact that the impact of the ILA is strongly correlated to the scale used for isotopic concentration evaluation (the effect is stronger at local scale). The impact of ILA on safety depends on the importance of the isotope for the application being considered.

6 Conclusion

The estimation of biases and uncertainties on nuclide inventories for PWR presented in this paper covers several sources and is presented both for UO₂ and MOX fuel at the assembly and the core level. They were computed both using the CASMO5 deterministic code, as well as the VESTA 2.2 Monte-Carlo depletion code, depending on the uncertainty source studied. They are listed as biases and uncertainties on isotopic concentrations at different burnup values, for a list of isotopes of interest in case of severe accident. For each of the sources of uncertainty, an estimate of the associated biases and uncertainties on nuclide inventories is provided.

It has been shown that among the sources of bias and uncertainties studied (nuclear data, technological uncertainties, bias due to the resolution method, and bias and uncertainties due to Infinite lattice approximation–ILA–at the assembly level), spread due to nuclear data as well as the bias and uncertainties due to ILA are the most significant ones, for the isotopes of interest. Depending on the isotope and on the burnup value, the estimated nuclear data spread, as well as the bias and uncertainties due to ILA, can reach more than 30%, or even 100%, for some isotopes. As an example, Supplementary Appendix S2 presents the different bias and uncertainties values obtained in the case of the UO₂ fuel at the assembly level at the end of irradiation, for the list of the 17 main contributors in case of severe accident.

The choice was made in this paper not to present the overall resulting biases and uncertainties, considering all the sources studied. An important assumption indeed necessary to perform for the estimation of the global biases and uncertainties is the independence and non-interaction of the different sources. To get rid of this assumption, it would be necessary to carry out a very complex and computationally expensive multidimensional analysis, which is not performed here.

Moreover, estimation of biases and uncertainties in isotopic inventories presented in this paper is not exhaustive and perfectible.

- Uncertainties due to nuclear data could be further developed through the implementation of advanced methods for nuclear data uncertainties propagation.

- About inter-code comparison, especially at the core level, only two fuel management types and a given loading plan, and with a single nuclear data library were considered. It would therefore be useful to verify that the biases remain of the same order of magnitude for other fuel managements and loading plans, as well as for different nuclear data libraries. This last point could highlight possible differences in the treatment of nuclear data by different codes. Moreover, this particular source of bias is completely dependent on the code used and cannot be generalized.

- Another modeling bias is the simulation of the core in two dimensions, which does not consider axial effects. However, depending on the axial coast, the conditions differ (water density, clusters, etc.), which consequently modifies the depletion of the fuel.

- Finally, an important source of uncertainty for nuclides with a relatively short half-life is related to power fluctuations within the reactor. Indeed, the concentrations of nuclides with very short half-lives such as Xe is directly correlated to the power level in the hours preceding the shutdown. Other FPs with somewhat longer half-lives are influenced by fluctuations on longer time scales. It should be noted that in general the simulation of irradiation at nominal power maximizes the concentrations of these isotopes.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: NEA databank.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor J-FM declared a shared OECD research group with the author RI at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1033306/full#supplementary-material

Footnotes

¹Fine burnup mesh (every 0.5 GWd/t) up to 10 GWd/t, then progressive enlargement of burnup step size up to 2.5 GWd/t until the end of irradiation.

²VESTA performs reaction rates calculations on a very fine energy groups grid (44,000 groups).

³In the ENDF/B-VII.1 library delivered with CASMO5, some isotopes are extracted from the JENDL-4.0 library [23] (as example ²³⁹Pu) or from TENDL-2012 [24].

⁴For the sake of clarity and consistency, concerning the sign of the provided biases, it must be reminded that a positive ${\epsilon }_{Code}$ represents an overestimation of CASMO5 concentrations with respect to the VESTA ones, whereas a positive ${\epsilon }_{Env}$ represents an underestimation of the concentrations obtained using ILA compared to more precise color-set calculations.

References

1. Ebiwonjumi, B., Kong, C., Zhang, P., Cherezov, A., and Lee, D. (2021). Uncertainty quantification of PWR spent fuel due to nuclear data and modeling parameters. Nuclear Engineering and Technology 53, 715–731. doi:10.1016/j.net.2020.07.012

CrossRef Full Text | Google Scholar

2. Huang, D., and Abdel-Khalik, H. S. (2020). Nuclear data uncertainty propagation and modeling uncertainty impact evaluation in neutronics core simulation. Progress in Nuclear Energy 128, 103443. doi:10.1016/j.pnucene.2020.103443

CrossRef Full Text | Google Scholar

3. Araj, K. J., Allen, A. O., Auer, P., Boulware, D. G., Finlayson, F., et al. (1985). Report to the American Physical Society of the study group on radionuclide release from severe accidents at nuclear power plants. Reviews of Modern Physics 57, S1–S144. doi:10.1103/revmodphys.57.s1

CrossRef Full Text | Google Scholar

4. Haeck, W., and Dechenaux, B. (2017). VESTA User’s Manual - Version 2.2.0”, IRSN report PSNEXP/SNC/2017-251. France: Institut de Radioprotection et de Sûreté Nucléaire.

Google Scholar

5. Hendricks, J. S., et al. (2005). MCNPX, VERSION 2.6.a”, LA-UR-05-8225. USA: LANL.

Google Scholar

6. Ichou, R. (2020). Validation of VESTA 2.2.0 - Volume 1: Methodology and overview of results”, IRSN report IRSN/2020-00269 Index A. France: Institut de Radioprotection et de Sûreté Nucléaire.

Google Scholar

7. Ichou, R., et al. Proceedings of PHYSOR 2020. Cambridge, United Kingdom. March 29^th – April 2^nd (2020).On the validation of VESTA 2.2.0 using the ARIANE GU3 sample

Google Scholar

8. Rochman, D., Vasiliev, A., Ferroukhi, H., Hursin, M., Ichou, R., Taforeau, J., et al. (2021). Analysis for the ARIANE GU3 sample: nuclide inventory and decay heat. Eur. Phys. J. Nuclear Sci. Technol. 7, 14. doi:10.1051/epjn/2021013

CrossRef Full Text | Google Scholar

9. Koning, A., et al. (2006). The JEFF-3.1 Nuclear Data Library”. France: OECD/NEA.

Google Scholar

10.NEA (2014). France. https://www.oecdnea.org/dbforms/data/eva/evatapes/jeff_32/. The JEFF-3.2 Nuclear Data Library.

Google Scholar

11. Chadwick, M.B., et al. (2006). ENDF/B-VII.0: Next Generation Evaluated Nuclear Data Library for Nuclear Science and Technology. Nuclear Data Sheets 107 (12), 2931–3060. ISSN 0090-3752.

Google Scholar

12. Chadwick, M.B., et al. (2011). ENDF/B-VII.1 Nuclear Data for Science and Technology: Cross Sections, Covariances, Fission Product Yields and Decay Data. Nuclear Data Sheets 112 (12), 2931–3060. ISSN 0090-3752.

Google Scholar

13. Studsvik, (2018). CASMO5, A fuel assembly burnup program, Methodology Manual. Idaho, USA: Idaho Falls.

Google Scholar

14. Marguet, S. (2019). La technologie des réacteurs à eau pressurisée. France: EDP Sciences. Chapter 5.7.

Google Scholar

15. Kerkar, N., and Paulin, P. (2008). Exploitation des cœurs REP, Chapters 2 and 3. France: EDP Sciences.

Google Scholar

16. Grard, H. (2014). Physique, fonctionnement et sûreté des REP – Le réacteur en production, Chapters 2 and 4. France: EDP Sciences.

Google Scholar

17. Groupement de, (2014)., 271. France, 25.Groupement de Scientifiques pour l’Information sur l’Energie Nucléaire (GSIEN)La Gazette Nucléaire.

Google Scholar

18. Haeck, W. (2018). GAIA 1.1.0 User’s Manual,” PSN-EXP/SNC/2017-198. Institut de Radioprotection et de Sûreté Nucléaire.

Google Scholar

19. Macfarlane, Robert, Muir, Douglas W., Boicourt, R. M., Albert, Comstock, and Conlin, Jeremy Lloyd (2017). The NJOY Nuclear Data Processing System. United States: N: Web. Version 2016. doi:10.2172/1338791

CrossRef Full Text | Google Scholar

20. NEA, (2000). The JEF-2.2 Nuclear Data Library. Paris: OECD Publishing.

Google Scholar

21. Plompen, A. J. M. (2020). The joint evaluated fission and fusion nuclear data library, JEFF-3.3. Eur. Phys. J. A 56, 181.

Google Scholar

22. Brown, D. A. (2018). ENDF/B-VIII.0: the 8th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data. Nucl. Data Sheets 148, 1–142.

CrossRef Full Text | Google Scholar

23. Shibata, K., Iwamoto, O., Nakagawa, T., Iwamoto, N., Ichihara, A., Kunieda, S., et al. (2011). JENDL-4.0: A new library for nuclear science and engineering. J. Nucl. Sci. Technol. 48, 1–30. doi:10.1080/18811248.2011.9711675

CrossRef Full Text | Google Scholar

24. Koning, A., et al. . TENDL-2012: TALYS-based evaluated nuclear data library. Nuclear Research and Consultancy Group (NRG) Petten, The Netherlands.

Google Scholar

25. NEA/NSC/, R (2015). 8 – « Evaluation guide for the Evaluated Spent Nuclear Fuel Assay Database (SFCOMPO)» - February (2016).

Google Scholar

26. Hebert, A. (2020). Applied reactor physics”. 3rd. Presses Internationales Polytechnique.

Google Scholar

27. Smith, K. (2016). “Nodal diffusion methods: understanding numerous unpublished details,” in PHYSOR 2016 (Sun Valley, ID. May 1–5.

Google Scholar

28. Bonthoux, R., and Taforeau, J. Proceedings of PHYSOR 2022. Pittsburg, USA. May 15^th – 20^th (2022).Impact of infinite lattice approximation on fuel composition for nuclear safety applications.

Google Scholar