Introduction
Due to its rich reserves and potential for effective application, shale oil has been targeted for unconventional oil and gas exploration (Salygin et al., 2019; Podoba and Lavrova, 2021). The main technologies for developing low permeability unconventional reservoirs are multi-fractured horizontal well (MFHW) and stimulated reservoir volume (SRV) fracturing stimulation since they improve low permeability reservoir conductivity for effective production and high recovery. The estimated amount of technically recoverable continental shale oil resources in China was about 60 × 108t by prediction (Zou et al., 2013). However, it is challenging to evaluate the production of shale because of the heterogeneity of reservoir, complex fracture network produced by hydraulic fracturing, and the strong non-linearity of low permeability shale oil flow (Yao et al., 2020).
To match actual performance, we need enough production data for historical matching and choose an appropriate prediction model. Once those geologic parameters, fracture parameters and fluid properties of the share reservoir are obtained from prediction model, we can predict the production decline trend and assess the effectiveness of the completion and stimulation design. In the following section, this paper discussed the physics of fluid storage and flow in shale, and then summarized the current popular production prediction models and techniques for MFHW and SRV in the shale reservoir. Eventually, we point out the problems existing productivity prediction model of horizontal well and emphasize the future research work. It is expected to provide methods and technical reference for the effective development of shale oil and gas resources in the future.
Physics of fluid storage and transport
The complexity of fluid phase behavior, the fluid flow mechanisms in shale matrix and the fracture geometry can make shale reservoir modeling and production forecast difficult. Compared with conventional reservoirs, shale oil has completely different rock and fluid properties, primarily reflected in: (1) Nanopore system becoming main storage space of shale oil; (2) complex chemical composition, containing abundant organic matters and different proportions of inorganic minerals; (3) The internal flow mechanism of shale reservoir. In the study of phase behavior of shale oil, previous studies have discovered the interfacial tension, contact angle, critical temperature, and pressure of fluids contained in shale nanopores are significantly different from those of bulk fluids. (Luo et al., 2016; Sobecki et al., 2019). Teklu et al. (2014) considered changes in the fluid’s critical temperature and pressure in nanopores, results suggesting that fluid’s bubble point pressure, tension between gas and oil, and minimum miscibility pressure all decreased as the pore gets smaller, while the upper dew point pressure rised and the lower dew point pressure fell. As for multi-scale fluid transport mechanisms, researchers have extensively studied different oil and gas flow regimes in shale matrices. Chen et al. (2015) used the lattice Boltzmann method to calculated apparent permeability considering Knudsen diffusion, slip flow. Due to fluid-solid interactions, shale oil flow behavior in nanoporous media is more complicated than gas transport. Yang et al. (2019) proposed a new pore network model to represent shale oil flow in nanoporous media considering microscopic fluid slippage and adsorption on pore surfaces by scaling up shale oil flow from single nanotubes to the pore scale. As to analysis anomalous transport in fracture system, the fractal theory and the fractional derivative method were applied (Cossio et al., 2013; Ozcan et al., 2014; Wang et al., 2015; Albinali and Ozkan, 2016). These works are helpful to account for the effect of reservoir heterogeneities on flow behavior and complex fracture geometries and pores in unconventional reservoirs.
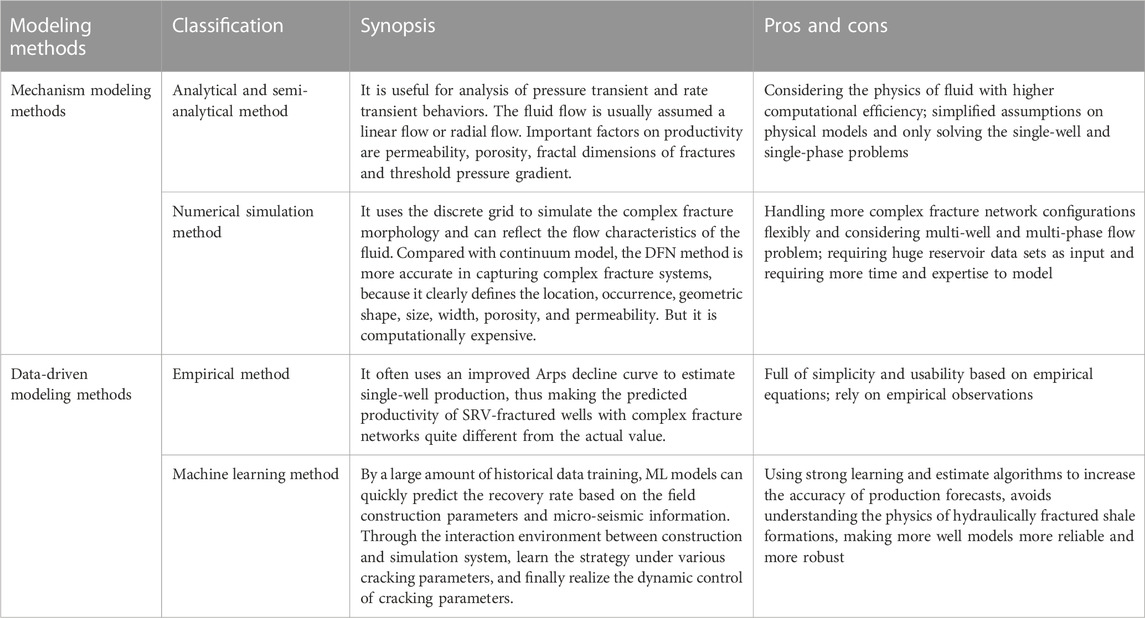
Production forecast techniques of MFHW
Mechanism modeling methods
The analytical and semi-analytical method is applied for analysis of pressure transient and rate transient behaviors. Analytical methods are usually based on certain assumptions, such as assuming that the formation is homogeneous and the fluid follows single-phase flow. The widely used analytical model for MFHW is the linear flow model, which integrates the geometry of the hydraulic fractures with the diffusion in the matrix and the natural fractures to create an analogous homogenous reservoir. Cinco-Ley and Samaniego-V (1981) first proposed the idea of treating the stimulated reservoir as a combination of different flow zones. They developed a bi-linear analytical model where the flow region was divided into by the fluid flowed from the matrix into the fracture and then into the wellbore. The tri-linear flow model (Ozkan et al., 2009; Brown et al., 2011) was the classic linear model to analyze production performance of MFHW, which was extended to multi regions considering more detail outer boundaries and simulate more complex flows (Yuan et al., 2015; Ji et al., 2017). Recently, to describe the flow behavior of reservoir beyond the fracture tip, (Yao et al., 2020), has proposed a composite model combining multi-linear model and radial flow model, where reservoir was divided into multiple subsystems, each of which is subdivided into zones, and the flow within each zone can be linear, radial, or continuous source/sink flow. Semi-analytical method can be utilized to accurately account for the effects of reservoir heterogeneity and different types of boundaries on productivity when predicting the productivity of MFHW traversed by two or three dimensional hydraulic fractures at any arbitrary angle. (Yao et al., 2012, 2015; Zhou et al., 2014). Yu et al. (2016) studied the effect of non-planar hydraulic-fracture geometry on shale production. Sheng et al. (2019) proposed a semi-analytical model of fractal diffusion to describe the distribution of induced fractures around the main hydraulic fracture. These analytical and semi-analytical solutions aim to continuously represent flow regimes (simple linear flow or radial flow), but they simplify the geometry of the complex fracture network and are only applied for the single-phase problems.
Compared with analytical methods, numerical simulation method may perform better in multiphase seepage. This method uses the discrete grid to simulate the complex fracture morphology and can reflect the flow characteristics of the fluid in shale reservoir. The frequently used models for numerical simulation are discrete fracture network model (DFN) and embedded discrete fracture network model (EDFN). The DFN is based on the unstructured mesh and divides the fractures finely. Compared with the continuous representation, the discrete fracture model can simulate large-scale complex fractures (Meyer and Bazan, 2011). Due to the complex fracture network morphology, many scholars have developed DFMs with different numerical methods to simulate multiphase flow (Hoteit and Firoozabadi, 2006; Xu S. et al., 2017). Xu Y. et al. (2017) and AlTwaijri et al. (2018) used DFN to study the effect of fracture geometry on productivity. To solve the problem of low computational efficiency of DFN, Li and Lee (2008) proposed the EDFN, which uses a structured matrix grid, and then the fractures are embedded in the matrix grid as an additional grid to support the processing of small scale fractures to large scale fractures. Though numerical simulation modeling has the advantage of handling more complicated fracture network morphologies and better representing the heterogeneous of shale reservoir, it is complex and requires huge reservoir data sets, i.e., hard and soft data (Mohaghegh, 2013). Moreover, these numerical modeling researches have not been properly considered the complex pore space structure, which has a great impact on fluid flow.
Data-driven modeling methods
The empirical method is a traditional data-driven analysis method, which applied different decline equations for curve-fitting production data. The early empirical method is Arps’ decline curve methodology (Arps, 1945), which gave the time-yield equations of exponential, hyperbolic and harmonic decline curves. However, it only matches the history of boundary dominant flow (Fetkovich, 1980). Consequently, various authors have proposed enhanced prediction models to account for transient flow, such as Duong’s decline model (Duong, 2010), Logistic growth model (Clark et al., 2011), and their composite models (Yu, 2013) etc. All of them are mainly reflected in the derivation of the form of decreasing equation and solution method of the coefficient. Yuan et al. (2017) used a new iterative algorithm for integrated evaluation, prediction and optimization of production in shale reservoir, which improved the existing production data analysis workflow (Clarkson, 2013). To reconcile different types of empirical decline methods, Yu et al. (2018) developed a workflow and it successfully applied it to many shale fields. Empirical method is full of simplicity and usability, allowing quick estimation in a short time, but it cannot accurately describe fluid flow patterns, hydraulic fractures due to their reliant on empirical observations of a particular scenario.
Machine learning (ML) method uses data relationships with strong learning and estimate algorithms to increase the accuracy of production forecasts. Bayesian algorithm, neural network algorithm (NNA), random forest algorithm (RFA) and support vector machine (SVM) are commonly used to predict productivity. Luo et al. (2019) used RFA and NNA to predict 6 months of oil production for the Ford Shale, whose result helped understand the impact of completion design and geological variables on Eagle Ford well production. Lee and Mallick (2021) proposed a Bayesian hierarchical model that leverages shale well data to estimate production decline curves at the individual well and reservoir level. Using the historical data of oil well production, Machado et al. (2020) compared and analyzed the fitting effects of ML algorithms, suggesting ML was effective and required less computational effort compared with conventional methods above. As an important data-driven method, ML avoids explicitly explain the physics of the storage and transport in shale the data characteristics and invests heavily on what we know and measure in the field, making more well models more reliable and more robust. However, data-driven modeling is not applicable to an asset with small number of wells. Data-driven modeling of the production from shale reservoir appears to be the most logical solution until more understanding from experiments can be scaled up and incorporated into our previous models. Table 1 summarizes the key features of aforementioned modeling methods.
Challenges of productivity forcast and future development
The existing productivity prediction theories and methods produced cannot match the expectations for stimulating shale reservoirs to improve production because of the complex fluid phase behavior, fluid flow mechanisms in shale matrix, and complex fracture network. In view of the challenges existing in current productivity prediction should focus on the following aspects:
(1) Theoretically, the fluid phase behavior in shale matrix needs further study. There are lack of full understanding about the main controlling factors for the change of critical parameters of alkanes, accuracy of capillary force estimation and reliability of phase state prediction, and the adsorption characteristics of alkanes (Zhang et al., 2017; Wang X. et al., 2018; Wu et al., 2019; Lu et al., 2022). As to fluid flow mechanisms through shale multiscale pore networks, it is necessary to develop better mathematical models for characterizing transport properties, because most prior research primarily concentrated on the transport processes of single-phase flow and few studied the behavior of multiphase flow.
(2) In production simulation, the structural descriptions of volume-fracturing-induced fracture network, key theories and characterization methods for complex fracture networks is necessary (Ren et al., 2016; Wang W. et al., 2018). It is required a compositional model accounting for characteristics of shale oil, including phase behavior, non-linear flow and stress sensitivity of shale matrix and fracture, especitally, establishing a multi-field coupling mechanism and studying multi-phase flow dynamics (Cui et al., 2018; Praditia et al., 2018; Shahamat and Clarkson, 2018). The process of fluid absorption in shale oil reservoirs, the mechanism and influencing variables of fracturing fluid absorption, and the damage and control of fracturing fluid filtrate to shale reservoirs need be investigated.
(3) It is of necessity to develop key technologies production with optimal and rapid drilling and completion of long horizontal wells and large-scale volume fracturing. Additionally, intelligent fracturing control technologies should be investigated further. New technologies big data, cloud computing, and machine learning should be comprehensively applied to establish the relationship between fracturing parameters and well production and optimize fracturing parameter design to boost MFHW production.
Summary
The physics of fluid storage and the flow in shale is discussed and main methodologies of shale oil production forecasting are summarized, including mechanism modeling methods and data-driven methods. Although there are many production forecasting methods, modeling fluid flows in complex fracture networks in shale reservoirs is still difficult since fundamental theories and characterization methods for complex fracture networks, especially the physics of fluid storage and flow in shale reservoirs have not yet been fully understood. In the future, searching in characterizing complex fracture networks methods, establishing a multi-field coupling mechanism and studying multi-phase flow dynamics and developing Intelligent fracturing control technologies are required for shale reservoir modeling to achieve effective production of shale oil.
Author contributions
FG analysed the relative data and drafted the manuscript. WY make important revisions to the paper and RC gives important suggestions in the writing of the paper. All authors discussed the results and contributed to the final manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Albinali, A., and Ozkan, E. (2016). Analytical modeling of flow in highly disordered, fractured nano-porous reservoirs. All Days (Anchorage, Alsk. U. S. A. SPE), SPE-180440-MS. doi:10.2118/180440-MS
AlTwaijri, M., Xia, Z., Yu, W., Qu, L., Hu, Y., Xu, Y., et al. (2018). Numerical study of complex fracture geometry effect on two-phase performance of shale-gas wells using the fast EDFM method. J. Petroleum Sci. Eng. 164, 603–622. doi:10.1016/j.petrol.2017.12.086
Brown, M., Ozkan, E., Raghavan, R., and Kazemi, H. (2011). Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs. SPE Reserv. Eval. Eng. 14, 663–676. doi:10.2118/125043-pa
Chen, L., Zhang, L., Kang, Q., Viswanathan, H. S., Yao, J., and Tao, W. (2015). Nanoscale simulation of shale transport properties using the lattice Boltzmann method: Permeability and diffusivity. Sci. Rep. 5, 8089. doi:10.1038/srep08089
Cinco-Ley, H., and Samaniego-V., F. (1981). Transient pressure analysis for fractured wells. J. Petroleum Technol. 33, 1749–1766. doi:10.2118/7490-pa
Clark, A. J., Lake, L. W., and Patzek, T. W. (2011). Production forecasting with logistic growth models. In, SPE-144790-MS. doi:10.2118/144790-ms
Clarkson, C. R. (2013). Production data analysis of unconventional gas wells: Review of theory and best practices. Int. J. Coal Geol. 109–110, 101–146. doi:10.1016/j.coal.2013.01.002
Cossio, M., Moridis, G. J. J., and Blasingame, T. A. A. (2013). A semianalytic solution for flow in finite-conductivity vertical fractures by use of fractal theory. SPE J. 18, 83–96. doi:10.2118/153715-pa
Cui, G., Wang, Y., Rui, Z., Chen, B., Ren, S., and Zhang, L. (2018). Assessing the combined influence of fluid-rock interactions on reservoir properties and injectivity during CO2 storage in saline aquifers. Energy 155, 281–296. doi:10.1016/j.energy.2018.05.024
Duong, A. N. (2010). An unconventional rate decline approach for tight and fracture-dominated gas wells. in, SPE-137748-MS. doi:10.2118/137748-ms
Fetkovich, M. J. (1980). Decline curve analysis using type curves. J. Petroleum Technol. 32, 1065–1077. doi:10.2118/4629-pa
Hoteit, H., and Firoozabadi, A. (2006). Compositional modeling of discrete-fractured media without transfer functions by the discontinuous Galerkin and mixed methods. SPE J. 11, 341–352. doi:10.2118/90277-pa
Ji, J., Yao, Y., Huang, S., Ma, X., Zhang, S., and Zhang, F. (2017). Analytical model for production performance analysis of multi-fractured horizontal well in tight oil reservoirs. J. Petroleum Sci. Eng. 158, 380–397. doi:10.1016/j.petrol.2017.08.037
Lee, S. Y., and Mallick, B. (2021). Bayesian hierarchical modeling: Application towards production results in the Eagle Ford shale of south Texas. in 84, 1–43. doi:10.1007/s13571-020-00245-8
Li, L., and Lee, S. H. (2008). Efficient field-scale simulation of black oil in a naturally fractured reservoir through discrete fracture networks and homogenized media. SPE Reserv. Eval. Eng. 11, 750–758. doi:10.2118/103901-pa
Lu, H., Xu, Y., Duan, C., Jiang, P., and Xu, R. (2022). Experimental study on capillary imbibition of shale oil in nanochannels. Energy fuels. 36, 5267–5275. doi:10.1021/acs.energyfuels.2c00309
Luo, G., Tian, Y., Sharma, A., and Ehlig-Economides, C. (2019). Eagle Ford well insights using data-driven approaches. In (OnePetro). doi:10.2523/iptc-19260-ms
Luo, S., Nasrabadi, H., and Lutkenhaus, J. L. (2016). Effect of confinement on the bubble points of hydrocarbons in nanoporous media. AIChE J. 62, 1772–1780. doi:10.1002/aic.15154
Machado, D. A. D., Souza Chaves, M. C., de Oliveira Monteiro, G., and Velasco Medani, D. (2020). Machine learning models to automatically validate petroleum production tests. Day 3 Wed, July 29, 2020 (Virtual SPE), D031S013R002. doi:10.2118/199112-ms
Meyer, B. R., and Bazan, L. W. (2011). A discrete fracture network model for hydraulically induced fractures - theory, parametric and case studies. doi:10.2118/140514-ms
Mohaghegh, S. D. (2013). Reservoir modeling of shale formations. J. Nat. Gas Sci. Eng. 12, 22–33. doi:10.1016/j.jngse.2013.01.003
Ozcan, O., Sarak, H., Ozkan, E., and Raghavan, R. (2014). A trilinear flow model for a fractured horizontal well in a fractal unconventional reservoir. All Days (Amsterdam, Neth. SPE), SPE-170971-MS. doi:10.2118/170971-ms
Ozkan, E., Brown, M., Raghavan, R., and Kazemi, H. (2009). Comparison of fractured horizontal-well performance in conventional and unconventional reservoirs. (OnePetro). doi:10.2118/121290-ms
Podoba, Z., and Lavrova, A. (2021). Shale revolution in the USA and its impact on the international trade flows of oil and gas. doi:10.38050/01300105202121
Praditia, T., Helmig, R., and Hajibeygi, H. (2018). Multiscale formulation for coupled flow-heat equations arising from single-phase flow in fractured geothermal reservoirs. Comput. Geosci. 22, 1305–1322. doi:10.1007/s10596-018-9754-4
Ren, L., Su, Y., Zhan, S., Hao, Y., Meng, F., and Sheng, G. (2016). Modeling and simulation of complex fracture network propagation with SRV fracturing in unconventional shale reservoirs. J. Nat. Gas Sci. Eng. 28, 132–141. doi:10.1016/j.jngse.2015.11.042
Salygin, V., Guliev, I., Chernysheva, N., Sokolova, E., Toropova, N., and Egorova, L. (2019). Global shale revolution: Successes, challenges, and prospects. Sustainability 11, 1627. doi:10.3390/su11061627
Shahamat, M. S., and Clarkson, C. R. (2018). Multiwell, multiphase flowing material balance. SPE Reserv. Eval. Eng. 21, 445–461. doi:10.2118/185052-pa
Sheng, G., Javadpour, F., Su, Y., Liu, J., Li, K., and Wang, W. (2019). A semianalytic solution for temporal pressure and production rate in a shale reservoir with nonuniform distribution of induced fractures. SPE J. 24, 1856–1883. doi:10.2118/195576-pa
Sobecki, N., Nieto-Draghi, C., Di Lella, A., and Ding, D. Y. (2019). Phase behavior of hydrocarbons in nano-pores. Fluid Phase Equilibria 497, 104–121. doi:10.1016/j.fluid.2019.05.025
Teklu, T. W., Alharthy, N., Kazemi, H., Yin, X., Graves, R. M., and AlSumaiti, A. M. (2014). Phase behavior and minimum miscibility pressure in nanopores. SPE Reserv. Eval. Eng. 17, 396–403. doi:10.2118/168865-pa
Wang, W., Su, Y., Sheng, G., Cossio, M., and Shang, Y. (2015). A mathematical model considering complex fractures and fractal flow for pressure transient analysis of fractured horizontal wells in unconventional reservoirs. J. Nat. Gas Sci. Eng. 23, 139–147. doi:10.1016/j.jngse.2014.12.011
Wang, W., Su, Y., Yuan, B., Wang, K., and Cao, X. (2018a). Numerical simulation of fluid flow through fractal-based discrete fractured network. Energies 11, 286. doi:10.3390/en11020286
Wang, X., Shi, F., Liu, C., Lu, D., Liu, H., and Wu, H. (2018b). Extended finite element simulation of fracture network propagation in formation containing frictional and cemented natural fractures. J. Nat. Gas Sci. Eng. 50, 309–324. doi:10.1016/j.jngse.2017.12.013
Wu, K., Chen, Z., Li, J., Lei, Z., Xu, J., Wang, K., et al. (2019). Nanoconfinement effect on n-alkane flow. J. Phys. Chem. C 123, 16456–16461. doi:10.1021/acs.jpcc.9b03903
Xu, S., Feng, Q., Wang, S., Zha, M., Cui, R., Gao, F., et al. (2017a). A stochastic permeability model for shale formations based on embedded discrete fracture model. SPE/AAPG/SEG Unconv. Resour. Technol. Conf. doi:10.15530/URTEC-2017-2691224
Xu, Y., Filho, C. J. S., Yu, W., and Sepehrnoori, K. (2017b). Discrete-fracture modeling of complex hydraulic-fracture geometries in reservoir simulators. SPE Reserv. Eval. Eng. 20, 403–422. doi:10.2118/183647-pa
Yang, Y., Wang, K., Zhang, L., Sun, H., Zhang, K., and Ma, J. (2019). Pore-scale simulation of shale oil flow based on pore network model. Fuel 251, 683–692. doi:10.1016/j.fuel.2019.03.083
Yao, S., Wang, X., Yuan, Q., Guo, Z., and Zeng, F. (2020). Production analysis of multifractured horizontal wells with composite models: Influence of complex heterogeneity. J. Hydrology 583, 124542. doi:10.1016/j.jhydrol.2020.124542
Yao, S., Zeng, F., and Liu, H. (2015). A semi-analytical model for hydraulically fractured horizontal wells with stress-sensitive conductivities. Environ. Earth Sci. 75, 34. doi:10.1007/s12665-015-4775-y
Yao, S., Zeng, F., Liu, H., and Zhao, G. (2012). A semi-analytical model for multi-stage fractured horizontal wells. In, SPE-162784-MS. doi:10.2118/162784-ms
Yu, S. (2013). Best practice of using empirical methods for production forecast and EUR estimation in tight/shale gas reservoirs. in, SPE-167118-MS. doi:10.2118/167118-ms
Yu, S., Jiang, Z., and Lee, W. J. (2018). Reconciling empirical methods for reliable EUR and production profile forecasts of horizontal wells in tight/shale reservoirs. Day 2 Wed, March 14, 2018 Calg. Alta. Can. SPE), D021S004R002. doi:10.2118/189802-ms
Yu, W., Wu, K., and Sepehrnoori, K. (2016). A semianalytical model for production simulation from nonplanar hydraulic-fracture geometry in tight oil reservoirs. SPE J. 21, 1028–1040. doi:10.2118/178440-pa
Yuan, B., Su, Y., Moghanloo, R. G., Rui, Z., Wang, W., and Shang, Y. (2015). A new analytical multi-linear solution for gas flow toward fractured horizontal wells with different fracture intensity. J. Nat. Gas Sci. Eng. 23, 227–238. doi:10.1016/j.jngse.2015.01.045
Yuan, B., Zheng, D., Moghanloo, R. G., and Wang, K. (2017). A novel integrated workflow for evaluation, optimization, and production predication in shale plays. Int. J. Coal Geol. 180, 18–28. doi:10.1016/j.coal.2017.04.014
Zhang, Q., Su, Y., Wang, W., Lu, M., and Sheng, G. (2017). Apparent permeability for liquid transport in nanopores of shale reservoirs: Coupling flow enhancement and near wall flow. Int. J. Heat Mass Transf. 115, 224–234. doi:10.1016/j.ijheatmasstransfer.2017.08.024
Zhou, W., Banerjee, R., Poe, B., Spath, J., and Thambynayagam, M. (2014). Semianalytical production simulation of complex hydraulic-fracture networks. SPE J. 19, 06–18. doi:10.2118/157367-pa
Keywords: shale oil reservoirs, horizontal well, hydraulic fracturing, production forecast, prediction model
Citation: Guo F, Chen R and Yan W (2023) Research progress and challenges on production forecast techniques of fractured horizontal wells in shale oil reservoirs. Front. Energy Res. 11:1028770. doi: 10.3389/fenrg.2023.1028770
Received: 26 August 2022; Accepted: 21 February 2023;
Published: 07 March 2023.
Edited by:
Fei Wang, Qingdao University of Science and Technology, ChinaReviewed by:
Ping Zhu, Technical University of Denmark, DenmarkCopyright © 2023 Guo, Chen and Yan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Weiwei Yan, eWFud3dAY2psdS5lZHUuY24=
 Fanrong Guo
Fanrong Guo Rou Chen
Rou Chen Weiwei Yan
Weiwei Yan