
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res., 07 October 2022
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.996556
This article is part of the Research TopicModern World Heat Transfer Problems: Role of Nanofluids and Fractional Order ApproachesView all 18 articles
 Mustafa Mutiur Rahman1
Mustafa Mutiur Rahman1 Wasim Jamshed2*
Wasim Jamshed2* Suriya Uma Devi. S3
Suriya Uma Devi. S3 Rabha W. Ibrahim4
Rabha W. Ibrahim4 Amjad Ali Pasha5
Amjad Ali Pasha5 Basma Souayeh6
Basma Souayeh6 Rabia Safdar7
Rabia Safdar7 Mohamed R. Eid8,9
Mohamed R. Eid8,9 Syed M. Hussain10
Syed M. Hussain10 El Sayed M. Tag El Din11
El Sayed M. Tag El Din11Because of its multivariate particle suspension approach, the developing class of fluid has a better level of stability as well as increased heat transfer. In this regard, hybrid nanofluid outperforms ordinary fluid and even well-known nanofluid. In a slick environment, we investigate its fluidity and heat transfer qualities. Nano-leveled particle morphologies, porousness materials, variable thermal conductivity, slippage velocity, and thermal radiative effects are all being studied. The Galerkin finite element method is a numerical methodology for numerically solving the governing equations (G-FEM). For this analysis, a Powell-Eyring hybrid nanofluid (PEHNF) flowing via a permeable stretchable surface is used, which comprises two types of nanoparticles (NP), copper (Cu), and titanium alloy (Ti6Al4V) dispersed in sodium alginate (C6H9NaO7). The heat transfer ratio of PEHNF (Ti6Al4V-Cu/C6H9NaO7) remained much greater than that of conventional nanofluids (Cu-C6H9NaO7), with a range of 43%–54%. When lamina particles are present, the thermal conductivity of the boundary layer increases dramatically, while spherical nanoparticles have the lowest thermal conductivity. As nanoparticles are added under their fractional sizes, radiative heat conductance, and flexible heat conductance, the system’s entropy increases. The flow system’s ability to transport mass decreases when molecule diffusivity decreases dramatically. This is theoretically related to a rise in Schmidt number against molecular diffusivity.
Different simulations, including the regulator rule scheme, Carreau’s scheme, Cross’ scheme, and Ellis’s scheme, are offered to shed light on the behavior of HNFs, however, few researchers have investigated the Williamson liquid scheme (WLS). Williamson (1929) thought about the flow of hybrid nanofluids (HNFs) such as (pseudo-plastic liquids), proposed an equation system to represent the flow of HNFs, and then empirically verified the results. In an advanced gravitational investigation, researchers proposed that an echoing level of a WLS should movement concluded an inspired superficial. A real fluid has both the lowest and highest operational viscosities that relate to its molecular structure. The WLS measures together the lowest and highest thicknesses. During the attendance of revolution, Said et al. (Said et al., 2021) planned a 3D-class of HNF to additional upsurge the heat transfer (HT) rate completed by widening slip. Mandal et al. (Mandal et al., 2022) exploited an artificial neural network to form investigational statistics. Saha et al. (Saha et al., 2022) described an investigation of HT and rheological possessions of HNFs for refrigeration presentations. Survey studies by Al‐Chlaihawi et al. (Al‐Chlaihawi et al., 2022), Kursus et al. (Kursus et al., 2022), Xiong et al. (Xiong et al., 2021), and Muneeshwaran et al. (Muneeshwaran et al., 2021) respectively, can be located in this direction, while Dubey et al. (Dubey and Sharma, 2022) offered a short survey in HNF on mechanics revisions. Syed and Jamshed (Hussain and Jamshed, 2021) considered the movement of MHD tangent HNF via a strained slip’s boundary layer. In accumulation, the demonstration of the extended HT of tangent hyperbolic fluids crossways a nonlinearly fluctuating slide containing HNFs was tested by Qureshi (Qureshi, 2022), Jamshed et al. (Jamshed et al., 2021a), and Parvin et al. (Parvin et al., 2021).
Puneeth et al. (Shankaralingappa et al., 2021) measured 3D-assorted convection movement of HNFs of a non-linear widening surface using a modified Buongiorno’s nanofluids model (MBNM). Rana et al. (Rana et al., 2021) presented a study of HNF movement past a perpendicular platter with nanoparticle aggregation kinematics, the current slide, and important buoyancy force possessions utilizing MBNM. Mahanthesh et al. (Mahanthesh et al., 2021) estimated the HT optimization of HNFs with the help of MBNM. Owhaib and Al-Kouz (Owhaib and Al-Kouz, 2022) and Owhaib et al. (Owhaib et al., 2021) employed the concept of MBNM in 3D systems of movement and HT of bi-directional overextended HNF film showing an exponential heat generation. Hussain et al. (Hussain et al., 2022a) characterized a biochemical response and current of HNFs flow-through solar gatherer as potential solar energy applying the idea of MBNM. Roşca et al. (Roşca et al., 2021) engaged the movement and HT of a stretching/shrinking slip by the virtue of MBNM. Akram et al. (Akram et al., 2022) analyzed the electroosmotic movement of silver-water HNF controlled by using two altered methods for NF including the MBNM. Areekara et al. (Areekara et al., 2022) suggested a study on NF movement with asymmetrical heat foundation and representative boundary conditions with the application by MBNM.
Nanofluids own the characteristics of the non-Newtonian fluid, together with the viscoelastic properties. Extended experimental work research is required to develop nanofluid viscosity models for use in simulation studies (Wang and Mujumdar, 2008; Bilgili et al., 2021). Therefore, the Powell-Eyring fluid is considered in the current model, together with the significance of non-Newtonian fluid properties. This type of fluid is proposed by Powell and Eyring (Hayat and Nadeem, 2018) in 1944. Moreover, Powell-Eyring fluid is one type of visco-elastic fluid. Eyring–Powell fluid model implements a higher-level complicated mathematical framework, but it is found to be the greater model over previous viscoelastic fluid models. This model is founded on the kinetic theories of liquids, not on empirical expressions. In addition, Eyring–Powell fluid model has Newtonian properties at low and great shear stress. Examples of Powell-Eyring fluids are polymer melts and solids suspended in non-Newtonian liquids. The significant implementations of Powell-Eyring fluid have been observed in engineering, manufacturing, and industrial areas such as polymers, pulp, plasma, and other biological technology. However, several researchers have investigated the properties of non-Newtonian Powell-Eyring nanofluid (Hayat et al., 2015; Malik et al., 2015; Hayat et al., 2017). Aziz and Afy (El-Aziz and Afify, 2019) chose the shooting technique, together with the Buongiorno nanofluid model to obtain the Casson nanofluid’s numerical solution over a stretching sheet. At the initial stages of flow (primary and secondary flow), they concluded that the Hall parameter upsurges in the convective rate of heat and mass transfer, together with the drag coefficient. Moreover, the nanoparticle volume concentration parameter increases for increasing velocity slip values. Consequently, the Sherwood number is reduced. Subsequently, the influences on the magnet field and Soret-Dufour have been reportedly on non-rotational Newton’s Oldroyd-B nanofluid stream bounded by the stretched sheet (Ali et al., 2021). This model is also being restricted under the modification of Fourier’s law. For the step of numerical findings, the Galerkin-Finite element system was developed.
Porous media models (PMMs), frequently referred to as porous materials, have pores (vacuums). The thin part of the material is referred to as the “matrix” or “frame.” Typically, a fluid is injected into the pores (fluid or fume). Though the material that makes up the frame is regularly hard, structures like foams might profit from the idea of PMM. To apply solar heat, Jamshed et al. (Jamshed et al., 2021b) employed PMM in solar aircraft combining tangent HNFs. Using the PMM in HNFs, Shahzad et al. (Shahzad et al., 2021) developed a comparative mathematical study of HT. Numerical conduct of a 2D-Magneto double-diffusive convection flow of HNF over PMM was provided by Parvin et al. (Parvin et al., 2021). Faisal et al. (Shahzad et al., 2022a) reported that using HNFs rather than PMM increased the thermal efficacy of solar water pumps. Banerjee and Paul (Banerjee and Paul, 2021) examined the most recent research and advancements concerning PMM combustion applications. For pebble-bed devices, Zou et al. (Zou et al., 2022) designed an explicit system of stone heat in the PMM. PMM substantiation using stress drip dimensions was suggested by Lee et al. (Lee et al., 2022). On a constructed soaking soil pile model, Cui et al. (Cui et al., 2021) investigated a numerical analysis of the solution for longitudinal quivering of a fluctuating pile based on PMM. A machine learning approach was taken by Alizadeh et al. (Alizadeh et al., 2021) to calculate transference and thermodynamic processes in metaphysical systems HT in HNFs movement in PMM. A non-homogenous HNF was proposed by Rashed et al. (Rashed et al., 2021) for 3D convective movement in enclosures with assorted PMM (AdnanKhan et al., 2021; Adnan and Ashraf, 2022a; Khan et al., 2022a; Alharbi et al., 2022; Ashraf et al., 2022a; Ashraf et al., 2022b; Adnan and Ashraf, 2022b; Khan et al., 2022b; Khan et al., 2022c; Murtaza et al., 2022). presented the latest updating that involves the traditional nanofluids with the features of heat and mass transmission in a different physical situation.
The rate of HT through a component thickness of a material per unit area per temperature variation is known as the variable thermal conductivity (VTC) of that material. Alternatively said, the VTC is inversely proportional to the temperature capacity. Gbadeyan et al. (Olabode et al., 2021) studied the effect of VTC and thickness on Casson NF movement with convective warming and velocity slide. Mabood et al. (Mabood et al., 2021) impacted the Stefan blowing and mass convention on the movement of HNF of VTC in a revolving disk. Abouelregal et al. (Abouelregal et al., 2021) checked the thermo-viscoelastic fractional model of revolving HNFs with VTC owing to mechanical and current loads. Swain et al. (Swain et al., 2021) utilized the HT and stagnation‐point movement of influenced HNFs with VTC. Also, Ahmed et al. (Ahmed et al., 2021) considered the HT of MHD movement of HNFs via an exponential penetrable widening arched surface with VTC. Mahdy et al. (Mahdy et al., 2021) employed the VTC and hyperbolic two-temperature philosophy throughout the magneto-photothermal model of semiconductors induced by laser pulses. Hobiny and Ibrahim (Hobiny and Abbas, 2022) analyzed the impacts of VTC in a semiconducting medium utilizing the finite element technique. Ahmad et al. (Ahmad et al., 2022a) studied the unsteady 3D-bio convective movement of HNFs by an exponentially widening sheet with VTC and chemical reaction. Din et al. (Din et al., 2022) assumed the entropy generation from convective released moving exponential porous fins with VTC and interior temperature compeers. For more details see Refs (Akgül et al., 2022; Attia et al., 2022; Ahmad et al., 2022b; Bilal et al., 2022; Qureshi et al., 2022; Safdar et al., 2022).
A statistical technique called quadratic regression estimation (QRE) is considered to identify the parabola equation that finest fits a given collection of data. Finding the equation of the conventional line that most closely fits a collection of information is the goal of this sort of regression, which is an extension of modest linear regression. Jamei et al. (Jamei et al., 2022) estimated the thickness of HNFs for current energy using the QRE. Nandi et al. (Nandi et al., 2022a; Nandi et al., 2022b) suggested different investigations on HNFs based on QRE. Bhattacharyya et al. (Bhattacharyya et al., 2022) introduced a numerical and statistical method to capture the movement characteristics of HNFs containing copper and grapheme HNs utilizing QRE. Kumbhakar and Nandi (Kumbhakar and Nandi, 2022) presented an unsteady MHD radiative-dissipative movement of HNFs of a widening sheet with slide and convective conditions employing QRE. Said et al. (Said et al., 2022) considered the application of the original outline by collaborative boosted QRE of HNFs. Chen et al. (Chen et al., 2022a; Chen et al., 2022b) gave a long approximation of the physical properties of HNFs.
By focusing on the flowing rapidity of a Powell-Eyring HNFs as well as thermal transmission with changing heat and current conductance flowing through a stretched permeable material, this work intends to bridge a gap in the previous survey and fill a knowledge gap. The flow of nanoliquid was geometrically modeled using a single-phase nanoliquid. The foundation liquid in the investigation of copper (Cu) and titanium alloy (Ti6Al4V) hybrid nanoparticles is sodium alginate (C6H9NaO7). The regulatory equations of the Powell-Eyring hybridization nanoliquid are transformed into ordinary differential equations (ODEs). The influences of porous parameters, thermal radiative fluxing, and variable thermal conductance are considered in the examination. Then, the effects of the slippage velocity and nanoparticle shape factors are probed in flowing and entropy aspects. The obtained ODEs are solved numerically using the Galerkin finite element technique and the necessary prevailing parametric parameters. Numerical results are shown graphically, and comments are built upon. In-depth research has been done on the possessions of particle morphologies, the convective slide boundary condition, the thermal energy movement, and the slippery velocity.
Analysis of movement shows how a superficial moves horizontally at an accelerating rate.
where
Under the following hypotheses and constraints, the theoretical framework is selected:
1) Unsteady two-dimensional laminar flowing.
2) Boundary-layer guesstimate.
3) Modified Buongiorno's structure.
4) Non-Newtonian PEHNFs.
5) Different effects i.e., porous medium, variable thermal conductivity, radiative flowing, and nanomolecules shaped influence.
6) Penetrable expanding surface.
7) Slip and convective boundary constraints.
The exact formulary of the stress tensor of fluid follows the Powell-Eyring relationship is provided as (Aziz et al., 2021):
Here,
Classic formulas (Aziz et al., 2021) of a viscidness P-EHNF beside with entropy assembly befittingly adapted underneath normal boundary-layer approximations via a penetrable substantial, porous medium, variable thermal conductivity, and radiative flowing are
the suitable boundary conditions are (Aziz et al., 2021):
Where a flow speed is of the structure
The mongrelized nanoliquid is combined principally with Cu nano molecules in machine grease standard liquid at a constant fractional size (
The combination of nanomolecules in the basefluid runs to a difference in the characteristics thermophysically. Table 1 summarises the relevant parameters for PENF (Reddy et al., 2014; Din et al., 2022).
Herein,
Heat conditional of heat conducting for hybrid nanoliquid blend is followed as (Jamshed et al., 2021c):
The significance of several nanomolecules shaped is identified as the nanomolecules shaped influence. Figure 2 gives the values of the practical shaped component for different element shapes are obtained as (Akgül et al., 2022): Figure 3 demonstrates the themophysical values of the used materials of HNF.
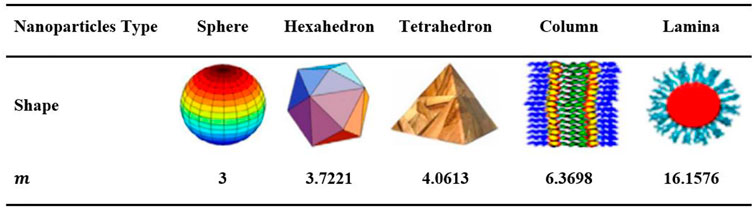
FIGURE 2. Standards of the practical shaped element for diverse particle shaped. The material possessions of the crucial sodium alginate (C6H9NaO7) and the various NP exploited in this research are indicated in Figure 3 (Xu and Chen, 2017; Makinde et al., 2018; Jamshed et al., 2021d).
PEHNF radiative flow only travels a little space resulting in the thickener of NF. Because this is happening, Rosseland’s guesstimate for radiative fluxing (Shahzad et al., 2022b), is used in Eq. 5 and it is given
Where
Boundary-value problem (BVP) formulas (3–6) are converted in the definition of the similarity procedure that converts the regulating PDEs to ODEs. Advancing streaming function
and similarity transformations are
with
where
Meticulous authentication is done on Eq. 3. Notation
It is noticed a variety of factors depend on the similarity variable
The drag force
where
Employing the dimensionless makeovers (11), one acquires
Where
The relevant constraints of the present system were studied numerically using the finite element technique. The finite element approach is based on the partitioning of the desired domain into elements (finite). The FES (finite element scheme) is covered in this section. Figure 4 depicts the flow chart of the finite element method. This method has been employed in numerous computational fluid dynamics (CFD) problems; the assistances of employing this methodology are discussed further below. II- A Galerkin finite element manner (G-FEM) is utilized to determine the solutions of highly elliptic equations (Brewster, 1992) (non-linear). Using a finite element technique, the domain of the current exemplary is broken into small parts. G-FEM is used in a variety of applications, including electrical systems, solid mechanics, chemical processes, and fluid-related challenges. The phases of the G-FEM strategy are as next:
Phase-I. Weak form is derived from strong form (mentioned ODEs), and residuals are computed.
Phase -II. Shape functions are linearly taken, and G-FEM is used to generate a weak form.
Phase -III. The assembly method is used to build stiffness elements, and a global stiffness matrix is created.
Phase -IV. Using the Picard linearizing technique, an algebraic structure (non-linear equalities) is produced.
Phase -V. Employing the next halting conditions, algebraic equations are simulated using 10−5 (computational tolerance).
Additionally, the Galerkin restricted constituent technique’s watercourse summary is represented in Figure 4.
On the one hand, the validity of the computational technique was tested by comparing the current method’s performance to the available data on heat transfer rate in Refs. (Hussain et al., 2022b; Bouslimi et al., 2022). Table 3 demonstrates the consistent comparison found across the investigations. The current study’s provided results, on the other hand, are quite accurate.
A crucial aspect that interests scientists and researchers is the reduction of energy resource waste. Therefore, these necessary outcomes for researchers are gained by enhancing the functionality of earlier systems. Systems’ entropy creation is examined in order to achieve energy irreversibility and reduce waste. Design is prearranged about entropy generation in NFs (Hussain, 2022)
The irreversibility of thermal transport is represented by the leading term in the preceding equation, while the frictional and porous media effects are represented by the following terms. The nondimensional entropy establishment is prearranged by
Eq. 11 is utilized to obtain a dimensionless equation regarding entropy formation as follows,
Here,
Quadratic regression analysis (QRA) is the statistical procedure that was used to test the elements that influence the flow in the system one at a time. Technically, this process works with the single key aspect and tends to explore its significance over the flow by keeping the other constraints as constants. In this section, the features of frictional force and Nusselt quantity are examined under Quadratic regression analysis (QRA).
Regarding the frictional factor
QRA for the predicted
Likewise, towards the Quadratic regression assessment of Nusselt quantity
with
Tables 4, 5 illustrate correspondences between the frictional factor
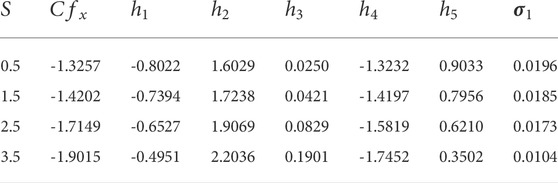
TABLE 5. Frictional factor
Because of the thermal outcome, the thermal slippage constrain plays a vital role in the heat transference rate. The reduced frictionless force mechanisms hold an upper hand over the QRA technique with fast and better convergence when the optimal regression estimate was introduced to the process and the percentage difference tends to be nearly zero.
Results of the numerical procedure adapted for the parametrical studies were showcased and discussed in this section. Influence constraints like
The illustration of the non-Newtonian Powell-Eyring fluid term (
The graphical results of permeability parameter
Finally, the achieved outcome of the impact of the changes in various parameters and 5 shape nanoparticles by the names of a sphere, hexahedron, tetrahedron, column, and lamina on the profile of temperature and entropy have been analyzed and investigated in Figure 7A,B. In Figure 7A, the influence of the increment in nanoparticle shape parameter
The visualization of the temperature profile against Biot numbers
The impacts of velocity slip parameters (ε) on the velocity field, temperature field, and entropy generation are plotted in Figure 9A–C, by choosing C6H9NaO7 as the base fluid. The effect of the strain parameter is reported from the PENF (Cu-C6H9NaO7) and PEHNF (Ti6Al4V-Cu/C6H9NaO7) momentum distribution (Figure 9A). This parameter is obtained from the boundary conditions of the current model. The gradual increment of the velocity slip enhances the fluid viscosity, thus decreasing the fluid velocity. The higher concentration of slip velocity (ε) values lowers the thermal boundary layer thickness (Figure 9B), which the diminution of the profile is associated with the Williamson nanofluids. At the same time, the slip velocity parameter slows the collisions with molecular diffusion. When the concentration of nanoparticles is higher in a system, the system is associated with the instantaneous possessions of thermal convection, transmission, and kinematic viscosity. Figure 9C shows the plot of entropy generated (
The effect of the Reynolds number (
Figure 11A exhibits dispersal of concentration
The coefficients in the components of the flow and heat transmission are namely dragged force
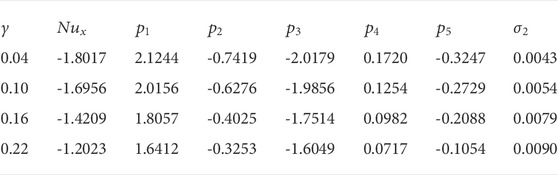
TABLE 6. Nusselt quantity
In this mathematical investigation, the heat transmission in a Powell-Eyring hybrid nanofluid (PEHNF) model bounded by an expanding surface is investigated. This model is implemented in a thermal system, which is inspired by the modified Buongiorno’s NF prototype. The presence of nanoparticles such as Cu-C6H9NaO7 and Ti6Al4V-Cu/C6H9NaO7 nanoparticles are implemented in this model. The influences of porous media, thermal radiative flow, and variable thermal conductivity are taken into account in the mathematical model. Furthermore, the effect of the nanoparticles’ shape factors is determined, and their impacts can be observed in thermal and entropy aspects. The numerical solutions for the current mathematical model can be achieved by following these steps: 1) Apply similarity solution to convert PDEs to ODEs, and 2) solve the ODEs with Galerkin finite element plan. The primary outcomes from this investigation are listed for the profiles such as velocity, temperature, and concentration, together with the coefficients of drag force and Nusselt number. These outcomes are listed below:
1) Along the far stream, the velocity field is reduced for the upsurging Powell-Eyring fluid (
2) The temperature profile of Powell-Eyring fluid for both cases of Cu-C6H9NaO7 (conventional nanofluid) and Ti6Al4V-Cu/C6H9NaO7 (hybrid nanofluid) intensifies under the increment of
3) The temperature distribution is affected by most of the physical quantities, which denotes that nanofluids have a high heat exchange rate. This property helps control the temperature during spin coating processes.
4) The entropy profile against Powell-Eyring fluid (
5) The shape of nanoparticles is namely sphere, hexahedron, tetrahedron, lamina, and column. Among them, lamina has the greatest impact on the function of temperature and entropy.
6) The ability of the flow system toward the mass transference gets reduced as the molecular diffusivity drops significantly. This can be technically connected with the increase in Schmidt number versus the molecular diffusivity.
7) The remarkable change in frictional force factor for Ti6Al4V-Cu/C6H9NaO7 and Cu-C6H9NaO7 nanofluids can be seen, compared to the Nusselt number coefficient for the porosity and volume fraction.
These outcomes can be a guideline for the industry and technology, to choose the appropriate working fluid for improved productivity in the associated device or prototype Subsequently, this research work can be extended by applying the model of rotating disk flow considering ferromagnetic nanoparticles (Jamshed et al., 2021e; Pasha et al., 2022). The FEM could be applied to a variety of physical and technical challenges in the future (Jamshed et al., 2022b; Hussain et al., 2022b; Hussain et al., 2022a).
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
WJ, MR and SS formulated the problem. WJ and RI solved the problem. WJ, MR, SS, RI, BS, RS, AP, ME, SH and ED computed and scrutinized the results. All the authors equally contributed in writing and proof reading of the paper. All authors reviewed the manuscript.
Authors are grateful to the Deanship of Scientific Research, Islamic University of Madinah, Ministry of Education, KSA for supporting this research work through research project grant under Research Group Program/1/804.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abouelregal, A. E., Ahmad, H., Nofal, T. A., and Abu-Zinadah, H. (2021). Thermo-viscoelastic fractional model of rotating nanobeams with variable thermal conductivity due to mechanical and thermal loads. Mod. Phys. Lett. B 35 (18), 2150297. doi:10.1142/s0217984921502973
Adnan, , and Ashraf, W. (2022a). Numerical thermal featuring in γAl2O3-C2H6O2 nanofluid under the influence of thermal radiation and convective heat condition by inducing novel effects of effective Prandtl number model (EPNM). Adv. Mech. Eng., 14(6), p.168781322211065, doi:10.1177/16878132221106577
Adnan, , and Ashraf, W., (2022b). Thermal efficiency in hybrid (Al2O3-CuO/H2O) and ternary hybrid nanofluids (Al2O3-CuO-Cu/H2O) by considering the novel effects of imposed magnetic field and convective heat condition. Waves in Random and Complex Media, pp.1–16.
Adnan, , Khan, U., Ahmed, N., Manzoor, R., and Mohyud-Din, S. T. (2021). Impacts of various shaped Cu-nanomaterial on the heat transfer over a bilateral stretchable surface: Numerical investigation. Adv. Mech. Eng. 13 (12), 168781402110674. doi:10.1177/16878140211067420
Ahmad, S., Naveed Khan, M., and Nadeem, S. (2022). Unsteady three dimensional bioconvective flow of Maxwell nanofluid over an exponentially stretching sheet with variable thermal conductivity and chemical reaction. Int. J. Ambient Energy in press, 1–11. doi:10.1080/01430750.2022.2029765
Ahmad, N., Mehmood, N., and Akgül, A. (2022). Applications of some new Krasnoselskii-type fixed-point results for generalized expansive and equiexpansive mappings. Adv. Contin. Discret. Model. 2022 (1), 30–19. doi:10.1186/s13662-022-03704-w
Ahmed, K., Akbar, T., Muhammad, T., and Alghamdi, M. (2021). Heat transfer characteristics of MHD flow of Williamson nanofluid over an exponential permeable stretching curved surface with variable thermal conductivity. Case Stud. Therm. Eng. 28, 101544. doi:10.1016/j.csite.2021.101544
Akgül, E. K., Akgül, A., Jamshed, W., Rehman, Z., Nisar, K. S., Alqahtani, M. S., et al. (2022). Analysis of respiratory mechanics models with different kernels. Open Phys. 20 (1), 609–615. doi:10.1515/phys-2022-0027
Akram, J., Akbar, N. S., and Tripathi, D. (2022). Analysis of electroosmotic flow of silver-water nanofluid regulated by peristalsis using two different approaches for nanofluid. J. Comput. Sci. 62, 101696. doi:10.1016/j.jocs.2022.101696
Al‐Chlaihawi, K. K., Alaydamee, H. H., Faisal, A. E., Al‐Farhany, K., and Alomari, M. A. (2022). Newtonian and non‐Newtonian nanofluids with entropy generation in conjugate natural convection of hybrid nanofluid‐porous enclosures: A review. Heat. Trans. 51 (2), 1725–1745. doi:10.1002/htj.22372
Alharbi, K. A. M., Khan, U., Ahammad, N. A., Ullah, B., Wahab, H. A., Zaib, M., et al. (2022). Heat transport mechanism in Cu/water and (Cu–Al2O3)/water under the influence of thermophysical characteristics and non-linear thermal radiation for Blasius/Sakiadis models: Numerical investigation. J. Indian Chem. Soc. 99 (8), 100578. doi:10.1016/j.jics.2022.100578
Ali, B., Hussain, S., Nie, Y., Hussein, A. K., and Habib, D. (2021). Finite element investigation of Dufour and Soret impacts on MHD rotating flow of Oldroyd-B nanofluid over a stretching sheet with double diffusion Cattaneo Christov heat flux model. Powder Technol. 377, 439–452. doi:10.1016/j.powtec.2020.09.008
Alizadeh, R., Abad, J. M. N., Ameri, A., Mohebbi, M. R., Mehdizadeh, A., Zhao, D., et al. (2021). A machine learning approach to the prediction of transport and thermodynamic processes in multiphysics systems-heat transfer in a hybrid nanofluid flow in porous media. J. Taiwan Inst. Chem. Eng. 124, 290–306. doi:10.1016/j.jtice.2021.03.043
Areekara, S., Mackolil, J., Mahanthesh, B., Mathew, A., and Rana, P. (2022). A study on nanoliquid flow with irregular heat source and realistic boundary conditions: A modified buongiorno model for biomedical applications. Z. Angew. Math. Mech. 102 (3), e202100167. doi:10.1002/zamm.202100167
Ashraf, W., Junaid Anjum, H., and Khan, I. (2022a). Energy transformation and entropy investigation in the nanofluid composed by γ-nanomaterial over a permeable convective surface with solar thermal radiation: Numerical analysis. Front. Energy Res. 10, 507.
Ashraf, W., Khan, I., Shemseldin, M. A., and Mousa, A. A. A. (2022b). Numerical energy storage efficiency of MWCNTs-propylene glycol by inducing thermal radiations and combined convection effects in the constitutive model. Front. Chem. 10, 879276. doi:10.3389/fchem.2022.879276
Attia, N., Akgül, A., Seba, D., Nour, A., and Asad, J. (2022). A novel method for fractal-fractional differential equations. Alexandria Eng. J. 61 (12), 9733–9748. doi:10.1016/j.aej.2022.02.004
Aziz, A., Jamshed, W., Aziz, T., Bahaidarah, H., and Ur Rehman, K. (2021). Entropy analysis of Powell–Eyring hybrid nanofluid including effect of linear thermal radiation and viscous dissipation. J. Therm. Anal. Calorim. 143 (2), 1331–1343. doi:10.1007/s10973-020-10210-2
Banerjee, A., and Paul, D. (2021). Developments and applications of porous medium combustion: A recent review. Energy 221, 119868. doi:10.1016/j.energy.2021.119868
Bhattacharyya, A., Sharma, R., Hussain, S. M., Chamkha, A. J., and Mamatha, E. (2022). A numerical and statistical approach to capture the flow characteristics of Maxwell hybrid nanofluid containing copper and graphene nanoparticles. Chin. J. Phys. 77, 1278–1290. doi:10.1016/j.cjph.2021.09.015
Bilal, S., Shah, I. A., Akgül, A., Tekin, M. T., Botmart, T., Yahia, I. S., et al. (2022). A comprehensive mathematical structuring of magnetically effected Sutterby fluid flow immersed in dually stratified medium under boundary layer approximations over a linearly stretched surface. Alexandria Eng. J. 61 (12), 11889–11898. doi:10.1016/j.aej.2022.05.044
Bilgili, F., Nathaniel, S. P., Kuşkaya, S., and Kassouri, Y. (2021). Environmental pollution and energy research and development: An environmental kuznets curve model through quantile simulation approach. Environ. Sci. Pollut. Res. 28 (38), 53712–53727. doi:10.1007/s11356-021-14506-0
Bouslimi, J., Alkathiri, A. A., Alharbi, A. N., Jamshed, W., Eid, M. R., and Bouazizi, M. L. (2022). Dynamics of convective slippery constraints on hybrid radiative Sutterby nanofluid flow by Galerkin finite element simulation. Nanotechnol. Rev. 11 (1), 1219–1236. doi:10.1515/ntrev-2022-0070
Chen, T. C., Hammid, A. T., Akbarov, A. N., Shariati, K., Dinari, M., and Ali, M. S. (2022). Estimating the physical properties of nanofluids using a connectionist intelligent model known as gaussian process regression approach. Int. J. Chem. Eng. 2022, 1–14. doi:10.1155/2022/1017341
Chen, T. C., Majdi, H. S., Ismael, A. M., Pouresmi, J., Ahangari, D., and Noori, S. M. (2022). Insights into the estimation of the enhanced thermal conductivity of phase change material-containing oxide nanoparticles using gaussian process regression method. Int. J. Chem. Eng. 2022, 1–10. doi:10.1155/2022/7119336
Cui, C., Meng, K., Xu, C., Liang, Z., Li, H., and Pei, H. (2021). Analytical solution for longitudinal vibration of a floating pile in saturated porous media based on a fictitious saturated soil pile model. Comput. Geotechnics 131, 103942. doi:10.1016/j.compgeo.2020.103942
Devi, S. S. U., and Devi, S. A. (2016). Numerical investigation of three-dimensional hybrid Cu–Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 94 (5), 490–496. doi:10.1139/cjp-2015-0799
Din, Z. U., Ali, A., De la Sen, M., and Zaman, G. (2022). Entropy generation from convective–radiative moving exponential porous fins with variable thermal conductivity and internal heat generations. Sci. Rep. 12 (1), 1791–1811. doi:10.1038/s41598-022-05507-1
Dubey, V., and Sharma, A. K. (2022). A short review on hybrid nanofluids in machining processes. Adv. Mater. Process. Technol., 1–14. doi:10.1080/2374068x.2022.2087315
El-Aziz, M. A., and Afify, A. A. (2019). Effect of Hall current on MHD slip flow of Casson nanofluid over a stretching sheet with zero nanoparticle mass flux. Thermophys. Aeromech. 26 (3), 429–443. doi:10.1134/s0869864319030119
Hayat, T., and Nadeem, S. (2018). Flow of 3D Eyring-Powell fluid by utilizing Cattaneo-Christov heat flux model and chemical processes over an exponentially stretching surface. Results Phys. 8, 397–403. doi:10.1016/j.rinp.2017.12.038
Hayat, T., Ashraf, B., Shehzad, S. A., and Abouelmagd, E. (2015). Three-dimensional flow of Eyring Powell nanofluid over an exponentially stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 25, 593–616. doi:10.1108/hff-05-2014-0118
Hayat, T., Ullah, I., Alsaedi, A., and Farooq, M. (2017). MHD flow of Powell-Eyring nanofluid over a non-linear stretching sheet with variable thickness. Results Phys. 7, 189–196. doi:10.1016/j.rinp.2016.12.008
Hobiny, A. D., and Abbas, I. (2022). The impacts of variable thermal conductivity in a semiconducting medium using finite element method. Case Stud. Therm. Eng. 31, 101773. doi:10.1016/j.csite.2022.101773
Hussain, S. M., and Jamshed, W. (2021). A comparative entropy based analysis of tangent hyperbolic hybrid nanofluid flow: Implementing finite difference method. Int. Commun. Heat Mass Transf. 129, 105671. doi:10.1016/j.icheatmasstransfer.2021.105671
Hussain, S. M., Jamshed, W., Safdar, R., Shahzad, F., Mohd Nasir, N. A. A., and Ullah, I. (2022). Chemical reaction and thermal characteristiecs of maxwell nanofluid flow-through solar collector as a potential solar energy cooling application: A modified Buongiorno's model. Energy & Environment, 0958305X221088113. doi:10.1177/0958305X221088113
Hussain, S. M., Jamshed, W., Pasha, A. A., Adil, M., and Akram, M. (2022b). Galerkin finite element solution for electromagnetic radiative impact on viscid Williamson two-phase nanofluid flow via extendable surface. Int. Commun. Heat Mass Transf. 137, 106243. doi:10.1016/j.icheatmasstransfer.2022.106243
Hussain, S. M. (2022). Irreversibility analysis of time-dependent magnetically driven flow of sutterby hybrid nanofluid: A thermal mathematical model. Waves in Random and Complex Media, 1. doi:10.1080/17455030.2022.2089369
Jamei, M., Karbasi, M., Mosharaf-Dehkordi, M., Olumegbon, I. A., Abualigah, L., Said, Z., et al. (2022). Estimating the density of hybrid nanofluids for thermal energy application: Application of non-parametric and evolutionary polynomial regression data-intelligent techniques. Measurement 189, 110524. doi:10.1016/j.measurement.2021.110524
Jamshed, W., and Nisar, K. S. (2021). Computational single‐phase comparative study of a Williamson nanofluid in a parabolic trough solar collector via the Keller box method. Int. J. Energy Res. 45 (7), 10696–10718. doi:10.1002/er.6554
Jamshed, W., Prakash, M., Devi, S., Ibrahim, R. W., Shahzad, F., Nisar, K. S., et al. (2021). A brief comparative examination of tangent hyperbolic hybrid nanofluid through a extending surface: Numerical keller–box scheme. Sci. Rep. 11 (1), 24032–32. doi:10.1038/s41598-021-03392-8
Jamshed, W., Nisar, K. S., Ibrahim, R. W., Shahzad, F., and Eid, M. R. (2021). Thermal expansion optimization in solar aircraft using tangent hyperbolic hybrid nanofluid: A solar thermal application. J. Mater. Res. Technol. 14, 985–1006. doi:10.1016/j.jmrt.2021.06.031
Jamshed, W., Devi, S. U., and Nisar, K. S. (2021). Single phase based study of Ag-Cu/EO Williamson hybrid nanofluid flow over a stretching surface with shape factor. Phys. Screen. 96 (6), 065202. doi:10.1088/1402-4896/abecc0
Jamshed, W., Şirin, C., Selimefendigil, F., Shamshuddin, M. D., Altowairqi, Y., and Eid, M. R. (2021). Thermal characterization of coolant Maxwell type nanofluid flowing in parabolic trough solar collector (PTSC) used inside solar powered ship application. Coatings 11 (12), 1552. doi:10.3390/coatings11121552
Jamshed, W., Nasir, N. A. A. M., Isa, S. S. P. M., Safdar, R., Shahzad, F., Nisar, K. S., et al. (2021). Thermal growth in solar water pump using Prandtl–eyring hybrid nanofluid: A solar energy application. Sci. Rep. 11 (1), 18704–18721. doi:10.1038/s41598-021-98103-8
Jamshed, W., Safdar, R., Rehman, Z., Lashin, M. M., Ehab, M., Moussa, M., et al. (2022). Computational technique of thermal comparative examination of Cu and Au nanoparticles suspended in sodium alginate as Sutterby nanofluid via extending PTSC surface. J. Appl. Biomaterials Funct. Mater. 20, 228080002211040. doi:10.1177/22808000221104004
Jamshed, W., Eid, M. R., Safdar, R., Pasha, A. A., Isa, S. S. P. M., Adil, M., et al. (2022). Solar energy optimization in solar-HVAC using sutterby hybrid nanofluid with smoluchowski temperature conditions: A solar thermal application. Sci. Rep. 12, 11484. doi:10.1038/s41598-022-15685-7
Khan, U., Abdul Wahab, H., Syed, H., Ullah, B., and Adnan, (2022). Numerical study of heat transport mechanism in hybrid nanofluid [(Cu-Al2O3)/water] over a stretching/shrinking porous wedge. Proc. Institution Mech. Eng. Part E J. Process Mech. Eng., 095440892211079. doi:10.1177/09544089221107981
Khan, U., Ahmed, N., and Khan, I. (2022). Heat transfer evaluation in MgZn6Zr/C8H18 [(Magnesium-Zinc-Zirconium)/Engine oil] with non-linear solar thermal radiations and modified slip boundaries over 3-dimensional convectively heated surface. Front. Energy Res., 351.
Khan, U., Adnan, Ullah, B., Abdul Wahab, H., Ullah, I., Almuqrin, M. A., and Khan, I. (2022). Comparative thermal transport mechanism in Cu-H2O and Cu-Al2O3/H2O nanofluids: Numerical investigation. Waves in Random and Complex Media, 1–16. doi:10.1080/17455030.2021.2023783
Kumbhakar, B., and Nandi, S. (2022). Unsteady MHD radiative-dissipative flow of Cu-Al2O3/H2O hybrid nanofluid past a stretching sheet with slip and convective conditions: A regression analysis. Math. Comput. Simul. 194, 563–587. doi:10.1016/j.matcom.2021.12.018
Kursus, M., Liew, P. J., Che Sidik, N. A., and Wang, J. (2022). Recent progress on the application of nanofluids and hybrid nanofluids in machining: A comprehensive review. Int. J. Adv. Manuf. Technol. 121, 1455–1481. doi:10.1007/s00170-022-09409-4
Lee, J., King, S., Hassan, Y. A., Nguyen, T., Balestra, P., Schunert, S., et al. (2022). “Pronghorn porous media model validation with pressure drop measurements,” in Paper in the 19th international topical meeting on nuclear reactor thermal hydraulics (NURETH-19), Brussels, Belgium, March 6 - 11.
Mabood, F., Rauf, A., Prasannakumara, B. C., Izadi, M., and Shehzad, S. A. (2021). Impacts of Stefan blowing and mass convention on flow of Maxwell nanofluid of variable thermal conductivity about a rotating disk. Chin. J. Phys. 71, 260–272. doi:10.1016/j.cjph.2021.03.003
Mahanthesh, B., Shehzad, S. A., Mackolil, J., and Shashikumar, N. S. (2021). Heat transfer optimization of hybrid nanomaterial using modified buongiorno model: A sensitivity analysis. Int. J. Heat Mass Transf. 171, 121081. doi:10.1016/j.ijheatmasstransfer.2021.121081
Mahdy, A. M. S., Lotfy, K., El-Bary, A., and Tayel, I. M. (2021). Variable thermal conductivity and hyperbolic two-temperature theory during magneto-photothermal theory of semiconductor induced by laser pulses. Eur. Phys. J. Plus 136 (6). doi:10.1140/epjp/s13360-021-01633-3
Makinde, O. D., Mahanthesh, B., Gireesha, B. J., Shashikumar, N. S., Monaledi, R. L., and Tshehla, M. S. (2018). MHD nanofluid flow past a rotating disk with thermal radiation in the presence of aluminum and titanium alloy nanoparticles. Defect Diffusion Forum 384, 69. doi:10.4028/www.scientific.net/DDF.384.69
Malik, M. Y., Khan, I., Hussain, A., and Salahuddin, T. (2015). Mixed convection flow of MHD eyring-powell nanofluid over a stretching sheet: A numerical study. AIP Adv. 5 (11), 117118. doi:10.1063/1.4935639
Mandal, D. K., Biswas, N., Manna, N. K., Gayen, D. K., Gorla, R. S. R., and Chamkha, A. J. (2022). Thermo-fluidic transport process in a novel M-shaped cavity packed with non-Darcian porous medium and hybrid nanofluid: Application of artificial neural network (ANN). Phys. Fluids 34 (3), 033608. doi:10.1063/5.0082942
Muneeshwaran, M., Srinivasan, G., Muthukumar, P., and Wang, C. C. (2021). Role of hybrid-nanofluid in heat transfer enhancement–A review. Int. Commun. Heat Mass Transf. 125, 105341. doi:10.1016/j.icheatmasstransfer.2021.105341
Murtaza, R., Hussain, I., Rehman, Z., Khan, I., and Andualem, M. (2022). Thermal enhancement in Falkner–Skan flow of the nanofluid by considering molecular diameter and freezing temperature. Sci. Rep. 12 (1), 9415–9514. doi:10.1038/s41598-022-13423-7
Nandi, S., Kumbhakar, B., and Seth, G. S. (2022). Quadratic regression analysis of unsteady MHD free convective and radiative–dissipative stagnation flow of hybrid nanofluid over an exponentially stretching surface under porous medium. Chin. J. Phys. 77, 2090–2105. doi:10.1016/j.cjph.2021.12.011
Nandi, S., Kumbhakar, B., and Sarkar, S. (2022). MHD stagnation point flow of Fe3O4/Cu/Ag-CH3OH nanofluid along a convectively heated stretching sheet with partial slip and activation energy: Numerical and statistical approach. Int. Commun. Heat Mass Transf. 130, 105791. doi:10.1016/j.icheatmasstransfer.2021.105791
Olabode, J. O., Idowu, A. S., Akolade, M. T., and Titiloye, E. O. (2021). Unsteady flow analysis of Maxwell fluid with temperature dependent variable properties and quadratic thermo-solutal convection influence. Partial Differ. Equations Appl. Math. 4, 100078. doi:10.1016/j.padiff.2021.100078
Owhaib, W., and Al-Kouz, W. (2022). Three-dimensional numerical analysis of flow and heat transfer of bi-directional stretched nanofluid film exposed to an exponential heat generation using modified Buongiorno model. Sci. Rep. 12 (1). doi:10.1038/s41598-022-13351-6
Owhaib, W., Basavarajappa, M., and Al-Kouz, W. (2021). Radiation effects on 3D rotating flow of Cu-water nanoliquid with viscous heating and prescribed heat flux using modified Buongiorno model. Sci. Rep. 11 (1). doi:10.1038/s41598-021-00107-x
Parvin, S., Isa, S. S. P. M., Jamshed, W., Ibrahim, R. W., and Nisar, K. S. (2021). Numerical treatment of 2D-Magneto double-diffusive convection flow of a Maxwell nanofluid: Heat transport case study. Case Stud. Therm. Eng. 28, 101383. doi:10.1016/j.csite.2021.101383
Pasha, A. A., Islam, N., Jamshed, W., Alam, M. I., Jameel, A. G. A., Juhany, K. A., et al. (2022). Statistical analysis of viscous hybridized nanofluid flowing via Galerkin finite element technique. Int. Commun. Heat Mass Transf. 137, 106244. doi:10.1016/j.icheatmasstransfer.2022.106244
Qureshi, Z. A., Bilal, S., Khan, U., Akgül, A., Sultana, M., Botmart, T., et al. (2022). Mathematical analysis about influence of Lorentz force and interfacial nano layers on nanofluids flow through orthogonal porous surfaces with injection of SWCNTs. Alexandria Eng. J. 61 (12), 12925–12941. doi:10.1016/j.aej.2022.07.010
Qureshi, M. A. (2022). Thermal capability and entropy optimization for Prandtl-Eyring hybrid nanofluid flow in solar aircraft implementation. Alexandria Eng. J. 61 (7), 5295–5307. doi:10.1016/j.aej.2021.10.051
Rana, P., Mahanthesh, B., Mackolil, J., and Al-Kouz, W. (2021). Nanofluid flow past a vertical plate with nanoparticle aggregation kinematics, thermal slip and significant buoyancy force effects using modified Buongiorno model. Waves in Random and Complex Media, 1. doi:10.1080/17455030.2021.1977416
Rashed, Z. Z., Alhazmi, M., and Ahmed, S. E. (2021). Non-homogenous nanofluid model for 3D convective flow in enclosures filled with hydrodynamically and thermally heterogeneous porous media. Alexandria Eng. J. 60 (3), 3119–3132. doi:10.1016/j.aej.2021.01.049
Reddy, N. B., Poornima, T., and Sreenivasulu, P. (2014). Influence of variable thermal conductivity on MHD boundary layer slip flow of ethylene-glycol based Cu nanofluids over a stretching sheet with convective boundary condition. Int. J. Eng. Math. 2014, 905158. doi:10.1155/2014/905158
Roşca, N. C., Roşca, A. V., Aly, E. H., and Pop, I. (2021). Flow and heat transfer past a stretching/shrinking sheet using modified buongiorno nanoliquid model. Mathematics 9 (23), 3047. doi:10.3390/math9233047
Safdar, R., Jawad, M., Hussain, S., Imran, M., Akgül, A., and Jamshed, W. (2022). Thermal radiative mixed convection flow of MHD Maxwell nanofluid: Implementation of buongiorno's model. Chin. J. Phys. 77, 1465–1478. doi:10.1016/j.cjph.2021.11.022
Saha, A., Manna, N. K., Ghosh, K., and Biswas, N. (2022). Analysis of geometrical shape impact on thermal management of practical fluids using square and circular cavities. Eur. Phys. J. Spec. Top. 231, 2509–2537. doi:10.1140/epjs/s11734-022-00593-8
Said, Z., Sundar, L. S., Tiwari, A. K., Ali, H. M., Sheikholeslami, M., Bellos, E., et al. (2021). Recent advances on the fundamental physical phenomena behind stability, dynamic motion, thermophysical properties, heat transport, applications, and challenges of nanofluids.Phys. Rep. 946, 1–94. doi:10.1016/j.physrep.2021.07.002
Said, Z., Sharma, P., Tiwari, A. K., Huang, Z., Bui, V. G., Hoang, A. T., et al. (2022). Application of novel framework based on ensemble boosted regression trees and Gaussian process regression in modelling thermal perfopHASErmance of small-scale Organic Rankine Cycle (ORC) using hybrid nanofluid. J. Clean. Prod. 360, 132194. doi:10.1016/j.jclepro.2022.132194
Shahzad, F., Jamshed, W., Ibrahim, R. W., Sooppy Nisar, K., Qureshi, M. A., Hussain, S. M., et al. (2021). Comparative numerical study of thermal features analysis between Oldroyd-B copper and molybdenum disulfide nanoparticles in engine-oil-based nanofluids flow. Coatings 11 (10), 1196. doi:10.3390/coatings11101196
Shahzad, F., Jamshed, W., DeviS, S. U., Safdar, R., Prakash, M., Ibrahim, R. W., et al. (2022). Raising thermal efficiency of solar water‐pump using Oldroyd‐B nanofluids' flow: An optimal thermal application. Energy Science & Engineering. doi:10.1002/ese3.1173
Shahzad, F., Jamshed, W., Nisar, K. S., Nasir, N. A. A. M., Safdar, R., Abdel-Aty, A. H., et al. (2022). Thermal analysis for Al2O3–sodium alginate magnetized Jeffrey’s nanofluid flow past a stretching sheet embedded in a porous medium. Sci. Rep. 12 (1), 1. doi:10.1038/s41598-022-06983-1
Shankaralingappa, B. M., Madhukesh, J. K., Sarris, I. E., Gireesha, B. J., and Prasannakumara, B. C. (2021). Influence of thermophoretic particle deposition on the 3D flow of sodium alginate-based Casson nanofluid over a stretching sheet. Micromachines 12 (12), 1474. doi:10.3390/mi12121474
Swain, K., Mahanthesh, B., and Mebarek‐Oudina, F. (2021). Heat transport and stagnation‐point flow of magnetized nanoliquid with variable thermal conductivity, Brownian moment, and thermophoresis aspects. Heat. Transf. 50 (1), 754–767. doi:10.1002/htj.21902
Wang, X. Q., and Mujumdar, A. S. (2008). A review on nanofluids-part II: Experiments and applications. Braz. J. Chem. Eng. 25, 631–648. doi:10.1590/s0104-66322008000400002
Xiong, Q., Altnji, S., Tayebi, T., Izadi, M., Hajjar, A., Sundén, B., et al. (2021). A comprehensive review on the application of hybrid nanofluids in solar energy collectors. Sustain. Energy Technol. Assessments 47, 101341. doi:10.1016/j.seta.2021.101341
Xu, X., and Chen, S. (2017). Cattaneo–Christov heat flux model for heat transfer of Marangoni boundary layer flow in a copper–water nanofluid. Heat. Trans. Asian. Res. 46 (8), 1281–1293. doi:10.1002/htj.21273
Keywords: Powell-Eyring hybridized nanofluid, modified Buongiorno’s structure, shape factor, irreversibility analysis, Galerkin finite element technique
Citation: Rahman MM, Jamshed W, Devi. S SU, Ibrahim RW, Pasha AA, Souayeh B, Safdar R, Eid MR, Hussain SM and Tag El Din ESM (2022) Quadratic regression estimation of hybridized nanoliquid flow using Galerkin finite element technique considering shape of nano solid particles. Front. Energy Res. 10:996556. doi: 10.3389/fenrg.2022.996556
Received: 17 July 2022; Accepted: 08 August 2022;
Published: 07 October 2022.
Edited by:
Adnan Abbasi, Mohi-ud-Din Islamic University, PakistanReviewed by:
Muhammad Hafeez, Gdansk University of Technology, PolandCopyright © 2022 Rahman, Jamshed, Devi. S, Ibrahim, Pasha, Souayeh, Safdar, Eid, Hussain and Tag El Din. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wasim Jamshed, d2FzaWt0a0Bob3RtYWlsLmNvbSYjeDAyMDBhOw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.