- 1School of Mechatronic Engineering and Automation, Foshan University, Foshan, China
- 2School of Intelligent Manufacturing, Guangzhou Vocational College of Technology & Business, Guangzhou, China
The sliding mode observer (SMO)–based sensorless control is essentially a discontinuous switching control algorithm. Therefore, there is large speed or torque chattering in the permanent magnet synchronous motor (PMSM) with existing sliding mode observer–based control methods. In order to solve this problem well, an algorithm based on an improved sliding mode observer is proposed. In detail, the piecewise power function approach is used to replace the traditional ones, that is, the sgn function or the sigmoid function approach. Simulation verifications are conducted to validate the effectiveness of the proposed observer. It shows that the piecewise power function–based sliding mode observer algorithm has obvious advantages in the stability of the three-phase current, namely, it improves the estimation accuracy of the rotor position, rotor speed, and dynamic response to various loads. For further verification, the proposed sliding mode observer algorithm is implemented and verified in a marine electric propulsion motor with a DSP chip of TMS320F28377D. Experimental results validate that the piecewise power function–based sliding mode observer algorithm has high control accuracy and fewer fluctuations, which are all vital in marine engineering.
Introduction
In order to implement a real-time closed-loop vector control in a PMSM, it usually needs some feedback parameters such as the position and speed by installing position or speed sensors in the motor rotor shaft. However, the sensors are vulnerable and easily damaged. Meanwhile, the measurement precision of the sensors easily interferes with temperature, humidity, and rotor vibration (Xing et al., 2020). Since the mechanical sensors will lead to stability problems in the control system, sensorless control technology has become a research hotspot for scholars and engineers in recent years (Song et al., 2018; Li et al., 2019; Liu et al., 2021).
At present, the main methods used in PMSM sensorless control include the model reference adaptive system (MRAS) method (Chenxing and Chen, 2018), extended Kalman filter (EKF) method (Cao et al., 2019), high-frequency signal injection method (Wang et al., 2019), and SMO method (Ye and Yao, 2021). Therein, SMO has the advantage of sliding motion invariance; the SMO is insensitive to external interferences or parameter perturbations (Gong et al., 2020). This advantage makes the SMO algorithm have strong robustness and is widely used in sensorless motor control. However, the SMO has an obvious disadvantage, that is, the chattering problem, which affects the accuracy of the observation. To reduce the effect of chattering on position estimation in SMO, scholars and engineers have proposed some methods. In Ma and Zhang (2018), a sgn function of current error in the feedback correction is adopted. However, by using the step sgn function, the SMO demands higher requirements of the low-pass filter. This will reduce the estimation precision of the rotor position due to the larger phase delay of the filter. In Iqbal and Memon (2019), a sigmoid function–based SMO is used for rotor position estimation. Meanwhile, the SMO is cascaded with an extended high gain observer (EHGO) to obtain a robust speed estimation. In Ye (2019), an iterative SMO for sensorless control is proposed. The iterative SMO enables the system to have a stronger anti-interference ability and adapt to changes in motor parameters. However, iterative SMO runs longer than traditional SMO. In Zhang and Jiang (2021), a fuzzy control algorithm is applied to SMO to reduce chattering and improve observation accuracy. The fuzzy sliding mode gain is designed to vary adaptively according to the system state, but the combination of fuzzy control and SMO increases the complexity of the algorithm. In Lu et al. (2021a), a global nonlinear piecewise function based on the SMO algorithm was proposed. Therein the current equation of the SMO was reconstructed to optimize the control system’s performance. In Ding et al. (2022), a second-order sliding mode controller based on a disturbance observer is proposed, and the disturbance observer can optimize the disturbance rejection performance of the PMSM system to a certain extent. However, the system becomes complicated as the order increases. In addition, in Liu and Chen (2022), the arcsine saturation function is used in the latter and stable stages of sliding mode motion. In Yi et al. (2022), combining the backstepping method and the sliding mode control, a new reaching law SMO is designed. Although the introduction of the backstepping method can improve the performance of the SMO, the design process is cumbersome.
As shown in the aforementioned SMOs, the estimated value will oscillate up and down around the actual value. Although chattering is inevitable, it can be limited to a certain range (Lu et al., 2021b; Ren et al., 2021). Therefore, in this study, an improved SMO algorithm is proposed by using a piecewise power function instead of the ideal switching function. Studies show that, beyond the boundary layer, the piecewise power function has the ability to saturate the error of the rotor current; within the boundary layer, the piecewise power function changes in the form of a power function. This property makes the back electromotive force (BEMF) more stable when switching the system. This article is organized as follows: first, the SMO model based on the piecewise power functions is derived in this study. Then the sliding mode gain
The traditional sliding mode observer
Generally, the mathematical model of the surface-mounted PMSM in the
where
In general, the response of the stator current is much faster than the rotor speed in a motor. Let the derivation of
According to Eqs 1, 2, the conventional SMO can be described as Eq. 3 (An et al., 2020):
where sgn () is the sgn function;
The stator current error between the estimated value and the actual value can be obtained by subtracting Eq. 1 from Eq. 3. The corresponding Eq. 4 is obtained.
In Eq. 4, according to the sliding mode dynamic condition, if
Since the actual control signal of the SMO is a high-frequency discontinuous switching signal, it is necessary to add a low-pass filter to extract the continuous estimated value of the extended BEMF from the control signal. The corresponding equation is shown as Eq. 6:
where
The arctangent function is used to extract the rotor position information from the estimated value of the extended BEMF. Hence, the rotor position information is obtained as Eq. 7.
Since Eq. 6 indicated a low-pass filter with a cutoff frequency
Then the estimated speed of the three-phase PMSM is expressed as Eq. 9:
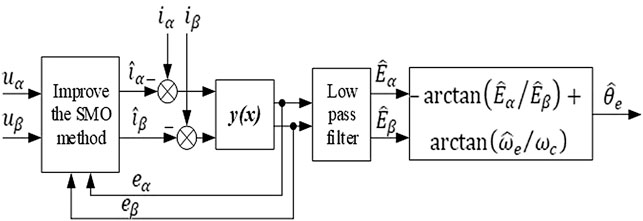
To sum up, the block diagram of the conventional SMO algorithm can be depicted as the diagram shown in Figure 1.
The improved sliding mode observer proposed in this study
Design of the improved sliding mode observer
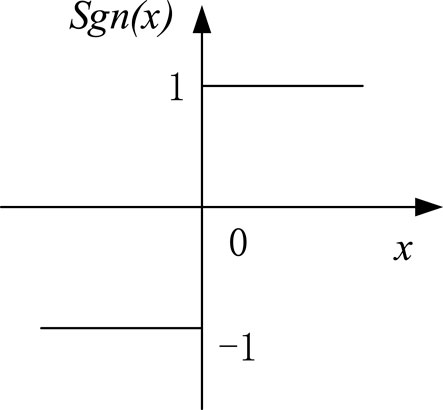
The traditional SMO sliding mode surface uses a symbolic function (sgn function). Figure 2 shows the sgn function curve used in traditional SMO. It can be seen in Figure 2 that the output value is saturated to 1 when the sgn function is
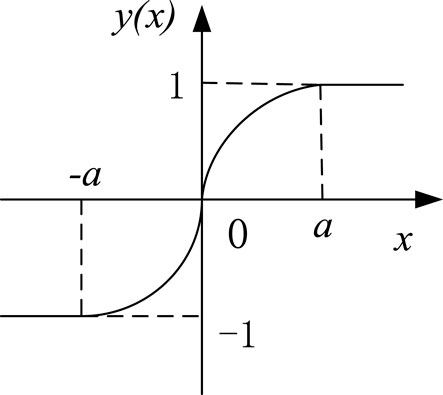
Figure 3 shows the sigmoid function curve expressed by Eq. 10.
where
By using saturation functions or other types of continuous functions instead of the sgn function, the system will achieve a continuous feedback control when the points in the state space enter the boundary layer adjacent to the sliding mode switching surface, thereby effectively suppressing system chattering (Chen and Zhao, 2016). In order to suppress the system chattering in SMO, we use a piecewise power function to replace the sgn function and design an improved SMO as follows. Within the boundary layer, the piecewise power function varies in the form of the power function, as shown in Eq. 11. This change can make the BEMF more stable when the system is switching. Meanwhile, beyond the boundary layer, the piecewise power function has the property of saturating the current value error.
where
Figure 4 shows that
According to Eqs 4, 11, the stator current error equation of the proposed SMO is calculated as Eq. 12.
Then the structural block diagram of the improved SMO is shown in Figure 5.
Stability evaluation of the proposed sliding mode observer
The Lyapunov stability criterion is used to analyze the stability of the control system with the proposed SMO. First, subtract Eq. 1 from Eq. 12 to obtain Eq. 13.
where
Then the Lyapunov stability equation is established as Eq. 14.
where
Hence, the stability condition is satisfied if
Combining Eqs 14, 15, Eqs 16, 17 can be derived.
Since
Simulation analysis
The boundary layer thickness ‘
Figures 6A–C shows the rotational speed estimated by SMO based on the sgn, sigmoid, and piecewise power functions, respectively. The simulation results show that the estimated speed is chattered seriously and significantly deviates from the actual speed of about ±3 r/min in Figure 6A with the sgn function. Meanwhile, Figure 6B shows that the chattering of the estimated speed is slight, but there is a particular error with the actual speed with the sigmoid function. Figure 6C displays that the estimated speed is only ±1 r/min deviating from the actual speed, and the system chattering is significantly suppressed. By comparison, the speed estimated by the SMO algorithm based on the piecewise power function is closest to the actual value, and the speed estimation accuracy is higher than others.
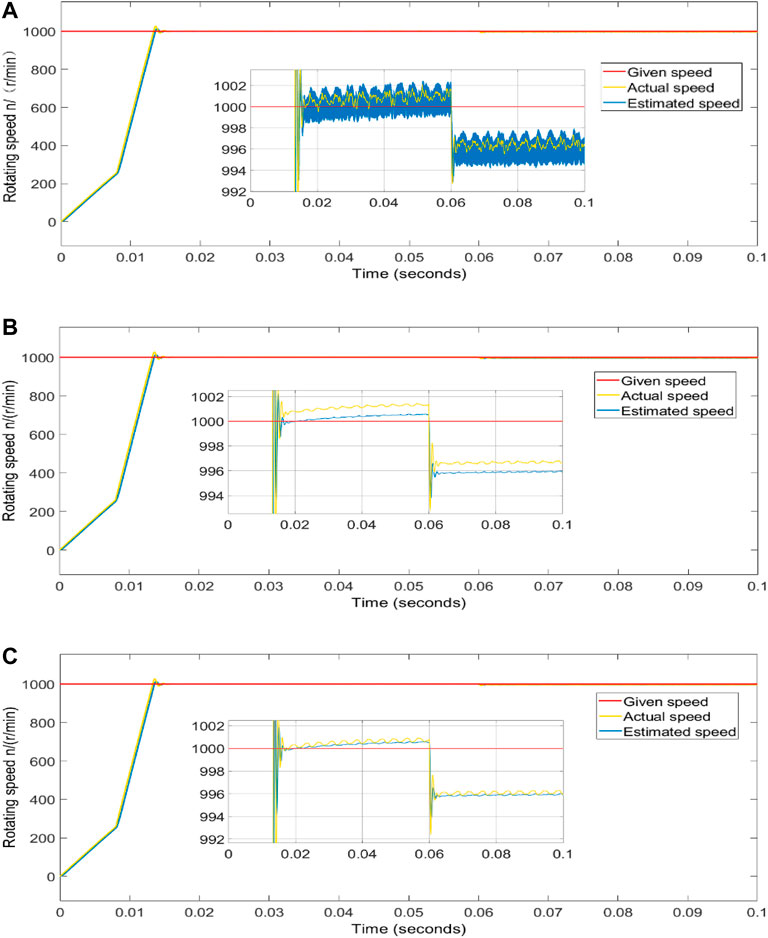
FIGURE 6. (A) Changes of rotational speed estimated by SMO based on sgn function; (B) changes of rotational speed estimated by SMO based on sigmoid function; (C) changes of rotational speed estimated by SMO based on piecewise power function.
Figures 7A–C shows the differences in rotor speed error of the SMO algorithm based on sgn, sigmoid, and piecewise power functions, respectively. Figure 7A displays that, with the sgn function, the rotor speed error of the control system varies at −2 to 2 r/min with serious chattering. Figure 7B shows that, with the sigmoid function, the error is about 1 r/min with a bit of chattering. Figure 7C shows that the error is stable at about 0.5r/min with a real slight chattering. By comparison, the chattering can be effectively suppressed when the proposed SMO algorithm is adopted in the control system.
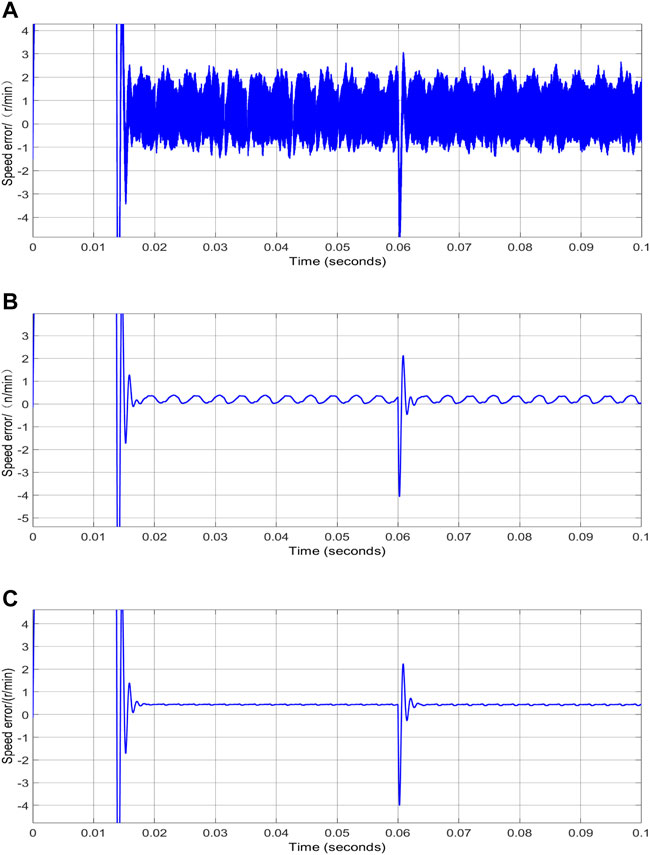
FIGURE 7. (A) Rotational speed error of the SMO based on the sgn function; (B) rotational speed error of the SMO based on the sigmoid function; (C) rotational speed error of the SMO based on the piecewise power function.
Figures 8A–C shows the harmonic analysis results A-phase stator current of the motor with the SMO algorithm based on the sgn, sigmoid, and piecewise power functions, respectively. The harmonic analysis ranges from 0.03 s to the end of the following cycle with a fundamental frequency of 67 Hz. Figure 8A displays that the current has many burrs, and the total harmonic distortion (THD) of the current is 19.84%. According to Figure 8B, the THD value of the current is 17.04%. Figure 8C shows that the THD value is 15.66%. The results show that the THD value of the output current with the SMO based on the piecewise power function is the smallest. Moreover, when the torque changes suddenly at 0.06 s, the phase current can quickly recover to a stable value, which indicates that the proposed SMO has a good dynamic performance against load fluctuation.
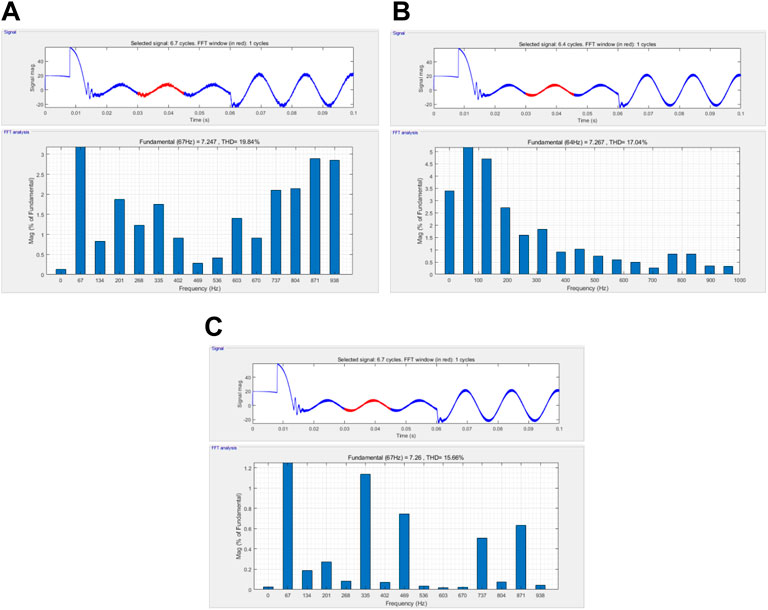
FIGURE 8. (A) Harmonic analysis of the motor stator A-phase current with the SMO based on the sgn function; (B) harmonic analysis of the motor stator A-phase current with the SMO based on the sigmoid function; (C) harmonic analysis of the motor stator A-phase current with the SMO based on the piecewise power function.
Figures 9A–C shows the output torque of the sensorless motor control system with the SMO based on sgn, sigmoid, and piecewise power functions, respectively. With the sgn function, the output torque chatters seriously, as is shown in Figure 9A, and the fluctuation range is as extensive as ±3 Nm. According to Figure 9B, the torque chattering of the system is relatively stable with the sigmoid function. Meanwhile, the torque chattering is very slight with the piecewise power function since the torque fluctuation is in the range of ±1 Nm in Figure 9C.
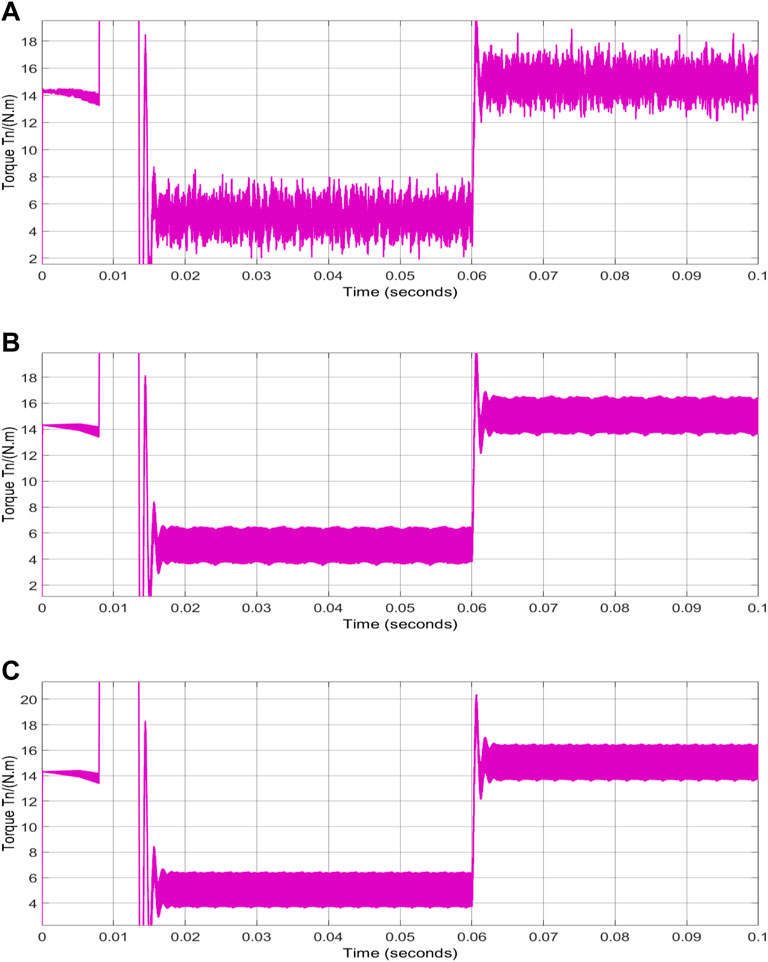
FIGURE 9. (A) Output torque changes of the sensorless motor control system with the SMO based on the sgn function; (B) output torque changes of the sensorless motor control system with the SMO based on the sigmoid function; (C) output torque changes of the sensorless motor control system with the SMO based on the piecewise power function.
The aforementioned simulation results show that compared with the SMO algorithm based on the sgn function and sigmoid function, respectively, the SMO algorithm based on the piecewise power function has obvious advantages in terms of estimation accuracy, suppression of torque chattering, maintaining the three-phase current stable, and responding to dynamic loads changes.
Experiment analysis
To verify the effectiveness and feasibility of the proposed SMO algorithm, we conducted experiments with a sensorless control platform of a marine electric propulsion motor, as shown in Figures 10, 11.
Figure 12 shows the motor’s three-phase stator current from stationary to a stable rotating speed. At the time of 0.5 s, the current switches from the low-speed I/F control to the high-speed SMO control. It is noticed in the picture that the motor responds quickly in the whole startup stage, and the current is stable in the startup process without large distortion. The whole switching process is smooth, and the current has no large fluctuations.
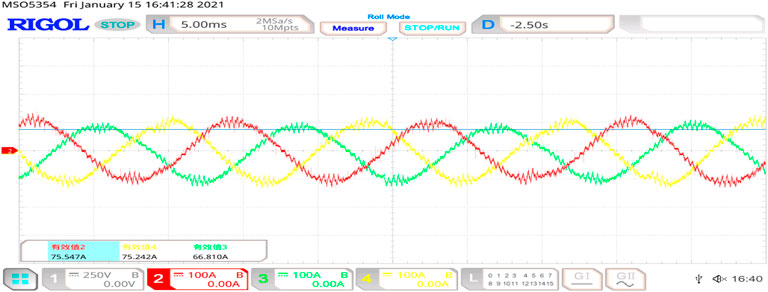
Figure 13 shows the three-phase stator current when the motor runs steadily at a speed of 300 r/min. The figure shows that the three-phase current is 75 A, and the current has no large pulse vibration, indicating the rotor position information is accurately estimated with the SMO in the steady state.
Conclusion
To achieve a higher degree of control accuracy for the marine electric propulsion motor, we tried to suppress the speed and torque chattering phenomenon of the traditional SMOs by replacing the sgn function or the sigmoid function with a piecewise power function. In the study, the stability of the piecewise power function–based SMO is verified by the Lyapunov method. After that, simulations and experiments are conducted to ascertain the feasibility of the proposed SMO. The results show that the proposed SMO can better suppress chattering by improving the speed estimation precision from 0.2% to 0.05% compared with traditional SMOs. Meanwhile, the torque chattering problem is resolved more effectively by improving the THD value of the stator current from 19.84% to 17.04% to 15.66%. The piecewise power function–based SMO is feasible for all situations where the senseless control algorithm is used. Moreover, the proposed SMO will perform better on estimation precision if the observer gain can be automatically adjusted using intelligent algorithms.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization: XL and HZ; methodology: XL and ZZ; software: XL and HZ; validation: XL, SZ, and ZZ; formal analysis: HL; investigation: HZ and FG; resources: XL and FG; data curation: XL; writing—original draft preparation: XL; writing—review and editing: XL, ZZ, and SZ; visualization: XL and LQ; supervision: XL, LQ, and HL; project administration: XL; funding acquisition: XL; All authors approved the submitted version and agreed to be responsible for all aspects.
Funding
This work was supported in part by the Key Project of National Natural Science Foundation of China (61733015), in part by Collaborative Innovation Center of Intelligent electrical equipment of Higher vocational colleges in Guangdong Province, in part by High-end Power System Technology Development Center of Guangdong Universities (2019GGCZX002) and in part by Innovation Team Project of Guangdong Universities (2021KCXTD027).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
An, Q., Zhang, J., An, Q., Liu, X., Shamekov, A., and Bi, K. (2020). Frequency-adaptive complex-coefficient filter-based enhanced sliding mode observer for sensorless control of permanent magnet synchronous motor drives. IEEE Trans. Ind. Appl. 56 (1), 335–343. doi:10.1109/tia.2019.2951760
Cao, R., Jiang, N., and Lu, M. (2019). Sensorless control of linear flux-switching permanent magnet motor based on extended Kalman filter. IEEE Trans. Ind. Electron. 67 (7), 5971–5979. doi:10.1109/TIE.2019.2950865
Chen, M., and Zhao, Y. (2016). “Simulation research on sensorless speed control system of permanent magnet synchronous motor based on SMO,” in 2016 Eighth International Conference on Measuring Technology and Mechatronics Automation (ICMTMA). doi:10.1109/ICMTMA.2016.149
Chenxing, S., and Chen, W. (2018). “Sensorless vector control of three-phase permanent magnet synchronous motor based on model reference adaptive system,” in 2018 IEEE 4th International Conference on Control Science and Systems Engineering. doi:10.1109/ccsse.2018.8724849
Ding, S., Hou, Q., and Wang, H. (2022). Disturbance-observer-based second-order sliding mode controller for speed control of PMSM drives. IEEE Trans. Energy Convers. 2022, 1–10. doi:10.1109/TEC.2022.3188630
Gong, C., Hu, Y., Gao, J., Wang, Y., and Yan, L. (2020). An improved delay-suppressed sliding-mode observer for sensorless vector-controlled PMSM. IEEE Trans. Ind. Electron. 67 (7), 5913–5923. doi:10.1109/tie.2019.2952824
Iqbal, M. A., and Memon, A. Y. (2019). “Robust backstepping sensorless speed control of PMSM using cascaded sliding mode and high gain observers,” in 2019 International Symposium on Recent Advances in Electrical Engineering (RAEE), Islamabad, Pakistan, Aug 2019. doi:10.1109/RAEE.2019.8886948
Li, Z., Zhou, S., Xiao, Y., and Wang, L. (2019). Sensorless vector control of permanent magnet synchronous linear motor based on self-adaptive super-twisting sliding mode controller. IEEE Access 7, 44998–45011. doi:10.1109/access.2019.2909308
Liu, G., Zhang, H., and Song, X. (2021). Position-estimation deviation-suppression technology of PMSM combining phase self-compensation SMO and feed-forward PLL. IEEE J. Emerg. Sel. Top. Power Electron. 9 (1), 335–344. doi:10.1109/jestpe.2020.2967508
Liu, Z., and Chen, W. (2022). Research on an improved sliding mode observer for speed estimation in permanent magnet synchronous motor. Processes 10 (6), 1182. doi:10.3390/pr10061182
Lu, W., Tang, B., Ji, K., Lu, K., Wang, D., and Yu, Z. (2021a). A new load adaptive identification method based on an improved sliding mode observer for PMSM position servo system. IEEE Trans. Power Electron. 36 (3), 3211–3223. doi:10.1109/tpel.2020.3016713
Lu, W., Zheng, D., Lu, Y., Lu, K., Guo, L., Yan, W., et al. (2021b). New sensorless vector control system with high load capacity based on improved SMO and improved FOO. IEEE Access 9, 40716–40727. doi:10.1109/access.2021.3065040
Ma, Z., and Zhang, X. (2018). FPGA implementation of sensorless sliding mode observer with a novel rotation direction detection for PMSM drives. IEEE Access 6, 55528–55536. doi:10.1109/ACCESS.2018.2871730
Park, J., and Lee, D. H. (2019). “Sensorless control of PMSM using voltage and current angle estimation,” in 2019 22nd International Conference on Electrical Machines and Systems (ICEMS). doi:10.1109/ICEMS.2019.8922294
Ren, N., Fan, L., and Zhang, Z. (2021). Sensorless PMSM control with sliding mode observer based on sigmoid function. J. Electr. Eng. Technol. 16 (2), 933–939. doi:10.1007/s42835-021-00661-4
Song, X., Han, B., Zheng, S., and Chen, S. (2018). A novel sensorless rotor position detection method for high-speed surface PM motors in a wide speed range. IEEE Trans. Power Electron. 33 (8), 7083–7093. doi:10.1109/tpel.2017.2753289
Wang, S., Yang, K., and Chen, K. (2019). An improved position-sensorless control method at low speed for PMSM based on high-frequency signal injection into a rotating reference frame. IEEE Access 7, 86510–86521. doi:10.1109/access.2019.2925214
Xing, J., Qin, Z., Lin, C., and Jiang, X. (2020). Research on startup process for sensorless control of PMSMs based on I-F method combined with an adaptive compensator. IEEE Access 8, 70812–70821. doi:10.1109/access.2020.2987343
Ye, S. (2019). Design and performance analysis of an iterative flux sliding-mode observer for the sensorless control of PMSM drives. ISA Trans. 94, 255–264. doi:10.1016/j.isatra.2019.04.009
Ye, S., and Yao, X. (2021). An enhanced SMO-based permanent-magnet synchronous machine sensorless drive scheme with current measurement error compensation. IEEE J. Emerg. Sel. Top. Power Electron. 9 (4), 4407–4419. doi:10.1109/jestpe.2020.3038859
Yi, L., Sun, T., Yu, W., Xu, X., Zhang, G., and Jiang, G. (2022). Induction motor fault detection by a new sliding mode observer based on backstepping. J. Ambient. Intell. Humaniz. Comput. 2022, 1–14. doi:10.1007/s12652-022-03755-7
Keywords: PMSM, sliding mode observer, sensorless control, piecewise power function, chatter suppression
Citation: Li X, Zhan S, Guo F, Zhuang Z, Zhang H, Liao H and Qu L (2022) Chattering suppression of the sliding mode observer for marine electric propulsion motor based on piecewise power function. Front. Energy Res. 10:994180. doi: 10.3389/fenrg.2022.994180
Received: 14 July 2022; Accepted: 02 September 2022;
Published: 21 September 2022.
Edited by:
Atif Jahanger, Hainan University, ChinaCopyright © 2022 Li, Zhan, Guo, Zhuang, Zhang, Liao and Qu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fang Guo, RnN1X2d1b2ZAMTYzLmNvbQ==
 Xiangfeng Li
Xiangfeng Li Shengqiang Zhan1
Shengqiang Zhan1