- School of Economics and Management, Fujian Agriculture and Forestry University, Fuzhou, China
Numerous studies show that it is reasonable and effective to apply decomposition technology to deal with the complex carbon price series. However, the existing research ignores the residual term containing complex information after applying single decomposition technique. Considering the demand for higher accuracy of the carbon price series prediction and following the existing research path, this paper proposes a new hybrid prediction model VMD-CEEMDAN-LSSVM-LSTM, which combines a new quadratic decomposition technique with the optimized long short term memory (LSTM). In the decomposition part of the hybrid model, the original carbon price series is processed by variational mode decomposition (VMD), and then the residual term obtained by decomposition is further decomposed by complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN). In the prediction part of the hybrid model, least squares support vector machine (LSSVM) is introduced, and LSSVM-LSTM model is constructed to predict the components obtained by decomposition. The empirical research of this paper selects two different case data from the European Union emissions trading system (EU ETS) as samples. Taking the results of Case Ⅰ in the 1-step ahead forecasting scenario as an example, the prediction evaluation indexes
1 Introduction
As one of the common threats to human life and security, climate change is faced by all countries in the world. From a global perspective, greenhouse gases are the main inducing factors that lead to abnormal changes in global climate (Huang and He, 2020). Carbon dioxide is one of the main greenhouse gases in the world, and excessive carbon emissions will accelerate the global warming process and threaten the sustainable development of human society. Therefore, reducing carbon emissions through reasonable regulation is the key to mitigating climate change (Chen et al., 2021). Numerous existing studies have shown that the carbon emission trading system, which is guided by market demand and traded through the pricing of carbon emissions, can control carbon dioxide emissions more efficiently and reasonably (Cui et al., 2014; Song et al., 2019a; Bauer et al., 2020; Sun and Wang, 2020).
Among the carbon emission trading systems that have emerged in recent years, the EU ETS involved in this paper is to price carbon dioxide by selling and trading carbon emission quotas. Compared with other trading markets around the world, it has stronger liquidity and influence (Zhang and Wei, 2010). As a signal that transmits important information in the trading market, the change of carbon price reflects the important information in the marginal cost of emission reduction (Aatola et al., 2013). Fluctuations in carbon prices will affect the cost of carbon emissions, causing changes in the market supply and demand relationship formed in carbon allowance trading. However, excessive volatility of carbon prices will bring risks to the trading market and reduce the effectiveness of the trading system (Song et al., 2019b; Liu et al., 2020). Reasonable prediction of carbon price can not only help traders in the carbon market to manage the price risk, but also help all kinds of market participants to make more rational investment decisions. In addition, effective carbon price forecasting can also create a stable carbon pricing mechanism for the market and improve the management ability of carbon assets (Zhu et al., 2018; Zhu et al., 2019). Therefore, it is of great practical significance and necessity to conduct prediction research on carbon price.
However, the volatility of carbon prices is affected by various uncertain variables from the internal market mechanism and the external environment. For example, the periodicity of economic development, the prices of various other energy sources, and related energy policies (Koch et al., 2014; Duan et al., 2018; Yang et al., 2020; Duc et al., 2021). The change of carbon price shows the characteristics of high volatility, nonlinearity and complexity (Zhu et al., 2017; Fan, et al., 2019; Tian and Hao, 2020; Huang et al., 2021). Therefore, how to optimize the prediction method of carbon price and improve the accuracy and reliability of the prediction results is the difficulty of research work.
According to the different variables involved, the prediction research of carbon price can be divided into multivariate prediction research and univariate prediction research (Zhu et al., 2017). Multivariable forecasting research involves other exogenous variables except price factors, and to some extent, it faces the dilemma of error accumulation. Univariate variable forecasting research only contains historical price series, thus getting rid of the dependence on exogenous variables (Li et al., 2021). The research scope of this paper belongs to the single variable price forecasting research.
Existing single variable models for forecasting energy prices can be divided into the following three categories: the traditional econometric models, the artificial intelligence models and the hybrid models (Zhu et al., 2017). Among them, the traditional econometric models include autoregressive conditional heteroskedasticity (ARCH), autoregressive moving average (ARMA), autoregressive integrated moving average (ARIMA), etc. (Byun and Cho, 2013; Jiang et al., 2018). The artificial intelligence models include artificial neural networks (ANNs), LSTM, and support vector machines (SVRs), et al. (Feijoo et al., 2016; Keles et al., 2016; Gundu and Simon, 2021).
The research of traditional econometric models shall be based on strict statistical theory. The premise of the research is that the carbon price data is normally distributed and linearly correlated. The premise of this linear assumption makes it difficult to capture the complex features hidden in the carbon price time series (Lin et al., 2011; Taylan, 2017). Aiming at overcoming this defect, the artificial intelligence model has established a series of mathematical models of nonlinear operations, and has made great progress in the innovation of algorithm development (Sun and Huang, 2020; Seyedan et al., 2022). However, most of the single artificial intelligence models have limited predictive validity and are prone to fall into the dilemma of local optimal solutions, long computation time and poor convergence speed.
In view of the timeliness and complexity of the fluctuation of carbon price series, it is difficult to capture the hidden features of its internal irregular series in the research using a single prediction model, not to speak of obtaining satisfactory prediction results (Sun and Xu, 2021). The third kind of hybrid model effectively integrates various technical advantages by combining different models, and has greater advantages in the research of price forecasting (Xu et al., 2020; Yang et al., 2020). The typical hybrid model is TEI@I complex system research methodology (Wang et al., 2005) which combines decomposition technology and prediction model. In the decomposition part, the main features of the time series are identified and extracted through decomposition technology, and a series of modal components of the complex price series are obtained, which reduces the complexity of the data series (da Silva et al., 2021; Gao et al., 2022). In the prediction part, the prediction model is used to predict the different components. This method combines the advantages of decomposition technology and prediction model to improve the prediction performance of complex price series by reducing the complexity of the series and optimizing the prediction method, and shows good performance in the prediction research of carbon price (Li et al., 2021; Sun and Xu, 2021).
In the existing research on decomposition techniques that constitute TEI@I complex system research methodology, empirical mode decomposition (EMD) algorithm is easy to fall into the dilemma of modal mixing, and does not have complete physical significance (Tian and Hao, 2020). Aiming at overcoming this defect, Wu and Huang (2004) proposed the ensemble optical mode decomposition (EEMD). However, due to its weak mathematical foundation, EEMD lacks the ability to separate components with similar frequencies, and to some extent, it still retains residual noise, which limits the decomposition effect. In order to overcome the shortcomings of the above decomposition algorithms, CEEMDAN borrowed the idea of adding Gaussian noise and canceling noise through multiple stacking and averaging in EEMD, which had better completeness of decomposition (Zhang et al., 2018; Cao et al., 2019). Furthermore, in a series of other developed decomposition algorithms developed, by adopting an adaptive decomposition mode for the effective components of each center frequency, VMD can capture the characteristics of data more effectively by adopting an adaptive decomposition mode for the effective components of each center frequency (da Silva et al., 2022). Its advantages have been confirmed in the existing research on carbon price prediction (Wang et al., 2019; Zhu et al., 2019; Sun and Huang, 2020).
Among the existing prediction models that constitute the TEI@I complex system research methodology, compared with the traditional econometric model, the artificial intelligence model can describe the nonlinear characteristics hidden in the carbon price series more effectively, and have better forecasting ability. Artificial neural network (ANN) is one of the representatives of machine learning methods, which describes the mapping relationship between data by adjusting the direct relationship between layers and the weights of nodes in each layer. However, it has problems such as vanishing gradients in the process of processing complex sequences (Zheng et al., 2022). Recurrent neural network (RNN) can maintain the memory of recently added information by establishing connection hidden units (Lin et al., 1998). Furthermore, as an improved model of RNN, LSTM can identify and extract more important historical data information in the process of data prediction by selectively filtering the input information (Li, 2020). Therefore, it has better ability in dealing with non-stationary and nonlinear sequences (Krishan et al., 2019; Liu and Shen, 2019).
However, there are still deficiencies in the existing research on carbon price prediction using the TEI@I complex system research methodology: First, although the superiority of VMD technology has been proved, the existing research on carbon price prediction using VMD technology does not have a further in-depth discussion on the residual term obtained after decomposition (Zhu et al., 2019; Chai et al., 2021; Huang et al., 2021), so the complex information contained in the residual term is ignored, which reduces the decomposition effect of the overall data. Second, although EEMD technology overcomes the defect that EMD technology is prone to modal aliasing to some extent, it does not completely eliminate the added white noise signal, resulting in some residual noise in the decomposition process. Thirdly, although a single LSTM model can fit the long-term historical path of the input sequence data to a certain extent, it is difficult to deeply characterize the effective information and relationships between discontinuous data (Stefenon et al., 2022).
The research objective of this paper is to make up for the deficiency of the existing research, and propose a new hybrid model VMD-CEEMDAN-LSTM model to improve the prediction accuracy of carbon price. The new proposed model incorporated a new quadratic decomposition technique combining VMD and CEEMDAN algorithm for the first time. Specifically, CEEMDAN is used to further decompose the residual term obtained after the application of VMD technology, which solves the technical gap in the application of VMD algorithm in the existing research on carbon price prediction. At the same time, the LSSVM-LSTM model combined with LSSVM (Suykens and Vandewalle, 1999) is used to predict each component obtained after decomposition. The error correction technique, can effectively extract valuable information from error values (Cai et al., 2016; Hao and Tian, 2019). Therefore, compared with the single artificial intelligence prediction model, the neural network hybrid model based on error correction technique fully considers the importance of error data and can improve the accuracy of the model more reasonably (Yu et al., 2015; Zhang et al., 2017). Among them, LSSVM is a kernel function learning machine that follows the principle of Structural Risk Minimization (SRM), which reduces the computational complexity and has excellent fitting ability for nonlinear data (Fang and Xie, 2011). Therefore, LSSVM is used to correct the error data predicted by LSTM to further improve the accuracy of carbon price prediction.
In addition, in order to verify the superiority of the proposed model over existing studies, this paper constructs other nine different benchmark models for comparison, namely LSTM, LSSVM-LSTM, EEMD-LSTM, EEMD-LSSVM-LSTM, CEEMDAN-LSTM, CEEMDAN-LSSVM-LSTM, VMD-LSTM, VMD-LSSVM-LSTM, VMD-EEMD-LSTM, VMD-EEMD-LSSVM-LSTM and VMD-CEEMDAN-LSTM.
The main innovation and contribution of this paper lies in constructing a new quadratic decomposition technique technology to process the carbon price data, and using a more advanced prediction model for research, and verifying the rationality and superiority of the proposed model based on real world transaction data. The details are as follows:
Firstly, a new quadratic decomposition technique combining VMD and CEEMDAN is proposed to decompose the carbon price, which makes up for the deficiency in the existing research of applying VMD technology to predict the carbon price. The empirical results show that, compared with the hybrid model which only adopts single decomposition algorithm (EEMD, CEEMDAN or VMD), the quadratic decomposition technique constructed in this paper fully combines the advantages of VMD and CEEMDAN, which can effectively reduce the complexity of data and better depict the essential characteristics implied in the carbon price sequence.
Secondly, the CEEMDAN is introduced into the carbon price forecasting research, which proves the superiority of the CEEMDAN compared to the EEMD. The results of the empirical study show that the CEEMDAN used in this paper can effectively reduce the reconstruction signal error caused by residual white noise and mine more hidden information.
Thirdly, the LSSVM-LSTM model is used to predict the carbon price for the first time. LSSVM model has been successfully applied in fault detection and MAGE classification (Calisir and Dogantekin, 2011; Long et al., 2014). This paper further adopts LSSVM-LSTM model as the prediction model in the hybrid model. The empirical results show that, compared with LSTM model, LSSVM-LSTM model has better performance in carbon price prediction, and can effectively improve the overall prediction ability of the hybrid model.
Furthermore, in order to verify the robustness of the VMD-CEEMDAN-LSSVM-LSTM model proposed in the study of carbon price prediction, this paper adopts
The rest of this paper is organized as follows. Section 2 reviews the literature on carbon price prediction. Section 3 introduces a series of sub-models involved in this study and the construction steps of the VMD-CEEMDAN-LSSVM-LSTM hybrid model. Section 4 introduces the relevant evaluation criteria and the concrete results of empirical research. Finally, the paper concludes in Section 5.
2 Literature review
As mentioned in the introduction, the prediction of carbon price can be divided into three different categories, namely, the first category of traditional econometric models, the second category of artificial intelligence models and the third category of hybrid models. Acoordingly, the literature review in this part will be divided into the above three parts.
In the research of applying traditional econometric model to predict carbon price, Benz and Trück (2009) applied Markov switching and AR-GARCH models to predict the spot price of carbon dioxide (CO2) emission allowances. Byun and Cho (2013) compared and analyzed the performance of GARCH-type models, an implied volatility from prices, and k-nearest neighbor models in predicting carbon option prices. Bulai et al. (2022) predicted the carbon price in the EU ETS through the proposed ARMA-GARCH model.
In the research of applying artificial intelligence model to predict carbon price, Atsalakis (2016) constructed an adaptive neuro-fuzzy inference system based on ANN in the study of carbon price prediction. Xu et al. (2020) took the carbon price data of the EU ETS as the research object, combined the technology of data reconstruction with extreme learning machine algorithm, and constructed CPN-ELM model to predict the carbon price. Yun et al. (2020) introduced an LSTM model with multi-layer and multi-variable characteristics into the prediction research of carbon price.
In the application of TEI@I complex systems research methodology to predict carbon price research. Yang et al. (2020) took the trading prices of carbon exchanges in different regions of China as the research object, and constructed a mixed model combining the modified ensemble empirical mode decomposition (MEEMD) and the LSTM optimized by the improved whale optimization algorithm (IWOA). Sun and Li (2020) combined CEEMD and LSTM network to forecast price series from China carbon exchanges. Furthermore, Wang et al. (2021) introduced a series of models (including fully integrated EMD, sample entropy, LSTM and random forest) to build a new hybrid model in the prediction of price series from different carbon exchanges in China. Furthermore, in the research of applying quadratic decomposition technology, Sun and Huang (2020) constructed a quadratic decomposition technique consisting of EMD and VMD, and also introduced partial autocorrelation analysis (PACF) and back propagation (BP) neural network model optimized by genetic algorithm (GA) to construct a new hybrid prediction model. Li et al. (2021) constructed a quadratic decomposition technique based on CEEMD and VMD, and used BPNN optimized by improved sine cosine algorithm (ISCA) as a prediction model to predict the carbon price.
Reviewing the above studies, it can be concluded that traditional econometric models and artificial intelligence models cannot fully capture the nonlinear characteristics hidden in the carbon price in the prediction of carbon price. Compared with other existing types of forecasting models, the hybrid model combining decomposition techniques and forecasting models has more advantages. However, there are still some problems neglected in the existing research, the residual term generated by the application of VMD technology still contains a lot of irregular and complex information, and the prediction ability of the LSTM model without optimization also has certain deficiencies. Therefore, in order to improve the ability and accuracy of carbon price prediction methods and fill in the gaps of existing research, our study integrated VMD technology, CEEMDAN technology, LSSVM model and LSTM model to predict the carbon price of the EU ETS by building the VMD-CEEMDAN-LSSVM-LSTM hybrid model.
3 Methodology
This part expounds the relevant sub-models that constitute the hybrid model. Specifically, it includes decomposition algorithms, prediction models and the construction of VMD-CEEMDAN-LSSVM-LSTM model.
3.1 Decomposition algorithms
3.1.1 VMD
According to the preset number of modes, VMD decomposes the signal into finite bandwidths with different center frequencies (Dragomiretskiy and Zosso, 2014). The essence of VMD is to create and solve variational problems. The specific solution process is as follows:
Further,
The expression for center frequency update is:
3.1.2 CEEMDAN
As an improved algorithm of EEMD and EMD, CEEMDAN can have smaller modal aliasing and lower component reconstruction error at the same time. The specific decomposition process is as follows:
3.2 Prediction models
3.2.1 LSSVM
In the SVM model, for a sample
Where
The function interval of the training set is equal to the minimum value of the function interval of all sample points:
Where
Where
The geometric interval can not only represent the correctness of the classification prediction, but also accurately represent the distance from the sample to the separating hyperplane. The optimization problem of SVM is transformed into maximizing the geometric distance of training samples:
The value of the function interval will not affect the solution of the optimal problem. If the function interval of the training sample is set to 1, the above problem will be transformed into:
It can be seen that the optimization problem of SVM is a QP (Quandratic Programming) problem with partition constraints. The specific form is as follows:
Where
Where
Where
Further, solve
Where
3.2.2 LSTM
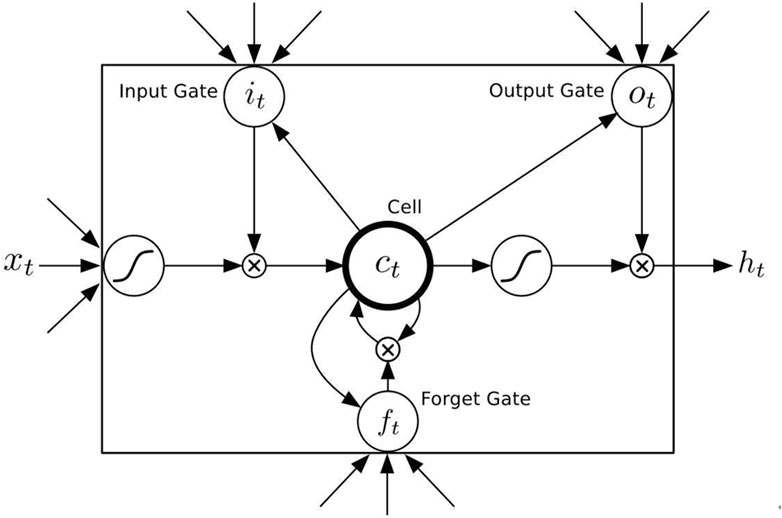
LSTM is a neural network model with memory, and its core unit include the input gate, forgetting gate and output gate. The basic network structure of LSTM is shown in Figure 1.
The function of the gate is to control which information is put into the state value of the cell. The specific mathematical model is as follows:
Where
Where
Where
where
Construction of the hybrid model VMD-CEEMDAN-LSSVM-LSTM
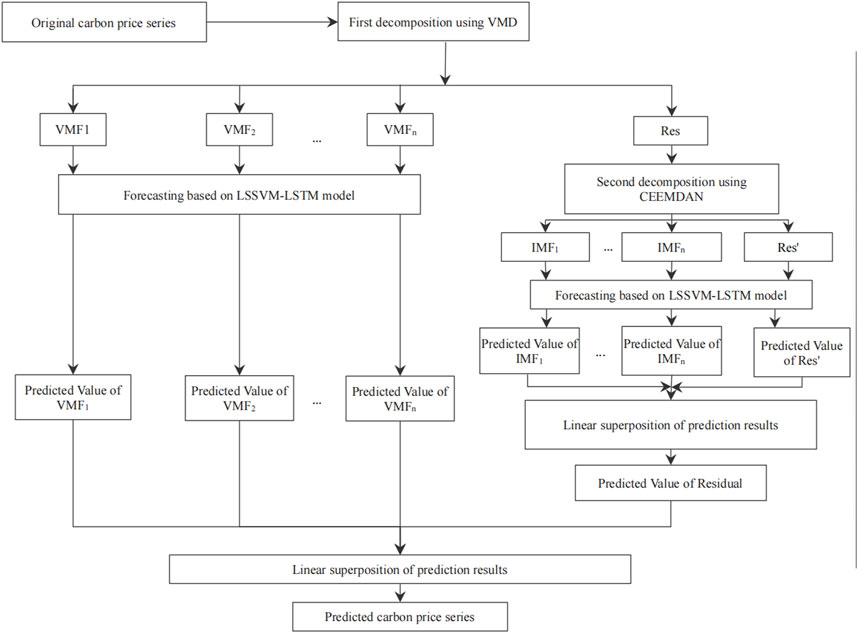
In this section, by combining VMD, CEEMDAN and LSSVM-LSTM, the hybrid VMD-CEEMDAN-LSSVM-LSTM model is developed to predict the carbon price series. The main structure of the model is shown in Figure 2. Firstly, VMD is used to decompose the original carbon price series, in which the residual term obtained by decomposition is further decomposed by CEEMDAN, and then LSSVM-LSTM model is applied to predict each component obtained after decomposing. The detailed steps are as follows:
4 Empirical study
4.1 Source of data
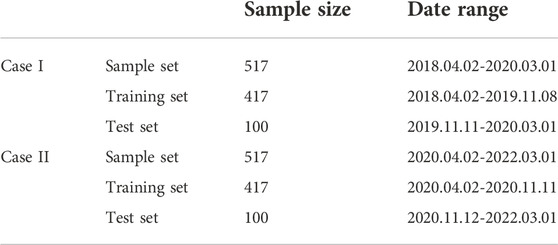
The empirical research of this paper is based on the trading data of EU ETS, and the specific daily futures price data comes from Wind database. As the largest emission trading system market in the world, the necessity and urgency of forecasting the price fluctuation of ETS has been confirmed by the literature (Zhu et al., 2017; Huang et al., 2021. The samples selected in this paper cover two different cases. The effectiveness and robustness of different models for carbon price prediction can be better tested through price data in different time intervals. Specifically, the time range of the two case samples is 2018.04.02-2020.03.01 and 2020.04.02-2022.03.01 respectively.
4.2 Data description and data processing
Due to the learning mechanism of the neural network, the data of each sample need to be divided into the training set and the testing set before prediction. The model is trained by the training set to capture the characteristics of data, and the performance of the model is verified by the testing set. Thus, all samples are divided into the training set and the testing set in this study. Table 1 shows the specific information of data set division of two case samples.
Table 2 shows the results of statistical analysis of sample data from different cases, showing the specific characteristics of the data. It can be inferred from the numerical results of the corresponding indicators that the data of the two case samples do not conform to the normal distribution and have obvious peak values.
In addition, in order to ensure the training effect of the hybrid prediction model, it is necessary to normalize the subsequence data of each modal component obtained by applying the decomposition technique. In the research of this paper, the Min-Max deviation standardization method is adopted to process the data linearly, and the specific expression is:
Where
4.3 Evaluation indicators
In order to evaluate the performance of different models involved in the research on carbon price prediction, this paper selects three common different evaluation indicators. Specifically, it includes,
Where
4.4 Benchmark model
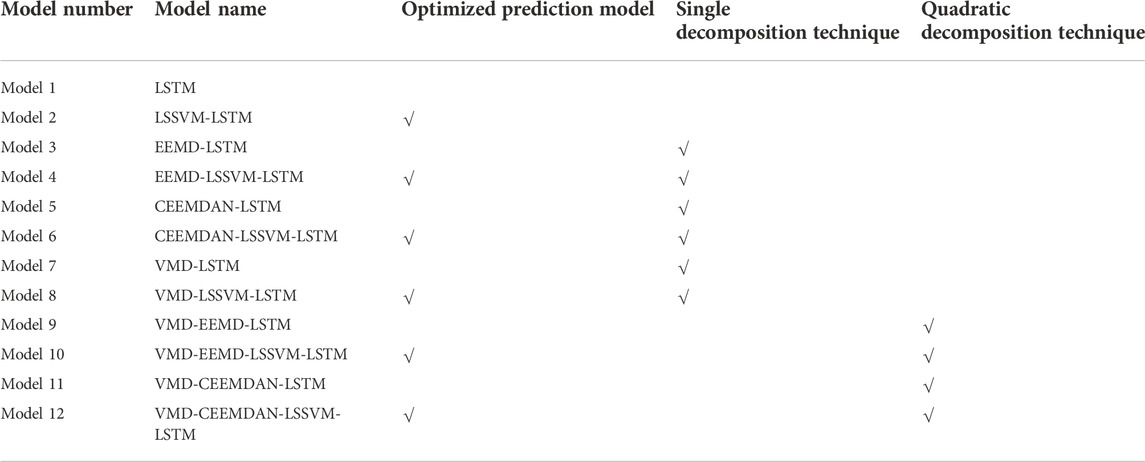
In order to verify the superiority of the VMD-CEEMDAN-LSSVM-LSTM hybrid model proposed in this paper over the existing research, a series of benchmark models are constructed in this paper, including two prediction models without decomposition technique (LSTM and LSSVM-LSTM), six hybrid models with single decomposition technique (EEMD-LSTM, EEMD-LSSVM-LSTM, CEEMDAN-LSTM, CEEMDAN-LSSVM-LSTM, VMD-LSTM and VMD-LSSVM-LSTM) and three other hybrid models with quadratic decomposition technique (VMD-EEMD-LSTM, VMD-EEMD-LSSVM-LSTM and VMD-CEEMDAN-LSTM).
Table 3 shows the characteristics of different models. Specifically, LSTM is the basic prediction model, and LSSVM-LSTM is the prediction model combined with LSSVM. Among the benchmark models that apply the single decomposition technique, EEMD-LSTM, CEEMDAN-LSTM and VMD-LSTM respectively applies the EEMD, CEEMDAN and VMD technologies to the carbon price series, discard the residual items, and then use LSTM model to predict a series of decomposed components. Correspondingly, EEMD-LSSVM-LSTM, CEEMDAN-LSSVM-LSTM and VMD-LSSVM-LSTM replace the prediction model from the LSTM model with the LSSVM-LSTM model.
In the benchmark model applying the quadratic decomposition technique, VMD-EEMD-LSTM retains the residual term obtained after applying the VMD technique to the carbon price sequence, decomposes the residual term with the EEMD technique, and uses the LSTM model to predict the decomposed components and the residual term. Correspondingly, the VMD-EEMD-LSSVM-LSTM uses the LSSVM-LSTM model to predict each component. The VMD-CEEMDAN-LSTM further uses CEEMDAN technology to decompose the residual term obtained by applying VMD technology. The VMD-CEEMDAN-LSSVM-LSTM is a hybrid model that combines the VMD-CEEMDAN quadratic decomposition technique and the LSSVM-LSTM model proposed in this paper.
4.4 Analysis of empirical results
This section shows the empirical results of the above two cases. The empirical research of all models is completed by the software matlab 2019a.In order to evaluate the effectiveness and robustness of the forecasting models more comprehensively, a rolling forecasting strategy was applied, and all the models have been studied with 1-step, 2-step and 4-step ahead forecasting. Compared with the static forecasting method, the rolling forecasting method continuously updates the data of the training samples by inputting the time series into the forecasting model in the form of a rolling window, and dynamically controls the data that is far away from the current moment through the weight, thus avoiding the cumulative iteration of prediction errors and improve the predictive ability of the model.
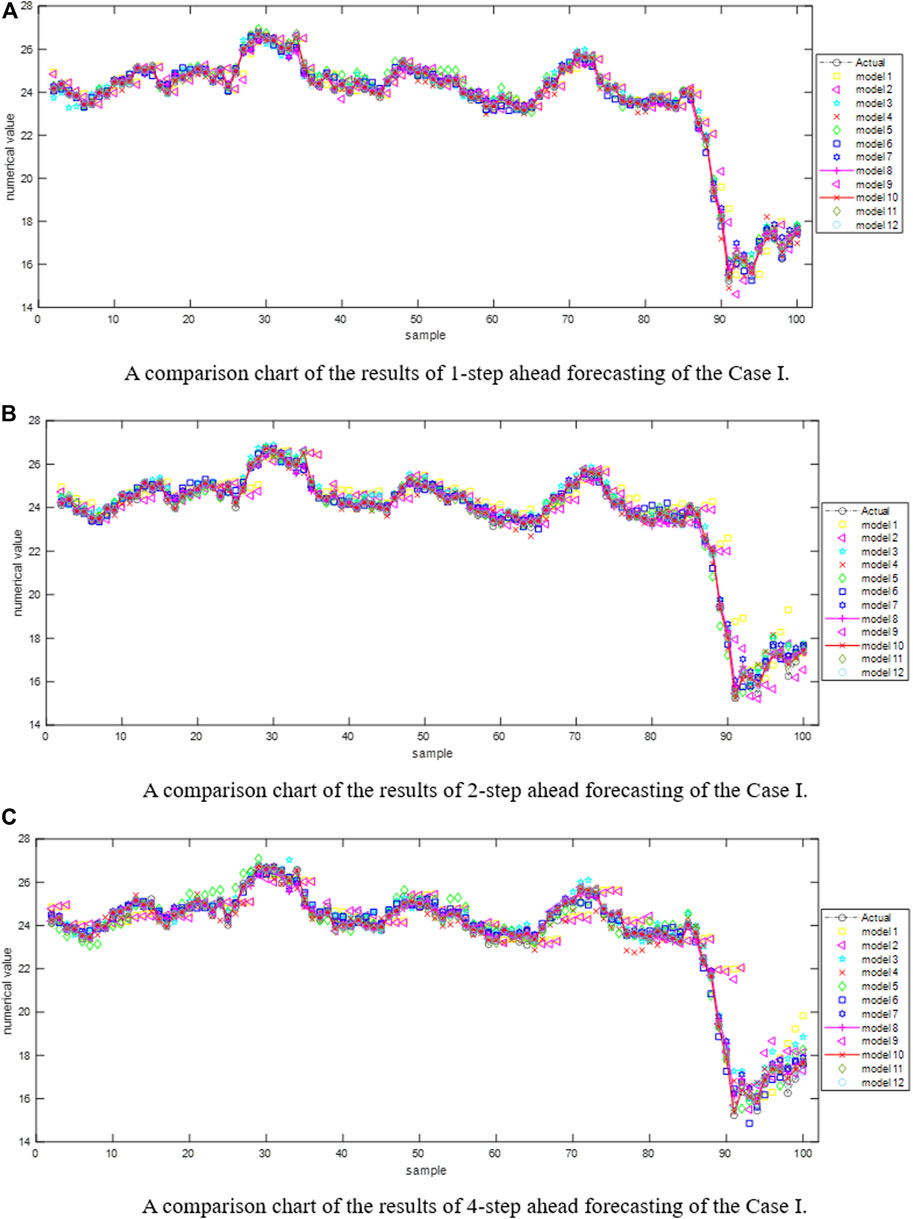
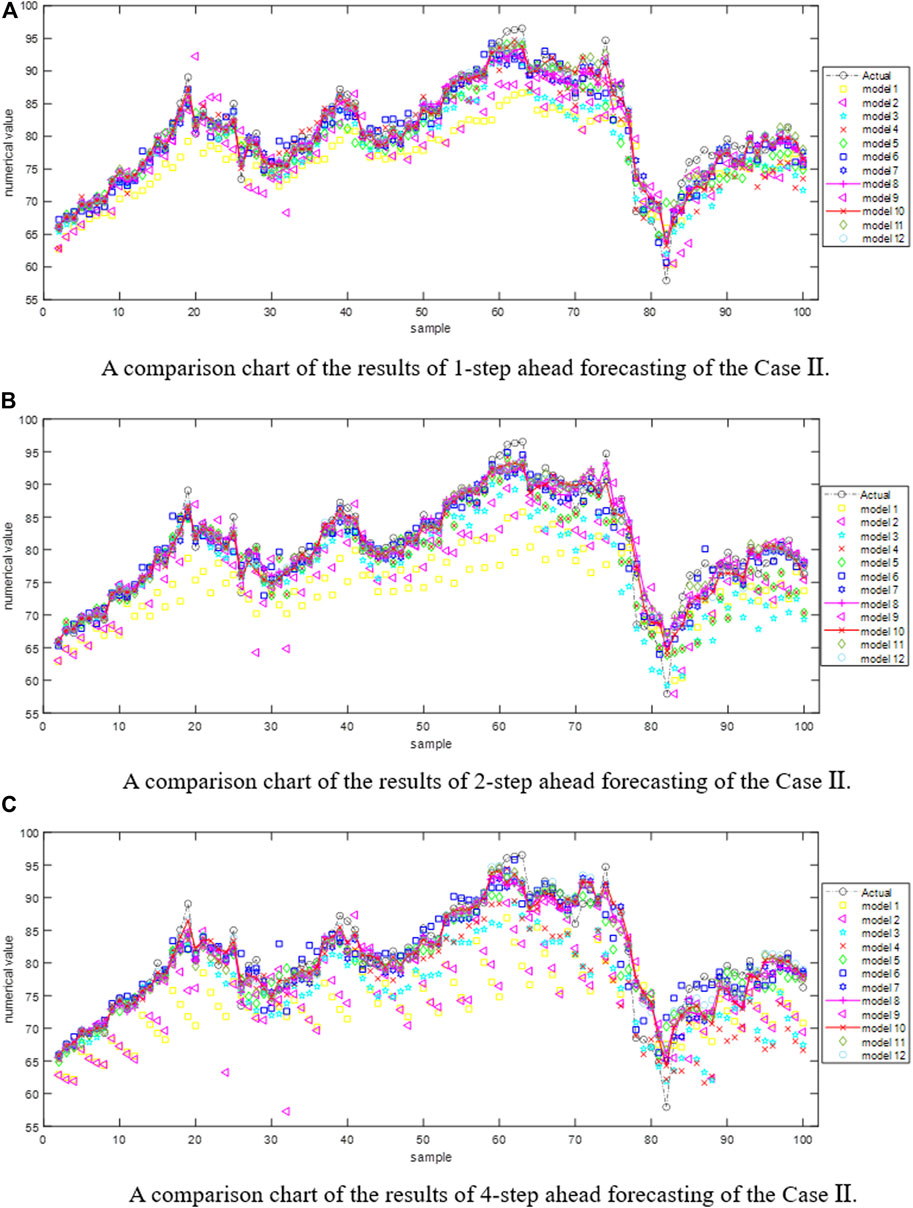
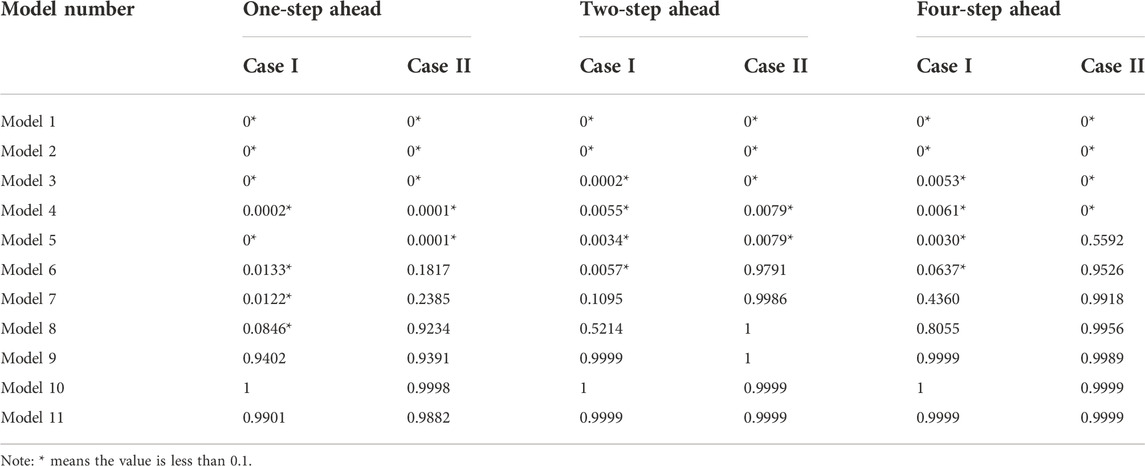
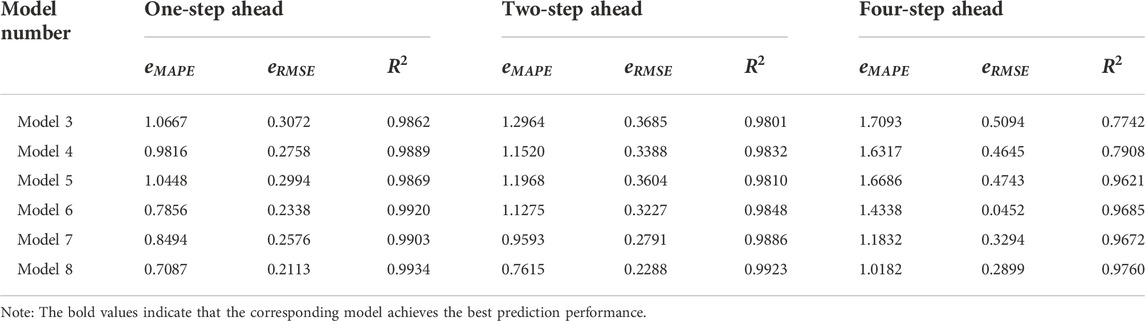
Figure 3 is the comparison charts of the results of 1-step, 2-step and 4-step ahead forecasting of Case Ⅰ by different models. Correspondingly, Figure 4 is the prediction results of Case Ⅱ. Table 4 shows the results of Dunnett test on different benchmark models. It can be seen from the numerical results that among the series of benchmark models constructed in this paper, the hybrid model incorporating the decomposition technique is significantly different from the single prediction model. Tables 5–10 show the concrete numerical results of multi-step ahead forecasting completed by different models for Case Ⅰ and Case Ⅱ. Specifically, among the empirical results of Case Ⅰ, Table 5 and Table 8 show the prediction results of the model without decomposition technique, Table 6 and Table 9 show the prediction results of the model with single decomposition technique, and Table 7 and Table 10 show the prediction results of the model with quadratic decomposition technique. In the prediction of carbon price series, the results based on different evaluation indexes (
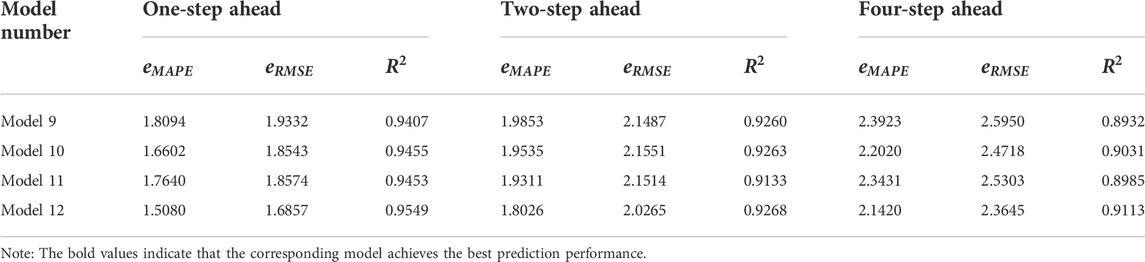
TABLE 10. Prediction results of the model combined with quadratic decomposition technique (Case II).
The remaining analysis content in this section will focus on the prediction results, The concrete analysis includes the prediction model and decomposition techniques which constitute the hybrid model.
4.4.1 Analysis of prediction model
In the series of models involved in this paper, two prediction models, LSTM and LSSVM-LSTM, are used respectively. The results of empirical studies based on different cases show that the LSSVM-LSTM model is more suitable for the prediction of carbon price series than the LSTM model. The specific analysis are as follows:
(1) By comparing the prediction results of LSTM and LSSVM-LSTM, it can be seen that the latter outperforms the former in both cases. Taking the results of case in the 1-step ahead forecasting scenario as an example, the results of the evaluation indicators
(2) In the hybrid model applying the single decomposition technique, by comparing the prediction results of the hybrid model with LSSVM-LSTM model and the hybrid model with LSTM model, it can be seen that the prediction results of the hybrid model with LSSVM-LSTM in two different cases are better than those of the hybrid model with LSTM model. Taking the numerical results of case I combined with the VMD technology in the 1-step 1-step ahead forecasting scenario as an example, the results of the evaluation indicators
(3) In the hybrid model using quadratic decomposition technique, VMD-EEMD-LSSVM-LSTM and VMD-CEEMDAN-LSSVM-LSTM combined with LSSVM-LSTM have better prediction results than VMD-EEMD-LSTM and VMD-CEEMDAN-LSTM combined with LSTM. This result shows that LSSVM-LSTM is more superior than LSTM for carbon price prediction, and it is not only applicable to the hybrid model combined with the single decomposition technology, but also applicable to the hybrid model combined with the quadratic decomposition technique.
The above conclusions are consistent in the research of different case samples. As a special commodity, the price of carbon allowances is bound to be affected by historical prices. It is difficult for a single LSTM model to fully describe the characteristics of carbon price data. Compared with LSTM, LSSVM-LSTM can better capture the long-term correlation between price data, mine valuable information in historical time series, and adapt to the complex change form of carbon price series, so it has better prediction performance.
4.4.2 Analysis of decomposition techniques
The hybrid models combined with decomposition techniques in this paper can be divided into two different types: the hybrid model using single decomposition technique and the hybrid model using quadratic decomposition technique. Based on the empirical research results of carbon price forecasting, it shows that VMD technology can effectively improve the prediction performance of the hybrid model with single decomposition technique. The quadratic decomposition technique VMD-CEEMDAN proposed in this paper has better performance than all single decomposition techniques and other different types of quadratic decomposition techniques, which confirms the effectiveness of the decomposition strategy constructed in this paper. The specific analysis is as follows:
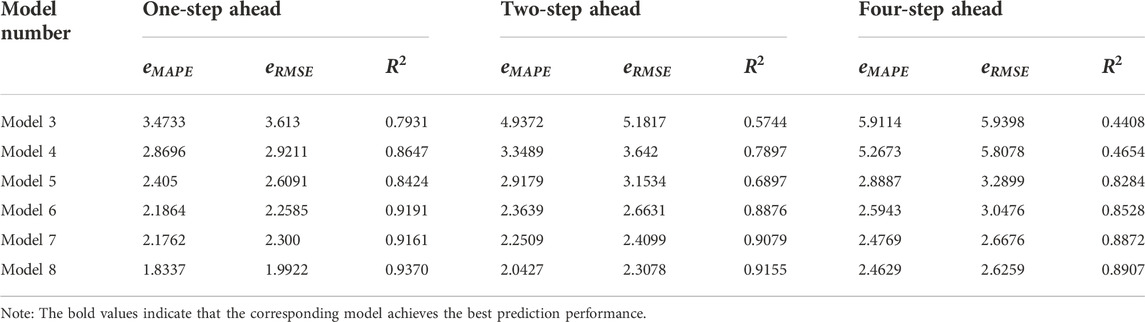
(1) Decomposition technology can effectively improve the prediction accuracy. Comparing the prediction results of the single model without the decomposition technique and the hybrid model with the decomposition technique, it can be seen that the hybrid model with the decomposition technique outperforms the single model in all multi-step ahead forecasting scenarios. This result demonstrates the validity of the TEI@I complex system research methodology for carbon price forecasting. By applying the decomposition technology to carbon prices, the complexity of the price series can be effectively reduced, and the prediction ability of the overall model can be improved.
(2) The decomposition effect of VMD technology is better than EEMD technology and CEEMDAN technology. In the hybrid model applying single decomposition technique, by comparing the prediction results of the hybrid model combining EEMD technology (EEMD-LSTM and EEMD-LSSVM-LSTM), CEEMDAN technology (CEEMDAN-LSTM and CEEMDAN-LSSVM-LSTM) and VMD technology (VMD-LSTM and VMD-LSSVM-LSTM), it can be seen that CEEMDAN technology has achieved better prediction performance than EEMD technology, while VMD technology has achieved better performance than EEMD technology and CEEMDAN technology in any prediction situation of different cases. This result shows that CEEMDAN technology selected in this paper is more effective than EEMD technology in the prediction of carbon price, while VMD technology can transform complex information contained in carbon price into more stable and regular modal information compared with other decomposition technologies.
(3) The effect of quadratic decomposition technique is significantly better than that of single decomposition technology. By comparing the results of the hybrid model using the single decomposition technique (EEMD-LSTM, EEMD-LSSVM-LSTM, CEEMDAN-LSTM, CEEMDAN-LSSVM-LSTM, VMD-LSTM and VMD-LSSVM-LSTM) and the hybrid model using the quadratic decomposition technique (VMD-EEMD-LSTM 、VMD-EEMD-LSSVM-LSTM 、VMD-CEEMDAN-LSTM and VMD-CEEMDAN-LSSVM-LSTM), it can be seen that the hybrid model combined with the quadratic decomposition technique has better decomposition effect than the single decomposition technique, which effectively reduces the value of evaluation indicators, and shows the effectiveness of the quadratic decomposition technique in the research of carbon price prediction.
(4) VMD-CEEMDAN technology has the best ability to decompose data. In the hybrid model applying the quadratic decomposition technique, by comparing the prediction results of the models applying the VMD-EEMD technology (VMD-EEMD-LSTM and VMD-EEMD-LSSVM-LSTM) and the VMD-CEEMDAN technology (VMD-CEEMDAN-LSTM and VMD-CEEMDAN-LSSVM-LSTM), it can be seen that VMD-CEEMDAN technology can deal with the residual term after VMD technology is applied more effectively than VMD-EEMD technology.
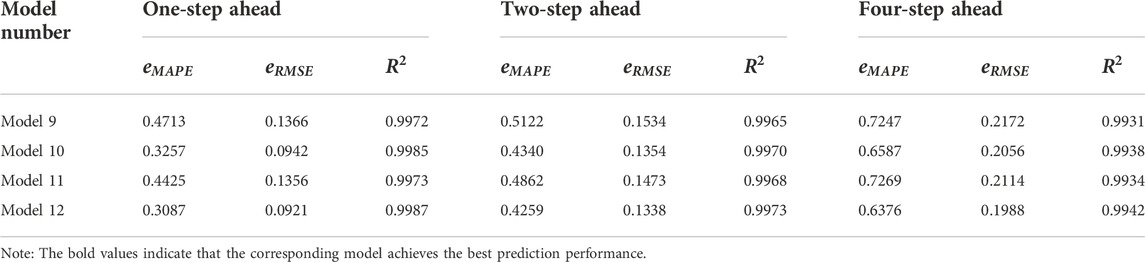
(5) The VMD-CEEMDAN-LSSVM-LSTM hybrid model has the best prediction performance. In the 1-step, 2-step and 4-step ahead forecasting scenarios, with the increase of the prediction step size, the values of the error indicators of each model show an upward trend due to the existence of error accumulation. The VMD-CEEMDAN-LSSVM-LSTM model proposed in this paper can maintain the smallest error value in all forward multi-step forecasting studies, indicating the robustness of this hybrid model in the research of carbon price forecasting.
To sum up, the data of carbon price is highly nonlinear and complex, which leads to the unsatisfactory prediction effect of traditional single prediction model on carbon price. The empirical results of different sample cases show that the single decomposition technology can reduce noise and improve the prediction accuracy of carbon price to a certain extent. Further, compared with the single decomposition technology, the quadratic decomposition technique can more accurately process data with high nonlinearity and irregularity, effectively break through the limitations of the model, and achieve higher-precision predictions.
5 Conclusion
The effective prediction of carbon price is of great significance to all parties involved in carbon market transactions and relevant policy makers. Aiming at overcoming deficiencies of the existing research on carbon price prediction using decomposition technology, this paper combines VMD, CEEMDAN and LSSVM-LSTM technology to construct a new hybrid model VMD-CEEMDAN-LSSVM-LSTM.
In this hybrid model, a new quadratic decomposition technique, VMD-CEEMDAN, is introduced for the first time. The complex information contained in the residual term of the original carbon price series obtained by VMD technology is considered, and the prediction research is carried out based on LSSVM-LSTM model. The empirical research results based on the carbon price of the EU ETS show that, compared with a series of other benchmark models, the hybrid model VMD-CEEMDAN-LSSVM-LSTM proposed in this paper can maintain the best performance in all multi-step ahead forecasting scenarios. The excellent performance shows that the hybrid model constructed in this paper can effectively describe the complex fluctuation information in the carbon price series, which significantly improves the overall prediction performance of the model.
It is worth mentioning that the carbon price prediction model proposed in this paper only takes the price data as the input of the model. Although this method of prediction based on historical price data can have excellent prediction results to a certain extent, the carbon trading market is jointly influenced by internal market mechanism and external environmental heterogeneity, such as supply and demand, climate change, government intervention and many other different factors. The impact mechanism of different factors on carbon price volatility is complex. Therefore, in the future research, the model proposed in this paper can be combined with other influencing factors, and a multi-factor model can be constructed to explore the influence of different factors on carbon price fluctuation, so as to further improve the rationality and effectiveness of carbon price prediction.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material further inquiries can be directed to the corresponding author.
Author contributions
TZ: Conceptualization, Validation, Writing—review and editing, Supervision, Methodology, Software, Formal analysis, Writing—original draft, Visualization. ZT: Data curation, Project administration, Investigation, Resource acquisition, Form suggestion, Funding acquisition.
Acknowledgments
The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China under Grant Nos. 71973028.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aatola, P., Ollikainen, M., and Toppinen, A. (2013). Price determination in the EU ETS market: Theory and econometric analysis with market fundamentals. Energy Econ. 36, 380–395. doi:10.1016/j.eneco.2012.09.009
Atsalakis, G. S. (2016). Using computational intelligence to forecast carbon prices. Appl. Soft Comput. 43, 107–116. doi:10.1016/j.asoc.2016.02.029
Bauer, N., Bertram, C., Schultes, A., Klein, D., Luderer, G., Kriegler, E., et al. (2020). Quantification of an efficiency–sovereignty trade-off in climate policy. Nature 588, 261–266. doi:10.1038/s41586-020-2982-5
Benz, E., and Trück, S. (2009). Modeling the price dynamics of CO2 emission allowances. Energy Econ. 31, 4–15. doi:10.1016/j.eneco.2008.07.003
Bulai, V. C., Horobet, A., Popovici, O. C., Belascu, L., and Dumitrescu, S. A. (2022). A VaR-based methodology for assessing carbon price risk across European Union economic sectors. Energies 14 (24), 8424. doi:10.3390/en14248424
Byun, S. J., and Cho, H. (2013). Forecasting carbon futures volatility using GARCH models with energy volatilities. Energy Econ. 40, 207–221. doi:10.1016/j.eneco.2013.06.017
Cai, G., Wang, W., and Lu, J. (2016). A novel hybrid short term load forecasting model considering the error of numerical weather prediction. Energies 9 (12), 994. doi:10.3390/en9120994
Calisir, D., and Dogantekin, E. (2011). A new intelligent hepatitis diagnosis system: PCA-LSSVM. Expert Syst. Appl. 38 (8), 10705–10708. doi:10.1016/j.eswa.2011.01.014
Cao, J., Li, Z., and Li, J. (2019). Financial time series forecasting model based on CEEMDAN and LSTM. Phys. A Stat. Mech. its Appl. 519, 127–139. doi:10.1016/j.physa.2018.11.061
Chai, S. L., Zhang, Z. X., and Zhang, Z. (2021). Carbon price prediction for China's ETS pilots using variational mode decomposition and optimized extreme learning machine. Ann. Oper. Res., 18. 1–22. doi:10.1007/s10479-021-04392-7
Chen, Z. F., Zhang, X., and Chen, F. L. (2021). Do carbon emission trading schemes stimulate green innovation in enterprises? Evidence from China. Technol. Forecast. Soc. Change 168, 120744. doi:10.1016/j.techfore.2021.120744
Cui, L., Fan, Y., Zhu, L., and Bi, Q. (2014). How will the emissions trading scheme save cost for achieving China’s 2020 carbon intensity reduction target? Appl. Energy 136, 1043–1052. doi:10.1016/j.apenergy.2014.05.021
da Silva, R. G., Moreno, S. R., Ribeiro, M. H. D., Larcher, J. H. K., Mariani, V. C., and Coelho, L. D. (2022). Multi-step short-term wind speed forecasting based on multi-stage decomposition coupled with stacking-ensemble learning approach. Int. J. Electr. Power & Energy Syst. 143, 108504. doi:10.1016/j.ijepes.2022.108504
da Silva, R. G., Ribeiro, M. H. D., Moreno, S. R., Mariani, V. C., and Coelho, L. D. (2021). A novel decomposition-ensemble learning framework for multi-step ahead wind energy forecasting. Energy 216, 119174. doi:10.1016/j.energy.2020.119174
Duan, H. B., Mo, J. L., Fan, Y., and Wang, S. Y. (2018). Achieving China’s energy and climate policy targets in 2030 under multiple uncertainties. Energy Econ. 70, 45–60. doi:10.1016/j.eneco.2017.12.022
Duc, Khuong, N., Toan, L. D. H., and Nasir, M. A. (2021). Carbon emissions determinants and forecasting: Evidence from G6 countries. J. Environ. Manag. 285, 111988. doi:10.1016/j.jenvman.2021.111988
Fan, X., Lv, X., Yin, J., Tian, L., and Liang, J. (2019). Multifractality and market efficiency of carbon emission trading market: Analysis using the multifractal detrended fluctuation technique. Appl. Energy 251, 113333. doi:10.1016/j.apenergy.2019.113333
Fang, K. A., and Xie, B. (2011). Research on dealing with missing data based on clustering and association rule. Stat. Res. 2, 89–94.
Feijoo, F., Silva, W., and Das, T. K. (2016). A computationally efficient electricity price forecasting model for real time energy markets. Energy Convers. Manag. 113, 27–35. doi:10.1016/j.enconman.2016.01.043
Gao, R. B., Du, L., Suganthan, P. N., Zhou, Q., and Yuen, K. F. (2022). Random vector functional link neural network based ensemble deep learning for short-term load forecasting. Expert Syst. Appl. 206, 117784. doi:10.1016/j.eswa.2022.117784
Gundu, V., and Simon, S. P. (2021). PSO-LSTM for short term forecast of heterogeneous time series electricity price signals. J. Ambient. Intell. Humaniz. Comput. 12 (2), 2375–2385. doi:10.1007/s12652-020-02353-9
Hao, Y., and Tian, C. (2019). A novel two-stage forecasting model based on error factor and ensemble method for multi-step wind power forecasting. Appl. Energy 238, 368–383. doi:10.1016/j.apenergy.2019.01.063
Huang, Y. C., and He, Z. (2020). Carbon price forecasting with optimization prediction method based on unstructured combination. Sci. Total Environ. 725, 138350. doi:10.1016/j.scitotenv.2020.138350
Huang, Y. M., Dai, X. Y., Wang, Q. W., and Zhou, D. Q. (2021). A hybrid model for carbon price forecasting using GARCH and long short-term memory network. Appl. Energy 285, 116485. doi:10.1016/j.apenergy.2021.116485
Jiang, S. M., Yang, C., Guo, J. T., and Ding, Z. W. (2018). ARIMA forecasting of China's coal consumption, price and investment by 2030. Energy Sources Part B Econ. Plan. Policy 13 (3), 190–195. doi:10.1080/15567249.2017.1423413
Ju, F. Y., and Hong, W. C. (2013). Application of seasonal SVR with chaotic gravitational search algorithm in electricity forecasting. Appl. Math. Model. 37, 9643–9651. doi:10.1016/j.apm.2013.05.016
Keles, D., Scelle, J., Paraschiv, F., and Fichtner, W. (2016). Extended forecast methods for day-ahead electricity spot prices applying artificial neural networks. Appl. Energy 162, 218–230. doi:10.1016/j.apenergy.2015.09.087
Koch, N., Fuss, S., Grosjean, G., and Edenhofer, O. (2014). Causes of the EU ETS price drop: Recession, CDM, renewable policies or a bit of everything?-New evidence. Energy Policy 73, 676–685. doi:10.1016/j.enpol.2014.06.024
Krishan, M., Jha, S., Das, J., Singh, A., Goyal, M. K., and Sekar, C. (2019). Air quality modelling using long short-term memory (LSTM) over NCT-Delhi, India. Air Qual. Atmos. Health 12 (8), 899–908. doi:10.1007/s11869-019-00696-7
Li, H. T., Jin, F., Sun, S. L., and Li, Y. W. (2021). A new secondary decomposition ensemble learning approach for carbon price forecasting. Knowledge-based Syst. 214, 106686. doi:10.1016/j.knosys.2020.106686
Li, Y. (2020). Forecasting Chinese carbon emissions based on a novel time series prediction method. Energy Sci. Eng. 8 (7), 2274–2285. doi:10.1002/ese3.662
Lin, K. P., Pai, P. F., and Yang, S. L. (2011). Forecasting concentrations of air pollutants by logarithm support vector regression with immune algorithms. Appl. Math. Comput. 217 (12), 5318–5327. doi:10.1016/j.amc.2010.11.055
Lin, T., Horne, B. G., and Giles, C. L. (1998). How embedded memory in recurrent neural network architectures helps learning long-term temporal dependencies. Neural Netw. 11 (5), 861–868. doi:10.1016/s0893-6080(98)00018-5
Liu, H., and Shen, L. (2019). Forecasting carbon price using empirical wavelet transform and gated recurrent unit neural network. Carbon Manag. 11 (1), 25–37. doi:10.1080/17583004.2019.1686930
Liu, J., Huang, Y., and Chang, C. (2020). Leverage analysis of carbon market price fluctuation in China. J. Clean. Prod. 245, 118557. doi:10.1016/j.jclepro.2019.118557
Long, B., Xian, W., Li, M., and Wang, H. (2014). Improved diagnostics for the incipient faults in analog circuits using LSSVM based on PSO algorithm with Mahalanobis distance. Neurocomputing 133 (10), 237–248. doi:10.1016/j.neucom.2013.11.012
Seyedan, M., Mafakheri, F., and Wang, C. (2022). Cluster-based demand forecasting using Bayesian model averaging: An ensemble learning approach. Decis. Anal. J. 3, 100033. doi:10.1016/j.dajour.2022.100033
Song, Y. Z., Liu, T. S., Liang, D. P., Li, Y., and Song, X. Q. (2019a). A fuzzy stochastic model for carbon price prediction under the effect of demand-related policy in China's carbon market. Ecol. Econ. 157, 253–265. doi:10.1016/j.ecolecon.2018.10.001
Song, Y. Z., Liu, T. S., Ye, B., Zhu, Y., Li, Y., and Song, X. Q. (2019b). Improving the liquidity of China’s carbon market: Insight from the effect of carbon price transmission under the policy release. J. Clean. Prod. 239, 118049. doi:10.1016/j.jclepro.2019.118049
Stefenon, S. F., Ribeiro, M. H. D., Nied, A., Yow, K. C., Mariani, V. C., Coelho, L. D., et al. (2022). Time series forecasting using ensemble learning methods for emergency prevention in hydroelectric power plants with dam. Electr. Power Syst. Res. 202, 107584. doi:10.1016/j.epsr.2021.107584
Sun, W., and Huang, C. (2020). A carbon price prediction model based on secondary decomposition algorithm and optimized back propagation neural network. J. Clean. Prod. 243, 118671–671. doi:10.1016/j.jclepro.2019.118671
Sun, W., and Li, Z. Q. (2020). An ensemble-driven long short-term memory model based on mode decomposition for carbon price forecasting of all eight carbon trading pilots in China. Energy Sci. Eng. 8 (11), 4094–4115. doi:10.1002/ese3.799
Sun, W., and Wang, Y. W. (2020). Factor analysis and carbon price prediction based on empirical mode decomposition and least squares support vector machine optimized by improved particle swarm optimization. Carbon Manag. 11 (3), 315–329. doi:10.1080/17583004.2020.1755597
Sun, W., and Xu, C. (2021). Carbon price prediction based on modified wavelet least square support vector machine. Sci. Total Environ. 754, 142052. doi:10.1016/j.scitotenv.2020.142052
Suykens, J. A. K., and Vandewalle, J. (1999). Least squares support vector machine classifiers. Neural Process. Lett. 9 (3), 293–300. doi:10.1023/a:1018628609742
Taylan, O. (2017). Modelling and analysis of ozone concentration by artificial intelligent techniques for estimating air quality. Atmos. Environ. 150, 356–365. doi:10.1016/j.atmosenv.2016.11.030
Tian, C., and Hao, Y. (2020). Point and interval forecasting for carbon price based on an improved analysis forecast system. Appl. Math. Model. 79, 126–144. doi:10.1016/j.apm.2019.10.022
Wang, J. J., Sun, X., Cheng, Q., and Cui, Q. (2021). An innovative random forest-based nonlinear ensemble paradigm of improved feature extraction and deep learning for carbon price forecasting. Sci. Total Environ. 762, 143099. doi:10.1016/j.scitotenv.2020.143099
Wang, S., E, J. W., and Li, S. G. (2019). A novel hybrid carbon price forecasting model based on radial basis function neural network. Acta Phys. Pol. A 135 (3), 368–374. doi:10.12693/aphyspola.135.368
Wang, S., Yu, L., and Lai, K. K. (2005). Crude oil price forecasting with TEI@I methodology. J. Syst. Sci. Complex. 18 (2), 145–166.
Wu, Z., and Huang, N. E. (2004). A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. A 460 (2046), 1597–1611. doi:10.1098/rspa.2003.1221
Xu, H., Wang, M., Jiang, S., and Yang, W. (2020). Carbon price forecasting with complex network and extreme learning machine. Phys. A Stat. Mech. its Appl. 545, 122830. doi:10.1016/j.physa.2019.122830
Yang, S. M., Chen, D. J., Li, S. L., and Wang, W. J. (2020). Carbon price forecasting based on modified ensemble empirical mode decomposition and long short-term memory optimized by improved whale optimization algorithm. Sci. Total Environ. 716, 137117. doi:10.1016/j.scitotenv.2020.137117
Yu, Z., Yang, C., Zhang, Z., and Jiao, J. (2015). Error correction method based on data transformational GM (1, 1) and application on tax forecasting. Appl. Soft Comput. 37, 554–560. doi:10.1016/j.asoc.2015.09.001
Yun, P., Zhang, C., Wu, Y. Q., Yang, X. Z., and Wagan, Z. A. (2020). A novel extended higher-order moment multi-factor framework for forecasting the carbon price: Testing on the multilayer long short-term memory network. Sustainability 12 (5), 1869. doi:10.3390/su12051869
Zhang, J. L., Li, D., Hao, Y., and Tan, Z. F. (2018). A hybrid model using signal processing technology, econometric models and neural network for carbon spot price forecasting. J. Clean. Prod. 204, 958–964. doi:10.1016/j.jclepro.2018.09.071
Zhang, Y. J., and Wei, Y. M. (2010). An overview of current research on EU ETS: Evidence from its operating mechanism and economic effect. Appl. Energy 87 (6), 1804–1814. doi:10.1016/j.apenergy.2009.12.019
Zhang, Y., Wang, P., Ni, T., Cheng, P., and Lei, S. (2017). Wind power prediction based on LS-SVM model with error correction. Adv. Electr. Comp. Eng. 17 (1), 3–8. doi:10.4316/aece.2017.01001
Zheng, X., Kok, S., Wen, C., Haslenda, H., and Yee, V. (2022). Forecasting heterogeneous municipal solid waste generation via Bayesian-optimised neural network with ensemble learning for improved generalization. Comput. Chem. Eng. 166, 107946. doi:10.1016/j.compchemeng.20
Zhu, B., Han, D., Wang, P., Wu, Z., Zhang, T., and Wei, Y. M. (2017). Forecasting carbon price using empirical mode decomposition and evolutionary least squares support vector regression. Appl. Energy 191, 521–530. doi:10.1016/j.apenergy.2017.01.076
Zhu, B., Wang, P., Chevallier, J., Wei, Y. M., and Xie, R. (2018). Enriching the VaR framework to EEMD with an application to the European carbon market. Int. J. Fin. Econ. 23, 315–328. doi:10.1002/ijfe.1618
Keywords: carbon price, quadratic decomposition technique, VMD-CEEMDAN, LSSVM-LSTM, multi-step ahead forecasting
Citation: Zhang T and Tang Z (2023) Multi-step carbon price forecasting based on a new quadratic decomposition ensemble learning approach. Front. Energy Res. 10:991570. doi: 10.3389/fenrg.2022.991570
Received: 11 July 2022; Accepted: 14 September 2022;
Published: 06 January 2023.
Edited by:
Leandro Dos Santos Coelho, Pontifical Catholic University of Parana, BrazilReviewed by:
Jorge Sandoval, Pontifical Catholic University of Parana, BrazilViviana Mariani, Pontifical Catholic University of Parana, Brazil
Matheus Ribeiro, Federal Technological University of Paraná, Brazil
Copyright © 2023 Zhang and Tang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhenpeng Tang, emhlbnB0YWZAMTI2LmNvbQ==
 Tingting Zhang
Tingting Zhang Zhenpeng Tang
Zhenpeng Tang