Oil-gas two-phase seepage model in fractured carbonate reservoirs

Fractures are developed in fractured carbonate reservoirs. Traditional fracture characterization methods and seepage mathematical models cannot accurately describe the complex spatial distribution of large-scale fractures and their stress sensitivity, and do not consider the two-phase seepage of oil and gas, resulting in the dynamic analysis results have large errors. Aiming at this problem, a two-phase seepage model of oil and gas in fractured carbonate reservoirs considering stress sensitivity is established in this paper, and the semi-analytical solution of the model is obtained by using three-dimensional source function theory and finite difference method. The accuracy of the model is verified by comparison with commercial numerical simulation software, the production performance curve of oil and gas two-phase is drawn, and the influence of key seepage parameters of reservoirs and fractures on production performance is analyzed. The results show that the hybrid solution method of 3D source function and finite difference can realize the accurate and efficient solution of 3D discrete fracture oil and gas two-phase seepage model. The stress sensitivity effect leads to serious loss of fracture permeability and increase of fluid seepage resistance, which seriously affects the production of oil wells. The greater the fracture permeability, the higher the initial value of production, and the higher the position of the production curve. The longer fracture length, the higher the production curve in the early and middle production stages, and the slower the production decline.

1 Introduction

In recent years, with the deepening of exploration and development, many fractured carbonate volatile oil reservoirs have been discovered and show huge resource potential (Zhou and Yang, 2012; Yang et al., 2018), the reservoir pressure is lower than the bubble point pressure and degassing occurs, which seriously affects the productivity of the oil well (Sun et al., 2022a). Affected by diagenesis and tectonic processes, such reservoirs usually have dense matrix and uneven fracture development. Large-scale natural fractures are generally developed near faults, and are usually distributed discontinuously. Such fractures are not only important flow channels but also storage spaces (Zhang et al., 2017). In addition, a large number of studies have shown that the fracture system of such reservoirs exhibits strong stress sensitivity (Yang et al., 2009; Li et al., 2014; Li and Shao, 2017), and the stress sensitivity effect has a serious negative effect on the fluid seepage ability, which directly affects the stable production ability of the oil well. Therefore, fracture seepage parameters, oil and gas two-phase flow characteristics, and stress-sensitive effects are the key factors affecting the accurate prediction of the productivity of fractured carbonate volatile oil reservoirs, which should be considered in the productivity evaluation model.

At present, the productivity prediction methods of carbonate reservoirs mainly include analytical, semi-analytical and numerical simulation methods. The analytical method is usually based on the steady-state seepage theory, and uses the point-sink method and the superposition principle of potential to establish the productivity calculation model of carbonate oil and gas wells (Sun et al., 2022b). For carbonate reservoirs, the development process is in an unsteady flow stage for a long time. The productivity equation established based on the steady-state seepage theory cannot truly reflect the production process of the gas reservoir, and most of the analytical models are based on multi-media models (Pallav and Khalid, 2006; Jia et al., 2016; Shi et al., 2018). The multi-media model considers fractures as the main seepage channel, matrix as the main reservoir space, and quasi-steady or unsteady channeling to the natural fracture system at the same time, the fractures and the matrix system are continuously and uniformly distributed, and the fractures The characteristic parameters of cannot be shown to characterize, and this method is not suitable for fractured carbonate reservoirs. Many semi-analytical methods are mainly based on two-dimensional discrete models (Hazlett and Babu, 2014; Zhou et al., 2014; Fang et al., 2015), and the characteristic parameters of each fracture in the reservoir can be explicitly represented. In order to improve the calculation efficiency, the idea of reducing the dimension is usually adopted to simplify the number of fractures meshes, considering that the fractures are distributed in two-dimensional space, and the inside of the fractures is a one-dimensional flow problem. Although the discrete processing of the fracture system in the two-dimensional space can improve the computational efficiency to a certain extent, the description of large-scale three-dimensional fracture characteristics lacks authenticity. Therefore, the mathematical model of seepage established from this is difficult to accurately describe the real flow state of the reservoir. In addition, these analytical and semi-analytical methods are only suitable for the productivity prediction of single-phase fluids. For the two-phase flow of oil and gas during the development of fractured carbonate reservoirs, due to the serious nonlinearity of the mathematical model itself, the above models are no longer applicable. Numerical simulation methods can explicitly characterize the parameters of artificial fractures and deal with multiphase fluid flow problems (Zhang et al., 2015; Zhang et al., 2018; Sun et al., 2022c), but the preprocessing process of numerical simulation methods is complicated. As a result, the number of grids is huge, and the calculation timeliness is low when dealing with thousands of case studies. In a word, the difficulties in accurately predicting the productivity of fractured carbonate oil wells are mainly manifested in: first, it is difficult to characterize and simulate large-scale fractures; second, it is difficult to simulate oil and gas two-phase flow and stress sensitivity. Therefore, it is urgent to establish an efficient and accurate oil and gas two-phase seepage model in fractured carbonate reservoirs to clarify the production performance characteristics of oil wells under complex seepage conditions.

In this paper, a three-dimensional discrete fracture oil and gas two-phase seepage model considering the stress sensitivity of large-scale fractures is studied. In order to further approximate the real state of large-scale fractures in the reservoir, the large-scale fractures are discretized into several micro-elements. The mathematical model of seepage in discrete fractures is established, and by coupling the reservoir flow model, a three-dimensional discrete fracture oil and gas two-phase seepage mathematical model and a semi-analytical solution method are formed. The accuracy of the model is verified by comparison with commercial numerical simulation software, and the influence of fractures and key reservoir seepage parameters on productivity prediction is analyzed based on the semi-analytical model studied.

2 Mathematical methods

2.1 Model assumptions

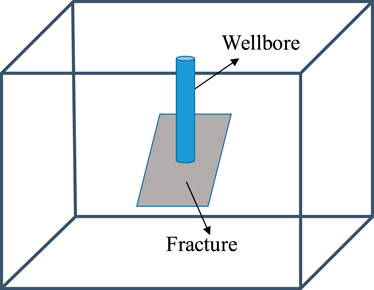
Considering large-scale fractures as three-dimensional discrete fractures with limited conductivity, the reservoir is equivalent to a single medium, and the physical model diagram is shown in Figure 1. Reservoir fluids include oil and gas phases, and gas dissolved in oil is represented by the dissolved gas-oil ratio (R_s). A vertical well is drilled in a large-scale fracture and produces at a constant pressure. The large-scale fracture only intersects with the perforation of the well, and other sections of the well are closed, that is, it is assumed that the fluid flows into the wellbore only through the large-scale fracture, and some other basic assumptions as follows:

(1) The reservoir is closed at the top, bottom and sides;

(2) Two-phase flow of oil and gas is considered in large-scale fractures, and the flow of fluid in three-dimensional fractures is a two-dimensional problem, and the flow in reservoirs is a three-dimensional problem;

(3) Consider the permeability stress sensitivity of large-scale fractures;

(4) The fluid flow in the matrix and fractures conforms to the isothermal Darcy flow;

(5) The effects of gravity and capillary forces are ignored.

FIGURE 1

FIGURE 1. Physical model diagram of 3D discrete fracture.

2.2 Mathematical model

The flow from the reservoir to the wellbore is regarded as composed of two parts: the reservoir flow and the large-scale fracture flow. The mathematical model of seepage of each system will be established in the following, and then the pressure and flow will be used to couple the reservoir and large-scale fractures in the continuous condition of the fracture surface. The flow equation of fractures forms a three-dimensional discrete fracture seepage mathematical model and a semi-analytical solution method.

2.2.1 Mathematical model of oil and gas two-phase seepage in fractured system

Introducing the permeability modulus, considering the permeability of stress-sensitive large-scale fractures as:

$k_{\text{F}}=k_{\text{Fi}}{e}^{-{\gamma }_{\text{F}}\left(p_{\text{i}}-p_{\text{F}}\right)}(1)$

According to previous research (Wang et al., 2021a), combined with Eq. 1, the differential equation of oil phase seepage in fracture system can be obtained as:

$\frac{\partial }{\partial \xi }\left[\beta \frac{k_{\text{Fi}}{e}^{-{\gamma }_{\text{F}}\left(p_{\text{i}}-p_{\text{F}}\right)}{k}_{\text{ro}}}{{\mu }_{\text{o}}{B}_{\text{o}}}\frac{\partial p_{\text{F}}}{\partial \xi }\right]+\frac{\partial }{\partial \eta }\left[\beta \frac{k_{\text{Fi}}{e}^{-{\gamma }_{\text{F}}\left(p_{\text{i}}-p_{\text{F}}\right)}{k}_{\text{ro}}}{{\mu }_{\text{o}}{B}_{\text{o}}}\frac{\partial p_{\text{F}}}{\partial \eta }\right]+{\tilde{\tilde{q}}}_{\text{SCFo}}+{\tilde{\tilde{q}}}_{\text{SCWo}}=\frac{\partial }{\partial t}\left[\frac{{\varphi }_{\text{F}}\left(1-S_{\text{g}}\right)}{B_{\text{o}}}\right](2)$

The gas-phase seepage differential equation is:

$\begin{array}{l}\frac{\partial }{\partial \xi }\left[\frac{\beta k_{\text{Fi}}{e}^{-{\gamma }_{\text{F}}\left(p_{\text{i}}-p_{\text{F}}\right)}{k}_{\text{rg}}{R}_{\text{s}}}{{\mu }_{\text{o}}{B}_{\text{o}}}\frac{\partial p_{\text{F}}}{\partial \xi }+\frac{\beta k_{\text{Fi}}{e}^{-{\gamma }_{\text{F}}\left(p_{\text{i}}-p_{\text{F}}\right)}{k}_{\text{rg}}}{{\mu }_{\text{g}}{B}_{\text{g}}}\frac{\partial p_{\text{F}}}{\partial \xi }\right]+\\ \frac{\partial }{\partial \eta }\left[\frac{\beta k_{\text{Fi}}{e}^{-{\gamma }_{\text{F}}\left(p_{\text{i}}-p_{\text{F}}\right)}{k}_{\text{rg}}{R}_{\text{s}}}{{\mu }_{\text{o}}{B}_{\text{o}}}\frac{\partial p_{\text{F}}}{\partial \eta }+\frac{\beta k_{\text{Fi}}{e}^{-{\gamma }_{\text{F}}\left(p_{\text{i}}-p_{\text{F}}\right)}{k}_{\text{rg}}}{{\mu }_{\text{g}}{B}_{\text{g}}}\frac{\partial p_{\text{F}}}{\partial \eta }\right]+R_{\text{s}}{\tilde{\tilde{q}}}_{\text{SCFo}}+{\tilde{\tilde{q}}}_{\text{SCWg}}=\frac{\partial }{\partial t}\left(\frac{{\varphi }_{\text{F}}{S}_{\text{g}}}{B_{\text{g}}}\right)\end{array}(3)$

Initial conditions

$P_F\left(\xi ,n,t=0\right)=P_i(4)$

The wellbore production conditions are (Peaceman, 1983):

${\tilde{\tilde{q}}}_{\text{SCWo}}=\frac{2\pi \beta k_{\text{Fi}}{e}^{-{\gamma }_{\text{F}}\left(p_{\text{i}}-p_{\text{F}}\right)}{k}_{\text{ro}}{w}_{\text{F}}}{{\mu }_{\text{o}}{B}_{\text{o}}\ln \left(r_{\text{eq}}/r_{\text{W}}\right)}\left(p_{\text{F}}-p_{\text{W}}\right)(5)$

${\tilde{\tilde{q}}}_{\text{SCWg}}=\frac{2\pi \beta k_{\text{Fi}}{e}^{-{\gamma }_{\text{F}}\left(p_{\text{i}}-p_{\text{F}}\right)}{k}_{\text{rg}}{w}_{\text{F}}}{{\mu }_{\text{g}}{B}_{\text{g}}\ln \left(r_{\text{eq}}/r_{\text{W}}\right)}\left(p_{\text{F}}-p_{\text{W}}\right)(6)$

$r_{eq}=0.14\sqrt{\mathrm{\Delta }{l}_F^2+\mathrm{\Delta }{h}_F^2}(7)$

In the formula, $p_{\text{i}}$ is the initial reservoir pressure, MPa; $p_{\text{F}}$ is the large-scale fracture pressure, MPa; $p_{\text{W}}$ is the wellbore pressure, MPa; $k_{\text{Fi}}$ is the initial permeability of the large-scale fracture, mD; $k_{\text{F}}$ is the large-scale fracture permeability, mD; $k_{\text{ro}}$ is the relative permeability of the oil phase; $k_{\text{rg}}$ is the relative permeability of gas phase; ${\varphi }_{\text{F}}$ is the inherent porosity of large-scale fractures; t is time, d; $w_{\text{F}}$ is the width of large-scale fractures, m; ${\tilde{\tilde{q}}}_{\text{SCFo}}$ represents the oil phase production per unit volume of matrix to fracture microelements, 1/d; ${\tilde{\tilde{q}}}_{\text{SCWo}}$ Oil production per unit volume of the wellbore, d⁻¹; ${\tilde{\tilde{q}}}_{\text{SCWg}}$ gas production per unit volume of fracture microelements to the wellbore, d⁻¹; _Bo is the crude oil volume coefficient, m³/m³; B_g is the gas volume coefficient, m³/m³; μ _o is crude oil viscosity, mPa·s; μ_g is gas viscosity, mPa·s; $S_{\text{o}}$ oil phase saturation; $S_g$ gas phase saturation; $R_S$ represents the dissolved gas-oil ratio, m³/m³. $r_{eq}$ is the equivalent radius, m; $r_W$ is the wellbore radius, m; is the large ${\gamma }_{\mathit{F}}$ scale fracture permeability modulus, MPa⁻¹; β is the conversion coefficient; ε and ξ represent the two directions of the fracture surface $\mathrm{\Delta }{\mathit{l}}_F$; Indicates $\mathrm{\Delta }{h}_F$ the height of the crack cell, m.

2.2.2 Mathematical model of reservoir seepage

The partial differential equation for seepage control in a single-medium reservoir in a rectangular closed formation is:

$\frac{{\partial }^2{p}_{\text{M}}}{\partial x^2}+\frac{{\partial }^2{p}_{\text{M}}}{\partial y^2}+\frac{{\partial }^2{p}_{\text{M}}}{\partial z^2}+\tilde{q}\delta (x-x_{\text{w}},y-y_{\text{w}},z-z_{\text{w}})=\frac{{\varphi }_{\text{M}}{\mu }_{\text{g}}{c}_{\text{tM}}}{k_{\text{M}}}\frac{\partial p_{\text{M}}}{\partial t}(8)$

Initial conditions:

$P_{\mathrm{M}}\left(x,y,z,0\right)=p_i(9)$

Outer boundary conditions:

Along the x-coordinate direction

$\frac{\partial p_{\text{M}}(0,y,z,t)}{\partial x}=0,\frac{\partial p_{\text{M}}(x_{\text{e}},y,z,t)}{\partial x}=0(10)$

Along the y-coordinate direction

$\frac{\partial p_{\text{M}}(x,0,z,t)}{\partial y}=0,\frac{\partial p_{\text{M}}(x,y_{\text{e}},z,t)}{\partial y}=0(11)$

Along the z coordinate direction

$\frac{\partial p_{\text{M}}(x,y,z_{\text{e}},t)}{\partial z}=0,\frac{\partial p_{\text{M}}(x,y,0,t)}{\partial z}=0(12)$

In the formula, $p_{\text{M}}$ is the pseudo-pressure of the matrix system, MP a; $k_M$ is the matrix permeability, mD; ${\varphi }_{\text{M}}$ is the matrix porosity; ${\varphi }_M$ represents the comprehensive compressibility of the matrix system, MPa⁻¹; x _e is the distance from the outer boundary in the x direction, m; y_e is the outer boundary distance in the y direction, m; z_e is the outer boundary distance in the z direction, m; $z$ is the position coordinate of the point source; δ () is the Dirac function.

2.3 Solution of seepage mathematical model

2.3.1 Numerical solution of oil and gas two-phase flow in fractured system

Divide the large-scale fracture into several micro-elements, and use the numerical discretization method to discretize the seepage differential equation of the large-scale fracture system in time and space. Taking the fracture micro-element (i, j) as an example, the oil phase seepage differential equation is transformed into

${\displaystyle \sum _{l\in {\psi }_{i,j}}{T}_{o_{l,\left(i,j\right)}}^{n+1}}\left(p_{F_l}^{n+1}-p_{F_{i.j}}^{n+1}\right)+q_{SCF{o}_{i,j}}^{n+1}+q_{SCW{o}_{i,j}}^{n+1}=\frac{V_{b_{i,j}}}{\mathrm{\Delta }t}\left\{{\left[\frac{{\varphi }_F\left(1-S_g\right)}{B_{\circ }}\right]}_{i,j}^{n+1}-{\left[\frac{{\varphi }_F\left(1-S\right)}{B_{\circ }}\right]}_{i,j}^n\right\}(13)$

The gas phase equation simplifies to

${\displaystyle \sum _{l\in {\psi }_{i,j}}\left[T_{g_{l,\left(i,j\right)}}^{n+1}\left(p_{F_l}^{n+1}-p_{F_{i.j}}^{n+1}\right)+T_{o_{l,\left(i,j\right)}}^{n+1}{R}_{s_{l,\left(i,j\right)}}^{n+1}\left(p_{F_l}^{n+1}\right)-p_{F_{i.j}}^{n+1}\right]}+R_{S_{l,\left(i,j\right)}}^{n+1}{q}_{SCF{o}_{i,j}}^{n+1}+q_{SCW{g}_{i,j}}^{n+1}=\frac{V_{b_{i,j}}}{{\alpha }_c\mathrm{\Delta t}}\left\{{\left(\frac{{\varphi }_F{S}_g}{B_g}\right)}_{i,j}^{n+1}-{\left(\frac{{\varphi }_F{S}_g}{B_g}\right)}_{i,j}^n+{\left[\frac{{\varphi }_F{R}_s\left(1-S_g\right)}{B_o}\right]}_{i,j}^{n+1}-{\left[\frac{{\varphi }_F{R}_s\left(1-S_g\right)}{B_o}\right]}_{i,j}^n\right\}(14)$

In the formula, ${\psi }_{i,j}$ is a two-dimensional array, and its value is the index of the fracture micro-element adjacent to the fracture micro -element [ $\left(q_{SCF{o}_{i,j}}^{n+1}\right)$ i, j], representing the volume flow of the matrix to the fracture micro-element, m³/d; $\left(q_{SCW{o}_{i,j}}^{n+1}\right)$, $\left(q_{SCF{g}_{i,j}}^{n+1}\right)$ represent the oil production and Gas production, m³/d; $V_{b_{i,j}}$ indicates the volume of fracture microelements, m³.

The stress-sensitive term is explicitly processed, updated by the pressure value calculated at the current time step, and included in the conductivity term as a whole.

$T_{o_{l,\left(i,j\right)}}^{n+1}=G_{l,\left(i,j\right)}{\left(k_{ro}\right)}_{l,\left(i,j\right)}^{n+1}{\left(\frac{1}{{\mu }_{\mathrm{o}}{B}_{\mathrm{o}}}\right)}_{l,\left(i,j\right)}^{n+1}(15)$

$T_{g_{l,\left(i,j\right)}}^{n+1}=G_{l,\left(i,j\right)}{\left(\frac{k_{\mathrm{rg}}}{{\mu }_{\mathrm{g}}{B}_{\mathrm{g}}}+\frac{k_{\mathrm{ro}}{R}_{\mathrm{s}}}{{\mu }_{\mathrm{o}}{B}_{\mathrm{o}}}\right)}_{l,\left(i,j\right)}^{n+1}(16)$

In the formula, G represents the geometric conductivity, which is usually calculated by harmonic mean:

$G_{l,\left(i,j\right)}=\frac{{\gamma }_l{\gamma }_{i,j}}{{\gamma }_l+{\gamma }_{i,j}}(17)$

${\gamma }_{i,j}=\beta {\left(\frac{k_{\mathrm{F}}{w}_{\mathrm{F}}\mathrm{\Delta }{h}_{\mathrm{F}}}{\mathrm{\Delta }{l}_{\mathrm{F}}}\right)}_{i,j}(18)$

$V_{b_{i,j}}={\left(\mathrm{\Delta }{l}_{\mathrm{F}}\mathrm{\Delta }{h}_{\mathrm{F}}{w}_{\mathrm{F}}\right)}_{i,j}(19)$

Simplify the right-hand terms of Eqs 13, 14 (Jia et al., 2017) to obtain a simplified form of the oil-gas two-phase differential equation, in which the oil phase equation is transformed into

${\displaystyle \sum _{l\in {\psi }_{i,j}}{T}_{o_{l,\left(i,j\right)}}^{n+1}}\left(p_{F_l}^{n+1}-p_{F_{i,j}}^{n+1}\right)+q_{SCF{o}_{i,j}}^{n+1}+q_{SCW{o}_{i.j}}^{n+1}=C_{o{p}_{i.j}}^{n+1}\left(p_{F_{i,j}}^{n+1}-p_{F_{i,j}}^n\right)+C_{o{g}_{i.j}}^{n+1}\left(S_{g_{i,j}}^{n+1}-S_{g_{i,j}}^n\right)(20)$

The gas phase equation is

${\displaystyle \sum _{l\in {\psi }_{i,j}}\left[T_{g_{l,\left(i,j\right)}}^{n+1}\left(p_{F_l}^{n+1}-p_{F_{i,j}}^{n+1}\right)+T_{o_{l,\left(i,j\right)}}^{n+1}{R}_{s_{l,\left(i,j\right)}}^{n+1}\left(p_{F_l}^{n+1}-p_{F_{i,j}}^{n+1}\right)\right]}+q_{SCW{g}_{i,j}}^{n+1}+R_{s_{l,\left(i,j\right)}}^{n+1}{q}_{SCF{o}_{i,j}}^{n+1}=C_{g{p}_{l,\left(i,j\right)}}^{n+1}\left(p_{F_{i,j}}^{n+1}-p_{F_{i,j}}^n\right)+C_{g{g}_{l,\left(i,j\right)}}^{n+1}\left(S_{g_{i,j}}^{n+1}-S_{g_{i,j}}^n\right)(21)$

In the formula, $N_{\mathrm{F}}$ and $N_{\mathrm{F}}$ represent the conductivities of oil and gas phases between fracture microelements (i, j) and adjacent fracture microelements at the n + 1th time step, respectively.

The boundary conditions are discretely processed as follows:

$\{\begin{array}{c}{q}_{SCW{o}_l}^{n+1}=-T_{o_{l,w}}^{n+1}\left[p_{F_l}^{n+1}-p_w^n\right]\\ q_{SCW{g}_l}^{n+1}=T_{g_{l,w}}^{n+1}\left[p_{F_l}^{n+1}-p_w^n\right]\end{array},l\in {\psi }_w(22)$

$\{\begin{array}{c}{T}_{o_{l,w}}^{n+1}={\left[\beta \frac{2\pi k_{\mathrm{F}}{w}_{\mathrm{F}}}{1n\left(r_{eq}/r_w\right)}\right]}_l{\left(k_{ro}\right)}_l^{n+1}{\left(\frac{1}{{\mu }_o{B}_o}\right)}_l^{n+1}\\ T_{g_{l,w}}^{n+1}={\left[\beta \frac{2\pi k_{\mathrm{F}}{w}_{\mathrm{F}}}{1n\left(r_{eq}/r_w\right)}\right]}_l{\left(k_{rg}\right)}_l^{n+1}{\left(\frac{1}{{\mu }_g{B}_g}\right)}_l^{n+1}\end{array}(23)$

where $T_{g_{l,w}}^{n+1}$ is the conductivity of the gas phase between the wellbore and the adjacent fracture micro-elements.

Eqs 20, 21 are established for $N_{\mathrm{F}}$ a crack micro-element, which contains two $N_{\mathrm{F}}$ equations and two unknowns the same time, the matrix equation can be expressed as

$\mathit{D}\cdot \overrightarrow{\mathit{X}}=\overrightarrow{\mathit{E}}+\overrightarrow{\mathit{q}}(24)$

Among them,

${\overrightarrow{\mathit{E}}}_{i,j}=\left[\begin{array}{c}-T_{o_{\left(i,j\right),w}}^{n+1}{p}_w^n-C_{o{p}_{i,j}}^{n+1}{p}_{F_{i,j}}^n-C_{o{g}_{i,j}}^{n+1}{S}_{g_{i,j}}^n\\ T_{g_{\left(i,j\right),w}}^{n+1}{p}_w^n-C_{g{p}_{i,j}}^{n+1}{p}_{F_{i,j}}^n-C_{g{g}_{i,j}}^{n+1}{S}_{g_{i,j}}^n\end{array}\right](25)$

${\overrightarrow{\mathit{X}}}_{i,j}=\left[\begin{array}{c}{p}_{F_{i,j}}^{n+1}\\ S_{g_{i,j}}^{n+1}\end{array}\right](26)$

${\overrightarrow{\mathit{q}}}_{i,j}=\left[\begin{array}{c}{p}_{F_{i,j}}^{n+1}\\ S_{g_{i,j}}^{n+1}\end{array}\right]=\left[\begin{array}{c}-q_{SCF{o}_{i,j}}^{n+1}\\ -R_{s_{l,\left(i,j\right)}}^{n+1}{q}_{SCF{o}_{i,j}}^{n+1}\end{array}\right](27)$

2.3.2 Analytical solution of reservoir flow

At present, for the research of three-dimensional point source function in real space, most of them are obtained by the Newman (Wang et al., 2021b) product method. The fracture element is regarded as a surface source, and the point source solution is integrated by curve, and the fracture surface pressure solution can be obtained:

$\begin{array}{l}{\stackrel{⌢}{p}}_{\text{M}}-p_{\text{M}}\left(x,y,z,t\right)=\frac{\alpha q_{SC}}{{\varphi }_{\text{M}}{c}_{\text{tM}}}{\displaystyle {\int }_{{\tau }_1}^{{\tau }_2}{\displaystyle {\int }_{-\frac{\mathrm{\Delta }l{\mathrm{F}}_{i,j}}{2}}^{\frac{\mathrm{\Delta }l{\mathrm{F}}_{i,j}}{2}}{\displaystyle {\int }_{-\frac{\mathrm{\Delta }{h}_{{\mathrm{F}}_{i,j}}}{2}}^{\frac{\mathrm{\Delta }{h}_{{\mathrm{F}}_{i,j}}}{2}}\frac{1}{x_{\text{e}}}\left\{1+2{\displaystyle \sum _{n=1}^{\infty }\exp \left[-\frac{n^2{\pi }^2\stackrel{⌢}{\chi }\left(t-\tau \right)}{x_e^2}\right]\cos \frac{n\pi x_{i,j}}{x_{\text{e}}}\cos \frac{n\pi x}{x_{\text{e}}}}\right\}}}}\\ \frac{1}{y_{\text{e}}}\cdot \left\{1+2{\displaystyle \sum _{n=1}^{\infty }\exp \left[-\frac{n^2{\pi }^2\stackrel{⌢}{\chi }\left(t-\tau \right)}{y_{\text{e}}^2}\right]\cos \frac{n\pi y_{i,j}}{y_{\text{e}}}\cos \frac{n\pi y}{y_{\text{e}}}}\right\}\\ \frac{1}{z_{\text{e}}}\cdot \left\{1+2{\displaystyle \sum _{n=1}^{\infty }\exp \left[-\frac{n^2{\pi }^2\stackrel{⌢}{\chi }\left(t-\tau \right)}{z_e^2}\right]\cos \frac{n\pi z_{i,j}}{z_{\text{e}}}\cos \frac{n\pi z}{z_{\text{e}}}}\right\}\text{d}\tau \text{d}\xi \text{d}\eta \end{array}(28)$

According to the superposition principle, the pressure drops generated by all fracture micro-elements to any point in the three-dimensional space is:

$\begin{array}{l}\mathrm{\Delta }{p}_{\text{M}}\left(x_o,y_o,z_o,t^{n+1}\right)={\stackrel{⌢}{p}}_{\text{M}}-p_{\text{M}}\left(x_o,y_o,z_o,t^{n+1}\right)=\\ \frac{\alpha }{{\varphi }_{\text{M}}{c}_{\text{tM}}}{\displaystyle {\sum }_{k=1}^{n+1}{\displaystyle {\sum }_{g=1}^{N_{\text{F}}}{\tilde{q}}_{SC{M}_g}^k}}{\displaystyle {\int }_{t^{k-1}}^{t^k}S}\left(x_o,y_o,z_o,t^{n+1}-\tau ,x_{\text{g}},y_{\text{g}},z_{\text{g}}\right)\text{d}\tau \end{array}(29)$

To simplify the form of the equation, let

$R_{o,g}^{n+1,k}=\frac{\alpha }{{\varphi }_{\text{M}}{c}_{\text{tM}}}{\displaystyle {\int }_{t^{k-1}}^{t^k}S}\left(x_o,y_o,z_o,t^{n+1}-\tau ,x_{\text{g}},y_{\text{g}},z_{\text{g}}\right)\text{d}\tau (30)$

Eq. 30 into Eq. 29, we have

$\mathrm{\Delta }{p}_{\text{M}}\left(x_o,y_o,z_o,t^{n+1}\right)={\stackrel{⌢}{p}}_{\text{M}}-p_{\text{M}}\left(x_o,y_o,z_o,t^{n+1}\right)={\displaystyle {\sum }_{k=1}^{n+1}{\displaystyle {\sum }_{g=1}^{N_{\mathrm{F}}}{\tilde{q}}_{SC{M}_g}^k}}\cdot R_{o,g}^{n+1,k}(31)$

At the current time step, the pressure generated by the joint action of all fracture micro-elements on the g-th segment fracture micro-element is:

$p_{{\text{M}}_{i,j}}^{n+1}={\stackrel{⌢}{p}}_{\text{M}}-{\displaystyle {\sum }_{g=1}^{N_{\text{F}}}{\tilde{q}}_{SC{M}_g}^k}\cdot R_{\left(i,j\right),g}^{n+1,n+1}-{\displaystyle {\sum }_{k=1}^n{\displaystyle {\sum }_{g=1}^{N_{\text{F}}}{\tilde{q}}_{SC{M}_g}^k}}\cdot R_{\left(i,j\right),g}^{n+1,k}(32)$

Applying Eq. 32 to all fracture elements, the solution matrix equation of the matrix system flow equation can be obtained:

$\mathit{R}\times \overrightarrow{\tilde{\mathit{q}}}\mathit{=-}\overrightarrow{\mathit{p}}\mathit{+}\left(\overrightarrow{\stackrel{⌢}{\mathit{p}}}\mathit{-}\overrightarrow{\mathit{r}}\right)(33)$

$\mathit{R}=\left[\begin{array}{ccccc}{\mathit{R}}_{\left(\mathrm{1,1}\right),\left(\mathrm{1,1}\right)}^{n+1,n+1}& \dots & {\mathit{R}}_{\left(\mathrm{1,1}\right),g}^{n+1,n+1}& \dots & {\mathit{R}}_{\left(\mathrm{1,1}\right),N_{\mathrm{F}}}^{n+1,n+1}\\ ⋮& \hspace{1em}& ⋮& \hspace{1em}& ⋮\\ {\mathit{R}}_{\left(i,j\right),\left(\mathrm{1,1}\right)}^{n+1,n+1}& \dots & {\mathit{R}}_{\left(i,j\right),g}^{n+1,n+1}& \dots & {\mathit{R}}_{\left(i,j\right),N_{\mathrm{F}}}^{n+1,n+1}\\ ⋮& \hspace{1em}& ⋮& \hspace{1em}& ⋮\\ {\mathit{R}}_{\left(n_x,n_y\right),\left(\mathrm{1,1}\right)}^{n+1,n+1}& \dots & {\mathit{R}}_{\left(n_x,n_y\right),g}^{n+1,n+1}& \dots & {\mathit{R}}_{\left(n_x,n_y\right),N_{\mathrm{F}}}^{n+1,n+1}\end{array}\right](34)$

$\overrightarrow{r}=\left[\begin{array}{c}{\displaystyle {\sum }_{k=1}^n{\displaystyle {\sum }_{g=1}^{N_{\mathrm{F}}}{\tilde{q}}_{SC{m}_g}^k\cdot {\mathit{R}}_{\left(\mathrm{1,1}\right),g}^{n+1,k}}}\\ ⋮\\ {\displaystyle {\sum }_{k=1}^n{\displaystyle {\sum }_{g=1}^{N_{\mathrm{F}}}{\tilde{q}}_{SC{m}_g}^k\cdot {\mathit{R}}_{\left(i,j\right),g}^{n+1,k}}}\\ ⋮\\ {\displaystyle {\sum }_{k=1}^n{\displaystyle {\sum }_{g=1}^{N_{\mathrm{F}}}{\tilde{q}}_{SC{m}_g}^k\cdot {\mathit{R}}_{\left(n_x,n_y\right),g}^{n+1,k}}}\end{array}\right](35)$

2.3.3 Discrete fracture-reservoir flow coupling solution

Combined with the two-phase flow equations of oil and gas in the fracture system and the flow equations in the matrix system, the reservoir and fracture seepage models are coupled to solve the equations:

$\{\begin{array}{l}\mathit{D}·\overrightarrow{\mathit{X}}\mathit{=}\overrightarrow{\mathit{E}}\mathit{+}\overrightarrow{\mathit{q}}\\ \mathit{R}·\overrightarrow{\tilde{\mathit{q}}}=\mathit{-}\overrightarrow{\mathit{p}}\mathit{+}\left(\overrightarrow{\stackrel{⌢}{\mathit{p}}}\mathit{-}\overrightarrow{\mathit{r}}\right)\end{array}(36)$

At the fracture surface, the pressure and flow are continuous, and there are

$p_{{\text{F}}_{i,j}}^{n+1}=p_{{\text{M}}_{i,j}}^{n+1}(37)$

$q_{SCF{o}_{i,j}}^{n+1}=\mathrm{\Delta }{l}_{{\text{F}}_{i,j}}\mathrm{\Delta }{h}_{{\text{F}}_{i,j}}{w}_{{\text{F}}_{i,j}}{\tilde{q}}_{SC{M}_{i,j}}^{n+1}(38)$

Combining Eqs 36–38, the coupling solution matrix of the three-dimensional discrete fracture oil and gas two-phase seepage model can be formed.

3 Analysis of production dynamic characteristics

3.1 Model validation

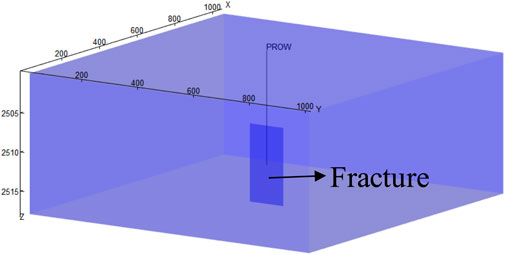
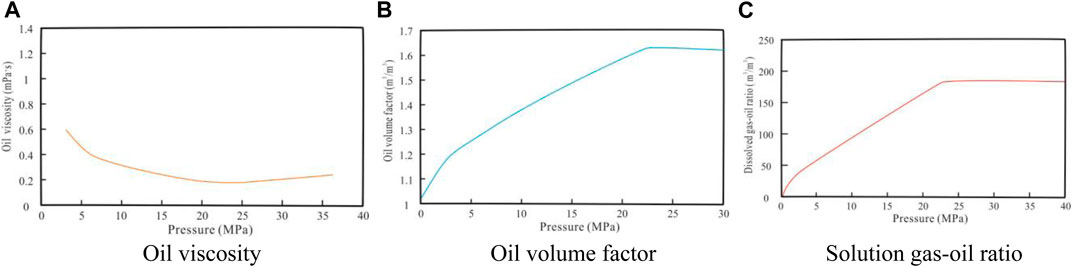
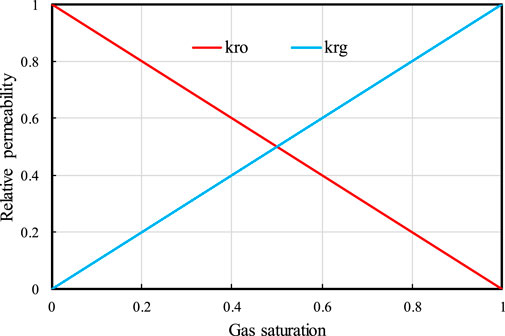
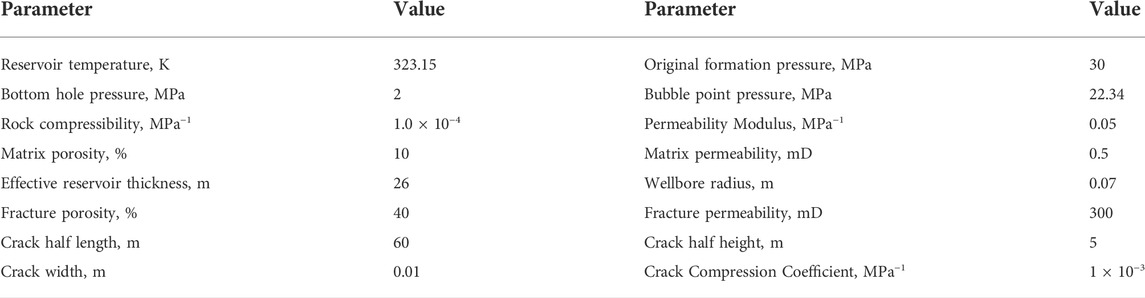
This section verifies the accuracy of the theoretical model by comparing it with the calculation results of the commercial numerical simulation software Eclipse. First, a three-dimensional vertical fracture numerical model as shown in Figure 2 was established using commercial numerical simulation software. Secondly, the 3D discrete fracture system and the matrix system are partitioned, and then the stress sensitivity of the 3D discrete fracture system is considered. Figure 3 shows the relationship curve of fluid high-pressure physical property parameters, and Figure 4 shows the relative permeability curve of oil and gas two-phase in the fracture system. The reservoir, fluid, and fracture-related parameters used for both methods are summarized in Table 1. The initial formation pressure is set higher than the bubble point pressure, so the initial fluid in the reservoir is oil phase; the production well produces at a constant bottom hole pressure.

FIGURE 2

FIGURE 2. Schematic diagram of fracture distribution and discretizing for numerical simulation.

FIGURE 3

FIGURE 3. Curves of oil properties versus pressure.

FIGURE 4

FIGURE 4. Relative permeability curve used for numerical model and semi-analytical model.

TABLE 1

TABLE 1. Input parameters of reservoir, fluid and fracture used for model verification.

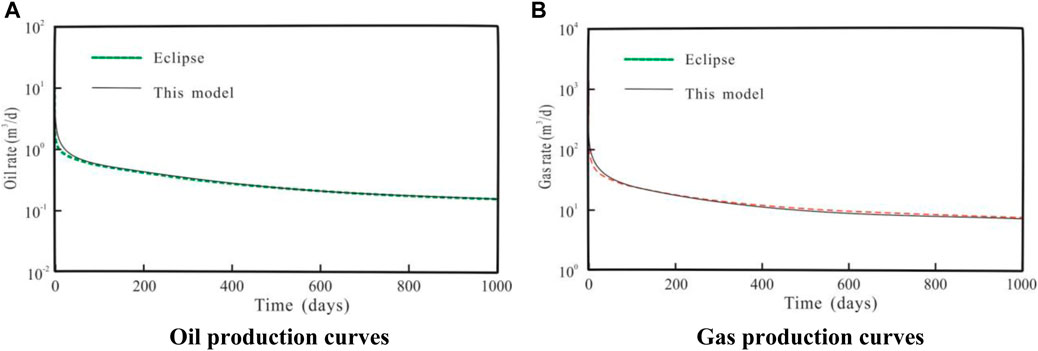
Figure 5 shows the comparison results between the model in this paper and the numerical simulation method. It can be seen that the production dynamic curves of the two methods are in good agreement. Except for a little deviation in the early stage, the degree of agreement in other stages is high, and the overall fitting error is in the engineering within the allowable range of error. Notably, although complex numerical formulas are utilized in the proposed numerical model, the model can be solved analytically, ensuring its fairly high computational performance.

FIGURE 5

FIGURE 5. Comparison of the proposed model and other methods.

3.2 Parameter sensitivity analysis

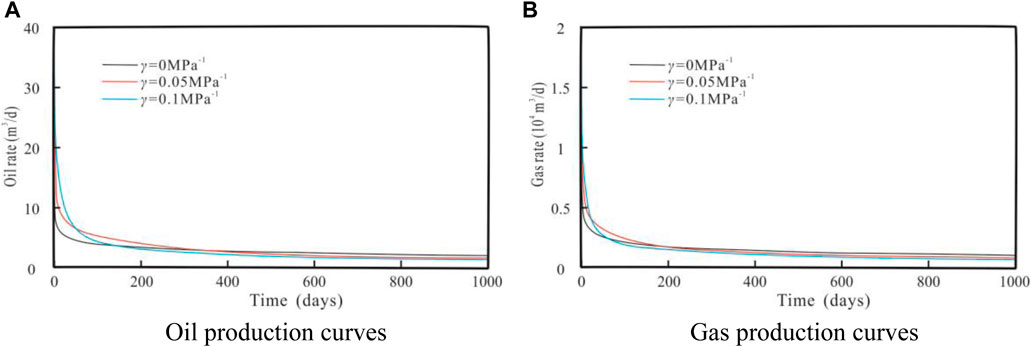
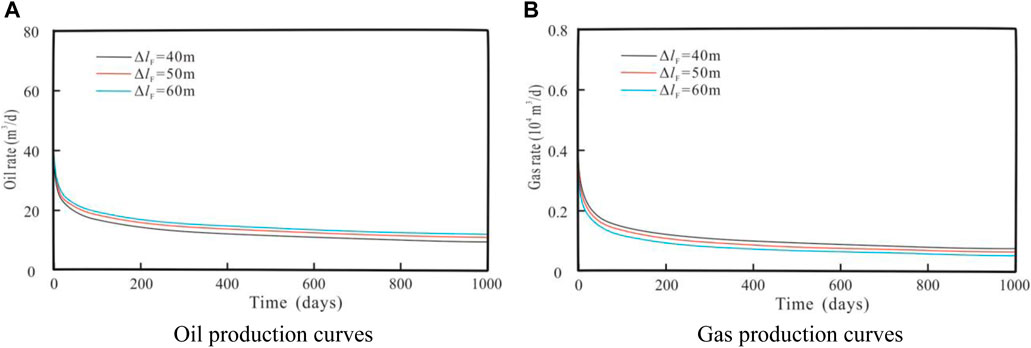
After verifying the accuracy of the theoretical model, based on the semi-analytical model studied, the influence of stress sensitivity coefficient, fracture half-length and fracture half-height parameters on the oil and gas two-phase production dynamic curve of the three-dimensional discrete fracture model is mainly analyzed, and the basic parameters are input to the model. All are listed in Table 1, and the value range of each sensitivity parameter is shown in Table 2.

TABLE 2

TABLE 2. Range of sensitivity parameters.

Figure 6 reflects the effect of fracture permeability stress sensitivity on the three-dimensional discrete fracture oil and gas two-phase production performance curve, and the magnitude of permeability modulus just reflects the strength of fracture permeability stress sensitivity. It can be seen from Figure 6 that the change of fracture permeability will affect the development process of the entire reservoir, especially in the early and middle production stages. In addition, the stronger the fracture stress sensitivity, the lower the oil and gas production curve position, and the faster the production decline rate. This is mainly because the strong stress sensitivity leads to a serious loss of fracture permeability, an increase in fluid seepage resistance, and more oil and gas cannot be produced, which eventually leads to a decrease in oil and gas production and a faster decline in production.

FIGURE 6

FIGURE 6. Effect of perm e ability modulus on production dynamic curves.

Figure 7 reflects the influence of the fracture half-length on the three-dimensional discrete fracture oil-gas two-phase production performance curve. It can be found that the change of fracture length affects the whole development stage, especially the early production stage. From the oil and gas two-phase production curves under different fracture half-lengths shown in Figure 7, it can be seen that the larger the fracture half-length, the larger the initial value of oil and gas two-phase production, and the more upward the production curve moves. This is mainly because the longer the fracture length is, the larger the linear seepage area of the fracture is. Under the production condition of constant bottom-hole flow pressure, production can be maintained with a small production decline, so the production curve moves upward.

FIGURE 7

FIGURE 7. Effect of fracture half-length on production dynamic curves.

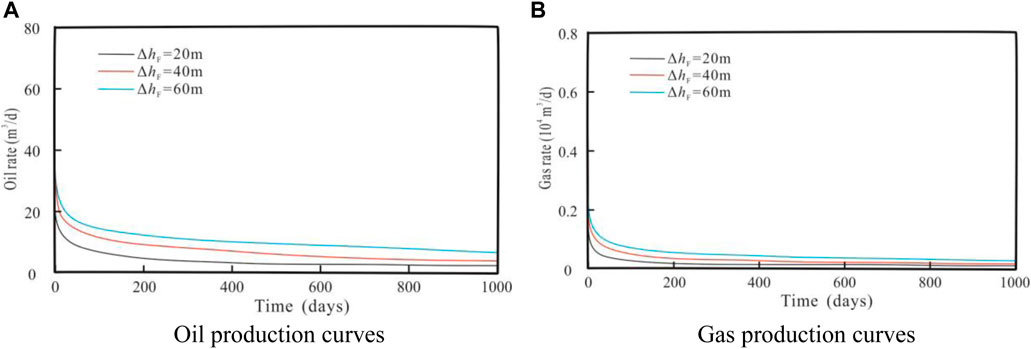
Figure 8 shows the effect of fracture half-height on the three-dimensional discrete fracture oil and gas two-phase production dynamic curve. Similar to the effect of fracture half-length on production performance, the change of fracture height has an impact on the entire production stage, especially in the early stage. As the fracture height increases, the initial value of oil and gas two-phase production increases, and the production curve moves upward. This is mainly because the larger the fracture height, the larger the linear seepage area of the fracture, and under the production condition of constant bottom-hole flow pressure, production can be maintained through a small production decline, so the production curve moves upward.

FIGURE 8

FIGURE 8. Effect of fracture half-height on production dynamic curves.

4 Conclusion

Dynamic response characteristics of oil and gas two-phase production in fractured carbonate reservoirs are obtained. Through the research of this paper, the following conclusion are mainly obtained:

(1) The fracture heterogeneity in carbonate reservoirs is relatively large, and the spatial distribution and flow characteristics of actual three-dimensional fractures can be reflected only by discrete treatment of fractures. Moreover, by combining the finite difference method and the point source function theory, the effective solution of the three-dimensional discrete fracture oil-gas two-phase seepage mathematical model can be achieved.

(2) The stress-sensitive effect leads to a serious loss of fracture permeability and an increase of fluid seepage resistance, which seriously affects the productivity of oil wells in fractured weakly volatile carbonate reservoirs.

(3) The key seepage parameters of fractures play an important role in the two-phase production performance of oil and gas in fractured carbonate reservoirs. The larger the fracture half-length and fracture half-height, the higher the production curve in the early and middle production stages. Production declines more slowly.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

BX: Supervision, Writing—Original Draft.

Conflict of interest

Author BX was employed by CNPC Greatwall Drilling Engineering Company Limited.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Fang, S., Cheng, L., and Li, C. (2015). Production model of horizontal wells fracturing with multi-angle fractures in stress-sensitive reservoirs [J]. J. Northeast Petroleum Univ. 39 (001), 87–94. doi:10.3969/j.issn.2095-4107.2015.01.011

CrossRef Full Text | Google Scholar

Hazlett, R. D., and Babu, D. K. (2014). Discrete wellbore and fracture productivity modeling for unconventional wells and unconventional reservoirs. SPE J. 19 (1), 19–33. doi:10.2118/159379-pa

CrossRef Full Text | Google Scholar

Jia, P., Cheng, L., Clarkson, C. R., and Williams-Kovacs, J. D. (2017). Flow behavior analysis of two-phase (gas/water) flowback and early-time production from hydraulically-fractured shale gas wells using a hybrid numerical/analytical model. Int. J. Coal Geol. 182, 14–31. doi:10.1016/j.coal.2017.09.001

CrossRef Full Text | Google Scholar

Jia, Y., Sun, G., and Nie, R. (2016). Seepage model and well test curve of quadruple medium reservoir [J]. Lithol. Reserv. 28 (01), 123–127. doi:10.3969/j.issn.1673-8926.2016.01.017

CrossRef Full Text | Google Scholar

Li, C., and Shao, H. (2017). Sensitivity analysis of permeability and stress in fractured carbonate reservoirs [J]. Chem. Manag. 000 (011), 142.

Google Scholar

Li, D., Kang, Y., and You, L. (2014). Experimental study on permeability stress sensitivity of carbonate reservoirs [J]. Nat. Gas. Geosci. 25 (3), 762106. doi:10.11764/j.issn.1672-1926.2014.03.0409

CrossRef Full Text | Google Scholar

Pallav, S., and Khalid, A. (2006). New transfer functions for simulation of naturally fractured reservoirs with dual-porosity models[J]. SPE J. 11 (3), 328–340. doi:10.2118/90231-PA

CrossRef Full Text | Google Scholar

Peaceman, D. W. (1983). Interpretation of well-block pressures in numerical reservoir simulation with nonsquare grid blocks and anisotropic permeability. Soc. Petroleum Eng. J. 23 (3), 531–543. doi:10.2118/10528-pa

CrossRef Full Text | Google Scholar

Shi, W., Yao, Y., and Cheng, S. (2018). Dynamic pressure characteristics of oil wells stimulated by acid fracturing in fractured low permeability carbonate reservoirs [J]. Nat. Gas. Geosci. 185 (04), 586–596. doi:10.11764/j.issn.1672-1926.2018.03.011

CrossRef Full Text | Google Scholar

Sun, Z., Huang, B., Li, Y., Lin, H., Shi, S., and Yu, W. (2022). Nanoconfined methane flow behavior through realistic organic shale matrix under displacement pressure: A molecular simulation investigation. J. Pet. Explor Prod. Technol. 12 (4), 1193–1201. doi:10.1007/s13202-021-01382-0

CrossRef Full Text | Google Scholar

Sun, Z., Huang, B., Wu, K., Shi, S., Wu, Z., Hou, M., et al. (2022). Nanoconfined methane density over pressure and temperature: Wettability effect. J. Nat. gas Sci. Eng. 99, 104426. doi:10.1016/j.jngse.2022.104426

CrossRef Full Text | Google Scholar

Sun, Z., Wang, S., Xiong, H., Wu, K., and Shi, J. (2022). Optimal nanocone geometry for water flow. AIChE J. 68 (3), e17543. doi:10.1002/aic.17543

CrossRef Full Text | Google Scholar

Wang, S., Bai, Y., and Xu, B. (2021). A semianalytical model for simulating fluid flow in tight sandstone reservoirs with a bottom aquifer. Geofluids 2021, 5549411. doi:10.1155/2021/5549411

CrossRef Full Text | Google Scholar

Wang, S., Bai, Y., Xu, B., Li, Y., Chen, L., Dong, Z., et al. (2021). A hybrid model for simulating fracturing fluid flowback in tight sandstone gas wells considering a three-dimensional discrete fracture. Lithosphere 2021 (4), 7673447. doi:10.2113/2021/7673447

CrossRef Full Text | Google Scholar

Yang, L., Kang, Z., and Xue, Z. (2018). Theory and practice of carbonate reservoir development in China [J]. Petroleum Explor. Dev. 045 (004), 669–678. doi:10.11698/PED.2018.04.12

CrossRef Full Text | Google Scholar

Yang, Z., Sun, J., and Zhang, J. (2009). Experimental study on stress sensitivity of fractured carbonate reservoirs [J]. Drill. Complet. Fluids 26 (006), 5–6.

Google Scholar

Zhang, L., Li, C., and Zhao, Y. (2017). Research progress on seepage mechanism of fractured carbonate reservoirs [J]. Earth Science-Journal China Univ. Geosciences 78, 8. doi:10.3799/dqkx.2017.101

CrossRef Full Text | Google Scholar

Zhang, N., Yao, J., and Huang, C. (2015). Mixed multi-scale finite element numerical simulation of fracture-cavity reservoir based on discrete fracture-cavity network model [J]. Chin. J. Comput. Mech. 32 (4), 473–478. doi:10.7511/jslx201504005

CrossRef Full Text | Google Scholar

Zhang, Q., Huang, C., and Yao, J. (2018). Multi-scale embedded discrete fracture model simulation method [J]. Chin. J. Comput. Mech. 35 (04), 507–513. doi:10.7511/jslx20170211002

CrossRef Full Text | Google Scholar

Zhou, W., Banerjee, R., Poe, B., Spath, J., and Thambynayagam, M. (2014). Semianalytical production simulation of complex hydraulic-fracture networks. SPE J. 19 (1), 06–18. doi:10.2118/157367-pa

CrossRef Full Text | Google Scholar

Zhou, X., and Yang, H. (2012). Practice and effect of integration of exploration and development of carbonate reservoirs in Tarim Oilfield [J]. China Pet. Explor. 017 (005), 1–9. doi:10.3969/j.jssn.1672-7703.2012.05.001

CrossRef Full Text | Google Scholar