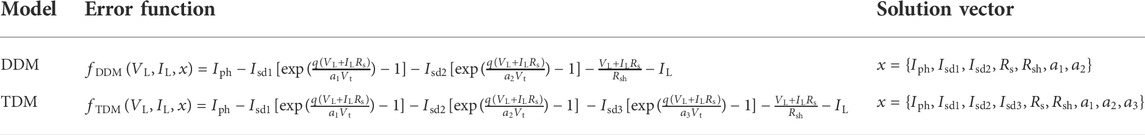- 1School of Electronic and Information Engineering, Ningbo University of Technology, Ningbo, China
- 2Ningbo Jianan Electronics Company Limited, Ningbo, China
Photovoltaic (PV) power generation can considerably reduce the consumption of traditional fossil energy and improve environmental problems. Reliable photovoltaic (PV) cell modelling owns great significance to the following output characteristics analysis and optimal operation of the whole PV system, while there are several unknown physical parameters within different PV cell models. Thus, the identification of the internal parameters of the PV cell model is the first and foremost step for PV cell modelling, nevertheless, the intrinsic highly complex and non-linear and multi-modal features make traditional approaches, such as analytical methods hard to achieve satisfactory performance in solving this problem. Hence, this work aims to employ a powerful tool to effectively and efficiently overcome this thorny problem based on the most advanced optimization method. A recently developed meta-heuristic algorithm called peafowl optimization algorithm (POA) is employed in this work for PV cell modelling parameter identification. For comprehensive validation, two different PV cell models, i.e., double diode model (DDM) and triple diode model (TDM) are utilized. Simulation results demonstrate that POA can more accurately identify the unknown parameters of PV cell models in a higher convergence speed compared against other algorithms.
Introduction
Due to the high speed of technological development in the world today, the over-exploitation of fossil energy sources has led to the subsequent depletion of resources and air pollution, which has become a vital task to be resolved. In order to relieve the pressure of energy supply as soon as possible and effectively, the change of energy structure in the new era is necessary for the construction and development of the current society (Zhang et al., 2020), and the development of various green and efficient renewable energy and clean energy technologies is very important. Among them, solar energy has been widely used in various application scales and purposes thanks to its excellent characteristics (Jordehi, 2016), such as rich reserves, clean and safe, no pollution to the environment during power generation, low cost, convenient and simple installation, etc.
Although PV power generation has achieved good results so far, it still faces many problems and challenges (Abbassi et al., 2018). First of all, the manufacturer does not usually provide comprehensive PV cell parameters, which are derived from standard test conditions that do not accurately reflect the changes caused by subsequent failure and ageing of PV panels (Qais et al., 2019). Therefore, it is difficult to achieve reliable PV cell modeling, which affects the following control and optimization of the whole system (Chen et al., 2018; Li et al., 2018). Therefore, it is of great significance to develop an accurate and efficient intelligent identification algorithm to reliably identify the unknown parameters of PV cells, so as to achieve accurate modeling of PV cells. Due to the multimodal and highly nonlinear characteristics of photovoltaic systems, researchers in recent years have focused on various types of photovoltaic models. The most representative equivalent models are the single diode (SDM) and the double diode model (DDM). However, complex photovoltaic parameter models also have certain reference significance, such as the three-diode model (TDM) with a large number of unknown parameters. The problem of this model is that the calculation process is complicated. In particular, this paper proposes TDM as the research object, which can effectively analyze the complex physical problems existing in photovoltaic systems. In addition, in the diagnosis and analysis of photovoltaic system faults, it is necessary to accurately extract the relevant electrical parameters of the model. This method is an important prerequisite for accurate maximum power point tracking. So far, scholars at home and abroad have developed many methods to solve the highly nonlinear and multimodal problem of PV cell parameter identification (Pourmousa et al., 2019). These methods can be divided into three categories, namely, analytical method, deterministic method and heuristic algorithm. The first two methods have obvious defects in the process of solving problems, such as low identification accuracy, large amount of calculation, strong model dependence, and extremely sensitive to initial operating conditions and gradient information. At first, the analytical method was used to extract model parameters (Wolf and Benda, 2013), and a series of interdependent mathematical equations were used to correlate different model parameters (Torabi et al., 2017). Most of the parameters used are: 1) short-circuit current, 2) open circuit voltage and 3) maximum power point voltage and current, and appropriate equations are derived with the data provided by the manufacturer. However, using mathematical methods to solve these equations will cost a lot of time and energy, and the accuracy is limited (Villalva et al., 2009). In order to overcome the shortcomings of analytical method, deterministic method is applied to this problem. This kind of method is an optimization method to extract parameters based on some reference points on the given current-voltage (I-V) curve (Gao et al., 2016). This method makes use of the two important analytical properties of convexity and monotonicity of the problem, which leads to two important research directions, convex function difference optimization method and monotone optimization method. Deterministic methods mainly include several types of traditional methods, including Lambert W-functions (El-Fergany, 2021) and iterative curve fitting (Chaibi et al., 2020), can effectively improve the calculation accuracy. However, they are very strict with the continuity, convexity and differentiability of the model characteristics and the objective function, and they are highly sensitive to gradient information and initial conditions, so they are easy to converge prematurely and fall into local optimization when solving highly nonlinear problems.
Meta-heuristic algorithms can transform the difficult problem of model parameter identification into a simple nonlinear constrained optimization problem. The great advantages of using meta-heuristic algorithm are: easy to implement, high efficiency, insensitive to initial conditions and gradient information, which can effectively avoid the shortcomings of the above two methods. They are considered to be the most promising and effective tool for PV cell parameter identification with the best comprehensive performance (Chan et al., 1986). So far, many heuristic algorithms have been used to identify the unknown parameters of PV cells (Pillai and Rajasekar, 2018; Yang et al., 2020), e.g., genetic algorithm (GA) (Jervase et al., 2001), particle swarm optimization (PSO) (Ye et al., 2009), artificial bee colony (ABC) (Oliva et al., 2014), whale optimization algorithm (WOA) (Xiong et al., 2018), backtracking search algorithm (BSA) (Yu et al., 2018), month flame optimizer (MFO) (Allam, Yousri, Eteiba), etc.
However, not all metaheuristic algorithms can be used for any optimization problem, because the optimizer in each algorithm mechanism cannot make the most rational optimization results for all problems. Especially due to various intractable problems such as high nonlinearity and multimodality. Therefore, the problem that has been widely concerned is how to solve the practical engineering problems and ensure the optimization effect at the same time. In particularly, this paper aims to propose a novel bionic optimization algorithm to achieve efficient and reliable optimization to solve the above highly complex practical engineering problems. Therefore, in this paper, a novel biomimetic optimization algorithm (POA) is used in the parameter identification of photovoltaic cell models, which has the following three contributions:
• POA is developed based on peafowl behavior which contains a variety of update factors that can effectively balance local exploration and global exploitation, thereby obtaining a satisfactory global optimal solution;
• POA with adaptive search is capable of dynamically adjusting its behavior to collect satisfactory search results at multiple stages;
• For PV cell parameter identification, two benchmark PV cell models, DDM and TDM, are used to comprehensively verify the effectiveness and reliability of POA for PV cell parameter identification. Case studies show that POA can effectively improve the accuracy and stability of parameter identification compared with other algorithms.
Photovoltaic cell modelling
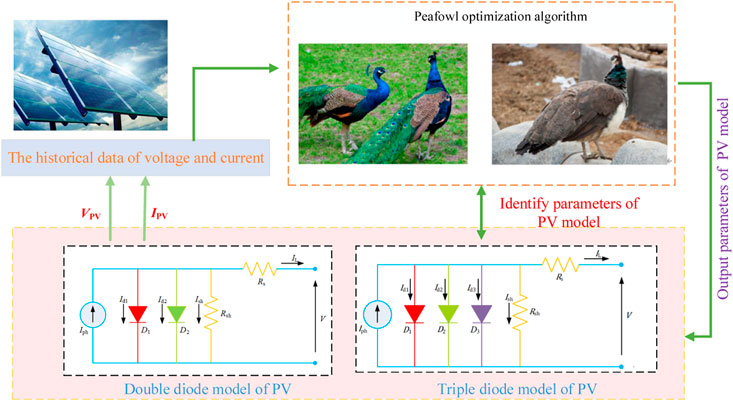
Building an exact PV cell model (Chen and Yu, 2019) is fundamental to its subsequent studies of output characteristics, fault diagnosis, etc. Only by accurately fitting the output I-V and power-voltage (P-V) curves of PV cells can the performance of PV systems be reliably evaluated and predicted, which largely depends on accurately identifying the required physical parameters from the PV cell model. In this paper, two kinds of equivalent circuit models, DDM and TDM are selected for modelling.
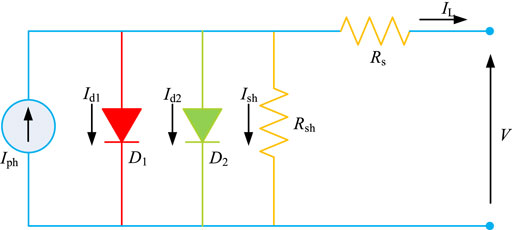
Double diode model
As demonstrated in Figure 1, DDM consists of an ideal constant current source
where
Hence, output I-V relationship of DDM can be calculated by
Thus, seven parameters need to be identified for DDM, e.g.,
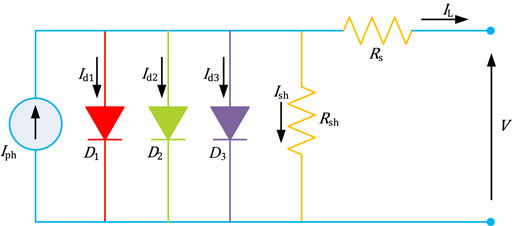
Triple diode model
The configuration of TDM is illustrated in Figure 2. Compared with DDM, a third diode is added in parallel due to the influence of grain boundaries and large leakage current (Qais et al., 2019).
Similarly, output I-V relationship of TDM is calculated by (Qais et al., 2019)
where
Therefore,
Objective function
In order to implement an exercise to efficiently minimize the error between experimental and simulated data, a parameter extraction technique is used to determine the optimal parameters for the PV model, which can be quantitatively evaluated with the assistance of an objective function. Here, the root mean square error (RMSE) is taken as the objective function, as follows:
where
In order to make the experimental data results more convincing, different error functions are given in Table 1.
Based on Table 1, for the sake of minimizing the error between experimental data and simulated data, objective function
Peafowl optimization algorithm
POA is based on the courtship, foraging and chasing behaviors of green peafowls (Wang et al., 2022). On this basis, a general mathematical model is established. Male peacocks have delicate feathers to show their unique position advantage in the population. Male peacocks usually take the initiative to attract female peahens after finding high-quality food, and then seek mating. The more beautiful a male peacock’s tail is, the more females it attracts by strutting and shaking its feathers. Once the male peacock finds food, they will not only open their feathers, but also further dance to expand the area to attract females (Wang et al., 2022). The dance mode can be divided into two types: rotating in place and walking in circles. Male peacocks also make cat like noises to attract female peahens. Male peacocks are polygamous, so they want to attract as many female peacocks as possible and mate with them.
The next aims to illustrate the main optimization mechanisms and principles of POA, to further demonstrate the superiority of this method. In order to more concisely introduce the core optimization principle of POA, only the core mechanisms are illustrated. More details can be referred to literature (Wang et al., 2022) for interested readers for more in-depth learning.
Courtship behavior of peacocks
When the peacock is in the mating season, the male peacock will hover near the food source through three behaviors: tail-spreading, rotating and flapping. There are two rotation modes around the food source, and the mechanism of these two rotation modes is dependent on the fitness function value. In particular, when the value of the fitness function is larger, the radius of the peacock’s rotation around the food is smaller, but the probability of the peacock’s rotation around the food is higher. The peacock with worse fitness function has a larger rotation radius, and this mathematical model is described as
where
Approaching behavior of peahens
Peacocks constantly adjust their behavior during courtship, adopting approach mechanisms and adaptive search mechanisms. In the process of courtship, the female peacock first approaches the male peacock and will look around. Therefore, the fitness of mutual attraction between male and female peacocks is proportional. The mathematical model of this process is as follows (Wang et al., 2022):
where
Random food searching behavior of peafowl cubs
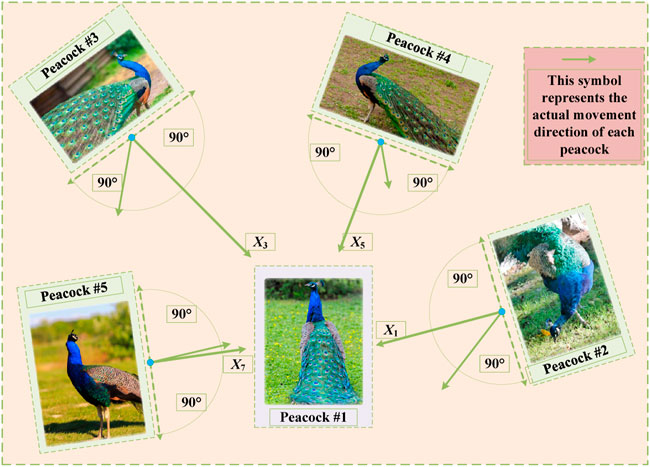
In order to play a random search role in the food search space, juvenile peacocks will actively approach male peacocks with good food sources (the highest fitness). In this paper, one of the five peacocks is used as the target object. These five peacocks guide the juvenile peacocks with equal probability. In this process, the random search behavior of the peacocks is described by the Levy flight, and the behavior of peafowl cub can be expressed as
where
Besides, the five peacocks also have the internal interactions among them. In addition, male peacock #1 has the best food source, the remaining four male peacocks will gradually move towards male peacock #1. The detailed pattern can be shown in Figure 3.
The optimization framework of PV cell parameter identification based on POA is shown in Figure 4. The historical data of the output voltage and current determined by the PV cell will be regarded as the input of the POA and converted into the objective function. According to the specific PV cell model, the optimization program is executed based on POA, and finally the identification parameters of PV cells are output.
Case studies
In this section, two different kinds of PV models, i.e., DDM and TDM are adopted for parameter identification based on POA. The experimental I-V data utilized for simulation are extracted from a 57 mm diameter R.T.C. France solar cell under the weather condition (G = 1000 W/
POA is in comparison with other two meta-heuristic algorithms, e.g., ABC (Oliva et al., 2014) and WOA (Xiong et al., 2018). Particularly, their maximum iteration number is designed to be the same, i.e., 200, while all approaches are executed in 30 independent runs to acquire statistical results. Besides, population size of each algorithm is designed to be 50 and 70 for DDM and TDM, respectively. Note that the best simulation results of all the methods are highlighted in bold. All case studies are undertaken by Matlab 2021a through a personal computer with IntelR CoreTMi7 CPU at 2.0 GHz and 32 GB of RAM.
Results discussion on double diode model
The optimal parameters and RMSE obtained by different algorithms are demonstrated in Table 2, among them the best result is highlighted in bold. Based on Table 2, it can be seen that POA can achieve the most satisfactory performance compared against its competitors in terms of accuracy. The RMSE obtained by POA is only 51.19% and 86.93% to that of ABC and WOA, respectively.
Figure 5 illustrate the I-V curve and P-V curve fitting results obtained by POA under DDM, which indicates that the identified results are highly matched with the real data. Thus, the model parameters identification accuracy of POA can be further improved.
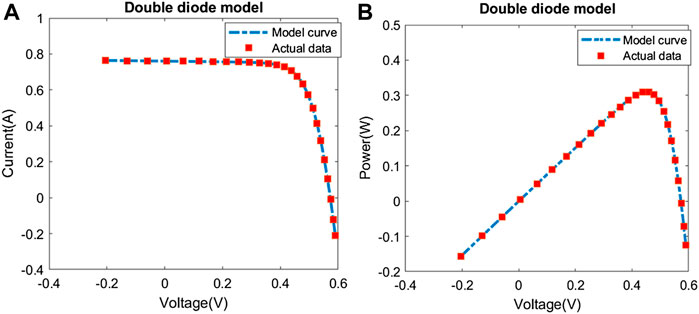
FIGURE 5. Comparison between actual data and model curve obtained by POA for DDM: (A) I-V curve and (B) P-V curve.
Besides, the boxplot graph and convergence curves obtained by various algorithm are respectively shown in Figures 6A,B. Boxplot graph shows that the distribution range of POA is the smallest among all the algorithms with the minimal lower and upper bounds, which indicates that POA can acquire the lowest RMSE with the highest stability. Convergence curves show that POA owns the highest convergence speed and stability.
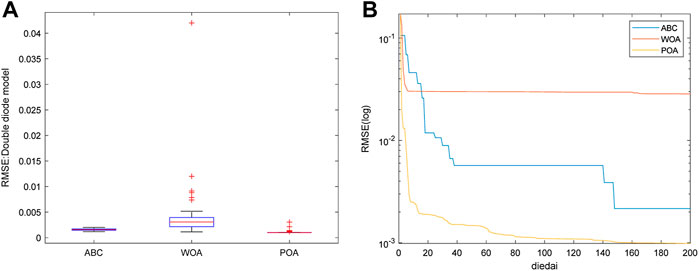
FIGURE 6. Boxplot graph and convergence curve obtained by POA for DDM: (A) boxplot graph and (B) convergence curve.
Results discussion on three-diode model
Table 3 shows the simulation results obtained by POA for TDM parameter estimation, in which the most accurate results along with its corresponding algorithm are highlighted in bold. Thus, it can be observed that POA can realize the highest quality estimation performance compared with ABC and WOA. The RMSE obtained by POA is only 84.47% and 81.64% to that of ABC and WOA, respectively.
The output I-V curve and P-V curve for TDM obtained by POA is shown in Figure 7, upon which it can be illustrated that the simulated data is extremely similar to the real data, which can effectively verify the parameters identification reliability of POA.
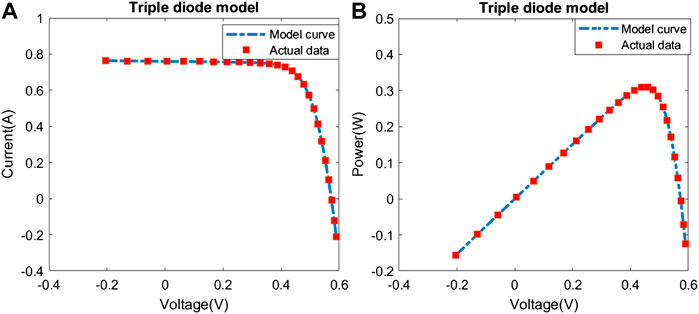
FIGURE 7. Comparison between actual data and model curve obtained by POA for TDM: (A) I-V curve and (B) P-V curve.
Furthermore, the boxplot graph and convergence curves of different algorithms are demonstrated in Figures 8A,B, respectively. Figure 8A shows that POA can obtain the smallest distribution range with the minimal lower and upper bounds, which can validate the high identification accuracy and stability of POA. From Figure 8B, it shows that POA can search the global optimum in a high convergence rate.
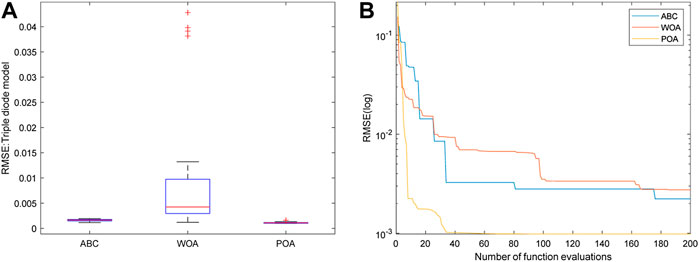
FIGURE 8. Boxplot graph and convergence curve obtained by POA for TDM: (A) boxplot graph and (B) convergence curve.
Conclusion
In this paper, the core component of the PV power generation system, namely the PV cell, is taken as the research object. The purpose of this paper is to accurately and effectively identify the unknown parameters in its model, so as to achieve its accurate modeling, so as to better guide the later optimal power generation and operation control. The main contributions of this paper are summarized as follows:
• Through the study of peacock behavior, I received relevant inspiration and used peacock behavior as a search mechanism. In this paper, a novel POA optimization algorithm is proposed. For the parameter identification problem of photovoltaic model, this algorithm is used to optimize the identification results, thereby improving the accuracy of photovoltaic cell parameter identification;
• The novelty of POA algorithm is that the algorithm includes efficient search operators and heuristics, in order to avoid getting trapped in local optima during the search process. The algorithm can dynamically adjust the optimization mechanism to find a balance between local search and global search, so as to improve the convergence accuracy of parameter identification;
• The algorithm is applied to the parameter identification of DDM and TDM PV cell models, and the effectiveness and reliability of POA for PV cell parameter identification are comprehensively verified. Case studies show that POA can effectively improve the accuracy and stability of parameter identification compared with other algorithms.
Further studies can be focused on the improvement and modification on the algorithm structure to lower the parameter tuning burden. Also, more different PV cell models can be applied for more comprehensive validation under more complex operation conditions, which is more beneficial for engineering applications.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
YZ: Conceptualization, Writing—Original Draft; EZ: Formal analysis, Software, Supervision; PA: Project administration, Resources, Writing—Review and; Editing.
Funding
The work was supported by Ningbo Natural Science Foundation 2019A610106 and the Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University, China (No. ICT2022B66).
Conflict of interest
EZ was employed by the Ningbo Jianan Electronics Company Limited.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbassi, R., Abbassi, A., Jemli, M., and Chebbi, S. (2018). Identification of unknown parameters of solar cell models: A comprehensive overview of available approaches. Renew. Sustain. Energy Rev. 90, 453–474. doi:10.1016/j.rser.2018.03.011
Allam, D., Yousri, D. A., and Eteiba, M. B. (2016). Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame optimization algorithm. Energy Convers. Manag. 123, 535–548. doi:10.1016/j.enconman.2016.06.052
Chaibi, Y., Allouhi, A., and Salhi, M. (2020). A simple iterative method to determine the electrical parameters of photovoltaic cell. J. Clean. Prod. 269, 122363. doi:10.1016/j.jclepro.2020.122363
Chan, D. S. H., Phillips, J. R., and Phang, J. C. H. (1986). A comparative study of extraction methods for solar cell model parameters. Solid-State Electron. 29 (3), 329–337. doi:10.1016/0038-1101(86)90212-1
Chen, X., and Yu, K. J. (2019). Hybridizing cuckoo search algorithm with biogeography-based optimization for estimating photovoltaic model parameters. Sol. Energy 180, 192–206. doi:10.1016/j.solener.2019.01.025
Chen, Z. C., Han, F. C., Wu, L. J., Yu, J. L., Cheng, S. Y., Lin, P. J., et al. (2018). Random forest based intelligent fault diagnosis for PV arrays using array voltage and string currents. Energy Convers. Manag. 178, 250–264. doi:10.1016/j.enconman.2018.10.040
Chin, V. J., Salam, Z., and Ishaque, K. (2015). Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 154, 500–519. doi:10.1016/j.apenergy.2015.05.035
El-Fergany, A. A. (2021). Parameters identification of PV model using improved slime mould optimizer and Lambert W-function. Energy Rep. 7, 875–887. doi:10.1016/j.egyr.2021.01.093
Gao, X., Cui, Y., Hu, J., Xu, G., and Yu, Y. (2016). Lambert W-function based exact representation for double diode model of solar cells: Comparison on fitness and parameter extraction. Energy Convers. Manag. 127, 443–460. doi:10.1016/j.enconman.2016.09.005
Jervase, J. A., Bourdoucen, H., and Al-lawati, A. M. (2001). Solar cell parameter extraction using genetic algorithms. Meas. Sci. Technol. 12, 1922–1925. doi:10.1088/0957-0233/12/11/322
Jordehi, A. R. (2016). Parameter estimation of solar photovoltaic (PV) cells: a review. Renew. Sustain. Energy Rev. 61, 354–371. doi:10.1016/j.rser.2016.03.049
Li, Y. F., Lin, P. J., Zhou, H. F., Chen, Z. C., Wu, L. J., Cheng, S. Y., et al. (2018). On-line monitoring system based on open source platform for photovoltaic array. Energy Procedia 145, 427–433. doi:10.1016/j.egypro.2018.04.070
Oliva, D., Cuevas, E., and Pajares, G. (2014). Parameter identification of solar cells using artificial bee colony optimization. Energy 72, 93–102. doi:10.1016/j.energy.2014.05.011
Pillai, D. S., and Rajasekar, N. (2018). Metaheuristic algorithms for PV parameter identification: A comprehensive review with an application to threshold setting for fault detection in PV systems. Renew. Sustain. Energy Rev. 82 (3), 3503–3525. doi:10.1016/j.rser.2017.10.107
Pourmousa, N., Ebrahimi, S. M., Malekzadeh, M., and Alizadeh, M. (2019). Parameter estimation of photovoltaic cells using improved Lozi map based chaotic optimization algorithm. Sol. Energy 180, 180–191. doi:10.1016/j.solener.2019.01.026
Qais, M. H., Hasanien, H. M., and Alghuwainem, S. (2019). Identification of electrical parameters for three-diode photovoltaic model using analytical and sunflower optimization algorithm. Appl. Energy 250, 109–117. doi:10.1016/j.apenergy.2019.05.013
Torabi, K. E., Eddine, I. A., Obbadi, A., Errami, A., Rmaily, R., Sahnoun, S., et al. (2017). Parameters estimation of the single and double diode photovoltaic models using a gauss-seidel algorithm and analytical method: A comparative study. Energy Convers. Manag. 148, 1041–1054. doi:10.1016/j.enconman.2017.06.064
Villalva, M. G., Gazoli, J. R., and Filho, E. R. (2009). Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 24, 1198–1208. doi:10.1109/TPEL.2009.2013862
Wang, J. B., Yang, B., Chen, Y. J., Zeng, K. D., Zhang, H., Shu, H. C., et al. (2022). Novel phasianidae inspired peafowl (pavo muticus/cristatus) optimization algorithm: design, evaluation, and SOFC models parameter estimation. Sustain. Energy Technol. Assessments 50, 101825. doi:10.1016/j.seta.2021.101825
Wolf, P., and Benda, V. (2013). Identification of PV solar cells and modules parameters by combining statistical and analytical methods. Sol. Energy 93, 151–157. doi:10.1016/j.solener.2013.03.018
Xiong, G. J., Zhang, J., Shi, D. Y., and He, Y. (2018). Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Convers. Manag. 174, 388–405. doi:10.1016/j.enconman.2018.08.053
Yang, B., Wang, J. B., Zhang, X. S., Yu, T., Yao, W., Shu, H. C., et al. (2020). Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595
Ye, M. Y., Wang, X. D., and Xu, Y. S. (2009). Parameter extraction of solar cells using particle swarm optimization. J. Appl. Phys. 105 (9), 094502–094508. doi:10.1063/1.3122082
Yu, K. J., Liang, J. J., Qu, B. Y., Cheng, Z. P., and Wang, H. S. (2018). Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. Energy 226, 408–422. doi:10.1016/j.apenergy.2018.06.010
Keywords: PV power generation, PV cell modelling, parameter identification, peafowl optimization algorithm, meta-heuristic algorithm
Citation: Zheng Y, Zhang E and An P (2022) Peafowl optimization algorithm based PV cell models parameter identification. Front. Energy Res. 10:985523. doi: 10.3389/fenrg.2022.985523
Received: 04 July 2022; Accepted: 18 July 2022;
Published: 15 August 2022.
Edited by:
Bin Zhou, Hunan University, ChinaReviewed by:
Xingshuo Li, Nanjing Normal University, ChinaJinlei Sun, Nanjing University of Science and Technology, China
Copyright © 2022 Zheng, Zhang and An. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peng An, NjE0NTQ1NTEzQHFxLmNvbQ==
 You Zheng
You Zheng Enyou Zhang2
Enyou Zhang2 Peng An
Peng An