- 1Institute of Applied System Analysis, Jiangsu University, Zhenjiang, China
- 2Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan
- 3Mechanical Engineering Department, College of Engineering, King Khalid University, Abha, Saudi Arabia
- 4Shoubra Faculty of Engineering, Benha University, Cairo, Egypt
- 5Mechanical Engineering Department, College of Engineering and Islamic Architecture, Umm Al-Qura University, Makkah, Saudi Arabia
- 6Faculty of Engineering and Technology, Future University in Egypt New Cairo, Cairo, Egypt
- 7Department of Mathematics, College of Science and Humanities in Al-Aflaj, Prince Sattam Bin Abdulaziz University, Al-Aflaj, Saudi Arabia
- 8Department of Mathematics, Faculty of Science, Damietta University, New Damietta, Egypt
By considering the Cattaneo–Christov approach and Buongiorno’s model, the thermal transport model is formulated for the flow of Oldroyd-B nanofluid over a bidirectional stretching surface. The flow profile of Oldroyd-B nanofluid is examined for various physical parameters, and the effects of heat source/sink are also utilized to explore the thermal transport properties subject to thermal relaxation time. Governing mathematical models are developed on the basis of basic laws and presented in the form of Partial differential equations (PDEs). The governing partial differential equations are transformed into ordinary differential equations considering suitable dimensionless transformations. The homotopic method is applied to study the feature of heat and velocity components in fluid flow. The influence of each physical parameter over the thermal and concentration profile is displayed graphemically. It is noticed that thermal transport is decreasing with increment in thermal relaxation time. The mass transfer becomes weak with magnifying values of the stretching strength parameter. Moreover, the larger thermophoretic parameter regulates the heat transfer during fluid flow.
1 Introduction
The heating and cooling fluids play a significant role in the advancement and development of engineering and industries. In general, usual fluids such as water,glycol, and ethylene have the incompetent ability of thermal conduction. However, metals possess a three-time greater ability of thermal transport compared to usual fluids. Therefore, it was required to make the mixture of a usual fluid and metal particle to enhance the thermal conductivity of the fluid. This mixture is called nanofluid. This concept of nanoparticle addition in a based fluid was introduced by Choi (1995). Choi et al. (2001) experimentally proved that the thermal transport of nanofluid is high, followed by a base fluid. Due to their high thermal conductivity, nanofluids have numerous applications in, for example, the advancement of thermal machines and the microelectromechanical system. The influence of the Brownian motion parameter on the heat transfer of nanofluid is studied by Evans et al. (2006). Sheikholeslami and Ganji (2013) investigated the flow of Cu-H2O nanofluid between flat surfaces and concluded that the concentration of nanoparticles was enhanced by magnifying the Nusselt number. Sheikholeslami et al. (2014) examined the effect of magnetic force over the convective energy transport during nanofluid flow and noticed that, by increasing the Hartmann number, the heat diffusion in the system rises. The flow of Burgers nanofluid under the influence of stretching surface is examined by Khan et al. (2016a). For a greater radiation parameter, the heat profile of the Burgers nanofluid is ascending. Earlier research (Hayat et al., 2016; Hayat et al., 2017a; Hayat et al., 2018; Hayat et al., 2019) studied the convective transport of nanofluid by considering slip mechanism over a surface. Moreover, it analyzed the ferromagnetic and cross nanofluid flows considering various physical influences. The thermal transport rate magnifies for a greater ratio of velocity. Hayat et al. (2017b) discussed the two-dimensional flow of the Burgers nanofluid with a modified heat and mass flux approach. They concluded that an increment in thermal relaxation time sufficiently decreases the thermal transport. Some studies (Khan et al., 2019; Khan et al., 2020a; Khan and Alzahrani, 2020) analyzed the transport of nanofluid considering porous media; the magnifying influence of the Eckert number gives strength to the heat conduction of the nanofluid. Bhattacharyya et al. (2019) considered the flow of nanofluid over the rotating and stretchable surface. Based on this study, the higher Reynolds number minimizes the magnitude of radial velocity. Sher et al. (2019) explored the features of the Burgers nanofluid model formulation for nanofluid with a stretching surface with an improved thermal flux theory, which was investigated by Ahmad et al. (2019). Khan et al. (2020b) proposed a new flow model for the Burgers nanofluid and investigated the thermal transport. They summarized that, for increasing magnitudes of stagnation, the parameter flow velocity of nanofluid is improved. Amjid et al. (2020) approximated the transport of Casson nanofluid over a curve surface. They examined that flow is decreasing because of magnifying the Casson constant. Muhammad et al. (2020) computed the bidirectional flow of nanofluid applying thermal radiation and concluded that the increment in thermophoresis force increases the heat conduction in the nanofluid flow. Khan and Alzahrani (2021), Khan et al. (2021), and Khan and Puneeth (2021) presented some current significant studies about nanofluids.
Thermal transport is a significant natural phenomenon with multiple applications in industries. The theory of heat transport was firstly introduced by Fourier (Grattan-Guinness, 2005) and introduced Fourier’s law of thermal transport. Laterally, based on Fourier’s law, numerous researchers studied the features of thermal transformation in different fluid flow phenomena (Rashidi et al., 2014; Ahmed et al., 2019; Nadeem and Khan, 2019; Khan et al., 2020; Khan et al., 2022; Raza et al., 2022). Cattaneo (1948) made amendments to Fourier’s law and stated that thermal transport depends on the time called the thermal relaxation time. Christov (2009) introduced further modifications to the Cattaneo model. The Cattaneo–Christov approach is proposed to investigate heat transformation using familiarizing thermal relaxation time. After that, researchers applied this Cattaneo–Christov approach to study the thermal transformation phenomena in different kinds of fluid flows. Straughan (2010) presented a study based on the Cattaneo–Christov theory. Haddad (2014) applied the Cattaneo–Christov thermal transport theory to examine the instability. Shehzad et al. (2016) applied Cattaneo–Christov to study the Darcy flow of viscoelastic fluid and concluded that the flow profile of such fluid changes by varying the values of the Forchheimer parameter. Saleem et al. (2017) employed Cattaneo–Christov approach to investigate the Maxwell fluid flow and found that thermal conduction decreased with ascending thermal relaxation time. Waqas et al. (2018) applied the Cattaneo–Christov approach to inquiry the thermal conduction in Burgers fluid and reported that a greater thermal relaxation time constant reduced the thermal flow of the fluid. Rasool and Zhang (2019) examined the Darcy flow of nanofluid over the surface by applying the Cattaneo–Christov approach. Shehzad et al. (2019) studied the fluid flow by applying the Cattaneo–Christov approach of thermal and mass transfer and investigated that the ascending values of the Prandtl parameter enhanced the thermal curve. Hafeez et al. (2020) investigated chemical reactions, applied the Cattaneo–Christov approach to study the fluid flow using rotating surfaces, and used the Midrich technique to examine the influence of different parameters. Ahmed et al. (2020) applied the Cattaneo–Christov approach to analyze fluid transport over a stretching sheet. Recently, Iqbal et al. (2020) analyzed the heat transfer while the Burgers nanofluid flow based on the Cattaneo–Christov approach. They found that the magnifying values of the thermal relaxation constant results minimized the thermal flow rate. Rehman et al. (2016) constructed the solution of the set of equations to study the heat transfer phenomena. Currently, Ali et al. (2021) applied a finite differencing approach to analyze the heat transfer. Some other studies are carried out to solve such problems for examining thermal transport (Kamran et al., 2015; Kamran et al., 2016a; Kamran et al., 2016b; Rehman and Kamran, 2019).
The heat transport during the nanofluid flow using stretched surfaces has been examined by numerous researchers (Khan et al., 2016a; Hayat et al., 2019; Khan et al., 2020b). The Cattaneo–Christov approach has been applied by researchers to study heat transfer in the Burgers fluid (Khan et al., 2016b; Khan and Khan, 2016). Still, no mathematical formulation has been developed to analyze the thermal transport by applying the Cattaneo–Christov theory for the flow of the Oldroyd-B nanofluid and Buongiorno’s model. In this article, we proposed a new model of heat transport applying the Cattaneo–Christov approach and Buongiorno’s model to investigate the thermal transport in the Burgers nanofluid under the influence of a stretching sheet. The homotopic algorithm is applied to solve governing problems.
2 Mathematical formulation
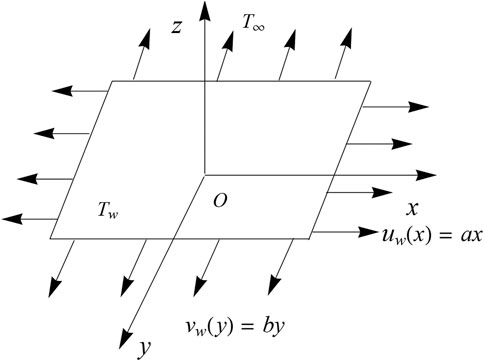
This section presents a mathematical formulation for three-dimensional convective transport of Oldroyd-B nanofluid employed by a bidirectional stretching sheet. In-compressible and steady flow phenomena are studied in this article. A model combining the Cattaneo–Christov approach with Buongiorno’s model is employed to present a mathematical formulation for solutal and thermal conduction in the flow of the Oldroyd-B nanofluid. A cartesian coordinate system was applied to formulate the proposed model. Axial velocities in the x and y direction are u = ax and v = by, where a and b denote constants. The flow region is taken as z > 0. The velocity vector is V = [u, v, w], Tw denotes temperature, and Cw represents concentration, respectively. The flow pattern is presented in Figure 1.
The rheology of Oldroyd-B fluid is represented by the following equation:
where S is tensor representing the extra stress, μ is dynamic viscosity,
The continuity and momentum governing model by neglecting pressure are given as follows (khan et al., 2020; Iqbal et al., 2020):
For the current problem, the law of energy conservation is (Iqbal et al., 2020)
where q denotes the thermal flux and satisfies the equation
The mass transfer model is as follows (Iqbal et al., 2020; Iqbal et al., 2021)
where J indicates mass flux and satisfies the following relation:
Here, λt, λc, and λ1 denote the thermal and the mass and fluid relaxation time, respectively. λ2 is the Oldroyd-B fluid parameter, ν denotes kinematics viscosity, T denotes temperature, and C) represents the concentration, respectively. DB denotes diffusion coefficient, whereas q is thermal flux and J represents mass flux, respectively.
Eliminating S from
with the boundary conditions
Here,
See the following transformations (Ahmad et al., 2019; Iqbal et al., 2021):
By invoking these transformations, Eq. 8 is satisfied and Eqs. (9) − (12) take the following forms:
with transformed boundary conditions are follows:
Here, β1 is the relaxation time, β2 the Oldroyd-B fluid material parameter, Pr the Prandtl number, Le the Lewis number, βt the thermal relaxation time constraint, and βc the mass relaxation time. Thermophoresis, Brownian motion, and ratio of stretching rates are (Nt),
3 Homotopic solution approach
In this manuscript,the homotopic analysis approach (Hayat et al., 2017b; Khan et al., 2020b; Khan et al., 2020) is applied to solve the Eqs 16–19 with boundary conditions defined in Eqs 20, 21. Initial guess and linear operators are needed to proceed with this approach. Hence, for analytic solutions’ linear operators
4 Physical analysis of results
The three-dimensional steady-state thermal transfer phenomena of nanofluid by a bidirectional stretching surface is analyzed. For the Oldroyd-B nanofluid flow features, the Cattaneo–Christov approach and Buongiorno’s model are employed together. The homotopic approach is used to analyze the impact of various physical parameters involved in Eqs. (16 – (19) with boundary conditions (20) and (21).
The axial velocity components
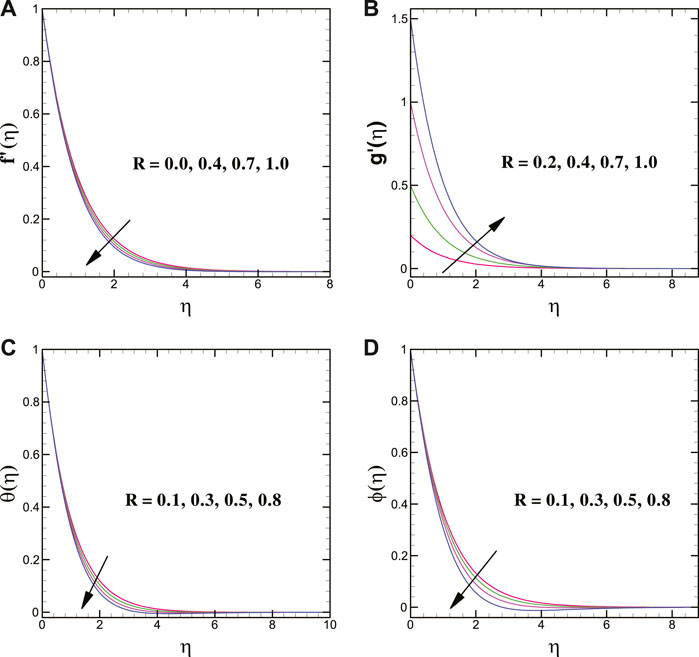
Figures 2A–D represent the effect of stretching strength (R) over
5 Validation of homotopic outcomes
In this section, approximated – f′′(0), − g′′(0), and − θ′(0) for different α are displayed in Tables 1, 2, and the obtained values are compared with other studies. This comparison indicates that our approximations are accurate and the adopted homotopic technique is a valid approach.
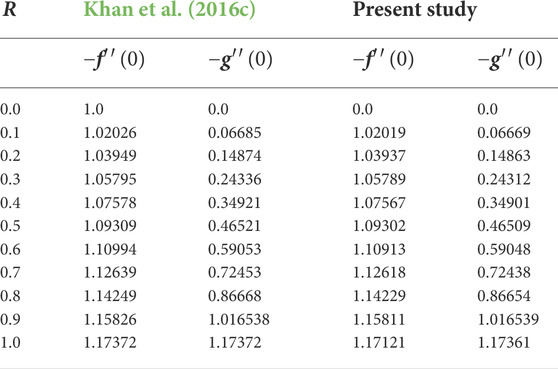
TABLE 1. An evaluation table for − f′′(0) and − g′′(0) for several magnitudes of R in reduced case when β1 = β2 = M = 0.

TABLE 2. An assessment table for − θ′(0) for pertinent ranges of R in reducing case when β1 = β2 = δ = βt = Nt = Nb = 0 and Pr = 1.
Concluding remarks
The Cattaneo–Christov approach and Buongiorno’s model were employed together to investigate the momentum and energy transport features of the three-dimensional flow of the Oldroyd-B nanofluid over a bidirectional stretched sheet. After utilizing the homotopy analysis method on the governing equation to solve them, we found some important results, which are noted here.
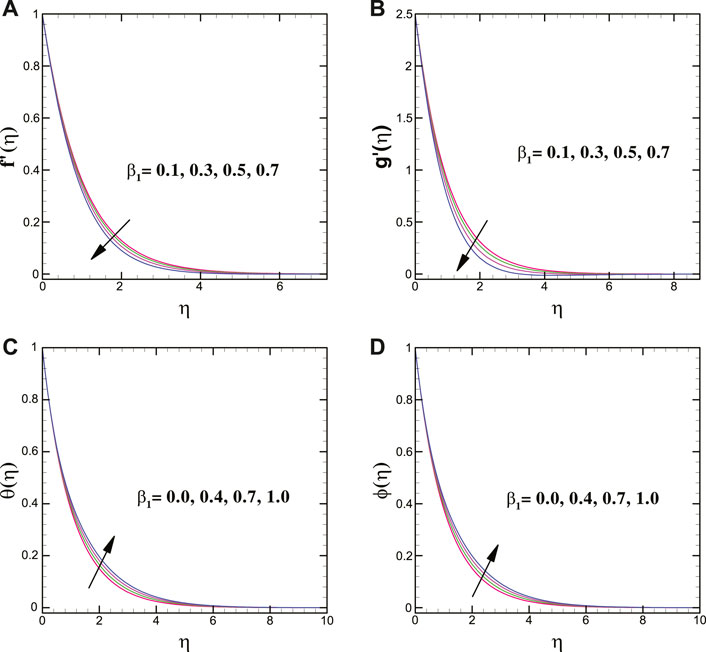
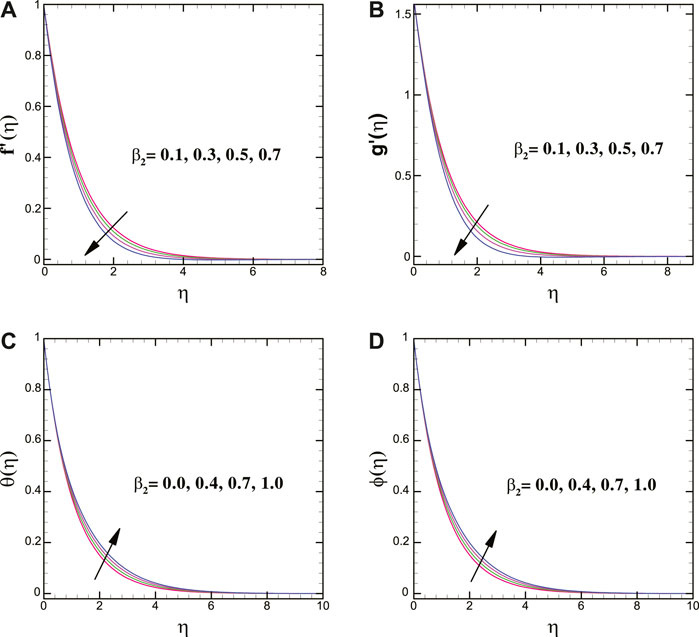
We found that, for magnifying stretching strength R, the vertical velocity in the y-direction magnifies, but it decreases in the x-direction. The flow curves of the Oldroyd-B nanofluid for the relaxation time parameter show an opposite behavior compared to the Oldroyd-B material parameter.
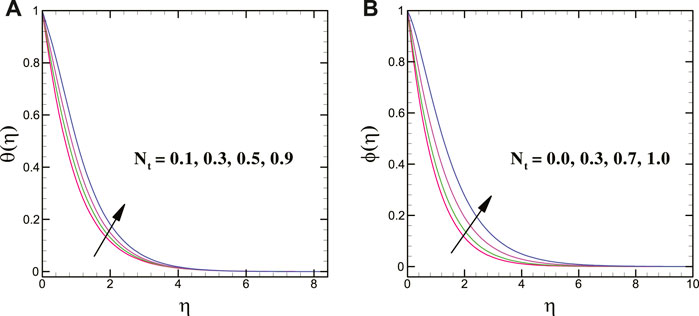
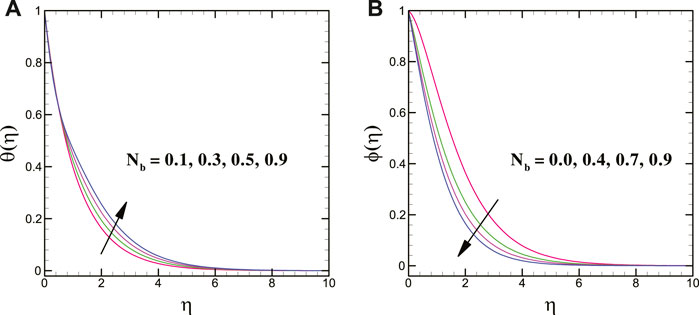
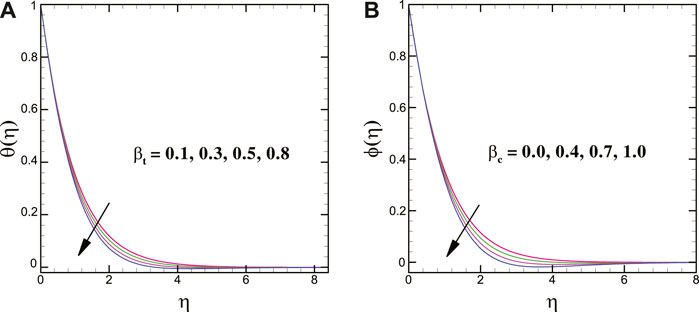
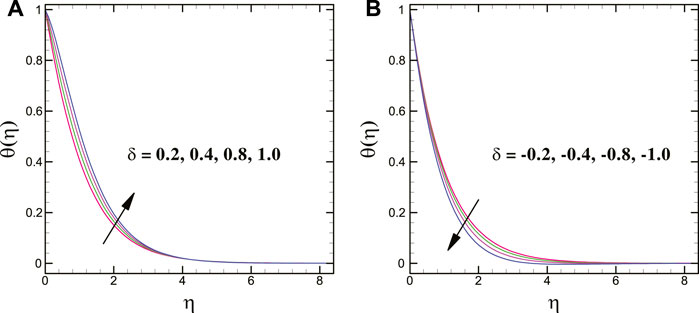
For varying values of the Brownian motion parameter, the solutal transport decays, whereas the thermal conduction shows enhancing trend for it. Moreover, the thermal and concentration transport = escalates for larger magnitudes of the thermophoretic force parameter. In addition, a larger thermal relaxation time parameter deteriorates the thermal transport. The mass transfer profile decreases for a greater solutal relaxation time parameter. The larger stretching strength decreases the thermal energy transport of the nanoliquid. Figures 8A,B clearly elucidate that the thermal profile is augmented for larger heat source parameter while it declines for heat sink parameter.
Data availability statement
The original contributions presented in the study are included in the article/supplementary materials. Further inquiries can be directed to the corresponding authors.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work is supported by National Natural Science Foundation of China (12071408), Natural Science foundation of Jiangsu (BK20201149) and Jiangsu Funding Program for excellent Postdoctoral Talent, Grant No: 2022ZB675. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code:22UQU4331317DSR67.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Large Groups (RGP.2/94/43). The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4331317DSR67.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmad, I., Faisal, M., and Javed, T. (2019). Bi-directional stretched nanofluid flow with Cattaneo-Christov double diffusion. Results Phys. 15, 102581. doi:10.1016/j.rinp.2019.102581
Ahmed, J., Khan, M., and Ahmad, L. (2019). MHD swirling flow and heat transfer in Maxwell fluid driven by two coaxially rotating disks with variable thermal conductivity. Chin. J. Phys. 60, 22–34. doi:10.1016/j.cjph.2019.02.010
Ahmed, S., Nadeem, S., Muhammmad, N., and Khan, M. N. (2020). Cattaneo-Christov heat flux model for stagnation point flow of micropolar nanofuid toward a nonlinear stretching surface with slip effects. J. Therm. Analy. Calorim. 143, 1187. doi:10.1007/s10973-020-09504-2
Ali, B., Raju, C. S. K., Ali, L., Hussain, S., and Kamran, T. (2021). G-Jitter impact on magnetohydrodynamic non-Newtonian fluid over an inclined surface: Finite element simulation. Chin. J. Phys. 71, 479–491. doi:10.1016/j.cjph.2021.03.020
Amjid, M., Zehra, I., Nadeem, S., and Abbas, N. (2020). Thermal analysis of Casson micropolar nanofluid flow over a permeable curved stretching surface under the stagnation region. J. Therm. Anal. Calorim. 143, 2485–2497. doi:10.1007/s10973-020-10127-w
Bhattacharyya, A., Seth, G. S., Kumar, R., and Chamkha, A. J. (2019). Simulation of Cattaneo–Christov heat flux on the flow of single and multi-walled carbon nanotubes between two stretchable coaxial rotating disks. J. Therm. Anal. Calorim. 139, 1655–1670. doi:10.1007/s10973-019-08644-4
Cattaneo, C. (1948). Sulla conduzione del calore. Atti Semin. Mat. Fis. Univ. Modena Reggio Emilia 3, 83–101.
Choi, S. U. S. (1995). “Enhancing thermal conductivity of fluids with nanoparticles, the proceedings of the 1995,” in ASME international mechanical engineering congress and exposition (San Francisco, USA: ASME), 99–105.
Choi, S. U. S., Zhang, Z. G., Yu, W., Lockwood, F. E., and Grulke, E. A. (2001). Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 4, 2252–2254. doi:10.1063/1.1408272
Christov, C. I. (2009). On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 36, 481–486. doi:10.1016/j.mechrescom.2008.11.003
Evans, W., Fish, J., and Keblinski, P. (2006). Role of Brownian motion hydrodynamics on nanofluid thermal conductivity. Appl. Phys. Lett. 88, 093116. doi:10.1063/1.2179118
Grattan-Guinness, I. (2005). Chapter 26 – joseph Fourier, Théorie analytique de la chaleur (1822). Landmark Writings West. Math. 1640-1940. 2005. 354. doi:10.1016/B978-044450871-3/50107-8
Haddad, S. A. M. (2014). Thermal instability in Brinkman porous media with Cattaneo-Christov heat flux. Int. J. Heat. Mass Transf. 68, 659–668. doi:10.1016/j.ijheatmasstransfer.2013.09.039
Hafeez, A., Khan, M., and Ahmed, J. (2020). Thermal aspects of chemically reactive Oldroyd-B fluid flow over a rotating disk with Cattaneo-Christov heat flux theory. J. Therm. Anal. Calorim. 144, 793–803. doi:10.1007/s10973-020-09421-4
Hayat, T., Ahmed, S., Khan, M. I., and Alsaedi, A. (2018). Simulation of ferromagnetic nanomaterial flow of Maxwell fluid. Results Phys. 8, 34–40. doi:10.1016/j.rinp.2017.11.021
Hayat, T., Aslam, N., Khan, M. I., Khan, M. I., and Alsaedi, A. (2019). Physical significance of heat generation/absorption and Soret effects on peristalsis flow of pseudoplastic fluid in an inclined channel. J. Mol. Liq. 275, 599–615. doi:10.1016/j.molliq.2018.11.055
Hayat, T., Aziz, A., Muhammad, T., and Alsaedi, A. (2017). On model for flow of Burgers nanofluid with Cattaneo–Christov double diffusion. Chin. J. Phys. 55, 916–929. doi:10.1016/j.cjph.2017.02.017
Hayat, T., Khan, M. I., Tamoor, M., Waqas, M., and Alsaedi, A. (2017). Numerical simulation of heat transfer in MHD stagnation point flow of Cross fluid model towards a stretched surface. Results Phys. 7, 1824–1827. doi:10.1016/j.rinp.2017.05.022
Hayat, T., Shehzad, S. A., and Alsaedi, A. (2014). Three-dimensional flow of an Oldroyd-B fluid over a bidirectional stretching surface with prescribed surface temperature and prescribed surface heat flux. J. Hydrology Hydromechanics 62, 117–125. doi:10.2478/johh-2014-0016
Hayat, T., Tamoor, M., Khan, M. I., and Alsaedi, A. (2016). Numerical simulation for nonlinear radiative flow by convective cylinder. Results Phys. 6, 1031–1035. doi:10.1016/j.rinp.2016.11.026
Iqbal, Z., Khan, M., Ahmed, A., Ahmed, J., and Hafeez, A. (2020). Thermal energy transport in Burgers nanofluid flow featuring the Cattaneo–Christov double diffusion theory. Appl. Nanosci. 10, 5331–5342. doi:10.1007/s13204-020-01386-y
Iqbal, Z., KhanAhmed, M. A., and Ullah, M. Z. (2021). The mechanical aspects of bidirectional stretching on thermal performance in Burgers nanofluid flow subject to ohmic heating and chemical reaction. Proc. Inst. Mech. Eng. Part E J. Proc. Mech. Eng. 2021, 0954408921999613. doi:10.1177/0954408921999613
Kamran, T., Amir, M. J., and Rehman, M. S. (2015). Solution of Eigen value problems by using new iterative method. Int. J. Sci. Eng. Res. 11, 1355–1361.
Kamran, T., Rehman, M. S., and Amir, M. J. (2016). Using new iterative method to find the exact s for a class of stiff systems of equations. Int. J. Math. Phys. Sci. Res. 3, 60–65.
Kamran, T., Yaseen, M., and Rehman, M. S. (2016). Solution of variational problems using new iterative method. Int. J. Sci. Eng. Res. 7, 1619–1624.
Khan, M. I., Alsaedi, A., Hayat, T., and Khan, N. B. (2019). Modeling and computational analysis of hybrid class nanomaterials subject to entropy generation. Comput. Methods Programs Biomed. 179, 104973. doi:10.1016/j.cmpb.2019.07.001
Khan, M. I., and Alzahrani, F. (2020). Binary chemical reaction with activation energy in dissipative flow of non-Newtonian nanomaterial. J. Theor. Comput. Chem. 19, 2040006. doi:10.1142/s0219633620400064
Khan, M. I., Alzahrani, F., and Hobiny, A. (2020). Simulation and modeling of second order velocity slip flow of micropolar ferrofluid with Darcy–Forchheimer porous medium. J. Mat. Res. Technol. 9, 7335–7340. doi:10.1016/j.jmrt.2020.04.079
Khan, M. I., and Alzahrani, F. (2021). Physical impact of double stratification in Darcy–Forchheimer hybrid nanofluid (Al2O3–Cu–H2O) subject to Arrhenius pre-exponential factor law and entropy generation. Waves Random Complex Media 1, 22. doi:10.1080/17455030.2021.2011985
Khan, M. I., Malik, M. Y., Chaudhry, F., Khan, S. U., and El-Zahar, E. R. (2021). Transportation of Marangoni convection with dust particles random motion in flow of hybrid nanomaterials. Waves Random Complex Media 1, 14. doi:10.1080/17455030.2021.2017072
Khan, M. I., and Puneeth, V. (2021). Isothermal autocatalysis of homogeneous–heterogeneous chemical reaction in the nanofluid flowing in a diverging channel in the presence of bioconvection. Waves Random Complex Media 1, 21. doi:10.1080/17455030.2021.2008547
Khan, M., Iqbal, Z., and Ahmed, A. (2020). A mathematical model to examine the heat transport features in Burgers fluid flow due to stretching cylinder. J. Therm. Anal. Calorim. 147, 827–841. doi:10.1007/s10973-020-10224-w
Khan, M., Iqbal, Z., and Ahmed, A. (2020). Stagnation point flow of magnetized Burgers’ nanofluid subject to thermal radiation. Appl. Nanosci. 10, 5233–5246. doi:10.1007/s13204-020-01360-8
Khan, M., Khan, W. A., and Alshomrani, A. S. (2016). Non-linear radiative flow of three-dimensional Burgers nanofluid with new mass flux effect. Int. J. Heat. Mass Transf. 101, 570–576. doi:10.1016/j.ijheatmasstransfer.2016.05.056
Khan, M., and Khan, W. A. (2016). Three-dimensional flow and heat transfer to Burgers fluid using Cattaneo-Christov heat flux model. J. Mol. Liq. 221, 651–657. doi:10.1016/j.molliq.2016.06.041
Khan, M. R., Mao, S., Deebani, W., and Elsiddieg, A. M. (2022). Numerical analysis of heat transfer and friction drag relating to the effect of Joule heating, viscous dissipation and heat generation/absorption in aligned MHD slip flow of a nanofluid. Int. Commun. Heat Mass Transf. 131, 105843. doi:10.1016/j.icheatmasstransfer.2021.105843
Khan, W. A., Alshomrani, A. S., and Khan, M. (2016). Assessment on characteristics of heterogeneous-homogenous processes in three-dimensional flow of Burgers fluid. Results Phys. 6, 772–779. doi:10.1016/j.rinp.2016.09.019
Khan, W. A., Khan, M., and Alshomrani, A. S. (2016). Impact of chemical processes on 3D Burgers fluid utilizing Cattaneo-Christov double-diffusion: Applications of non-Fourier’s heat and non-Fick’s mass flux models. J. Mol. Liq. 223, 1039–1047. doi:10.1016/j.molliq.2016.09.027
Liu, I. C., and Andersson, H. I. (2008). Heat transfer over a bidirectional stretching sheet with variable thermal conditions. Int. J. Heat. Mass Transf. 51, 4018–4024. doi:10.1016/j.ijheatmasstransfer.2007.10.041
Muhammad, T., Waqas, H., Khan, S. A., Ellahi, R., and Sait, S. M. (2020). Significance of nonlinear thermal radiation in 3D Eyring–Powell nanofluid flow with Arrhenius activation energy. J. Therm. Anal. Calorim. 143, 929–944. doi:10.1007/s10973-020-09459-4
Nadeem, S., and Khan, A. U. (2019). MHD oblique stagnation point flow of nanofluid over an oscillatory stretching/shrinking sheet: Existence of dual solutions. Phys. Screen. 94, 075204. doi:10.1088/1402-4896/ab0973
Rashidi, M. M., Rostami, B., Freidoonimehr, N., and Abbasbandy, S. (2014). Free convective heat and mass transfer for MHD fluid flow over a permeable vertical stretching sheet in the presence of the radiation and buoyancy effects. Ain Shams Eng. J. 5, 901–912. doi:10.1016/j.asej.2014.02.007
Rasool, G., and Zhang, T. (2019). Darcy-Forchheimer nanofluidic flow manifested with Cattaneo-Christov theory of heat and mass flux over non-linearly stretching surface. PLoS ONE 14, e0221302. doi:10.1371/journal.pone.0221302
Raza, A., Ghaffari, A., Khan, S. U., Haq, A. U., Khan, M. I., and Khan, M. R. (2022). Non-singular fractional computations for the radiative heat and mass transfer phenomenon subject to mixed convection and slip boundary effects. Chaos, Solit. Fractals 155, 111708. doi:10.1016/j.chaos.2021.111708
Rehman, M. S., and Kamran, T. (2019). Solution of nonlinear Riccati differential equations using new iterative method. Int. J. Eng. Fut. Tech. 16.
Rehman, M. S., Yaseen, M., and Kamran, T. (2016). New iterative method for solution of system of linear differential equations. Int. J. Sci. Res. 5.
Saleem, S., Awais, M., Nadeem, S., Sandeep, N., and Mustafa, M. T. (2017). Theoretical analysis of upper-convected Maxwell fluid flow with Cattaneo–Christov heat flux model. Chin. J. Phys. 55, 1615–1625. doi:10.1016/j.cjph.2017.04.005
Shehzad, S. A., Abbasi, F. M., Hayat, T., and Alsaedi, A. (2016). Cattaneo-Christov heat flux model for Darcy-Forchheimer flow of an Oldroyd-B fluid with variable conductivity and non-linear convection. J. Mol. Liq. 224, 274–278. doi:10.1016/j.molliq.2016.09.109
Shehzad, S. A., Mushtaq, T., Abbas, Z., and Rauf, A. (2019). Double-diffusive Cattaneo–Christov squeezing flow of micropolar fluid. J. Therm. Anal. Calorim. 143, 445–454. doi:10.1007/s10973-019-09183-8
Sheikholeslami, M., Bandpy, M. D., Ellahi, R., and Zeeshan, A. (2014). Simulation of MHD CuO–water nanofluid flow and convective heat transfer considering Lorentz forces. J. Magn. Magn. Mat. 369, 69–80. doi:10.1016/j.jmmm.2014.06.017
Sheikholeslami, M., and Ganji, D. D. (2013). Heat transfer of Cu-water nanofluid flow between parallel plates. Powder Technol. 235, 873–879. doi:10.1016/j.powtec.2012.11.030
Sher, M., Muhammad, I., Asif, H. S., Muhammad, T., Muhammad, T., Muhammad, N., et al. (2019). Semi analytical solution of steady Burgers’ nanofluid flow between parallel channels with heat generation/absorption under the influence of thermal radiation. J. Nanofluids 8, 1468–1478. doi:10.1166/jon.2019.1706
Straughan, B. (2010). Thermal convection with the cattaneo–christov model. Int. J. Heat. Mass Transf. 53, 95–98. doi:10.1016/j.ijheatmasstransfer.2009.10.001
Waqas, M., Hayat, T., Shehzad, S. A., and Alsaedi, A. (2018). Analysis of forced convective modified Burgers liquid flow considering Cattaneo-Christov double diffusion. Results Phys. 8, 908–913. doi:10.1016/j.rinp.2017.12.069
Nomenclature
u, v, w Velocity components (ms−1)
μ Dynamic viscosity (kg m−1 s−1)
x, y, z Cartesian coordinates (ms−1)
Nb Brownian motion parameter
α1 Thermal diffusivity (m2 s−1)
β1 Fluid relaxation time parameter
k Thermal conductivity
Cw Concentration at surface
l Specific length (m)
DB The mass diffusion coefficient (m2 s −1)
q Heat flux
σ Fluid electric conductivity (Sm−1)
C∞ Ambient concentration
cp Specific heat capacity (JK−1 kg−1)
C Concentration
S Extra stress tensor
ν Kinematic viscosity (m2 s−1)
U0 Reference velocity (ms−1)
Le Lewis number
λ1 Fluid relaxation time (s)
λ2 The material parameter of Oldroyd-B fluid (s2)
ρ Fluid density (kg m−3)
θ Dimensionless temperature
J Mass flux
Tw Surface temperature (K)
T∞ Ambient temperature (K)
DT Thermophoresis coefficient (m2 s−1)
βt Thermal relaxation time parameter (s)
hf Heat convection coefficient
η Dimensionless similarity variable
ax, by linear stretching velocities (ms−1)
T Fluid temperature (K)
A1 First Rivlin–Ericksen tensor
f′ Dimensionless fluid velocity component
Pr Prandtl number
βc Solutal relaxation time parameter (s)
ϕ Dimensionless concentration
Keywords: energy transport, Oldroyd-B nanofluid, heat source/sink, bidirectional stretching, Cattaneo–Christov theory, Buongiorno’s model for nanofluids
Citation: Hussain A, Iqbal Z, Abdelmohimen MAH, Guedri K, Tag-eldin E and Yassen MF (2022) Energy transport features of Oldroyd-B nanofluid flow over bidirectional stretching surface subject to Cattaneo–Christov heat and mass fluxes. Front. Energy Res. 10:985146. doi: 10.3389/fenrg.2022.985146
Received: 03 July 2022; Accepted: 08 August 2022;
Published: 21 October 2022.
Edited by:
Umar Khan, Hazara University, PakistanReviewed by:
Kasra Ghasemi, University of Guelph, CanadaNajma Saleem, Prince Mohammad bin Fahd University, Saudi Arabia
Saranya Shekar, United Arab Emirates University, United Arab Emirates
Copyright © 2022 Hussain, Iqbal, Abdelmohimen, Guedri, Tag-eldin and Yassen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zahoor Iqbal, aXphaG9vckBtYXRoLnFhdS5lZHUucGs=; Elsayed Tag-eldin, ZWxzYXllZC50YWdlbGRpbkBmdWUuZWR1LmVn
 Arafat Hussain1
Arafat Hussain1 Zahoor Iqbal
Zahoor Iqbal