State-of-charge estimation method for lithium-ion batteries based on competitive SIR model

In order to meet the needs of life and production and ensure the battery is stable when using the battery, a scheme for reckoning the state of charge of lithium-ion batteries derived from the competitive SIR model is proposed. During the charging process of the battery, the electrolyte and the diaphragm reach the negative electrode of the battery, and the electrolyte escapes from the graphite of the negative electrode to the positive electrode in the case of discharge. The analysis shows that the SIR model belongs to the internal information evolution process, which can infect the surrounding data and evaluate the state of charge better. Through experiments, it is substantiated that the scheme is able to better estimate the state of lithium-ion batteries, the error value is 0.0189, the accuracy is good, and the battery usage can be predicted in time.

1 Introduction

With the continuous growth of the population, the human society and the world economy have also developed rapidly (Xiong et al., 2021). However, energy crisis and environmental pollution have become increasingly serious problems faced by people. Therefore, both the government and scientists have paid attention to it (Zhang et al., 2015a).

In order to solve the above problems, electric vehicles with clean energy as the power source came into being. With the emergence of energy crisis and environmental problems, the new energy automobile university gradually occupies an important position in the global automobile industry (Yang et al., 2022).

In recent years, the development of hybrid electric vehicles has boosted the research and development of batteries. At the same time, more lithium batteries are required to meet the quality of life (Dey et al., 2015). In terms of principle and characteristics, different types of batteries have their own characteristics, such as chemical composition, performance (Li et al., 2021a), cost and safety. Later, dry batteries and nickel-cadmium batteries appeared. Later, for environmental protection, the research focus turned to batteries.

The battery state of charge (SOC) is an important parameter of the battery management system (Li et al., 2021b). However, the SOC peak cannot be directly measured, and it is affected by factors such as application environment, declining degree, self-discharge, current amplification. Therefore, SOC reckoning, especially online reckoning, is a hot and difficult issue in lithium battery research. Based on this, a proportional-integral (PI) observer was proposed in (Xu, 2014) to estimate the SOC of Li-ion batteries in EDVs (End-diastolic volume). In literature (Ya-Xiong and Zhang, 2016), in order to reckon SOC of lithium batteries, the primary battery model is improved to develop the accuracy of the model and enable the battery model to reflect the actual internal state of the battery. The corresponding battery test experiments are carried out. Reference (Jiang et al., 2022) uses the EDVs Extended Rauch-Tung-Striebel Smoother (ERTSS) to estimate SOC. Using a Genetic Algorithm (GA) to search for the smoothing time interval for the optimal ERTSS, various dynamic unit tests were performed. Reference (Hu et al., 2022) extracts higher-level spatial features between multi variables into the current SOC and historical input, to achieve state assessment. However, the above-mentioned methods have low accuracy and large errors, so they cannot be accurately evaluated. Therefore, in this paper, the competitive SIR model is used to reckon the state of charge, and its advantages are clarified by analyzing the condition of lithium-ion batteries, and the SIR model is used to reckon SOC of the battery, providing a better method for battery condition assessment.

2 Lithium-ion batteries working principle and performance

2.1 Analysis of the advantages of lithium batteries

Lithium-ion batteries have superior properties that drive their rapid development. Its advantages are as follows:

1) High energy density (Zou et al., 2014). There are many kinds of materials that make up lithium-ion batteries, and different materials have different electrical conductivity. The power density of lithium-ion batteries is superior to other batteries in terms of mass and volume.

2) The open circuit voltage is too high. The materials that make up a lithium-ion battery determine its high open-circuit voltage, about three times that of the same nickel-chromium and nickel-metal hydride batteries.

3) The output power is large. This is also determined by the materials that make up the lithium-ion battery.

4) No memory effect (Yang et al., 2021). This feature allows the battery to function when it is not fully charged, avoiding the need to fully charge and discharge the battery every time, which is simpler to use and maintain than normal batteries.

5) The self-discharge rate of the battery is low. Self-discharge is not obvious and the efficiency is low. Even if it does not work for a long time, the average monthly excretion is only 5–10%.

6) Wide operating temperature range. It can work in a wide temperature range and can work normally at −20°C∼+50°C.

7) The charging speed is fast. Lithium-ion batteries have high charging efficiency. They can be charged with 1C or more and can reach full state in a short period of time.

8) Long cycle life. Its cycle life is significantly better than other batteries. The cycle life of ordinary lithium batteries can reach 500 times or even more than 1,000 times. However, the theoretical charge-discharge cycles of batteries can reach more than 2000 times.

9) Safe and pollution-free. This is an environmentally friendly battery that can provide energy without producing heavy metals (Zhang et al., 2015b), harmful gases and other pollutants.

The superior performance of lithium-ion batteries is suitable for electric vehicles, which has prompted more research on them.

2.2 Lithium-ion batteries working principle

This paper mainly introduces the internal structure of lithium iron phosphate battery. Its cathode (Vo et al., 2015) material is composed of lithium iron phosphate. On the left is $LiFeP{o}_4$ , and the positive electrode of the battery is composed of olivine-structured bubbles. Aluminum foil connects it to the battery positive. On the right is the battery negative. Its material is graphite (Xie et al., 2018). Copper foil connects it to the battery negative. The middle part is the polymer membrane (Hu et al., 2018). It separates the positive and negative electrodes, allowing Li + to pass but preventing e- from passing through. The battery electrolyte is usually an organic electrolyte, which is located at the upper and lower ends of the battery. The working process of the battery is shown in Eq. 1 and Eq. 2:

In charge state:

$LiFeP{o}_4-xL{i}^{+}-x{e}^{-}\to xFeP{o}_4+\left(1-x\right)LiFeP{o}_4(1)$

In discharge state:

$FeP{o}_4+xL{i}^{+}+x{e}^{-}\to xLiFeP{o}_4+\left(1-x\right)FeP{o}_4(2)$

During the charging situation, the Li + escaped from the anode reaches the negative electrode of the battery through the electrolyte and the diaphragm through the action of the electric field, and the current flows reversely from the cathode to the anode. During the discharging situationf, Li + escapes from the graphite of the cathode to the anode through the electrolyte, and the current flows from the anode to the cathode.

3 State of charge estimation research status

3.1 State of charge definition

State-of-charge batteries are usually expressed as a percentage, with values ranging from 0 to 1. Remaining power is an important parameter reflecting battery performance. In many cases, SOC is often used to indicate the remaining power of the battery. Strictly speaking, however, the two definitions are different and the units adopted are inconsistent.

At present, the definition of SOC is not unified (Sakile and Sinha, 2021). Only a few simple definitions are introduced below, and the following definitions are given from different perspectives.

Definition 1. The most classic expression in the definition of SOC is as follows:

$SOC=\frac{Q_{remain}}{Q_{rated}}\times 100\mathrm{\%}(3)$

where $Q_{remain}$ is the remaining charge scope (Le et al., 2021). $Q_{rated}$ is the rated charge capacity. If we think that $Q_{rated}$ is a fixed value (Gholizadeh and Salmasi, 2013), the definition (3) of SOC can be rewritten as Eq. 4:

$SOC=\frac{Q_{remain}}{Q_{ramain}+Q_d}\times 100\mathrm{\%}(4)$

Among them, compared with the Eq. 3, the extra denominator $Q_d$ in the Eq. 4 represents the amount that has been released in the electric charge after the latest charging point.

Definition 2. Definition from the perspective of electricity: the battery is discharged at a certain rate, the current remaining battery capacity of the battery is used as the numerator (Zhang et al., 2022), and the total available capacity is used as the denominator. The corresponding mathematical expression is shown in Eq. 5.

$SOC=\frac{Q_t}{Q_0}\times 100\mathrm{\%}(5)$

In Eq. 5, $Q_t$ represents the remaining power of the battery during calculation, that is, the battery is fully discharged to the discharge cut-off (Mitsuru and Yuhu, 2019) voltage under the conditions of a certain discharge rate and temperature specified in the actual experiment; $Q_0$ indicates the total capacity of the battery.There is also a definition of SOC as shown in the following Eq. 6:

$SOC=\frac{Q\left(t\right)-Q_0}{Q_E-Q_0}\times 100\mathrm{\%}(6)$

Among them, $Q\left(t\right)$ is the remaining scope, $Q_E$ represents the maximum scope, and $Q_0$ represents the total capacity of the battery.

Definition 3. , according to the definition of SOC:

$SOC=SO{C}_0-\frac{1}{C_N}{\displaystyle {\int }_0^t\eta id\tau }(7)$

In the above formula: $C_N$ is the rated scope; $i$ is the battery current; $\eta$ represents the efficiency during charge-discharge situation, and $SO{C}_0$ is the initial state under working conditions.Definition 4, defined in terms of energy:

$SOC=\frac{\text{remaining}\text{available}\text{energy}}{\text{total}\text{available}\text{energy}}\times 100\mathrm{\%}=1-\frac{W_h}{W_{hE}}(8)$

In Eq. 8, $W_h$ represents the used energy, and $W_{hE}$ represents the total usable energy.

3.2 Reckoning scheme

Battery SOC evaluation plays a primary role in battery systems. The state of charge can only be estimated indirectly (Zheng et al., 2016), which needs to be estimated with the help of information such as voltage, current, internal resistance, and temperature. This is a physical quantity that cannot be directly measured (Hu et al., 2018). Many scholars and experts have done a series of related researches and discussions on the online reckoning scheme. In line with the different algorithm modeling methods, SOC estimation methods can be divided into simple calculation methods, fitting methods and nonlinear filtering methods (Tian et al., 2022). The specific classification is as follows.

3.2.1 Simple calculation method

The so-called calculation methods (such as the open circuit voltage method, the internal resistance method (Wu et al., 2021), the ampere-hour integration method, the discharge experiment method and the ultrasonic detection method) calculate the SOC of the battery through the definition formula of SOC. The simple parameter used in the formula is the charge and discharge current collected by the “black box”, without using any intelligent model or equivalent model (Chen et al., 2022), and not caring about the internal structure of the battery, but treating the battery as a whole as a “black box”, which is a relatively basic estimation method. The direct calculation method is a method that realizes SOC estimation only by defining the formula calculation. The direct calculation method referred to in this article is the ampere-hour integration method.

According to the ampere-hour integration method, SOC is defined as follows:

$SOC\left(t\right)=SOC\left(t_0\right)-\frac{\eta {\displaystyle {\int }_{t_0}^{t}Idt}}{Q_N}(9)$

$\eta$ is the Coulomb efficiency coefficient, $Q_N$ is the nominal capacity of the battery, $I$ is the discharge current, and $SOC\left(t_0\right)$ is the state of charge at $t_0$.

The nonlinear relationship between OCV and SOC is first fitted, and then the relationship is used to reckon SOC indirectly, the so-called open circuit voltage method. In general, the open circuit voltage method has a clear relationship with SOC in the early and late stages of charging, and it is best to estimate SOC within this range. The ampere-hour integration method has become the most widely used method in practice due to its simplicity and ease of implementation. Combining the advantages and disadvantages of the two methods, it is found that the two methods are obviously complementary. Therefore, many scholars have proposed new ideas to combine these two methods. The use of high-performance current sensors to measure current solves the problem of current inaccuracy, but also increases the cost. The advantage is that the principle is simple, and the calculation of the internal resistance value is simple. However, due to the influence of other factors, it is difficult to determine the relationship with SOC. Ultrasonic testing is a relatively new method. According to the advantage that ultrasound is very sensitive to porosity changes, it can detect the SOC state of the battery with high sensitivity.

3.2.2 Fitting method

The fitting estimation method fits the internal relationship between the external characteristics and SOC (such as load voltage method and the linear model method) according to the experimental data of the battery under various operating conditions, or uses various intelligent learning algorithms (such as neural network, network method, fuzzy inference method, support vector machine, etc.) offline training of the relationship model between battery performance parameters and state of charge, and then based on the relationship model, using experimental data to reckon SOC, which is called the fitting scheme. With the development of modern sensor technology and data storage and processing technology, data-driven system health prediction methods (neural network method, fuzzy inference method, support vector machine, correlation vector machine, etc.) have been widely used and popularized. The SOC reckoning scheme can be enforced to various lithium-ion batteries, the estimation accuracy is improved.

Fuzzy inference methods can estimate the time-varying parameters of circuit models well, but lack the ability of self-learning and self-adaptation. The SVM method uses a limited number of samples. The algorithm is simple and stable, but requires much data for computation. Support vector regression has the ability to learn from small samples, but the algorithm is not adaptive when battery performance parameters change (Liu et al., 2021).

3.2.3 Nonlinear filtering method

The nonlinear filtering method treats the battery as a dynamic system. The state variables of the system include SOC, which is updated by observing the variable value (usually selecting the battery terminal voltage as the observation variable), and finally the standard error of the state variable is minimized, sliding mode observer method, H filter method, etc, are used in nonlinear stochastic systems, and this kind of SOC estimation method is more suitable in terms of estimation accuracy.

To sum up, among the existing SOC estimation methods, the simple calculation scheme is straightforward to implement, and is widely used in occasions with low precision requirements. In occasions with high accuracy requirements, this method is usually used as an auxiliary tool for other SOC estimation methods; the fitting method is straightforward to perform and has high accuracy, but requires much data for computation, training data and method will directly affect the estimation accuracy; The nonlinear filtering method can track the changes of battery voltage and current in real time, update the SOC estimation value, and realize online SOC estimation, but the implementation process of this method is relatively complicated and the amount of calculation is large.

3.2.4 SI model

Assuming that the total population of an area is a constant, then in the process of spreading infectious diseases, it is divided into susceptible groups (Susceptible) and infected persons (Infective). Susceptible populations are those who are not yet infected but are at risk of infection. $S\left(t\right)$ represents the number of people who are vulnerable at $t$ , and $I\left(t\right)$ represents to the number of people who are infected at $t$. Obviously:

$S\left(t\right)+I\left(t\right)=N(10)$

Assuming that the infection rate is $\beta$ , the number of people who are newly infected is:

$\frac{dI\left(t\right)}{dt}=\beta I\left(t\right)S\left(t\right)(11)$

The change of susceptible population per unit time is:

$\frac{dS\left(t\right)}{dt}=-\beta I\left(t\right)S\left(t\right)(12)$

Assuming the initial infection number $I_0=I\left(0\right)$ , the simultaneous Eqs 10–12 can be obtained:

$I\left(t\right)=\frac{N}{1+\left(\frac{N}{I_0}-1\right)e^{-\beta Nt}}(13)$

As time $t$ approaches infinity, the number of infected people will approach $N$ . Based on this feature, this paper uses the SI model to represent the dissemination model of rumor-refuting information in competitive information, that is, after the rumor-refuting information begins to spread, the number of users who finally receive the information approaches $N$ .

3.2.5 SIR model

Similar to the SI model, the SIR model has an additional removal population. Removal populations are those who received treatment after infection and then migrated from the infected population. For example, such a population would not become infected after developing antibodies to infectious diseases. $R\left(t\right)$ represents the number of people who are removed at time $t$ , $\gamma$ and represents the probability of an infected person being removed per unit time. Based on the advantages of the SIR model over the SI model, this paper adopts the SIR model as the propagation model.

Since the SIR model is similar to the SI model, the change equation can be rewritten as:

$\frac{dI\left(t\right)}{dt}=\beta I\left(t\right)S\left(t\right)-\gamma I\left(t\right)(14)$

$\frac{dS\left(t\right)}{dt}=-\beta I\left(t\right)S\left(t\right)(15)$

$\frac{dR\left(t\right)}{dt}=\gamma I\left(t\right)(16)$

$S\left(t\right)+I\left(t\right)+R\left(t\right)=N(17)$

Under normal circumstances, since the initial infected population is not 0, so $I_0=I\left(0\right)\mathrm{>0}$ , $S_0=S\left(0\right)\mathrm{>}0$ .

Based on this, this paper proposes a SOC reckoning for Li-ion batteries under a competitive SIR model. The SIR model was first used to study the spread and evolution of infectious diseases (Du et al., 2021). Since the 18th century, many research results have been formed, most of which focus on the improvement of the model and the application of the model in different fields. SIR is an infectious disease model developed from the SI model, which uses mathematical methods to analyze changes in the number of infections, predict peak periods, and identify regulatory and preventive mechanisms (Chen et al., 2020).

In the traditional SIR model, all participants in the system are divided into three parties: S is the susceptible group, I is the infected, i.e. the disseminator of opinions, and R is the immune, i.e. the person who is immune to the current information and no longer transmits it information. The mutual transformation of the three groups reflects the evolution of public opinion or information within the group.

4 Results and analysis

In this paper, a competitive SIR model is used to estimate the SOC during steady-state discharge of lithium-ion batteries. Experimental data was gathered during discharge situation of a set of lithium-ion batteries. The specification of the lithium-ion battery used in the experiment is shown in Table 1.

TABLE 1

TABLE 1. Lithium-ion battery parameters.

The SOC recorded during the entire discharge process is calculated by Eq. 18:

$SOC=SO{C}_0+\frac{1}{C_R}{\displaystyle {\int }_{t_0}^t{I}_{cm}d\tau },C_R={\displaystyle {\int }_0^{t_{EDV}}{I}_{cm}d\tau }(18)$

In Eq. 18, $SO{C}_0$ represents the original SOC, $C_R$ is the rated scope, $I_{cm}$ is the discharge current, and $t_{EDV}$ represents the discharge time.

The root-mean-square error (RMSE) was used to evaluate the accuracy of the SIR model estimation. RMSE is defined as follows:

${\delta }_{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left|f\left(x_i\right)-y_i\right|}^2}}(19)$

In Eq. 19, $f\left(x_i\right)$ represents the estimated value based on the model, $y_i$ represents the true value of the equation SOC, $n$ is the number of reckoned points.

Design experiments to complete the state of the battery, and continuously charge and discharge the battery under specific set conditions.

The capacity is obtained by the corresponding standard measurement, and the specific steps are as follows:

1) Charging experiment, keep the lithium-ion battery charged at a constant current of 0.2°C at an ambient temperature of 36°C, and switch to constant voltage charging when the voltage reaches 4.2 V. When the charging current reaches 0.12 A, stop charging. It was left to stand for 15 min, cycling this process until the charge cut off current.

2) The discharge experiment is also carried out at the same ambient temperature. When the battery terminal voltage drops to 2.75 V, the discharge is stopped.

It was left to stand for 30 min; this process was applied to two batteries, called No. 4 and No. 5, respectively, to discharge the No. 4 battery at a constant current of 1.0°C, and the No. 5 battery to discharge at a constant current of 2.0°C.

Based on this step, the accelerated aging test of the battery under the corresponding conditions was carried out.

Data such as degree, number of charge and discharge cycles and time are saved and recorded. The experiment was carried out for a month, and the 4th and 5th batteries were respectively charged and discharged cyclically. However, due to the failure of the experimental platform, the 4th battery was overcharged, resulting in damage to the internal mechanism of the battery, and it could not continue to charge. A total of 200 times were charged. Discharge, only 200 sets of data. It took nearly a year for the AA battery to complete 789 charge and discharge experiments. So far, the capacity of the battery has dropped to the failure value. The aging experiment of the battery has been completed, and a total of 789 sets of data have been obtained.

During stable discharge experiment, the data used is the lithium-ion battery data provided by the database prediction center (Kim et al., 2021). The data of the No. 5 lithium-ion battery during discharge situation is used as the basis for the experimental data. In data set No. 5, the first to fourth groups of discharge data are used as the training set of the model, the seventh group of discharge data is used for the accuracy estimation of the model, and the seventh group of discharge process data are as follows Figure 1.

FIGURE 1

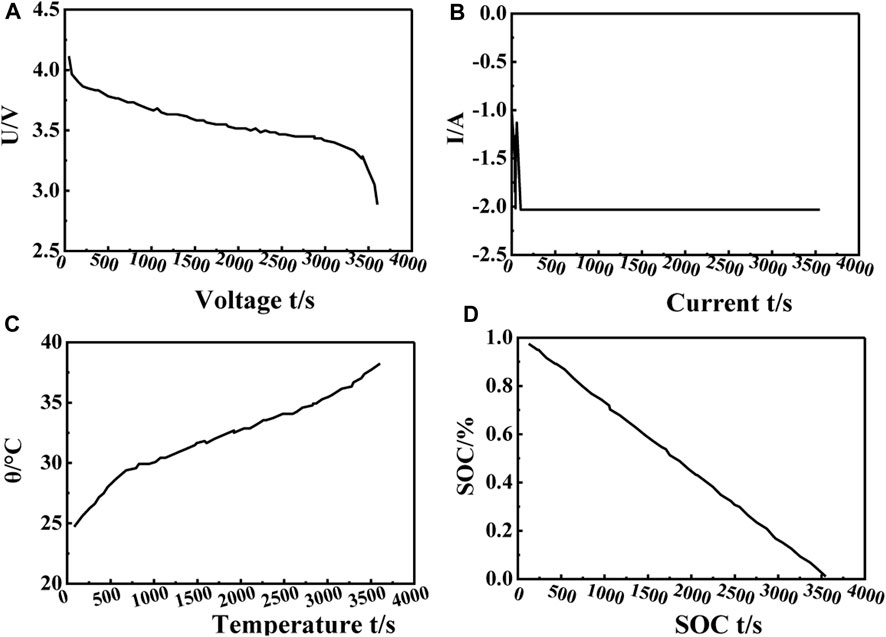
FIGURE 1. Discharge data. When the current is constant, the voltage drops slowly with time, and at 3500s, the voltage reaches 2.8 V. The temperature gradually increased with time, and the highest value could reach 3.7°C. The SOC value increases with time, from the initial 0.92 to 0 at 3500s

The battery voltage, current, and temperature are the characteristic input of the model, and the SOC value is the model output. The number of random forest trees is set to 500 (the test results show that the model is guaranteed to converge), and the randomly selected features are set to 2. In order to verify the evaluation performance of the random forest regression algorithm in the SOC reckoning scheme of lithium-ion batteries, the BP neural network and the T-S fuzzy neural network use the same parameters as the benchmark for comparison. The obtained sixth group of experimental prediction results and experimental errors are shown in Figure 2.

FIGURE 2

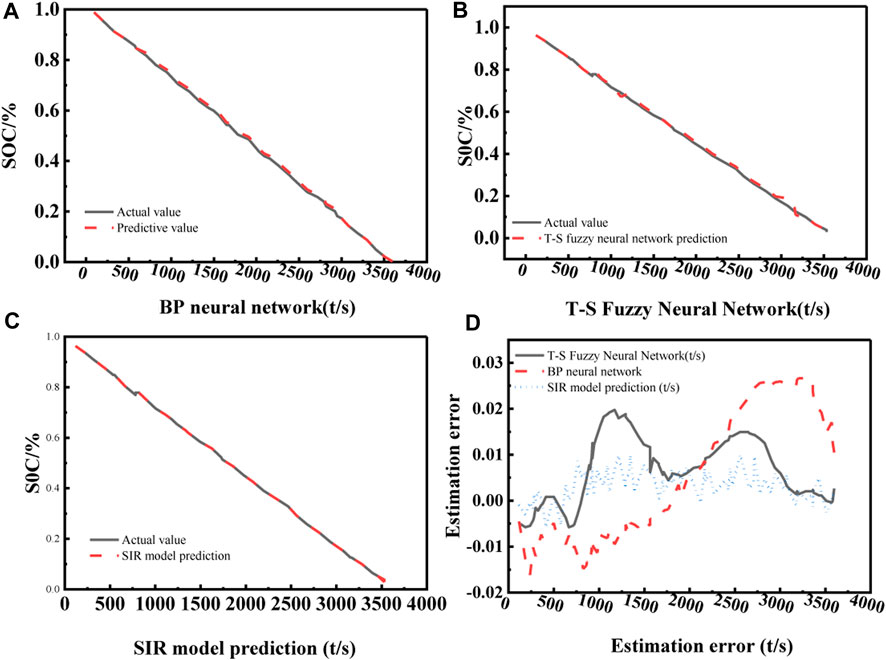
FIGURE 2. Prediction results of the sixth group of experiments. (A) the BP neural network has an error between the SOC prediction and the real value, but the value is small. Observing (B), it can be seen that the T-S fuzzy neural network has obvious errors at 3000s, indicating that there is a small gap with the real value. (C) shows the SIR model. The SOC prediction of the SIR model is almost close to the real value, and is basically in a coincident state. The SIR model can ensure that the error is within a certain range. It can be seen from (D) that the maximum estimation errors of the SIR model, BP neural network and T-S fuzzy neural network are 0.0189, 0.021, and 0.026, respectively. Through the simulation results of the MATLAB platform, it is concluded that the root mean square error (RMSE) of the SIR model, BP neural network and T-S fuzzy neural network are 0.003203, 0.044561, and 0.018213, respectively.

Figure 2 shows that the SIR model, BP neural network and T-S fuzzy neural network all have high estimation accuracy. Compared with the BP neural network and the T-S fuzzy neural network, the SOC prediction of the SIR model is almost close to the true value. The reckoning lapse of BP neural network and T-S fuzzy neural network is in a large range with the change of input vector, and the SIR model can assure that the lapse is within a certain range. Figure 2D shows that the maximum reckoning lapse of the SIR model, BP neural network and T-S fuzzy neural network are 0.0189, 0.021 and 0.026, respectively. Through the simulation results of the MATLAB platform, it is concluded that the root mean square error (RMSE) of the SIR model, BP neural network and T-S fuzzy neural network are 0.003203, 0.044561, and 0.018213, respectively.

The calculation error of the nuclear state of the lithium-ion battery calculated by the SIR model is shown in Figure 3. It can be seen from Figure 3 that with the increase of the number of iterations, the calculation error gradually becomes in a stable state, that is, to say, when the number of iterations reaches a certain number, the estimated error result will not be greatly improved.

FIGURE 3

FIGURE 3. Iterations and errors.

5 Discussion

The scheme for reckoning SOC of lithium-ion batteries should be studied in depth, because the parameters will change when the capacity fades and temperature changes, which allows the circuit parameters in the model to be adjusted as the conditions change, so that the static circuit model can be adjusted. Converting into a dynamic model, inevitably, this will increase the difficulty of the processor’s operation, and at the same time, more experiments are required as a basis, which also means that more manpower, material resources and time are required. In estimating SOC, there are many parameters that need to be measured, such as current and voltage. However, due to noise, electromagnetic interference and other factors, the accuracy of the measured value may be distorted, which will affect the estimated result. Improve the measurement accuracy as much as possible, and try to eliminate the influence of noise and other factors on it is the direction of future efforts.

6 Conclusion

This paper proposes a scheme for reckoning SOC of lithium-ion battery using the competitive SIR model, and compares the error value between the method proposed in this paper and the BP neural network and T-S fuzzy neural network method through experiments. The experimental results of the designed research show that:

1) We have compared the SIR model, BP neural network and T-S fuzzy neural network to reckon SOC of lithium-ion batteries, and concluded that the estimation error of the SIR model is the smallest compared to 0.0189. Through the simulation results of the MATLAB platform, it is concluded that the root mean square error of the SIR model is 0.003203.

2) Compared with BP neural network and T-S fuzzy neural network, the competitive SIR model has higher accuracy in estimating the battery charge; in the case of a limited number of estimated samples, the SIR model can effectively avoid the problem of overfitting.

3) The variable importance analysis of the SIR model can analyze the importance of the features, which can improve the accuracy of the parameters by improving the accuracy of the parameters when measuring the parameters, thereby improving the estimation accuracy of the results.

The method in this paper has higher accuracy and can avoid the probability of fitting problems. The competitive SIR model in this paper can be adopted to estimate SOC of lithium-ion batteries, which provides a reference for the model building of future lithium-ion battery charge reckoning systems.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

GX conceived the idea, completed the experiments and wrote the final manuscript.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, L., Wu, X., Lopes, A. M., Yin, L., and Li, P. (2022). Adaptive state-of-charge estimation of lithium-ion batteries based on square-root unscented Kalman filter. Energy 252, 123972. doi:10.1016/j.energy.2022.123972

CrossRef Full Text | Google Scholar

Chen, Z., Zhou, J., Zhou, F., and Xu, S. (2020). State-of-charge estimation of lithium-ion batteries based on improved H infinity filter algorithm and its novel equalization method. J. Clean. Prod. 290, 125180. doi:10.1016/j.jclepro.2020.125180

CrossRef Full Text | Google Scholar

Dey, S., Ayalew, B., and Pisu, P. (2015). Nonlinear robust observers for state-of-charge estimation of lithium-ion cells based on a reduced electrochemical model. Control systems technology. IEEE Trans.23, 1935–1942. doi:10.1109/TCST.2014.2382635

CrossRef Full Text | Google Scholar

Du, B., Yu, Z., Yi, S., He, Y., and Luo, Y. (2021). State-of-charge estimation for second-life lithium-ion batteries based on cell difference model and adaptive fading unscented Kalman filter algorithm. Int. J. Low-Carbon Technol. 16, 927–939. doi:10.1093/ijlct/ctab019

CrossRef Full Text | Google Scholar

Gholizadeh, M., and Salmasi, F. R. (2013). Estimation of state of charge, unknown nonlinearities, and state of health of a lithium-ion battery based on a comprehensive unobservable model. IEEE Trans. Ind. Electron. 61 (3), 1335–1344. doi:10.1109/tie.2013.2259779

CrossRef Full Text | Google Scholar

Hu, C., Cheng, F., Ma, L., and Li, B. (2022). State of charge estimation for lithium-ion batteries based on TCN-LSTM neural networks. J. Electrochem. Soc. 169, 030544. doi:10.1149/1945-7111/ac5cf2

CrossRef Full Text | Google Scholar

Hu, X., Yuan, H., Zou, C., Li, Z., and Zhang, L. (2018). Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order calculus. IEEE Trans. Veh. Technol. 67, 10319–10329. doi:10.1109/tvt.2018.2865664

CrossRef Full Text | Google Scholar

Jiang, Y., Song, W., Zhu, H., Zhu, Y., Du, Y., and Yin, H. (2022). Extended rauch–tung–striebel smoother for the state of charge estimation of lithium-ion batteries based on an enhanced circuit model. Energies 15, 963. doi:10.3390/en15030963

CrossRef Full Text | Google Scholar

Kim, W. Y., Lee, P. Y., Kim, J., and Kim, K. S. (2021). A robust state of charge estimation approach based on nonlinear battery cell model for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 70, 5638–5647. doi:10.1109/tvt.2021.3079934

CrossRef Full Text | Google Scholar

Le, S., Wu, Y., Guo, Y., and Del Vecchio, C. (2021). Game Theoretic Approach for a service function chain routing in NFV with coupled constraints. Circuits and Systems II: Express Briefs. IEEE Trans.68, 3557–3561. doi:10.1109/TCSII.2021.3070025

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D., and Cheng, Q. (2021). Short-term nacelle orientation forecasting using bilinear transformation and ICEEMDAN framework. Front. Energy Res. 9, 780928. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. (2021). Monitoring and identifying wind turbine generator bearing faults using deep belief network and EWMA control charts. Front. Energy Res. 9, 799039. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Liu, Y., Li, J., Zhang, G., Hua, B., and Xiong, N. (2021). State of charge estimation of lithium-ion batteries based on temporal convolutional network and transfer learning. IEEE Access 9, 34177–34187. doi:10.1109/access.2021.3057371

CrossRef Full Text | Google Scholar

Mitsuru, T, and Yuhu, W (2019). Mayer-type optimal control of probabilistic boolean control network with uncertain selection probabilities. IEEE Trans. Cybern. 51, 3079–3092. doi:10.1109/tcyb.2019.2954849

CrossRef Full Text | Google Scholar

Sakile, R., and Sinha, U. K. (2021). Estimation of state of charge and state of health of lithium-ion batteries based on a new adaptive nonlinear observer. Adv. Theory Simul. 4 (11), 2100258. doi:10.1002/adts.202100258

CrossRef Full Text | Google Scholar

Tian, Y., Huang, Z., Tian, J., and Li, X. (2022). State of charge estimation of lithium-ion batteries based on cubature Kalman filters with different matrix decomposition strategies. Energy 238, 121917. doi:10.1016/j.energy.2021.121917

CrossRef Full Text | Google Scholar

Vo, T. T., Chen, X., Shen, W., and Kapoor, A. (2015). New charging strategy for lithium-ion batteries based on the integration of Taguchi method and state of charge estimation. J. Power Sources 273, 413–422. doi:10.1016/j.jpowsour.2014.09.108

CrossRef Full Text | Google Scholar

Wu, Y., Guo, Y., and Toyoda, M. (2021). Policy iteration approach to the infinite horizon average optimal control of probabilistic boolean networks. IEEE Trans. Neural Netw. Learn. Syst. 32, 2910–2924. doi:10.1109/tnnls.2020.3008960

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, J., Ma, J., and Bai, K. (2018). Enhanced Coulomb counting method for state-of-charge estimation of lithium-ion batteries based on peukert's law and coulombic efficiency. J. POWER Electron. 18 (3), 910–922. doi:10.6113/JPE.2018.18.3.910

CrossRef Full Text | Google Scholar

Xiong, R., Wang, J., Shen, W., Tian, J., and Mu, H. (2021). Co-estimation of state of charge and capacity for lithium-ion batteries with multi-stage model fusion method. Engineering 7, 1469–1482. doi:10.1016/j.eng.2020.10.022

CrossRef Full Text | Google Scholar

Xu, J., Mi, C. C., Cao, B., Deng, J., Chen, Z., and Li, S. (2014). The state of charge estimation of lithium-ion batteries based on a proportional-integral observer. IEEE Trans. Veh. Technol. 63, 1614–1621. doi:10.1109/tvt.2013.2287375

CrossRef Full Text | Google Scholar

Ya-Xiong, G. U., and Zhang, Y. J. (2016). Estimation of state of charge of lithium-ion battery based on dual extend Kalman filter. Chin. J. Power Sources.

Google Scholar

Yang, B., Wang, Y., and Gao, H. (2021). State-of-charge estimation of lithium-ion batteries based on PSO-BP neural network. Sci. Publ. Group 10 (6), 115–120. doi:10.11648/j.ijepe.20211006.13

CrossRef Full Text | Google Scholar

Yang, K., Tang, Y., Zhang, S., and Zhang, Z. (2022). A deep learning approach to state of charge estimation of lithium-ion batteries based on dual-stage attention mechanism. Energy 244, 123233. doi:10.1016/j.energy.2022.123233

CrossRef Full Text | Google Scholar

Zhang, C., Li, K., Pei, L., and Zhu, C. (2015). An integrated approach for real-time model-based state-of-charge estimation of lithium-ion batteries. J. Power Sources 283 (1), 24–36. doi:10.1016/j.jpowsour.2015.02.099

CrossRef Full Text | Google Scholar

Zhang, C., Wang, L. Y., Li, X., Chen, W., Yin, G. G., and Jiang, J. (2015). Robust and adaptive estimation of state of charge for lithium-ion batteries. IEEE Trans. Ind. Electron. 62 (8), 4948–4957. doi:10.1109/tie.2015.2403796

CrossRef Full Text | Google Scholar

Zhang, Y., Qian, T., and Tang, W. (2022). Buildings-to-distribution-network integration considering power transformer loading capability and distribution network reconfiguration. Energy 244, 123104. doi:10.1016/j.energy.2022.123104

CrossRef Full Text | Google Scholar

Zheng, L., Zhang, L., Zhu, J., Wang, G., and Jiang, J. (2016). Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model. Appl. Energy 180 (15), 424–434. doi:10.1016/j.apenergy.2016.08.016

CrossRef Full Text | Google Scholar

Zou, Z., Xu, J., Mi, C., Cao, B., and Chen, Z. (2014). Evaluation of model based state of charge estimation methods for lithium-ion batteries. Energies 7 (8), 5065–5082. doi:10.3390/en7085065

CrossRef Full Text | Google Scholar