
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 31 August 2022
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.979938
The steel plant integrated energy system (SPIES) is an important form in the steel industry. Improving the utilization efficiency of steam, electricity, coal gas and other energy flows is of great significance for both economic and environmental benefits. In this paper, a SPIES scheduling model is established according to the operation characteristics of coal gas holders, boilers and other equipment in steel plants. Meanwhile, to cope with the uncertainty of byproduct coal gas, this paper adopts an imprecise Dirichlet model (IDM) to construct a fuzzy set containing multisource coal gas production information. Then, according to duality theory and the big-M method, the original distributed robust optimization (DRO) model is transformed into a traditional mixed integer linear programming (MILP) model, which is solved by the column-and-constraint generation (CC&G) algorithm. Finally, a real steel production system is given in a case study. Case study illustrate that compared with the traditional robust method, the method proposed in this paper for a SPIES can effectively reduce the conservatism of the scheduling decision. Numerical simulation show that the proposed method can reduce total cost by 55,307.1¥, accounting for 1.91% of the total cost compared with robust optimization method and save 1,326.94 s of computational time compared with the stochastic optimization method, thus reaching balance between conservatism and computational efficiency.
With the wide application of renewable energy power generation technologies, integrated energy systems (IESs) is of great significance for improving energy efficiency, realizing the complementary and coupling operation between various energy flows, thus peaking carbon dioxide emissions and achieving carbon neutrality (Wang et al., 2022)- (Clegg and Mancarella, 2016). However, the uncertainty and complex coupling relationship between multiple energy sources make it difficult to solve IESs optimal scheduling problem quickly and accurately. Therefore, it is of realistic importance to study the accurate and intelligent optimal scheduling decision-making method of IESs (Mo et al., 2022).
In this backdrop, some scholars have carried out research around IESs. Most of existing research objects of IESs mainly focus on buildings (Hannan et al., 2018), parks (Chen et al., 2020) and large communities (Ma et al., 2019). But large industrial loads are often ignored. Among them, steel industry in China has developed very quickly, along with the durative and steady growth of the national economy. Compared with the above objects, steel plants have more diversified production modes and intensive energy consumption. In the industrial process of iron and steel production, a large number of secondary energy source can be reused, including blast furnace gas (BFG), coke oven gas (COG), Linz Donawitz process gas (LDG) and steam, accounting for approximately 50%–60% of the total energy consumption of steel plants, which indicate great utilization potential (Li et al., 2021)- (He et al., 2015). Therefore, establishing an IES model for steel plant and scheduling the multi-coupling energy flow in the plant will significantly improve the economic and environmental benefits. Current researches on the energy management for steel plants mainly focus on single energy flow scheduling. From the perspective of coal gas scheduling, reference (Xia et al., 2016) uses a multi-step optimization algorithm to solve the coal gas scheduling problem in steel plants, which effectively improves the utilization efficiency of coal gas; (Wang et al., 2013) proposed a hierarchical scheduling method for coal gas in energy-intensive enterprises and solved it online in real time using the simplex method. On the other hand, some literature analyzed the electrical power consumption behavior of steel plant. In (Jin et al., 2017)- (Chen et al., 2015), considering the production privacy of enterprises and the uncertainty of renewable energy output, steel plant can be seen as flexible and adjustable resources in the area of demand response. Through the electricity price incentive signal, they are guided to participate in the consumption of new energy and peak shaving ancillary services, effectively alleviating the pressure on the power supply and demand of the regional power system. Meanwhile, energy management mathematical model in the power system or industrial production processes was complex, especially including some unilinear parts or integer variables. To overcome this issue, some intelligence methods have been applied in energy system, for example, tree-seed algorithm proposed in (Kiran and Yunusova, 2022) was investigated on the long-term energy estimation model of Turkey and (Dehghani et al., 2019) illustrated the current status of each biofuel technologies and demonstrating each trend with using the technology life cycle, which avoid unreasonable energy production and inefficient energy use.
However, the abovementioned strategies do not consider the uncertainty of byproduct coal gas. In fact, the uncertainty of the coal gas production in steel plants mainly comes from the following two aspects: 1) In the process of coal gas generation, storage and transmission, coal gas needs to go through the pipe network, gas holder, etc. There are many pieces of measuring equipment installed in each link, causing inevitable measurement errors between the general meter and submeter, even as high as 10%–20% (Xuan et al., 2020). 2) The production of coal gas is closely related to the production equipment status. Affected by the adjustment of the production and maintenance plan, the production of coal gas will fluctuate accordingly. In addition, the production of gas is also affected by the external environment, such as pressure and temperature, which all lead to uncertainty of the gas production (Sun et al., 2019). If the coal gas production uncertainty is ignored, it will lead to an increase in coal gas discharge loss and a reduction in the economic benefits, which is not conducive to the long-term development of steel plants.
Therefore, it is necessary to consider the uncertainty of byproduct coal gas when formulating a steel plant integrated energy system (SPIES) scheduling strategy. The mature methods dealing with uncertainty mainly include robust optimization (RO) (Kamwa et al., 2000)- (Niu et al., 2019) and stochastic optimization (SO) (Liu et al., 2016)- (Garcia-Torres et al., 2021). RO can ensure that a feasible solution exists under the worst scenario, but the final solution tends to be conservative; SO obtains the optimization strategy by obtaining the probability distribution of uncertain parameters. SO can satisfy the existence of feasible solutions under some scenarios. Compared with RO, SO reduces the conservatism of feasible solutions and improves the economy of the scheduling scheme. However, in practice, it is difficult to obtain the probability distribution of uncertainty directly, and scenario selection increases the computational complexity. DRO combines the advantages of RO and SO and achieves a balance between robustness and economy, and it has been widely used in the optimal dispatching of IESs (Huang et al., 2022)- (Zhou et al., 2020). By constructing fuzzy sets, DRO only needs partial probability distribution information for uncertain variables. According to the different methods for constructing fuzzy sets, DRO can be divided into moment uncertainty-based DRO models and probability distance-based DRO models. The former usually uses expectation and covariance to describe the distribution characteristics of samples, and the constructed uncertain probability distribution confidence set cannot converge to the real distribution, resulting in the accuracy deviation of the final result (Wang et al., 2016); the latter, represented by Kullback-Leibler divergence and Wasserstein probability distance, uses normal form distance to describe the difference size of elements in the set, and the result is still conservative (Chen et al., 2018).
To overcome these issues and make full use of byproduct coal gas, a DRO scheduling method considering the byproduct coal gas uncertainty is proposed in this paper. The contributions of this paper can be summarized as follow: 1). Different from previous studies that only focus on single energy flow in the steel plant, this paper establishes a detailed SPIES mathematical model, which fully considers the coupling relationship between various energy flows, thus avoiding unreasonable energy production and ineffectual energy use; 2). In this paper, a distributed robust optimization model of SPIES is given, which takes into account the multiple production uncertainties of coal gas. Compared with the traditional RO and SO methods, this paper uses the imprecise Dirichlet model (IDM) to construct fuzzy set, which not only ensures the safe operation of the system, but also reduces the conservatism of scheduling decisions.
The remainder of the paper is organized as follows. First, the SPIES operation framework is given. Then, an IDM method is adopted to construct the cumulative distribution function (CDF) of coal gas production, and the fuzzy set is mapped to the upper and lower bounds of the uncertainty model. Next, a two-stage DRO scheduling model for a SPIES is established. The initial model with bilinear terms is transformed into MILP form using dual theory and the big-M method, and the CC&G algorithm is introduced to improve the solution efficiency. Finally, the feasibility of the proposed method is verified by an actual steel plant.
Figure 1 shows the SPIES operation framework, which is composed of a gas system, steam system and power system. Among them, the gas system mainly includes a blast furnace, coke oven, converter and coal gas holder. The gas holder is responsible for the storage and release of coal gas. When the gas production exceeds a certain threshold, to ensure the pressure safety of the pipe and maintain the dynamic balance of the coal gas, the excess gas should be released. The steam system mainly produces enough steam with a certain enthalpy and pressure to meet the steam demand of vaporization cooling, steel rolling and other production links. The steel plant usually owns a self-serviced power plant, which can provide power for plant and load in the industrial park distribution network. Meanwhile, steel plant can adjust power generation according to electricity price information, production demand and tie line power constraints, and surplus power can be sold to the main network to obtain a profit.
Meanwhile, considering that the mathematical model of SPIES is extremely complex, a detailed nomenclature is provided below to help the readers gain a better understanding.
In this paper, an imprecise Dirichlet model (IDM) is used to construct fuzzy sets for DRO. Compared with the deterministic Dirichlet model, the IDM adopts a set of prior density functions for parameter estimation, which overcomes the problem of parameter estimation deviation caused by the traditional Dirichlet model using a single density function under limited data samples. The specific principle is briefly described as follows.
For event
According to the principle of Bayesian statistics, the prior Dirichlet probability density function of event state probability can be written in the form shown in Eq. 3.
After obtaining the observed value of the Mth sample, the posterior Dirichlet probability density function about the event state probability is derived, as shown as follows in Eq. 5:
In (5),
Obviously, the maximum and minimum values of
When the system operators give the confidence
Here, H represents the cumulative distribution function (CDF) of the beta distribution with
Here,
The uncertain variables considered in this paper are the production of BFG, COG and LDG. The gas production fuzzy set is constructed by using historical data samples and the IDM method mentioned above, and then the gas production uncertainty interval can be determined by the given confidence level. After obtaining the interval, the gas production uncertainty set is constructed according to the box model shown in Eq. 11.In Eq. 11,
As shown in Figure 2, the SPIES DRO scheduling framework considering of byproduct coal gas uncertainty is mainly composed of two parts. The first part is based on the day-ahead scheduling stage, with the goal of minimizing the total scheduling cost. The second part is the real-time rescheduling stage, in which units and equipment can be readjusted to cope with the gas production uncertainty. It should be noted that the SPIES needs to send the power purchase and sale information to the upper power grid in the day-ahead stage, i.e., the electricity sale and buy quantity are determined in the day-ahead stage and remain unchanged in the real-time stage. Therefore, the SPIES DRO mathematical model can be written in the general form shown in Eq. 12.
The objective function of the day-ahead scheduling model is shown in Eq. 13.
Here, Cost(G) is the position adjustment cost of the gas holder; Cost(F) is the total combustion cost of gas and coal; Cost(P) is the cost of purchasing and selling electricity; Cost(S) is the production cost of steam; Cost(R) is the compensation cost of steam and electricity demand response. Steam S1 represents high-pressure steam with a pressure value of 2.5–3.5 Mpa and steam S2 represents medium-pressure steam with pressure value of 0.8–1.3 Mpa.
It should be noted that the position adjustment of the gas holder can effectively improve the pressure distribution of the pipe network and plays an important role in ensuring the stable supply of gas. However, due to the existence of adjustment capacity and safety constraints, the position offset from the central position should not be too large. Therefore, this paper describes the relationship between the adjustment cost and position offset of a coal gas holder by the piecewise linearization method. As shown in Figure 3, the gas holder position is divided into five levels, representing the lowest position
In the day-ahead stage, the production constraints and some other physical constraints of boilers Eqs. 14–19 are mainly considered.
Here, Eq. 14 represents the steam production constraint; Eq. 15 represents the climbing constraint of the boilers; Eqs 16, 17 represent the gas consumption and regulation constraints of each boiler; Eq. 18 represents the energy balance constraint and Eq. 19 represents the calorific value constraint of mixed coal gas.
For combined heat and power (CHP) units, the day ahead scheduling constraints include the following:
As mentioned above, the SPIES power generation not only provides the power needed by the equipment and industrial processes in the plant but also needs to supply power to the distribution network of the external park. To simplify the distribution power flow calculation process, this paper adopts the second-order cone relaxation method shown as follows in Eqs 28–32:
In addition, the dynamic balance constraints of various energy flows need to be considered, including Eqs 33–36:
Eq. 33 represents the dynamic production and consumption balance of the three types of coal gas; Eq. 34 represents the dynamic balance of steam; Eq. 35 represents the power balance; Eq. 36 represents the power purchase and sale status constraint, i.e., the SPIES cannot purchase and sell power at the same time.
To reduce the discharge loss of byproduct coal gas caused by uncertainty in the real-time stage, it is necessary to make real-time adjustments on the basis of day-ahead scheduling. The objective function of this stage is given in Eq. 37.
Objective Eq. 37 minimizes the sum of the depreciation cost of the units Costadj(F), the penalty cost of gas discharge loss Costadj(D), the readjustment cost of the gas holder Costadj(G) and the compensation cost for the demand response of the steam/electric load Costadj(R).
The constraints in the real-time rescheduling stage are similar to those in the day-ahead scheduling stage, mainly including steam/power production constraints, ramping constraints, energy balance constraints of controllable units, etc. The difference is that, as shown in Eq. 38, the value of the decision variable y in the real-time rescheduling stage should be the sum of the decision variable xc in the day-ahead stage and the adjustment amount
On the other hand, according to the uncertainty description method in Section 3, the IDM method and uncertainty interval transformation are adopted to modify the coal gas production and consumption dynamic balance constraint Eq. 33 into the form shown in Eq. 39.
Solving the full problem of two-stage DRO directly is very difficult. In order to solve the practical large scale problem, CC&G algorithm is introduced. For the convenience of explanation, the form shown in Eq. 12 is extended to a general DRO model with a coefficient matrix, as shown as follows in Eq. 40:
In (40), c, d and e represent the coefficient matrix in the objective function; A, B, C, D, E, F and G represent the coefficients in the constraints; and H, I, J and K represent the constant terms of the corresponding constraints, and the specific values can be obtained by Eqs 13–39. Among them, A, C and E represent the variable coefficient matrix of equality constraints, and H and J represent the constant matrix of equality constraints; B, E, F, and G represent the variable coefficient matrix of equality constraints, and I, K represent the constant matrix of inequality constraints. The determination of each matrix needs to consider the types of variables contained in the constraints.
Obviously, the variables in the DRO model Eq. 40 are mutually coupled and cannot be solved directly. Therefore, the CC&G algorithm (Zhou et al., 2020) is adopted in this paper to decompose the original problem Eq. 40 into a master problem (MP) and a slave problem (SP), i.e., Eqs 41,42.
In 41) and (42),
Eq. 43 contains the bilinear term
After the above transformation, the SP is transformed into a MILP model. Finally, through the iterative solution of the MP and SP, the final results can be obtained, and the flow chart of the CC&G algorithm is given in Figure 4 below.
In this paper, a real steel plant is used for a case study, and the IEEE-33 node test system is integrated as the park distribution network. The detailed system topology is shown in Figure 5. The scheduling cycle is 24 h. Detailed information about the parameters of each unit, coal gas production prediction curve, power/steam demand curve and time-of-use (TOU) price are given in the Tables 1–5; Supplementary Material S1. The conservative parameter of uncertainty
Figure 6 shows the operation state of each piece of equipment under the day-ahead scheduling stage. In the SPIES, the CHP unit is mainly responsible for steam production and power supply, so its BFG and COG consumption amounts are the largest. The LDG and coal consumption of the CHP unit are complementary because the cost of LDG is lower than the cost of purchased coal, i.e., when LDG production is high, the CHP unit reduces coal consumption to make profits. Similarly, when the production of LDG is low, the purchased coal is used to guarantee the production demand. Figure 6 1) shows the consumption of BFG. BFG consumption of 130 t boiler and start-up boiler changes with coal gas production fluctuation. Comparing the BFG and COG consumption of the 130 t boiler in Figures 6A,B, it can be found that their consumption basically shows a complementary trend to achieve the efficient utilization of coal gas. Obviously, CHP unit consumes the most BFG and COG, and the consumption remains at a stable level for most of the time. This is because the production task of CHP unit is heavy, and it is necessary to take into account both power production and steam production, which need to consume a great amount of coal gas. It can also be seen from Figure 6D that the gas holder position is basically maintained near the central gas holder position
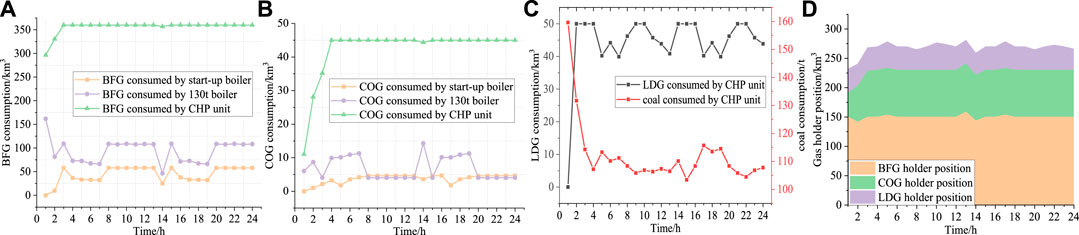
FIGURE 6. The operation status of each piece of equipment under day-ahead scheduling. (A): Consumption of BFG (B): Consumption of COG (C): Consumption of LDG and coal (D): Gas holder position.
Affected by the production state of the blast furnace, coke oven and converter and the measurement error of the monitoring equipment, there is a certain difference between the actual gas production and predicted gas production. Under the uncertainty of byproduct coal gas, the operation status of each piece of equipment needs to be adjusted in the real-time rescheduling stage. The specific results of this stage are shown in Figure 7. Figure 7A shows the adjustment of BFG. Compared with the other two types of coal gas, BFG has the maximum yield, so its adjustment amount in the real-time stage is also the largest. Figure 7B and Figure 7C show that a large regulation fluctuation occurred at 0:00–2:00 for controllable units that consume COG and LDG. This is mainly because during this period of time, the production status of the coke oven and that of the converter change sharply due to the production task adjustment of the next day, resulting in large fluctuations in the corresponding byproduct coal gas production. As shown in Figure 7D, at the beginning and end of the day, the adjustment range of the COG gas holder position and that of the LDG gas holder position are also large to reduce the negative impact of production fluctuation and coordinate controllable units to ensure gas supply and system safety.
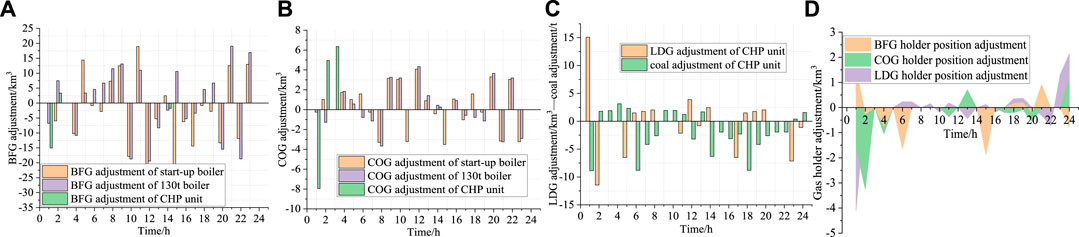
FIGURE 7. The operation status of each piece of equipment under real-time rescheduling. (A): Adjustment of BFG (B): Adjustment of COG (C): Adjustment of LDG and coal (D): Adjustment of the gas holder position.
The SPIES also carries the burden of responsibility to meet the power demand of the park distribution network. Figure 8 shows the power supply information from the SPIES to the park distribution network and the power sales information to the upper power grid. It should be noted that the maximum amount of electricity provided to the park distribution network during 8–10 h and 16–20 h is 12.75MW, which is determined by transmission power constraints of the tie line. Since the unit power generation cost of the SPIES in this paper is lower than the unit power purchase cost of the power grid, the power generation amount of the SPIES can meet its own industrial production demand and it is always in the state of electricity selling, which is consistent with the actual situation. In fact, steel plants, electrolytic aluminum plants and other energy-intensive enterprises tend to own self-served power plants to reduce the cost of purchasing power. Meanwhile, excess electric energy will be sold to the upper power grid. The SPIES will increase electricity sales during periods when the electricity sales price is high, such as 8–10 h and 16–20 h, to obtain more profits.
To further illustrate the effectiveness of the proposed method, other methods, including the deterministic programming method (DP), RO method, and SO method, are used for comparison. It should be noted that the value range of
Table 7 shows that the IDM method adopted in this paper can fully explore the potential of limited historical data samples. With the increasing number of samples, the cost of day-ahead scheduling and real-time rescheduling decreases and gradually approaches the total cost of the SO method. With the IDM method, it is not necessary to determine or assume the specific probability distribution type of uncertainty, especially when the number of samples is small, and its advantages are more outstanding. When the number of samples is less than 1,000, the decreasing trend of the total cost is very obvious; when the number of samples exceeds 1,000, the decreasing trend of the total cost gradually slows down, which also shows that this method can meet the requirement of small sample data analysis and improve the applicability. On the other hand, under different sample numbers, the total calculation time does not fluctuate greatly and basically remains within 100 s, which shows the efficiency of the CC&G algorithm.
Meanwhile, the value of the conservative parameter
Considering the uncertainty of byproduct coal gas production, a DRO scheduling model for SPIES is established, including day-ahead scheduling stage and real-time rescheduling stage. First, the fuzzy set of byproduct coal gas production is constructed by the IDM method, which is equivalent to the deterministic interval of production. Then, the CC&G algorithm is adopted to improve the solving efficiency. Finally, the following conclusions are drawn through the case study:
(1) The IDM method can accurately describe the uncertainty of coal gas production. When the data samples are small or the specific distribution of variables is unknown, the advantages of the proposed method are more obvious. In case study part, the solution results under different data samples are analyzed. In general, the more data samples, the less the total cost. When the number of samples is 200, the total cost is 2,834,843.9¥; when the number of samples is 2,500, the total cost is 2,829,942.0¥, which reduces total cost by 4,901.9¥. This also means that this method can meet the requirement of small sample data analysis and improve the applicability.
(2) Compared with the RO method and the SO method, the proposed DRO method can take into account the advantages of both, that is, it strikes a balance between the robustness of the RO method and the computational complexity of the SO method and controls the solution time within 100 s. More specifically, compared with the traditional RO method, method proposed in this paper reduces total cost by 55,307.1¥, accounting for 1.91% of the total cost. In addition, the proposed method can effectively reduce the computational complexity. Computational time of the proposed method is slightly longer than the traditional RO method but far faster than the SO method and saves 1,326.94 s compared to the SO method. Meanwhile, when the number of data samples is larger than 1,000, the total cost of the method proposed will continue to approach the total cost of the SO method, thus improving the practicability of the model.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
FL and TN designed the experiments, research methods. TN performed the format analysis. The tools analysis, data processing, and writing the original draft were carried out by FL. YL solved the application problem of research methods. SF performed the writing-review on references. WW contributed to proof reading and project/organization management. All authors have read and agreed to the published version of the manuscript.
This work is supported by the National Natural Science Foundation of China (under grant no. 52007017).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.979938/full#supplementary-material
Chen, R., Sun, H., Guo, Q., Jin, H., Wu, W., and Zhang, B. (2015). Profit-seeking energy-intensive enterprises participating in power system scheduling: Model and mechanism. Appl. Energy 158, 263–274. doi:10.1016/j.apenergy.2015.08.018
Chen, Y., Guo, Q., Sun, H., Li, Z., Wu, W., and Li, Z. (2018). A distributionally robust optimization model for unit commitment based on kullback–leibler divergence. IEEE Trans. Power Syst. 33, 5147–5160. doi:10.1109/TPWRS.2018.2797069
Chen, Z., Sun, Y., Ai, X., Malik, S. M., and Yang, L. (2020). Integrated demand response characteristics of industrial park: A review. J. Mod. Power Syst. Cle. 8, 15–26. doi:10.35833/MPCE.2018.000776
Clegg, S., and Mancarella, P. (2016). Integrated electrical and gas network flexibility assessment in low-carbon multi-energy systems. IEEE Trans. Sustain. Energy 7, 718–731. doi:10.1109/TSTE.2015.2497329
Dehghani, M., Alireza, A., Mohammad, H., and Narjes, S. (2019). Current status and future forecasting of biofuels technology development. Int. J. Energy Res. 43, 1142–1160. doi:10.1002/er.4344
Garcia-Torres, F., Bordons, C., Tobajas, J., Real-Calvo, R., Santiago, I., and Grieu, S. (2021). Stochastic optimization of microgrids with hybrid energy storage systems for grid flexibility services considering energy forecast uncertainties. IEEE Trans. Power Syst. 36, 5537–5547. doi:10.1109/TPWRS.2021.3071867
Hannan, M. A., Faisal, M., Ker, P. J., Mun, L. H., Parvin, K., Mahlia, T. M. I., et al. (2018). A review of internet of energy based building energy management systems: Issues and recommendations. IEEE Access 6, 38997–39014. doi:10.1109/ACCESS.2018.2852811
He, K., Zhu, H., and Wang, L. (2015). A new coal gas utilization mode in China’s steel industry and its effect on power grid balancing and emission reduction. Appl. Energy 154, 644–650. doi:10.1016/j.apenergy.2015.05.022
Huang, B., Li, Y., Zhan, F., Sun, Q., and Zhang, H. (2022). A distributed robust economic dispatch strategy for integrated energy system considering cyber-attacks. IEEE Trans. Ind. Inf. 18, 880–890. doi:10.1109/TII.2021.3077509
Jin, H., Li, Z., Sun, H., Guo, Q., Chen, R., and Wang, B. (2017). A robust aggregate model and the two-stage solution method to incorporate energy intensive enterprises in power system unit commitment. Appl. Energy 206, 1364–1378. doi:10.1016/j.apenergy.2017.10.004
Kamwa, I., Trudel, G., and Gerin-Lajoie, L. (2000). Robust design and coordination of multiple damping controllers using nonlinear constrained optimization. IEEE Trans. Power Syst. 15, 1084–1092. doi:10.1109/59.871737
Kiran, M. S., and Yunusova, P. (2022). Tree-seed programming for modelling of Turkey electricity energy demand. Int. J. Intel. Syst. Appl. Engin. 10, 142–152. doi:10.18201/ijisae.2022.278
Li, F., Chu, M., Tang, J., Liu, Z., Zhou, Y., and Wang, J. (2021). Exergy analysis of hydrogen-reduction based steel production with coal gasification-shaft furnace-electric furnace process. Int. J. Hydrogen Energy 46, 12771–12783. doi:10.1016/j.ijhydene.2021.01.083
Lin, L., Fei, H., Liu, R., and Pan, X. (2018). A regional wind power typical scenarios’ selection method based on hierarchical clustering algorithm. Power Syst. Prot. Cont. 46, 1–6. doi:10.7667/PSPC170454
Liu, C., Lee, C., Chen, H., and Mehrotra, S. (2016). Stochastic robust mathematical programming model for power system optimization. IEEE Trans. Power Syst. 31, 821–822. doi:10.1109/TPWRS.2015.2394320
Ma, L., Liu, N., Zhang, J., and Wang, L. (2019). Real-time rolling horizon energy management for the energy-hub-coordinated prosumer community from a cooperative perspective. IEEE Trans. Power Syst. 34, 1227–1242. doi:10.1109/TPWRS.2018.2877236
Mo, L., Xin, L., Chen, H., Zhao, Z., Chen, J., and Deng, Z. (2022). An analysis and evaluation method of park integrated energy system based on energy economics. Front. Energy Res. early access. doi:10.3389/fenrg.2022.968102
Niu, T., Guo, Q., Sun, H., Wang, B., and Zhang, B. (2019). Robust voltage control strategy for hybrid AC/DC sending-side systems to prevent cascading trip failures. IEEE Trans. Sustain. Energy 10, 1319–1329. doi:10.1109/TSTE.2018.2865795
Sun, X., Hu, J., and Wang, Z. (2019). Fuzzy optimization model for by-product gas scheduling in iron and steel making process. Indus. Saf. Envi. Prot. 45, 1–5. doi:10.3969/j.issn.1001-425X.2019.06.024
Walley, P. (1996). Inferences from multinomial data: Learning about a bag of marbles. J. R. Stat. Soc. Ser. B 58, 3–34. doi:10.1111/j.2517-6161.1996.tb02065.x
Wang, B., Lei, Z., Li, X., and Yin, Y. (2013). Research of optimizing and modeling of gas scheduling system in iron and steel enterprises. Cont. Engin. China 20, 13–17. doi:10.14107/j.cnki.kzgc.2013.01.003
Wang, Z., Wang, S., Feng, W., and Fu, Y. (2016). “The study on estimation of unknown parameters for uncertainty distribution,” in Proceeding of the 2016 International Conference on Information System and Artificial Intelligence (ISAI), Hong Kong, China, June 2016 (IEEE), 503–508.
Wang, Z., Zhu, Z., Xiao, G., Bai, B., and Zhang, Y. (2022). A transformer-based multi-entity load forecasting method for integrated energy systems. Front. Energy Res. 10, 952420. doi:10.3389/fenrg.2022.952420
Xia, X., Gao, Z., Xu, F., Zheng, T., and Dai, Z. (2016). Gas scheduling based generation dispatching of self-provided power plants for energy-intensive enterprises. Autom. Elect. Power Syst. 40, 160–167. doi:10.7500/AEPS20160428007
Xuan, W., Haoze, Y., and Cantao, S. (2020). Analysis on the realization path of gas prediction and optimal scheduling in iron and steel enterprises. Available at: http://www.csteelnews.com/sjzx/hyyj/202006/t20200611_33453.html.
Zhou, H., Li, Z., Zheng, J., Wu, Q., and Zhang, H. (2020). Robust scheduling of integrated electricity and heating system hedging heating network uncertainties. IEEE Trans. Smart Grid 11, 1543–1555. doi:10.1109/TSG.2019.2940031
Keywords: steel plant integrated energy system, distributed robust optimization, imprecise dirichlet model, MILP model, column-and-constraint generation algorithm
Citation: Li F, Li Y, Niu T, Fang S and Wu W (2022) Distributed robust optimization scheduling of a steel plant integrated energy system considering the uncertainty of byproduct coal gas. Front. Energy Res. 10:979938. doi: 10.3389/fenrg.2022.979938
Received: 28 June 2022; Accepted: 01 August 2022;
Published: 31 August 2022.
Edited by:
Thomas Alan Adams, McMaster University, CanadaReviewed by:
Mohammad Hossein Ahmadi, Shahrood University of Technology, IranCopyright © 2022 Li, Li, Niu, Fang and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tao Niu, bml1dHRodUBjcXUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.