Applying the natural transform iterative technique for fractional high-dimension equations of acoustic waves

In the present study, the natural transform iterative method (NTIM) has been implemented for the solution of a fractional Zakharavo–Kuznetsov (FZK) equation. NTIM is a relatively new technique for handling non-linear fractional differential equations. The method is tested upon the two non-linear FZK equalities. The solution of the proposed technique has been compared with the existing perturbation–iteration algorithm (PIA) method and residual power series method (RPSM). From the numerical results, it is clear that the method handles non-linear differential equations very suitably and provides the results in very closed accord with the accurate solution. As a result, the NTIM approach is regarded as one of the finest analytical techniques for solving fractional-order linear and non-linear problems.

1 Introduction

Entropy and fractional calculus are appealing concepts that are increasingly being used to investigate the dynamics of complicated systems. Fractional calculus (FC) has been increasingly used in numerous sectors of research in recent years. Fractional differential equalities (FDEs) efficiently depict the natural evolution associated with viscoelasticity, models of porous electrodes, thermal stresses, electromagnetism, energy transmission in viscous dissipation systems, relaxing oscillations, and thermoelasticity. Most of the mathematical models are obtained through real-world problems which can be modeled via differential equations of the integer order or of the fractional order. The differential equations may arise in diverse areas of technological sciences and biological sciences. In engineering sciences, they may be in the field of fluid dynamics, aerodynamics, the nuclear decay, climate changes, electronic circuits, etc. In biosciences, these models may be of the blood flow, population growth, and decay problems of some kind of species of organisms like bacteria or virus and may be the study of some rate of flow of some gas models or may be the concentration control of some liquids in some other liquids. Similarly, differential equations may also model some problems related to social sciences as in the fields of banking and finance. The customer may be satisfied by preparing a fractional model of interest or premium according to the required efforts of a person. Fractional calculus plays an essential role in these kinds of problems.

Fractional calculation is the generalization of the classical calculus which is an ancient branch of mathematics. The fractional calculus received much more attention of researchers during the last few decades. Fractional calculus has great achievements in the fields of physics, engineering, biology, medicine, hydrology, economics, and finance [1-5]. The models of differential equations may be linear or nonlinear; linear models can be solved easily by different methods and do not require too much difficulty for obtaining the exact solution. But most of the problems of the real world occur non-linearly and cannot be solved easily. They are very hard to solve by simple methods. Most of the non-linear problems do not have exact solutions. Therefore, researchers use different approaches to solve them.

Researchers use numerical methods to solve non-linear problems, but they have discretization issue, are costly, and time-consuming. The famous numerical methods are the following: the collocation method, finite difference technique, finite element procedure, and radial basis function technique [6-8]. Similarly, perturbation methods need small or large parameter assumptions which are very difficult [9, 10]. Non-perturbation methods are the Adomian decomposition methodology (ADM) and differential transformation methodolgy (DTM). These methods work on repetition and that is why these types of problems can be solved with the help of computer software easily. Some well-known iterative methods are the variational iterating methodology (VIM), new iterating methodology, modified variational iteration method (MVIM), etc. [11, 12]. The Zakharov–Kuznetsov (ZK) equation is an enticing modeling formula for studying vortices in geophysics flows. The ZK difficulties appear in many areas of material sciences, implemented arithmetic, and design. It occurs particularly in the realm of physical sciences. The ZK issues govern the behavior of weak non-linear particle acoustic plasma waves, such as cold nanoparticles and hot adiabatic electrons, in the presence of smooth magnetism. The non-direct higher order of the expanded KdV criteria for geometrical removal was used to generate solitary wave configurations. The accurate expository structures of various non-linear advancement equations in numerical materials engineering, namely, space time-fractional Zakharov–Kuznetsov and altered Zakharov–Kuznetsov formulas, were found using a fractional technique. Many approaches, including the new iterating Sumudu understanding of the complex, homotopy perturbation transform method, expanded direct algebra methodology, natural decomposition technique, and q-homotopy analysis transform methodology, have been used to examine it during the last few decades. In this research work, we will find the approximate solution to the fractional order of the Zakharova–Kuznetsova FZK equation (13). The general form of the FZK equation is

$D_t^{\beta }\phi +a{\left({\phi }^p\right)}_x+b{\left({\phi }^q\right)}_{xxx}+c{\left({\phi }^r\right)}_{yyx}=0,0\le t,0<\beta \le 1,(1)$

where $\phi =\phi \left(x,y,t\right),0<\beta \le 1$ signifies an order of the fractional derivative, and $a,b$ and $c$ are optional fixed factors. The integers $p,q,r$ control the behavior of weak non-linear ion acoustical waves in hemoglobin-containing coolant ions and hotness isotherm electrons in the existence of a consistent magneto force. Numerous researchers have tried to solve the FZK equation by using different approaches such as VIM, OHAM, PIA method, and RPSM [14]. We have obtained the solution of the FZK equation by NTIM which is an extension of the natural iterating methodology NIM presented by Gejji and Jafari [15, 16] to obtain the estimated solution of linear and non-linear differential equalities. NTIM was recently applied by Nawaz et al. [17] for solving the fractional order differential equation. In the proposed methodology, NIM is combined with the natural transform for the solution of the FZK equation. We observed that the proposed method was easy to implement and provide an encouraging approximate solution for the linear and non-linear differential equalities of fractional- and integer-order derivatives.

2 Basic definitions

Definition 2.1 [14]: The fractional integral operator $I^{\alpha }$ of order $\alpha \ge 0$ in the Riemann–Liouville idea of a function is described as

$I^{\alpha }f((\chi )()=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^{\chi }(\chi -s{)}^{\alpha -1}f(s)ds,\alpha ,\chi >0,(2)$

where $I^{0}f\left(\chi \right)=f\left(\chi \right)$ and $\mathrm{\Gamma }$ is the well-known function.

Definition 2.2 [14]: Riemann–Liouville fractional derivative can be defined if $g\left(r\right)\in C\left[a,b\right]$ then

$I_a^{\alpha }=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_a^r\frac{g\left(\chi \right)}{{\left(r-\chi \right)}^{1-\alpha }}d\chi .(3)$

Some properties of the fractional derivative and integral are given as $f\in C_{\mu },\mu \ge 1,\alpha ,\beta \ge 0$ and $\lambda >-1$ then

$\begin{array}{c}•I^{\alpha }{I}^{\beta }=I^{\alpha +\beta }f\left(\chi \right),\\ •I^{\beta }{I}^{\alpha }=I^{\alpha +\beta }f\left(\chi \right),\\ •I^{\alpha }{\chi }^{\lambda }=\frac{\mathrm{\Gamma }\left(\lambda +1\right)}{\mathrm{\Gamma }\left(\lambda +1+\alpha \right)}{\chi }^{\lambda +\alpha }.\end{array}$

Definition 2.3: Natural transubstantiate is specified as [18]

$N^{+}\left[\varphi \left(t\right)\right]=\mathfrak{R}\left(s,u\right)=\frac{1}{u}\underset{0}{\overset{\infty }{{\displaystyle \int }}}{e}^{\frac{-st}{u}}\left(\varphi \left(t\right)\right)dt,s,u>0.(4)$

$u$ and $s$ are the transformation variables.

Definition 2.4 [18]: The inverse of the natural transubstantiate $\mathfrak{R}\left(s,u\right)$ is defined as

$N^{-}\left[\mathfrak{R}\left(s,u\right)\right]=\varphi \left(t\right)=\frac{1}{2\pi i}{\int }_{c-i\infty }^{c+i\infty }{e}^{\frac{st}{u}}\left(\mathfrak{R}\left(s,u\right)\right)ds.(5)$

$s=a+bi$ is the complex plan for executing the integral along $s=c$, where $c\in R$.

Definition 2.5 [18]: If $\varphi \left(t\right)$ is a function and ${\varphi }^n\left(t\right)$ is its nth derivative, then the natural transubstantiate of $\varphi \left(t\right)$ is

$N^{+}\left({\phi }^n\left(t\right)\right)={\mathfrak{R}}_n\left(s,u\right)=\frac{s^n}{u^n}\mathfrak{R}\left(s,u\right)-{\sum }_{k=0}^{n-1}\frac{s^{n-\left(k+1\right)}}{u^{n-k}}\left({\phi }^n\left(0\right)\right),n\ge 1.(6)$

Theorem 2.6: If $k\left(t\right)$ and $h\left(t\right)$ are defined on a set $A$ and have the natural transforms $K\left(s,u\right)$ and $H\left(s,u\right)$, respectively, then

$N\left[k*h\right]=uK\left(s,u\right)H\left(s,u\right),$

where $\left[h*k\right]$ is the convolution of $h$ and $k$.

2.1 Natural Transform Iterative Method (NTIM)

Consider the fractional order PDE in the manner

$D_t^{\beta }\left[\phi \left(y,t\right)\right]=g\left(y,t\right)+L\left[\phi \left(y,t\right)\right]+N\left[\phi \left(y,t\right)\right],n-1<\beta \le n,(7)$

where $D_t^{\beta }$ is the Caputo’s fractional derivative operator of order $\beta ,$ $k\in N$, and $y=y_{{}_1}+y_2+\cdots +y_k.$ $L$ and $N$ represent the non-linear function. $g\left(y,t\right)$ is the resource bound. The initialization constraint is

$\phi \left(y,0\right)=f\left(y\right).(8)$

Taking the natural transform of (7), we have

$N^{+}\left[D_t^{\beta }\left(\phi \left(y,t\right)\right)\right]=N^{+}\left[g\left(y,t\right)\right]+N^{+}\left[L\left(\phi \left(y,t\right)\right)+N\left(\phi \left(y,t\right)\right)\right].(9)$

By employing the differentiate characteristic of the natural conversion to Eq. (9), we have

$\frac{s^{\beta }}{u^{\beta }}{N}^{+}\left[\phi \left(y,t\right)\right]-\frac{s^{\beta -1}}{u^{\beta }}\phi \left(y,0\right)=N^{+}\left[g\left(y,t\right)\right]+N^{+}\left[L\phi \left(y,t\right)+N\phi \left(y,t\right)\right].(10)$

Using the initial condition and rearranging Eq. (10), we obtain

$N^{+}\left[\phi \left(y,t\right)\right]=\frac{f\left(y\right)}{s}+\frac{u^{\beta }}{s^{\beta }}\left(N^{+}\left[g\left(y,t\right)\right]\right)+\frac{u^{\beta }}{s^{\beta }}\left(N^{+}\left[L\left(\phi \left(y,t\right)\right)+N\left(\phi \left(y,t\right)\right)\right]\right).(11)$

As the linear term $L\phi \left(y,t\right)$ can be created in the structure of infinite series as

$L\left({\sum }_{m=0}^{\infty }{\phi }_m\left(y,t\right)\right)={\sum }_{m=0}^{\infty }L\left({\phi }_m\left(y,t\right)\right)(12)$

and $N\left(\phi \left(y,t\right)\right)$, the non-linear term is proposed as

$N\left({\sum }_{m=0}^{\infty }{\phi }_m\left(y,t\right)\right)=N\left({\phi }_0\left(y,t\right)\right)+{\sum }_{m=1}^{\infty }\left\{N\left({\sum }_{j=0}^i{\phi }_j\left(y,t\right)\right)-N\left({\sum }_{j=0}^{m-1}{\phi }_j\left(y,t\right)\right)\right\}.(13)$

Applying Eq. (13) in Eq. (11), we obtain

$0.9!N^{+}\left[{\sum }_{i=1}^{\infty }{\phi }_i\right]=\frac{f}{s}+\frac{u^{\beta }}{s^{\beta }}\left(N^{+}\left[g\right]\right)+\frac{u^{\beta }}{s^{\beta }}\left[N^{+}\left[{\sum }_{m=0}^{\infty }L\left({\phi }_m\right)+N\left({\phi }_0\right)+{\sum }_{m=1}^{\infty }\left\{N\left({\sum }_{j=0}^m{\phi }_j\right)-N\left({\sum }_{j=0}^{m-1}{\phi }_j\right)\right\}\right]\right].(14)$

The recursive relation of Eq. (14) by the use of natural transform is

$0.9!\{\begin{array}{l}{N}^{+}\left[{\phi }_0\left(y,t\right)\right]=\frac{g\left(y\right)}{s}+\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[g\left(y,t\right)\right],\\ N^{+}\left[{\phi }_1\left(y,t\right)\right]=\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[\mathfrak{I}\left({\phi }_0\right)+N\left({\phi }_0\right)\right],\\ N^{+}\left[{\phi }_2\left(y,t\right)\right]=\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[L\left({\phi }_1\right)+N\left({\phi }_0+{\phi }_1\right)-N\left({\phi }_0\right)\right]\\ ⋮\\ N^{+}\left[{\phi }_{i+1}\left(y,t\right)\right]=\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[\begin{array}{c}L\left({\phi }_i\right)+\aleph \left({\phi }_0+{\phi }_1+\cdots +{\phi }_i\right)\\ -N\left({\phi }_0+{\phi }_1+\cdots +{\phi }_{i-1}\right)\end{array}\right],i\ge 0.\end{array}(15)$

Utilizing the inverted natural transmute to Eq. (15), the solution component can be obtained as

$0.9!\{\begin{array}{l}{\phi }_0\left(y,t\right)=N^{-}\left[\frac{g\left(x\right)}{s}+\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[g\right]\right],\\ {\phi }_0\left(y,t\right)=N^{-}\left[\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[L\left({\phi }_0\right)+N\left({\phi }_0\right)\right]\right],\\ {\phi }_0\left(y,t\right)=N^{-}\left[\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[L\left({\phi }_1\right)+N\left({\phi }_0+{\phi }_1\right)-N\left({\phi }_0\right)\right]\right],\\ ⋮\\ {\phi }_{\mathrm{i}+1}\left(y,t\right)=N^{-}\left[\frac{u^{\beta }}{s^{\beta }}N+\left[L\left({\phi }_0+{\phi }_1+\cdots +{\phi }_i\right)-N\left({\phi }_0+{\phi }_1+\cdots +{\phi }_{i-1}\right)\right]\right],i\ge 0.\end{array}(16)$

The $n$ bounds approximated the solution of Eqs. 7 and 8 by the proposed method, which is obtained by adding the components as

$\stackrel{\sim }{\phi }\left(y,t\right)={\phi }_0\left(y,t\right)+{\phi }_1\left(y,t\right)+...+{\phi }_{n-1}\left(y,t\right).(17)$

2.2 Convergence of the NTIM

Theorem 2.7 [18]: If $N$ is analytic in a neighborhood of ${\varphi }_0$ and

$\Vert N^{{}^m}\left({\phi }_0\right)\Vert =\mathrm{s}\mathrm{u}\mathrm{p}\left\{N^{{}^m}\left({\phi }_0\right)\left(b_1,b_2,.....b_n\right)/\Vert b_k\Vert \le \mathrm{1,1}\le k\le m\right\}\le l$

for any $m$ and for certain real $l>0\&\Vert {\phi }_k\Vert \le M<\frac{1}{e},k=\mathrm{1,2},...$, then the series ${\displaystyle \sum }_{m=0}^{\infty }{G}_m$ is absolutely convergent and more over

$\Vert G_m\Vert \le l{M}^m{e}^{m-1}\left(e-1\right),m=\mathrm{1,2},\cdots$

To appear in the boundaries of $\Vert {\phi }_k\Vert$, for every $k$, the conditions on $N^{\left(j\right)}\left({\phi }_0\right)$ are provided which are appropriate to assure convergence of the sequence. The satisfactory constraint for the convergent is provided in the subsequent theory.

Theorem 2.8: If $N$ is $C^{\infty }$ and $\Vert N^{{}^m}\left({\phi }_0\right)\Vert \le M\le e^{-1}\forall m$, then the sequence ${\displaystyle \sum }_{m=0}^{\infty }{G}_m$ is absolutely convergent. These are the required conditions for the convergence of the series $\sum {\phi }_j$.

3 Implementation of the NTIM to the FZK equation

Example 3.1. Consider the FZK equation in the following form [13]:

$D_t^{\beta }\phi +{\left({\phi }^k\right)}_x+\frac{1}{8}{\left({\phi }^k\right)}_{xxx}+\frac{1}{8}{\left({\phi }^k\right)}_{yyx}=0,0\le t,0<\beta \le 1.(18)$

Together, the initial condition is

$\phi \left(x,y,0\right)=f\left(x,y\right).(19)$

Eq. (18) is written in the implicit form as

$D_t^{\beta }\phi =-{\left({\phi }^k\right)}_x-\frac{1}{8}{\left({\phi }^k\right)}_{xxx}-\frac{1}{8}{\left({\phi }^k\right)}_{yyx}.(20)$

Using natural conversion to Eq. (20), we get

$N^{+}\left[D^{\beta }\left(\phi \right)\right]=N^{+}\left[-{\left({\phi }^k\right)}_x-\frac{1}{8}{\left({\phi }^k\right)}_{xxx}-\frac{1}{8}{\left({\phi }^k\right)}_{yyx}\right].(21)$

Utilize the differentiation characteristic of the natural convert as

$\frac{s^{\beta }}{u^{\beta }}{N}^{+}\left[\phi \right]-\frac{s^{\beta -1}}{u^{\beta }}\phi \left(x,y,0\right)=N^{+}\left[-{\left({\phi }^k\right)}_x-\frac{1}{8}{\left({\phi }^k\right)}_{xxx}-\frac{1}{8}{\left({\phi }^k\right)}_{yyx}\right].(22)$

Using the initial condition in Eq. (20) and rearranging, we have

$N^{+}\left[\phi \right]=\frac{f\left(x,y\right)}{s}+\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[-{\left({\phi }^k\right)}_x-\frac{1}{8}{\left({\phi }^k\right)}_{xxx}-\frac{1}{8}{\left({\phi }^k\right)}_{yyx}\right].(23)$

As $\phi \left(x,y,t\right)$ is the infinite series given as

${\sum }_{m=0}^{\infty }{\phi }_m\left(x,y,t\right),(24)$

applying natural transform to Eq. (25) and using the idea explained in the method

$\{\begin{array}{l}{N}^{+}\left[{\phi }_0\left(x,y,t\right)\right]=\frac{f\left(x,y\right)}{s},\\ N^{+}\left[{\phi }_1\left(x,y,t\right)\right]=\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[-{\left({\phi }_0^k\right)}_x-\frac{1}{8}{\left({\phi }_0^k\right)}_{xxx}-\frac{1}{8}{\left({\phi }_0^k\right)}_{yyx}\right],\\ N^{+}\left[{\phi }_2\left(x,y,t\right)\right]=\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[\begin{array}{l}-{\left({\left({\phi }_0+{\phi }_1\right)}^k\right)}_x-\frac{1}{8}{\left({\left({\phi }_0+{\phi }_1\right)}^k\right)}_{xxx}-\frac{1}{8}{\left({\left({\phi }_0+{\phi }_1\right)}^k\right)}_{yyx}\\ -\left(-{\left({\phi }_0^k\right)}_x-\frac{1}{8}{\left({\phi }_0^k\right)}_{xxx}-\frac{1}{8}{\left({\phi }_0^k\right)}_{yyx}\right)\end{array}\right].\\ ⋮\end{array}$

(25)Now, by taking the inverted natural transmute of Eq. 25, we obtain the solution elements as

$\{\begin{array}{l}{\phi }_0\left(x,y,t\right)=N^{-}\left[\frac{f\left(x,y\right)}{s}\right],\\ {\phi }_1\left(x,y,t\right)=N^{-}\left[\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[-{\left({\phi }_0^k\right)}_x-\frac{1}{8}{\left({\phi }_0^k\right)}_{xxx}-\frac{1}{8}{\left({\phi }_0^k\right)}_{yyx}\right]\right],\\ {\phi }_2\left(x,y,t\right)=N^{-}\left[\frac{u^{\beta }}{s^{\beta }}{N}^{+}\left[\begin{array}{l}-{\left({\left({\phi }_0+{\phi }_1\right)}^k\right)}_x-\frac{1}{8}{\left({\left({\phi }_0+{\phi }_1\right)}^k\right)}_{xxx}-\frac{1}{8}{\left({\left({\phi }_0+{\phi }_1\right)}^k\right)}_{yyx}\\ -\left(-{\left({\phi }_0^k\right)}_x-\frac{1}{8}{\left({\phi }_0^k\right)}_{xxx}-\frac{1}{8}{\left({\phi }_0^k\right)}_{yyx}\right)\end{array}\right]\right].\\ ⋮\end{array}$

(26)The $n-terms$ approximate solution of Eqs. 18 and 19 by NTIM is presented as

$\phi \left(x,y,t\right)={\phi }_0+{\phi }_1+...+{\phi }_{m-1}.(27)$

Example 3.2. Regarding the FZK (2, 2, 2) equality of the structure [13]

${}^c{D}_t^{\beta }\phi +{\left({\phi }^2\right)}_x+\frac{1}{8}{\left({\phi }^2\right)}_{xxx}+\frac{1}{8}{\left({\phi }^2\right)}_{yyx}=0,0<\beta \le 1.(28)$

With preliminary conditions

$\phi \left(x,y,0\right)=\frac{4}{3}\lambda {\sinh }^2\left(x+y\right).(29)$

Here, $\lambda$ is an optional fixed value. The accurate solution for $\beta =1.0$ is given by

$\phi \left(x,y,t\right)=\frac{4}{3}\lambda {\sinh }^2\left(x+y-\lambda t\right).(30)$

Utilizing the procedure of NTIM, we obtain the solution components for Eq. (28) as

${\phi }_0\left(x,y,t\right)=\frac{4}{3}\lambda {\sinh }^2\left(x+y\right),(31)$

${\phi }_1\left(x,y,t\right)=\frac{8{\lambda }^2{t}^{\beta }\left(4\sinh \left(2\left(x+y\right)\right)-5\sinh \left(4\left(x+y\right)\right)\right)}{9\mathrm{\Gamma }\left(\beta +1\right)},(32)$

${\phi }_2(x,y,t)=\frac{64{\lambda }^3{t}^{2\beta }(\begin{array}{l}3\mathrm{\Gamma }(\beta +1{)}^2\mathrm{\Gamma }(3\beta +1)(13\cosh (2(x+y))\\ -70\cosh (4(x+y))+75\cosh (6(x+y)))\\ -20\lambda \mathrm{\Gamma }(2\beta +1{)}^2{t}^{\beta }(4\sinh (2(x+y))\\ +8\sinh (4(x+y))-60\sinh (6(x+y))\\ +85\sinh (8(x+y)))\end{array})}{81\mathrm{\Gamma }(\beta +1{)}^2\mathrm{\Gamma }(2\beta +1)\mathrm{\Gamma }(3\beta +1)}.(33)$

Adding the elements, the second-order approximated solution can be written as

$\stackrel{\sim }{\phi }\left(x,y,t\right)={\phi }_0+{\phi }_1+{\phi }_2.$

Example 3.3. Consider the FZK (3, 3, 3) equation of the structure [13]

${}^c{D}_t^{\beta }\phi +{\left({\phi }^3\right)}_x+2{\left({\phi }^3\right)}_{xxx}+2{\left({\phi }^3\right)}_{yyx}=0.(34)$

Together with initial conditions

$\phi \left(x,y,0\right)=\frac{3}{2}\lambda \sinh \left(\frac{x+y}{6}\right).(35)$

Here, $\lambda$ is an optional fixed amount. The exact solution for $beta=1.0$ is given by

$\phi \left(x,y,t\right)=\frac{3}{2}\lambda \sinh \left(\frac{1}{6}\left(x+y-\lambda t\right)\right).(36)$

Using the procedure of the NTIM, the solution elements can be acquired as

${\phi }_0\left(x,y,t\right)=\frac{3}{2}\lambda \sinh \left(\frac{1}{6}\left(x+y\right)\right),(37)$

${\phi }_1\left(x,y,t\right)=\frac{3{\lambda }^3{t}^{\beta }\cosh \left(\frac{x+y}{6}\right)\left(7-9\cosh \left(\frac{x+y}{3}\right)\right)}{16\mathrm{\Gamma }\left(\beta +1\right)},(38)$

${\phi }_2(x,y,t)=\left[\begin{array}{l}-\frac{3{\lambda }^5{t}^{2\beta }}{131072\mathrm{\Gamma }(\beta +1{)}^3\mathrm{\Gamma }(2\beta +1)\mathrm{\Gamma }(3\beta +1)\mathrm{\Gamma }(4\beta +1)}\times \\ {\lambda }^4\mathrm{\Gamma }(2\beta +1)\mathrm{\Gamma }{(3\beta +1)}^2{t}^{2\beta }(\begin{array}{l}9(\begin{array}{l}\frac{1700}{6}\sinh (5(x+y))+\frac{9135}{6}\sinh (7(x+y))\\ -\frac{3412}{2}(\sinh (x+y))-\frac{10935}{2}(\sinh (3(x+y)))\end{array})\\ +\frac{3550}{6}\sinh (x+y)\end{array})\\ +16{\lambda }^2\mathrm{\Gamma }(\beta +1)\mathrm{\Gamma }(2\beta +1{)}^2\mathrm{\Gamma }(4\beta +1)t^{\beta }(\begin{array}{l}9(\begin{array}{l}\frac{75}{2}\cosh (x+y)+\frac{1827}{6}\cosh \\ (7(x+y))-\frac{1615}{6}(\cosh (5(x+y)))\end{array})\\ +\frac{1385}{6}\cosh (x+y)\end{array})\\ -256\mathrm{\Gamma }(\beta +1{)}^3\mathrm{\Gamma }(3\beta +1)\mathrm{\Gamma }(4\beta +1)(\begin{array}{l}\frac{70}{6}\sinh (x+y)+\frac{765}{6}\sinh (5(x+y))\\ -\frac{621}{2}(\sinh (x+y))\end{array})\end{array}\right].$

(39)Adding the components, the second-order series solution can be written as

$\stackrel{\sim }{\phi }\left(x,y,t\right)={\phi }_0\left(x,y,t\right)+{\phi }_1\left(x,y,t\right)+{\phi }_2\left(x,y,t\right).(40)$

4 Results and discussion

In this work, two problems of the FZK equation have been tested by the new developed methodology NTIM. The obtained results are assessed by diverse plots and tabulated data for testing the reliability of the proposed method. Figure 1 shows the 3D surfaces obtained by the NTIM and the accurate result correspondingly for Example 3.2 in the 3D graph by keeping the y parameter constant. By keeping the time parameter constant, the approximate and accurate results are shown in Figure 2 respectively, for problem 3.2. In Figure 3, the absolute error is shown by a 3D plot by the variation of $x$ and $y$ parameters while time is kept constant. A comparison for the variation of the fractional value $\beta$ is shown by 2D plots for Example 3.2 which shows the consistency of the method by agreeing to the amount of $\beta$ tactics to the standard amount 1 of a differential equation; the approximated result converges to the accurate solution of the problem. Similarly, Figure 4 shows the approximates and exacted solution by variation of the $x$ and $t$ components, while Figure 5 shows the 3D graphs of the approximated solution and exacted solution by keeping the time parameter constant for problem 3.3. Figure 6 shows the absolute error of the NTIM result and the exacted solution for problem 2. Table 1 shows the comparison of data on the computational amounts of the approximated solution of the PIA and RPS methods for diverse amounts of $\beta$, while in Table 2, the absolute errors of our suggested methodology have been matched with the absolute errors of the PIA and RPS methods. Similarly, in Table 3, the fractional value of NTIM has been compared with the third-order RPSM and PIA methods. In Table 4, the absolute errors of NTIM, RPSM, and PIA methods have been compared. The approximate solution in this article is executed up to second order for both problems. The accuracy may be increased by obtaining a higher order of the approximate solution. From the tables and graphs, it is so far clear that the NTIM reveals encouraging approximated results as evaluated with other existing methodologies in the previously published works Table 5.

FIGURE 1

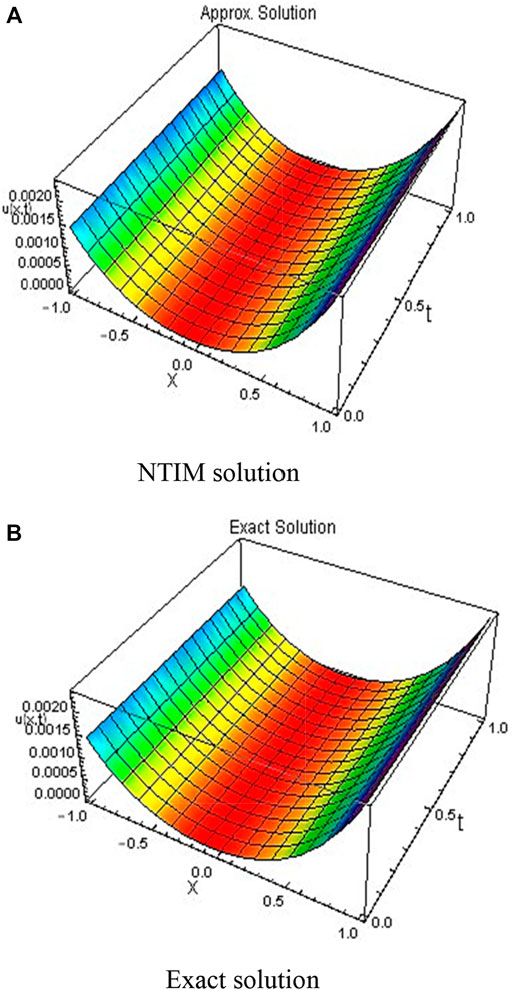
FIGURE 1. 3D plots obtained by the first order (A) NTIM and (B) exact solution for $\beta =1.0,y=0.1,\lambda =0.001$ for Example 3.2.

FIGURE 2

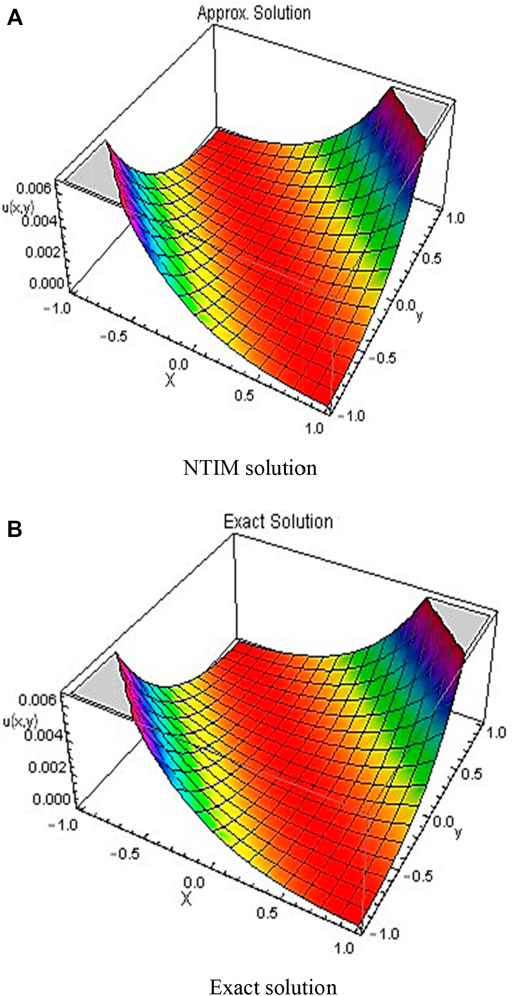
FIGURE 2. 3D plots obtained by the first order (A) NTIM and (B) exact solution for $\beta =1.0,t=0.1,\lambda =0.001$ for Example 3.2.

FIGURE 3

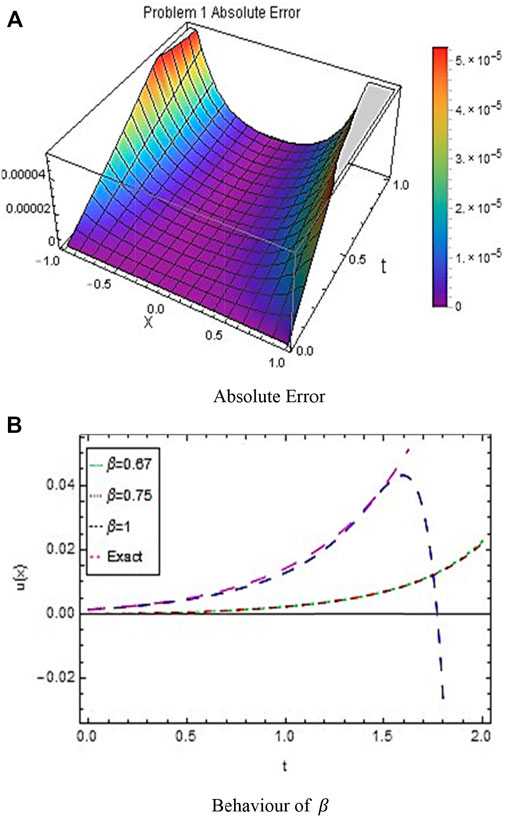
FIGURE 3. (A) shows the absolute error and (B) shows the behavior of $\beta$ on the solution of the NTIM for diverse amounts of $\beta$ when $x=y=0.1,\lambda =0.001$ for Example 3.2.

FIGURE 4

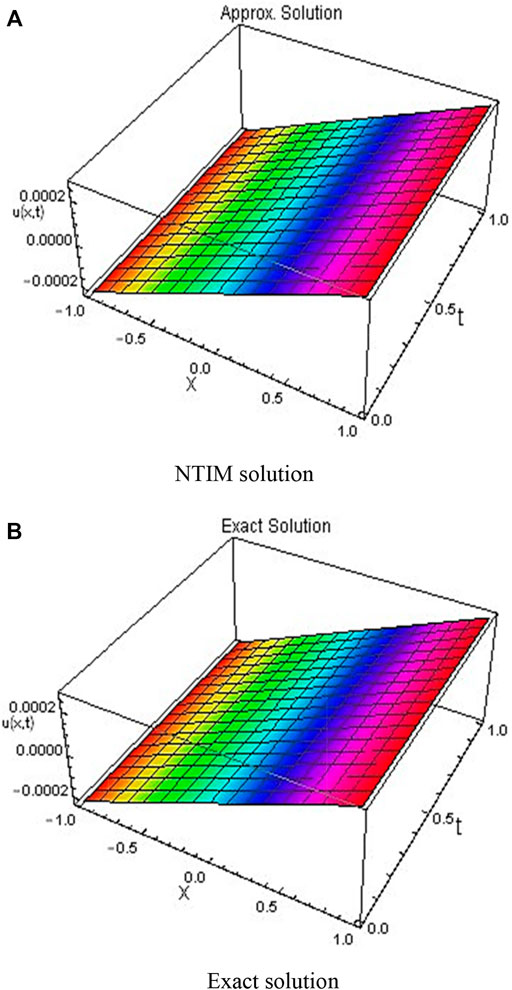
FIGURE 4. 3D plots obtained by the first order (A) NTIM and (B) exact solution for $\beta =1.0,y=0.1,\lambda =0.001$ for Example 3.3.

FIGURE 5

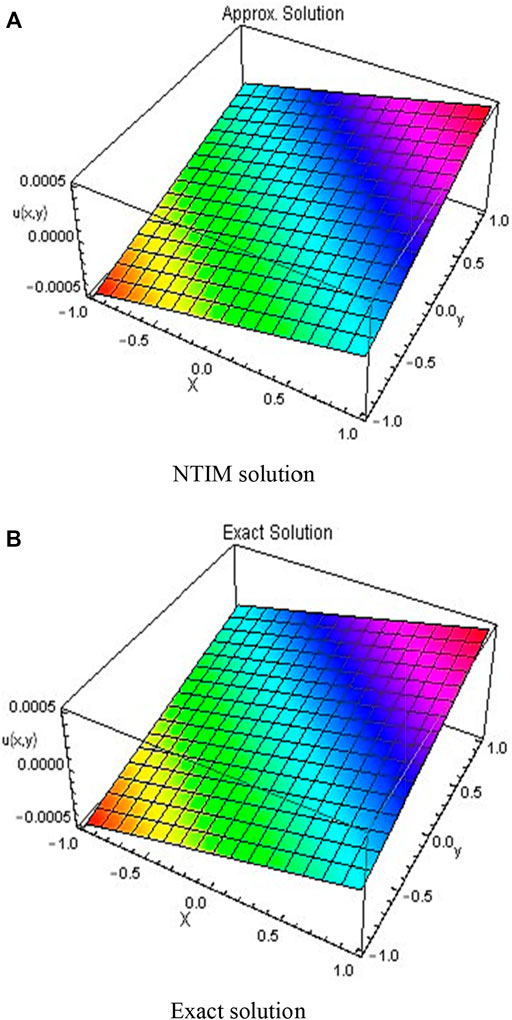
FIGURE 5. 3D plots obtained by the first order (A) NTIM and (B) exact solution for $\beta =1.0,t=0.1,\lambda =0.001$ for Example 3.3.

FIGURE 6

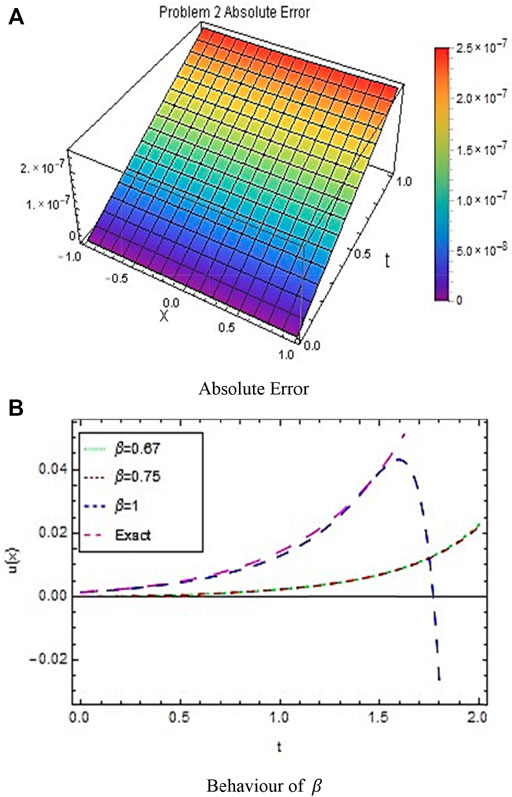
FIGURE 6. (A) shows the absolute error and (B) shows the behavior of $\beta$ on the solution of the NTIM for diverse amounts of $\beta$ when $x=y=0.1,\lambda =0.001$ for Example 3.3.

TABLE 1

TABLE 1. Few important expressions and their natural transubstantiates.

TABLE 2

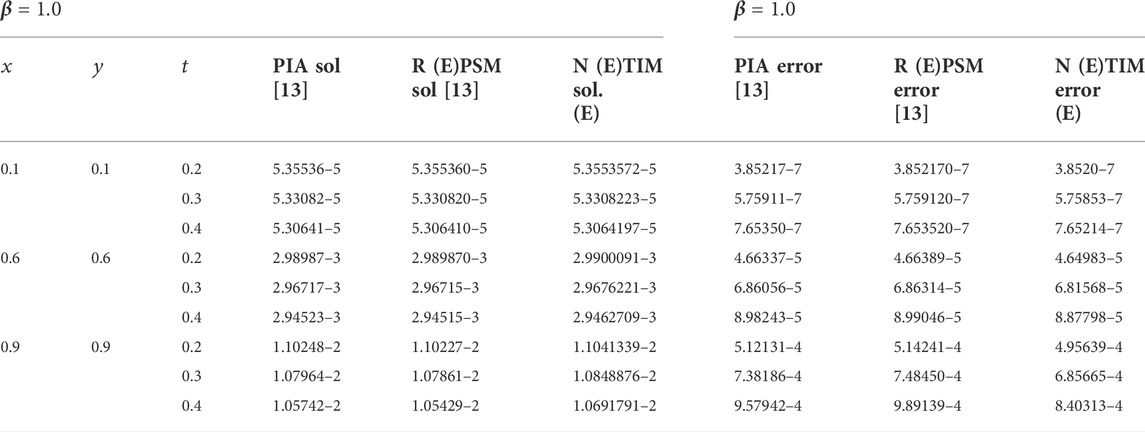
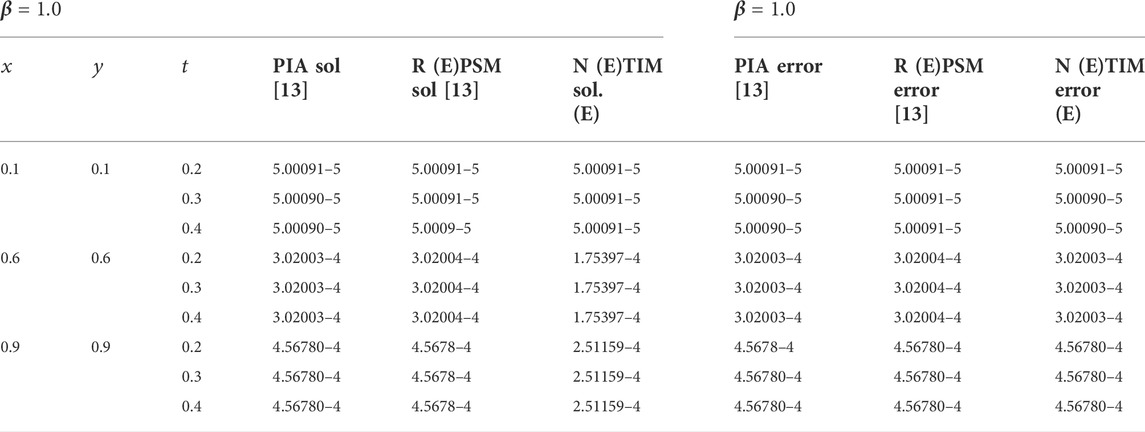
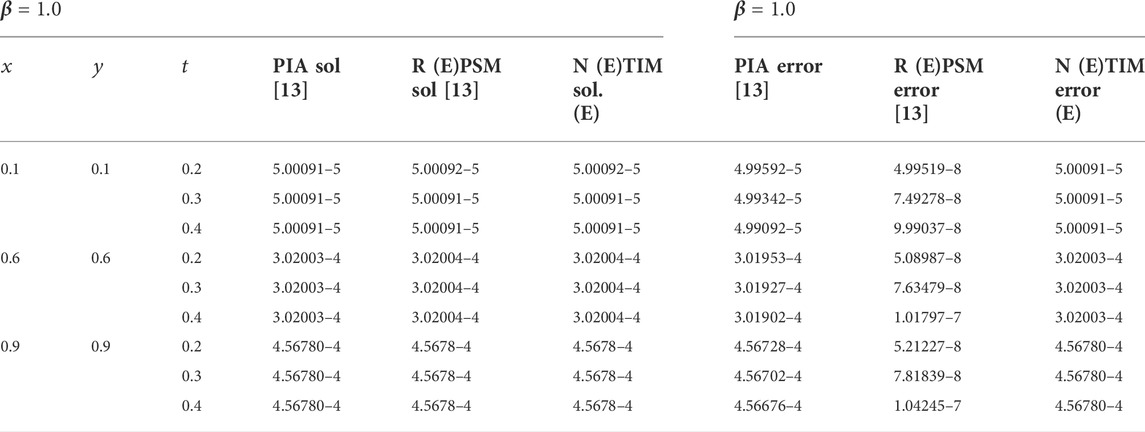
TABLE 2. Comparison of the second-order NTIM with the third-order RPSM and PIA method for diverse amounts of $\beta$.

TABLE 3

TABLE 3. Comparison of the second-order NTIM with the third-order RPSM and PIA method.

TABLE 4

TABLE 4. Comparison of the second-order NTIM with the third-order RPSM and PIA method.

TABLE 5

TABLE 5. Comparison of the second-order NTIM with the third-order RPSM and PIA method.

5. Conclusion

In the current investigation, the NTIM has been applied successfully to the FZK equations. Two problems have been tested. The proposed results reveal that the method handles the non-linear equations in a good way and provides an efficient approximate solution to non-linear PDEs. The numerical values of approximate and exact solutions through tables show the efficiency and reliability of the method. Also, the graphs verify the efficiency of the proposed method through 3D and 2D plots. The fractional approximation through 2D graphs also shows the consistency of the method by approaching the fractional value $\beta$ of the equation to the conventional amount 1, so an approximate result converges to the exacted result of the problems. This strategy is also effective when the answer to the integer order model is unknown. As a result, we decided that the current technique is trustworthy and effective in obtaining estimated solutions for various classes of linear and non-linear fractional formulations of ordinary and partial differential equations.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

LZ and RN formulated the problem. NA and WJ solved the problem. LZ, NA, RN, WJ, MRE, ESMTED, HAEWK, and FAAE, computed and scrutinized the results. All the authors equally contributed in writing and proof reading of the paper. All authors reviewed the manuscript.

Acknowledgments

The researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Gorenflo, R., and Mainardi, F. (2005). Simply and multiply scaled diffusion limits for continuous time random walks. J. Phys, Conf. Ser. 7, 1–16. doi:10.1088/1742-6596/7/1/001

CrossRef Full Text | Google Scholar

Barkai, E., Metzler, R., and Klafter, J. (2000). From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E 61 (1), 132–138. doi:10.1103/physreve.61.132

PubMed Abstract | CrossRef Full Text | Google Scholar

Benson, D.A., Wheatcraft, S.W., and Meerschaert, M.M. (2000). Application of a fractional advection‐dispersion equation. Water Resour. Res. 36 (6), 1403–1412.

CrossRef Full Text | Google Scholar

Almeida, R. (2017). A caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 44, 460–481. doi:10.1016/j.cnsns.2016.09.006

CrossRef Full Text | Google Scholar

Muslih, S., Baleanu, D., and Rabei, E. (2007). Gravitational potential in fractional space. Open Physics 5 (3), 285–292. doi:10.2478/s11534-007-0014-9

CrossRef Full Text | Google Scholar

Hu, H.Y., Chen, J.S., and Hu, W. (2007). Weighted radial basis collocation method for boundary value problems. Int. J. Numer. Methods Eng. 69 (13), 2736–2757. doi:10.1002/nme.1877

CrossRef Full Text | Google Scholar

Zhao, E., Shi, B., Qu, K., Dong, W., and Zhang, J. (2018). Experimental and numerical investigation of local scour around submarine piggyback pipeline under steady current. J. Ocean Univ. China 17 (2), 244–256. doi:10.1007/s11802-018-3290-7

CrossRef Full Text | Google Scholar

Kwon, Y.W., and Bang, H. (2018). The finite element method using MATLAB. Florida: CRC, press.

Google Scholar

D.S. Carter, (1965). Perturbation techniques in mathematics, physics and engineering. New York: Richard bellman.

Google Scholar

Benabidallah, M., and Cherruault, Y. (2004). Application of the adomian method for solving a class of boundary problems. Kybernetes 33, 118–132. doi:10.1108/03684920410514553

CrossRef Full Text | Google Scholar

Abassy, T.A. (2010). Modified variational iteration method (nonlinear homogeneous initial value problem). Comput. Math. Appl. 59 (2), 912–918. doi:10.1016/j.camwa.2009.10.002

CrossRef Full Text | Google Scholar

Molliq, R.Y., Noorani, M.S.M., Hashim, I., and Ahmad, R.R. (2009). Approximate solutions of fractional zakharov–kuznetsov equations by vim. J. Comput. Appl. Math. 233 (2), 103–108. doi:10.1016/j.cam.2009.03.010

CrossRef Full Text | Google Scholar

Senol, M., Alquran, M., and Kasmaei, H.D. (2018). On the comparison of perturbation-iteration algorithm and residual power series method to solve fractional zakharov-kuznetsov equation. Results Phys. 9, 321–327. doi:10.1016/j.rinp.2018.02.056

CrossRef Full Text | Google Scholar

Nawaz, R., Zada, L., Khattak, A., Jibran, M., and Khan, A. (2019). Optimum solutions of fractional order Zakharov–Kuznetsov equations. Complexity 2019, 1–9. doi:10.1155/2019/1741958

CrossRef Full Text | Google Scholar

Daftardar-Gejji, V., and Bhalekar, S. (2008). Solving fractional diffusion-wave equations using a new iterative method. Fract. Calc. Appl. Anal. 11 (2), 193–202.

Google Scholar

Bhalekar, S., and Daftardar-Gejji, V. (2011). Convergence of the new iterative method. International Journal of Differential Equations 2011, 1–10. doi:10.1155/2011/989065

CrossRef Full Text | Google Scholar

Nawaz, R., Ali, N., Zada, L., Nisar, K.S., Alharthi, M.R., and Jamshed, W. (2021). Extension of natural transform method with daftardar-jafari polynomials for fractional order differential equations. Alexandria Engineering Journal 60 (3), 3205–3217. doi:10.1016/j.aej.2021.01.051

CrossRef Full Text | Google Scholar

Nawaz, R., Ali, N., Zada, L., Shah, Z., Tassaddiq, A., and Alreshidi, N.A. (2020). Comparative analysis of natural transform decomposition method and new iterative method for fractional foam drainage problem and fractional order modified regularized long-wave equation. Fractals 28 (07), 2050124. doi:10.1142/s0218348x20501248

CrossRef Full Text | Google Scholar