Formation pressure distribution and productivity prediction of fractured horizontal wells in stress sensitive reservoirs

Aiming at the problems of formation pressure distribution and productivity prediction after Horizontal Well Volume Fracturing in stress sensitive reservoirs, the methods of dynamic permeability and dynamic threshold pressure gradient are used to deal with the influence of stress sensitivity, a numerical simulation method of oil-water two-phase flow based on finite element method is established. History matching is performed on the basis of the prediction of formation pressure distribution after horizontal well volume fracturing of, which ensures high matching accuracy. Taking the ultra-low permeability sandy glutenite reservoir of Baikouquan Formation in M18 area of Aihu Oilfield as research object, the influence law of formation pressure level on productivity and stress sensitivity on formation pressure distribution is studied. Analysis of the calculation results shows that: the influence of formation pressure level on well productivity is mainly in the first year of production, and the effect of energy increasing by volume fracturing is clarified. Stress sensitivity mainly affects the middle and later stage of production. With the increase of sensitivity, the permeability loss of the formation tends to be concentrated in the low-pressure area near the artificial fracture, forming an isolation zone with high flow resistance, which make the development effect of far well zone worse.

Introduction

Generally speaking, the lower the reservoir permeability, the weaker the stress sensitivity (Li, 2005, Li, 2009; Gao et al., 2014; Dou et al., 2016; Luo et al., 2019). However, due to its special geological characteristics, abnormally high pressure and low permeability reservoirs often have higher effective stress during development, and generally show stronger stress sensitivity. With the increase of effective stress, the loss rate of reservoir permeability gradually increases, showing greater seepage resistance, which affects the productivity of oil wells. Clarifying the influence of stress sensitivity on formation pressure distribution and productivity is of great significance for reservoir protection and design reasonable production system.

The research methods of stress sensitivity on productivity mainly include analytical method, semi analytical method, and numerical method. Analytical methods are used to establish productivity models for vertical wells (Liu et al., 2014; Shan et al., 2017; Chai et al., 2018; Zhu et al., 2018) and horizontal wells (Yang et al., 2017; Jiang et al., 2012; Ning et al., 2020; Guo and Wu 2007), most of which have to be studied for non-fractured wells. Fang et al. (2015) based on the perturbation theory and combined with the source function, established a semi-analytical method for calculating the production of fracturing horizontal wells in Laplace space, and analyzed the pressure and production dynamic curves of multi-angle and multi-stage fracturing horizontal wells in stress sensitive oil reservoirs. Numerical methods mainly use finite difference, finite volume method and finite element method. Song (2012) established the oil-water relative permeability curve under the combined effect of stress sensitivity and starting pressure on the basis of the stress sensitivity experimental results. Wang et al. (2013) established the dynamic model of threshold pressure gradient and dynamic permeability on the basis of laboratory experiments, and used the finite difference method to solve numerically. Liu et al. (2017) established a three-phase seepage mathematical model for shale oil considering the threshold pressure gradient and stress sensitivity, used the finite volume method to obtain the numerical solution, and compiled a numerical simulator. The finite element method has flexible grid division and is easy to deal with complex boundaries. It has unique advantages in the study of seepage problems in artificially fractured wells (Zhang et al., 2017; Feng et al., 2019; Su et al., 2019), and is very suitable for the development of numerical calculation programs.

The finite element-based numerical method is used to study the seepage problem of fractured wells in stress sensitive reservoirs. Innovatively establish the equivalent characterization method of stress sensitivity effect using dynamic permeability and dynamic starting pressure gradient based on the experimental data of core stress sensitivity, and improve the accuracy of history fitting of fractured horizontal wells based on the prediction of formation pressure distribution before production. In order to improve the programming efficiency, the calculation program is developed based on the Finite Element Automatic Generation System (FEPG) (Liang, 2011) of the Chinese Academy of Sciences, which can save a lot of programming work (Zhang et al., 2010; Zhang 2013; Shi et al., 2016).

Mathematical model

Basic assumptions: There is an oil-water two-phase fluid in a homogeneous reservoir, and both fluid and rock are weakly compressible. The influence of starting pressure gradient and capillary force is considered, and the influence of gravity is ignored. The motion equation is brought into the continuity equation, the fluid densities ρ_o, ρ_w are treated as constants, and the rock state equation is considered to process the right-hand term of the equation, and the oil phase pressure equation is obtained:

$\nabla \cdot \left[K\lambda \nabla p_{\text{o}}\left(1-\frac{G}{\left|\nabla p_{\text{o}}\right|}\right)\right]-\nabla \cdot \left(K\lambda {\lambda }_{\text{w}}\nabla p_{\text{c}}\right)=\varphi C_{\text{t}}\frac{\partial p_{\text{o}}}{\partial t}(1)$

Where $C_{\text{t}}=\frac{1}{\varphi }{C}_{\text{f}}+S_{\text{w}}{C}_{\text{w}}+S_{\text{o}}{C}_{\text{o}}$, $\lambda =\frac{K_{\text{ro}}}{{\mu }_{\text{o}}}+\frac{K_{\text{rw}}}{{\mu }_{\text{w}}}$, ${\lambda }_{\text{o}}=\frac{K_{\text{ro}}}{{\mu }_{\text{o}}\lambda }$, ${\lambda }_{\text{w}}=\frac{K_{\text{rw}}}{{\mu }_{\text{w}}\lambda }$

Define the total seepage velocity as u, then

$\mathit{u}={\mathit{v}}_{\text{o}}+{\mathit{v}}_{\text{w}}=-K\lambda \nabla p_{\text{w}}\left(1-\frac{G}{\left|\nabla p_{\text{w}}\right|}\right)-K\lambda {\lambda }_{\text{o}}\nabla p_{\text{c}}(2)$

Get:

$\nabla p_{\text{w}}\left(1-\frac{G}{\left|\nabla p_{\text{w}}\right|}\right)=-\frac{\mathit{u}}{K\lambda }-{\lambda }_{\text{o}}\nabla p_{\text{c}}(3)$

${\mathit{v}}_{\text{w}}={\lambda }_{\text{w}}\mathit{u}+\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}\nabla p_{\text{c}}(4)$

$\nabla \cdot \left({\mathit{v}}_w\right)=\nabla \cdot \left({\lambda }_w\mathit{u}\right)+\nabla \cdot \left(\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}\nabla p_{\text{c}}\right)(5)$

In order to improve the calculation stability of saturation equation, the relative mobility of water phase in the first term at the right end of the above formula λ_w is implicitly treated as a function of S_w. In the second term, the capillary pressure is also implicitly treated. Expand p_c into Taylor series near S_wⁿ⁻¹, and then take its first-order expansion and ignore the second-order small quantity, can get $\nabla p_{\text{c}}=\nabla p_c^{n-1}+p_c^{\prime }\nabla S_{\text{w}}-p_c^{\prime }\nabla S_{\text{w}}^{n-1}$, then Eq. 5 becomes:

$\nabla \cdot \left({\mathit{v}}_w\right)={\lambda }_{\text{w}}^{\prime }\mathit{u}\nabla S_{\text{w}}+\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}\nabla \cdot \left(\nabla p_{\text{c}}^{n-1}\right)+\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}{p}_c^{\prime }\nabla \cdot \left(\nabla S_{\mathbf{W}}\right)+\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}{p}_c^{\prime }\nabla \cdot \left(\nabla S_{\text{w}}^{n-1}\right)$

The water phase saturation equation can be obtained:

$-{\lambda }_{\text{w}}^{\prime }\mathit{u}\nabla S_{\text{w}}-\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}\nabla \cdot \left(\nabla p_{\text{c}}^{n-1}\right)-\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}{p}_{\text{c}}^{\prime }\nabla \cdot \left(\nabla S_{\text{w}}\right)-\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}{p}_{\text{c}}^{\prime }\nabla \cdot \left(\nabla S_{\text{w}}^{n-1}\right)=\varphi \frac{\partial \left(S_{\text{w}}\right)}{\partial t}(6)$

Artificial fracture characterization

The traditional fracture characterization method regards the fracture as a high-permeability zone, which has certain limitations in simulating complex fractures. The mixed element finite element method is used to simulate cracks with line elements. In order to facilitate mesh division, the implicit fracture line element is adopted, that is, the division of matrix mesh element and the fracture line element are carried out at the same time, and the fracture line element is hidden in the matrix element. This fracture treatment method needs to superimpose the stiffness of the fracture line element into the overall stiffness of the matrix, so as to improve the stiffness of the matrix element and improve the overall permeability of the matrix.

In the two-dimensional mathematical model of oil-water two-phase, artificial fractures are treated with line elements. The basic differential equations of artificial fractures have the same form as the matrix, and the dimension is one dimension lower than matrix. Due to the high fracture permeability, the threshold pressure gradient is not considered.

Oil phase pressure equation of artificial fracture:

$\nabla \cdot \left(K_{\text{f}}\lambda \nabla p_{\text{fo}}\right)-\nabla \cdot \left(K_{\text{f}}\lambda {\lambda }_{\text{w}}\nabla p_{\text{fc}}\right)=\varphi C_{\text{t}}\frac{\partial p_{\text{fo}}}{\partial t}(7)$

Water phase saturation equation of artificial fracture:

$-{\lambda }_{\text{w}}^{\prime }\mathit{u}\nabla S_{\text{w}}-{\mathit{K}}_{\text{f}}\mathit{\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}\nabla \cdot \left(\nabla p_{\text{fc}}^{n-1}\right)-{\mathit{K}}_{\text{f}}\mathit{\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}{p}_{\text{fc}}^{\prime }\nabla \cdot \left(\nabla S_{\text{w}}\right)-{\mathit{K}}_{\text{f}}\mathit{\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}{p}_{\text{fc}}^{\prime }\nabla \cdot \left(\nabla S_{\text{w}}^{n-1}\right)=\varphi \frac{\partial \left(S_{\text{w}}\right)}{\partial t}(8)$

Weak solution integral form of differential equations

Write the oil phase pressure Eq. 1 in integral form:

${\displaystyle \underset{V}{\iint }\nabla \cdot \left[K\lambda \nabla p_{\text{o}}\left(1-\frac{G}{\left|\nabla p_{\text{o}}\right|}\right)\right]\delta p_{\text{o}}\mathit{dV}}-{\displaystyle \underset{V}{\iint }\nabla \cdot \left(K\lambda {\lambda }_{\text{w}}\nabla p_{\text{c}}\right)\delta p_{\text{o}}\mathit{dV}}={\displaystyle \underset{V}{\iint }\varphi C_{\text{t}}\frac{\partial p_{\text{o}}}{\partial t}\delta p_{\text{o}}\mathit{dV}}(9)$

Integral by parts of the left-hand side of Eq. 9, can get:

$-{\displaystyle \underset{V}{\iint }K\lambda \nabla p_{\text{o}}\left(1-\frac{G}{\left|\nabla p_{\text{o}}\right|}\right)}\nabla \delta p_{\text{o}}\mathit{dV}+{\displaystyle \underset{\mathit{\Gamma }}{\int }K\lambda \frac{\partial p_{\text{o}}}{\partial n}\delta p_{\text{o}}\mathit{d\Gamma }}+{\displaystyle \underset{V}{\iint }K\lambda {\lambda }_{\text{w}}\nabla p_{\text{c}}\nabla \delta p_{\text{o}}\mathit{dV}}-{\displaystyle \underset{\mathit{\Gamma }}{\int }K\lambda {\lambda }_{\text{w}}\frac{\partial p_{\text{c}}}{\partial n}\delta p_{\text{o}}\mathit{d\Gamma }}={\displaystyle \underset{V}{\iint }\varphi C_{\text{t}}\frac{\partial p_{\text{o}}}{\partial t}\delta p_{\text{o}}\mathit{dV}}(10)$

When the oil-water well is at a constant pressure boundary, by selecting δp appropriately, make δp = 0 on the boundary and ignore the integral along the boundary ${\displaystyle \underset{\mathit{\Gamma }}{\int }K\lambda \frac{\partial p_{\mathrm{o}}}{\partial n}\delta p_{\mathrm{o}}\mathit{d\Gamma }}$ .The capillary pressure gradient is small compared to the formation pressure gradient near the bottom hole, so the boundary integral term $-{\displaystyle \underset{\mathit{\Gamma }}{\int }K\lambda {\lambda }_{\text{w}}\frac{\partial p_{\text{c}}}{\partial n}\delta p_{\text{o}}\mathit{d\Gamma }}$ is ignored. The weak solution integral form of the oil phase pressure equation can be obtained:

$-{\displaystyle \underset{V}{\iint }K\lambda \nabla p_{\text{o}}\left(1-\frac{G}{\left|\nabla p_{\text{o}}\right|}\right)}\nabla \delta p_{\text{o}}\mathit{dV}+{\displaystyle \underset{V}{\iint }K\lambda {\lambda }_{\text{w}}\nabla p_{\text{c}}\nabla \delta p_{\text{o}}\mathit{dV}}={\displaystyle \underset{V}{\iint }\varphi C_{\text{t}}\frac{\partial p_{\text{o}}}{\partial t}\delta p_{\text{o}}\mathit{dV}}(11)$

When the oil-water well is producing at a constant production rate q, and the bottom hole is the constant flow boundary, the integral term along the bottom hole boundary can be changed to ${\displaystyle \underset{\mathit{\Gamma }}{\int }\frac{q}{A}}\delta p_{\text{o}}d\mathit{\Gamma }$, can get:

$-{\displaystyle \underset{V}{\iint }K\lambda \nabla p_{\text{o}}\left(1-\frac{G}{\left|\nabla p_{\text{o}}\right|}\right)}\nabla \delta p_{\text{o}}\mathit{dV}+{\displaystyle \underset{V}{\iint }K\lambda {\lambda }_{\text{w}}\nabla p_{\text{c}}\nabla \delta p_{\text{o}}\mathit{dV}}+{\displaystyle \underset{\mathit{\Gamma }}{\int }\frac{q}{A}\delta p_{\text{o}}\mathit{d\Gamma }}={\displaystyle \underset{V}{\iint }\varphi C_{\text{t}}\frac{\partial p_{\text{o}}}{\partial t}\delta p_{\text{o}}\mathit{dV}}(12)$

Similarly, the weak solution integral expression of the water phase saturation equation can be obtained:

$-{\displaystyle \underset{V}{\iint }{\lambda }_{\text{w}}^{\prime }\mathit{u}\nabla S_{\text{w}}\delta S_{\text{w}}dV}+{\displaystyle \underset{V}{\iint }\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}\nabla p_{\text{c}}^{n-1}\nabla \delta S_{\text{w}}dV}+{\displaystyle \underset{V}{\iint }\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}{p}_{\text{c}}^{\prime }\nabla S_{\text{w}}\nabla \delta S_{\text{w}}dV}-{\displaystyle \underset{V}{\iint }\mathit{K\lambda }{\lambda }_{\text{o}}{\lambda }_{\text{w}}{p}_{\text{c}}^{\prime }\nabla S_{\text{w}}^{n-1}\nabla \delta S_{\text{w}}dV}={\displaystyle \underset{V}{\iint }\varphi \frac{\partial \left(S_{\text{w}}\right)}{\partial t}\delta S_{\text{w}}dV}(13)$

The u in the first term of the formula is treated explicitly, so this term does not need to be integral by parts. In the same way, the integral form of the weak solution of the fracture system can be obtained.

Algorithm

The oil phase pressure equation and the water phase saturation equation were solved by implicit pressure and explicit water saturation. The time was discretized by the Crank-Nicolson scheme. The linear equations were solved by the direct method of LDL^T decomposition. Both the water cut and the pressure gradient were solved using the least squares method.

Results and discussion

Numerical model building

Baikouquan formation in well block M18 of Aihu oil field is a low porosity, ultra-low permeability and abnormally high-pressure sandy conglomerate reservoir with a pressure coefficient of 1.63. The reservoir rocks of the Baikouquan Formation are mainly glutenite, gravel-bearing coarse sandstone and sandstone, and the pore types are mainly residual intergranular pores, intragranular dissolved pores, matrix shrinkage pores and crushed fractures. The reservoir porosity is mainly distributed between 8 and 14%, with an average of 11.9%, and the permeability is distributed between 0.01 × 10⁻³ μm² and 46 × 10⁻³ μm², with an average of 0.5 × 10⁻³ μm². Crude oil has low viscosity and good fluidity. Medium water sensitivity, velocity sensitivity and strong stress sensitivity. Stress Sensitivity index b = 0.385 ($K=K_0{\mathrm{e}}^{-b\varphi (p_0-p)}$) (Shi et al., 2016). With the natural energy development method of horizontal well + volume fracturing, the main problems faced are the large decline in the early stage and the prominent stress sensitivity problem. The fracturing construction time of each stage is 3 h, the time from the end of fracturing construction to putting into production is 10d, and the viscosity of fracturing fluid after gel breaking is 1 mPa s. Adjust the injection pressure and time of fracturing operation, and keep the total fracturing fluid volume unchanged to match the bottom hole flow pressure when it is put into production, so as to ensure the accuracy of pressure distribution prediction. A typical well in M18 well block is selected to establish a single well numerical model. The length of the horizontal section is 938 m, formation permeability is 0.5 × 10⁻³ μm², porosity is 0.095, reservoir thickness is 14.2 m, oil saturation is 58.6%, original formation pressure is 64 MPa, formation crude oil viscosity is 0.66 mPa s, threshold pressure gradient is 0.027 MPa/m, fracture Conductivity is 25μm² m, rock compressibility 1 × 10^–41/MPa, crude oil compressibility 18 × 10^–41/MPa, irreducible water saturation 26%, residual oil saturation 37.13%, water relative permeability at residual oil saturation is 12.99%.

The stress sensitive data adopts the results of laboratory experiments. When the net confining pressure is 44 MPa, the formation permeability is reduced to 20% of the initial value. In the numerical calculation, according to the net formation confining pressure value of each node, interpolate the data in stress sensitive data to obtain the formation permeability loss, and then update the formation permeability and threshold pressure gradient data of the node.

Well M1 fracturing 12 stages and 22 clusters, of which the 6th and 11th stages fracturing one cluster, and the half-length of the fractures is 55–164 m. In the M18 well block, natural fractures are not developed in the reservoir, and the rock is partially plastic and has a low brittleness value. The large stress difference between the two horizontal directions makes it difficult to achieve volume fracturing with complex artificial fracture network patterns in this area. The artificial fractures are mainly plane fractures. Building a 2D Model of Well M1.

History matching and productivity forecast

Well M1 adopts slick water + guar gum fracturing fluid, with a total fluid volume of 13,500 m³. In order to improve the accuracy of history matching, simulate the fracturing fluid injection process during fracturing construction, predict the formation pressure distribution before production under the influence of fracturing fluid energization, and use the total injected fluid volume and bottom-hole flow pressure during production to constrain Numerical calculation results.

The current production time of well M1 is 2.4 years, and the history matching is shown in Figure 1. The initial production of the well increased rapidly, and then decreased rapidly after reaching the peak. The history matching is carried out on the basis of the prediction of formation pressure distribution, which makes the matching effect in the initial stage better. When fracturing energization is not considered, the initial peak oil rate is only 60 t/d, and when fracturing energization is considered, it is 100 t/d, this is a very big difference. Therefore, if the influence of fracturing energization on the formation pressure distribution before production is not considered, history matching is difficult.

FIGURE 1

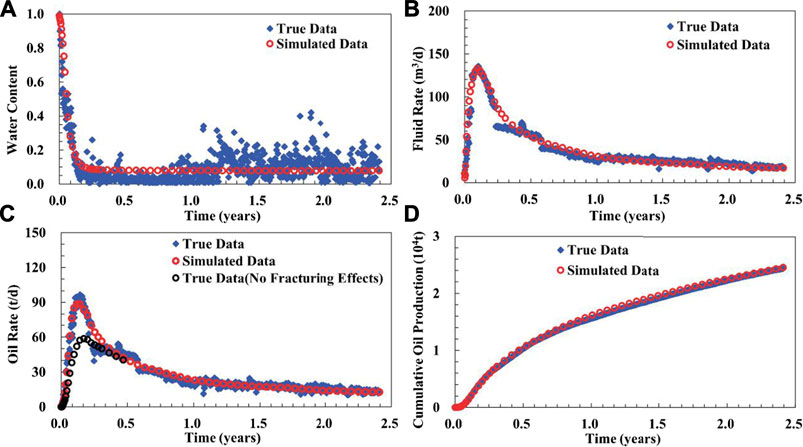
FIGURE 1. Historical matching curve of single well.(A) Water Content; (B) Fluid Rate; (C) Oil Rate; (D) Cumulative Production.

The two replacements of the nozzles caused large fluctuations in well production, and the matching effect was relatively poor in about half a year. This well lacks bottom-hole flow pressure data, which makes it difficult to accurately match production fluctuations, and can only match production trends. The cumulative oil production of well M1 in 2.4 years is 24,455 t, the cumulative oil production calculated by simulation is 24,564 t, and the fitting error is 0.45%.

The formation pressure and pressure gradient distribution of Well M1 are shown in Figure 2. At 2.4 years, the formation pressure in the simulation area of Well M1 was 35–61.23 MPa, and the permeability loss rate caused by stress sensitivity was 17.70%–2.22%.

FIGURE 2

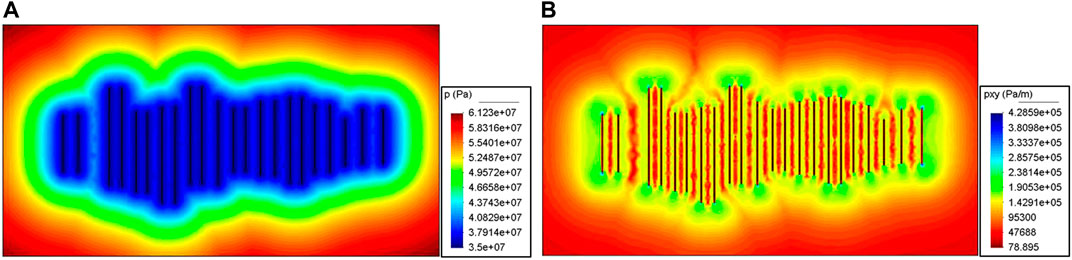
FIGURE 2. Distribution of formation pressure and pressure gradient. (A). Distribution of formation pressure, (B). Distribution of formation pressure gradient.

On the basis of single well history matching, predicted cumulative oil production in 8 years is 43,187 t, and the recovery degree is 12.77%.

Influence of formation pressure level on productivity

An ideal model of a single well was established, the length of the horizontal section was 1,000 m, 24 clusters in 12 fracturing stages, and the half-length of the fractures were all 120 m, and other calculation parameters were the same as those of Well M1. Four pre-production formation pressure level schemes were established, and the average formation pressures $\overline{p}$ within the influence range of fracturing energization during production were: 64, 66.56, 68.34, and 70.15 MPa. Among them, scheme one, 64 MPa, is the original formation pressure, which does not consider the influence of fracturing fluid on the formation pressure Scheme $\overline{p}$ = 66.56 MPa, the maximum formation pressure is 68.07 MPa, and the maximum influence range at the fracture end is 65.0 m; scheme $\overline{p}$ = 68.34 MPa, the maximum formation pressure is 71.05 MPa, and the influence range is 78.5 m; scheme $\overline{p}$ = 70.15 MPa, the maximum formation pressure. The value is 74.00 MPa, and the influence range is 85.8 m. From the one-year production performance (Figure 3), it can be seen that the impact of different formation pressure levels on the productivity of oil wells is mainly in the first half of the year. The higher the formation pressure level, the greater the peak production and the sharper the peak. Compared with not considering fracturing, the cumulative oil production of the 68.34 MPa (close to the formation pressure level of Well M1) increased by 2,421 t, an increase of 16.70%. Judging from the actual situation in the M18 well area, the average flowback rate of the fracturing fluid is low, about 12% in half a year, which makes the fracturing energy enhancement have a good oil-increasing effect.

FIGURE 3

FIGURE 3. Influence of formation pressure level on initial productivity.

Influence of stress sensitivity on formation pressure distribution

The bottom hole flow pressure drop is 20 MPa when the horizontal well has been in production for 8 years. Four schemes are selected for the permeability loss caused by stress sensitivity. The maximum permeability loss rates (K_s) near the bottom hole are 20%, 40%, 60%, and 80%, of which 80% scheme is close to the actual situation of well block M18. The numerical calculation model and other parameters are the same as those in the previous section, and the influence of fracturing on formation pressure is not considered. The formation pressure is taken as the original formation pressure.

Comparing the formation pressure distribution of the four stress sensitivity schemes in 8 years (Figure 4), it can be seen that the formation pressure consumed increases with the increase of stress sensitivity. The average formation pressure of the four schemes in 8 years is 35.17, 30.30, 27.40, and 25.37 MPa.

FIGURE 4

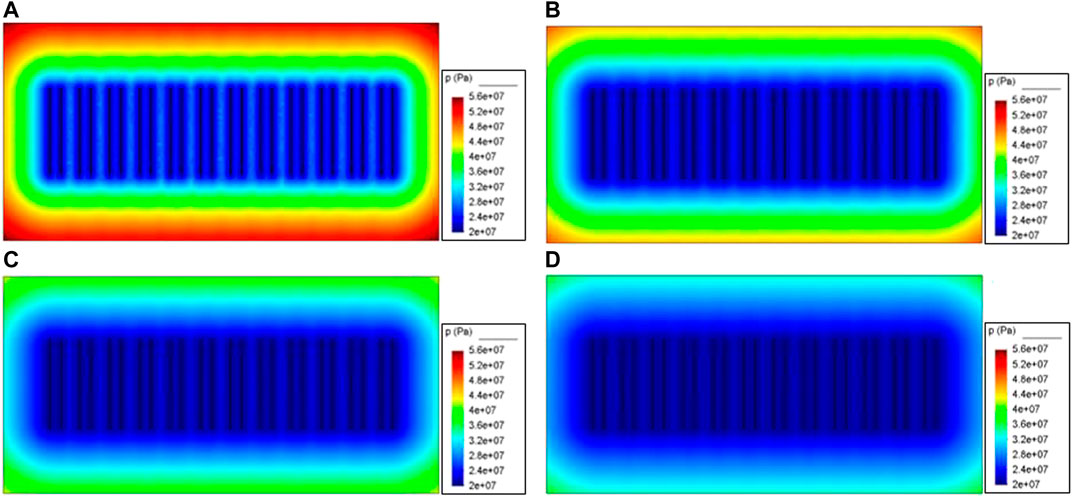
FIGURE 4. Effect of stress sensitivity on formation pressure distribution. (A) Max K_s = 20%; (B) Max K_s = 40%; (C) Max K_s = 60%; (D) Max K_s = 80%.

The loss of formation permeability is calculated according to the distribution of formation pressure. As the stress sensitivity increases, the difference between the maximum and minimum loss rates of the four schemes becomes larger and larger. The lowest loss rate of scheme 4 is only 26.41%, which is lower than that of scheme 2 and 3. On the one hand, the existence of stress sensitivity reduces the pore volume and reduces the reservoir permeability, which is not conducive to oil recovery. On the other hand, it is beneficial to maintain pore pressure and oil production, so stress sensitivity within a certain range may be beneficial to increase productivity (Wang et al., 2003; Li and Tu 2008). However, when the stress sensitivity is very strong, an isolation zone with lower permeability and higher fracturing gradient with high flow resistance tends to be formed near the fracture, which makes the oil production in the far-well area worse and reduces the productivity of the oil well. This situation can also be explained from the formation energy consumption, that is, the average formation pressure of scheme 4 is higher and the total pressure difference is lower. In the middle and late stages of production in the M18 well area, it is necessary to formulate a reasonable oil recovery rate and supplement formation energy to reduce the impact of stress sensitive oil wells.

Conclusion

Based on the basic principle of finite element method, a numerical method for predicting formation pressure distribution and oil well productivity of ultra-low permeability sandy conglomerate reservoir considering stress sensitivity is established. An innovative method to characterize the fracturing reformed area with permeability and threshold pressure gradient that vary with spatial location. The single well history matching is carried out on the basis of the formation pressure distribution prediction considering the influence of fracturing energy increase. In the peak yield stage, which is difficult to fit, the historical matching coincidence rate is high, and the overall historical fitting effect is good.

The fracturing energization effect in the M18 well area has a good oil-increasing effect. In view of the low fracturing fluid flowback rate, it is recommended to combine the imbibition theory to study the feasibility of oil displacement fracturing to further improve the oil recovery.

In the middle and late stages of oil well production, stress sensitivity strengthens the threshold pressure gradient and seepage resistance in the low-pressure zone near artificial fractures, so that the pressure is mainly consumed near the artificial fractures, and the production effect becomes poor. Optimizing the oil well production system, supplementing the formation energy, and reducing the influence of stress sensitivity are the key issues that need to be paid attention to in the M18 well area.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WH, LZ, and ZZhij contributed to conception and design of the study. DC organized the database. WH, LT, SZ, and ZZhim performed the numeral calculations and statistical analysis. WH, LT, WC, and SZ wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work is financially supported by the Daqing guiding science and technology plan project (No. zd-2021-51).

Conflict of interest

Author WC was employed by NO. 1 Oil Production Plant PetroChina Daqing Oilfield Company. Author DC was employed by Xinjiang Oilfield Company, PetroChina.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chai, R. K., Liu, Y. T., Wang, J. Q., and Xin, J. (2018). Study on productivity model of oil well in low-permeability reservoirs based on two-phase threshold pressure gradient and stress sensitivity (in Chinese). J. Xi'an Shiyou Univ. Nat. Sci. Ed. 33 (3), 44–50. doi:10.3969/j.issn.1673—064X.2018.03.007

CrossRef Full Text | Google Scholar

Dou, H., Zhang, H., Yao, S., Zhu, D., Sun, T., Ma, S., et al. (2016). Measurement and evaluation of the stress sensitivity in tight reservoirs. Petroleum Explor. Dev. 43 (6), 1116–1123. doi:10.1016/s1876-3804(16)30130-6

CrossRef Full Text | Google Scholar

Fang, S. D., Cheng, L. S., Li, C. Y., Cao, R. Y., Yang, J., and He, C. G. (2015). The productivity model of multi-angled fractured horizontal well in stress-sensitive reservoir (in Chinese). J. Northeast Petroleum Univ. 39 (1), 87–94. doi:10.3969/j.issn.2095-4107.2015.01.011

CrossRef Full Text | Google Scholar

Feng, F. P., Lei, Y., Chen, D. F., Hu, C. Y., Wang, H. Z., and Huang, R. (2019). Parameter analysis of SRV fracturing effect of tight reservoirs based on finite element numerical simulation (in Chinese). Reserv. Eval. Dev. 9 (1), 29–33. doi:10.13809/j.cnki.cn32-1825/te.2019.01.006

CrossRef Full Text | Google Scholar

Gao, T., Guo, X., Liu, J. N., Li, H. T., Xie, C., and Liu, H. (2014). Stress sensitivity experiment for ultra-low permeability core (in Chinese). Petroleum Geol. Oilfield Dev. Daqing 33 (4), 87–90. doi:10.3969/j.issn.1000-3754.2014.04.018

CrossRef Full Text | Google Scholar

Guo, X., and Wu, Y. (2007). Influence of start-up pressure gradient and stress sensitivity on productivity of low-permeability gas reservoirs(in Chinese). Oil Gas Geol. 28 (4), 539–543. doi:10.11743/ogg20070417

CrossRef Full Text | Google Scholar

Jiang, R., Wang, Y. Q., Zhang, Q., Huang, P., and Xu, Z. P. (2012). A capacity formula for horizontal well in stress-sensitive reservoir considering threshold pressure gradient and quadratic pressure gradient (in Chinese). Tuha Oil Gas 17 (1), 68–72.

Google Scholar

Li, C. L., and Tu, X. W. (2008). Two types of stress sensitivity mechanisms for reservoir rocks: being favorable for oil recovery(in Chinese). Lithol. Reserv. 20 (1), 111–113. doi:10.3969/j.issn.1673-8926.2008.01.019

CrossRef Full Text | Google Scholar

Li, C. L. (2005). Low permeability rocks are less sensitive to stress(in Chinese). Oil Drill. Prod. Technol. 27 (4), 62–63. doi:10.3969/j.issn.1000-7393.2005.04.019

CrossRef Full Text | Google Scholar

Li, C. L. (2009). Stress sensitivity influence on oil well productivity(in Chinese). J. Southwest Petroleum Univ. Sci. Technol. Ed. 31 (1), 170–172. doi:10.3863/j.issn.1674-5086.2009.01.041

CrossRef Full Text | Google Scholar

Liang, G. P. (2011). Finite element analysis software platform FEPG(in Chinese). Comput. Aided Eng. 20 (3), 92–96.

Google Scholar

Liu, F., Wang, Y. L., Chen, X. F., Yunhe, S., and Yue, W. (2014). Analysis on oil well productivity of low-permeability reservoirs with stress-sensitivity being taken into considerations(in Chinese). Oil Gas. Geol. 34 (1), 124–128. doi:10.11743/ogg20130117

CrossRef Full Text | Google Scholar

Liu, L. J., Yao, J., Sun, H., Bai, Y. H., Xu, B. Y., and Chen, L. (2017). The effect of threshold pressure gradient and stress sensitivity on shale oil reservoir productivity (in Chinese). Pet. Drill. Tech. 45 (5), 84–91. doi:10.11911/syztjs.201705015

CrossRef Full Text | Google Scholar

Luo, C., Zhou, P. G., Yang, H., and Shi, J. G. (2019). Stress sensitivity characteristics of low permeability reservoirs (in Chinese). J. Southwest Petroleum Univ. Sci. Technol. Ed. 41 (6), 1–7. doi:10.11885/j.issn.16745086.2019.01.21.03

CrossRef Full Text | Google Scholar

Ning, B., Xiang, Z. P., Liu, X. S., Zhijun, L., Zhonghua, C., Bocai, J., et al. (2020). Production prediction method of horizontal wells in tight gas reservoirs considering threshold pressure gradient and stress sensitivity. J. Pet. Sci. Eng. 187, 106750. doi:10.1016/j.petrol.2019.106750

CrossRef Full Text | Google Scholar

Shan, A. P., Shi, L. H., Kang, K., and Lu, C. (2017). A new production model of ultra-low permeability reservoirs under con sideration of start-up pressure gradient and stress sensitivity effect (in Chinese). Xinjiang Oil Gas 13 (4), 41–46.

Google Scholar

Shi, W. H., Yang, T. H., Liu, H. L., and Yang, B. (2016). Non-Darcy flow model and numerical simulation for water-inrush in fractured rock mass. Chin. J. Rock Mech. Eng. 35 (3), 446–455. doi:10.13722/j.cnki.jrme.2015.0389

CrossRef Full Text | Google Scholar

Song, C. T. (2012). Numerical reservoir simulation considering threshold pressure gradient and stress sensitive phenomenon(in Chinese). Sci. Technol. Eng. 12 (25), 6319–6326.

Google Scholar

Su, Y. L., Lu, M. J., Li, M., Zhang, Q., Wang, W. D., and Dong, M. Z. (2019). Numerical simulation of shale oil coupled flow in multi-pore media (in Chinese). Oil Gas. Geol. 40 (3), 645–652+660. doi:10.11743/ogg20190319

CrossRef Full Text | Google Scholar

Wang, X. J., Zhao, Y. S., Wen, W., Chi, B., and Sun, Y. (2003). Stress sensitivity and poroperm lower limit of deliverability in the low-permeability reservoir (in Chinese). Oil & Gas. Geol. 24 (2), 162–165. doi:10.11743/ogg20030212

CrossRef Full Text | Google Scholar

Wang, J., Liu, H. Q., Liu, R. J., and Xu, J. (2013). Numerical simulation for low-permeability and extra-low permeability reservoirs with considering starting pressure and stress sensitivity effects (in Chinese). J. Rock Mech. Eng. 32, 3317–3327.

Google Scholar

Yang, Z. P., Yang, H., Chen, H. P., and Zhang, H. (2017). New method for evaluating rock stress sensitivity for low- permeability tight gas reservoirs. Chem. Technol. Fuels Oils 53 (1), 68–76. doi:10.1007/s10553-017-0782-x

CrossRef Full Text | Google Scholar

Zhang, C. L., Wang, J. Y., and Fang, G. Y. (2010). Numerical simulation of fluid flow through shale coupled with multi-field based on FEPG (in Chinese). Drill. Fluid & Complet. Fluid 27 (3), 69–71.

Google Scholar

Zhang, Q. F., Huang, Z. Q., Yao, J., Wang, Y., and Li, Y. (2017). Two-phase numerical simulation of discrete fracture model based on multiscale mixed finite element method. Chin. Sci. Bull. 62 (13), 1392–1401. doi:10.1360/n972016-00584

CrossRef Full Text | Google Scholar

Zhang, S. L. (2013). Numerical simulation and analysis of structural fractures based on FEPG(in Chinese). J. Xi’an Univ. Sci. Technol. 33 (4), 86–91+100.

Google Scholar

Zhu, M. Q., Wang, N. T., and Zhang, H. (2018). Influences of the start-up pressure gradient and stress sensitive effect on the productivity of the oil reservoir(in Chinese). Petroleum Geol. Oilfield Dev. Daqing 37 (3), 59–63. doi:10.19597/j.issn.1000-3754.201709044

CrossRef Full Text | Google Scholar

Nomenclature

ϕ porosity, fraction

ϕ₀ initial porosity, fraction

S_o oil saturation, fraction

S_w water saturation, fraction

t time, s

K permeability, m²

K₀ initial permeability, m²

K_ro oil-phase relative permeability

K_rw water-phase relative permeability

μ_o oil-phase viscosity, Pa s

μ_w

water-phase viscosity, Pa s

p_o oil-phase pressure, Pa

p₀ original formation pressure, Pa

p_w water-phase pressure, Pa

p_c capillary pressure, Pa

$\overline{\mathit{p}}$ average formation pressure, Pa

G threshold pressure gradient, Pa/m

C_f rock compressibility, Pa⁻¹

C_t comprehensive compressibility, Pa⁻¹

C_o oil-phase compressibility, Pa⁻¹

C_w water-phase compressibility, Pa⁻¹

λ oil-water two-phase fluidity

λ_o oil-phase relative fluidity

λ_w water-phase relative fluidity

u total seepage velocity, m/s

v_o oil-phase seepage velocity, m/s

v_w water-phase seepage velocity, m/s

A seepage area, m²

Superscripts and subscripts

f_o oil-phase of fracture system

f_w water-phase of fracture system

f_c fracture capillary pressure

‘ derivative

n-1 previous time step