Economic dispatch using modified bat algorithm

Due to the frequent opening and shutting of turbine valves in the power system, valve point effect (VPE) that makes the economic dispatching (ED) problem non-linear, non-smooth and non-convex may be generated. Moreover, various constraints appear in the operation process, such as network transmission loss, and power balance during unit operation, which make it more difficult to find the global optimum through traditional mathematical methods. Nowadays, intelligent algorithms have successfully become a useful optimization tool to deal with nonlinear problems. In this paper, an improved bat algorithm (IBA), into which random black hole strategy and Gaussian mutation are introduced, is proposed to solve the ED problem. Furthermore, the random black hole strategy can enhance the diversity of the population and improve the convergence speed of IBA. Gaussian mutation is adopted to help jumping out of the local optimum. IBA is tested in 50 and 100 dimensions on 10 sets of well-known benchmark functions respectively, and compared with the methods in literature to verify its feasibility. Then, three different scales economic dispatching problems (3 units, 13 units, 40 units) are solved by this method, which further proves its effectiveness. The results show that IBA has obvious advantages and practical application value compared with other optimization methods.

1 Introduction

Economic Dispatch problem is a typical optimization problem in power system operation and has been one of the hot topics of research in recent years. The objective of the ED problem is to find the appropriate generation value to minimize the cost of generation while satisfying the equation and inequality constraints that may arise in power system operation (Ma et al., 2017; Chen and Tang, 2022). Generally, the thermal power unit would be affected by the valve point effect, which make the ED problem be a complex optimization problem with non-smooth, non-linear, non-convex and non-differentiable. There are two general methods to solve this problem: one is the classical mathematical method, such as quadratic programming, nonlinear programming, etc., and the other is the intelligent optimization algorithm, such as genetic algorithm, particle swarm algorithm, etc. (Singh and Dhillon, 2019; Yang et al., 2021). The former requires continuous differentiable function, which is obviously not suitable for the practical application scene. However, the latter has no special requirements on the objective function, so this paper chooses intelligent optimization algorithm instead of classical mathematical method to solve the ED problem.

In recent years, with the rapid development of intelligent optimization algorithms, more and more scholars are using it to solve ED problems (Niu et al., 2014; Dou and Qin, 2020). grey wolf optimization (GWO) (Singh and Dhillon, 2019), sailfish algorithm (SFA) (Li et al., 2021), fireworks algorithm (FWA) (Zare et al., 2021), whale optimization algorithm (WOA) (Medani et al., 2018), artificial bee colony algorithm (ABC) (Hassan et al., 2020), ant colony optimization (ACO) (Zhou et al., 2017), social spider algorithm (SSA) (Adhvaryyu and Adhvaryyu, 2020), marine predator algorithm (MPA) (Pan et al., 2021), ant lion optimizer (ALO) (Mouassa et al., 2017), bat algorithm (BA) (Rugema et al., 2021), and other optimization algorithms have been applied to the solution of ED problems. Ref. (Singh and Dhillon, 2021) proposes an improved directed bat optimizer with contrastive learning to solve the minimization power scheduling problem, and the results show that the proposed algorithm is a potential algorithm to solve the ED problem. An improved hybrid particle swarm optimization algorithm based on PSO and HPSOBA is proposed to solve economic dispatch problems containing conventional as well as hybrid and renewable energy sources. The results demonstrate the superior performance of the developed algorithm in terms of fuel cost reduction, faster convergence and computation time (Ellahi et al., 2021). Ref. (Guerraiche et al., 2021) presents a bat algorithm combined with a generalized evolutionary wandering algorithm to solve the multi-objective redundancy design problem with series-parallel power systems. A chaotic bat algorithm based on chaotic sequence improvement is applied to solve optimal reactive power scheduling problems with small, medium and large scale power systems. Simulation results reveal the effectiveness and interference resistance of the chaotic bat algorithm for solving such problems (MugemanyiQu et al., 2020). Ref. (Liang et al., 2018) proposes a bat optimization algorithm based on a combination of chaotic mapping and stochastic black hole model for solving economic dispatch problems in power systems, and the effectiveness of the proposed method is illustrated on three test cases.

The bat algorithm (BA) has the advantages of few parameters and fast convergence, so it is more often used in various power system problems (Xu and Xiang, 2021). However, the convergence speed of BA algorithm is too fast, which leads it to fall into local optimum easily. From this, a new improved BA (IBA) algorithm is proposed in this paper. To address the problem that the original BA algorithm easily falls into local optimum, two improvements are made to the BA algorithm: first, Random black hole strategy is used to increase the diversity of the algorithm and accelerate the convergence speed; second, Gaussian mutation is introduced to reduce the local optimum probability and improve the global search capability. To verify the effectiveness of IBA, we tested it on 10 sets of benchmark functions and three different sizes of ED problems and compared it with other methods in the literature, and the results show that IBA has a high convergence accuracy and can obtain better optimization results compared with other algorithms.

The rest of the paper is organized as follows. Section 2 describes in detail the mathematical model of the ED problem. Section 3 introduces the standard BA algorithm and proposes IBA. Section 4 evaluates comprehensively the performance of the IBA on benchmark functions. Section 5 gives the summary of the work and makes some briefings to the later research work.

2 Problem statement

The economic dispatch problem is the task of allocating reasonably the output of each unit under the premise of meeting various constraints in power system operation, so as to achieve the goal of minimizing the total generation cost of the power system.

2.1 SED problem formulation

The SED problem is mainly considered in this paper, which can be described as a cost minimization problem, and its objective function is defined as:

$\mathbf{Min}{\displaystyle \sum _{\mathbf{i=1}}^{\mathbf{\text{N}}}{\mathbf{F}}_{\mathbf{i}}}\left({\mathbf{P}}_{\mathbf{i}}\right)(1)$

where ${\mathbf{F}}_{\mathbf{i}}\left({\mathbf{P}}_{\mathbf{i}}\right)$ is the fuel cost function of the ${\mathbf{i}}^{\mathbf{th}}$ unit and ${\mathbf{P}}_{\mathbf{i}}$ is the output power generated by the ${\mathbf{i}}^{\mathbf{th}}$ unit.

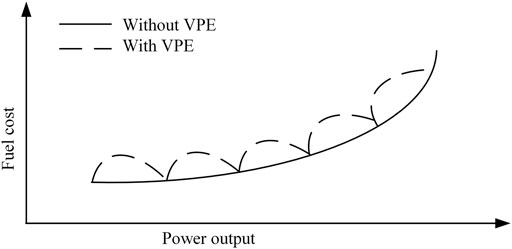
In real life, the power system produces VPE because of the steam turbine in the power system. Whenever the steam valve is turned on or off, which could change the input and output characteristics of the unit. Therefore, the fuel cost function has two forms: one is a quadratic function without VPE defined as Eq. 2, the other with VPE is described as Eq. 3.

$\mathbf{F}\left({\mathbf{P}}_{\mathbf{i}}\right)\mathbf{=}{\displaystyle \sum _{\mathbf{i=1}}^{\mathbf{N}}{\mathbf{a}}_{\mathbf{i}}}\mathbf{+}{\mathbf{b}}_{\mathbf{i}}{\mathbf{P}}_{\mathbf{i}}\mathbf{+}{\mathbf{c}}_{\mathbf{i}}{\mathbf{P}}_{\mathbf{i}}^{\mathbf{2}}\mathbf{ }(2)$

$\mathbf{F}\left({\mathbf{P}}_{\mathbf{i}}\right)={\displaystyle \sum }_{\mathbf{i}=1}^{\mathbf{N}}\left\{{\mathbf{a}}_{\mathbf{i}}+{\mathbf{b}}_{\mathbf{i}}{\mathrm{P}}_{\mathrm{i}}+{\mathbf{c}}_{\mathbf{i}}{\mathbf{P}}_{\mathbf{i}}^2+\left|{\mathbf{d}}_{\mathbf{i}}\mathbf{sin}\left[{\mathbf{e}}_{\mathbf{i}}\left({\mathbf{P}}_{\mathbf{i}}^{\mathbf{min}}-{\mathbf{P}}_{\mathbf{i}}\right)\right]\right|\right\}(3)$

where ${\mathbf{a}}_{\mathbf{i}}$, ${\mathbf{b}}_{\mathbf{i}}$, and ${\mathbf{c}}_{\mathbf{i}}$ are the fuel-cost coefficients of the ${\mathbf{i}}^{\mathbf{th}}$ unit, ${\mathbf{d}}_{\mathbf{i}}$ and ${\mathbf{e}}_{\mathbf{i}}$ are the fuel cost-coefficients of the ${\mathbf{i}}^{\mathbf{th}}$ unit with valve point effects. In addition, the cost functions without and with VPE are shown in Figure 1. In this paper, Eq. 3 is used as the cost function.

FIGURE 1

FIGURE 1. Cost function with and without valve point effect.

2.2 Constraints

(a) Power balance constraints

${\displaystyle \sum _{\mathbf{i=1}}^{\mathbf{N}}{\mathbf{P}}_{\mathbf{i}}\mathbf{-}{\mathbf{P}}_{\mathbf{L}}\mathbf{=}{\mathbf{P}}_{\mathbf{D}}}(4)$

where ${\mathbf{P}}_{\mathbf{D}}$ is the total system load demand, and ${\mathbf{P}}_{\mathbf{L}}$ is the transmission loss. While power network is concentrated, thus ${\mathbf{P}}_{\mathbf{L}}$ is ignored in this paper.

(b) Generating capacity constraints

${\mathbf{P}}_{\mathbf{i}}^{\mathbf{min}}\le {\mathbf{P}}_{\mathbf{i}}\le {\mathbf{P}}_{\mathbf{i}}^{\mathbf{max}}(5)$

where ${\mathit{P}}_{\mathit{i}}^{\mathit{max}}$ and ${\mathbf{P}}_{\mathbf{i}}^{\mathbf{min}}$ are the maximum and minimum power outputs of the ${\mathbf{i}}^{\mathbf{th}}$ unit.

3 Improved bat algorithm

3.1 Conventional bat algorithm

Bat algorithm (BA) is a heuristic search algorithm based on group intelligence proposed by Yang in 2010, which mimics the behavior of miniature bats to find small insects as prey or avoid obstacles through echolocation system. Furthermore, bats perform various activities through echolocation, which can be summarized as follows (Yang, 2010).

(a) Miniature bats can use echolocation to measure distance and distinguish between prey and obstacles.

(b) Miniature bats make random flight catch prey at a certain speed ${\mathbf{v}}_{\mathbf{i}}$, fixed frequency ${\mathbf{f}}_{\mathbf{min}}$, variable wavelength $\mathbf{\lambda }$ and loudness ${\mathbf{A}}_0$. Furthermore, the emissivity $\mathbf{\epsilon }\in \left[\mathrm{0,1}\right]$ can be adjusted. Meanwhile, the frequency and wavelength of the pulses are related to the distance to the prey.

(c) Here, the loudness may be anywhere from a big positive ${\mathbf{A}}_0$ to a constant value ${\mathbf{A}}_{\mathbf{min}}$ of the minimum.

Like most evolutionary algorithms, the population ${\mathbf{X}}_{\mathbf{i},\mathbf{j}}\left(\mathbf{i}=\mathrm{1,2},\mathrm{...},\mathbf{N};\mathbf{j}=\mathrm{1,2},\mathrm{...},\mathbf{D}\right)$ of BA is composed of $\mathbf{N}$ individuals with $\mathbf{D}$ variable. In $\mathbf{D}$ dimensional search space, each bat adjusts its frequency $\mathrm{f}$ before updating its speed, and then updates its speed according to its current speed and the distance between its current position and the current optimal position. The position and speed are updated as follows:

${\mathbf{f}}_{\mathbf{i}}\mathbf{=}{\mathbf{f}}_{\mathbf{min}}\mathbf{+\beta }\left({\mathbf{f}}_{\mathbf{max}}\mathbf{-}{\mathbf{f}}_{\mathbf{min}}\right)(6)$

${\mathbf{v}}_{\mathbf{i}}^{\mathbf{t}}\mathbf{=}{\mathbf{v}}_{\mathbf{i}}^{\mathbf{t-1}}\mathbf{+}{\mathbf{f}}_{\mathbf{i}}\left({\mathbf{X}}_{\mathbf{i}}^{\mathbf{t}}\mathbf{-}{\mathbf{X}}_{\mathbf{\ast }}\right)(7)$

${\mathbf{X}}_{\mathbf{i}}^{\mathbf{t}}\mathbf{=}{\mathbf{X}}_{\mathbf{i}}^{\mathbf{t-1}}\mathbf{+}{\mathbf{v}}^{\mathbf{t}}(8)$

where ${\mathbf{f}}_{\mathbf{i}}$ is the frequency of the ${\mathbf{i}}^{\mathbf{th}}$ bat, ${\mathbf{f}}_{\mathbf{min}}$ is the minimum frequency, ${\mathbf{f}}_{\mathbf{max}}$ is the maximum frequency. For convenience, ${\mathbf{f}}_{\mathbf{min}}$ = 0, ${\mathbf{f}}_{\mathbf{max}}$ = 100, as described in reference (Yang, 2010). $\mathit{\beta }$ is a uniformly distributed random number in $\left[\mathrm{0,1}\right]$, ${\mathbf{X}}_{\ast }$ is the current global optimal position.

If the random number is greater than the pulse number, bats can carry out random flight. The formula for random flight is as follows:

${\mathbf{X}}_{\mathbf{new}}={\mathbf{X}}_{\mathbf{old}+}\mathbf{\epsilon }{\mathbf{A}}^{\mathbf{t}}(9)$

where $\mathbf{\epsilon }$ is a random number in $\left[-\mathrm{1,1}\right]$, ${\mathbf{A}}^{\mathbf{t}}$ is the average loudness of all bats at ${\mathbf{t}}^{\mathbf{th}}$ iteration. With the iteration going on, the loudness and rate of pulse emission need to be updated accordingly, and the formulas are as follows:

${\mathbf{A}}_{\mathbf{i}}^{\mathbf{t+1}}\mathbf{=\alpha }{\mathbf{A}}_{\mathbf{i}}^{\mathbf{t}}(10)$

${\mathbf{r}}_{\mathbf{i}}^{\mathbf{t+1}}\mathbf{=}{\mathbf{r}}_{\mathbf{i}}^{\mathbf{0}}\left(\mathbf{1-exp}\left(\mathbf{-\gamma t}\right)\right)(11)$

where $\mathbf{\alpha }$ and $\mathbf{\gamma }$ are constants, $\mathbf{\alpha }$ = $\mathit{\gamma }$ = 0.9, as described in reference (Yang, 2010). ${\mathbf{A}}_{\mathbf{i}}^0$ and ${\mathbf{r}}_{\mathbf{i}}^0$ are random number in $\left[\mathrm{1,2}\right]$ and random number in $\left[\mathrm{0,1}\right]$, respectively.

The pseudo code of bat algorithm (Yang, 2010) is shown in Figure 2.

FIGURE 2

FIGURE 2. Pseudo codes of BA.

3.2 Improved bat algorithm proposed

BA algorithm can be regarded as a reduced version of particle swarm. In addition to adding frequency to control bat flight speed, two variables of pulse rate ${\mathbf{r}}_{\mathbf{i}}$ and loudness ${\mathbf{A}}_{\mathbf{i}}$ are added. It also removes the fact that particle swarm optimization can move towards local and global optimal positions, which leads to faster convergence, but it is easy to fall into local optimization, which is its disadvantage. Therefore, based on the above deficiencies, some strategies need to be modified to get out of the local optimal problem and improve the performance of the BA algorithm.

This section proposes a new and improved bat algorithm for SED problem. Firstly, the random black hole strategy is used to update the bat position randomly, and then the Gaussian distribution function is used to jump out of the local optimum. In summary, two major improvements to IBA can be described as follows.

3.2.1 Random black hole strategy

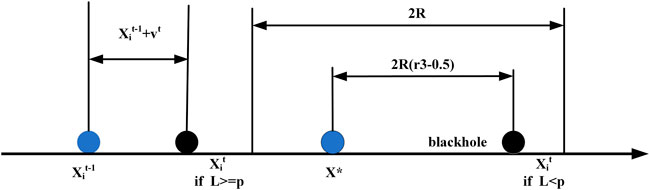
According to the black hole theory, particles could be absorbed by the black hole within a certain range, namely capture, but may also be spit out with a certain probability by the black hole, namely escape. Suppose that the bat swarm is a swarm of particles, and a bat near the current optimal bat is a black hole. The radius of the black hole is $\mathrm{R}$. Within radius $\mathrm{R}$, bats are captured by the black hole, but those caught still have a chance to escape. Introducing the random black hole strategy, if bats are captured, is conducive to accelerating the convergence; Conversely, it can increase the diversity of the population (Chen and Cheng, 2013; Zong et al., 2016; Liang et al., 2018; LV et al., 2019). The principle of the random black hole model is shown in Figure 3.

FIGURE 3

FIGURE 3. Position ${\mathbf{X}}_{\mathbf{i}}^{\mathbf{t}-1}$ updated by random black holes.

The position updating formula by the random black hole strategy can be formulated as follows:

${\mathbf{X}}_{\mathbf{i}}^{\mathbf{t}}\mathbf{=}\{\begin{array}{cc}{\mathbf{X}}_{\mathbf{i}}^{\mathbf{t-1}}\mathbf{+}{\mathbf{v}}^{\mathbf{t}}\mathbf{,}& \mathbf{L\ge p}\\ {\mathbf{X}}_{\mathbf{\ast }}\mathbf{+2R}\left({\mathbf{r}}_{\mathbf{3}}\mathbf{-0}\mathbf{.5}\right)\mathbf{,}& \mathbf{L<p}\end{array}(12)$

where $\mathbf{R}$ is the radius of the black hole, ${\mathbf{r}}_3$, $\mathbf{L}$ and $\mathbf{p}$ are all random numbers in $\left[\mathrm{0,1}\right]$. And the threshold $\mathbf{p}$ represents the capture capability of the black hole. If $\mathbf{L} < p$, bats are attracted to the black hole.

3.2.2 Gaussian mutation

Since the bat algorithm itself is easy to fall into local optimum, in view of this, Gaussian distribution function is introduced to help IBA to escape from local optimum (Kaur and Narang, 2019; Xie et al., 2021), which is depicted below:

${\mathbf{X}}_{\mathbf{i}}^{\mathbf{t}}={\mathbf{X}}_{\mathbf{i}}^{\mathbf{t}}\cdot \left(\mathbf{0.5}+\mathbf{\tau }\cdot \mathbf{N}\left(\mathbf{0,1}\right)\right)(13)$

where ${\mathbf{X}}_{\mathbf{i}}^{\mathbf{t}}$ is the position of ${\mathbf{i}}^{\mathbf{th}}$ bat at the ${\mathbf{t}}^{\mathbf{th}}$ iteration, $\mathbf{\tau }$ is a random number in $\left[\mathrm{0,1}\right]$, and $\mathbf{N}\left(\mathrm{0,1}\right)$ represents the normal distribution with mean value of $0$ and variance of $1$.

The pseudo code of the improved bat algorithm is shown in Figure 4.

FIGURE 4

FIGURE 4. Pseudo code of IBA.

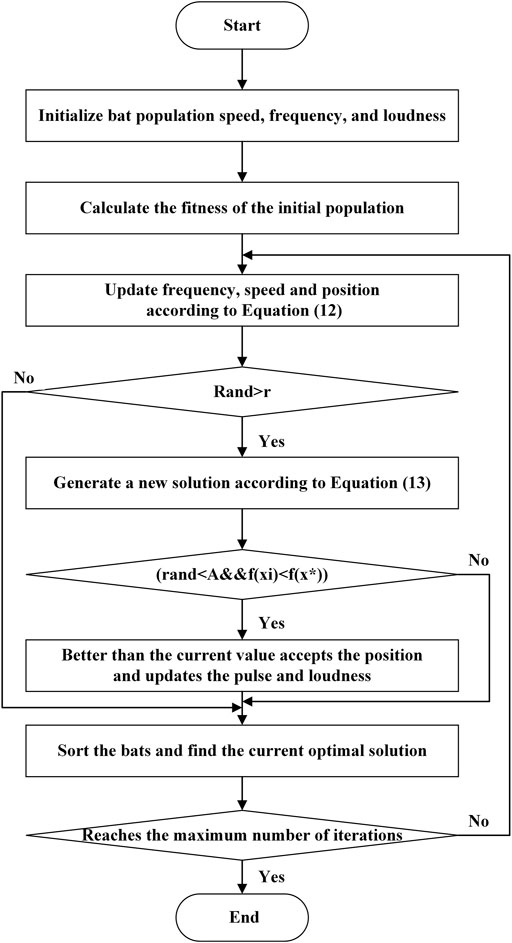
The flow chart of the improved bat algorithm is shown in Figure 5.

FIGURE 5

FIGURE 5. Flow chart of improved bat algorithm.

4 Experimental analysis

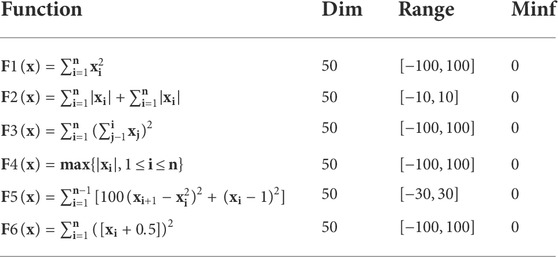
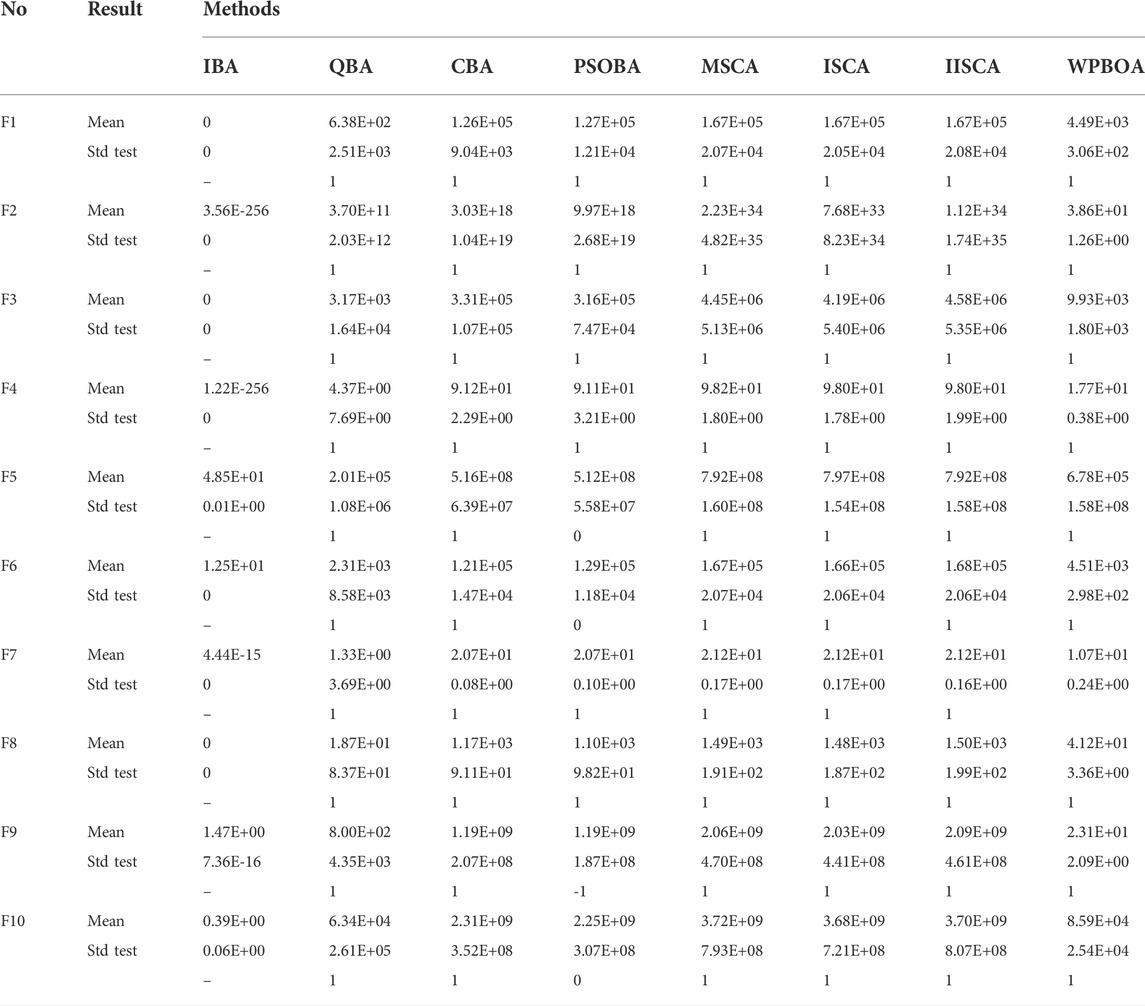
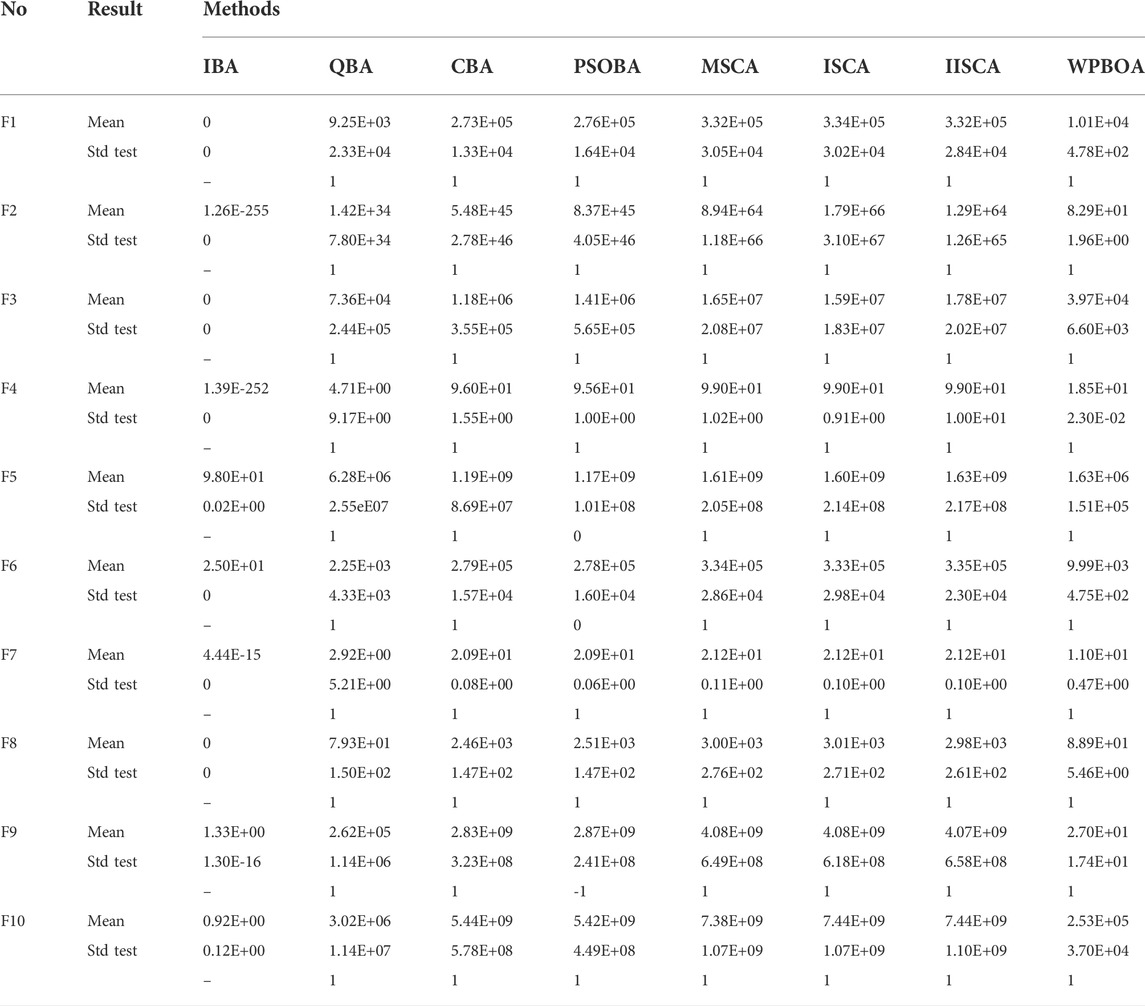
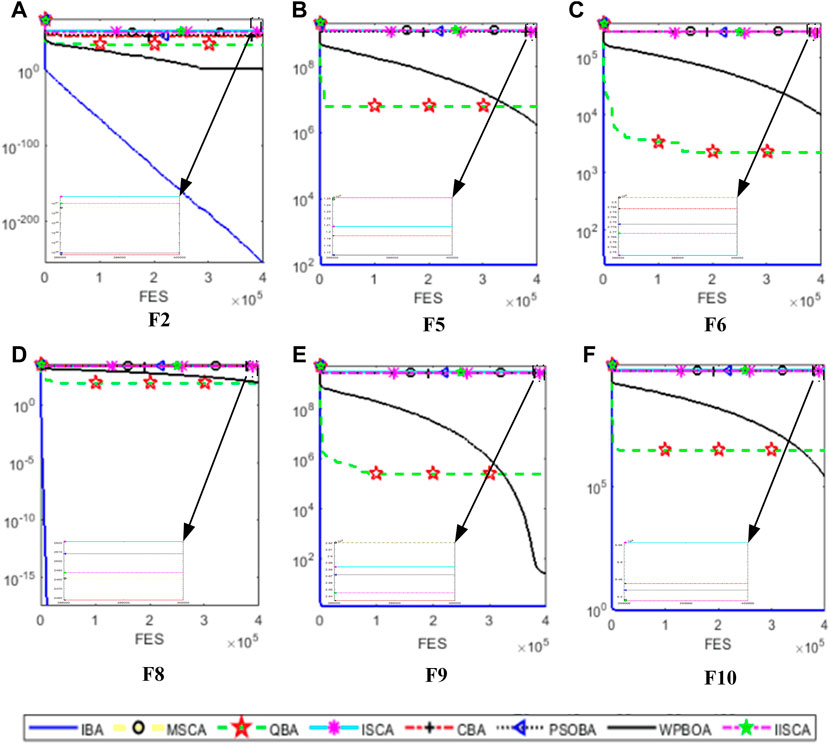
This section conducts simulation experiments based on 10 commonly used benchmark functions (Mirjalili and Lewis, 2016). Firstly, the definitions of these 10 functions are given in Table 1 and Table 2, and then IBA performance is compared with other seven algorithms including CBA (Adarsh et al., 2016), QBA (Zhu et al., 2016), PSOBA (Tchapda et al., 2017), WPBOA (Guo et al., 2021), MSCA (Wang and Lu, 2021), ISCA (Zadehparizi and Jam, 2022) and IISCA (Long et al., 2019). All experiments in this study are conducted in a PC with Windows 10 system, 3.8 GHz Intel Core, 8 GB RAM, and MATLAB R2018b.

TABLE 1

TABLE 1. Description of single-modal benchmark function.

TABLE 2

TABLE 2. Description of multimodal benchmark function.

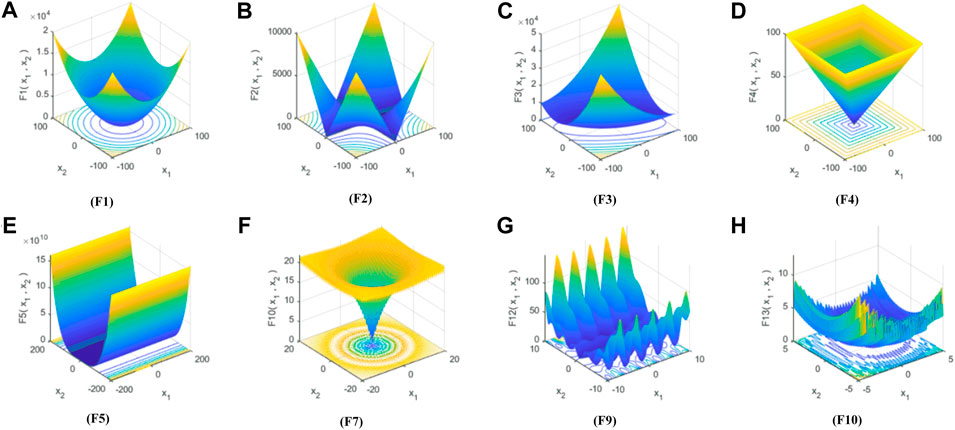
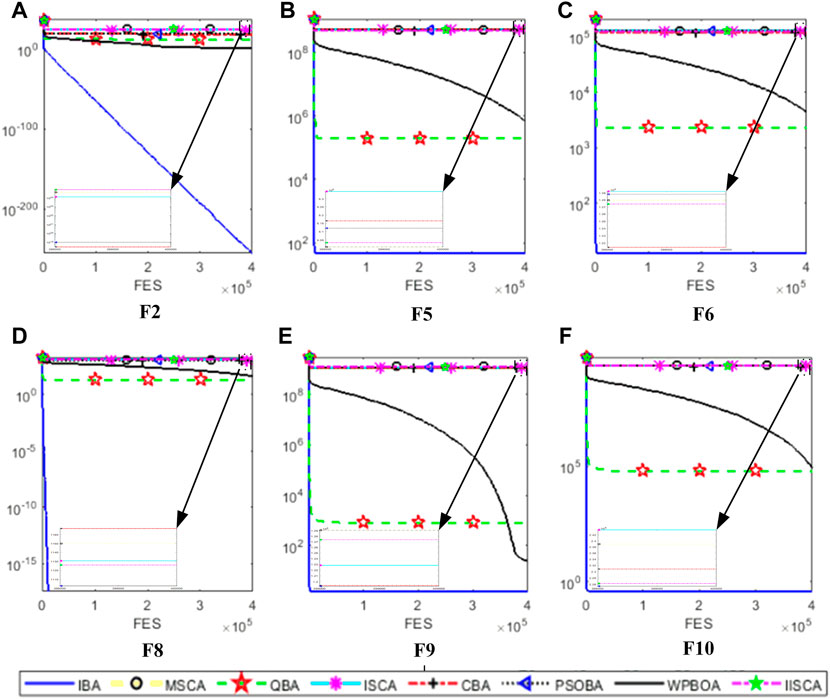
Generally speaking, benchmark functions can be divided into four groups: single-modal, multimodal, fixed dimensional multimodal and composite functions. In this paper, the performance of the proposed IBA method is analyzed and verified by using single-mode and multi-mode functions. The definitions of single-mode and multi-mode benchmark functions are listed in Tables 1 and 2, respectively. Figure 6 shows a typical two-dimensional diagram of some benchmark functions in this paper. Among these 10 benchmarks, F1 to F6 are unimodal functions, and the unimodal function has only one optimal value. However, for the multi-modal functions F7 to F10, the number of local minima increases as the problem dimension increases. In order to make a fair comparison between different algorithms, the function evaluation number (FES) (Kazikova et al., 2021) is utilized to measure the running time of the algorithm. All test functions in this paper have the same FES when searching for the global minimum.

FIGURE 6

FIGURE 6. (A–H) Typical two-dimensional diagram of benchmark function.

4.1 Performance verification of IBA

IBA method is further evaluated on 10 benchmark functions and compared with other seven methods the above mentioned. In this paper, Wilcoxon signed rank test (Yang et al., 2021) is utilized to compare the differences between IBA and other algorithms in the literature, and the significant level $\mathrm{\alpha }$ is set to 0.05, max_FESs on 10 benchmark functions under 50 and 100 dimensions are all 4E+05. In order to obtain better results, each algorithm runs independently for 30 times. The population sizes of IBA and the other seven methods are all $\mathbf{N}$ 20, and the other parameters of the seven methods are derived from the literature.

Table 3 and Table 4 summarize the average results, standard deviation and Wilcoxon signed rank test results of 30 independent runs on 50 and 100 dimensional benchmark functions. The best results of the average and standard deviation are marked in bold. When the $\mathrm{test}$ = 1, 0 and −1, IBA is superior, equivalent and lower than the methods in the above literature respectively. Among the 10 benchmark functions solved by IBA, the results of three functions (F1, F3, and F8) reach the theoretical optimal value, which is better than CBA, QBA, PSOBA, WPBOA, MSCA, ISCA, and IISCA. The results of the other seven functions that do not reach the theoretical optimal value are significantly better than the results of the compared algorithms, and are closer to the theoretical optimal value. The Wilcoxon signed rank test is used to test IBA and the methods in the literature. The results show that IBA is better than most algorithms compared. Equally unsurprisingly, only IBA can obtain optimal solutions or suboptimal solutions with the scale of the problems. It can be seen that the improved IBA algorithm has higher computation accuracy. In the case of statistical results, no method is better than the proposed IBA. In order to more intuitively express the convergence rate of IBA, Figure 7 and Figure 8 show the convergence characteristic curves of the average value of 30 independent tests of six functions. It can be seen from the figure that five algorithms are very close on some benchmark functions, which look like a curve. However, the convergence curves of IBA are all located at the bottom of the figure with the fastest convergence speed and the highest calculation accuracy. It can be concluded that IBA algorithm proposed in this paper is better than the algorithms in the literature, which shows that IBA has strong optimization ability. To sum up, it proves that IBA not only has high precision, but strong stability.

TABLE 3

TABLE 3. Comparison of the results (Dim=50,FES=4e+5).

TABLE 4

TABLE 4. Comparison of the results (Dim=100,FES=4e+5).

FIGURE 7

FIGURE 7. (A–F) Comparison of convergence curves on 50-dimensional.

FIGURE 8

FIGURE 8. (A–F) Comparison of convergence curves on 100-dimensional.

4.2 Application to SED

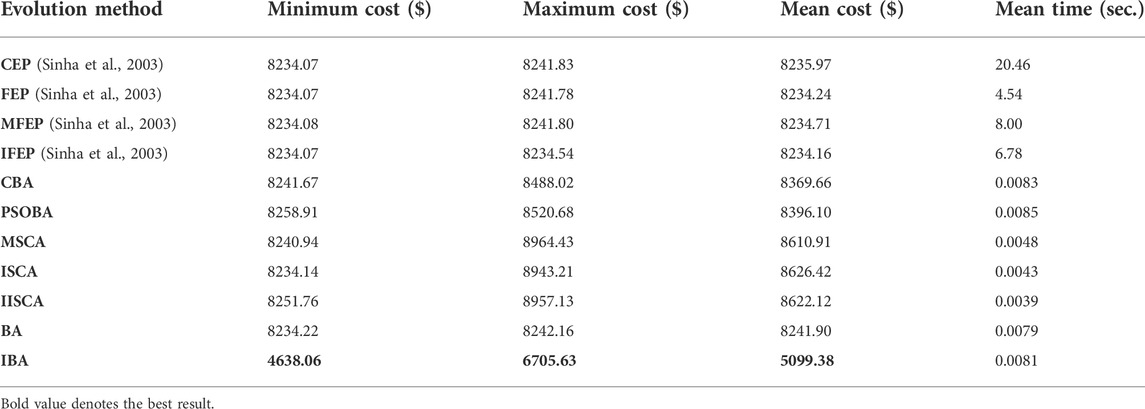
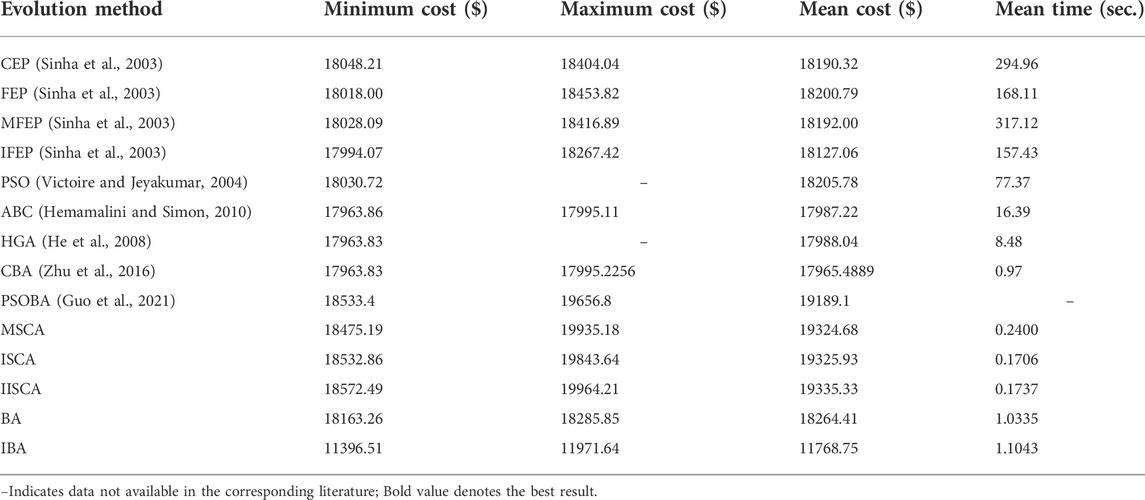
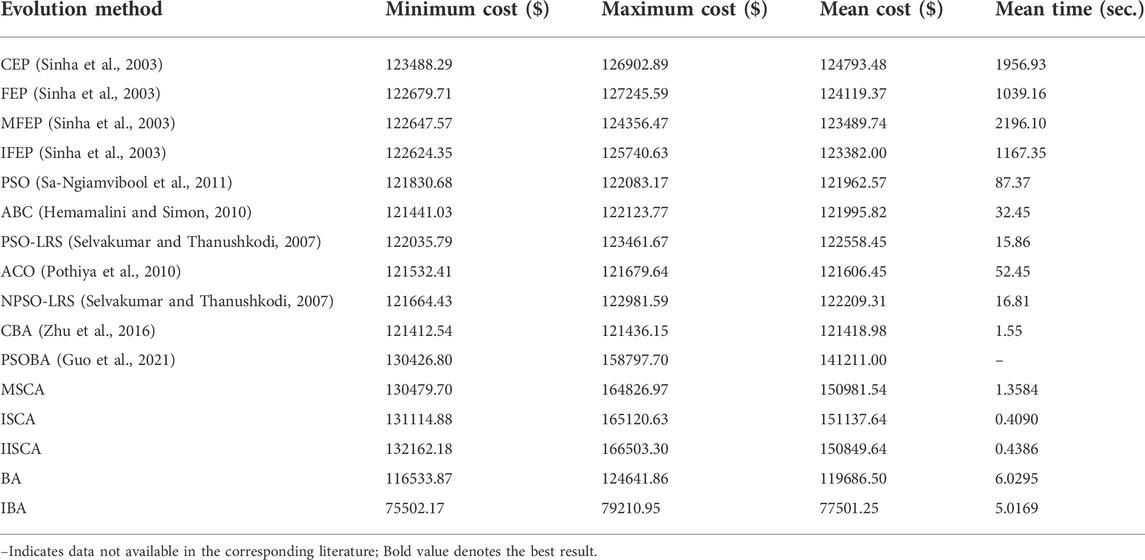
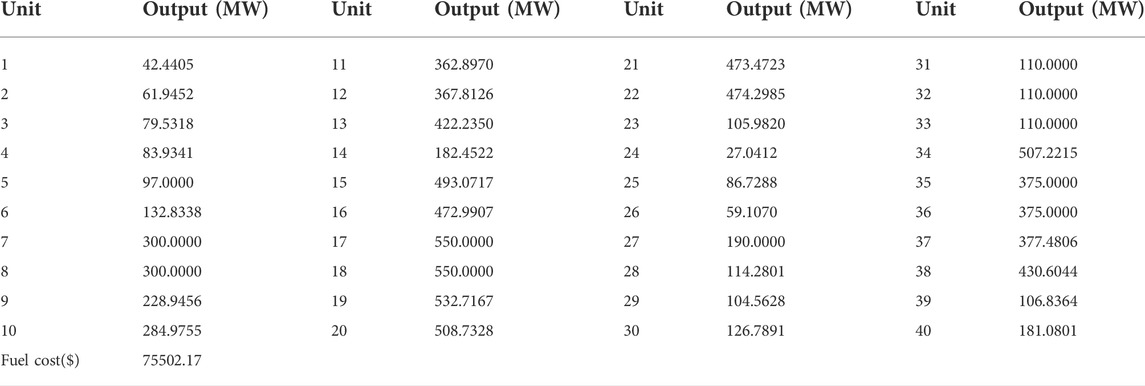
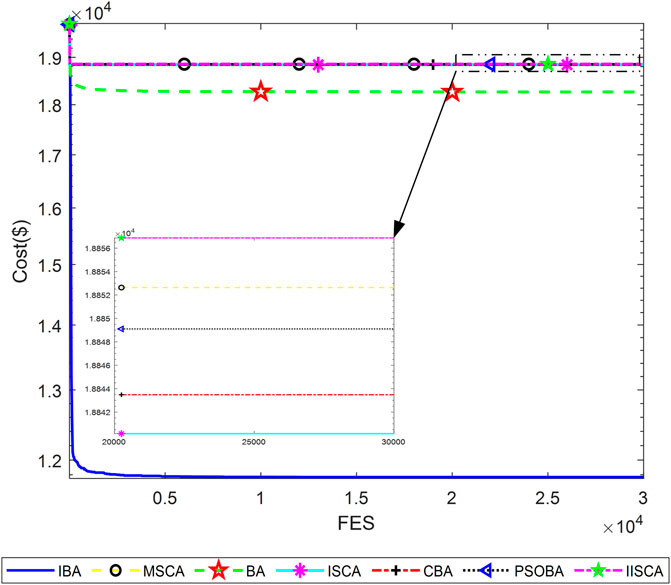
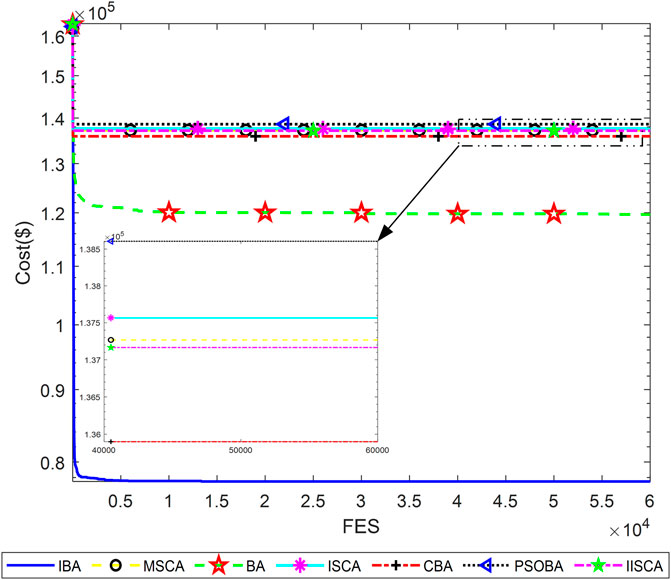
Three power system cases considering the valve point effects from the reference, that are as follows: 1) 3 units and power load demand 850MW; 2) 13 units and power load demand 1800MW; 3) 40 units and power load demand 10500 MW. The details of the three cases can be obtained from reference (Sinha et al., 2003; Niu et al., 2014). All test data are from the literature published for fair comparison. Furthermore, termination criteria max_FESs of 3-unit, 13-unit, and 40-unit systems are respectively set to 100, 30000, and 60000.

The results of minimum, maximum, average cost and average calculation time are shown in Table 5, Table 7 and Table 9. The best results of three cases obtained by IBA are better than all other algorithms. Even the maximum fuel costs of IBA is better than the method in the literature. Although the computation time of IBA is not as fast as other algorithms, its results are still competitive. Table 6, Table 8, and Table 10 show the dispatch of the best results obtained by IBA meeting all constraints. Therefore, it can be concluded that IBA is effective to solve the SED problem. Figure 9, Figure 10, and Figure 11 show the convergence curves of IBA algorithm and other algorithms. It can be seen that compared with other algorithms, IBA can jump out of the local optimum and find the global optimum quickly. From the above discussion, it is evident that the improved BA is effective, for which the detailed reasons are listed as the following: First, Random black hole strategy disables the population to be gathered in the process of evolution to some extent, which further improves the convergence of the IBA; second, Gaussian mutation is adopted in IBA to increase its ability of local search and to improve the quality of the solution. In brief, IBA algorithm overcomes the poor local search capability and the precocious phenomena of the traditional BA, and also effectively improves the global search ability of the BA.

TABLE 5

TABLE 5. Results of case I with 850 mw load demand (3-unit system with valve point effect).

TABLE 6

TABLE 6. Distribution of best results of 3 unit SED problems.

TABLE 7

TABLE 7. Results of case 2 with load demand of 1800 MW (13 unit system with valve point effect).

TABLE 8

TABLE 8. Distribution of best results of 13 unit problems.

TABLE 9

TABLE 9. Results of case III with 10500 MW load demand (40 unit system with valve point effect).

TABLE 10

TABLE 10. Distribution of best results of 40 unit problems.

FIGURE 9

FIGURE 9. Convergence of IBA and other six algorithms in test case 1 (unit 3).

FIGURE 10

FIGURE 10. Convergence of IBA and other six algorithms in test case 2 (unit 13).

FIGURE 11

FIGURE 11. Convergence of IBA and other six algorithms in test case 3 (unit 40).

5 Conclusion

This paper proposes an improved bat algorithm (IBA) with random black hole strategy and Gaussian mutation. Random black hole strategy can make the algorithm converge quickly and increase the population diversity. Gaussian mutation can improve the global search ability of the IBA. Furthermore, IBA is tested on ten benchmark functions compared with the algorithms from the literature. The results show that the performance of IBA algorithm has been improved significantly. Finally, the proposed IBA method is used to solve three different scale of power system problems, in which valve point effect and power balance constraints are considered. The experimental results show that for the SED problem with valve point effect, IBA has better effect on the SED problem in terms of fast convergence speed and high-quality solution. In addition, the good performance of IBA also shows its potential in solving large-scale optimization problems. To sum up, it can be proved that IBA has achieved satisfactory results on benchmark function and SED problem, and provides a competitive alternative to solve nonlinear and nonconvex optimization problems. Furthermore, the combination of large-scale and renewable resources is also a topic for future research.

Data availability statement

The datasets presented in this article are not readily available because these datasets are also a part of the ongoing study. Requests to access the datasets should be directed to XM, mouxiaolin@sztu.edu.cn.

Author contributions

WY and XM designed experiments; RL and YY carried out experiments; RL and YY analyzed experimental results and wrote the manuscript.

Funding

The National Key Research and Development Project of China (No. 2018YFB1700500) and the Scientific and Technological Project of Henan Province (No. 222102110095), Higher Learning Key Development Project of Henan Province (No. 22A120007), the University Scientific Research Platform of Guangdong Province (No. 2019KZDXM033), the University Stability Support Plan Key Project of Shenzhen (No. SZWD2021017).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.977883/full#supplementary-material

References

Adarsh, B. R., Raghunathan, T., Jayabarathi, T., and Yang, X. S. (2016). Economic dispatch using chaotic bat algorithm. Energy 96, 666–675. doi:10.1016/j.energy.2015.12.096

CrossRef Full Text | Google Scholar

Adhvaryyu, S., and Adhvaryyu, P. K. (2020). Application of bio-inspired social spider algorithm in multi-area economic emission dispatch of solar, wind and CHP-based power system. Soft Comput. 24, 9611–9624. doi:10.1007/s00500-019-04468-4

CrossRef Full Text | Google Scholar

Chen, M. Y., and Cheng, S. (2013). Multi - objective particle swarm optimization algorithm based on random black hole mechanism and step-by-step elimination strategy. Control Decis. 28, 1729–1734.

Google Scholar

Chen, X., and Tang, G. (2022). Solving static and dynamic multi-area economic dispatch problems using an improved competitive swarm optimization algorithm. Energy 238, 122035. doi:10.1016/j.energy.2021.122035

CrossRef Full Text | Google Scholar

Dou, X. M., and Qin, N. N. (2020). Enhanced quantum-behaved particle swarm optimization algorithm for power system dispatch problem. J. Chongqing Univ. Posts Telecommun. Sci. Ed. 32, 528–535. doi:10.3979/j.issn.1673-825X.2020.04.004

CrossRef Full Text | Google Scholar

Ellahi, M., Abbas, G., Satrya, G. B., Usman, M. R., and Gu, J. (2021). A modified hybrid particle swarm optimization with bat algorithm parameter inspired acceleration coefficients for solving eco-friendly and economic dispatch problems. IEEE Access 9, 82169–82187. doi:10.1109/access.2021.3085819

CrossRef Full Text | Google Scholar

Guerraiche, K., Dekhici, L., Chatelet, E., and Zeblah, A. (2021). Multi-objective electrical power system design optimization using a modified bat algorithm. Energies 14 (13), 3956. doi:10.3390/en14133956

CrossRef Full Text | Google Scholar

Guo, Y., Liu, X., and Chen, L. (2021). Improved butterfly optimisation algorithm based on guiding weight and population restart. J. Exp. Theor. Artif. Intell. 33, 127–145. doi:10.1080/0952813x.2020.1725651

CrossRef Full Text | Google Scholar

Hassan, H., Alquthami, T., Butt, S. E., Tahir, M. F., and Mehmood, K. (2020). Short-term optimal scheduling of hydro-thermal power plants using artificial bee colony algorithm. Energy Rep. 6, 984–992. doi:10.1016/j.egyr.2020.04.003

CrossRef Full Text | Google Scholar

He, D., Wang, F., and Mao, Z. (2008). A hybrid genetic algorithm approach based on differential evolution for economic dispatch with valve-point effect. Int. J. Electr. Power & Energy Syst. 30, 31–38. doi:10.1016/j.ijepes.2007.06.023

CrossRef Full Text | Google Scholar

Hemamalini, S., and Simon, S. P. (2010). Artificial bee colony algorithm for economic load dispatch problem with non-smooth cost functions. Electr. Power Components Syst. 38, 786–803. doi:10.1080/15325000903489710

CrossRef Full Text | Google Scholar

Kaur, A., and Narang, N. (2019). Optimum generation scheduling of coordinated power system using hybrid optimization technique. Electr. Eng. 101, 379–408. doi:10.1007/s00202-019-00789-7

CrossRef Full Text | Google Scholar

Kazikova, A., Pluhacek, M., and Senkerik, R. (2021). How does the number of objective function evaluations impact our understanding of metaheuristics behavior. IEEE Access 9, 44032–44048. doi:10.1109/access.2021.3066135

CrossRef Full Text | Google Scholar

Li, L. L., Shen, Q., Tseng, M. L., and Luo, S. (2021). Power system hybrid dynamic economic emission dispatch with wind energy based on improved sailfish algorithm. J. Clean. Prod. 316, 128318. doi:10.1016/j.jclepro.2021.128318

CrossRef Full Text | Google Scholar

Liang, H., Liu, Y., Shen, Y., Li, F., and Man, Y. (2018). A hybrid bat algorithm for economic dispatch with random wind power. IEEE Trans. Power Syst. 33 (5), 5052–5061. doi:10.1109/tpwrs.2018.2812711

CrossRef Full Text | Google Scholar

Long, W., Wu, T., Liang, X., and Xu, S. (2019). Solving high-dimensional global optimization problems using an improved sine cosine algorithm. Expert Syst. Appl. 123, 108–126. doi:10.1016/j.eswa.2018.11.032

CrossRef Full Text | Google Scholar

Lv, F. L., Luo, F. M., and Zhang, B. C. (2019). Gravitational search algorithm based on random black hole and adaptive strategy. J. Xihua Univ. Nat. Sci. Ed. 38 (3), 55–60.

Google Scholar

Ma, H., Yang, Z., You, P., and Fei, M. (2017). Multi-objective biogeography-based optimization for dynamic economic emission load dispatch considering plug-in electric vehicles charging. Energy 135, 101–111. doi:10.1016/j.energy.2017.06.102

CrossRef Full Text | Google Scholar

Medani, K., Sayah, S., and Bekrar, A. (2018). Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electr. Power Syst. Res. 163, 696–705. doi:10.1016/j.epsr.2017.09.001

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Mouassa, S., Bouktir, T., and Salhi, A. (2017). Ant lion optimizer for solving optimal reactive power dispatch problem in power systems. Eng. Sci. Technol. Int. J. 20, 885–895. doi:10.1016/j.jestch.2017.03.006

CrossRef Full Text | Google Scholar

MugemanyiQu, S., Qu, Z., Rugema, F. X., Dong, Y., Bananeza, C., and Wang, L. (2020). Optimal reactive power dispatch using chaotic bat algorithm. IEEE Access 8, 65830–65867. doi:10.1109/access.2020.2982988

CrossRef Full Text | Google Scholar

Niu, Q., Zhang, H., Wang, X., Li, K., and Irwin, G. W. (2014). A hybrid harmony search with arithmetic crossover operation for economic dispatch. Int. J. Electr. Power & Energy Syst. 62, 237–257. doi:10.1016/j.ijepes.2014.04.031

CrossRef Full Text | Google Scholar

Pan, J. S., Shan, J., Chu, S. C., Jiang, S., Zheng, S., and Liao, L. (2021). A multigroup marine predator algorithm and its application for the power system economic load dispatch. Energy Sci. Eng. 10, 1840–1854. doi:10.1002/ese3.957

CrossRef Full Text | Google Scholar

Pothiya, S., Ngamroo, I., and Kongprawechnon, W. (2010). Ant colony optimisation for economic dispatch problem with non-smooth cost functions. Int. J. Electr. Power & Energy Syst. 32, 478–487. doi:10.1016/j.ijepes.2009.09.016

CrossRef Full Text | Google Scholar

Rugema, F. X., Yan, G., Mugemanyi, S., Jia, Q., Zhang, S., and Bananeza, C. (2021). A cauchy-Gaussian quantum-behaved bat algorithm applied to solve the economic load dispatch problem. IEEE Access 9, 3207–3228. doi:10.1109/access.2020.3034730

CrossRef Full Text | Google Scholar

Sa-Ngiamvibool, W., Pothiya, S., and Ngamroo, I. (2011). Multiple tabu search algorithm for economic dispatch problem considering valve-point effects. Int. J. Electr. Power & Energy Syst. 33, 846–854. doi:10.1016/j.ijepes.2010.11.011

CrossRef Full Text | Google Scholar

Selvakumar, A. I., and Thanushkodi, K. (2007). A new particle swarm optimization solution to nonconvex economic dispatch problems. IEEE Trans. Power Syst. 22, 42–51. doi:10.1109/TPWRS.2006.889132

CrossRef Full Text | Google Scholar

Singh, D., and Dhillon, J. S. (2019). Ameliorated grey wolf optimization for economic load dispatch problem. Energy 169, 398–419. doi:10.1016/j.energy.2018.11.034

CrossRef Full Text | Google Scholar

Singh, D., and Dhillon, J. S. (2021). Improved directional bat algorithm based electric power dispatch. Electr. Power Components Syst. 48 (19-20), 2089–2105. doi:10.1080/15325008.2021.1910381

CrossRef Full Text | Google Scholar

Sinha, N., Chakrabarti, R., and Chattopadhyay, P. K. (2003). Evolutionary programming techniques for economic load dispatch. IEEE Trans. Evol. Comput. 7, 83–94. doi:10.1109/tevc.2002.806788

CrossRef Full Text | Google Scholar

Tchapda, G., Wang, Z., and Sun, Y. (2017). Application of improved particle swarm optimization in economic dispatch of power system. Proceeding of the 10th Int. Symposium Comput. Intell. Des. (ISCID), December 2017, Hangzhou, China, IEEE 2, 500–503.

CrossRef Full Text | Google Scholar

Victoire, T., and Jeyakumar, A. E. (2004). Hybrid PSO–SQP for economic dispatch with valve-point effect. Electr. Power Syst. Res. 71, 51–59. doi:10.1016/j.epsr.2003.12.017

CrossRef Full Text | Google Scholar

Wang, M., and Lu, G. (2021). A modified sine cosine algorithm for solving optimization problems. IEEE Access 9, 27434–27450. doi:10.1109/access.2021.3058128

CrossRef Full Text | Google Scholar

Xie, J. X., Gao, Y. L., and Yu, H. L. (2021). A hybrid particle swarm optimization algorithm based on Gaussian mutation and Levy flight strategy. J. Baoji Univ. Arts Sci. Sci. Ed. 41, 5–10. doi:10.13467/j.cnki.jbuns.2021.01.002

CrossRef Full Text | Google Scholar

Xu, T., and Xiang, Z. (2021). Modified constant modulus algorithm based on bat algorithm. J. Intelligent Fuzzy Syst. 41 (3), 4493–4500. doi:10.3233/jifs-189709

CrossRef Full Text | Google Scholar

Yang, W., Peng, Z., Yang, Z., Guo, Y., and Chen, X. (2021). An enhanced exploratory whale optimization algorithm for dynamic economic dispatch. Energy Rep. 7, 7015–7029. doi:10.1016/j.egyr.2021.10.067

CrossRef Full Text | Google Scholar

Yang, X. S. (2010). A new metaheuristic bat-inspired algorithm, 284. Springer: Springer Berlin Heidelberg, 65–74.

CrossRef Full Text | Google Scholar

Zadehparizi, F., and Jam, S. (2022). Basic and improved sine–cosine optimization algorithms for antenna design. Iran. J. Sci. Technol. Trans. Electr. Eng. 46, 303–309. doi:10.1007/s40998-022-00485-6

CrossRef Full Text | Google Scholar

Zare, M., Narimani, M. R., Malekpour, M., Azizipanah-Abarghooee, R., and Terzija, V. (2021). Reserve constrained dynamic economic dispatch in multi-area power systems: An improved fireworks algorithm. Int. J. Electr. Power & Energy Syst. 126, 106579. doi:10.1016/j.ijepes.2020.106579

CrossRef Full Text | Google Scholar

Zhou, J., Wang, C., Li, Y., Wang, P., Li, C., Lu, P., et al. (2017). A multi-objective multi-population ant colony optimization for economic emission dispatch considering power system security. Appl. Math. Model. 45, 684–704. doi:10.1016/j.apm.2017.01.001

CrossRef Full Text | Google Scholar

Zhu, B., Zhu, W., Liu, Z., Duan, Q., and Cao, L. (2016). A novel quantum-behaved bat algorithm with mean best position directed for numerical optimization. Comput. Intell. Neurosci. 2016, 1–17. doi:10.1155/2016/6097484

CrossRef Full Text | Google Scholar

Zong, C. F., Dai, M., and Zhao, H. L. (2016). Application of improved black hole particle swarm optimization algorithm in environmental economic dispatch of power system. Electrotech. Electr. 2016, 33–36. doi:10.3969/j.issn.1007-3175.2016.01.009

CrossRef Full Text | Google Scholar