Edge intelligence enabled optimal scheduling with distributed price-responsive load for regenerative electric boilers

Heat supply accounts for a substantial amount of terminal energy usage. However, along with price rises in primary energy, there is an urgent need to reduce the average cost of energy consumption during the purchasing of thermal services. Electric heating, an electricity-fed heating production and delivery technology, has been suggested as a promising method for improving heating efficiency, due to the ease of scheduling. However, the traditional centralized operating methods of electricity purchasing rely on explicit physical modeling of every detail, and accurate future predictions, the implementation of which are rarely practical in reality. To facilitate model-free decisions in the field of electricity purchasing, heat storage, and supply management, aimed at cost saving in a real-time price environment, this study proposes a scheduling framework based on deep reinforcement learning (DRL) and the existence of responsive users. First, the structure of a distributed heating system fed by regenerative electric boilers (REBs), which facilitate shiftable heat-load control, is introduced. A terminal heat demand response model based on thermal sensation vote (TSV), characterizing the consumption flexibility of responsive users, is also proposed. Second, due to thermal system inertia, the sequential decision problem of electric heating load scheduling is transformed into a specific Markov decision process (MDP). Finally, the edge intelligence (EI) deployed on the demand side uses a twin delayed deterministic policy gradient (TD-3) algorithm to address the action space continuity of electric heating devices. The combination of a DRL strategy and the computing power of EI enables real-time optimal scheduling. Unlike the traditional method, the trained intelligent agent makes adaptive control strategies according to the currently observed state space, thus avoiding prediction uncertainty. The simulation results validate that the intelligent agent responds positively to changes in electricity prices and weather conditions, reducing electricity consumption costs while maintaining user comfort. The adaptability and generalization of the proposed approach to different conditions is also demonstrated.

1 Introduction

Heat, the most significant component of energy end-use, accounted for nearly half of all global final energy consumption in 2021 (IEA, 2021). Worldwide, nearly 90% of heat is generated by fossil fuels, and China consumes nearly 70% of coal used for district heating globally. Generally, the source-side centralized unit generates the heat that is delivered through the heat network, with inevitable losses in traditional heating systems. Moreover, during winter in northern China, the operation mode of the thermal power unit—‘fixing power based on heat’—limits its ability to promptly follow the changing load and peak regulation capacity (Li J. et al., 2021). Because of the requirement to meet carbon neutrality targets, Beijing has proposed renovating more than 120 million square meters of buildings with intelligent heating by the end of the 14th Five-Year Plan. In addition, with traditional fossil energy sources depleted and primary energy prices growing, the cost of traditional heating is skyrocketing. Therefore, improving energy use efficiency, and reducing the cost of heating services have become huge challenges.

To alleviate this problem, electric heating devices (EHDs) on the load side provide an excellent means of improving thermal efficiency. Liu et al. (2019) analyzes the influence of power-to-heat devices on the operational reliability of energy hubs. EHDs can be integrated with renewable energy resources, thereby contributing to a significant reduction in the carbon emissions of the heating sector (Javanshir et al., 2022). Due to the ease of electricity scheduling, EHDs can also provide flexibility to the distribution grid through demand response (DR) (Chen et al., 2019). Li et al. (2020) exploit the thermal inertia of buildings in district heating networks to improve the flexibility of the distribution network. Alipour et al. (2019) propose a DR management model for electricity and heat consumers, demonstrating the impact of electricity price fluctuations on heat loads over different time scales. In addition, the combination of heat storage and EHDs can further improve the system’s operational flexibility (Tan et al., 2022). Regenerative electric boilers (REBs) are typical of such hybrid systems supplying distributed electrical heating users. Hence, it is expected that in the near future REBs will play an integral role in the efficiency of district heating systems.

However, access to a large number of REBs is prone to spike loads, due to the large-scale and potentially undiversified nature of electric heating loads (Li S. et al., 2022). Hence, reliable automation control technology is essential for secure grid operation. In general, numerous model-based methodologies are applied to electric heating load management problems. Li Z. et al. (2021), for example, transform the nonlinear microgrid operation problem involving thermal energy flow into a mixed-integer linear programming (MILP) model, effectively coordinating active/reactive power and thermal flow scheduling. Gonzato et al. (2019) present a hierarchical model predictive control (MPC) methodology to manage the heat demand of the building network, and thereby reduce peak demand. Ostadijafari et al. (2020) propose an approximate economic linearized model for temperature control of intelligent buildings based on price response, while meeting occupant comfort levels. Li et al. (2022b) propose an MPC method combined with approximate dynamic programming (ADP), to enable coordinated management of electrical and thermal energy in practical microgrids. Despite several potential benefits, model-based optimization methods also have certain pitfalls: 1) costly detailed physical models are a prerequisite, and it is challenging to ensure accuracy (Zhang et al., 2021), especially given the high-order nature of such modeling (Zhang et al., 2019). 2) For load scheduling problems, model-based optimization relies heavily on the accuracy of price forecasting data (Song et al., 2021). Thus, prediction deviations can easily contribute to significantly unsatisfactory heating performance. 3) The long computing time of the iterative algorithm barely enables online applications (Liu et al., 2022).

In contrast to model-based methods, a forecasting process before decision-making is not compulsory in reinforcement learning (RL), i.e., a “model-free” control approach. Hence, data-driven methods do not rely on prediction accuracy. Deep reinforcement learning (DRL) replaces agent reward tables or function settings in traditional Q-learning with deep neural networks (DNNs). As a result, it has better representational capabilities to adapt to more complex control problems, thus enabling “end-to-end” control (Duan et al., 2016). In recent times, DRL has been widely used in energy management to improve the operational performance of power systems , and without the need to acquire precise physical system models (Du and Li, 2020; Wang et al., 2021). Compared to electrical loads, heat loads offer greater flexibility in the balancing process, i.e., a larger state-action space, which fits well with the fast decision-making ability of DRL in a high-dimensional solution space. Claessens et al. (2018) demonstrate the validity of a convolutional neural network (CNN) in Q-iteration under thermal loads response settings. Zhang et al. (2019) apply DRL to the thermal management of office buildings, based on the building energy model, thereby increasing the possibility of reducing heating demand. Zhao et al. (2022) utilize a dueling network to cope with the hysteresis of the heat transfer process in a district heating system (DHS) in order to optimize the scheduling of heating loads in industrial parks. Yang et al. (2021) propose a double deep Q-network (DDQN) with an experience replay mechanism to adaptively control the indoor environment of temperature and CO₂.

However, there are a few drawbacks to the data-driven scheduling approach: a large amount of data from different scenarios, as well as computational power, is required to train the model. Therefore, it is imperative to combine DRL and edge computing with powerful computational power in a technology known as edge intelligence (EI) (Lee, 2022). In recent years, the application of EI in smart power systems has been emerging rapidly worldwide. Cen et al. (2022) demonstrate the applicability of microservices and edge computing apparatuses in the distribution grid computational resource configuration. An integrated cloud-edge architecture, combined with reinforcement learning to facilitate cost-effective smart buildings, is proposed by Zhang et al. (2021). Fang et al. (2020) exploit the distributed structure of EI to reduce the computing burden on the cloud, thus enabling economic scheduling of virtual power plants. A single-edge computing apparatus allows integration of multiple input sources, and accomplishes application in multiple scenarios simultaneously. Hence, EI is well-suited for the automatic control of numerous distributed EHDs. Nevertheless, research into this has not been widely conducted. To better exploit the potential of distributed electric heating loads, and to respond effectively to changes in dynamic electricity prices, we propose an EI-based DRL process of optimizing REB scheduling.

The main contribution of the study is as follows. First, a study of the optimized distribution of terminal electric heating to customers under dynamic environmental conditions is conducted. In light of building characteristics, meteorological conditions, and user preferences, we propose a demand response model for electric heating users based on a thermal sensation vote (TSV). Second, the multi-objective optimal scheduling problem is formulated as a specific Markov decision process (MDP), with a reward in energy costs and a discomfort penalty. We propose a DRL control strategy based on a twin delayed deterministic policy gradient (TD3) algorithm to address the action space continuity of EHDs. The combination of the powerful computing power of EI with DRL enables optimal control of EHDs in real time. In comparison with work relying on accurate forecasting data and a detailed model, here the trained agent makes an adaptive control strategy decision according to the observed state-space. In this way undesirable actions attributed to prediction uncertainty can be avoided. Finally, the feasibility of the proposed approach in frequently changing external environments is validated, for it maintains good adaptability to extreme weather and user preferences that are significantly different from the training process. By learning electricity price patterns, DRL performs better at decreasing electricity costs than traditional methods.

2 Problem formulation

The system shown in Figure 1 is taken as an example. The existing electric heating market consists of the power grid, load aggregator (LA), and heat loads. LAs sign heating contracts with distributed users and receive dynamic electricity prices from the grid. As aggregation service providers, LAs negotiate with the power grid on behalf of a group of small-scale heating users to participate in DR schemes with the aim of cost reduction. In the DR model, LAs compensate terminal users when demand cannot be satisfied so as to encourage them to participate in demand response based on their different heating requirements. During peak hours, customers participating in DR are often asked to reduce their demand appropriately in exchange for lower heating bills. Furthermore, due to the high price of electricity, LAs would sometimes rather work at low levels of heating power and pay compensation to achieve reduced costs. With thermal storage capacity, LAs can take advantage of the peak-to-valley difference in electricity prices to reduce their costs.

FIGURE 1

FIGURE 1. Distributed heating system model.

LAs apply edge intelligence technology to coordinate the direct control of distributed electric heating devices to satisfy the needs of terminal users. Thus, the EI is integrated into the control module of the REB. The REB near to the distributed heat load is responsible for consuming electricity, storing heat and supplying thermal loads. Temperature sensors are deployed in the load building to collect relevant data. Outdoor temperature and solar radiation information is available from a weather station. Information on electricity prices is published by the grid. The EI of the LAs summarizes and analyzes all the above information. Accordingly, a thermal service management strategy to autonomously control the REB operation is developed. In this study, the indoor temperature field distribution is assumed to be uniform.

2.1 Building heating load

The indoor temperature variation of a building is mainly influenced by the heat supplied, the outdoor temperature, the building’s thermal characteristics, and the category of heating devices (Li et al., 2022c). Typically, there is a positive correlation between heat demand and the difference between the indoor and outdoor temperature of the building. The greater the temperature difference, the more energy is required for heating. However, accurate thermodynamic models representing a natural system are fairly complicated, while the black-box models barely understand the underlying processes. Therefore, by combining the above properties, the gray-box model is available to simplify the precise physical model (Lork et al., 2020). Meanwhile, the state-space representing the temperature of a building can be transformed into a discrete set of difference equations. The indoor temperature variation can be calculated by the following equation:

${\mathit{T}}_{\mathit{i},\mathit{t}+\mathit{1}}^{\mathbf{in}}={\mathit{T}}_{\mathit{i},\mathit{t}}^{\mathbf{in}}-\frac{{\mathit{T}}_{\mathit{i},\mathit{t}}^{\mathbf{in}}-{\mathit{T}}_{\mathit{i},\mathit{t}}^{\mathbf{out}}}{{\mathit{R}}^{\mathit{i}-\mathit{a}}\times {\mathit{C}}_{\mathit{i}}}-\frac{{\mathit{T}}_{\mathit{i},\mathit{t}}^{\mathbf{in}}-{\mathit{T}}_{\mathit{i},\mathit{t}}^{\mathit{e}}}{{\mathit{R}}^{i-e}\times {\mathit{C}}_{\mathit{i}}}+\frac{\left({\mathit{u}}_{\mathit{b},\mathit{t}}^{\mathit{i}}·{\mathit{Q}}_{\mathit{i},\mathit{t}}^{\mathit{heat}}+{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathbf{inter} }+{\mathit{A}}_{\mathit{w}}\times {\mathit{I}}_{\mathit{t}}^{\mathbf{sol} }\right)\times \mathit{\beta }}{{\mathit{C}}_{\mathit{i}}},(1)$

${\mathit{T}}_{\mathit{i},\mathit{t}+1}^{\mathit{e}}={\mathit{T}}_{\mathit{i},\mathit{t}}^{\mathit{e}}-\frac{{\mathit{T}}_{\mathit{i},\mathit{t}}^{\mathit{e}}-{\mathit{T}}_{\mathit{i},\mathit{t}}^{\mathbf{in} }}{{\mathit{R}}^{\mathit{i}-\mathit{e}}\cdot {\mathit{C}}_{\mathit{e}}}+\frac{\left({\mathit{u}}_{\mathit{b},\mathit{t}}^{\mathit{i}}\cdot {\mathit{Q}}_{\mathit{t}}^{\mathit{h}\mathit{e}\mathit{a}\mathit{t}}+{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathbf{inter} }+{\mathit{A}}_{\mathit{w}}\cdot {\mathit{I}}_{\mathit{t}}^{\mathbf{sol} }\right)\cdot (1-\mathit{\beta })}{{\mathit{C}}_{\mathit{e}}},(2)$

where $T_{i,t}^{in}$ and $T_{i,t}^{out}$ are the indoor and outdoor temperature of building $i$ at time $t$, respectively. $T_{i,t}^e$ is the non-observable building envelope temperature. $R^{i-a}$ is the overall thermal resistance between the interior and the ambient conditions of the building, including conduction and ventilation losses. $C_e$ and $C_i$ are the building materials and interior heat capacity, respectively. $R^{i-e}$ is the thermal resistance between the air and the building envelope. $Q_{i,t}^{heat}$ is the heat demand of user i. $P_{i,t}^{inter }$ is the internal heat gain associated with indoor appliance utilization and occupant activity. $I_t^{sol }$ is the energy flux from the sun through the windows. $A_w$ is the effective window area. Lastly,$\beta$ is a coefficient that sets the share between the heat injected into the interior, and the material, which in this study is assumed to be 1.

2.2 Regenerative electric boiler

The REB consists of an electric boiler (EB) and a heat accumulator (HA) device. The structure of the REB is shown in Figure 2. The advantage of the REB is that it can be used not only as a heat source for direct heat supply but also to achieve adjustable load shift with the storage property of the heat accumulator. Furthermore, the REB boosts power consumption at low electricity prices and releases stored heat during peak hours to reduce peak-to-valley load variation. In this study, the electrode-type electric boiler with water tank storage is used. It utilizes the property of high thermal resistance of the medium to achieve heating electrification. By adjusting the depth of submergence of the electrode in water, the current through it can be changed to achieve continuous regulation of the heating power. The thermal power of an electric boiler can be expressed by the following constraints:

${\mathit{Q}}_{\mathit{t}}^{\mathit{E}\mathit{B}}={\mathit{\eta }}_{\mathit{e}\mathit{b}}{\mathit{P}}_{\mathit{t}}^{\mathit{E}\mathit{B}},(3)$

${\mathit{Q}}_{\mathit{t}}^{\mathit{E}\mathit{B}}={\mathit{Q}}_{\mathit{d},\mathit{t}}^{\mathit{E}\mathit{B}}+{\mathit{Q}}_{\mathit{i}\mathit{n},\mathit{t}}^{\mathit{T}},(4)$

$\mathbf{0}\le {\mathit{P}}_{\mathit{t}}^{\mathit{E}\mathit{B}}\le {\mathit{P}}^{\mathit{E}\mathit{B},\mathit{max}},(5)$

${\mathit{Q}}_{\mathit{t}}^{\mathit{h}\mathit{e}\mathit{a}\mathit{t}}={\mathit{Q}}_{\mathit{d},\mathit{t}}^{\mathit{E}\mathit{B}}+{\mathit{Q}}_{\mathit{o}\mathit{u}\mathit{t},\mathit{t}}^{\mathit{T}},(6)$

FIGURE 2

FIGURE 2. Regenerative electric boiler structure.

where $Q_t^{EB}$ and $P_t^{EB}$ are the thermal and electrical power of the electric boiler at time step $t$, respectively, and ${\eta }_{eb}$ is the conversion efficiency of the electric boiler. The heat output of the electric boiler comprises two parts $Q_{d,t}^{EB}$ and $Q_{in,t}^T$, one of which is supplied directly to the heat load, and the rest stored in the water tank.

The HA stores surplus heat produced by the boiler and supplies it to users when needed. In this study, the heat accumulator employs water as the heat accumulator medium. There is an inevitable loss during energy conversion with the outside of the tank, which is caused by the difference in water temperature between the injected and output tanks (Alipour et al., 2019). Hence, the efficiency of heat charging and discharging is considered. The loss is represented by the relationship with the previous state of heat stored. At time t, the amount of available heat in the tank is calculated by the following equation:

${\mathit{E}}_{\mathit{t}}=(\mathbf{1}-{\mathit{\eta }}_{\mathit{s}}){\mathit{E}}_{\mathit{t}-\mathbf{1}}+({\mathit{I}}_{\mathit{c},\mathit{t}}{\mathit{\eta }}_{\mathit{c}}{\mathit{Q}}_{\mathit{i}\mathit{n},\mathit{t}}^{\mathit{T}}-\frac{{\mathit{I}}_{\mathit{d},\mathit{t}}{\mathit{Q}}_{\mathit{o}\mathit{u}\mathit{t},\mathit{t}}^{\mathit{T}}}{{\mathit{\eta }}_{\mathit{d}}})\mathit{\Delta }\mathit{t},(7)$

where $E_t$ and $E_{t-1}$ are the heat stored in the thermal tank at time step $t$ and $t-1$, respectively, and ${\eta }_s$, ${\eta }_c$, and ${\eta }_d$ are the dissipation efficiency, the heat charging and discharging efficiency of the HA, respectively. $I_{c,t}$ and $I_{d,t}$ are binary decision variables indicating the charging and discharging modes of the tank at time $t$; $I_{c,t}, I_{d,t}\in \left\{\mathrm{0,1}\right\}$. $I_{c,t}=1$ when the tank operates in the charging model; otherwise, $I_{d,t}=1$. However, the water tank is unable to store and release heat at the same time due to mechanical limitations, so the following constraint needs to be ensured:

${\mathit{I}}_{\mathit{c},\mathit{t}}\times {\mathit{I}}_{\mathit{d},\mathit{t}}=0.(8)$

Furthermore, to model the practical state of the heat accumulator facility, the limit charging and discharging rate, and the capacity of storage are constrained as

${\mathit{E}}^{\mathit{min}}\le {\mathit{E}}_{\mathit{t}}\le {\mathit{E}}^{\mathit{max}},(9)$

$\mathbf{0}\le {\mathit{Q}}_{\mathit{i}\mathit{n},\mathit{t}}^{\mathit{T}}\le {\mathit{Q}}_{\mathit{i}\mathit{n}}^{\mathit{T},\mathit{max}},(10)$

$\mathbf{0}\le {\mathit{Q}}_{\mathit{o}\mathit{u}\mathit{t},\mathit{t}}^{\mathit{T}}\le {\mathit{Q}}_{\mathit{o}\mathit{u}\mathit{t}}^{\mathit{T},\mathit{max}},(11)$

where $E^{max}$ and $E^{min}$ are, respectively, the upper and lower capacity bounds of the HA. $Q_{in}^{T,max}$ and $Q_{out}^{T,max}$ are the maximum heat charging and discharging rates, respectively. Since the heat accumulator can transfer energy in two directions, the REB has the integrated characteristics of source and load, i.e., it can be regarded as both a heat producer and consumer.

2.3 Heat demand response model

Aside from economic factors, user comfort levels cannot be ignored when optimizing the scheduling of heat loads. There is a certain degree of variability in users’ temperature perceptions: User comfort is not affected by changing the indoor temperature within a specific range, which thus provides flexibility to regulate the heat demand as part of the price response. Thus, the thermal sensation vote (TSV) is introduced to evaluate user satisfaction with the indoor temperature, as shown in Figure 3.

FIGURE 3

FIGURE 3. Thermal sensation vote.

When TSV = 0, the coziest experience for occupants is provided, and $T_{com}$ is the most comfortable indoor temperature. When TSV<0.1, the temperature range is $[T_{low}^b,T_{high}^b]$, and the user has no significant sensation of temperature variation. When TSV<0.5, the temperature range is $[T_{min},T_{max}]$, in which users perceive the temperature change, but it is still acceptable. When this is exceeded, the user experiences noticeable discomfort. $T_{max}$ and $T_{min}$ are the upper and lower limits of temperatures permitted by users. For users not participating in the DR, the room temperature will be kept within a small range close to the coziest temperature. Therefore, user preferences for non-participation in DR are set as follows:

${\mathit{T}}_{\mathit{l}\mathit{o}\mathit{w}}^{\mathit{b}}\le {\mathit{T}}_{\mathit{i},\mathit{t}}\le {\mathit{T}}_{\mathit{h}\mathit{i}\mathit{g}\mathit{h}}^{\mathit{b}}.(12)$

During peak hours, the indoor temperature of customers participating in DR is allowed to fluctuate within an acceptable range, i.e., $[T_{min},T_{max}]$. From the view of economic cost, the indoor temperature is unlikely to remain in the interval $[T_{high}^b,T_{max}]$. Therefore, the indoor temperature preference setting for users participating in DR satisfies the following constraint:

${\mathit{T}}_{\mathit{min}}\le {\mathit{T}}_{\mathit{i},\mathit{t}}\le {\mathit{T}}_{\mathit{h}\mathit{i}\mathit{g}\mathit{h}}^{\mathit{b}}.(13)$

When the temperature of the load departs from the set comfort zone, the user will experience discomfort. It is comparatively easier to describe the level of the user’s discomfort. Therefore, the discomfort level of the heat load can be represented as

${\mathit{\rho }}_{\mathit{n}}=\frac{{\mathit{e}}^{\mathit{so}{\mathit{t}}_{\mathit{t}}}-1}{\mathit{e}-1},\forall \mathit{t}>0,(14)$

$\mathit{s}\mathit{o}{\mathit{t}}_{\mathit{h}}=\frac{\left|{\mathit{T}}_{\mathit{t}}-{\mathit{T}}_{\mathit{c}\mathit{o}\mathit{m}}\right|}{{\mathit{T}}_{\mathit{h}\mathit{i}\mathit{g}}-{\mathit{T}}_{\mathit{min}}},\forall \mathit{t}>0,(15)$

where $so{t}_h$ indicates the percentage of deviation from the preferred temperature.

Then, according to Eq. 1,2, the demand regulation of the heat user’s response can be obtained:

${\mathit{Q}}_{\mathit{i}}^{\mathit{min}}\le {\mathit{Q}}_{\mathit{i},\mathit{t}}^{\mathit{h}\mathit{e}\mathit{a}\mathit{t}}\le {\mathit{Q}}_{\mathit{i}}^{\mathit{h}\mathit{i}\mathit{g}\mathit{h}}.(16)$

The EI determines the initial heating action based on economic goals. However, in order to maintain the comfort level of the end-user, the edge intelligence center adjusts the heating mode according to the comfort constraint:

${\mathit{\chi }}_{\mathit{f},\mathit{t}}^{\mathit{i}}=\{\begin{array}{ccc}0& \mathit{i}\mathit{f}& {\mathit{T}}_{\mathit{t}}^{\mathit{l}}>{\mathit{T}}_{\mathit{h}\mathit{i}\mathit{g}\mathit{h}}\\ {\mathit{\chi }}_{\mathit{t}}^{\mathit{i}}& \mathit{i}\mathit{f}& {\mathit{T}}_{\mathit{min}}<{\mathit{T}}_{\mathit{t}}^{\mathit{i}}<{\mathit{T}}_{\mathit{h}\mathit{i}\mathit{g}\mathit{h}}\\ 1& \mathit{i}\mathit{f}& {\mathit{T}}_{\mathit{t}}^{\mathit{i}}<{\mathit{T}}_{\mathit{min}}\end{array},(17)$

where $T_t^i$ is the operational temperature of the building at time t, and${\chi }_{f,t}^i$ is the final decision action of the controller.

2.4 Objective function

The objective of thermal service management for LAs is to minimize operating costs while maintaining indoor temperature within the desired range for users. Specifically, the LAs compensate customers for deviations from the preferred temperature range. The goal is to minimize the energy costs and compensation fees. The objective function can be defined as follows:

$\mathbf{min}\mathit{f}={\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}\left\{{\mathit{\omega }}_1\left[{\mathit{\lambda }}_{\mathit{t}}\cdot {\mathit{P}}_{\mathit{t}}^{\mathit{E}\mathit{B}}\cdot \mathit{\Delta }\mathit{t}\right]+{\mathit{\omega }}_2\cdot \mathit{\zeta }\cdot {\mathit{\rho }}_{\mathit{n},\mathit{d}\mathit{c}}\right\},(18)$

where the first item on the right side of the equation is associated with the cost of electricity consumption, and the second item is the penalty due for a violation of the comfort zone. $T$ is the total time steps in a complete heat load management period. ${\omega }_1$ and ${\omega }_2$ are weighting factors for each item based on the user’s preference; ${\lambda }_t$ is the real-time electricity price from the grid. The factor $\zeta$ is introduced to compensate for the indoor temperature discomfort level. Different kinds of trade-offs between energy profit and discomfort penalty can be achieved by adapting the weighting factors in Eq. 17. Raising the weight of ${\omega }_2$ means a higher priority on comfort. Under some tariff conditions, and to minimize long-term costs, the REB would rather cease operating and pay compensation for violations. The constraints of the electric heating load management problem are shown as Eqs. 1–17.

3 Methods

The optimal scheduling problem of EHL is to control the electric boiler’s direct supply power and the heat storage’s heat exchange rate at each time step to minimize total operating costs. Thus, the optimization problem can be viewed as a sequential decision problem and formulated as a Markov decision process. Due to the excellent computing ability of DRL, it is a promising application with traditional edge computing. The deployment of EI enables an effective combination of the two methods. In this study, an algorithm of an AC structure is adapted and detailed in the following.

3.1 Conversion to Markov decision process

In this section, the electric heating load scheduling problem is formulated as a MDP, which considers the operational constraints of regenerative electric boiler heating systems, varying weather conditions, and dynamic electricity prices.

Typically, the MDP consists of state, action, and reward functions, which can be represented as $S,A,r$, where S represents a set of states, A represents a set of actions, and r represents the reward function, i.e., the results of the interaction of state and action. At each step t, the agent observes the environment state, $s_t\in S$, and chooses an action, $a_t\in A\left(s\right)$, based on policy $\pi$, where $A\left(s\right)$ represents the set of all admissible actions at state $s_t$. The agent then receives the reward, $r(s,a)$, and the system evolves to the next state, ${s^{\prime }}_t\in S$. In this scenario, the agent is the edge intelligence control center, and the environment is the ambient conditions observed by the agent.

State space: A state comprises a set of physical quantities that reflect the environment. In the process of heat load scheduling, the observed state consists of outdoor temperature, indoor temperature, preferred indoor temperature set by users, electricity price, solar radiation, and the available capacity of HA. Since the scheduling of heat load involves time dependence, the behavior of the end-users usually follows a repetitive diurnal pattern. The agent can capture this by adding a time-state component to the state vector.

${\mathit{s}}_{\mathit{t}}=[{\mathit{T}}_{\mathit{t}}^{\mathit{i}\mathit{n}},{\mathit{T}}_{\mathit{t}}^{\mathit{o}\mathit{u}\mathit{t}},{\mathit{T}}^{\mathit{p}\mathit{r}\mathit{e}},{\mathit{\lambda }}_{\mathit{t}},{\mathit{I}}_{\mathit{t}}^{\mathit{s}\mathit{o}\mathit{l}},{\mathit{E}}_{\mathit{t}},\mathit{t}](19)$

Action space: The agent decides the action to perform based on the observed state. For electric heating load management, the action includes the input power of the electric boiler, and the charging or discharging heat rate of the HA. Due to the regulating continuity of the electrode submersion depth, and the volume of input or output water, the actions are continuous within predefined ranges. Thus, the agent’s action at state $s_t$ can be denoted as

${\mathit{a}}_{\mathit{t}}=[{\mathit{P}}_{\mathit{t}}^{\mathit{E}\mathit{B}},{\mathit{Q}}_{\mathit{t}}^{\mathit{T}}].(20)$

Reward function formulation: The agent’s objective is to minimize the total operating cost, including the energy cost related to total power consumption, and the penalty for indoor temperature deviation from the comfort zone. Therefore, the reward $r_t$ obtained by the agent at step $t$ can be defined as

${\mathit{r}}_{\mathit{t}}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})=-({\mathit{w}}_1\cdot {\mathit{\lambda }}_{\mathit{t}}\cdot {\mathit{a}}_{\mathit{t}}\left[0\right]\cdot \mathit{\Delta }\mathit{t})-{\mathit{w}}_{\mathbf{2}}\cdot \mathit{\tau }\left({\mathit{s}}_{\mathit{t}}\right),(21)$

$\mathit{\tau }\left({\mathit{S}}_{\mathit{t}}\right)=\{\begin{array}{l}\mathbf{0},\mathit{i}\mathit{f}{\mathit{T}}_{\mathit{min}}\le {\mathit{T}}_{\mathit{t}}^{\mathit{i}\mathit{n}}{\le }_{\mathit{h}\mathit{i}\mathit{g}\mathit{h}}\\ \mathit{\zeta }.{\mathit{\rho }}_{\mathit{n},\mathit{d}\mathit{c}},\mathit{o}\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{w}\mathit{i}\mathit{s}\mathit{e}\end{array}(22)$

where the minus sign at the front of the right side of Eq. 21 is to convert the cost minimization problem into the classical reward maximization form of MDP, and $\tau \left(s_t\right)$ is the penalty for temperature violation.

The decision about which action to perform in a specific state is determined by the policy π. The agent interacts with the environment on the basis of the policy, and forms trajectories of states, actions, and rewards $\left(s_1, a_1, r_1, s_2, a_2, r_2\dots \right)$. From the perspective of MDP, the efficacy of the action $a_t$ under a state $s_t$ can be evaluated by using the state-action value function $Q_{\pi }(s,a)$:

${\mathit{Q}}_{\mathit{\pi }}(\mathit{s},\mathit{a})={\mathit{E}}_{\mathit{\pi }}\left[{\displaystyle \sum }_{\mathit{k}}^{\mathit{T}}{\mathit{\gamma }}^{\mathit{k}}{\mathit{r}}_{\mathit{t}+\mathit{k}}|{\mathit{s}}_{\mathit{t}}=\mathit{s},{\mathit{a}}_{\mathit{t}}=\mathit{a}\right],(23)$

where $\gamma \in \left[\mathrm{0,1}\right]$ is the discount factor for future rewards, and the agent is to explore the optimal control policy ${\pi }^{\ast }$ to maximize the reward received, defined as ${\pi }^{\ast }=arg\underset{a\in A}{max}{Q}_{\pi }(s,a)$.

3.2 Reinforcement learning structure

The DDPG is a model-free and off-policy algorithm using actor-critic architecture. Compared to the DQN-like algorithm, the DDPG can learn policy in continuous state-action space without discretization, hence alleviating the curse of dimensionality. However, the DDPG has the problem of overestimation. To solve this, Fujimoto et al. (2018) propose a twin delayed DDPG (TD-3), adopting the idea of double Q-learning. TD3 consists of a pair of critic-networks along with an actor-network ($Q_{{\theta }_1,}{Q}_{{\theta }_2,}{\pi }_{\varphi }$), all of which are accompanied by their target network (${Q^{\prime }}_{{\theta }_1,}{Q^{\prime }}_{{\theta }_2,}{{\pi }^{\prime }}_{\varphi }$). The critic network minimizes the loss of updating itself via (23). The actor updates the deterministic policy gradient with a sampled policy gradient, as presented in (24),

$\mathit{ℒ}\left(\mathit{\theta }\right)=\mathit{arg}\mathit{min} {\mathit{N}}^{-1}{\displaystyle \sum {(\mathit{y}-{\mathit{Q}}_{{\mathit{\theta }}_{\mathit{i}}}(\mathit{s}, \mathit{a}))}^2},(24)$

${\mathit{\nabla }}_{\mathit{\varphi }}\mathit{J}\left(\mathit{\varphi }\right)={\mathit{N}}^{-\mathbf{1}}\mathit{\Sigma }\left({\mathit{\nabla }}_{\mathit{a}}{\mathit{Q}}_{\mathit{\theta }}(\mathit{s},\mathit{a}){|}_{\mathit{s}={\mathit{s}}^{\mathit{t}},\mathit{a}={\mathit{\pi }}_{\mathit{\varphi }}\left({\mathit{s}}^{\mathit{t}}\right)}{\mathit{\nabla }}_{\mathit{\varphi }}{\mathit{\pi }}_{\mathit{\varphi }}\left(\mathit{s}\right){|}_{\mathit{s}={\mathit{s}}^{\mathit{t}}}\right),(25)$

$\mathit{y}=\mathit{r}+\mathit{\gamma }\underset{\mathit{i}=\mathbf{1,2}}{\mathit{min}}{\mathit{Q}}_{{{\mathit{\theta }}^{\prime }}_{\mathit{i}}}({\mathit{s}}^{\prime },{\mathit{a}}^{\prime }),(26)$

${\mathit{a}}^{\prime }={\mathit{\pi }}_{{\mathit{\varphi }}^{\prime }}\left({\mathit{s}}^{\prime }\right)+\mathit{\nu },\mathit{\nu }=\mathit{c}\mathit{l}\mathit{i}\mathit{p}(\mathit{o}(\mathit{\mu },\mathit{\sigma },\mathit{\omega }),-\mathit{c},\mathit{c}).(27)$

The agent selects the minimum value of the twin target network outputs as shown in (25), where $a^{\prime }$ is the target action, which improves the algorithm’s stability. Due to the policy update delaying strategy, the actor-network is updated after several critic updates, which reduces the potential for mistake spreading. Plus, the noise is introduced to the target policy when forming the target. In this study, the noise is generated by the Ornstein–Uhlenbeck process, which can improve the exploration efficiency in inertial systems, where $\nu$ is the clipped OU noise and $c$ is the edge value. This smoothing method will keep the action close to the original target, improving algorithm stability and convergence in the stochastic domain.

The framework of the TD3-based autonomous EHL management approach for the REB system is shown in Figure 4, where the key step is the clipped double Q-learning process and the delayed policy update. Specifically, the trained actor-network chooses an action under the current observed state $s_t$. The action is then executed by the EB and HA systems. The environment transits to the next state, which the agent regards as $s_{t+1}$, and the agent receives present rewards. Finally, the transition of states, actions, rewards, and next states are stored in the experience memory P. For centralized training, each agent will sample a mini-batch of size $N\ast (s_t,a_t,s_{t+1},r_t)$ from P. The parameters of the critic will be updated by minimizing the time difference error via (23), and the actor will be updated by the policy gradient via (24). The target networks will be updated as follows:

${{\mathit{\theta }}^{\prime }}_{\mathit{i}\mathbf{1}}\leftarrow \mathit{\tau }{\mathit{\theta }}_{\mathit{i}\mathbf{1}}+(\mathbf{1}-\mathit{\tau }){{\mathit{\theta }}^{\prime }}_{\mathit{i}\mathbf{1}},(28)$

${{\mathit{\theta }}^{\prime }}_{\mathit{i}\mathbf{2}}\leftarrow \mathit{\tau }{\mathit{\theta }}_{\mathit{i}\mathbf{2}}+(\mathbf{1}-\mathit{\tau }){{\mathit{\theta }}^{\prime }}_{\mathit{i}\mathbf{2}},(29)$

${{\mathit{\varphi }}^{\prime }}_{\mathit{i}}\leftarrow \mathit{\tau }{{\mathit{\varphi }}^{\prime }}_{\mathit{i}}+(\mathbf{1}-\mathit{\tau }){{\mathit{\varphi }}^{\prime }}_{\mathit{i}},(30)$

where $\tau \ll 1$ is the target update parameter. Thus, the slow update of the target will improve learning stability. As time progresses, this process continues. As we can see from the agent’s interaction with the environment, the proposed method requires only instantaneous observation for the decision at each time step. Therefore, the developed data-driven method enables direct mapping from known states to heat load management decisions without the uncertainty of predictive information. The training procedure of the proposed TD3-based approach can be found in Algorithm 1.

FIGURE 4

FIGURE 4. Framework of TD3-based DRL approach.

ALGORITHM 1

Algorithm 1. Training procedure of the proposed TD3-based EHD scheduling strategy

3.3 Edge intelligence solution

The proposed DRL approach can gradually explore the correct policy by interacting with the environment. The appropriate decision-making model is developed in an extensive training process. Because of the excellent ability of edge computing, it is inevitable that DRL will be combined with edge computing. Moreover, the REB can be integrated by EI with effective technologies, such as information technology and suitable software control. Edge Intelligence consists of edge nodes and terminal nodes. The terminal nodes collect the output, the state of the heating equipment, and the users’ data, such as preference setting and temperature state. The edge nodes receive the information uploaded by the terminal nodes, and carry out effective filtering and calculation. After processing, the edge nodes transmit the required gradient information back to the terminal devices. This is beneficial for real-time control and online training of the model.

Because of the actor-critic structure of DRL, we implement the model in a hybrid way. The actor is deployed on the terminal nodes to make adaptive control decisions locally in real time. It is not necessary to upload all the data collected from the devices and users to the edge. The critic is deployed on the edge nodes to collect all the decisions made by the terminal nodes. The critic trains the model with the gradient information from the actor. Instead of complete data information, only limited gradient and state information is transmitted between edge and terminal nodes for training and expanding the experience pool. Thus, the requirement for communication delays and bandwidth is reduced.

4 Case study

4.1 Simulation setup

In this study, a simulation where the LA provides a service for 10 terminal electric heating users in a region is created to test the proposed approach. The LA receives the price signal from the power grids, and the weather information from the local meteorologic station. The edge intelligence center is deployed on the REB for optimal scheduling. The parameters of the REB and the heating load characteristics of a single house in this study are shown in Table 1. The day-ahead electricity price data and weather data of Norway are applied. Data from November 2018 to December 2019 are used as the training dataset, and data from the same period in the following year are used for testing verification. The distribution of the dataset is shown in Figure 5. Furthermore, the users’ preferred comfort temperature is set to 21°C. When the temperature deviates from the comfort zone, the LA needs to compensate the user, where the compensation factor $\zeta$ is set to 0.05.

TABLE 1

TABLE 1. Parameters of DHS.

FIGURE 5

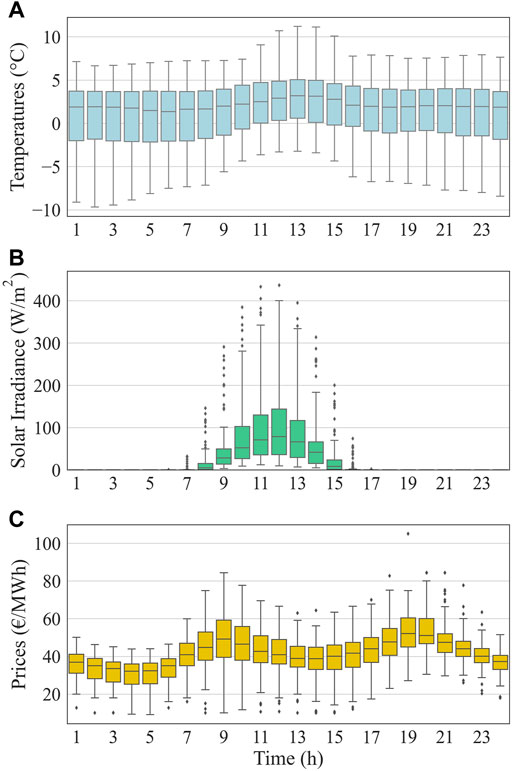
FIGURE 5. Distribution of the training dataset: (A) ambient temperature, (B) solar radiation, and (C) electricity price.

The proposed algorithm applied by edge intelligence is based on the actor-critic structure. The actor-double critic network of the proposed method has different hidden layers, however. A rectified linear unit (ReLU) is used as the activation function for the hidden layers, while the tanh function of the actor-network in the output layer is used to solve the vanishing gradient problem, and fits exactly with the action space of the heat accumulator. The structure of the actor-critic network is shown in Figure 6, while the rest of the hyperparameters of the agent training are shown in Table 2.

FIGURE 6

FIGURE 6. Actor and critic network structure.

TABLE 2

TABLE 2. DRL training parameters.

4.2 Results

4.2.1 Comparison with other approaches

In this study, the feasibility and accessibility of the EI learning scheme is illustrated by feeding the well-trained DRL-based agent with arbitrary testing data of the external environment, including time-varying prices and heat demand. In detail, the average time for determining a temporal set of strategies containing the output power of EB and the exchange power of HA is 16 ms, demonstrating that the real-time electric heating load scheduling is effectively enabled by the approach as presented. Specifically, the optimal results of the desired relatively long-term rewards over the course of a week are obtained through 168 iterations, without any prerequisite for forecasting information.

The comparative results of three different methods—MPC, DDPG, and the TD3 approach—are shown in Table 3, while Figure 7 details the information about energy cost and temperature deviation of each iteration. It can easily be seen that although the MPC method results in lower electricity costs by providing 7.9% less heat than DDPG, it causes higher temperature deviation and variation compared to the relatively fixed coziest temperature. Hence, the temperature constraint is violated. Unless the LA raises the compensation fee considerably, the terminal users will not accept the heating service, which means that MPC-based scheduling is hardly applicable.

TABLE 3

TABLE 3. Simulation results.

FIGURE 7

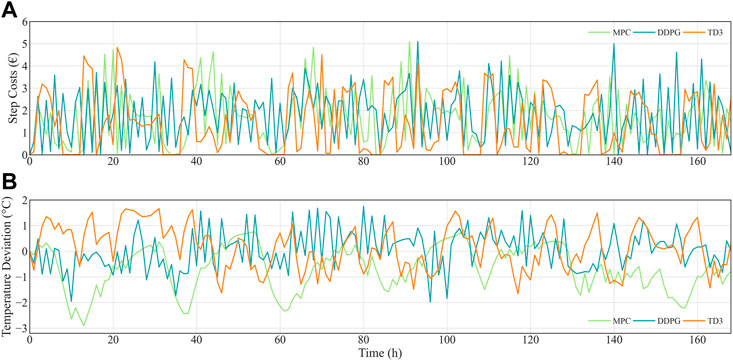
FIGURE 7. Comparison of different methods of testing results: (A) each step average energy cost and (B) average temperature deviation from the most comfortable level.

By contrast, the DRL approach is able to output the indoor temperature, which is much closer to the preset preference value, and guarantee the fluctuation is maintained within quite a small range. As a result of higher quality thermal services, the compensation expenses and total thermal service costs are significantly reduced through a DRL-based approach. In particular, the TD3-based approach saves 26.2% in energy costs, but compensate users a bit more than the DDPG method. Nevertheless, the method presented here achieves the lowest total cost of heating service among all methods mentioned. This demonstrates that the TD3 approach makes the felicitous trade-off between energy costs and terminal users’ comfort. Moreover, although the TD3 approach consumes 0.79% more power than the MPC method, energy costs are reduced by 13.5%. It can be concluded that the proposed approach is more adept at taking advantage of changes in electricity prices, and at exploiting the capacity potential of heat storage.

4.2.2 Strategy sensitivity analysis

The effects of environmental conditions on the control strategy of EBs and HAs, including electricity prices, and indoor and ambient temperatures, are examined in this section. An example of the decision-making model generated by a well-trained agent through the training set is shown in Figure 8, which neglects solar radiation. The generated strategy determines the control decisions on the output power of EBs, and the exchange power of HAs in confronting different state spaces. As shown in Figure 8, fluctuations in price and temperature have different influence on the REB action-space. Regardless of the electricity price, the EB always inclines toward the same output action under the same temperature. However, when the temperature drops, there is a significant increase in EB output power. By contrast, the higher the electricity price, the more likely the HA is to work in discharging mode. Typically, there is a clear difference in HA action patterns with 45 €/GWh as the boundary at a fixed ambient temperature. The HA is inclined to release more heat at a lower electricity price, implying a higher response priority to electricity price changes. In short, the action-spaces of EBs and HAs are more sensitive to temperature and price variations, respectively. The different sensitivities to diverse factors guarantees that the proposed approach ensures a higher level of user comfort while exploiting the energy storage capacity to save costs. Nevertheless, the final strategy decision is not only associated with temperature and price, but is also limited by the currently available heat in the HA. The optimal daily scheduling results are presented in the following section.

FIGURE 8

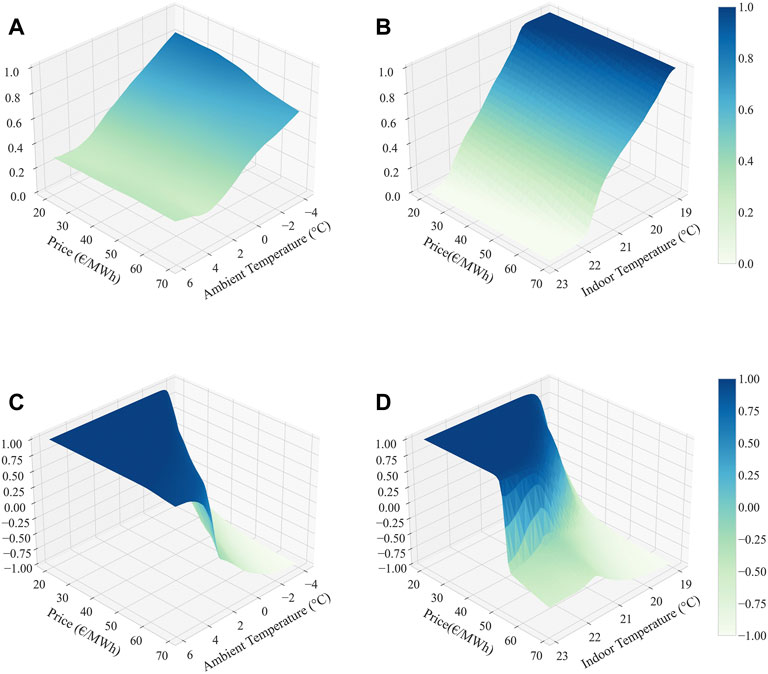
FIGURE 8. Control strategy of electric boiler and heat storage under (A/C) fixed indoor temperature of 21°C and (B/D) fixed ambient temperatures of 0°C.

4.2.3 Adaptability to different conditions

The EI deployed on the distributed REBs employs the decision-making model generated by a trained agent for optimal scheduling. In this section, different scenarios demonstrate the adaptability of DRL-based decision strategies to address system uncertainty. Specifically, the demonstration is performed in 4 different scenarios, with diverse weather conditions, electricity prices, and terminal user preferences that deviate from the training process. The different scenarios and results are as follows.

Scenarios 1&2: These scenarios are set up to test the optimal scheduling validity of the proposed approach under different weather and price conditions. Specifically, the variation in the action and state space within a 1-day cycle of dispatch is shown in more detail. The entire heating season is divided into two parts: the early heating period, with an average ambient temperature of 4°C, and the late heating period, with an average ambient temperature of 0°C, corresponding to scenarios 1 and 2, respectively. The scheduling results of a random day during different period are shown in Figure 9. Due to the relatively lower electricity prices and the greater indoor–outdoor temperature difference, the REB in scenario 2 operates at a higher power, and supplies 35.34% more heat than scenario 1. Moreover, the electricity price has significant peaks from 8:00 to 11:00 and 18:00 to 20:00, resulting in the strategy following habitual daily patterns. Since the solar irradiance and outdoor temperature are higher from 9:00 to 16:00, the EB operates at low power during this period. At peak hours, the heat storage releases more heat, while the EB is inclined to work at lower power. It will even shut down if the available heat in the HA is sufficient in the daytime. Due to the low electricity price from 1:00 to 7:00 and 13:00 to 15:00, the energy consumption during this period is substantial and the HA stores the surplus heat.

FIGURE 9

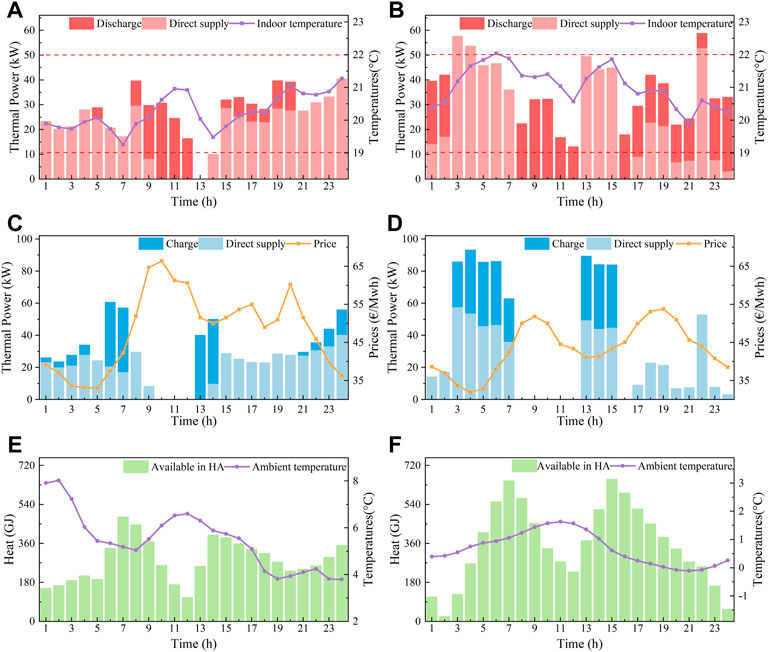
FIGURE 9. Scheduling results of 1 day in Scenarios 1 (left column) and 2 (right column) heating period: (A/B) output power of REB and average indoor temperatures, (C/D) input power of REB and electricity prices, and (E/F) available heat stored in heat accumulator and ambient temperatures.

Scenario 3: There is sometimes abnormal extreme weather, such as low temperatures caused by a cold wave, which challenges the electric heating system operation. Therefore, this scenario is designed to test the adaptability of the proposed approach to the sort of extreme weather not observed during the training process. The ambient temperature is assumed to be on average 6°C lower than the training dataset, and the solar irradiance is assumed to be weak. The optimal scheduling results of scenario 3 are shown in Figure 10. It can be observed that the indoor temperature is still maintained close to the preferred 21°C, but is widely variable. In addition, the indoor temperature is violated a little bit at 12:00. Compared to the case above, the REB provides substantially more heat, and the EB sometimes even operates at full capacity. To be more specific, the heat supply is increased by 69.13% and 24.96% in contrast to scenarios 1 and 2, respectively. Moreover, the HA is fully charged at low prices to adequately exploit its capacity potential. Consequently, the HA continues to release heat at peak hours until there is no available capacity. This demonstrates that the proposed approach has generalization ability for extreme weather conditions deviating from the training process. The applicability under actual anomalous weather conditions is achieved by the DRL-based stochastic exploration process.

FIGURE 10

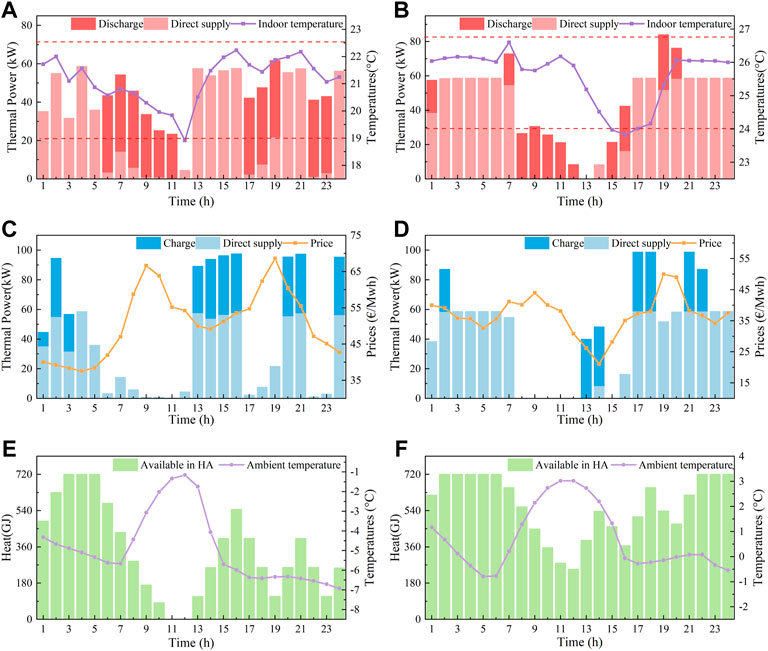
FIGURE 10. Scheduling results of 1 day in Scenarios 3 (left column) and 4 (right column) heating period: (A/B) output power of REB and average indoor temperatures, (C/D) input power of REB and electricity prices, and (E/F) available heat stored in heat accumulator and ambient temperatures.

Scenario 4: The load scale accessed by LA and user preference settings are dynamically changing. Accordingly, the LA has to adjust the REB scheduling policy properly. This scenario aims to evaluate the adaptability of the proposed approach in satisfying heating quality and quantity demands that differ from the training setup. Hence, there are 2 new terminal users added to the aggregated group. Furthermore, the most comfortable preferred temperature for all users is increased to 26°C. The optimal scheduling results of scenario 4 are shown in Figure 10. It can be observed that the indoor temperature is maintained within [24°C, 26.5°C] except from 16:00 to 17:00. The REB operating mode is more variable than scenarios 1 and 2, given the higher quality of heat service demand. Thus, there is a bit of indoor temperature violation, i.e., 0.03°C and 0.15°C. This scenario validates the excellent adaptability of the proposed method to different user scales and preferences. However, given the capacity limitation of the device, the temperature variation is greater than the case above. Therefore, it is recommended that LA expands the capacity of REB for larger regulation capability.

In brief, the scheduling results of 4 different scenarios provide evidence that the proposed TD3-based optimal scheduling approach makes adaptive strategies in different conditions to minimize users’ electricity costs while satisfying their preferences. In addition, the agent can make appropriate trade-offs between energy costs and comfort. In other words, the EI employing DRL-based strategy has learned the formulation of the autonomous optimal electric heating service scheduling policy.

5 Conclusion

In this study, an automated EI-based DRL control framework is presented, allowing direct optimization decisions on distributed electric heating users in a cost-effective way. A heat demand-response model based on TSV is proposed to quantitatively characterize the price response of users with different preferences. The data-driven TD3-based reinforcement learning approach employed by EI addresses the continuity of REBs action-space properly. The combination of the powerful computing power of edge computing and reinforcement learning enables optimal control of EHD in real time. The decision-making and critic aspects of EI are deployed at the terminal and edge nodes, respectively, to improve response efficiency and accuracy. The simulation results show that electric boiler and heat storage control strategies are more sensitive to temperature and price, respectively. Compared to the traditional method, the proposed approach will save 13.5% in electricity purchasing costs, and maintain the indoor temperature close to the desired comfort level with minor deviation. In particular, the proposed approach demonstrated excellent adaptability and generalization in face of extreme weather, and changes in user preferences.

However, this study does not account for the computing resource and communication costs of an applied edge computing apparatus, which are sometimes considerable, nor does it consider the issue of competitive strategies among multiple aggregators. In future work, we will further investigate the computational resource cooperation and allocation problem in edge intelligence and apply the achievements of this work to the optimization problem of cloud-edge collaboration systems in distributed electric heating networks.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

DF and TL contributed to the conception and design of the study. DF completed the original draft. RW and HQ were responsible for case study organization and data curation. XD was responsible for program compilation. YC was responsible for visualization and supervision. YL and TL performed the review and edit of the manuscript. All authors contributed to the manuscript and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (Grant Nos. 51977133 and U2066209).

Acknowledgments

We gratefully acknowledge the support of National Natural Science Foundation of China (NSFC) (Grant No. 51977133 and Grant No. Grant No. U2066209).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alipour, M., Zare, K., Seyedi, H., and Jalali, M. (2019). Real-time price-based demand response model for combined heat and power systems. Energy 168, 1119–1127. doi:10.1016/j.energy.2018.11.150

CrossRef Full Text | Google Scholar

Cen, B., Hu, C., Cai, Z., Wu, Z., Zhang, Y., Liu, J., et al. (2022). A configuration method of computing resources for microservice-based edge computing apparatus in smart distribution transformer area. Int. J. Electr. Power & Energy Syst. 138, 107935. doi:10.1016/j.ijepes.2021.107935

CrossRef Full Text | Google Scholar

Chen, Q., Xia, M., Wang, S., Wang, H., Liu, W., Wang, Z., et al. (2019). Optimization modeling method for coal-to-electricity heating load considering differential decisions. Glob. Energy Interconnect. 2, 188–196. doi:10.1016/j.gloei.2019.07.006

CrossRef Full Text | Google Scholar

Claessens, B. J., Vrancx, P., and Ruelens, F. (2018). Convolutional neural networks for automatic state-time feature extraction in reinforcement learning applied to residential load control. IEEE Trans. Smart Grid 9, 3259–3269. doi:10.1109/TSG.2016.2629450

CrossRef Full Text | Google Scholar

Du, Y., and Li, F. (2020). Intelligent multi-microgrid energy management based on deep neural network and model-free reinforcement learning. IEEE Trans. Smart Grid 11, 1066–1076. doi:10.1109/TSG.2019.2930299

CrossRef Full Text | Google Scholar

Duan, Y., Chen, X., Houthooft, R., Schulman, J., and Abbeel, P. (2016). Benchmarking deep reinforcement learning for continuous control. ArXiv160406778 Cs, Available at: http://arxiv.org/abs/1604.06778 (Accessed May 11, 2022).

Google Scholar

Fang, D., Guan, X., Lin, L., Peng, Y., Sun, D., and Hassan, M. M. (2020). Edge intelligence based economic dispatch for virtual power plant in 5G internet of energy. Comput. Commun. 151, 42–50. doi:10.1016/j.comcom.2019.12.021

CrossRef Full Text | Google Scholar

Fujimoto, S., van Hoof, H., and Meger, D. (2018). Addressing function approximation error in actor-critic methods. ArXiv180209477 Cs Stat. Available at: http://arxiv.org/abs/1802.O9477 (Accessed May 7, 2022).

Google Scholar

Gonzato, S., Chimento, J., O’Dwyer, E., Bustos-Turu, G., Acha, S., and Shah, N. (2019). Hierarchical price coordination of heat pumps in a building network controlled using model predictive control. Energy Build. 202, 109421. doi:10.1016/j.enbuild.2019.109421

CrossRef Full Text | Google Scholar

IEA (2021). Heat. - fuels technol. Available at: https://www.iea.org/fuels-and-technologies/heating (Accessed April 18, 2022).

Google Scholar

Javanshir, N., Syri, S., Teräsvirta, A., and Olkkonen, V. (2022). Abandoning peat in a city district heat system with wind power, heat pumps, and heat storage. Energy Rep. 8, 3051–3062. doi:10.1016/j.egyr.2022.02.064

CrossRef Full Text | Google Scholar

Lee, S. H. (2022). Real-time edge computing on multi-processes and multi-threading architectures for deep learning applications. Microprocess. Microsyst. 92, 104554. doi:10.1016/j.micpro.2022.104554

CrossRef Full Text | Google Scholar

Li, J., Fu, Y., Li, C., Li, J., Xing, Z., and Ma, T. (2021a). Improving wind power integration by regenerative electric boiler and battery energy storage device. Int. J. Electr. Power & Energy Syst. 131, 107039. doi:10.1016/j.ijepes.2021.107039

CrossRef Full Text | Google Scholar

Li, S., Bao, G., Zhang, X., Wu, G., and Ren, B. (2022a). Distributed response strategy of electric heating loads based on temperature queue sorting. Electr. Power Syst. Res. 211, 108196. doi:10.1016/j.epsr.2022.108196

CrossRef Full Text | Google Scholar

Li, X., Li, W., Zhang, R., Jiang, T., Chen, H., and Li, G. (2020). Collaborative scheduling and flexibility assessment of integrated electricity and district heating systems utilizing thermal inertia of district heating network and aggregated buildings. Appl. Energy 258, 114021. doi:10.1016/j.apenergy.2019.114021

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., Xu, Y., Moazeni, S., and Tang, Z. (2022b). Multi-stage real-time operation of a multi-energy microgrid with electrical and thermal energy storage assets: A data-driven MPC-ADP approach. IEEE Trans. Smart Grid 13, 213–226. doi:10.1109/TSG.2021.3119972

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., and Xu, Y. (2021b). Risk-averse coordinated operation of a multi-energy microgrid considering voltage/var control and thermal flow: An adaptive stochastic approach. IEEE Trans. Smart Grid 12, 3914–3927. doi:10.1109/TSG.2021.3080312

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., Xu, Y., and Zheng, X. (2022c). Stochastic-weighted robust optimization based bilayer operation of a multi-energy building microgrid considering practical thermal loads and battery degradation. IEEE Trans. Sustain. Energy 13, 668–682. doi:10.1109/TSTE.2021.3126776

CrossRef Full Text | Google Scholar

Liu, J., Tang, Z., Zeng, P. P., Li, Y., and Wu, Q. (2022). Fully distributed second-order cone programming model for expansion in transmission and distribution networks. IEEE Syst. J., 1–12. doi:10.1109/JSYST.2022.3154811

CrossRef Full Text | Google Scholar

Liu, Y., Su, Y., Xiang, Y., Liu, J., Wang, L., and Xu, W. (2019). Operational reliability assessment for gas-electric integrated distribution feeders. IEEE Trans. Smart Grid 10, 1091–1100. doi:10.1109/TSG.2018.2844309

CrossRef Full Text | Google Scholar

Lork, C., Li, W.-T., Qin, Y., Zhou, Y., Yuen, C., Tushar, W., et al. (2020). An uncertainty-aware deep reinforcement learning framework for residential air conditioning energy management. Appl. Energy 276, 115426. doi:10.1016/j.apenergy.2020.115426

CrossRef Full Text | Google Scholar

Ostadijafari, M., Dubey, A., and Yu, N. (2020). Linearized price-responsive HVAC controller for optimal scheduling of smart building loads. IEEE Trans. Smart Grid 11, 3131–3145. doi:10.1109/TSG.2020.2965559

CrossRef Full Text | Google Scholar

Song, H., Liu, Y., Zhao, J., Liu, J., and Wu, G. (2021). Prioritized replay dueling DDQN based grid-edge control of community energy storage system. IEEE Trans. Smart Grid 12, 4950–4961. doi:10.1109/TSG.2021.3099133

CrossRef Full Text | Google Scholar

Tan, H., Yan, W., Ren, Z., Wang, Q., and Mohamed, M. A. (2022). A robust dispatch model for integrated electricity and heat networks considering price-based integrated demand response. Energy 239, 121875. doi:10.1016/j.energy.2021.121875

CrossRef Full Text | Google Scholar

Wang, X., Liu, Y., Zhao, J., Liu, C., Liu, J., and Yan, J. (2021). Surrogate model enabled deep reinforcement learning for hybrid energy community operation. Appl. Energy 289, 116722. doi:10.1016/j.apenergy.2021.116722

CrossRef Full Text | Google Scholar

Yang, T., Zhao, L., Li, W., Wu, J., and Zomaya, A. Y. (2021). Towards healthy and cost-effective indoor environment management in smart homes: A deep reinforcement learning approach. Appl. Energy 300, 117335. doi:10.1016/j.apenergy.2021.117335

CrossRef Full Text | Google Scholar

Zhang, X., Biagioni, D., Cai, M., Graf, P., and Rahman, S. (2021). An edge-cloud integrated solution for buildings demand response using reinforcement learning. IEEE Trans. Smart Grid 12, 420–431. doi:10.1109/TSG.2020.3014055

CrossRef Full Text | Google Scholar

Zhang, Z., Chong, A., Pan, Y., Zhang, C., and Lam, K. P. (2019). Whole building energy model for hvac optimal control: A practical framework based on deep reinforcement learning. Energy Build. 199, 472–490. doi:10.1016/j.enbuild.2019.07.029

CrossRef Full Text | Google Scholar

Zhao, H., Wang, B., Liu, H., Sun, H., Pan, Z., and Guo, Q. (2022). Exploiting the flexibility inside park-level commercial buildings considering heat transfer time delay: A memory-augmented deep reinforcement learning approach. IEEE Trans. Sustain. Energy 13, 207–219. doi:10.1109/TSTE.2021.3107439

CrossRef Full Text | Google Scholar