Island microgrid power control system based on adaptive virtual impedance

When the microgrid is in the islanding operation mode, affected by the line impedance difference between the distributed power sources (DGs), the traditional droop control strategy will lead to the fact that the reactive power of the system cannot be reasonably distributed according to the droop gain, which makes the power grid prone to failure. To solve this problem, an improved sag control strategy based on adaptive virtual impedance is proposed in this paper. The central controller calculates the given power according to the capacity of each inverter and the total load capacity of the line, and then sends it to each inverter, and the inverter determines the value range of the virtual impedance according to the given reactive power. A voltage compensation link is added to the control strategy to compensate for the voltage drop difference caused by the line impedance difference, thereby ensuring the stability of the output power and realizing the power control of the microgrid. The MATLAB/Simulink simulation platform was built to establish the microgrid simulation model in island mode. The simulation results show that when the inverters with the same capacity are connected in parallel, the output active power is the most stable, and the reactive power maintains an equalized state; When inverters of different capacities are connected in parallel, the output active power takes the shortest time to stabilize, and the reactive power basically matches the rated capacity ratio. Therefore, it is fully demonstrated that this method has a good control effect on the power control and operation of the islanded microgrid.

1 Introduction

Large-scale development and utilization of renewable energy is an important means for mankind to deal with energy crisis and environmental pollution. Therefore, the distributed generation technology of various renewable energy sources has been widely concerned (Zeng and Yang, 2018). The microgrid is composed of distributed generation DG (distributed generation), energy storage devices, energy conversion devices, protection devices, loads and other equipment, and can operate in grid-connected and islanded modes (Pei and Zhang, 2018). When the microgrid is connected to the grid, the voltage and frequency are determined by the system, and the power can be easily shared equally. In the island-type microgrid, DG needs to proportionally distribute the total load in the microgrid according to their respective capacities. When the line impedance of each DG is inconsistent, reactive power cannot be evenly divided according to the sag coefficient, and reactive power circulation will occur between inverters, thus affecting the power quality and system stability of the power grid (Zhang et al., 2018). Therefore, the rational allocation of reactive power is one of the hotspots in microgrid research.

Scholars at home and abroad have put forward a variety of methods for the problem that the reactive power cannot be equally divided due to impedance mismatch. Zeng Xiaoxu, studied the influence of DG output changes on the AC bus voltage of the microgrid, and proposed an overall control strategy for the SMES system based on DG current feedforward to realize the stability control of the voltage of the new energy grid (Zhang et al., 2021). Li Hui, analyzed the control law of microgrid operation and proved that the microgrid control model based on the PQ control method can be used for the operation of microgrid, realizing the decoupling control of active power and reactive power (Geng, 2020). Huang Shuang, studied the microgrid layered control technology based on multi-agent system, proposed a microgrid layered control framework based on multi-agent system, and discussed the structure function of MAS in microgrid and its coordinated control strategy (Zhu et al., 2019). Although the above experts have studied the power and operation control methods of new energy microgrids. However, it can be found that there are still some drawbacks in the traditional method. For example, when the DG is connected to the power grid, it is difficult to control, causing the voltage and frequency of the power grid to be offset, affecting the safety and reliability of the power grid during operation. When the PQ control method is used in the case of high penetration rate of renewable energy in the microgrid, because the response speed of the micro source and the time scale of system power fluctuation do not match, it is easy to cause the phenomenon of system instability. The multi-agent system control technology ignores the communication speed and reliability between agents, and the traditional methods generally ignore the impact of virtual impedance on the operation of the microgrid, which makes it difficult to realize the combination of distributed power sources at random locations and makes the microgrid prone to accidents, resulting in the overall paralysis of the microgrid (Tu et al., 2018)∼ (Liu et al., 2018). The shortcomings of traditional methods are summarized and it is found that the reliability of new energy microgrid still needs to be improved. The reliability of new energy microgrid plays a very important role in the normal operation of power grid, so it is extremely urgent to improve the reliability of new energy microgrid.

Aiming at the above problems, a microgrid power control method based on adaptive virtual impedance is proposed. In this paper, virtual impedance is introduced and the function of virtual impedance is analyzed, the value range of virtual resistance is determined by the rated capacity ratio of inverter, which can effectively guarantee the power quality of the output of microgrid. The virtual impedance adaptive ability is poor in the traditional method. Insufficient estimation of line impedance when multiple inverters are connected in parallel, resulting in poor output power matching. This paper uses the integral controller to calculate the reference value of the output power. The central controller then calculates the given capacity of each inverter based on the load power and the inverter capacity. Finally, it is sent to the inverter for local control, so as to adjust the virtual impedance value and realize the accurate distribution of load power. The simulation results verify the effectiveness of the proposed control strategy.

2 Traditional droop control and reactive power distribution

The droop control principle and power transmission characteristics are analyzed when the low-voltage microgrid operates in island mode (Zhou et al., 2021). Taking the parallel operation of two micro-power inverters as an example, the DG is connected to the common load through the inverter and transmission feeder, and the inverter is equivalent to a voltage source. The equivalent circuit is shown in Figure 1 (Li et al., 2017).

FIGURE 1

FIGURE 1. Equivalent circuit of micropower inverter running in parallel.

The output current of the micro-power inverter is shown in Eq. 1:

${\dot{I}}_i=\frac{E\angle {\delta }_i-V\angle 0}{Z_i\angle {\theta }_i}=\frac{E}{Z_i}\angle \left({\delta }_i-{\theta }_i\right)-\frac{V}{Z_i}\angle \left(-{\theta }_i\right)\left(i=\mathrm{1,2}\right)(1)$

The complex power output by the micro-power inverter is shown in Formula Eq. 2:

$\begin{array}{l}{S}_i=P_i+j{Q}_i=\dot{V}*{\dot{I}}_i\\ =V\left(\frac{E_i\cos {\delta }_i+j{E}_i\sin {\delta }_i-V}{Z_i\cos {\theta }_i+j{Z}_i\sin {\theta }_i}\right)\\ =\frac{1}{Z_i}\left(E_{i}V\cos {\delta }_i\cos {\theta }_i-V^2\cos {\theta }_i+E_{i}V\sin {\delta }_i\sin {\theta }_i\right)\\ +j\frac{1}{Z_i}\left(E_{i}V\cos {\delta }_i\sin {\theta }_i-V^2\sin {\theta }_i+E_{i}V\sin {\delta }_i\cos {\theta }_i\right)\left(i=\mathrm{1,2}\right)\end{array}(2)$

According to Formula Eq. 1 and Eq. 2, the output active power and reactive power of the inverter can be obtained as shown in Formula Eq. 3:

$\{\begin{array}{l}{P}_i=\frac{1}{Z_i}\left(E_{i}V\cos {\delta }_i\cos {\theta }_i-V^2\cos {\theta }_i+E_{i}V\sin {\delta }_i\sin {\theta }_i\right)\left(i=\mathrm{1,2}\right)\\ Q_i=\frac{1}{Z}\left(E_{i}V\cos {\delta }_i\sin {\theta }_i-V^2\sin {\theta }_i+E_{i}V\sin {\delta }_i\cos {\theta }_i\right)\left(i=\mathrm{1,2}\right)\end{array}(3)$

Since the resistance value is much smaller than the reactance value in the high-voltage system, it can be known that $R\ll X$. When the power angle is small, we know $\sin \delta =\delta ,\cos \delta =1$. Then formula Eq. 3 can be transformed into formula Eq. 4:

$\{\begin{array}{l}{P}_i=\frac{E_{i}V}{Z_i}\delta \\ Q_i=\frac{E_{i}V}{Z_i}-\frac{V^2}{Z_i}\end{array}(4)$

It can be known from formula Eq. 4 that the active power $P_i$ and reactive power $Q_i$ output by the micro-power inverter can be controlled by the power angle $\delta$ and the voltage amplitude $V$ respectively. Therefore, the mathematical model of traditional P-f, Q-V droop control can be expressed by formula Eq. 5:

$\{\begin{array}{l}f=f^{*}-m\left(P-P_n\right)\\ V=V^{*}-m\left(Q-Q_n\right)\end{array}(5)$

In the formula, $f$ and $f^{*}$ are the actual value and reference value of the inverter output frequency respectively, the unit is Hz. $V$ and $V^{*}$ are the actual value and reference value of the inverter output voltage amplitude respectively, and the unit is V. $P$ and $P_n$ are the actual value and rated value of the output active power of the inverter, in unit W. $Q$ and $Q_n$ are the actual value and rated value of the output reactive power of the inverter respectively, in Var. $m$ is active frequency droop coefficient, the unit is Hz/W; $n$ is the reactive voltage amplitude droop coefficient, the unit is V/Var.

The traditional droop control structure represented by Formula Eq. 5 is shown in Figure 2, where $i_{\mathrm{o}}$ is the inverter output filter inductor current, $u_{\mathrm{o}}$ is the inverter output filter capacitor voltage. $\omega$ and $U$ are respectively the voltage angular frequency and amplitude adjusted by the droop controller, which are used to synthesize the reference voltage of the double-loop control of voltage and current.

FIGURE 2

FIGURE 2. Traditional droop control structure.

The traditional droop control is proposed under the condition that the sum of inverter output impedance and line impedance is inductive. Low-voltage transmission lines are usually used in microgrids, and the line impedance in low-voltage microgrids is mainly resistive. If traditional droop control is used, the adjustment of voltage amplitude will affect the adjustment of active power, reactive power and frequency, and even cause the coupling of active power and reactive power, affecting the stability of the system. Therefore, decoupling of active and reactive power is usually achieved by adding virtual impedance, so that the droop control method expressed in Equation Eq. 5 can continue to be used.

3 Improved droop control strategy based on virtual impedance

3.1 Principle of virtual impedance

The key to microgrid power control is to control the output power of the inverter to match the rated capacity (Li et al., 2021). In practical situations, the line impedance has a very close relationship with the path, length, etc. However, due to the lack of accurate measurement, it is difficult to realize the power control of the new energy microgrid, so the virtual impedance analysis microgrid power control method is introduced. Virtual impedance is a form to simulate the impedance of microgrid by adding a feedback loop to the current loop and voltage loop of microgrid. The purpose of voltage and current double loop control is to make the output voltage of inverter track the ideal voltage of microgrid completely (Cui and Peng, 2018; Chang, 2019; Wu and Luo, 2021).

The ideal circuit diagram and the actual equivalent circuit diagram before adding the virtual impedance are shown in Figure 3.

FIGURE 3

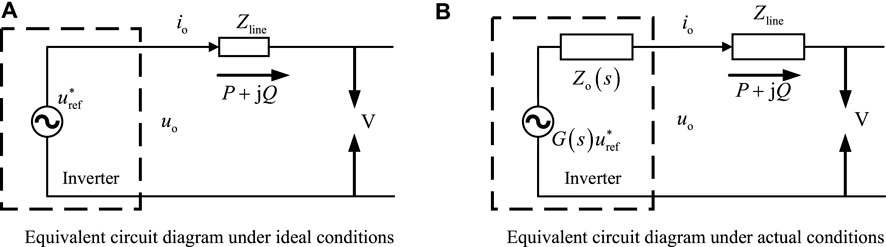
FIGURE 3. Ideal and actual equivalent circuit diagrams before adding virtual impedance.(A) Equivalent circuit diagram under ideal conditions (B) Equivalent circuit diagram under actual conditions.

Figure 3A is equivalent circuit diagram under ideal conditions. But in general, the equivalent output impedance of the inverter is changed to G(s) due to the voltage gain in the voltage double loop control link. And the effect of the equivalent output impedance Z(s) of the inverter should be considered.

In Figure 3B, the output voltage of the inverter is:

$u_{\mathrm{o}}\left(s\right)=G\left(s\right)u_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}\left(s\right)-Z_{\mathrm{o}}\left(s\right)·i_{\mathrm{o}}\left(s\right)(6)$

After the virtual impedance is introduced, the output voltage of the inverter is:

$u_{\mathrm{o}}\left(s\right)=G\left(s\right)u_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}\left(s\right)-\left[Z_{\mathrm{v}}\left(s\right)G\left(s\right)+Z_{\mathrm{o}}\left(s\right)\right]·i_{\mathrm{o}}\left(s\right)(7)$

Therefore, the total output impedance of the inverter after the introduction of virtual impedance is:

$Z_{\mathrm{o}}^{\prime }\left(s\right){=\mathrm{Z}}_{\mathrm{v}}\left(s\right)\mathrm{G}\left(s\right){+\mathrm{Z}}_{\mathrm{o}}\left(s\right)(8)$

The equivalent circuit diagram after adding the virtual impedance is shown in Figure 4.

FIGURE 4

FIGURE 4. Equivalent circuit diagram after adding virtual impedance.

3.2 Add virtual impedance

The coordinate system of the microgrid inverter in this study is the rotating coordinate system dq0, in which the virtual impedance control loop expression as:

$\{\begin{array}{l}{u}_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{d}}=u_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{d}}^{*}-R_{\mathrm{v}\mathrm{i}\mathrm{r}}{i}_{\mathrm{o}\mathrm{d}}+\omega L_{\mathrm{v}\mathrm{i}\mathrm{r}}{i}_{\mathrm{o}\mathrm{q}}\\ u_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{q}}=u_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{q}}^{*}-R_{\mathrm{v}\mathrm{i}\mathrm{r}}{i}_{\mathrm{o}\mathrm{q}}+\omega L_{\mathrm{v}\mathrm{i}\mathrm{r}}{i}_{\mathrm{o}\mathrm{q}}\end{array}(9)$

In formula (9), $u_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{d}}$ and $u_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{q}}$ represent the $d$ axis component and $q$ axis component of the reference value of the outer loop of the output voltage respectively; $u_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{d}}^{*}$ and $u_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{q}}^{*}$ represent the $d$ axis component and $q$ axis component of the reference voltage respectively; $R_{\mathrm{v}\mathrm{i}\mathrm{r}}$ represents the virtual resistance; $i_{\mathrm{o}\mathrm{d}}$ and $i_{\mathrm{o}\mathrm{q}}$ respectively represent the $d$ axis component and $q$ axis component of the output current reference value; $\omega$ is the angular frequency of the rotating coordinate system; $L_{\mathrm{v}\mathrm{i}\mathrm{r}}$ represents the virtual inductance.

The structural block diagram of the virtual impedance controller is shown in Figure 5.

FIGURE 5

FIGURE 5. Controller structure with virtual impedance added.

In Figure 5, $u_{\mathrm{o}\mathrm{d}}$ and $u_{\mathrm{o}\mathrm{q}}$ respectively represent the $d$ axis and $q$ axis components of the output voltage;$K_{\mathrm{v}\mathrm{p}}$ represents the voltage loop ratio; $K_{\mathrm{v}\mathrm{i}}$ is the integral coefficient of the voltage loop; $s$ represents the inverter capacity; $i_d^{*}$ and $i_q^{*}$ respectively represent the $d$ axis and $q$ axis components of the reference value of the current loop.

According to the structure diagram of the controller, the transfer function of the equivalent output impedance of the inverter can be described as Equation Eq. 10.

$\begin{array}{l}{Z}_{\mathrm{o}}^{`}\left(s\right)=G\left(s\right)Z_{\mathrm{v}}\left(s\right)+Z_{\mathrm{o}}\left(s\right)\\ =\frac{\left(K{K}_{\mathrm{p}\mathrm{w}\mathrm{m}}C{s}^2+K{K}_{\mathrm{v}\mathrm{p}}{K}_{\mathrm{p}\mathrm{w}\mathrm{m}}s+K{K}_{\mathrm{v}\mathrm{i}}{K}_{\mathrm{p}\mathrm{w}\mathrm{m}}\right)Z_{\mathrm{v}}\left(s\right)+s^2}{s^2+K{K}_{\mathrm{p}\mathrm{w}\mathrm{m}}C{s}^2+\left(1+K{K}_{\mathrm{v}\mathrm{p}}{K}_{\mathrm{p}\mathrm{w}\mathrm{m}}\right)s+K{K}_{\mathrm{v}\mathrm{i}}{K}_{\mathrm{p}\mathrm{w}\mathrm{m}}}\end{array}(10)$

In formula Eq. 10, $Z_{\mathrm{o}}^{`}\left(s\right)$ represents the total equivalent output impedance of the inverter; $G\left(s\right)$ represents the voltage gain; $Z_{\mathrm{v}}\left(s\right)$ represents the pure inductive virtual impedance; $Z_{\mathrm{o}}\left(s\right)$ represents the pure resistive virtual impedance; $K$ represents the droop coefficient of the inverter; $K_{\mathrm{p}\mathrm{w}\mathrm{m}}$ represents the influence factor of the resistance value in the virtual impedance; $C$ represents the determinant factor of the droop factor of the inverter.

P-V droop control is more suitable for low voltage microgrid. However, the line resistance-inductance ratio is very high under low-voltage microgrid conditions. The existence of line inductance may cause power coupling and even affect the stable operation of the microgrid system (Cui and Peng, 2018; Li, 2020; Liu and Zhao, 2022). Therefore, the introduction of virtual resistance can change the equivalent output impedance of the inverter. After introducing the virtual resistance, the Bode diagram of the output impedance of the microgrid inverter is obtained as shown in Figure 6.

FIGURE 6

FIGURE 6. Bode diagram of inverter output impedance.

Figure 6 reflects the change of the output impedance of the inverter when the virtual resistance value R increases from 0 Ω to 1 Ω. After the research and analysis in Figure 6, it can be seen that the equivalent output impedance of the original inverter is close to the inductive characteristic at a frequency of 50 Hz, and its amplitude is approximately equal to zero. After the introduction of the virtual resistor, the inverter impedance is close to the resistive characteristic when the frequency is 50 Hz, and the output voltage amplitude and the resistance value have a significant positive correlation, which is beneficial to the decoupling of the inverter output power. From the above analysis, it can be seen that the output impedance of the inverter in the microgrid changes significantly after the virtual impedance is added, which greatly reduces the coupling degree of the inverter output power.

3.3 The value range of the virtual resistance is determined

In order to accurately control the power of the new energy microgrid, it is necessary to determine the value range of the virtual resistance for the microgrid after introducing the virtual impedance.

Set the rated active power and rated reactive power of the microgrid inverter as $P$ and $Q$ respectively, and the no-load active power and no-load reactive power as $P_N$ and $Q_N$ respectively, then the inverter output power satisfies the following formula:

$\{\begin{array}{l}P\ge P_N\\ Q\ge Q_N\end{array}(11)$

As the sag control of the inverter has certain limits on the reference voltage $u_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}$, the reference voltage is set lower than $m$ times the reference voltage $u^{*}$, where the value range of $m$ is (1,1.1). The existing literature research shows that the range of the phase angle $\theta$ between the output voltage of the inverter and the coupling point is extremely small, and the maximum value ${\theta }_0$ is set to 10°. According to the above conditions, the rated active power and rated reactive power of the inverter are taken as objective functions, and taking the phase angle and the output voltage amplitude as variables to obtain the partial derivative, we can get:

$\{\begin{array}{l}\frac{\partial P^{*}}{\partial \theta }=\frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}\left[\left(R_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}+R_{\mathrm{v}}\right)V\sin \theta +V{X}_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}\cos \theta \right]}{{\left(R_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}+R_{\mathrm{v}}\right)}^2+X_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}^2}\\ \frac{\partial Q^{*}}{\partial \theta }=\frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}\left[\left(R_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}+R_{\mathrm{v}}\right)V\cos \theta +V{X}_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}\sin \theta \right]}{{\left(R_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}+R_{\mathrm{v}}\right)}^2+X_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}^2}\\ \frac{\partial P^{*}}{\partial u_{\mathrm{r}\mathrm{e}\mathrm{f}}}=\frac{2u_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}\left(R_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}+R_{\mathrm{v}}\right)+V{X}_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}\sin \theta -V\cos \theta }{{\left(R_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}+R_{\mathrm{v}}\right)}^2+X_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}^2}\\ \frac{\partial Q^{*}}{\partial u_{\mathrm{r}\mathrm{e}\mathrm{f}}}=\frac{-\left(R_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}+R_{\mathrm{v}}\right)V\sin \theta -X_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}V\cos \theta }{{\left(R_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}+R_{\mathrm{v}}\right)}^2+X_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}^2}\end{array}(12)$

In formula Eq. 12, $R_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}$ represents the real-time impedance of the inverter; $V$ represents the bus voltage; $X_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}$ represents the inductance value.

When the rated capacity relationship of the two inverters is $S_1^{*}=k{S}_2^{*}$, the relationship between the virtual resistances can be expressed as:

$\frac{R_{\mathrm{v}1}}{R_{\mathrm{v}2}}=\frac{n_1}{n_2}=\frac{1}{k}(13)$

In the formula, $k$ represents the ratio of the rated capacity of the inverter. The value range of virtual resistance is determined by the rated capacity ratio of the inverter so as to achieve the accurate distribution of output power of the parallel inverter.

3.4 Voltage drop difference

Although the virtual resistance can make the output impedance of the inverter meet the power matching conditions, it will also cause a short-term drop in the inverter voltage, resulting in a decrease in the quality of the output power of the microgrid (Liu, 2020)∼(Deng et al., 2018). In order to obtain better power quality, it is necessary to calculate the output voltage of the microgrid.

The relationship between the output voltage of the inverter and the bus voltage is expressed as:

$\{\begin{array}{l}{E}_{\mathrm{d}}=V+\mathrm{\Delta }{V}_{\mathrm{d}}=V+I_{\mathrm{d}}R+I_{\mathrm{d}}X\\ E_{\mathrm{q}}=-I_{\mathrm{q}}R+I_{\mathrm{q}}X\end{array}(14)$

In formula Eq. 14, $E_{\mathrm{d}}$ and $E_{\mathrm{q}}$ represent the $\mathrm{d}$ axis and $\mathrm{q}$ axis components of the inverter output voltage; $\Delta V_{\mathrm{d}}$ represents the $\mathrm{d}$ axis component of the bus voltage; $X$ represents the reactance value in the output line; $I_{\mathrm{d}}$ and $I_{\mathrm{q}}$ represent the $d$ axis and $q$ axis components of the inverter output current; $R$ represents the resistance value in the line impedance. Then the output voltage amplitude of the new energy microgrid inverter is

$E=\sqrt{E_{\mathrm{d}}^2+E_{\mathrm{q}}^2}=\sqrt{{\left(V+\frac{\mathit{PR}}{V}+\frac{QX}{V}\right)}^2+{\left(-\frac{QR}{V}+\frac{PX}{V}\right)}^2}(15)$

In the low-voltage microgrid, the line resistance and inductance are relatively high, so the inductive component can be ignored. Equation Eq. 15 translates into:

$E=\sqrt{E_{\mathrm{d}}^2+E_{\mathrm{q}}^2}=\sqrt{{\left(V+\frac{\mathit{PR}}{V}\right)}^2+{\left(-\frac{QR}{V}\right)}^2}\approx V+\frac{\mathit{PR}}{V}(16)$

Combine Equation Eqs 15, 16 to obtain:

$V=E_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}-n_{\mathrm{u}}P=E_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}-\left(n_{\mathrm{E}}+\frac{R}{V}\right)P(17)$

In formula Eq. 17, $E_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}$ represents the reference voltage amplitude; $n_{\mathrm{u}}$ represents the droop coefficient of voltage and active power at PCC point; $n_{\mathrm{E}}$ represents the droop coefficient of the output voltage and active power of the microgrid inverter.

It can be seen from the above formula that if the value of the virtual impedance is large, the inverter will be unstable, so it is necessary to comprehensively consider the relationship between the output voltage and power.

3.5 Power control

In order to improve the precision of power control of new energy microgrid, an integral controller is designed. It makes the value of the virtual impedance resistance adaptively change, so that the output power of the inverter approaches a given value and remains stable, and finally realizes the power control of the new energy microgrid.

There is an obvious inverse proportional relationship between the line impedance and the output active power of the inverter. In order to realize the adaptive virtual impedance, the reference value of the output power is first calculated by the integral controller. The central controller is then connected to the inverter via a low broadband line. Finally, use the power information to correct the virtual resistance value of the inverter (Zhang et al., 2022)∼(Huang et al., 2022).

The formula for calculating the reference value of the inverter output power is:

$P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}=\frac{1}{n_{\mathrm{n}}}\times \left(1/\left(\frac{1}{n_1}+\frac{1}{n_2}+\cdots +\frac{1}{n_N}\right)\right)\times {\displaystyle \sum }_{j=1}^N{P}_j(18)$

In formula Eq. 18, $P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}$ represents the output power of the $j-\mathrm{t}\mathrm{h}$ inverter; $n$ represents the harmonic value; $N$ represents the maximum value range of the number of inverters.

The formula for calculating the output active power of the inverter is

$P_{\mathrm{i}}=\frac{1}{T}{{\displaystyle \int }}_{-\left(T/2\right)}^{T/2}u\left(t\right)i\left(t\right)\mathit{d}t\left(i=\mathrm{1,2},\cdots n\right)(19)$

In formula Eq. 19, $T$ represents the period of the periodic AC signal; $u\left(t\right)$ represents the instantaneous voltage; $i\left(t\right)$ represents the instantaneous current.

According to the calculation results of formula Eq. 18 and formula Eq. 19, the value range of the adaptive virtual impedance can be obtained as follows:

$R_{\mathrm{v}\mathrm{n}}=\frac{K_{\mathrm{i}}}{s}\left(P_{\mathrm{i}}-P_{\mathrm{r}\mathrm{e}\mathrm{d}}^{*}\right)(20)$

In formula Eq. 20, $R_{\mathrm{v}\mathrm{n}}$ represents the value of the adaptive virtual impedance; $K_{\mathrm{i}}$ represents the parameter of the integral controller.

According to the above algorithm, two inverters with the same capacity are taken as the research object, which are connected in parallel. Initially, the two inverters have different line impedances, resulting in a low degree of output power matching. The output power reference value $P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}$ obtained by the integral controller becomes the control target of the inverter, and the specific control realization process is shown as follows.

When the output active power of inverter 1 is less than the reference power, it is denoted as $P_1<P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}$. The output of the adaptive virtual impedance is negative after being adjusted by the integral controller, then the virtual impedance gradually decreases and the active power output of inverter 1 increases. When the output active power of inverter 2 is greater than the reference power, it is denoted as $P_2>P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}$; After the adaptive virtual impedance is adjusted by the integral controller, the output is positive, which reduces the active power output of inverter 1. Finally, when $P_1=P_2=P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{*}$, the output power of the two inverters remains stable and the integral controller stops working.

When multiple inverters are connected in parallel, the integral controller adaptively adjusts the virtual impedance value according to the reference power until the output power of the paralleled inverters is equal to the reference power, and keeps the output power of the inverters stable (Hou et al., 2015)∼(Pham and Lee, 2020).

The above process realizes the power control of the new energy microgrid by introducing adaptive virtual impedance. It not only ensures the stability of output power, but also improves the quality of electric power, providing an effective means to ensure the safety of power grid operation and the quality of power consumption of users.

3.6 Stability analysis of improved control strategy

In order to analyze the stability of the improved control strategy, a small signal model was established by linearization near the static operating point (Chen et al., 2017; Wu et al., 2017; Liu et al., 2019; Huang et al., 2020; Ge et al., 2021). The power of DG flowing into the transmission line can be expressed as:

$\{\begin{array}{l}P=\frac{R_{\mathrm{c}}{U}^2-R_{\mathrm{c}}UE\cos \phi +X_{\mathrm{c}}UE\sin \phi }{R_{\mathrm{c}}^2+X_{\mathrm{c}}^2}\\ Q=\frac{X_{\mathrm{c}}{U}^2-X_{\mathrm{c}}UE\cos \phi +R_{\mathrm{c}}UE\sin \phi }{R_{\mathrm{c}}^2+X_{\mathrm{c}}^2}\end{array}(21)$

Where, $U$ and $E$ are the output voltage of the inverter and the voltage at PCC respectively. $R_{\mathrm{c}},X_{\mathrm{c}}$ is the line impedance after adding the virtual impedance, and $R_{\mathrm{c}}=R+L_{\mathrm{v}},X_{\mathrm{c}}=X+L_{\mathrm{v}}$.

Set ${\phi }_0,U_0$ and $E_0$ as the stable operation points of the system, according to the droop control Eq. 5 and Eq. 21, the related small signal equation can be obtained as:

$\{\begin{array}{l}\Delta \omega =-\frac{\partial \omega }{\partial P}\Delta P\\ \Delta U=\frac{\partial U}{\partial Q}\Delta Q\\ \Delta P=\frac{\partial P}{\partial U}\Delta U+\frac{\partial P}{\partial \phi }\Delta \phi +\frac{\partial P}{\partial L_{\mathrm{v}}}\Delta L_{\mathrm{v}}\\ \Delta Q=\frac{\partial Q}{\partial U}\Delta U+\frac{\partial Q}{\partial P}\Delta \phi +\frac{\partial Q}{\partial L_{\mathrm{v}}}\Delta L_{\mathrm{v}}\\ \Delta L_{\mathrm{v}}=\frac{K_i}{s}\Delta P\end{array}(22)$

Equation Eq. 22 can be simplified as:

$\{\begin{array}{l}\Delta \omega =-m\Delta P\\ \Delta U=-n\Delta Q\\ \Delta P=k_{\mathrm{p}\mathrm{u}}\Delta U+k_{\mathrm{p}\phi }\Delta \phi +k_{\mathrm{p}\mathrm{l}}\Delta L_{\mathrm{v}}\\ \Delta Q=k_{\mathrm{q}\mathrm{u}}\Delta U+k_{\mathrm{q}\phi }\Delta \phi +k_{\mathrm{q}\mathrm{l}}\Delta L_{\mathrm{v}}\\ \Delta L_{\mathrm{v}}=\frac{K_i}{s}\Delta P\end{array}(23)$

in,

$\{\begin{array}{l}{k}_{\mathrm{p}\mathrm{u}}=\frac{2R_{\mathrm{c}}U-R_{\mathrm{c}}E\cos \phi +X_{\mathrm{c}}E\sin \phi }{R_{\mathrm{c}}^2+X_{\mathrm{c}}^2}\\ k_{\mathrm{q}\mathrm{u}}=\frac{2X_{\mathrm{c}}U-X_{\mathrm{c}}E\cos \phi -R_{\mathrm{c}}E\sin \phi }{R_{\mathrm{c}}^2+X_{\mathrm{c}}^2}\\ k_{\mathrm{p}\phi }=\frac{R_{\mathrm{c}}UE\sin \phi +X_{\mathrm{c}}UE\cos \phi }{R_{\mathrm{c}}^2+X_{\mathrm{c}}^2}\\ k_{\mathrm{q}\phi }=\frac{X_{\mathrm{c}}UE\sin \phi -R_{\mathrm{c}}UE\cos \phi }{R_{\mathrm{c}}^2+X_{\mathrm{c}}^2}\\ k_{\mathrm{p}\mathrm{l}}=\frac{-2\left(R_{\mathrm{c}}+X_{\mathrm{c}}\right)P+U^2-UE\cos \phi +UE\sin \phi }{R_{\mathrm{c}}^2+X_{\mathrm{c}}^2}\\ k_{\mathrm{q}\mathrm{l}}=\frac{-2\left(R_{\mathrm{c}}+X_{\mathrm{c}}\right)Q+U^2-UE\cos \phi +UE\sin \phi }{R_{\mathrm{c}}^2+X_{\mathrm{c}}^2}\end{array}(24)$

The power in droop control is obtained by passing the measured instantaneous power through a first-order low-pass filter, so Eq. 23 can be transformed into:

$\{\begin{array}{l}\Delta \omega \left(s\right)=-\frac{m{\phi }_{\mathrm{c}}}{s+{\phi }_{\mathrm{c}}}\left[k_{\mathrm{p}\mathrm{u}}\Delta U\left(s\right)+k_{\mathrm{p}\phi }\Delta \phi \left(s\right)+k_{\mathrm{p}\mathrm{l}}\Delta L_{\mathrm{v}}\left(s\right)\right]\\ \Delta U\left(s\right)=-\frac{n{\phi }_{\mathrm{c}}}{s+{\phi }_{\mathrm{c}}}\left[k_{\mathrm{q}\mathrm{u}}\Delta U\left(s\right)+k_{\mathrm{q}\phi }\Delta \phi \left(s\right)+k_{\mathrm{q}\mathrm{l}}\Delta L_{\mathrm{v}}\left(s\right)\right]\\ \Delta L_{\mathrm{v}}\left(s\right)=\frac{K_i}{s}\left[k_{\mathrm{p}\mathrm{u}}\Delta U\left(s\right)+k_{\mathrm{p}\phi }\Delta \phi \left(s\right)+k_{\mathrm{p}\mathrm{l}}\Delta L_{\mathrm{v}}\left(s\right)\right]\end{array}(25)$

where ${\phi }_{\mathrm{c}}$ is the cutoff frequency of the low-pass filter, and $\Delta \omega \left(s\right)=s\Delta \phi \left(s\right)$. Simplifying Equation Eq. 25, the characteristic equation of the system can be obtained as:

$A{s}^4+B{s}^3+C{s}^2+Ds+E=0(26)$

in,

$\{\begin{array}{l}A=\frac{1}{{\omega }_{\mathrm{c}}^2}\\ B=\frac{2}{{\omega }_{\mathrm{c}}}+\frac{n{k}_{\mathrm{q}\mathrm{u}}}{{\omega }_{\mathrm{c}}}-\frac{k_{\mathrm{q}\mathrm{l}}{K}_i}{{\omega }_{\mathrm{c}}^2}\\ C=1+\frac{m{k}_{\mathrm{p}\phi }}{{\omega }_{\mathrm{c}}}+n{k}_{\mathrm{q}\mathrm{u}}-\frac{2k_{\mathrm{q}\mathrm{l}}{K}_i}{{\omega }_{\mathrm{c}}}\\ D=m{k}_{\mathrm{p}\phi }+nm{k}_{\mathrm{q}\mathrm{u}}{k}_{\mathrm{p}\phi }-nm{k}_{\mathrm{p}\mathrm{u}}{k}_{\mathrm{q}\phi }-k_{\mathrm{q}\phi }{K}_i-\frac{m{k}_{\mathrm{q}\mathrm{l}}{K}_i{k}_{\mathrm{p}\phi }}{{\omega }_{\mathrm{c}}}+\frac{m{k}_{\mathrm{p}\phi }{K}_i}{{\omega }_{\mathrm{c}}}\\ E=-m{k}_{\mathrm{q}\mathrm{l}}{K}_i{k}_{\mathrm{p}\phi }+m{k}_{\mathrm{p}\mathrm{l}}{k}_{\mathrm{q}\phi }{K}_i\end{array}(27)$

Analyze the system stability by taking the root locus of the characteristic equation of the above system (Chen et al., 2017; Liu et al., 2019; Huang et al., 2020; Zhou et al., 2020; Ge et al., 2021; Gao, 2022). Figure 7 shows the root locus distribution corresponding to the change of $K_i$ from 0.001 to 0.010 when other control parameters are fixed. The direction of the arrow in Figure 7 is the direction in which the corresponding parameter increases.

FIGURE 7

FIGURE 7. The root locus of the characteristic equation of the system.

In the root locus diagram, the characteristic roots close to the virtual axis have the greatest influence on the stability of the system and are generally defined as the dominant poles. In Figure 7, ${\lambda }_1$ and ${\lambda }_2$ have a greater impact on the system stability. As the integral coefficient $K_i$ increases within the specified range, the real parts of the two pairs of conjugated virtual roots are all less than 0, indicating that the system can run stably. During the increase of $K_i$, the distance of the eigenvalue from the real axis does not change much, indicating that the change of $K_i$ has little effect on the damping characteristics of the system. When $K_i$ increases, the dominant poles ${\lambda }_1$ and ${\lambda }_2$ get closer and closer to the imaginary axis, and the system stability decreases. Therefore, the value of the integral coefficient $K_i$ cannot be too large, otherwise the stability will be affected. The value of $K_i$ in the text is 0.005.

4 Simulation analysis

The island-type microgrid simulation model shown in Figure 8 is built on the MATLAB/Simulink software simulation platform to verify the effectiveness of the improved droop control. The simulation model consists of two DGs operating in parallel to supply linear loads. And the load parameter is $P_1=20\mathrm{k}\mathrm{W},Q_1=20\mathrm{k}\mathrm{V}\mathrm{a}\mathrm{r};P_2=10\mathrm{k}\mathrm{W},Q_2=10\mathrm{k}\mathrm{V}\mathrm{a}\mathrm{r}$.

FIGURE 8

FIGURE 8. Simulation model of islanded microgrid.

Example 1 is a comparative analysis of the influence of the traditional control strategy and the improved control strategy on the power distribution and voltage amplitude of the microgrid when the capacity of the two DGs is the same. Example 2 simulation verifies the accuracy of the load distribution of the inverter using the improved control strategy when the DG capacity is different. The simulation parameters are shown in Table 1.

TABLE 1

TABLE 1. Simulation parameters.

4.1 Simulation example 1

Two DGs with the same capacity run in parallel. Before the 1 s, only load 1 is put into operation, and the active power and reactive power are 20 kW and 20 kVar respectively. At the 1 s, load 2 is also put into operation, and the active power and reactive power of the system become 20 kW and 20 kVar respectively after the steady-state operation of the system. At the 2 s, the load 2 is out of operation, and the active power and reactive power become 30 kW and 30 kVar after the steady-state operation of the system, and the simulation time is 3 s. When both DGs use traditional droop control, the DG output power and voltage waveforms are shown in Figure 9.

FIGURE 9

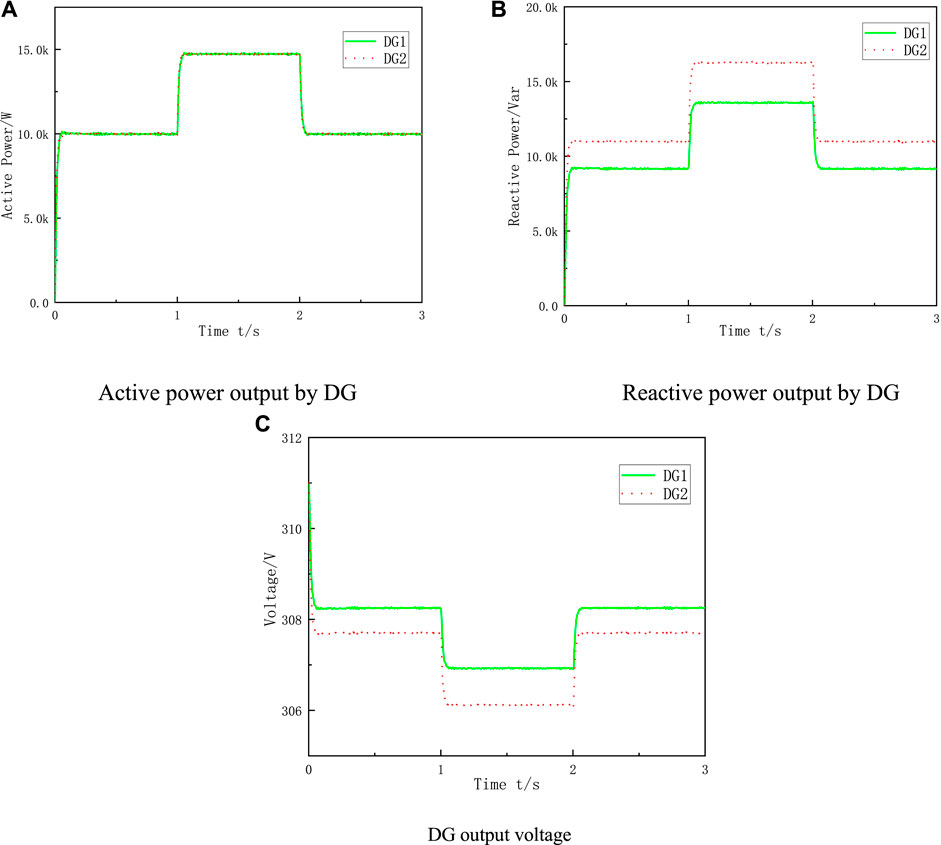
FIGURE 9. Simulation results of traditional droop control. (A) Active power output by DG (B) Reactive power output by DG. (C) DG output voltage.

Since DG 1 and DG 2 have the same capacity, in order to allocate reactive power reasonably, it is necessary to make the allocation of reactive power to each DG equal when the system is in a stable state. It can be concluded from Figure 9 that two DGs with the same capacity are operated in parallel using the traditional droop control method. Before and after the load changes, the DG can share the active power equally according to the active droop coefficient. However, due to the existence of line impedance difference, there is a certain deviation in the output voltage amplitude of the two DGs after stabilization. A small output voltage amplitude has a certain deviation after stabilization, and a small output voltage deviation will cause a large power distribution deviation. Since the line impedance of DG 2 is larger than that of DG 1, DG 2 allocates less reactive power, which leads to the fact that the reactive power cannot be divided equally according to the droop coefficient.

When both DGs adopt the improved droop control strategy, the output power and voltage waveforms of DG1 and DG2 are shown in Figure 10.

FIGURE 10

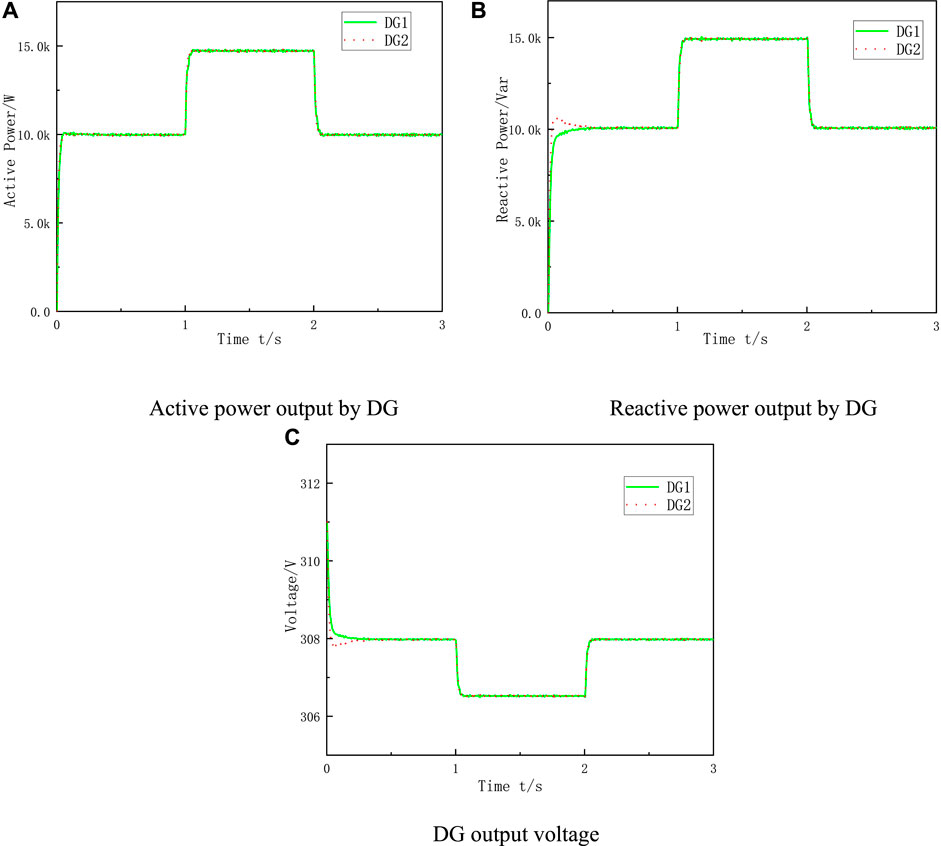
FIGURE 10. Simulation results of improved droop control when two DGs have the same capacity. (A) Active power output by DG. (B) Reactive power output by DG. (C) DG output voltage.

It can be seen from Figure 10 that when two DGs with the same capacity are operated in parallel using the improved droop control strategy, before and after the load changes, the DG can divide the active power equally according to the active power droop coefficient. And the adaptive virtual impedance is added to the droop control to compensate the voltage drop difference caused by the line impedance difference. The difference between the output voltage amplitudes of the two DGs is small after stabilization. When the line impedance is different, the reactive power can also be accurately distributed according to the droop coefficient.

4.2 Simulation example 2

DG1 and DG2 run in parallel, and the rated capacity ratio is 2:1. Using the improved droop control strategy, the simulation process is the same as that of Example 1, and the output active and reactive power waveforms of the inverter are shown in Figure 11.

FIGURE 11

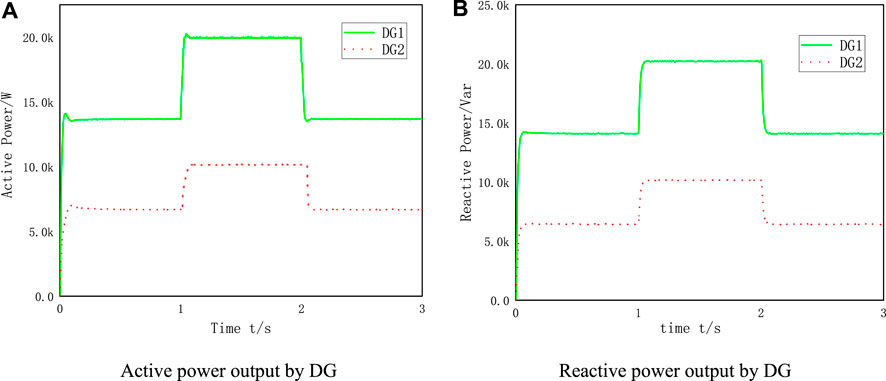
FIGURE 11. Simulation results of improving droop control with two DGs with different capacities. (A) Active power output by DG. (B) Reactive power output by DG.

To achieve reasonable power distribution, the power distribution ratio of DG 1 and DG 2 should be 1:2. It can be seen from Figure 11A that the active power output by the inverter can be distributed according to the DG capacity ratio before and after the load power factor changes, and the ratio of the distributed power between DG 1 and DG 2 is 2:1. It can be seen from Figure 11B that with the improved droop control strategy, the output reactive power of the inverter meets the requirement of 2:1. In the 1 s and 2 s, the load increases and decreases respectively, and the reactive power of the inverter can still be distributed in proportion to the DG capacity. The transition process is smooth and the time is short.

5 Conclusion

The mechanism that the traditional droop control cannot realize the reasonable distribution of reactive power due to the difference in the impedance of each DG line is analyzed. It is concluded that the fundamental reason for the unreasonable distribution of reactive power is the voltage drop difference caused by the inconsistent impedance of each DG line. The improved droop control strategy proposed in this paper is suitable for island-type microgrids. It does not need to measure the line impedance parameter value. It can automatically adjust the virtual impedance value according to the load power, eliminate the voltage drop difference caused by the line impedance difference, so that the distribution of reactive power is not affected by the inconsistent line impedance, and finally realize the equal distribution of reactive power. Through the comparative simulation analysis of the traditional droop control and the improved control strategy in this paper, it can be seen that the improved control strategy can realize the accurate distribution of reactive power, which verifies the effectiveness of the method.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

HS: Put forward research ideas and design research schemes; ZZ: The control strategy is improved according to the proposed ideas, and the correctness of the improved strategy is verified by simulation; SW: Responsible for final version revision.

Funding

This research was supported by the National Natural Science Foundation of China (61867003), and the 2020 Gansu Provincial College Innovation Fund Program (2020A-044).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chang, Z. (2019). Research on droop control strategy of low-voltage microgrid inverter based on virtual impedance. Lanzhou: Lanzhou Jiao tong University. doi:10.27205/d.cnki.gltec.2019.000666

CrossRef Full Text | Google Scholar

Chen, K., Cao, Y., and Jiang, Y. (2017). Improved droop control strategy for parallel inverter in microgrid. Power Electron. Technol. 51 (01), 29–32.

Google Scholar

Cui, M., and Peng, B. (2018). Improved droop control based on adaptive virtual impedance and phase compensation [J/OL]. Electr. Meas. Instrum.: 1-13. [2022-06-08]. Available at: http://kns.cnki.net/kcms/detail/23.1202.TH.20210126.1541.002.html.

Google Scholar

Deng, Q., Long, X., Yang, G., Liu, T., Xiang, Q., and Xie, Z. (2021). Based on network parallel inverter is improved droop control strategy study. Natural Science Journal of Xiangtan University 5, 59–69.

Google Scholar

Gao, S. (2022). Micro grid more parallel inverter circulation suppression method research. Shenyang: Shenyang university of technology. dc nki. 10.27322/Gsgyu.2022.000039.

Google Scholar

Ge, J., Dong, X., and Zhu, J. (2021). Research on secondary control of shunt inverter in islanding microgrid. Electr. Autom. 43 (04), 87–90.

Google Scholar

Geng, Y. (2020). Research on power regulation of low-voltage microgrid parallel inverters based on virtual impedance. Jinan: Shandong University. doi:10.27272/d.cnki.gshdu.2020.002463

CrossRef Full Text | Google Scholar

Hou, G., Xing, F., Yang, Y., and Zhang, J. (2015). “Industrial electronics and applications (ICIEA)”, in Proceedings of the 2015 IEEE 10th Conference on.Virtual negative impedance droop method for parallel inverters in microgrids, (IEEE).

Google Scholar

Huang, Y., Zheng, S., and He, L. (2020). Grid inverter feed-forward control strategy based on virtual impedance study. J. sun yat-sen Univ. Nat. Sci. Ed. (both Engl. Chin). 21 (02), 90–99.

Google Scholar

Huang, Y., Zheng, S., and He, L. (2022). Research on feedforward control strategy of grid-connected inverter based on virtual impedance. J. Sun Yat-Sen Univ. Nat. Sci. Ed. Chin. Engl. 61 (02), 90–99. doi:10.13471/j.cnki.acta.snus.2020b148

CrossRef Full Text | Google Scholar

Li, H., Yang, H., and Zeng, Q. (2017). Improved droop control strategy in islanded microgrid. J. Electr. Power Syst. Autom. 29 (04), 49–54.

Google Scholar

Li, Y., Yang, M., and Sun, W. (2021). Research on reactive power distribution of islanded AC microgrid based on improved droop control. J. Sol. Energy 42 (08), 7–15. doi:10.19912/j.0254-0096.tynxb.2019-0524

CrossRef Full Text | Google Scholar

Li, Z. (2020). Research on microgrid droop control strategy based on adaptive virtual impedance. Wuhu: Anhui Engineering University. doi:10.27763/d.cnki.gahgc.000185

CrossRef Full Text | Google Scholar

Liu, Q., and Zhao, W. (2022). Power control system of new energy microgrid based on adaptive virtual impedance. J. Power Suppl. 1-16. [2022-06-08] Available at: http://kns.cnki.net/kcms/detail/12.1420.TM.20210608.1533.004.html.

Google Scholar

Liu, H., Li, L., Ye, J., et al. (2018). Precise power distribution and frequency and voltage recovery control in independent microgrids. J. North Univ. China (Natural Sci. Ed.) 39 (01), 54–60.

Google Scholar

Liu, Y., Guan, L., Guo, F., Zheng, J., Chen, J., Liu, C., et al. (2019). A reactive power-voltage control strategy of an AC microgrid based on adaptive virtual impedance. Energies 12, 3057. doi:10.3390/en12163057

CrossRef Full Text | Google Scholar

Liu, P. (2020). Research on parallel control strategy of multiple inverters with different capacities. Xiangtan: Xiangtan University. doi:10.27426/d.cnki.gxtdu.2020.001315

CrossRef Full Text | Google Scholar

Pei, S., and Zhang, J. (2018). Research on microgrid control strategy based on adaptive virtual impedance. Electr. Meas. Instrum. 55 (12), 82–87.

Google Scholar

Pham, D. M., and Lee, H. (2020). Effective coordinated virtual impedance control for accurate power sharing in islanded microgrid. IEEE Trans. Indust. Electron., 1–1. doi:10.1109/tie.2020.2972441

CrossRef Full Text | Google Scholar

Tu, C., Xiao, F., and Lan, Z. (2018). Research on voltage quality control strategy of power electronic transformers in microgrid. New Technol. Electr. Eng. 37 (06), 1–9.

Google Scholar

Wu, Z., and Luo, Y. (2021). Research on inverter parallel control strategy based on virtual impedance. Power Capacitor React. Power Compens. 42 (06), 166–172. doi:10.14044/j.1674-1757.pcrpc.2021.06.024

CrossRef Full Text | Google Scholar

Wu, X., Chen, S., and Iravani, R. (2017). Feasible range and optimal value of the virtual impedance for droop-based control of microgrids. IEEE Trans. Smart Grid 8 (3), 1242–1251. doi:10.1109/tsg.2016.2519454

CrossRef Full Text | Google Scholar

Zeng, X., and Yang, S. (2018). Voltage stability analysis and control strategy of new energy microgrid. Electron. Technol. 47 (12), 1–4.

Google Scholar

Zhang, J., Yu, A., and Tu, Y. (2018). Distributed power control of microgrid based on adaptive virtual impedance. J. Shanghai Electr. Power Univ. 34 (06), 523–530.

Google Scholar

Zhang, Q., Yu, Q., and Wang, J. (2021). Improved droop control based on segmented virtual impedance. Acta Electr. Power Syst. Autom. 33 (09), 87–93. doi:10.19635/j.cnki.csu.epsa.000637

CrossRef Full Text | Google Scholar

Zhang, J., Zhao, R., and Liu, Y. (2022). Parallel operation control strategy of resistive inverters in low voltage microgrid. High. Volt. Technol. 48 (01), 136–146. doi:10.13336/j.1003-6520.hve.20211241

CrossRef Full Text | Google Scholar

Zhou, Z., Peng, Y., Liu, B., and Li, X. (2020). Design of improved droopdown controller based on adaptive virtual impedance. Electr. Drive 52 (17), 40–45. doi:10.19457/J.1001-2095.dqCD22931

CrossRef Full Text | Google Scholar

Zhou, G., Yan, G., and Zhao, S. (2021). Improved droop control in low-voltage microgrid island operation mode. Jilin Electr. Power 49 (01), 6–10. doi:10.16109/j.cnki.jldl.2021.01.002

CrossRef Full Text | Google Scholar

Zhu, X., Han, D., and Meng, F. (2019). A method of series virtual impedance of grid-connected converters to improve the stability of DC microgrid. Power Grid Technol. 43 (12), 4523–4531. doi:10.13335/j.1000-3673.pst.2018.1752

CrossRef Full Text | Google Scholar