Research on power system flexibility considering uncertainties

In order to help achieve the goal of carbon peak and carbon neutrality, the large-scale development and application of clean renewable energy, like wind generation and solar power, will become an important power source in the future. Large-scale clean renewable energy generation has the uncertain characteristics of intermittency, randomness, and volatility, which brings great challenges to the balance regulation and flexible operation of the power system. In addition, the rapid development of renewable energy has led to strong fluctuations in electricity prices in the power market. To ensure the safe, reliable, and economic operation of the power system, how to improve the power system flexibility in an uncertain environment has become a research hotspot. Considering the uncertainties, this article analyzes and summarizes the research progress related to power system flexibility from the perspective of power system planning, operation, and the electricity market. Aiming at the modeling technology of uncertainty, the related modeling methods including stochastic programming, robust optimization, and distributionally robust optimization are summarized from the perspective of mathematics, and the application of these methods in power system flexibility is discussed.

1 Introduction

In order to deal with energy depletion and environmental problems, many countries have formulated carbon emission strategies. On 22 September 2020, Chairman Xi announced to the world that China will strive to achieve peak carbon dioxide emissions before 2030 and carbon neutrality by 2060. The United States and the European Union have proposed a Zero Carbon Action Plan (ZCAP) and a net zero emission target for 2050, respectively. Canada is expected to commit to a net zero emission target by 2050 and develop a legally binding 5-year carbon budget. Sweden set a net zero emission target in 2017. According to the Paris Agreement, it promised to achieve carbon neutrality by 2045, with at least 85% of the emission reduction to be achieved through domestic policies and the rest to be made up by international emission reduction. Germany promises to “pursue” greenhouse gas neutrality by 2050. Singapore avoided promising a clear decarbonization date but made it the ultimate goal of the long-term strategy submitted to the United Nations in March 2020. By 2040, diesel locomotives will be phased out and replaced by electric vehicles. Therefore, a high proportion of renewable energy power generation has become a future power system scenario of widespread concern around the world. Under the new scenario, the characteristics of the power system have changed significantly. The randomly fluctuating wind and solar energy have become the main power sources, the “base load” power plants have been basically cancelled, the conventional thermal power units are started and stopped within a day, and the stochastic volatility of renewable energy is complemented through the flexible resource regulation of hydropower plants, gas-fired power plants, energy storage, etc.; flexibility has become the core issue of planning and operation.

In China, guided by the goal of carbon peaking and carbon neutrality, China has put forward the development strategy of building a new power system with new energy as the main body. The goal of “carbon peak and carbon neutrality” is a systematic project, and the power industry shoulders an important historical mission. According to the statistics of the International Energy Agency (IEA) in 2019, the total carbon emission in China was 11.3 billion tons, and the carbon emission in the energy field was 9.8 billion tons, accounting for 87% of the national total. Among them, the carbon emission in the power industry was 4.2 billion tons, accounting for 37% of the national total (United Nations Environment Programme, 2019). At present, China’s energy consumption and carbon dioxide emissions per unit of GDP have been reduced by 13.5 and 18%, respectively, which has been written into the main objectives of economic and social development during the 14th Five-Year Plan (Xinhuanet, 2021). According to EIA data, the carbon emission of the United States in 2019 was 6.558 billion tons, down 11.96% from 2007. In 2020, renewable energy accounted for 12.49% of primary energy consumption in the United States. Biomass energy accounts for the highest proportion of renewable energy, accounting for 39%, followed by wind energy (26%), hydropower (22%), light energy (11%), and geothermal energy (2%). In 2020, the carbon emission of the EU was 2.551 billion tons, a decrease of 32.05% compared with 1990.

Therefore, to achieve the goal of carbon peak and carbon neutrality, the power industry has the heaviest task and the greatest responsibility and will play an important role of the main force. Therefore, the intermittent renewable energy power generation represented by wind power and solar energy will enter the fast lane of large-scale development and gradually form a clean and sustainable power supply mode dominated by renewable energy power generation. Also, the power system will change from a high-carbon power system to a deep low-carbon or zero-carbon power system.

However, due to the strong uncertainty and strong fluctuation characteristics of intermittent renewable energy power generation, realizing the status of the power subject and responsibility subject of renewable energy power generation faces complex technical challenges and needs a long-term development process. In addition to continuing to pay attention to safety, reliability, and economy, the flexibility of the power system has become a new focus. Under this background, it has become an urgent problem to explore the flexibility mechanism, planning, and operation theory and method of the new power system in a complex environment and multi-space–time interaction (Xu et al., 2020).

Security, reliability, economy, and flexibility are the internal requirements of modern power systems and are important indexes to measure whether the operation mode of the power system is reasonable or not (Telukunta et al., 2017). There is an extremely close relationship between them. In order to analyze the power system flexibility, we briefly introduce the other three research statuses. The security of the power system represents the ability of the power system to maintain a continuous power supply in case of an accident in a short time. From the perspective of security, aiming at the rapid development of power systems, Shu and Tang (2017) analyzed the main standards of power system security in China and discussed the development direction in the future. Shahidehpour et al. (2005) discussed the important role of security in power system planning and operation, studied the challenges and problems faced by security in different time- and space scales, and put forward the corresponding solutions. Yorino et al. (2018) proposed a bi-level robust optimization model to solve the problem of reserve margin under the environment of uncertain renewable energy output to ensure the safe operation of the whole system. From the economic viewpoint, Wang et al. (2017) described the scheduling problem containing a large amount of random wind power as a chance-constrained economic scheduling problem. The joint probability density function of multiple wind farms was established by using the Gaussian mixture model, and the results verify that the system can achieve a better economy. In order to solve the problem of excess wind power generation, power-to-gas technology was introduced into the integrated electricity and natural gas system, and a stochastic dynamic economic dispatching model based on the conditional value at risk method security risk constraints was established in Chen (2019). From the reliability side, AmandaSteele et al. (2021) discussed the impact of the growth of renewable energy on power system reliability. In order to maintain the safe operation of the system in the short and medium term, considering the uncertainty of wind power, a multi-state model of hybrid power generation and standby suppliers was proposed in Ding et al. (2014), and a time-varying reliability evaluation technology was used for system reliability evaluation.

Under the background of zero-carbon transformation of energy structure, building a new power system with renewable energy as the main body will become an important means to achieve the goals of carbon peaking and carbon neutrality. A high proportion of renewable energy has become the main feature of the power system. Different from conventional thermal power, renewable energy power generation is affected by meteorological conditions and environmental factors, and its output shows the characteristics of intermittence and fluctuation, which makes the power system change from a deterministic system to a strong uncertain system. The random variation characteristics of high-proportion renewable power will bring unprecedented challenges to the power system. However, due to the lack of flexibility in the power system, it is difficult to absorb renewable energy efficiently. Enhancing flexibility and improving system regulation capacity are inevitable requirements for realizing power zero-carbon transformation. However, the problem of insufficient flexibility in the power system restricting the consumption of renewable energy has not been fundamentally solved. Flexibility has become one of the indispensable indexes of the power system. At present, researchers have made relevant research and summary on the aspects of flexibility resources and flexibility evaluation methods (Brunner et al., 2020; Michael et al., 2020; Semich et al., 2020). Li et al. (2018) summarized the flexibility indicators and evaluation methods. Mohandes et al. (2019) analyzed the concept, indexes, and related economic technologies of power system flexibility in high penetration of the renewable energy environment and focused on the impact of uncertain renewable energy on storage and reserve. Taking the impact of renewable energy growth on power systems as the starting point, Alireza et al. (2019) analyzed the role of various flexibility resources in system flexibility from the point of timescales. The existing review on power system flexibility research mainly focuses on the definitions of power system flexibility, flexibility resources, and power balance mechanism in an uncertain environment, but there is no discussion on the application of the uncertainty modeling method in power system flexibility research. On this basis, this article further discusses the modeling technology of uncertainty factors in detail. Therefore, aiming at the planning flexibility, operation flexibility, and electricity market flexibility of power systems in an uncertain environment, this article summarizes the main modeling methods of uncertainties and analyzes the advantages and disadvantages of various methods.

In the following, Section 2 presents the concept and the characteristics of power system flexibility. Section 3 summarizes the uncertainty modeling methods from the perspective of mathematics. Section 4 summarizes the related research on power system flexibility under an uncertainty environment, and Section 5 narrates the concluding remarks.

2 Power system flexibility

2.1 Definition of power system flexibility

Flexibility is the ability of a power system to use all resources to respond to changes in net demand in a certain environment (Lannoye et al., 2012). At present, the research on power system flexibility is still in its infancy. The North American Electric Reliability Council (NERC) and International Energy Agency (IEA) define flexibility from different perspectives as follows: the NERC believes that power system flexibility is the ability to use system resources to meet load changes, which is mainly reflected in operation flexibility, and it focuses on the methods to improve power system flexibility (Milligan et al., 2010). IEA believes the power system flexibility means that, under its boundary constraints, the power system can quickly respond to large fluctuations in supply or load demand and can quickly respond to predictable changes (International Energy Agency, 2014). Hence, some researchers have declared their views on the definition of power system flexibility from different perspectives. In terms of power capacity and ramp rate, power system flexibility is described as the ability to increase energy production with a certain rate and ramp duration, that is, the ability to sustain ramping for a given duration (Dvorkin et al., 2014). Zhao et al. (2016) defined flexibility as the maximum uncertainty range that the power system can cope with. Generally speaking, the research on power system flexibility focuses more on the dynamic response and adequacy of the generation side and demand side.

2.2 Characteristics of power system flexibility

Power system flexibility has three characteristics: inherent characteristics of the power system, directionality, and spatio-temporal characteristics (Lu et al., 2018).

Flexibility is an inherent characteristic of a power system (Denholm and Hand, 2011). For the power system, it has the ability to resist a certain risk, that is, the power system has an internal tolerance that allows the power system to deviate from the preset operating point to a certain extent without any change. This tolerance is considered as the inherent flexibility of the power system. From the perspective of power system active power balance, the climbing capacity, output range, and load characteristics of units are the inherent characteristics of power system flexibility.

Directionality (Lannoye et al., 2010): the power system is affected by many uncertain factors. The intermittent power sources have changed the traditional power structure and increased the randomness and uncertainty of power system operation from the power generation side, resulting in a power imbalance in the power system in a short time. Under different operating conditions, the power system flexibility is different. In view of this characteristic of flexibility, it can be considered that power system flexibility has two directions: upward and downward, that is, the flexibility is directional. The upregulation ability and downregulation ability reflect the flexibility of the system in different directions.

Spatio-temporal characteristic means the power system flexibility needs to be described on a certain timescale (Thatte and Xie, 2016). The power change caused by uncertainty in the power system rarely increases or decreases monotonically, and the change duration is also different. Therefore, the evaluation of power system flexibility is different in different timescales. According to the timescales, it can be divided into the flexibility of frequency modulation and unit climbing. On the spatial scale, due to the influence of resource distribution and transmission conditions, flexible resources cannot be dispatched freely in the system (Chen et al., 2020).

2.3 Evaluation methods of power system flexibility

In the research of power system flexibility, evaluation methods are the key point (Semich et al., 2020). According to the power system flexibility characteristics, many research studies have put forward different flexibility evaluation indexes. Velocity ramps (positive ramp and negative ramp) and load duration (the duration of continuous maximum and minimum loads) were presented as the evaluation indexes to evaluate the flexibility of the system (Martin et al., 2019). From the perspective of the attributes of the five flexible resources (supply, demand, grid, storage, and markets), Papaefthymiou et al. (2018) divided them into 14 flexibility index systems. Similar to Papaefthymiou et al. (2018), the authors also adopt the attribute classification method and put forward four flexibility attribute indexes, namely: positive flexibility, negative flexibility, production flexibility, and time-varying flexibility in Zhou et al. (2021). Some other evaluation indexes, such as upward and downward reserves (Ma et al., 2013), optimal costs, time-dependent flexibility potentials, costs of flexibility provision (Wanapinit et al., 2021), and flexibility metrics (flexibility regulation range increase rate and flexibility promotion cost) (Guo et al., 2020), were presented to evaluate power system flexibility.

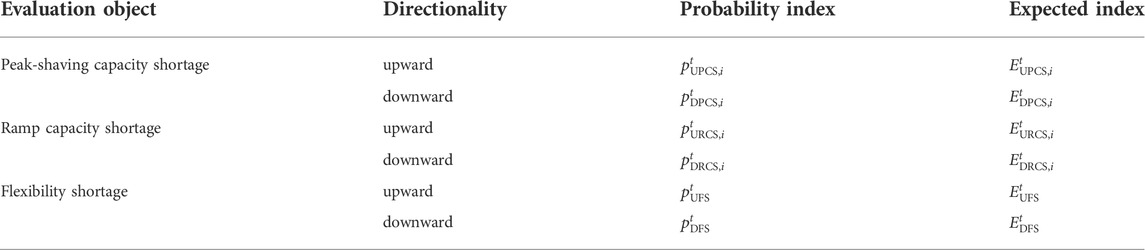
We briefly list several commonly used power system flexibility evaluation indexes in Table 1.

TABLE 1

TABLE 1. Some power system flexibility evaluation indexes.

3 Modeling methods of uncertainties

Renewable energy generation, load demand forecasting, electricity price fluctuation, and other uncertain factors make the power system in a strong uncertain environment. The traditional deterministic method is no longer appropriate, and it is necessary to consider the influence of uncertain factors. How to optimize the problem under uncertainty becomes important. To solve the problem of uncertainties in the power system, the key is to accurately describe the impact of uncertain factors and how to effectively use the information on uncertain variables to provide theoretical data for power departments to make safe and economic decision-making schemes.

For the traditional deterministic optimization problem, its mathematical expression is generally as follows (Anthony Man, 2011):

$\begin{array}{l}\min f\left(x\right)\\ s.t.h\left(x\right)\le 0,\end{array}(1)$

where x is the decision vector, $f\left(x\right)$ is the objective function, and $h\left(x\right)$ is the constraint function. In model (1), the corresponding parameters of both constraints and objective function are determined.

However, due to the emergence of various uncertain factors, the problems related to power systems have changed from traditional certainty to uncertainty, and the general expression of the uncertain optimization mathematical model is as follows(Sun et al., 2022):

$\begin{array}{l}\min f\left(x,\xi \right)\\ s.t.h\left(x,\xi \right)\le 0\\ \forall \xi \in U,\end{array}(2)$

where $\xi$ is an uncertain parameter, and U is an uncertain set.

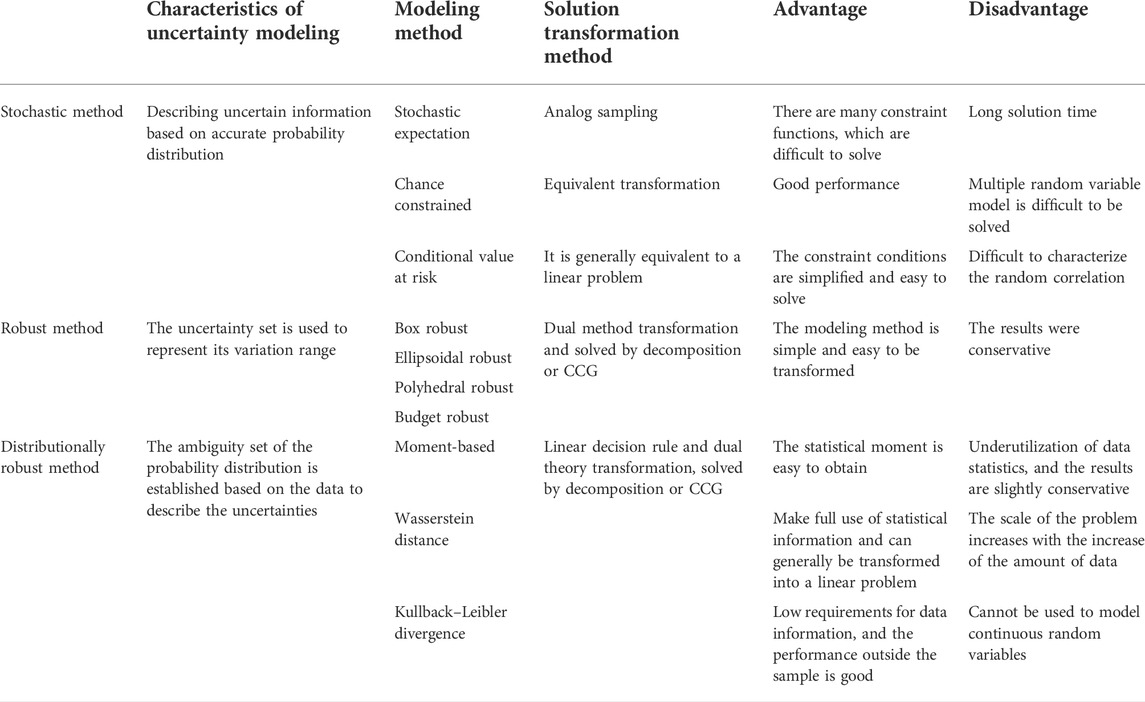
According to the different modeling of uncertain factors, the uncertain optimization methods mainly include stochastic programming, robust optimization, and distributionally robust optimization, and the comparisons of these methods are shown in Appendix 1.

3.1 Stochastic programming

In stochastic programming, random variables are often fitted to obtain the probability density distribution through the statistical analysis of historical data (Birge and Dempstert, 1996). The accurate acquisition of probability distribution and the accuracy of sampling calculation optimal solution are the main problems of stochastic programming methods (Jiang and Li, 2021). At present, the common stochastic programming methods mainly include the following.

3.1.1 Stochastic expectation model

In the stochastic expectation model, the distribution function model of uncertain parameters is determined, and the uncertain parameters are described by selecting a discrete or continuous probability distribution function. The stochastic expectation model is described as follows (Zhu et al., 2007):

$\{\begin{array}{l}\max \mathbb{E}\left[f\left(x,\xi \right)\right],\\ s.t.\mathbb{E}\left[g_j\left(x,\xi \right)\right]\le 0,j=\mathrm{1,2},\dots ,p,\end{array}(3)$

where $\xi$ is an uncertain parameter, x is the decision vector, $f\left(x,\xi \right)$ is the objective function, and $g_j\left(x,\xi \right)$ is the constraint condition function.

If there are random parameters in the objective function and constraints, it is only necessary to take the expected value of the corresponding function, and the uncertain model can be transformed into a deterministic model and be solved.

3.1.2 Chance constrained

Chance constrained programming refers to the situation where constraints contain random variables, and the decisions must be made before the realization of random variables is predicted. However, considering that the decision may not meet the constraints when adverse circumstances occur, the decision needs to meet the constraints to a certain extent, but the decision should make the probability of the establishment of the constraints not less than a certain confidence level (Guo et al., 2021). The generalized chance-constrained programming model is described as follows (Mohanty et al., 2020):

$\{\begin{array}{l}\min \overline{f}\\ s.t.\mathit{\mathbb{P}}\left\{f\left(x,\xi \right)\ge \overline{f}\right\}\ge \beta \\ \mathit{\mathbb{P}}\left\{g_i\left(x,\xi \right)\le 0,i=\mathrm{1,2},\cdots ,p\right\}\ge {\alpha }_i,\end{array}(4)$

where $\overline{f}$ is the objective value, x is the decision variable, $\xi$ is the uncertain variable, $\mathit{\mathbb{P}}\{\cdot \}$ is the probability of event occurrence, $\beta$ is the confidence level that the objective function is not lower than the threshold $\overline{f}$, and ${\alpha }_i$ is the ith constraint that satisfies the given confidence level.

There are two main solutions to chance-constrained programming. The first one is to transform the chance constrained into deterministic programming and then solve it by the theory of deterministic programming (Huo et al., 2021). The second one is an intelligent algorithm. The optimal value of the objective function and the optimal solution set of decision variables are obtained by stochastic simulation technology and solving them by intelligent algorithms, such as the simulated annealing algorithm (Özcan, 2010), genetic algorithm (Shing Chih and Fu, 2014), and random hill climbing algorithm (Kaur and Dhillon, 2021). The main disadvantage of these intelligent algorithms is their low efficiency.

3.1.3 Conditional value at risk

The theory of conditional value at risk (CVaR) is derived from the value at risk (VaR), which refers to the maximum expected loss at a given confidence level (Fernández, 2016; Belhajjam et al., 2017). The mathematical description of the VaR method is as follows (Crespi and Mastrogiacomo, 2020):

$Va{R}_{\beta }\left(x\right)=\min \{\xi \in \mathrm{ℝ}|\phi \left(x,\xi \right)\ge \beta \},(5)$

where x is the decision variable, $\xi$ is the uncertain variable, $\phi \left(x,\xi \right)$ is the function of the random variable $\xi$, and$\beta$ is the value of the confidence level. $\phi \left(x,\xi \right)$ can be obtained by the following formula (Belhajjam et al., 2017):

$\phi \left(x,\xi \right)={\displaystyle \underset{h\left(x,\xi \right)\le \alpha }{\int }p\left(\xi \right)}d\xi ,(6)$

where$p\left(\xi \right)$ is the probability density function of a random variable, $h\left(x,\xi \right)$ is the lost function, and $\alpha$ is the threshold.

The VaR method considers the probability density characteristics of random variables and can describe the minimum value of loss under a given value. However, the defects of VaR, such as lack of convexity and subadditivity, limit its further application in practical optimization problems (Khodabakhsh and Sirouspour, 2016).

In view of the fact that VaR cannot describe the tail risk, CVaR, which reflects the expected value of loss exceeding the VaR threshold at a given confidence level, as an alternative risk measure, is presented to avoid the problems of VaR. The mathematical description of CVaR is as follows (Crespi and Mastrogiacomo, 2020):

$CVa{R}_{\beta }\left(x\right)=\mathbb{E}\left[f\left(x,\xi \right)|f\left(x,\xi \right)\ge Va{R}_{\beta }\left(x\right)\right]=\frac{1}{1-\beta }{\displaystyle \underset{f\left(x,\xi \right)\ge Va{R}_{\beta }\left(x\right)}{\int }f\left(x,\xi \right)}p\left(x\right)d\xi .(7)$

To calculate the value of CVaR, Rockafellar and Uryasev (2000) established a linear programming model by using the sample average approximation method to avoid the calculation of the VaR and get the CvaR directly:

$\begin{array}{l}CVa{R}_{\beta }\left(x\right)=\min \{z_0+\frac{1}{n\left(1-\beta \right)}{\displaystyle \sum _{i=1}^n{z}_i}\}\\ s.t.z_i\ge f\left(x,{\xi }_i\right)-z_0\\ z_i\ge 0,i=\mathrm{1,2},\cdots n.\end{array}(8)$

The CVaR method can describe the impact of random variables from the perspective of risk, solve the problem that the VaR method cannot accurately describe the tail risk, and provide rich decision-making information for decision-makers (Ang et al., 2021). This method can use the constraints in the optimization model as the risk index to describe its risk, simplify the constraints in the model, obtain the risk decision information, and has the same good characteristics as the VaR method in mathematics.

3.1.4 Dependent-chance programming

Dependent-chance programming is a programming method generated when decision-makers face multiple events and want to maximize the probability of meeting these events. Dependent-chance programming is a stochastic optimization theory to optimize the chance function of events in an uncertain environment. The general model is given as follows (Liu, 1997):

$\{\begin{array}{l}\max \mathit{\mathbb{P}}\left\{h\left(x_i,\xi \right)\le 0\right\}\\ s.t.g_j\left(x_i,\xi \right)\le 0,j=\mathrm{1,2},\dots ,p,\end{array}(9)$

where $x_i$ is the decision variable, and$\xi$ is the uncertain variable. The dependent-chance programming model can be expressed as maximizing the probability of a random event $h\left(x_i,\xi \right)\le 0$ under an uncertain environment $g_j\left(x_i,\xi \right)\le 0$.

At present, the genetic algorithm is mainly used to solve the dependent-chance programming model. In Zhang and Song (2017), the author proposed a Sugeno measure space-based algorithm to solve the dependent-chance programming model.

3.2 Robust optimization

The stochastic programming method requires the accurate distribution of random variables, but this is very unrealistic in practice. For example, incomplete data may lead to an inaccurate probability distribution, which may affect the decision-making results (Yang et al., 2019). The robust optimization method is different from stochastic programming. When facing uncertain parameters, the robust optimization method does not need to know its accurate distribution but only its uncertain space (Ben-Tal and Nemirovski, 2002). Robust optimization assumed that the range of uncertain parameters is a specific uncertain set. Within the range of the uncertain set, the objective function or constraints in the worst-case scenario are constructed, which can generally be expressed as a min-max-min optimization problem (Gabrel et al., 2014):

$\begin{array}{l}\underset{x\in R,\xi \in \mathcal{U}}{\min \max \min }f\left(x,\xi \right)\\ s.t.g_i\left(x,\xi \right)\le 0\\ \forall \xi \in \mathcal{U}\\ i=\mathrm{1,2},\cdots m,\end{array}(10)$

where x is the decision variable, $\xi$ is the uncertain variable, and $\mathcal{U}$ is the uncertain set.

By choosing a different uncertain set to describe the uncertainties, robust optimization models with different modeling characteristics and solving difficulties can be obtained. According to different selection types of uncertainty sets, robust optimization methods can generally be divided into the box robust optimization method, ellipsoid robust optimization method, polyhedron robust optimization method, and budget robust optimization method. There are mainly the following types of robust sets to characterize uncertain variables.

3.2.1 Box robust set

The box uncertainty set is the simplest uncertainty set, also known as an interval set. Because robust optimization is an optimization solution method considering the worst case, it is possible for some models to optimize all uncertain parameters in the upper and lower bounds of the interval set. The generalized box robust optimization model is described as follows (Xiao et al., 2013):

$\mathcal{U}=\{\xi |{\xi }^0+\widehat{\xi },e^T\widehat{\xi }=0,\underset{-}{\xi }\le \widehat{\xi }\le \stackrel{-}{\xi }\},(11)$

where e is the column vector with element 1, and $\underset{-}{\xi }$ and $\stackrel{-}{\xi }$ are the upper and lower bounds of the given set, respectively.

However, in practice, the probability of this situation may not happen. Therefore, the results are easy to be excessively conservative (Gu et al., 2016).

3.2.2 Ellipsoidal robust set

To reduce the aggressive conservatism in Xiao et al. (2013), the ellipsoidal robust optimization method is presented as follows (Ben-Tal and Nemirovski, 1998):

$\mathcal{U}=\{\xi |{\xi }^0+A\widehat{\xi },e^{T}A\widehat{\xi }=0,\Vert \widehat{\xi }\Vert \le 1\},(12)$

where A is the control matrix of ellipsoidal size. Selecting different matrices can effectively control the distribution of uncertain parameters from the center of the sphere and the radius from the center of the sphere. Different values of A can realize the optimal decision of ellipsoid robust optimization with the coordination of conservatism and optimality (Hanks et al., 2017). Compared with the box robust optimization method, the ellipsoidal robust optimization method can describe uncertain parameters more accurately. However, the ellipsoidal robust optimization method increases the complexity of problem-solving, which limits the application of this method.

3.2.3 Polyhedral robust set

For robust uncertain optimization problems, not only the robustness of the results needs to be considered but also the trade-off between optimization performance and robustness. The polyhedral robust optimization method can meet such requirements at the same time. The generalized polyhedral robust optimization model is described as follows (Jalilvand-Nejad et al., 2016):

$\mathcal{U}=\{\xi |{\Vert \xi \Vert }_1\le \mathrm{\Gamma },\left|\xi \right|\le e\}.(13)$

The polyhedral uncertain set can be regarded as a special form of the ellipsoidal uncertain set. Although the polyhedral uncertainty set is difficult to characterize the correlation between uncertain parameters, they are widely favored in practical engineering problems because of their linear structure and easy-to-control uncertainty (Saric and Stankovic, 2008).

3.2.4 Budget robust set

The budget robust optimization method builds the uncertainty set based on the relative value of the offset of uncertain parameters, which can more accurately describe the fluctuation of uncertainties and is described as follows (Goerigk et al., 2020):

$\mathcal{U}=\{\xi |{\displaystyle \sum \left|\frac{{\xi }_i-{\widehat{\xi }}_i}{\stackrel{-}{{\xi }_i}-\underset{-}{{\xi }_i}}\right|}\le \mathrm{\Gamma },\left|\xi \right|\le e\},(14)$

where ${\widehat{\xi }}_i$ is the forecast value of an uncertain variable, and $\underset{-}{\xi }$ and $\stackrel{-}{\xi }$ are the upper and lower bounds of the given set, respectively.

3.2.5 Combined robust set

In addition to the aforementioned common uncertain sets, in order to adapt to different situations and describe the uncertainties more accurately, some researchers have also derived many kinds of combined uncertain sets, such as the “box + ellipsoidal” uncertain set and “box + polyhedral” uncertain set (Papadimitriou and Fortz, 2015; Dong et al., 2020).

3.3 Distributionally robust optimization

In recent years, the distributionally robust optimization (DRO) method has been proposed to overcome the shortcomings of stochastic optimization and robust optimization (Goh and Sim, 2010). Considering that in practical problems, some statistical information of random variables is often known, such as expectation and variance, and historical sample data. By establishing the ambiguity set of a random variable probability distribution based on some statistical information, the DRO method seeks the minimum expected value of system operation cost under the worst probability distribution. Therefore, the DRO method not only makes use of the statistical information of random variables but also ensures the reliability of the scheduling scheme to a certain extent (Wiesemann et al., 2014). Constructing the ambiguity set is the basis and key of the DRO method. At present, the ambiguous set construction methods mainly include as followed.

3.3.1 Moment-determination ambiguity set

Although it is impossible to accurately obtain the distribution of random variables through limited historical data, it can determine the mean and variance of random variables. Therefore, the DRO moment-determination method is derived, and the ambiguity set is described as follows (Wei et al., 2016):

$\mathrm{D}=\{P\left(\xi \right)|\begin{array}{c}P\left(\xi \in \mathrm{\Xi }\right)=1\\ \mathbb{E}\left(\xi \right)=\mu \\ \mathbb{E}\left({\left(\xi -\mu \right)}^2\right)={\sigma }^2\end{array}\},(15)$

where $\mathrm{D}$ is the ambiguity set, and $\mu$ and ${\sigma }^2$ are the mean and variance of random variables, respectively.

The uncertainty of the correlation moment is not considered in the DRO moment-deterministic method, which has a great impact on the decision results.

3.3.2 Moment-uncertainty ambiguity set

In practice, due to many reasons such as limited data and missing data, the moment-determination ambiguity set obtained from historical data statistics is not completely accurate and has certain uncertainty. Therefore, the DRO method considering moment uncertainty is particularly important. The moment-uncertainty ambiguity set can be expressed as follows (Chang et al., 2019):

$\mathrm{D}=\{\mathrm{\mathbb{P}}\in \mathrm{\Omega }|\begin{array}{c}\begin{array}{c}\mathrm{\mathbb{P}}\left(\xi \in \mathrm{\Xi }\right)=1\\ {\left(\mathbb{E}\left[\xi \right]-{\mu }_0\right)}^{\mathrm{T}}{\sigma }_0^{-1}\left(\mathbb{E}\left[\xi \right]-{\mu }_0\right)\le {\gamma }_1\\ \mathbb{E}\left[\left(\xi -{\mu }_0\right){\left(\xi -{\mu }_0\right)}^{\mathrm{T}}\right]\le {\gamma }_2{\sigma }_{\text{0}}\end{array}\\ {\gamma }_1\ge \text{0,}{\gamma }_2\ge 1\end{array}\},(16)$

where the second line assumes that the mean value of the random variable is located in an ellipsoid with ${\mu }_0$ as the center and ${\gamma }_1$ as the size. The third line describes the possibility that the random variable $\xi$ is close to ${\mu }_0$ based on the correlation ${\sigma }_{\text{0}}$. The parameters ${\gamma }_1$ and ${\gamma }_2$ quantify the decision-making trust in ${\mu }_0$ and ${\sigma }_{\text{0}}$, respectively.

3.3.3 Wasserstein distance-based ambiguity set

The Wasserstein distance-based method constructs the initial empirical distribution based on the sampled data and can make full use of the available historical data. Moreover, this method uses the Wasserstein sphere to limit the fluctuation range of probability distribution (Graf and Luschgy, 2009; Zhou et al., 2020). The selection of sphere radius has an important impact on the conservatism of system decision-making results. The ambiguity set is defined as a ball in the probability distribution space, which contains all distributions close to the real distribution or the most likely distribution in terms of probability distance. The decision-maker can control the conservatism of the optimization problem by adjusting the radius of the ball. If the radius is zero, the ambiguity set will be reduced to a single element set containing only the real distribution. The Wasserstein distance-based ambiguity set can be expressed as follows (Zheng and Chen, 2020):

${\mathrm{ℳ}}_{\mathrm{ϵ}}\left({\stackrel{\mathrm{\sim }}{\mathrm{\mathbb{P}}}}_S\right)=\{\mathrm{\mathbb{P}}\in \mathrm{ℛ}\left(\mathrm{\Xi }\right):W(\mathrm{\mathbb{P}},{\stackrel{\mathrm{\sim }}{\mathrm{\mathbb{P}}}}_S)\le \mathrm{ϵ}\},(17)$

where ${\mathrm{ℳ}}_{\mathrm{ϵ}}\left({\stackrel{\mathrm{\sim }}{\mathrm{\mathbb{P}}}}_S\right)$ represents the Wasserstein ball with $\mathrm{ϵ}$ as the radius and ${\stackrel{\mathrm{\sim }}{\mathrm{\mathbb{P}}}}_S$ as the center of the sphere.

The worst expectation of constructing an ambiguity set based on first-order Wasserstein distance has the following form and theorem (Mohajerin Esfahani and Kuhn, 2018):

$\mathcal{Z}\left(x\right)={\max }_{\mathrm{\mathbb{P}}}{\mathbb{E}}_{\mathrm{\mathbb{P}}}\left[Z\left(x,\xi \right)\right].(18)$

Through the strong duality theory, we can get the following equation:

$\mathcal{Z}\left(x\right)=\underset{\lambda \in {\mathrm{ℝ}}^{+}}{\inf }\mathrm{ϵ}\lambda +\frac{1}{I}{\displaystyle \sum _{s\in S}\sup Z\left(x,\xi \right)-\lambda d\left(\xi ,\stackrel{\sim }{\xi }\right)}.(19)$

Using Wasserstein distance to construct the ambiguity set has two advantages: 1) the distribution constructed by this method is more reasonable than that constructed by other common methods; 2) the robust problem can be transformed into finite convex programming or even linear programming, which is easy to calculate (Duan et al., 2018).

3.3.4 Kullback–Leibler distance-based ambiguity set

Different from the DRO method based on Wasserstein distance, the DRO method based on the Kullback–Leibler divergence assumes that the probability is discrete, and the Kullback–Leibler divergence is defined as follows (Kullback, 1987):

$D_{KL}\left(p|P_0\right)={\displaystyle \underset{\mathrm{\Omega }}{\int }P\left(\theta \right)}\log \frac{P\left(\theta \right)}{P_0\left(\theta \right)}d\theta ,(20)$

where p and p₀ are probability distribution functions of the random variable $\xi$, and $D_{KL}\left(p|P_0\right)$ represents the Kullback–Leibler divergence from p to p₀.

The ambiguity set of a probability distribution based on Kullback–Leibler divergence is as follows (Yang et al., 2019):

$\mathrm{D: }=\{P\in \mathrm{D|}{D}_{KL}\left(p|P_0\right)\le \eta \},(21)$

where $\eta$ is the divergence tolerance to control the size of the ambiguity set.

This kind of model transforms the original problem through simple dual derivation and the discrete probability scene value technique, and the solution is relatively simple. However, although the subproblem can be accelerated by solving each discrete scene separately, the solution time of the whole model is long.

4 Study on power system flexibility considering uncertainties

Uncertainty affects the power system in many ways. The current research mainly includes power system planning, power system operation, electricity market, load forecasting, and supply-demand balance.

The research on the uncertainty of power system load forecasting is mainly divided into two aspects: probabilistic load forecasting and the uncertainty of load forecasting results. There are few studies on the uncertain supply-demand balance of power systems, especially the system balance and operation problems caused by renewable energy. From a certain point of view, the purpose of power system load forecasting and supply-demand balance is mainly to provide a scientific basis for power system planning and operation. Therefore, aiming at the problem of power system flexibility in an uncertain environment, this study mainly summarizes the research progress of power system planning, operation, and electricity market flexibility.

4.1 Planning flexibility

Generally, power system planning consists of generation planning, capacity planning, and reserve planning (Dong and Tong, 2020). In the uncertain environment, the uncertainties increase the need for planning flexibility in electric power systems, and great progress has been made in the research of power system flexibility planning (Sun et al., 2021).

External flexibility resources, such as energy storage and demand response, are exploited in generation expansion planning for coping with renewable energy increases (Dai et al., 2021). Due to variable renewable energy source integration, a power-based unit commitment generation expansion planning model was presented to overcome the problem of overestimating the actual flexibility of the system, and from the perspective of directional characteristics, the indicators of insufficient flexibility of up- and downregulation and their expression forms are defined (Tejada-Arango et al., 2020). In Hua et al. (2018), from the viewpoint of representing system flexibility, a unit commitment generation expansion planning model was presented, and a convex relaxation was used to solve the problem computationally challenging of unit commitment, which is different from the model in Tejada-Arango et al. (2020). Flexibility is rarely fully considered in capacity planning models because of the computational demands of including mixed integer unit commitment within the capacity expansion; considering the carbon emission constraints and the penetration of renewable energy in power systems, the problems of generation of planning flexibility (Palmintier and Webster, 2016) and capacity planning flexibility (Hargreaves et al., 2015; Chen et al., 2018) were discussed, respectively. Based on a computational efficient modeling formulation, the chanced programming (Chen et al., 2018) and robust method (Hargreaves et al., 2015) were used to present the uncertainty of the wind power output.

A flexible power system should have sufficient ramp capacity and reserve capacity to meet the occurrence of uncertain conditions. Therefore, traditional reserve planning is deemed impeding to the system's flexibility (Khoshjahan et al., 2019). The concept of flexibility envelopes, which can capture reserve requirements, was presented as an alternative approach to the traditional reserve scheduling method (Nosair and Bouffard, 2015a; Nosair and Bouffard, 2015b). In Ghaemi and Salehi (2021) and Yang and Sun (2022), flexibility constraints were considered as a limit to reduce costs of the system, and MILP expansion planning was proposed, where an interval optimization has been utilized to address uncertainties due to the computational efficiency. In Dehghan et al. (2020), (2020), and Pourahmadi et al. (2020a), the problem of generation expansion planning was studied by the robust method, stochastic method, and distributionally robust method, respectively. Through different uncertainty modeling techniques, these literature reports analyzed the flexibility improvement methods from different viewpoints, and the flexibility of the system is evaluated from the time scale.

From the perspective of power system planning flexibility, the aforementioned research considers the uncertain factors including wind, transmission lines, and load demand but rarely considers the correlation between wind power. For power system planning, this is an important factor worthy of consideration. Whether it can effectively improve flexibility is worth discussing.

4.2 Operation flexibility

Compared with the problem of power system planning flexibility, the problem of power system operational flexibility in an uncertain environment, such as unit commitment and economic dispatch, has changed more obviously (Li et al., 2021). Operation flexibility is an important characteristic of the power system. It is an important means to reduce the power supply interruption caused by uncertainties in the power system. Improving the availability of renewable energy is one of the methods to meet the requirements of operational flexibility in power systems (Huo et al., 2020). It is the most important link to accurately model the uncertainties and describe their characteristics with corresponding mathematical methods (Pourahmadi et al., 2019; Pourahmadi et al., 2020b). The robust method, as a mature uncertainty modeling technology, has been widely used. To discuss the flexible unit commitment problem, box-based, ellipsoidal-based and polyhedral-based approaches as the uncertainties’ modeling have been used in Li et al. (2015), Angulo Cárdenas et al. (2016), and Cho et al. (2019) to model the uncertainty of renewable power and load demand, and the results showed that a flexible scheduling strategy was obtained which balances the economic and efficiency. From the perspective of the model solving efficiency, these three modeling methods have good performance. Demand response, as a flexible resource, its uncertainty is characterized by the stochastic method, and the role of improving system flexibility in multi-energy systems and unit commitment problems was studied in Good and Mancarella, (2019) and Saeed Poorvaezi et al. (2019). In the research, the difficult solution form of the problem is simplified by applying methods such as random scene reduction.

In the power system, with the rapid development of distributed generation, user-side management has become an important way to improve system flexibility (Rashidizadeh-Kermani et al., 2020). To assess the operational flexibility capacity of the system, a fixed robust uncertainty set and an adjustable uncertainty set were constructed; the wind power model based on a two-stage robust unit commitment was introduced in Pourahmadi et al. (2022), and the author adopts the improved method based on the CCG algorithm to solve the adjustable robust model. Considering energy storage and reserves, Zhang et al. (2016) presented a flexibility-oriented unified scheduling model to study the features required for flexibility assessment.

With the development of energy storage technology, much attention has been paid to the research of power system reserve flexibility from the perspective of the economy (Krad et al., 2017). Flexibility reserve, both with the function of supplying the energy imbalance in real-time operation and determining flexible ramping requirements (Khatami et al., 2020), and a continuous-time stochastic multi-fidelity model for co-optimization of energy and flexibility reserve were proposed by Khatami and Parvania (2020). Compared with these two similar stochastic modeling forms, the solution is more difficult and less efficient when considering the time scale.

4.3 Electricity market flexibility

Flexibility is the key to the operation of a high proportion renewable energy electricity market. Large power abandonment, frequent occurrence of negative electricity prices, and price fluctuation are all manifestations of inflexibility after the power system is connected to a high proportion of renewable energy (Bistline, 2019; Mamounakis et al., 2019; Ordoudis et al., 2020; Zhang et al., 2020). In the uncertain environment, how to improve the flexibility of the power market is worthy of attention for the realization of a new power system and the goal of dual carbon (Muñoz et al., 2021).

The flexibility of the electricity market can be improved by strengthening transmission investment and improving generation side flexibility and mechanism innovation (Papadaskalopoulos and Strbac, 2013; Chen and Jing, 2022; Tu, 2022). In addition, flexible ramping products, such as traditional thermal power units, electric vehicles, energy storage, electricity-gas combined system, and demand response, have made great progress as a method to improve system flexibility in an uncertain environment (Wang and Hodge, 2017; Wang et al., 2021). Considering the spatio-temporal correlations of wind power and demand uncertainties, a distributionally robust chance constrained multi-interval model was proposed to solve the deliverability issues of flexible ramping products (Fang et al., 2020), and the Wasserstein distance ambiguity set was transformed into a MILP problem. By aggregating demand-side flexibility resources, Di Somma et al. (2019) formulated a stochastic MILP problem, and the uncertainties of day-ahead market price and intermittent renewable energy generation were modeled through a set of scenarios to improve the flexibility operation of the electricity market. For the same MILP model, the difference between the two modeling methods leads to different difficulties and efficiency of the solution. Due to a large number of random scenes, the solution time is obviously long (Di Somma et al., 2019; Fang et al., 2020).

With the increasing proportion of renewable energy, energy storage, and natural gas, the main body of electricity market transactions is both an energy producer and energy consumer (Iria et al., 2019). At the same time, a large number of uncertain factors have challenged the effectiveness of various traditional operation measures. In the multi-energy environment, how to improve the flexibility of operation of the electricity market under uncertainties has attracted great attention (Baringo et al., 2019; Qin et al., 2021; Sayed et al., 2021; Yang et al., 2021). By using a set of inexact distributions based on historical data to portray the volatile market price, an electricity and heat market self-scheduling model was modeled as a distributionally robust problem, and the results validated that a more flexible electricity market can be obtained by this method (Li et al., 2022). For market flexibility, price and load demand are two major sources of uncertainty. The robust method (Velloso et al., 2020; Liu et al., 2022) and stochastic method (Hartwig and Kockar, 2016; Dvorkin, 2020; Jiang et al., 2022) were used to describe the uncertainty of market price and renewable energy generation, respectively. Numerical results showed that these methods have good performance in improving the flexibility of the electricity market in an uncertain environment.

5 Conclusion

This article reviews the concepts and characteristics of power system flexibility. Aiming at the problem of power system flexibility in an uncertain environment, the uncertainty modeling methods, including the robust method, stochastic method, and distributionally robust method, are summarized, and the corresponding mathematical modeling expressions are given. From the perspective of economy and conservatism, the advantages and disadvantages of these methods are compared and analyzed. Furthermore, from the perspective of planning, operation, and electricity market flexibility, the existing literature reports are summarized and analyzed in detail, and the following conclusions are obtained as follows:

1) Deepening the reform of the power system and building a new power system with renewable energy as the main body are important measures to achieve the goal of dual carbon. In this context, various uncertain factors, such as the output randomness and price instability of new energy, have a great impact on the power system flexibility.

2) The research on power system flexibility considering uncertainty factors and the research on using stochastic programming and robust optimization methods to solve such uncertain problems are mature at present. The application of constrained programming, value at risk method, conditional value at risk method, and robust optimization method in the power system will have further development. The new method combining the characteristics of stochastic programming and the robust optimization method can also be a way for subsequent related research. The distributionally robust method is the main research field of power system operation and planning flexibility, considering uncertainties, but there is little application research in electricity market flexibility. In addition, the random variable modeling method of distributionally robust optimization can be deeply studied to describe the uncertainty more accurately.

In recent years, with the improvement of computer computing power and the development of artificial intelligence technology, which has been gradually applied to power system uncertainty modeling, combining probability prediction technology with the optimal method, a decision-making method based on probability prediction has been constructed from mathematical theory so as to improve the flexibility ability of the power system to deal with the actual uncertainty factors in the future. For the research of power system flexibility in an uncertainty environment, the innovation of the modeling method, the efficiency of the solution algorithm, and the accurate combination of application scenarios are worth considering.

Author contributions

CY contributed to manuscript writing. WS contributed to review and editing. DH contributed to the supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (51777126).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alireza, A., Meysam, D., and Farrokh, A. (2019). Power system flexibility: an overview of emergence to evolution[J]. J. Mod. Power Syst. Clean. Energy 7 (5), 987–1007.

Google Scholar

AmandaSteele, J. H., Wesley Burnett, J., and Bergstrom, J. C. (2021). The impact of variable renewable energy resources on power system reliability. J. Energy Policy 151, 111947.

Google Scholar

Ang, X., Shen, X., Guo, Q., and Sun, H. (2021). A conditional value-at-risk based planning model for integrated energy system with energy storage and renewables[J]. Appl. Energy 294, 116971.

Google Scholar

Angulo Cárdenas, A. A., Mancilla-David, F., Palma-Behnke, R. E., and Espinoza, D. G. (2016). A polyhedral-based approach applied to quadratic cost curves in the unit commitment problem. IEEE Trans. Power Syst. 31 (5), 3674–3683. doi:10.1109/tpwrs.2015.2499442

CrossRef Full Text | Google Scholar

Anthony Man, C. S. (2011). Deterministic approximation algorithms for sphere constrained homogeneous polynomial optimization problems. Math. Program. 129, 357–382. doi:10.1007/s10107-011-0464-0

CrossRef Full Text | Google Scholar

Baringo, A., Baringo, L., and Arroyo, J. M. (2019). Day-ahead self-scheduling of a virtual power plant in energy and reserve electricity markets under uncertainty. IEEE Trans. Power Syst. 34 (3), 1881–1894. doi:10.1109/tpwrs.2018.2883753

CrossRef Full Text | Google Scholar

Belhajjam, A., Belbachir, M., and Ouardirhi, S. E. (2017). Robust multivairiate extreme value at risk allocation[J]. Fina. Res. Lett., S1544612316303622.

Google Scholar

Ben-Tal, A., and Nemirovski, A. (1998). Robust convex optimization. Math. OR. 23 (4), 769–805. doi:10.1287/moor.23.4.769

CrossRef Full Text | Google Scholar

Ben-Tal, A., and Nemirovski, A. (2002). Robust optimization–methodology and applications[J]. Math. Program. 11, 453–480.

CrossRef Full Text | Google Scholar

Birge, J. R., and Dempstert, M. A. H. (1996). Stochastic programming approaches to stochastic scheduling. J. Glob. Optim. 9, 417–451. doi:10.1007/bf00121682

CrossRef Full Text | Google Scholar

Bistline, J. E. (2019). Turn down for what? The economic value of operational flexibility in electricity markets[J]. IEEE Trans. Power Syst. 34 (1), 527–534. doi:10.1109/tpwrs.2018.2856887

CrossRef Full Text | Google Scholar

Brunner, C., Deac, G., Braun, S., and Zophel, C. (2020). The future need for flexibility and the impact of fluctuating renewable power generation. Renew. Energy 149, 1314–1324. doi:10.1016/j.renene.2019.10.128

CrossRef Full Text | Google Scholar

Chang, Z., Ding, J., and Song, S. (2019). Distributionally robust scheduling on parallel machines under moment uncertainty. Eur. J. Operational Res. 272 (13), 832–846. doi:10.1016/j.ejor.2018.07.007

CrossRef Full Text | Google Scholar

Chen, D., and Jing, Z. (2022). An improved market mechanism for energy storage based on flexible state of energy[J]. CSEE J. Power Energy Syst. 8 (3), 838–848.

Google Scholar

Chen, X., Dall’Anese, E., Zhao, C., and Li, N. (2020). Aggregate power flexibility in unbalanced distribution systems. IEEE Trans. Smart Grid 11 (1), 258–269. doi:10.1109/tsg.2019.2920991

CrossRef Full Text | Google Scholar

Chen, X., Lv, J., McElroy, M. B., Han, X., Nielsen, C. P., and Wen, J. (2018). Power system capacity expansion under higher penetration of renewables considering flexibility constraints and low carbon policies. IEEE Trans. Power Syst. 33 (6), 6240–6253. doi:10.1109/tpwrs.2018.2827003

CrossRef Full Text | Google Scholar

Chen, Z. (2019). Stochastic dynamic economic dispatch of wind-integrated electricity and natural gas systems considering security risk constraints[J]. CSEE J. Power Energy Syst. 5 (3), 324–334.

Google Scholar

Cho, Y., Ishizaki, T., Ramdani, N., and Imura, J. (2019). Box-based temporal decomposition of multi-period economic dispatch for two-stage robust unit commitment. IEEE Trans. Power Syst. 34 (4), 3109–3118. doi:10.1109/tpwrs.2019.2896349

CrossRef Full Text | Google Scholar

Crespi, G. P., and Mastrogiacomo, E. (2020). Qualitative robustness of set-valued value-at-risk. Math. Methods Oper. Res. (Heidelb). 91, 25–54. doi:10.1007/s00186-020-00707-9

CrossRef Full Text | Google Scholar

Dai, W., Shi, B., Zhang, D., Goh, H. H., Liu, H., and Li, J. (2021). Incorporating external flexibility in generation expansion planning. IEEE Trans. Power Syst. 36 (6), 5959–5962. doi:10.1109/tpwrs.2021.3101700

CrossRef Full Text | Google Scholar

Dehghan, S., Amjady, N., and Aristidou, P. (2020). A robust coordinated expansion planning model for wind farm-integrated power systems with flexibility sources using affine policies. IEEE Syst. J. 14 (3), 4110–4118. doi:10.1109/jsyst.2019.2957045

CrossRef Full Text | Google Scholar

Denholm, P., and Hand, M. (2011). Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 39 (3), 1817–1830. doi:10.1016/j.enpol.2011.01.019

CrossRef Full Text | Google Scholar

Di Somma, M., Graditi, G., and Siano, P. (2019). Optimal bidding strategy for a DER aggregator in the day-ahead market in the presence of demand flexibility. IEEE Trans. Ind. Electron. 66 (2), 1509–1519. doi:10.1109/tie.2018.2829677

CrossRef Full Text | Google Scholar

Ding, Y., Singh, C., Goel, L., Østergaard, J., and Wang, P. (2014). Short-term and medium-term reliability evaluation for power systems with high penetration of wind power. IEEE Trans. Sustain. Energy 5 (3), 896–906. doi:10.1109/tste.2014.2313017

CrossRef Full Text | Google Scholar

Dong, H., and Tong, X.-J. (2020). Review of mathematical methodology for electric power optimization problems[J]. J. Operations Res. Soc. China 8 (2), 295–309.

Google Scholar

Dong, H., Yang, C., and Sun, W. (2020). Modelling the operation of small-scale integrated energy systems based on data-driven robust optimization[J]. IEEJ Trans Electr. Electron. Eng. 15 (3), 442–450.

Google Scholar

Duan, C., Fang, W., Jiang, L., Yao, L., and Liu, J. (2018). Distributionally robust chance-constrained approximate AC-OPF with Wasserstein metric. IEEE Trans. Power Syst. 33 (5), 4924–4936. doi:10.1109/tpwrs.2018.2807623

CrossRef Full Text | Google Scholar

Dvorkin, Y., Kirschen, D. S., and Ortega-Vazquez, M. A. (2014). Assessing flexibility requirements in power systems. IET Gener. Transm. &amp. Distrib. 8 (11), 1820–1830. doi:10.1049/iet-gtd.2013.0720

CrossRef Full Text | Google Scholar

Dvorkin, Y. (2020). A chance-constrained stochastic electricity market. IEEE Trans. Power Syst. 35 (4), 2993–3003. doi:10.1109/tpwrs.2019.2961231

CrossRef Full Text | Google Scholar

Fang, X., Sedzro, K. S., Yuan, H., Ye, H., and Hodge, B. M. (2020). Deliverable flexible ramping products considering spatiotemporal correlation of wind generation and demand uncertainties. IEEE Trans. Power Syst. 35 (4), 2561–2574. doi:10.1109/tpwrs.2019.2958531

CrossRef Full Text | Google Scholar

Fernández, J. A. (2016). Economic lot sampling inspection from defect counts with minimum conditional value-at-risk[J]. Eur. J. Oper. Res., S0377221716308761.

Google Scholar

Gabrel, V., Murat, C., and Thiele, A. (2014). Recent advances in robust optimization: An overview. Eur. J. Operational Res. 235 (3), 471–483. doi:10.1016/j.ejor.2013.09.036

CrossRef Full Text | Google Scholar

Ghaemi, S., and Salehi, J. (2021). Incorporating ramp problem into the expansion planning of distributed energy resources for improving flexibility of renewable-based distribution network using interval optimization. Electr. Eng. 103, 341–355. doi:10.1007/s00202-020-01079-3

CrossRef Full Text | Google Scholar

Goerigk, M., Kurtz, J., and Poss, M. (2020). Min–max–min robustness for combinatorial problems with discrete budgeted uncertainty. Discrete Appl. Math. 285, 707–725. doi:10.1016/j.dam.2020.07.011

CrossRef Full Text | Google Scholar

Goh, J., and Sim, M. (2010). Distributionally robust optimization and its tractable Approximations. Operations Res. 58 (4), 902–917. doi:10.1287/opre.1090.0795

CrossRef Full Text | Google Scholar

Good, N., and Mancarella, P. (2019). Flexibility in multi-energy communities with electrical and thermal storage: A stochastic, robust approach for multi-service demand response. IEEE Trans. Smart Grid 10 (1), 503–513. doi:10.1109/tsg.2017.2745559

CrossRef Full Text | Google Scholar

Graf, S., and Luschgy, H. (2009). Quantization for probability measures in the prokhorov metric. Theory Probab. Appl. 53 (2), 216–241. doi:10.1137/s0040585x97983687

CrossRef Full Text | Google Scholar

Gu, C., Yang, W., Song, Y., and Li, F. (2016). Distribution network pricing for uncertain load growth using fuzzy set theory. IEEE Trans. Smart Grid 7 (4), 1932–1940. doi:10.1109/tsg.2016.2518175

CrossRef Full Text | Google Scholar

Guo, G., Zephyr, L., Morillo, J., Wang, Z., and Lindsay Anderson, C. (2021). Chance constrained unit commitment approximation under stochastic wind energy. Comput. Operations Res. 134, 105398. doi:10.1016/j.cor.2021.105398

CrossRef Full Text | Google Scholar

Guo, Z., Zheng, Y., and Li, G. (2020). Power system flexibility quantitative evaluation based on improved universal generating function method: A case study of zhangjiakou. Energy 205, 117963. doi:10.1016/j.energy.2020.117963

CrossRef Full Text | Google Scholar

Hanks, R. W., Weir, J. D., and Lunday, B. J. (2017). Robust goal programming using different robustness echelons via norm-based and ellipsoidal uncertainty sets[J]. Eur. J. Operational Res. 262, 34–39.

CrossRef Full Text | Google Scholar

Hargreaves, J., Hart, E. K., Jones, R., and Olson, A. (2015). Reflex: An adapted production simulation methodology for flexible capacity planning. IEEE Trans. Power Syst. 30 (3), 1306–1315. doi:10.1109/tpwrs.2014.2351235

CrossRef Full Text | Google Scholar

Hartwig, K., and Kockar, I. (2016). Impact of strategic behavior and ownership of energy storage on provision of flexibility. IEEE Trans. Sustain. Energy 7 (2), 744–754. doi:10.1109/tste.2015.2497967

CrossRef Full Text | Google Scholar

Hua, B., Baldick, R., and Wang, J. (2018). Representing operational flexibility in generation expansion planning through convex relaxation of unit commitment. IEEE Trans. Power Syst. 33 (2), 2272–2281. doi:10.1109/tpwrs.2017.2735026

CrossRef Full Text | Google Scholar

Huo, D., Gu, C., Greenwood, D., Wang, Z., Zhao, P., and Li, J. (2021). Chance-constrained optimization for integrated local energy systems operation considering correlated wind generation. Int. J. Electr. Power & Energy Syst. 132, 107153. doi:10.1016/j.ijepes.2021.107153

CrossRef Full Text | Google Scholar

Huo, Y., Bouffard, F., and Joós, G. (2020). Spatio-temporal flexibility management in low-carbon power systems. IEEE Trans. Sustain. Energy 11 (4), 2593–2605. doi:10.1109/tste.2020.2967428

CrossRef Full Text | Google Scholar

International Energy Agency (2014). The power of transformation: wind, sun and the economics of flexible power systems[J].

Google Scholar

Iria, J. P., Soares, F. J., and Matos, M. A. (2019). Trading small prosumers flexibility in the energy and tertiary reserve markets. IEEE Trans. Smart Grid 10 (3), 2371–2382. doi:10.1109/tsg.2018.2797001

CrossRef Full Text | Google Scholar

Jalilvand-Nejad, A., Shafaei, R., and Hamid, S. (2016). Robust optimization under correlated polyhedral uncertainty set. Comput. Industrial Eng. 92, 82–94. doi:10.1016/j.cie.2015.12.006

CrossRef Full Text | Google Scholar

Jiang, J., and Li, S. J. (2021). On complexity of multistage stochastic programs under heavy tailed distributions. Operations Res. Lett. 49 (2), 265–269. doi:10.1016/j.orl.2021.01.016

CrossRef Full Text | Google Scholar

Jiang, T., Yuan, C., Bai, L., Chowdhury, B. H., Zhang, R., and Li, X. (2022). Bi-level strategic bidding model of gas-fired units in interdependent electricity and natural gas markets. IEEE Trans. Sustain. Energy 13 (1), 328–340. doi:10.1109/tste.2021.3110864

CrossRef Full Text | Google Scholar

Kaur, G., and Dhillon, J. S. (2021). Economic power generation scheduling exploiting hill-climbed Sine–Cosine​ algorithm. Appl. Soft Comput. 111, 107690. doi:10.1016/j.asoc.2021.107690

CrossRef Full Text | Google Scholar

Khatami, R., Parvania, M., and Narayan, A. (2020). Flexibility reserve in power systems: Definition and stochastic multi-fidelity optimization. IEEE Trans. Smart Grid 11 (1), 644–654. doi:10.1109/tsg.2019.2927600

CrossRef Full Text | Google Scholar

Khatami, R., and Parvania, M. (2020). Stochastic multi-fidelity scheduling of flexibility reserve for energy storage. IEEE Trans. Sustain. Energy 11 (3), 1438–1450. doi:10.1109/tste.2019.2927598

CrossRef Full Text | Google Scholar

Khodabakhsh, R., and Sirouspour, S. (2016). Optimal control of energy storage in a microgrid by minimizing conditional value-at-risk. IEEE Trans. Sustain. Energy 3 (7), 1264–1273. doi:10.1109/tste.2016.2543024

CrossRef Full Text | Google Scholar

Khoshjahan, M., Dehghanian, P., Moeini-Aghtaie, M., and Fotuhi-Firuzabad, M. (2019). Harnessing ramp capability of spinning reserve services for enhanced power grid flexibility. IEEE Trans. Ind. Appl. 55 (6), 7103–7112. doi:10.1109/tia.2019.2921946

CrossRef Full Text | Google Scholar

Krad, I., Gao, D. W., and Wu, H. (2017). An assessment of flexibility reserves in stochastic modeling at multiple timescales. CSEE J. Power Energy Syst. 3 (1), 84–92. doi:10.17775/cseejpes.2017.0011

CrossRef Full Text | Google Scholar

Kullback, S. (1987). The kullback-leibler distance[J]. Am. Statistician 41 (4), 340–341.

Google Scholar

Lannoye, E., Milligan, M., and Adams, J. (2010). Integration of variable generation: capacity value and evaluation of flexibility[J]. Proc. Power Energy Soc. General Meeting. Minneapolis Minnesota, USA: IEEE, 25–29.

Google Scholar

Lannoye, J. E., Flynn, D., and O'Malley, M. (2012). Evaluation of power system flexibility. IEEE Trans. Power Syst. 27 (2), 922–931. doi:10.1109/tpwrs.2011.2177280

CrossRef Full Text | Google Scholar

Li, H., Lu, Z., Qiao, Y., Zhang, B., and Lin, Y. (2021). The flexibility test system for studies of variable renewable energy resources. IEEE Trans. Power Syst. 36 (2), 1526–1536. doi:10.1109/tpwrs.2020.3019983

CrossRef Full Text | Google Scholar

Li, J., Liu, F., Li, Z., Shao, C., and Liu, X. (2018). Grid-side flexibility of power systems in integrating large-scale renewable generations: A critical review on concepts, formulations and solution approaches. Renew. Sustain. Energy Rev. 93, 272–284. doi:10.1016/j.rser.2018.04.109

CrossRef Full Text | Google Scholar

Li, P., Guan, X., Wu, J., and Zhou, X. (2015). Modeling dynamic spatial correlations of geographically distributed wind farms and constructing ellipsoidal uncertainty sets for optimization-based generation scheduling. IEEE Trans. Sustain. Energy 6 (4), 1594–1605. doi:10.1109/tste.2015.2457917

CrossRef Full Text | Google Scholar

Li, Z., et al. (2020). Probability-Interval-Based optimal planning of integrated energy system with uncertain wind power[J]. IEEE Trans. Industry Appl. 56 (1), 4–13.

CrossRef Full Text | Google Scholar

Li, Z., Chen, L., Wei, W., and Mei, S. (2022). Risk constrained self-scheduling of AA-CAES facility in electricity and heat markets: A distributionally robust optimization approach[J]. CSEE J. Power Energy Syst., 1–9. doi:10.17775/CSEEJPES.2020.06130

CrossRef Full Text | Google Scholar

Liu, B. (1997). Dependent-chance programming: A class of stochastic optimization. Comput. Math. Appl. 34 (12), 89–104. doi:10.1016/s0898-1221(97)00237-x

CrossRef Full Text | Google Scholar

Liu, F., Wang, X., Xiao, Y., and Bie, Z. (2022). Robust pricing of energy and ancillary services in combined electricity and natural gas markets. IEEE Trans. Power Syst. 37 (1), 603–616. doi:10.1109/tpwrs.2021.3091021

CrossRef Full Text | Google Scholar

Lu, Z., Li, H., and Qiao, Y. (2018). Probabilistic flexibility evaluation for power system planning considering its association with renewable power curtailment. IEEE Trans. Power Syst. 33 (3), 3285–3295. doi:10.1109/tpwrs.2018.2810091

CrossRef Full Text | Google Scholar

Ma, J., Silva, V., Belhomme, R., Kirschen, D. S., and Ochoa, L. F. (2013). Evaluating and planning flexibility in sustainable power systems. IEEE Trans. Sustain. Energy 4 (1), 200–209. doi:10.1109/tste.2012.2212471

CrossRef Full Text | Google Scholar

Mamounakis, I., Efthymiopoulos, N., Vergados, D. J., Tsaousoglou, G., Makris, P., and Varvarigos, E. M. (2019). A pricing scheme for electric utility's participation in day-ahead and real-time flexibility energy markets. J. Mod. Power Syst. Clean. Energy 7 (5), 1294–1306. doi:10.1007/s40565-019-0537-2

CrossRef Full Text | Google Scholar

Martin, D., Pfeiffer, D., Lauer, M., et al. (2019). How to measure flexibility-performance indicators for demand driven power generation from biogas plants[J]. Renew. Energy 134, 135–146.

Google Scholar

Michael, E., Kate, D., Cakir, B., Markovic, M., and Hodge, B. M. (2020). A review of power system planning and operational models for flexibility assessment in high solar energy penetration scenarios. Sol. Energy 210 (1), 169–180. doi:10.1016/j.solener.2020.07.017

CrossRef Full Text | Google Scholar

Milligan, M., O Malley, M., and Adams, J. M. (2010). Flexibility requirements and potential metrics for variable generation: implications for system planning studies[J]. NERC.

Google Scholar

Mohajerin Esfahani, P., and Kuhn, D. (2018). Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations. Math. Program. 171, 115–166. doi:10.1007/s10107-017-1172-1

CrossRef Full Text | Google Scholar

Mohandes, B., Moursi, M. S. E., Hatziargyriou, N., and Khatib, S. E. (2019). A review of power system flexibility with high penetration of renewables. IEEE Trans. Power Syst. 34 (4), 3140–3155. doi:10.1109/tpwrs.2019.2897727

CrossRef Full Text | Google Scholar

Mohanty, D. K., Pradhan, B. M. P., and Biswal, M. P. (2020). Chance constrained programming with some non-normal continuous random variables. Opsearch 57, 1281–1298. doi:10.1007/s12597-020-00454-9

CrossRef Full Text | Google Scholar

Muñoz, F. D., Suazo-Martínez, C., Pereira, E., and Moreno, R. (2021). Electricity market design for low-carbon and flexible systems: Room for improvement in Chile. Energy Policy 148, 111997. doi:10.1016/j.enpol.2020.111997

CrossRef Full Text | Google Scholar

Nosair, H., and Bouffard, F. (2015). Flexibility envelopes for power system operational planning. IEEE Trans. Sustain. Energy 6 (3), 800–809. doi:10.1109/tste.2015.2410760

CrossRef Full Text | Google Scholar

Nosair, H., and Bouffard, F. (2015). Reconstructing operating reserve: Flexibility for sustainable power systems. IEEE Trans. Sustain. Energy 6 (4), 1624–1637. doi:10.1109/tste.2015.2462318

CrossRef Full Text | Google Scholar

Ordoudis, C., Delikaraoglou, S., Kazempour, J., and Pierre, P. (2020). Market-based coordination of integrated electricity and natural gas systems under uncertain supply. Eur. J. Operational Res. 287 (3), 1105–1119. doi:10.1016/j.ejor.2020.05.007

CrossRef Full Text | Google Scholar

Özcan, U. (2010). Balancing stochastic two-sided assembly lines: A chance-constrained, piecewise-linear, mixed integer program and a simulated annealing algorithm. Eur. J. Operational Res. 205 (1), 81–97. doi:10.1016/j.ejor.2009.11.033

CrossRef Full Text | Google Scholar

Palmintier, Bryan S., and Webster, Mort D. (2016). Impact of operational flexibility on electricity generation planning with renewable and carbon targets. IEEE Trans. Sustain. Energy 7 (2), 672–684. doi:10.1109/tste.2015.2498640

CrossRef Full Text | Google Scholar

Papadaskalopoulos, D., and Strbac, G. (2013). Decentralized participation of flexible demand in electricity markets—Part I: Market mechanism. IEEE Trans. Power Syst. 28 (4), 3658–3666. doi:10.1109/tpwrs.2013.2245686

CrossRef Full Text | Google Scholar

Papadimitriou, D., and Fortz, B. (2015). “Robust cooperative monitoring problem[J],” in 7th international workshop on reliable networks design and modeling (RNDM), 186–193.

Google Scholar

Papaefthymiou, G., Haesen, E., and Sach, T. (2018). Power System Flexibility Tracker: Indicators to track flexibility progress towards high-RES systems. Renew. Energy 134, 1026–1035. doi:10.1016/j.renene.2018.04.094

CrossRef Full Text | Google Scholar

Pourahmadi, F., Heidarabadi, H., Hosseini, S. H., and Dehghanian, P. (2020). Dynamic uncertainty set characterization for bulk power grid flexibility assessment. IEEE Syst. J. 14 (1), 718–728. doi:10.1109/jsyst.2019.2901358

CrossRef Full Text | Google Scholar

Pourahmadi, F., Hosseini, S. H., Dehghanian, P., Shittu, E., and Fotuhi-Firuzabad, M. (2022). Uncertainty cost of stochastic producers: Metrics and impacts on power grid flexibility. IEEE Trans. Eng. Manag. 69 (3), 708–719. doi:10.1109/tem.2020.2970729

CrossRef Full Text | Google Scholar

Pourahmadi, F., Hosseini, S. H., and Fotuhi-Firuzabad, M. (2019). Economically optimal uncertainty set characterization for power system operational flexibility. IEEE Trans. Ind. Inf. 15 (10), 5456–5465. doi:10.1109/tii.2019.2906058

CrossRef Full Text | Google Scholar

Pourahmadi, F., Kazempour, J., Ordoudis, C., Pinson, P., and Hosseini, S. H. (2020). Distributionally robust chance-constrained generation expansion planning. IEEE Trans. Power Syst. 35 (4), 2888–2903. doi:10.1109/tpwrs.2019.2958850

CrossRef Full Text | Google Scholar

Qin, Zhijun, Mo, Yuhong, Liu, Hui, and Zhang, Yihui (2021). Operational flexibility enhancements using mobile energy storage in day-ahead electricity market by game-theoretic approach. Energy 232, 121008. doi:10.1016/j.energy.2021.121008

CrossRef Full Text | Google Scholar

Rashidizadeh-Kermani, H., Vahedipour-Dahraie, M., Shafie-Khah, M., and Siano, P. (2020). A regret-based stochastic Bi-level framework for scheduling of DR aggregator under uncertainties. IEEE Trans. Smart Grid 11 (4), 3171–3184. doi:10.1109/tsg.2020.2968963

CrossRef Full Text | Google Scholar

Rockafellar, R. T., and Uryasev, S. (2000). Optimization of conditional value-at-risk. J. Risk 2 (3), 21–41. doi:10.21314/jor.2000.038

CrossRef Full Text | Google Scholar

Saeed Poorvaezi, R., Abdollahi, Amir, and Rashidinejad, Masoud (2019). Probabilistic-possibilistic flexibility-based unit commitment with uncertain negawatt demand response resources considering Z-number method[J]. Int. J. Electr. Power & Energy Syst. 113, 71–89.

Google Scholar

Saric, A. T., and Stankovic, A. M. (2008). Applications of ellipsoidal approximations to polyhedral sets in power system optimization. IEEE Trans. Power Syst. 23 (3), 956–965. doi:10.1109/tpwrs.2008.926435

CrossRef Full Text | Google Scholar

Sayed, A. R., Wang, C., Wei, W., Bi, T., and Shahidehpour, M. (2021). Robust operational equilibrium for electricity and gas markets considering bilateral energy and reserve contracts. IEEE Trans. Power Syst. 36 (4), 2891–2905. doi:10.1109/tpwrs.2020.3043230

CrossRef Full Text | Google Scholar

Semich, I., Secil Varbak, N., and Oral, B. (2020). Challenges of renewable energy penetration on power system flexibility: A survey [J]. Energy Strategy Rev. 31, 100539.

Google Scholar

Shahidehpour, M., Tinney, F., and Fu, Y. (2005). Impact of security on power systems operation. Proc. IEEE 93 (11), 2013–2025. doi:10.1109/jproc.2005.857490

CrossRef Full Text | Google Scholar

Shing Chih, T., and Fu, S. Y. (2014). Genetic-algorithm-based simulation optimization considering a single stochastic constraint[J]. Eur. J. Operational Res. 236 (1), 113–125.

Google Scholar

Shu, Y., and Tang, Y. (2017). Analysis and recommendations for the adaptability of China's power system security and stability relevant standards. CSEE J. Power Energy Syst. 3 (4), 334–339. doi:10.17775/cseejpes.2017.00650

CrossRef Full Text | Google Scholar

Sun, Q., Wu, Z., Gu, W., Zhu, T., Zhong, L., and Gao, T. (2021). Flexible expansion planning of distribution system integrating multiple renewable energy sources: An approximate dynamic programming approach. Energy 226, 120367. doi:10.1016/j.energy.2021.120367

CrossRef Full Text | Google Scholar

Sun, X., Feng, X., and Teo, K. L. (2022). Robust optimality, duality and saddle points for multiobjective fractional semi-infinite optimization with uncertain data. Optim. Lett. 16, 1457–1476. doi:10.1007/s11590-021-01785-2

CrossRef Full Text | Google Scholar

Tejada-Arango, D. A., Morales-Espana, G., Wogrin, S., and Centeno, E. (2020). Power-based generation expansion planning for flexibility requirements. IEEE Trans. Power Syst. 35 (3), 2012–2023. doi:10.1109/tpwrs.2019.2940286

CrossRef Full Text | Google Scholar

Telukunta, V., Pradhan, J., Agrawal, A., Singh, M., and Srivani, S. G. (2017). Protection challenges under bulk penetration of renewable energy resources in power systems: A review. CSEE J. Power Energy Syst. 3 (4), 365–379. doi:10.17775/cseejpes.2017.00030

CrossRef Full Text | Google Scholar

Thatte, A. A., and Xie, L. (2016). A metric and market construct of inter-temporal flexibility in time-coupled economic dispatch. IEEE Trans. Power Syst. 31 (5), 3437–3446. doi:10.1109/tpwrs.2015.2495118

CrossRef Full Text | Google Scholar

Tu, T. (2022). Collusion potential assessment in electricity markets considering generation flexibility[J]. CSEE J. Power Energy Syst., 1–15. doi:10.17775/CSEEJPES.2020.01550

CrossRef Full Text | Google Scholar

United Nations Environment Programme (2019). “United Nations environment Programme,” in Emissions gap report 2019 (New York, United States: United Nations.

Google Scholar

Velloso, A., Street, A., Pozo, D., Arroyo, J. M., and Cobos, N. G. (2020). Two-stage robust unit commitment for Co-optimized electricity markets: An adaptive data-driven approach for scenario-based uncertainty sets. IEEE Trans. Sustain. Energy 11 (2), 958–969. doi:10.1109/tste.2019.2915049

CrossRef Full Text | Google Scholar

Wanapinit, Natapon, Thomsen, Jessica, Kost, Christoph, and Weidlich, A. (2021). An MILP model for evaluating the optimal operation and flexibility potential of end-users. Appl. Energy 282, 116183. doi:10.1016/j.apenergy.2020.116183

CrossRef Full Text | Google Scholar

Wang, Q., and Hodge, B. (2017). Enhancing power system operational flexibility with flexible ramping products: A review. IEEE Trans. Ind. Inf. 13 (4), 1652–1664. doi:10.1109/tii.2016.2637879

CrossRef Full Text | Google Scholar

Wang, S., Tan, X., Liu, T., and Tsang, D. H. K. (2021). Aggregation of demand-side flexibility in electricity markets: Negative impact analysis and mitigation method. IEEE Trans. Smart Grid 12 (1), 774–786. doi:10.1109/tsg.2020.3018227

CrossRef Full Text | Google Scholar

Wang, Z., Shen, C., Liu, F., Wu, X., Liu, C., and Gao, F. (2017). Chance-constrained economic dispatch with non-Gaussian correlated wind power uncertainty. IEEE Trans. Power Syst. 32 (6), 4880–4893. doi:10.1109/tpwrs.2017.2672750

CrossRef Full Text | Google Scholar

Wei, W., Liu, F., and Mei, S. (2016). Distributionally robust Co-optimization of energy and reserve dispatch. IEEE Trans. Sustain. Energy 7 (1), 289–300. doi:10.1109/tste.2015.2494010

CrossRef Full Text | Google Scholar

Wiesemann, W., Kuhn, D., and Sim, M. (2014). Distributionally robust convex optimization. Operations Res. 62 (6), 1358–1376. doi:10.1287/opre.2014.1314

CrossRef Full Text | Google Scholar

Xiao, Z., Chen, W., and Li, L. (2013). A method based on interval-valued fuzzy soft set for multi-attribute group decision-making problems under uncertain environment. Knowl. Inf. Syst. 34, 653–669. doi:10.1007/s10115-012-0496-7

CrossRef Full Text | Google Scholar

Xinhuanet (2021). Xinhuanet. Available at: http://www.xinhuanet.com/2021-03/13/c11272055642.htm.

Google Scholar

Xu, X. Y., Yan, Z., Shahidehpour, M., Li, Z., and Kong, X. (2020). Data-Driven risk-averse two-stage optimal stochastic scheduling of energy and reserve with correlated wind power. IEEE Trans. Sustain. Energy 11 (1), 436–447. doi:10.1109/tste.2019.2894693

CrossRef Full Text | Google Scholar

Yang, Ce, and Sun, W. (2022). Risk-averse two-stage distributionally robust economic dispatch model under uncertain renewable energy[J]. CSEE J. Power Energy Syst., 1–10. doi:10.17775/CSEEJPES.2020.03430

CrossRef Full Text | Google Scholar

Yang, C., Han, D., Sun, W. Q., and Tian, K. (2019). Distributionally robust model of energy and reserve dispatch based on kullback–leibler divergence. Electronics 8 (12), e1454. doi:10.3390/electronics8121454

CrossRef Full Text | Google Scholar

Yang, J., Liu, C., Mi, Y., Zhang, H., and Terzija, V. (2021). Optimization operation model of electricity market considering renewable energy accommodation and flexibility requirement. Glob. Energy Interconnect. 4 (3), 227–238. doi:10.1016/j.gloei.2021.07.007

CrossRef Full Text | Google Scholar

Yorino, N., Abdillah, M., Sasaki, Y., and Zoka, Y. (2018). Robust power system security assessment under uncertainties using Bi-level optimization. IEEE Trans. Power Syst. 33 (1), 352–362. doi:10.1109/tpwrs.2017.2689808

CrossRef Full Text | Google Scholar

Zhang, H., and Song, J. (2017). Dependent-chance programming on Sugeno measure space. J. Uncertain. Anal. Appl. 4, 7. doi:10.1186/s40467-017-0061-8

CrossRef Full Text | Google Scholar

Zhang, L., Capuder, T., and Mancarella, P. (2016). Unified unit commitment formulation and fast multi-service LP model for flexibility evaluation in sustainable power systems. IEEE Trans. Sustain. Energy 7 (2), 658–671. doi:10.1109/tste.2015.2497411

CrossRef Full Text | Google Scholar

Zhang, Z., Li, R., and Li, F. (2020). A novel peer-to-peer local electricity market for Joint trading of energy and uncertainty. IEEE Trans. Smart Grid 11 (2), 1205–1215. doi:10.1109/tsg.2019.2933574

CrossRef Full Text | Google Scholar

Zhao, J., Zheng, T., and Litvinov, E. (2016). A unified framework for defining and measuring flexibility in power system. IEEE Trans. Power Syst. 31 (1), 339–347. doi:10.1109/tpwrs.2015.2390038

CrossRef Full Text | Google Scholar

Zheng, X., and Chen, H. (2020). Data-Driven distributionally robust unit commitment with Wasserstein metric: Tractable formulation and efficient solution method. IEEE Trans. Power Syst. 35 (6), 4940–4943. doi:10.1109/tpwrs.2020.3014808

CrossRef Full Text | Google Scholar

Zhou, A., Yang, M., Wang, M., and Zhang, Y. (2020). A linear programming approximation of distributionally robust chance-constrained dispatch with Wasserstein distance. IEEE Trans. Power Syst. 35 (5), 3366–3377. doi:10.1109/tpwrs.2020.2978934

CrossRef Full Text | Google Scholar

Zhou, Y., Wang, J., Dong, F., Qin, Y., Ma, Z., Ma, Y., et al. (2021). Novel flexibility evaluation of hybrid combined cooling, heating and power system with an improved operation strategy. Appl. Energy 300, 117358. doi:10.1016/j.apenergy.2021.117358

CrossRef Full Text | Google Scholar

Zhu, H., Gu, M., and Peterson, B. (2007). Maximum likelihood from spatial random effects models via the stochastic approximation expectation maximization algorithm. Stat. Comput. 17 (2), 163–177. doi:10.1007/s11222-006-9012-9

CrossRef Full Text | Google Scholar

Appendix 1: Comparison of uncertainty modeling methods