- 1School of Electronic and Information Engineering, Ningbo University of Technology, Ningbo, China
- 2Ningbo Jianan Electronics Company Limited., Ningbo, China
In view of the low efficiency of thermoelectric generation systems in different regions, this paper designs an optimization and reconfiguration of thermoelectric power generation system under heterogeneous temperature difference (HTD) based on particle swarm optimization (PSO) algorithm, so as to make full use of various thermal energy resources and obtain higher electrical output power, which realize multi-directional utilization of energy. In addition, PSO algorithm is a simple optimization strategy with a straightforward operation mechanism and fewer parameters to control during calculation. The research shows that when TEG array is in multiple HTD states, PSO algorithm has a stronger ability to get rid of local optimization, which can reduce power loss and improve energy conversion efficiency. On this basis, PSO algorithm is used to reconfigure the 15 × 15 symmetric TEG array. The experimental simulation analysis based on MATLAB platform is carried out to verify the feasibility of PSO algorithm.
1 Introduction
With the growth of the global population and the improvement of human living standards (Shahbaz et al., 2020; Sun et al., 2020), energy consumption is also growing rapidly. For more than 100 years, traditional fossil energy (Liu et al., 2020) has been dominant in energy consumption, even disasters to a certain extent (Yang et al., 2020), but the consumption of traditional fossil energy will generate a large amount of carbon dioxide, which will lead to obvious greenhouse gas effects and bring huge challenges (Zhang et al., 2019) to the living environment of human beings, even to a certain degree of disaster. Thus, based on new materials and new technologies, the development of clean and renewable energy that can replace traditional fossil energy (El-Dein et al., 2013) (i.e., hydropower, nuclear energy, solar energy, wind energy, hydrogen energy, etc.) is imminent, which plays a vital role in the optimization of energy structure as well as the protection of the ecological environment.
It is worth noting that modern human activities generate a large amount of waste heat (Jian et al., 2021), especially industrial production activities are the main reason for creating a large amount of waste heat. Based on this, many scholars currently use semiconductor thermoelectric generation (Ge et al., 2021) technology to convert this waste heat into electricity. Thermoelectric generator (TEG) (Fernández-Yáñez et al., 2021), also known as waste heat power generation, is based on the theory of thermoelectric power generation, that is, using the temperature difference between high and low temperature heat sources, upon which low boiling point working fluid is used as the circulating work fluid. And then, on the basis of Rankine Cycle (RC), the steam generated by the high temperature heat source is heated and evaporated to generate electricity, which can directly convert the heat source into electricity, while the power generation process is vibration-free, pollution-free, highly reliable, long service life, etc. In addition, TEG system (Luo et al., 2021) has numerous application scenarios, such as temperature differences between upper and lower ocean waters, waste heat from automobile engines, and waste heat generated from industrial equipment after the operation.
Although TEG has tremendous potential in the field of waste heat recovery, its inherent deficiencies such as low energy conversion efficiency and low waste heat utilization rate restrict its more extensive application. One of the ideas being researched to enhance energy conversion efficiency is to search for the maximum power point (MPP) based on the maximum power point tracking (MPPT) algorithm. For the TEG array in uniform temperature difference conditions (i.e., similar to photovoltaic (PV) (Li et al., 2018) panels exposed to various solar radiation), scholars have concentrated a large number of their attention. Traditional gradient control techniques (Mamura et al., 2022) such as perturbation observation (PO) method, incremental conductance (INC.) method, open circuit voltage (OCV) method, and other optimization methods are exploited to obtain the optimal energy output of the TEG system. Although the traditional methods mentioned above are straightforward (Matthew and Jae, 2015) in principle and easy to implement, they are less accurate in control, which oscillates significantly around the MPP and even misjudges it, thus causing some power loss. Besides, in practical engineering applications, the external ambient temperature is not constant, rather it changes dynamically, which renders the gradient control techniques unsuitable for MPPT under various heterogeneous temperature difference (HTD) conditions.
The inevitable actual HTD states can produce multiple local maximum power points (LMPPs) on the power curve, into which the above method can be trapped very easily, so more sophisticated and intelligent techniques are required to search for the global maximum power point (GMPP). The meta-heuristic algorithms are powerful tools for achieving high-quality solutions in a short time, in part by identifying locally optimal solutions in the absence of an exact mathematical model. They offer an insightful and promising direction of work for tackling complicated high-dimensional optimization problems. Reference (Yang et al., 2019) proposed an improved adaptive compass search (ACS) to realize an efficient and stable GMPP search on power-current (P-I) of centralized TEG system under HTD. The proposed arithmetic optimization algorithm (AOA) in literature (Zhang et al., 2022), based on arithmetic operators in mathematics, enabled simple and rapid adaptive local exploration and global exploitation, thereby avoiding low quality LMPP to raise the energy utilization efficiency and generation efficiency of TEG systems. In addition, the musical chairs algorithm (MCA), particle swarm optimization (PSO) (Lamzouri et al., 2020), cuckoo search algorithm (CSA), as well as genetic algorithm (GA) are also applied to the MPPT of TEG systems.
With further research into energy efficiency and generation efficiency improvements in TEG systems, inspired by PV array reconfiguration for maximum power output, reconfiguration of TEG arrays is also a promising approach. In special, the reconfiguration technology can be divided into static reconfiguration and dynamic reconfiguration. The former reduces the power loss by rearranging the physical location of the PV modules. Although this method can disperse the shadows to other rows, the wiring is not flexible and inefficient for large PV arrays. Therefore, in practical engineering applications, dynamic reconfiguration has greater potential, which is to dynamically change the electrical connection mode by changing the switch matrix with strong flexibility and reliability. It is worth affirming that meta-heuristic algorithms have significant advantages and potential in dealing with array reconfiguration. For instance, butterfly optimization algorithm (BOA) (Fathy, 2020), grasshopper optimization algorithm (GOA) (Fathy, 2018), gravitational search algorithm (GSA) (Hasanien et al., 2016) artificial ecosystem-based optimization (AEO) (Yousri et al., 2022), ant colony algorithm (ACO) (Krishnan et al., 2020), and so on.
Inspired by the reconfiguration of PV arrays, this paper proposes a novelist PSO algorithm (Zeddini et al., 2016) for the reconfiguration of TEG arrays to reduce power losses and boost power generation efficiency. The main novelties/contributions of the proposed method are stated as follows:
The concept of reconfiguring TEG array to maximize power output is proposed for the first time;
PSO algorithm is a simple group optimization strategy with a simple operation mechanism and few parameters to be controlled in the calculation process;
The experimental results illustrate that PSO algorithm has a stronger ability to get rid of falling into local optimization, which can reduce power loss and improve energy conversion efficiency when TEG array is in multiple HTD states.
The rest of this paper is presented as follows: the mathematical model of TEG array is provided in Section 2. Besides, Section 3 describes the execution mechanism of PSO algorithm in detail. Section 4 illustrates results and discussion of simulation in comprehensive cases. Lastly, Section 5 summarizes various conclusions and future perspectives.
2 TEG Array Modelling
2.1 TEG Module Modelling
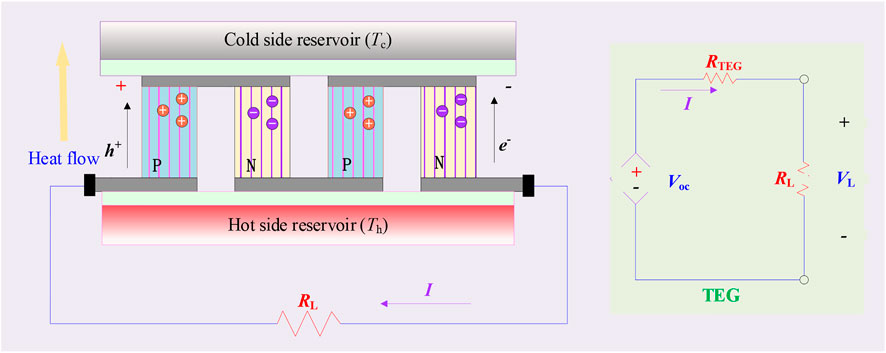
The TEG module is composed of two different thermoelectric materials, i.e., p-type and n-type. In addition, based on the Seebeck effect principle, the potential difference is caused by the migration of carriers in thermoelectric materials to convert heat energy into electric energy, as presented in Figure 1. A TEG module can be equivalent to a series resistance of the current source, which can be written as follows (Liu et al., 2016):
where
The Seebeck coefficient
where T is the average temperature of the hot side and cold side.
In practice, the Seebeck coefficient varies dynamically, mainly according to the average temperature on the low temperature side as well as on the high temperature side, which can be indicated as (Chakraborty et al., 2006)
where
Figure 1 represents the equivalent circuit of the TEG module, where the output current ITEG as well as the output power
where
When the external load is equivalent to the internal resistance of the thermoelectric material, the maximum power value can be obtained in the thermoelectric circuit as follows:
2.2 Mathematical Modelling of TEG Array
The low output voltage and low power of a single TEG module make it difficult to satisfy the practical requirements of the application, so several modules are connected in parallel and in series to form a TEG array. Figure 2A shows the
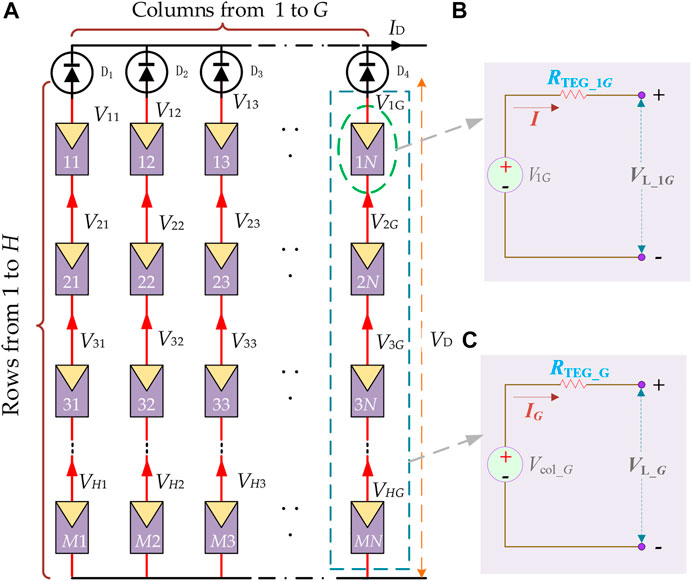
FIGURE 2. The
The output voltage and corresponding internal resistance in each column of the TEG array can be written as the sum of the voltages and corresponding internal resistances of the TEG modules in that column, which represents as
where
There is no doubt that the output power of a TEG array is highly dependent on the load voltage. Because when the output voltage of the column is less than the load voltage, the column is considered to be resistive. On the contrary, this column can output power. The equivalent internal resistance of each TEG module is calculated as
Furthermore, each column of TEG array can be equated to a current source in parallel with the corresponding internal resistance, whereas the current source can be expressed as
The equivalent circuit of the
The TEG array can output the maximum power when the total internal resistance is equal to the load resistance. Hence, the maximum output power of the TEG array can be described as
2.3 Objective Function
The significance of TEG array reconfiguration lies in seeking for GMPP, whose mathematical formula can be constructed as
2.4 Power Enhancement
Furthermore, a key criterion to measure the efficiency and performance of reconfiguration is power enhancement, which can be expressed as
where
3 Particle Swarm Optimization Algorithm
3.1 Optimization Mechanism
PSO algorithm is a well established swarm intelligence optimization algorithm that exploits the information communication capabilities of a population to discover the optimal solution to a problem. PSO algorithm (Gavhane et al., 2017) is constructed from the concept of real-life bird foraging whereby each particle in the swarm is initialized with its corresponding fitness value, which corresponds to the solution to the problem. In addition, each particle memorizes the solution during each iteration (i.e., the individuals in the swarm retain their own best position for searching for food Pbest as well as the best position obtained from the group Gbest), which then begins to iterate. The iterative process is the process of each particle searching for the optimal solution, with the particles regulating their position and speed in accordance with the variation in fitness values to seek the optimal position, when all particles have converged to that position, that is the optimal solution to the problem. In particular, the velocity of the particle is denoted as
Based on the principle of PSO algorithm, the mathematical model can be developed as follows: in a space of dimension D, a swarm of n particles searches for the optimal target, while the velocity and position of each particle are represented as
where
In addition, the velocity and position of each particle are limited by boundary conditions in each iteration, as the particle may exceed the allowed search space and produce invalid solutions, while Vmax is called velocity clamp as well as Xmax and Xmin mean position clamp.
3.2 Overall Optimization Procedure
For this reason, the overall implementation process of the reconfiguration design of TEG array based on PSO algorithm is depicted in Table 1.
4 Case Studies
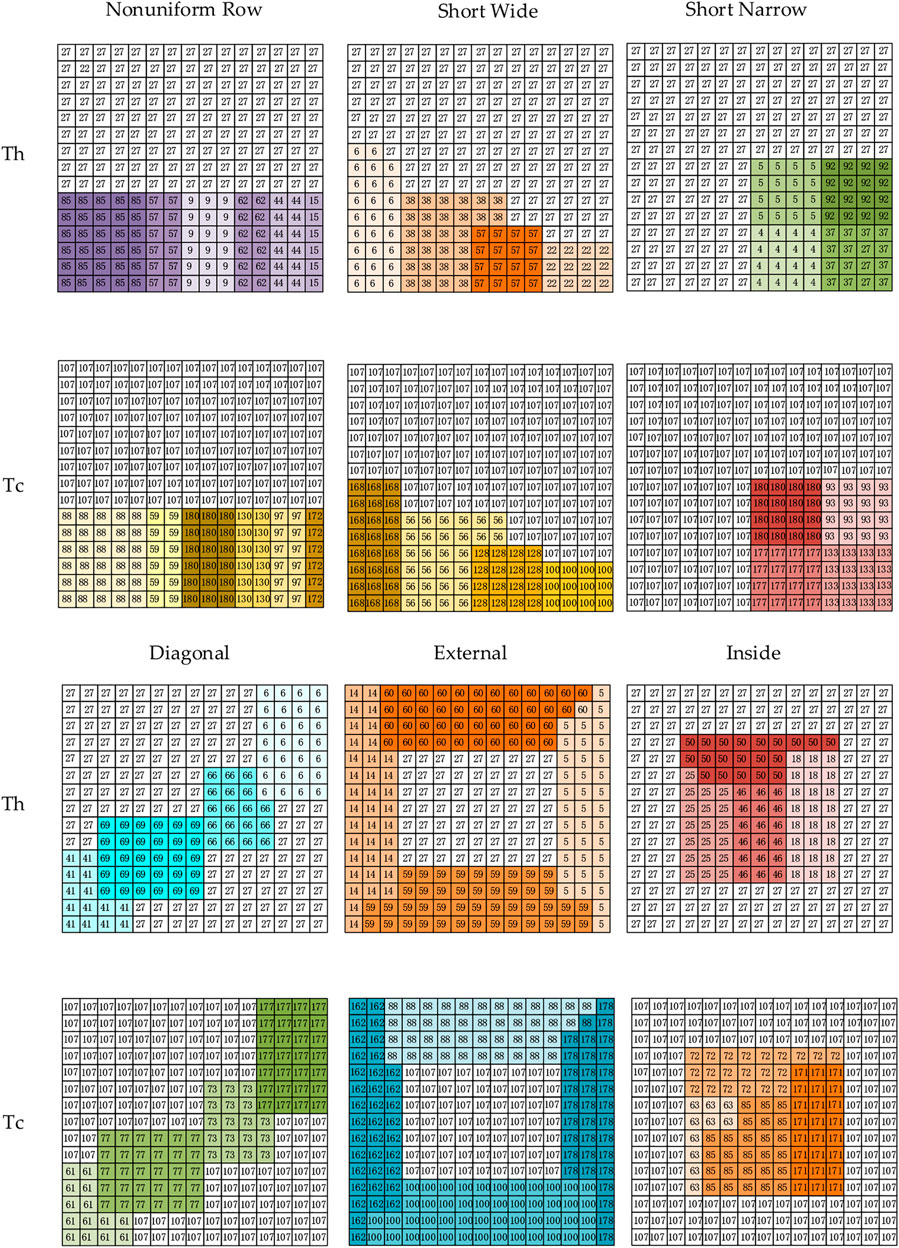
The array reconfiguration was carried out for six different HTD patterns (i.e., 1) Nonuniform row, 2) Short width, 3) Short narrow, 4) Diagonal, 5) External, 6) Inside) for a TEG array with a
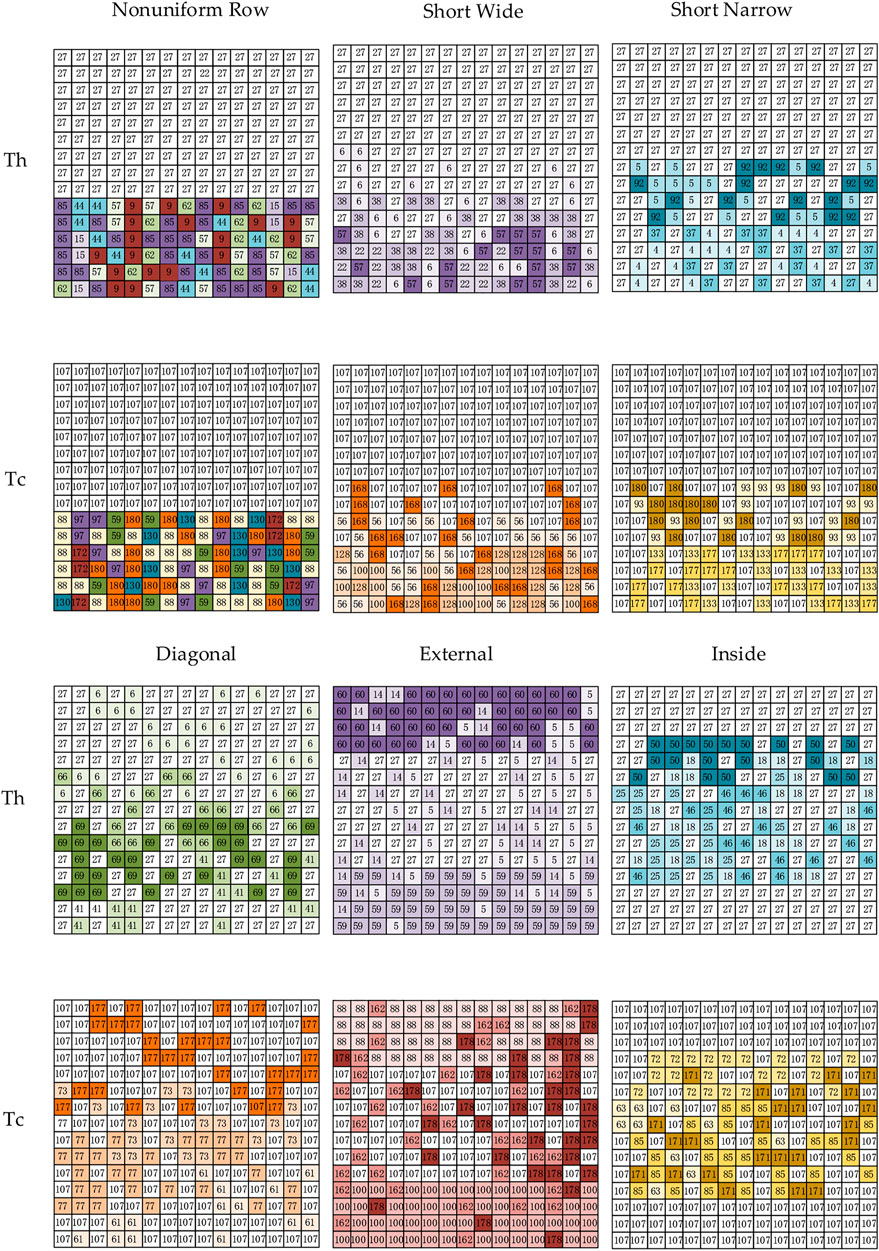
Compared with the output power without reconfiguration, a comprehensive and holistic comparison of the reconfiguration performance of PSO algorithm in six HTD patterns is carried out. Furthermore, the six HTD distributions in the 15 × 15 symmetric TEG array are shown in Figure 3, where different colors indicate different temperatures and the number on each block represents the temperature of that module. Figure 4 shows the output characteristics curves (i.e., V-I and P-I curves) of a 15 × 15 symmetric TEG array after reconfiguration. In particular, the maximum output power gained after PSO algorithm reconfiguration optimization is 4.305% higher than that gained without reconfiguration optimization under external temperature difference conditions, as illustrated in Figure 5. Figure 6 depicts the high and low temperature distribution of the 15 × 15 symmetric TEG array for each UTD state after reconfiguration based on the PSO algorithm.
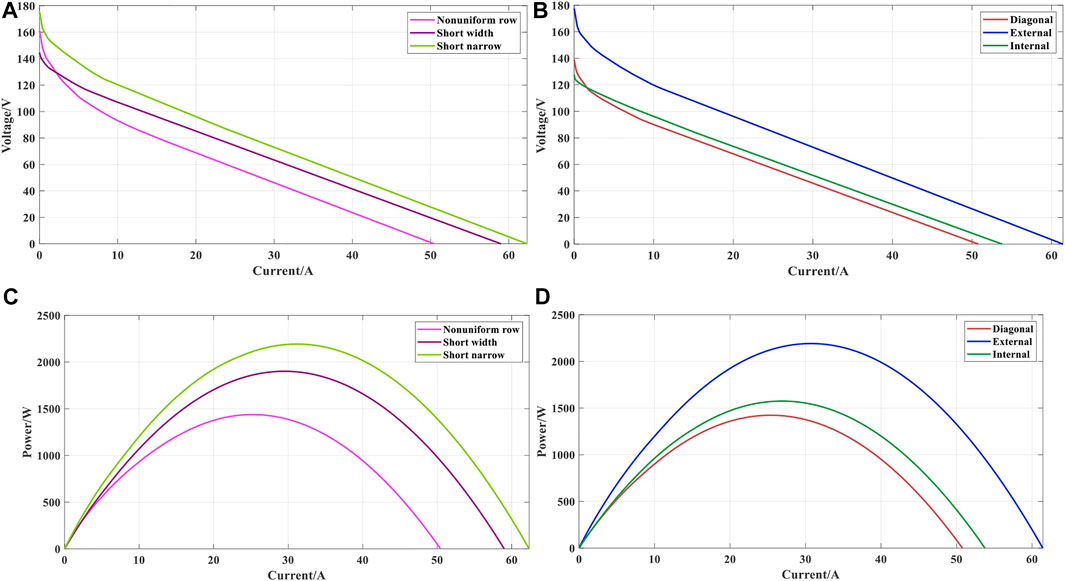
FIGURE 4. Output characteristics curves of a 15 × 15 symmetric TEG array. (A) V-I curves from the a to c pattens, (B) V-I curves from the d to f pattens, (C) P-I curves from the a to c pattens, and (D) P-I curves from the d to f pattens.
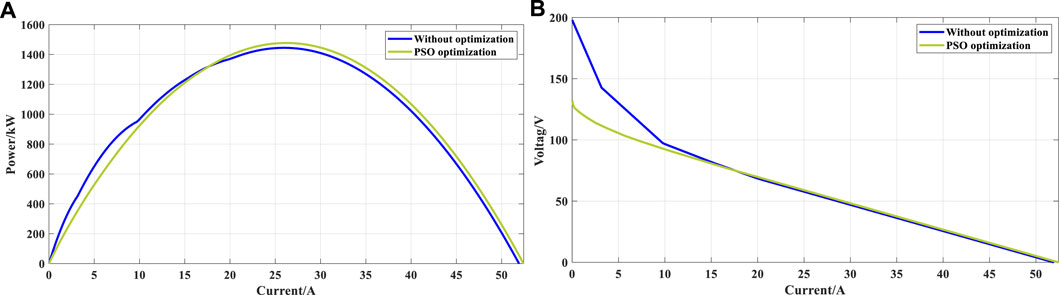
FIGURE 5. The V-I and P-I curves with and without the optimization at pattern e (A) V-I curve at pattern e, (B) P-I curve at pattern e.
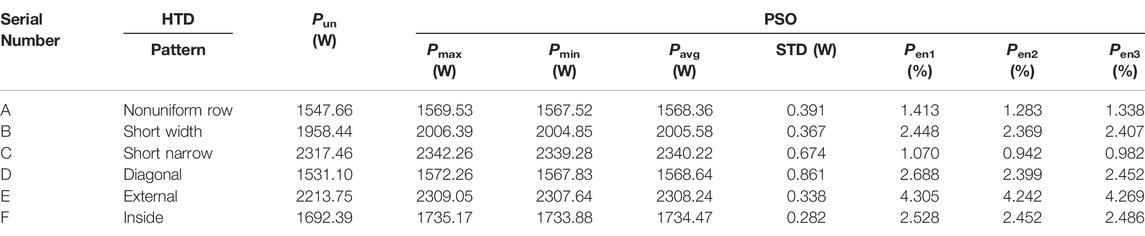
In addition, Pmax, Pmin, Pavg, and STD in Table 2 are the maximum, minimum, average, and standard deviation of the output power of the PSO algorithm in 20 independent runs, while Pen1, Pen2, and Pen3 in Table 2 indicate the power enhancement values of the maximum output power, minimum output power, and average output power respectively, which are valuable for assessing the reliability and effectiveness of the TEG array using PSO algorithm. Under six UTD patterns (e.g., 1) Nonuniform row, 2) Short width, (c)Short narrow, 4) Diagonal, 5) External, 6) Inside), the power enhancement values of the maximum power are 1.413, 2.448, 1.070, 2.688, 4.305, 2.528% in turn. To sum up, PSO algorithm can be closer to GMPP through population search, which can remarkably enhance the reconfigured power of TEG array and effectively reduce power loss through a simple optimization mechanism and single search law.
5 Conclusion
This paper proposes a meta-heuristic optimization approach called PSO algorithm for TEG system reconfiguration under HTD conditions, which contains the following three contributions/novelties:
(1) This paper proposed a PSO to optimize TEG system reconfigures symmetric arrays, which has not been previously employed to achieve a fast and effective tracking of the MPPT under HTD conditions;
(2) This paper comprehensively considers the impact caused under HTD conditions and simulates the actual temperature distribution including six types of wasted heat. Besides, a design of electrical switching arrangement is performed for 15 × 15 symmetric TEG arrays so that it can easily deal with any HTD conditions;
(3) The switch matrix of electrical connection is controlled in real-time by PSO algorithm to realize the optimal reconfiguration of TEG system affected by HTD conditions, which effectively approximates GMPP;
(4) Compared with the common reconfiguration methods, PSO algorithm has good performance in global exploration and local exploitation, which can apparently reduce the probability of falling into LMPP.
PSO algorithm is also a model-free algorithm, which is highly independent of the specific mathematical model of the optimization problem. Hence, it has high application flexibility and can be employed for other optimization problems of energy conversion, such as MPPT of PV systems.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
YZ: Conceptualization, Writing- Reviewing and Editing; EZ: Writing- Original draft preparation, Investigation; PN: Supervision.
Funding
This work is supported by Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University, China (No. ICT 2022B66), Ningbo Natural Science Foundation (2019A610106), and Ningbo Science and Technology Major Project (20212ZDYF020044).
Conflict of Interest
Authors EZ is employed by Ningbo Jianan Electronics Company Limited.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bijukumar, B., Raam, A. G. K., Ilango, G. S., and Nagamani, C. (2018). A Linear Extrapolation Based MPPT Algorithm for Thermoelectric Generators under Dynamically Varying Temperature Conditions. IEEE Trans. Energy Convers. 33 (4), 1641–1649. doi:10.1109/TEC.2018.2830796
Chakraborty, A., Saha, B. B., Koyama, S., and Ng, K. C. (2006). Thermodynamic Modelling of a Solid State Thermoelectric Cooling Device: Temperature-Entropy Analysis. Int. J. Heat Mass Transf. 49, 3547–3554. doi:10.1016/j.ijheatmasstransfer.2006.02.047
El-Dein, M. Z. S., Kazerani, M., and Salama, M. M. A. (2013). Optimal Photovoltaic Array Reconfiguration to Reduce Partial Shading Losses. IEEE Trans. Sustain. Energy 4 (1), 145–153. doi:10.1109/TSTE.2012.2208128
Fathy, A. (2020). Butterfly Optimization Algorithm Based Methodology for Enhancing the Shaded Photovoltaic Array Extracted Power via Reconfiguration Process. Energy Convers. Manag. 220, 113115. doi:10.1016/j.enconman.2020.113115
Fathy, A. (2018). Recent Meta-Heuristic Grasshopper Optimization Algorithm for Optimal Reconfiguration of Partially Shaded PV Array. Sol. Energy 171, 638–651. doi:10.1016/j.solener.2018.07.014
Fernández-Yáñez, P., Romero, V., Armas, O., and Cerretti, G. (2021). Thermal Management of Thermoelectric Generators for Waste Energy Recovery. Appl. Therm. Eng. 196, 117291. doi:10.1016/j.applthermaleng.2021.117291
Gavhane, P. S., Krishnamurthy, S., Dixit, R., Ram, J. P., and Rajasekar, N. (2017). EL-PSO Based MPPT for Solar PV under Partial Shaded Condition. Energy Procedia 117, 1047–1053. doi:10.1016/j.egypro.2017.05.227
Ge, M. H., Li, Z. H., Wang, Y. T., Zhao, Y., Zhu, Y., Wang, S., et al. (2021). Experimental Study on Thermoelectric Power Generation Based on Cryogenic Liquid Cold Energy. Energy 220, 119746. doi:10.1016/j.energy.2020.119746
Hasanien, H. M., Al-Durra, A., and Muyeen, S. M. (2016). “Gravitational Search Algorithm-Based PV Array Reconfiguration for Partial Shading Losses Reduction,” in 5th IET International Conference on Renewable Power Generation (RPG), London, UK, 21-23 Sept. 2016, 703–708. doi:10.1049/cp.2016.0577
Jian, L., Zhen, Y., Li, H., Hu, S., Duan, Y., and Yan, J. (2021). Optimal Schemes and Benefits of Recovering Waste Heat from Data Center for District Heating by CO2 Transcritical Heat Pumps. Energy Convers. Manag. 245, 114591. doi:10.1016/j.enconman.2021.114591
Krishnan, S., Kinattingal, S. G., Simon, S. P., and Nayak, P. S. R. (2020). MPPT in PV Systems Using Ant Colony Optimisation with Dwindling Population. IET Renew. Power Gener. 14 (7), 1105–1112. doi:10.1049/iet-rpg.2019.0875
Lamzouri, F-E., Boufounas, E-M., Brahmi, A., and Amrani, A. E. (2020). Optimized TSMC Control Based MPPT for PV System under Variable Atmospheric Conditions Using PSO Algorithm. Procedia Comput. Sci. 170, 887–892. doi:10.1016/j.procs.2020.03.116
Li, X., Wen, , Hu, Y., and Jiang, L. (2018). A Novel Beta Parameter Based Fuzzy-Logic Controller for Photovoltaic MPPT Application. Renew. Energy 130, 416–427. doi:10.1016/j.renene.2018.06.071
Liu, Y. H., Chiu, Y. H., Huang, J. W., and Wang, S. C. (2016). A Novel Maximum Power Point Tracker for Thermoelectric Generation System. Renew. Energy 97, 306–318. doi:10.1016/j.renene.2016.05.001
Liu, J., Yao, W., Wen, J. Y., Fang, J., Jiang, L., He, H., et al. (2020). Impact of Power Grid Strength and PLL Parameters on Stability of Grid-Connected DFIG Wind Farm. IEEE Trans. Sustain. Energy 11 (1), 545–557. doi:10.1109/TSTE.2019.2897596
Luo, D., Wang, R., Yan, Y., Yu, W., and Zhou, W. (2021). Transient Numerical Modelling of a Thermoelectric Generator System Used for Automotive Exhaust Waste Heat Recovery. Appl. Energy 297, 117151. doi:10.1016/j.apenergy.2021.117151
Mamura, H., Üstünera, M. A., and AminBhuiyanb, L. R. (2022). Future Perspective and Current Situation of Maximum Power Point Tracking Methods in Thermoelectric Generators. Sustain. Energy Technol. Assessments 50, 101824. doi:10.1016/j.seta.2021.101824
Matthew, B., and Jae, D. P. (2015). Current-sensorless Power Estimation and MPPT Implementation for Thermoelectric Generators. IEEE Trans. Industrial Electron. 62 (9), 5539–5548. doi:10.1109/TIE.2015.2414393
Shahbaz, M., Raghutla, C., Chittedi, K. R., Jiao, Z., and Vo, X. V. (2020). The Effect of Renewable Energy Consumption on Economic Growth: Evidence from the Renewable Energy Country Attractive Index. Energy 207, 118162. doi:10.1016/j.energy.2020.118162
Sun, K., Yao, W., Fang, J. K., Ai, X., Wen, J., and Cheng, S. (2020). Impedance Modeling and Stability Analysis of Grid-Connected DFIG-Based Wind Farm with a VSC-HVDC. IEEE J. Emerg. Sel. Top. Power Electron. 8 (2), 1375–1390. doi:10.1109/JESTPE.2019.2901747
Yang, B., Wang, J. T., Zhang, X. S., Zhang, M., Shu, H., Li, S., et al. (2019). MPPT Design of Centralized Thermoelectric Generation System Using Adaptive Compass Search under Non-uniform Temperature Distribution Condition. Energy Convers. Manag. 199, 111991. doi:10.1016/j.enconman.2019.111991
Yang, B., Wang, J. B., Zhang, X. S., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energy Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595
Yousri, D., Babu, T. S., Mirjalili, S., Rajasekar, N., and Elaziz, M. A. (2022). A Novel Objective Function with Artificial Ecosystem-Based Optimization for Relieving the Mismatching Power Loss of Large-Scale Photovoltaic Array. Energy Convers. Manag. 225, 113385. doi:10.1016/j.enconman.2020.113385
Zeddini, M. A., Pusca, R., Sakly, A., and Mimouni, M. F. (2016). PSO-Based MPPT Control of Wind-Driven Self-Excited Induction Generator for Pumping System. Renew. Energy 95, 162–177. doi:10.1016/j.renene.2016.04.008
Zhang, H. X., Lu, Z. X., Hu, W., and Tang, M. (2019). Coordinated Optimal Operation of Hydro-Wind-Solar Integrated Systems. Appl. Energy 242, 883–896. doi:10.1016/j.apenergy.2019.03.064
Keywords: thermoelectric generation system, heterogeneous temperature difference, reconfiguration, particle swarm optimization algorithm, symmetric
Citation: Zheng Y, Zhang E and An P (2022) Optimal Reconfiguration of Thermoelectric Generation System Under Heterogeneous Temperature Difference. Front. Energy Res. 10:967167. doi: 10.3389/fenrg.2022.967167
Received: 12 June 2022; Accepted: 22 June 2022;
Published: 11 July 2022.
Edited by:
Xueqian Fu, China Agricultural University, ChinaReviewed by:
Yaxing Ren, University of Warwick, United KingdomYixuan Chen, University of Hong Kong, Hong Kong SAR, China
Copyright © 2022 Zheng, Zhang and An. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peng An, NjE0NTQ1NTEzQHFxLmNvbQ==
 You Zheng1
You Zheng1 Peng An
Peng An