- 1College of Power and Energy Engineering, Harbin Engineering University, Harbin, China
- 2AVIC Shenyang Engine Design Institute, Shenyang, China
Reducing carbon emissions is an urgent need in the field of marine power. Gas turbines are of great importance in the marine industry. The use of clean or industrial-associated fuels can increase the fuel adaptability of designed, manufactured, or in-service gas turbines to realize the goal of expanding fuel sources, reducing fuel waste, lowering energy demand, and remitting environmental pressure. By changing from fossil fuel to alternative energy, the change in the physical properties of the combustion products will lead to changes in the working medium of the turbines, which result in a profound effect on the performance. In this study, based on the actual law of working medium property change, the evolution mechanism of turbine characteristics is lucubrated in depth, focusing on the key parameters of the influence of working medium properties on turbine characteristics under alternative fuel conditions, and a correction method is proposed to predict the evolution law of the turbine characteristics as working medium varies.
Background
In recent years, carbon peaks and neutrality have been among the most important issues in the energy sector. To reduce carbon emissions, a wide application of clean and industrial-associated fuels are the necessary pathway for marine power. It can meet the future economic and social needs for various types of energy, further improve the comprehensive utilization efficiency of energy, realize the cascade utilization of energy, and play an increasingly important role in social and economic development and energy security (Siemens, 2021).
In the existing research, the field of marine gas turbines rarely involves a large change in the physical properties of turbines. There are a few studies on the mechanism of the influence of the properties of the working mass on the turbine characteristics of the marine gas turbines. However, in the field of fuel-rich working medium turbines and some closed Breton cycle areas, there are some cases of turbine or circulating working medium changes, so there is a certain research basis.
In the previous studies, the fluid model directly determines the calculation of its thermal properties and influences the performance simulation of the turbine. Gas can be divided into two categories: ideal gas and real gas. For the former,
Calorimetry perfect gas is a gas, in which
When the components change, the thermal properties of the gas mixture, such as constant pressure specific heat and insulation index, change, which will affect the enthalpy of the gas, Mach number, pressure, and other important parameters, and finally change the aerodynamic characteristics of the turbine. Existing studies have shown that the use of the calorimetry perfect gas model, thermal perfect gas model, and real gas model can be applied to different application backgrounds to obtain corresponding research conclusions. The models have advantages and disadvantages in different application backgrounds. The existing research focused on selecting the mathematical model of the same working medium during simulation rather than correcting different working mediums described by the same mathematical model. However, conclusions are instructive, which show that
Analysis of influencing factors of turbine characteristics in gas turbine
The similitude theory is a good perspective to have a clear view of the core influencing factors of the evolution of turbine characteristics.
Differential equation analysis is one of the methods to obtain the similitude criteria. It requires that the basic system of differential equations of the phenomenon and all the single-value conditions be written first. Then, all similar criteria can be found in two ways. One is the so-called differential equation similar transfer method, and the other is the integral analogy method, which is the latter method used in the study.
By using a system of fundamental differential equations describing turbine flow and all single-value conditions for dimensionless processing, all similitude criteria for this phenomenon can be derived. The basic system of equations for viscous fluid mechanics is a system of second-order nonlinear partial differential equations. The continuous equation, the equation of motion, and the energy equation are used as the original description equations for dimensionlessness, and at the same time, similitude criteria are derived. First, a set of characteristic quantities is selected, and the characteristic quantities are simplified according to the basic assumptions. The basic physical quantities are selected as length, velocity, pressure, density, and time, divided by the corresponding variables in the boundary conditions. The resulting dimensionless variables are redefined, and the dimensionless equations and dimensionless boundary conditions are obtained. At the same time, a series of dimensionless combinations are obtained, and the terms in the equation are compared by orders of magnitude, simplifying the similitude criteria as a basis for similarity in model experiments (Liang et al., 2008; Ming et al., 2019a; Ming et al., 2019b).
The basic differential equations are
which are the mass conservation, momentum conservation, and energy conservation equations.
In the equations,
To nondimensionalize with the following proportions:
conservation equations can be nondimensionalized as
They can also be written as
When all the coefficients in the equation are equal, the same solution should be obtained under the same fixed solution conditions.
In the mass conservation equation and momentum conservation equation,
In the actual operation process, especially when the physical properties of the working medium change, theoretically, it is impossible to completely make all the similar criterion dimensionless numbers equal at the same time. The difference in the coefficients of the control equation caused by the physical properties of the working medium is mainly reflected in
The Brinkman number characterizes the ratio of the heat transferred by dissipation to the heat released by heat conduction. Because the working medium rapidly passes through the turbine runner during turbine operation, the Brinkman number has a limited impact on the entire energy equation. However, the assumption is based on the adiabatic process, and the difference between the adiabatic process and the isothermal process is the isochoric process, which means that
The Prandtl number is, in most cases, a physical quantity that is only related to the state of the fluid. Because Prandtl contains two important migratory properties, viscosity and thermal conductivity, and constant pressure-specific heat, and as a dimensionless quantity, it reflects the interrelationship between energy transport and momentum transport processes. Therefore, it has been widely used in thermal calculations. The Eckert number represents the relationship between the flow kinetic energy and the enthalpy difference of the boundary layer. It is used to characterize the compressibility and heat dissipation capacity of the working medium. The changes in the Prandtl and Eckert numbers are usually ignored when studying the aerodynamic properties of the same working medium in the turbine.
Therefore,
In the simulation study of the overall performance of the gas turbine, the physical properties of the combustion products are calculated with the assumption that air and gas are treated according to the gas mixture of variable specific heat when the temperature does not exceed 1,600°C. The assumption is widely and fully verified in many industrial productions. In the assumption,
In this article, the study of the turbine performance evolution is conducted from the perspective of the overall performance simulation of the gas turbine. The CFD numerical calculation method is used to obtain the evolutionary law of turbine characteristics, and the correction methods were proposed to estimate the evolutionary trend of turbine characteristics.
CFD calculation model of turbine
In this article, a 1.5-stage subsonic axial multi-stage turbine in the FINE/TURBO program calculation examples is selected, which is a publicly available study verified by Gallus and Walraevens in 1995 and 1998 by experimental and numerical calculations, respectively. The low-scale chordal ratio blades and constant tip and hub end wall profiles in this study enhance the strong secondary flow, so as a sufficiently representative multistage axial flow turbine is included as a study by the FINE/TURBO program. The model is a flow channel of equal inner and outer diameters, including one stage of guide blades, one stage of rotating blades, and one stage of static blades, of which the guide and static stages contain 36 blades per circumference and the rotating stage contains 41 blades, all of which are equal in width and unscrewed.
This study demonstrates the Ability of Fine/TURBO to simulate the flow of a multi-unit axial turbine in a steady-state subsonic range using experimentally validated calculations using the Spalart–Allmaras turbulence model. The turbine stage uses an HOH topology discrete, with each cell automatically generated using IGG/AutoGrid5 for a total of approximately 1.1 million grid points. The working medium is treated as an ideal gas of air. Along the inlet boundary, the pitch average experimental absolute total pressure, total temperature, and flow angle are applied. Along the outlet boundary, static pressure is applied to a radius, and its radial distribution is calculated using radial equilibrium conditions.
Because the guide stage of the geometric model has the same shape and parameters as the static stage, the rotating and static stages are repeated once after the original geometric model to obtain a 2.5-stage turbine. The 2.5-stage turbine contains one guide stage, two rotating stages, and two static stages. The geometric parameters of each level are consistent with the original information, and the relevant settings are also the same as in the original study. The 1.5-stage turbine is calculated to obtain the correction method and the 2.5-stage turbine is calculated to verify the applicability. The geometry of turbines is shown in Figure 1.
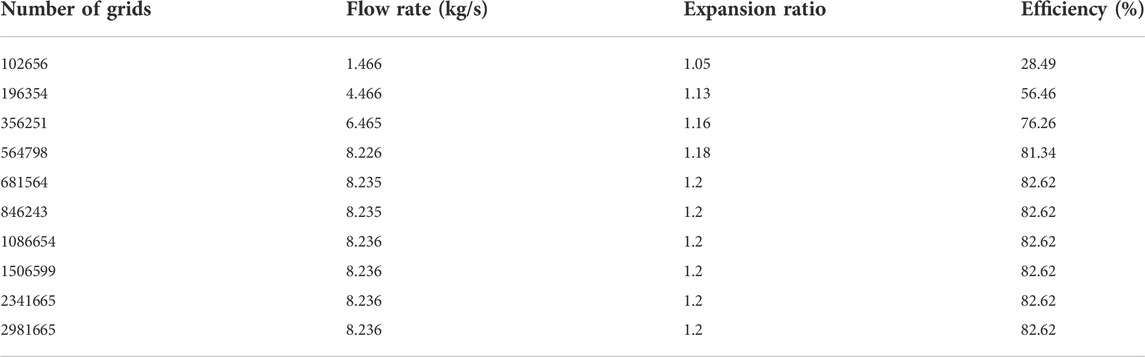
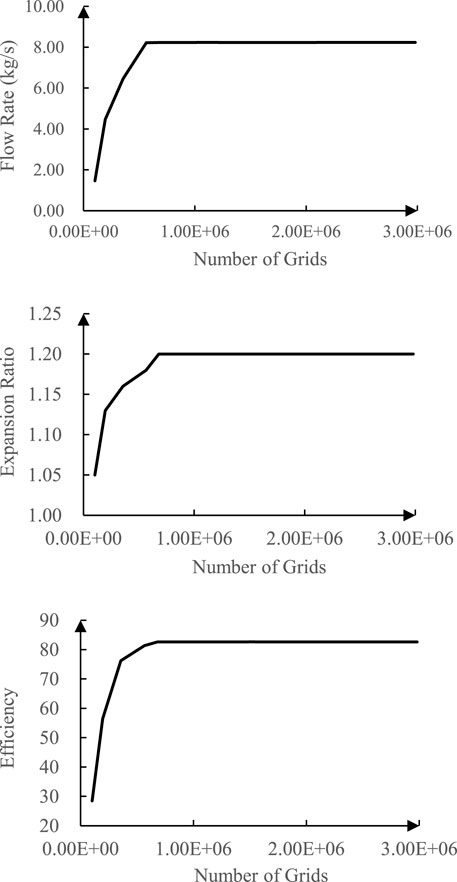
The mesh independence study of the 1.5-stage turbine in the design condition is carried out with a number of grids from about 100,000 to over 2,000,000.
The results are shown in Table 1 and Figure 2.
The number of grids of the 1.5-stage turbine is chosen as 1,500,000 for the following study, and the number of grids of the 2.5-stage turbine is redistricted with the same mesh density as the 1.5-stage turbine.
Firstly, the aerodynamic performance of the turbine is calculated using the default settings in the example to calculate the aerodynamic performance of the turbine based on the designed rotating speed of 3,500 r/min, the average inlet total pressure of 169,500 Pa, and the average outlet static pressure of 112,500 Pa. The design point speed is 3,500 r/min (equivalent to 3,308.15 r/min), the mass flow rate is 8.205 kg/s (equivalent to 5.052 kg/s), the expansion ratio is 1.198, and the efficiency is 83.63%. The working medium is air with
On the basis, change
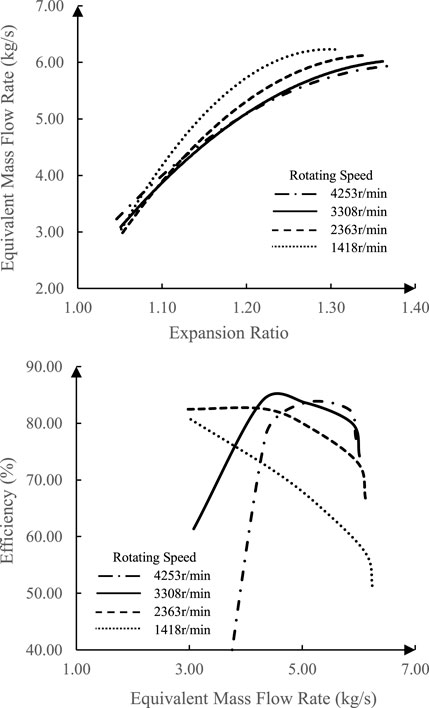
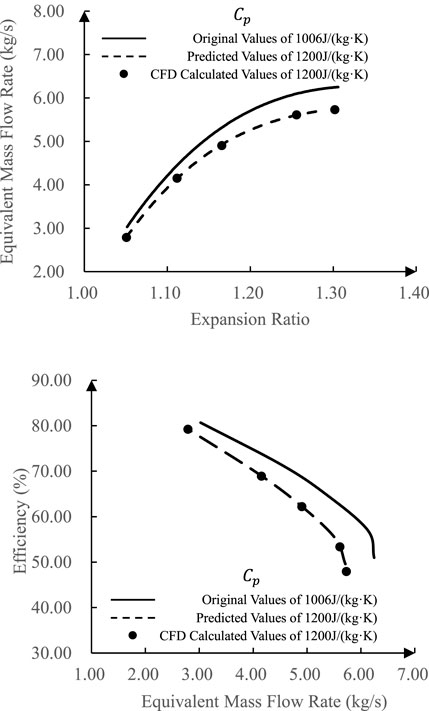
At the rotating speed of 3,308.15 r/min, the evolution of aerodynamic properties of the turbine is shown in Figure 4 when
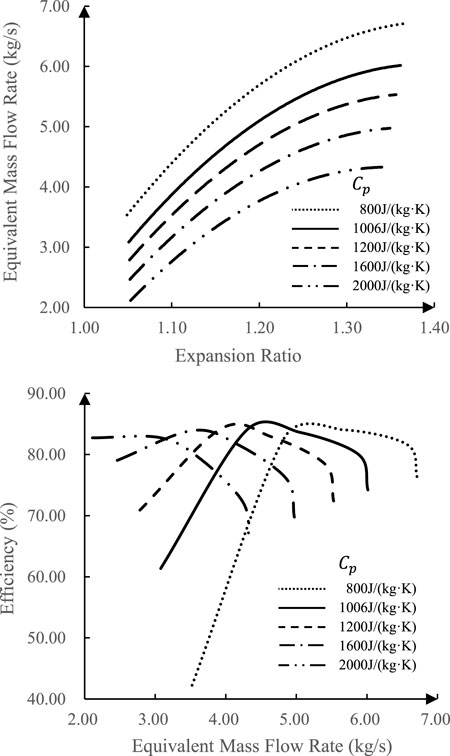
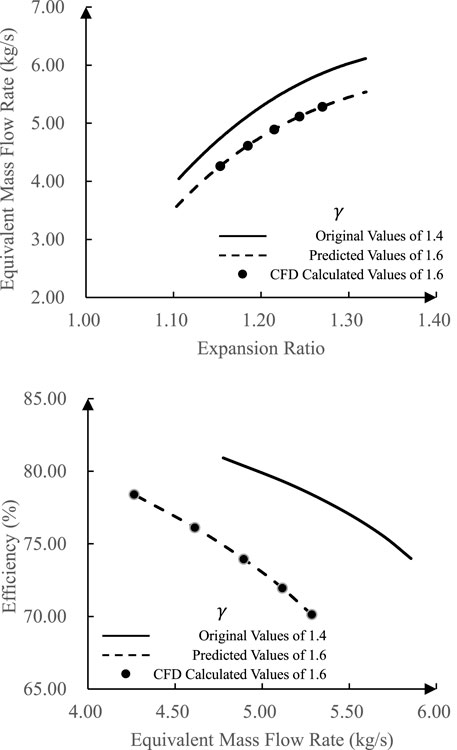
At the rotating speed of 3,308.15 r/min, the evolution of aerodynamic properties of the turbine is shown in Figure 5 when
In Figure 4 and Figure 5, the equivalent mass flow rate drops at the same expansion ratio, and the efficiency shifts with a lower equivalent mass flow rate as
Correction method of turbine characteristics
In the previous section,
First, the original characteristic line should be densified by the beta line method. The design points of the pending turbine may be different from the original characteristic line, so the seek points are scaled and the pending points are mapped to the original property map.
Then, by using the polynomial fitting, the relationship between the pressure ratio, flow rate, and efficiency value of the same beta point is predicted as a result of the eigenvalue.
The pending flow rate point is known after scaling, the correspondence is obtained by interpolating the beta value to the flow rate point, and the multinomial coefficients are obtained by the beta value and the other known quantity. The pressure ratio, flow rate, and efficiency of the operating point can be calculated as a result of the eigenvalue change. The correction formulas are obtained by multivariate polynomial analysis, allowing the property to be corrected by giving a certain operating and design point.
In this case, the correction method of turbine characteristics is solved with fine-grained scaling as follows:
where
Superscript
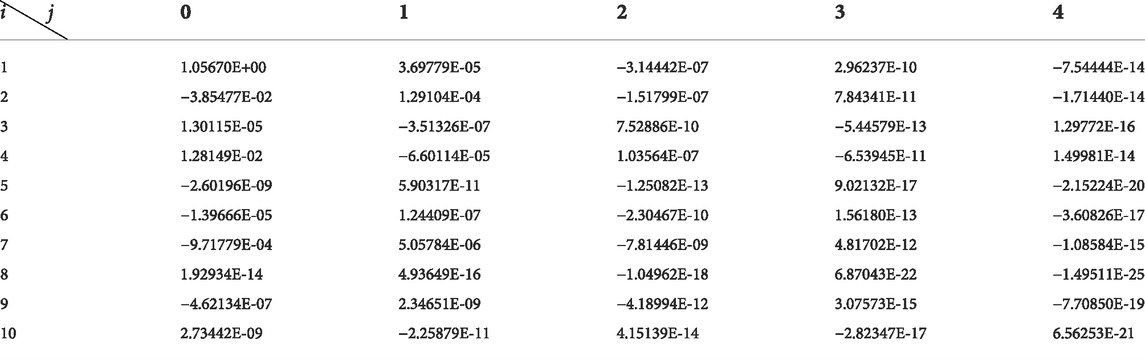
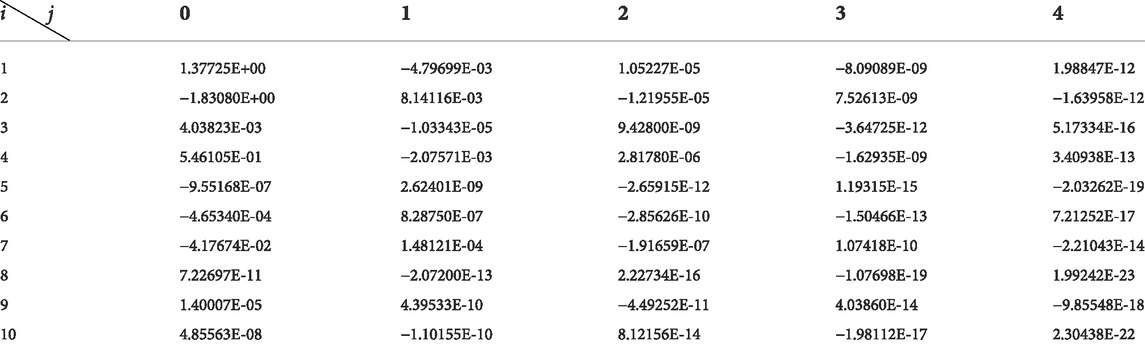
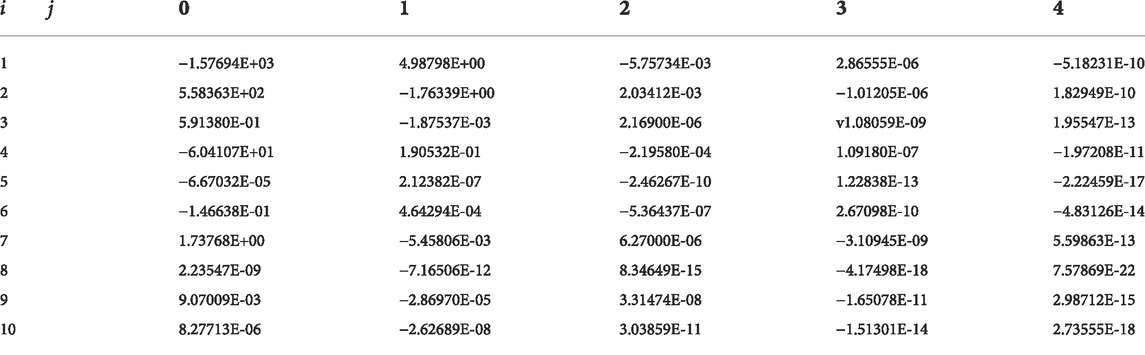
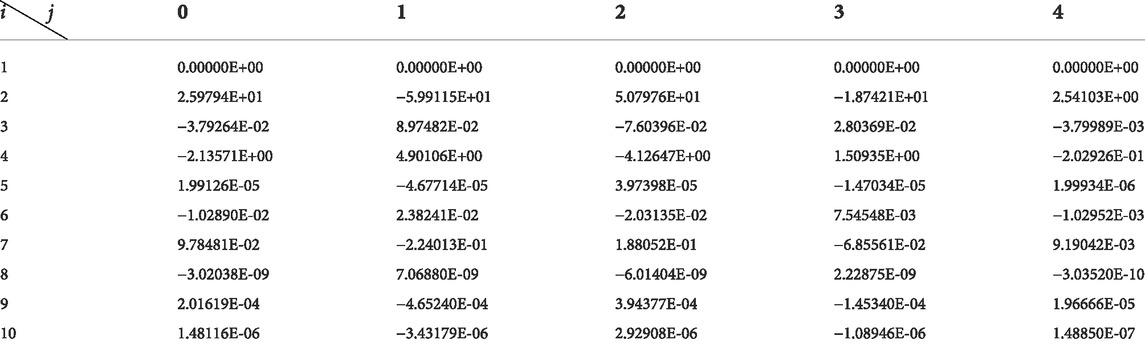
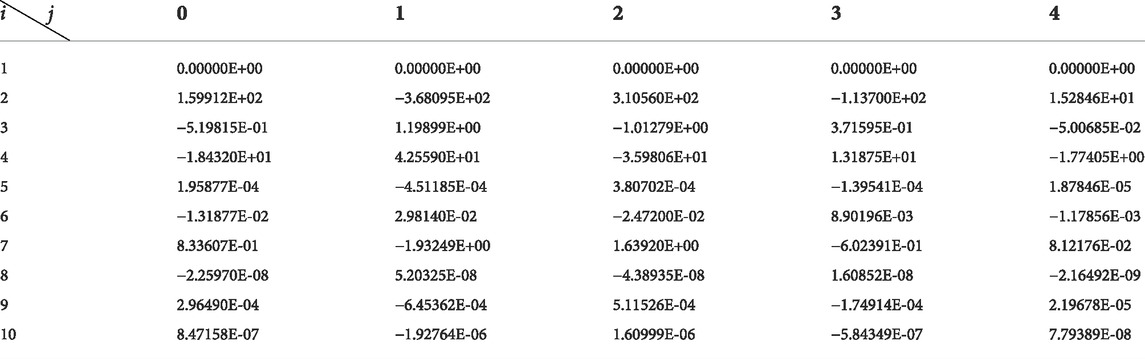
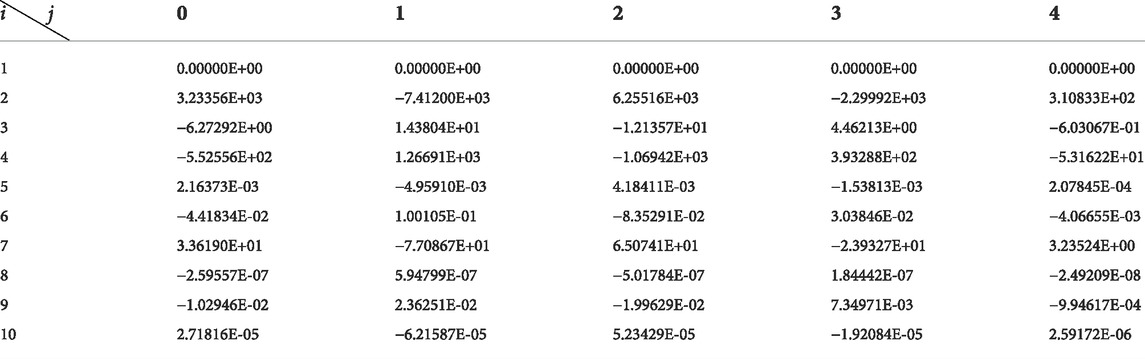
Correction factors are shown in Tables 2–7.
By putting the correction formula into the other speeds of the 1.5-stage turbine, turbine characteristics adopting different working mediums with different
Putting the correction formula into the other speeds of the 1.5-stage turbine, turbine characteristics adopting different working mediums with different
In order to verify the universality of the correction method, the correction formula is put into the design working point and non-design working conditions of the 2.5-stage turbine. The comparison at a rotating speed of 3,308 r/min is shown Figure 8.
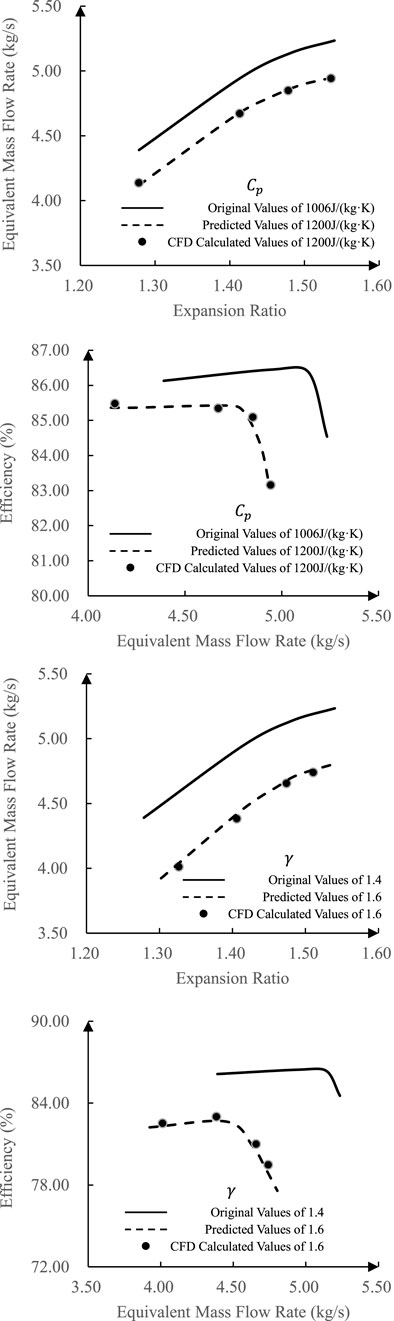
FIGURE 8. Comparison between prediction and CFD calculations as
Conclusion
In this article, from the perspective of the application of the low-carbon clean fuel or industrial-associated fuel, the gas turbine performance is significantly affected because the thermal physical properties of the working medium vary.
In this article, a theoretical study on the mechanism of influencing turbine characteristics is conducted when the turbine working medium changes, and conclusions are obtained as
A turbine characteristic correction method based on fine scaling is proposed aiming at the working medium changing problem of the turbine. After scaling is carried out using the design points, the coefficients of polynomial fitting are solved with the scaled equivalent flow rate. By giving certain operating and design points, the characteristics are corrected and the turbine characteristic line correction method suitable for this working medium property change problem is obtained. This correction method has been validated to apply to repetitive multi-stage turbines based on the same set structure. The applicability of the correction method using the same correction coefficient for turbines with different geometries has yet to be verified. The fine scaling method proposed in this article can realize the method of polynomial fitting for the working mass changing problem and obtain the corresponding correction method.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.
Author contributions
LM: methodology; ZW: conceptualization; JZ: data curation; PZ: supervision; KZ: resources.
Funding
National Science and Technology Major Project (J2019-I-0007-0007).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Boncinelli, P., Rubechini, F., Amone, A., Cecconi, M., and Cortese, C. (2004). Real gas effects in turbomachinery flows: A computational fluid dynamics model for fast computations[C]. ASME Paper GT2003-38101.
Canepa, R., and Satta, A. (2012). Influence of working fluid composition on the performance of turbomachinery in semi-closed gas turbine cycles[C]. ASME Paper GT2012-69453.
Colonna, P., Harinck, J., Rebay, S., and Guardone, A. (2008). Real-gas effects in organic rankine cycle turbine nozzles. J. Propuls. Power 24 (2), 282–294. doi:10.2514/1.29718
Gallar, L., Volpe, V., Salussolia, M., Pachidis, V., and Jackson, A. (2012). Thermodynamic gas model effect on gas turbine performance simulations. J. Propuls. Power 28 (4), 719–727. doi:10.2514/1.b34359
Harinck, J., Colonna, P., Guardone, A., and Rebay, S. (2010). Influence of thermodynamic models in two-dimensional flow simulations of turboexpanders[J]. ASME J. Turbomach. 132 (1), 011001.1–011001.17.
Jackson, J. B., Neto, A. C., Whellens, M. W., and Audus, H. (2000). Gas turbine performance using carbon dioxide as working fluid in closed cycle operation[C]. ASME Papar GT2000-153.
Liang, M., Zhang, Y., Wang, J., and Yang, X. (2008). “Researches of similitude laws obtained by differential equations for axial-flow helium compressors,” in The Proceedings of the International Conference on Nuclear Engineering(ICONE), 2015–1977.
Ming, L., Yang, X. Y., Zhang, Y. J., and Wang, J. (2019). Experimental study on performance of helium high pressure compressors of HTR-10GT. Ann. Nucl. Energy 125, 318–327. doi:10.1016/j.anucene.2018.11.007
Ming, L., Yang, X. Y., Zhang, Y. J., and Wang, J. (2019). Experimental study on performance of helium low pressure compressor of HTR-10GT. Prog. Nucl. Energy 111 (111), 156–164. doi:10.1016/j.pnucene.2018.11.008
Mirko, Z. S., Linke, P., Athanasios, I. P., and Aleksandar, S. G. (2012). On the role of working fluid properties in organic rankine cycle performance[J]. Appl. Therm. Eng. 36, 406–413.
Northall, J. D. (2005). The influence of variable gas properties on turbomachinery computational fluid dynamics[C]. ASME Paper GT2005-68478.
Roberts, S. K., and Sjolander, S. A. (2002). Semi-closed cycle 02/C02 combustion gas turbines: Influence of fluid properties on the aerodynamic performance of the turbomachinery[C]. ASME Paper GT2002-30410.
Rubechini, F., Marconcini, M., Amone, A., Maritano, M., and Cecchi, S. (2006). The impact of gas modelling in the numerical analysis of a multistage gasturbine[C]. ASME Paper GT2006-90129.
Sethi, V., Diara, F., Atabak, S., Jackson, A., Bala, A., and Pilidis, P. (2008). Advanced modelling of fluid thermodynamic properties for gas turbine performance simulation[C]. ASME Paper GT2008-51126.
Yao, Y., and Amos, I. (2004). Numerical study of axial turbine flow with variable gas property[C]. ASME Paper GT2004-53748.
Zhang, L., Zhuge, W., Peng, J., and Zhang, Y. (2014). The influence of real gas thermodynamics on ICE-ORC turbine flow fields[C]. ASME Paper GT2014-26470.
Nomenclature
Keywords: turbine characteristics, evolution law, correction method, alternative fuels, gas turbine
Citation: Ming L, Wang Z, Zhang J, Zheng P and Zhang K (2023) Numerical study on the evolution law and correction method of turbine characteristics of the gas turbine under alternative fuel conditions. Front. Energy Res. 10:966713. doi: 10.3389/fenrg.2022.966713
Received: 11 June 2022; Accepted: 03 August 2022;
Published: 06 January 2023.
Edited by:
Lei Luo, Harbin Institute of Technology, ChinaCopyright © 2023 Ming, Wang, Zhang, Zheng and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhitao Wang, d2FuZ3poaXRhb0BocmJldS5lZHUuY24=
 Liang Ming
Liang Ming Zhitao Wang
Zhitao Wang Jingkai Zhang1
Jingkai Zhang1