Abstract
The study of fluid dynamics due to the stretching surface is one of the most eminent topics due to its potential industrial applications viz. drawing wire and plastic films, metal and polymer extrusion, fiber and glass production. In the present article, the author is going to study the effects of hybrid nanofluids flow on an inclined plate including CuO (Copper Oxide), and Cu (Copper). The Casson fluid with a couple-stress term has been used in the flow analysis. The surface of the plate is considered slippery. The convection has been taken nonlinear with thermal radiation. The governing equation of the flow of hybrid nanofluids with energy equation has been transformed into highly nonlinear ODEs through similarity transformation. The proposed model has been solved through a numerical RK-4 method. Significant variables of the physical process such as solar radiation, nonlinear convection parameters, heat transfer rates, and their effect on the solar power plant have been noticed.
Introduction
Rising energy needs around the world, including irreversible means of energy such as natural fuels, energy storage, heat exchangers, and thermal resources. The production of these real resources, the result in huge detrimental effects on the environment, such as air pollution and global warming. To mitigate these losses, scientists have focused on techniques that improve renewable energy skills, like the production of solar energy. The spotless and cheapest renewable source of energy is solar energy, which may be converted into environmentally sociable thermal energy. These kinds of energies can be found in the shape of (solar collectors) and heat-changing liquids.
The collectors acquire solar rays by an absorbent plate and convey heat further to the absorbent solution such as water, water mixture). Nevertheless, their significant loss is the lower thermal capability of these conventional fluids, as they reveal low thermal efficiency in the alteration development. Converting conventional working liquids into nanofluids is one of the initiatives that has received much attention over the past few years to enhance the thermal efficiency of this technology. Nanofluids refer to a stable dispersion of solid particles of sizes between 1 and 100 nm (Choi, 1995). Nanofluids are widely used in various physical processes such as energy storage (Gul et al., 2019). Mebarek-Oudina (Mebarek-Oudina, 2019) studied the flow of nanofluids using different base liquids Sheikholeslami et al. (2014) presented a complete numerical simulation of nanofluid flow with magnetic and viscous dissipation effects. Because of the excellent use of nano liquid, Li et al. (2019) studied the flow of nano liquid within a porous duct by using external power in the form of the Buongiorno model. The impacts of magnetic hydrodynamics (MHD) on the heat trade-off dynamics of chemically reactive water base nano-liquids containing Cu/Ag in a rotating disk inside the permeable channel have been investigated by Reddy et al. (2017). Many recent studies have been conducted in the area of energy and thermal environments using analytical and numerical methods for handling heat exchange and nano-fluids. For instance, Zaim et al. (2020) and Khan et al. (2019), Hybrid nanofluid is obtained by combining two types of nanomaterials, which are added to conventional liquids, and are used in many heat exchange areas. Khan et al. (2017a) and Khan et al. (2020a) formulated and analyzed the transient flow of, and concluded that the Nusselt number performance improved considerably through the addition of 5% nanomaterials. Hayat and Nadeem (Hayat and Nadeem, 2017) investigated the inspiration of energy exchange through the increasing surface of hybrid nanofluids . Ali Lunda et al. (2020) studied the impacts of viscous dissipation on the flow of hybrid nano liquid by analyzing the stability of the shrinking plate. Aziz et al. (2020) and Khan et al. (2017b) considered the flow of hybrid nano-fluids on an extended plate. Sundar et al. (2020) has been examined the resistive aspect and energy transport phenomenon of hybrid nano liquid. Sohail et al. (2020) examined the three-dimensional movement of nanofluid in a flexible medium along with thermal radiation. Besides the aforementioned research papers, the following current articles can also be cited for getting more knowledge on the hybrid nano liquid process in various geometries. For example, Khan et al. (2021), Tahir et al. (2017), Khan et al. (2020b).
Recently, particles of different shapes on a closed porous surface and liquid moving in the permeable medium have attracted the attention of scientists. Their use can be measured in various fields such as nuclear engineering, and environmental sciences. Various physical processes that require the liquid movement on a porous medium include the use of blood flow in the veins or lungs, chemically catalysts connectors, geothermal energy, porous heat pipes, and porous heat pipes. As a Forchheimer term, it was introduced in Forchheimer (1901). Many researchers have used Darcy-Forchheimer concepts in various geometries for the study of fluid flow in a porous space. We are going to mention a few of them. Saif et al. (2019) discussed the movement of nano-fluids through a porous space. The variation in the motion of a liquid was created an expandable curved surface. Rasool et al. (2019) reported the flow of Darcy-Forchheimer nano-fluids produced by the stretching medium. The Darcy-Forchheimer liquid that flows through a spinning disc was discovered by Sadiq et al. (2020). Sheikholeslami et al. (2020) (Rasool et al., 2022) observed the behavior of non-Darcy liquid within a clear cavity. Hayat et al. (2020b), Sheikholeslami et al. (2020) examined the influence of Darcy-Forchheimer and EMHD on the flow of viscous liquids with joule heating and thermal flux over an extending surface. The numerical outcomes of CNTs nano-liquid flow across the divergent and convergent channels with thermal radiation have been calculated by Kumar et al. (2020) (Hayat et al., 2020a). There are various technical methods available for estimating temperature. The significance of radiation for heat and flow transmission is understood, especially in the fields of glass manufacturing, rocket engineering, furnace construction, nuclear plant, solar farms, physical science, and manufacturing, etc. Of such importance, the imposition of thermal radiation for heat transport is shown in Kumar et al. (2020). The different properties of such fluids were further studied by many researchers. Nanofluid flow reduces (Bilal, 2020; Khan et al., 2020c; Algehyne et al., 2022) the resistance to heat transfer for different flow systems. With the passage of time researchers came to know that the spread of two different types of nanoparticles in a pure fluid further augment the thermal flow characteristics. They termed such fluid as hybrid nanofluid. Rasool et al. (2022) and Wakif et al. (2022) have inspected the dynamics of hybrid nanofluid flow with the influence of thermal radiations and viscous dissipation past a stretching surface and have determined the influence of various parameters. It has been observed by the authors that the upper branch of the solution has been highlighted to be more applicable due to its stable nature (Alghamdi et al., 2021; Xia et al., 2021; Shah et al., 2022). have deliberated an incredible work to discuss the thermal flow improvement for hybrid nanofluid flow by means of different flow geometries and flow conditions. Recently, it has been noticed by researchers that the suspension of three different types of nanoparticles in a pure fluid can enhance the thermal conductivity of such fluid to the best possible limit. Such fluids are termed tri-hybrid nanofluids.
The main aim of the ongoing study is to observe the impact of (Cu, CuO) nano-components on the flow and heat transmission of water as a base fluid. Such formulation of fluid is used further on the inclined plate to improve the efficiency of solar collectors. Thermal radiation, nonlinear convection, and slip conditions are considered while formulating basic equations. The flow-related issues were formulated via differential equations which were solved numerically using the BVP-4 technique. Different significant quantities are discussed in terms of temperature and velocity.
Model analysis
The flow of the hybrid nanofluids containing nanoparticles is considered over an inclined plate that makes an angle with the upright axis as shown in the. Figure 1. The surface of the plate is considered slippery to reduce the stability of the external dust particles. The thermal convection is expanded and taking nonlinear. The basic equations in the presence of thermal radiation and Couple stress are displayed as.
FIGURE 1
Acceptable boundary conditions are
The velocity components in the x and y-direction,
Mathematical formulation of thermos-physical properties HNF
In the above mathematical expression, denotes the nanomaterials (Cu) volume fraction whereas denotes the volume fraction of (CuO) nanocomponents.
Introduction to useful similarity transformation variables as follows:
In the light of Eq.11, the Eqs 1–5 become
In terms of mutual boundary conditions:
The above-mentioned physical numbers are Grashof numbers, Couple stress term, Radiation factor, Slip velocity, parameter, and Prandtl number, Velocity slip, and Biot number.
In addition, some of the most useful physical numbers are, as, (Sherwood number), Skin friction coefficient (), and Nusselt number ().Where represents heat flux close to the surface, and denotes shear stress, employing Eqs. 9 and Eq. 14 gives,
Numerical method
The RK-4 numerical method has been used. The modeled Eqs 10, 11 are transformed to the first order by considering.
The first order ODEs system (Zaydan et al., 2022) has been solved with the efforts of the projected variables as shown in Eq. 16. The first order system using the RK4 method has been obtained as:
The first order system solution obtained and the results are analyzed for various embedded parameters.
Results and discussion
The hybrid nanofluid flow over a slippery surface of an inclined plane is considered for the applications of heat transfer. The impact of (velocity profile) and (temperature profile) quantitatively via differents tables and graphs for various active variables such as (slip parameter), (Gravitational parameters), (Biot number), (Volume fractions), and (Radiation factor) while considering (Cu + Water), (CuO + Water) nano liquid and hybrid nanofluid. The schematic diagram of the flow field is shown in Figure 1. Figure 2 The flow of fluid is increases over the slippery surface and this increase is more effective due to the larger values of the slip parameter . As the fluid moves over the surface, it traps more heat from the sheet, causing significant thermal dispersion. Intriguingly, even under favorable thermal transmission conditions, the entropy rate decreases to improve the quality of the slow-moving barrier. This can improve the slip to influence the suspended components and consequently the fluid motion is increases. Figure 3 The influence of the couple stress parameter versus velocity profile is shown in Figure 3. It is perceived that the development in couple stress terms results, decreases in the fluid motion at all locations. The rise in the couple stress parameter values improves the resistance force, to decline the velocity of the fluid. Figure 4 Incremented fractional volume through particle strength in porosity, hybrid nano-fluids also affects the flow rate. As a result, it increases the production of thermal transport and entropy in both types of flowing fluids and reduces the velocity profile by incrementing the volume fraction. Figure 5 Incremented Casson fluid parameter, increasing the resistive force and declining the fluid motion. The decline effect is compared for both Cu and CuO hybrid nano-fluids (Figures 6, 7).The increment in the positive value of the gravity parameters will raise the velocity profile and the velocity of the liquid is improved by the positive value of the gravity parameter. The opposite impact declines the fluid motion. The comparative analysis for both Cu and Cu-CuO shown has been displayed in Figures 6, 7 which signifies that the velocity profile decrement due to the negative value of the gravity parameter.
FIGURE 2
FIGURE 3
FIGURE 4
FIGURE 5
FIGURE 6
FIGURE 7
Figure 8 Biot number denotes an incremental convectively thermal rates that can affect the area of interest related to temperature. According to the limitation to heat production, the Biot number tends to increase the current thermal rates in the flow region but makes the lower portion of the sheet. According to previous entropy and thermal plots, the Biot number is also a factor in the elevation of the thermal diffusion, which simultaneously increases the rate of entropy. Figure 9 As the volume friction value rises which reduces the temperature profile. will decrease. This is because when nanoparticles are put in the conventional fluid, the nanoparticles increase in temperature, which will increase the temperature profile.
FIGURE 8
FIGURE 9
Figure 10 illustrates the state of thermal radiation sequentially, for the growing values of the thermal radiation barrier. Radiation heat raises the thermal state of the environment of interest, which places a greater thermal transfer load on the passing fluid, which increases the thermal conductivity to the radiation barriers. The thermal properties of the solid materials and base fluid are displayed in Table. 1. The skin friction improved with the increasing values of the parametersas displayed in Table. 2. Physically, the greater values of these factors enrich the resistance force and subsequently skin friction enhancing. The heat transfer rate growths with the cumulative values of the nanoparticle volume fraction and Radiation factors as displayed in Table 3. The heat transfer rate enhancing for the nanofluids up to 8.1501% using and 8.473% increases for hybrid nanofluids using . Similarly, the rate of heat transfer escalats gradually with the growing amount of nanoparticle volume fraction. From Table 4 it has been detected that hybrid nanofluids are more proficient for heat transfer enhancement. The comparison of the current results is compared with the existing literature considering base fluid only and shown in Table 4.
FIGURE 10
TABLE 1
| Property | ||
|---|---|---|
| 6320 | 3580 | |
| 531.8 | 960 | |
| 76.5 | 48.4 |
thermo-physical properties.
TABLE 2
| 0.2 | 0.0 | 0.2 | 0.2 | 0.472836 | 0.473952 |
| 0.3 | 1.473962 | 1.4745742 | |||
| 0.4 | 1.4749321 | 1.47575322 | |||
| 0.01 | 1.4735318 | 1.474421331 | |||
| 0.02 | 1.4744321 | 1.47538012 | |||
| 0.4 | 1.483120 | 1.4846352 | |||
| 0.6 | 1.49431275 | 1.49532125 | |||
| 0.4 | 1.47343546 | 1.47446874 | |||
| 0.6 | 1.47412023 | 1.4753214091 |
numerical outcomes versus different values of emerging parameters.
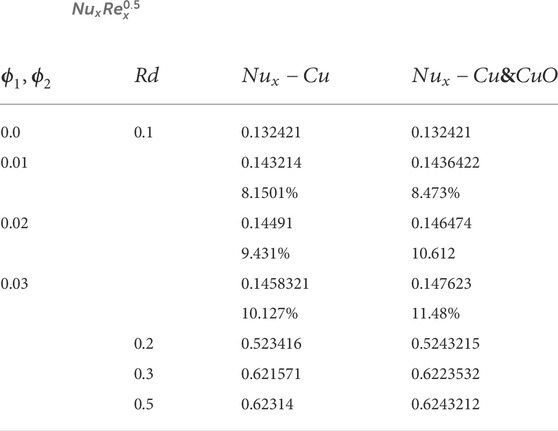
TABLE 3
| 0.0 | 0.1 | 0.132421 | 0.132421 |
| 0.01 | 0.143214 | 0.1436422 | |
| 8.1501% | 8.473% | ||
| 0.02 | 0.14491 | 0.146474 | |
| 9.431% | 10.612 | ||
| 0.03 | 0.1458321 | 0.147623 | |
| 10.127% | 11.48% | ||
| 0.2 | 0.523416 | 0.5243215 | |
| 0.3 | 0.621571 | 0.6223532 | |
| 0.5 | 0.62314 | 0.6243212 |
numerical outcomes versus different values of emerging parameters and % enhancement in heat transfer rate.
TABLE 4
| Wang Wang (1989) | Golra and sidawi Gorla and Sidawi (1994) | Recent | |
|---|---|---|---|
| 6.3 | 0.24532 | 0.24545 | 0.24548 |
| 6.5 | 0.194522 | 0.194642 | 0.194653 |
| 6.7 | 0.135281 | 0.135393 | 0.135412 |
Quantitative analogy with [39], [40] using .
Conclusion
The impact of the Cu and CuO hybrid nanofluid flow for the enhancement of heat transfer rate has been examined through a slippery surface of the inclined plate. The convection is taken quadratic and due to the stretching of the plate, the gravity force is assumed negative and positive. The significant physical characteristics of Nusselt number versus radiation and other physical constraints have been noticed. In this article, some significant points present our conclusion in the following remarks. For impact have been analyzed and the comparative results for the Cu& CuO hybrid nanofluid are observed. The higher value of the nanoparticle volume fractions incremented the temperature distribution . The heat transfer rate enhancing for up to 10.127% using and 11.48% increases for hybrid nanofluids using . The Biot number increases the temperature distribution for its larger amount. The larger value of the parameter enhances the rate of heat transfer and, as a result, the Nusselt number rises. Nanoliquids are more viscous than ordinary liquids, which reflects that the boiling point of nanoliquids is more than that of conventional base liquids. This would improve the heat transfer power of the solar collectors.
Statements
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
TG, modeling and solution; SM, writing draft WA, editing. ZR, Validated, SEA and ETE, participated in revision and provide funding source.
Acknowledgments
This work was supported by the King Khalid University through a grant KKU/RCAMS/22 under the Research Center for Advance Materials (RCAMS) at King Khalid University, Saudi Arabia. The author Sharifah E. Alhazmi sehazmi@uqu.edu.sa would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4282396DSR24).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Nomenclature
Greek symbols
- ,
Velocities components
Dynamic viscosity of nanofluid
Dimensional velocity profiles
Dynamic viscosity of base fluid
Fluid temperature
Nanofluid density
Wall surface temperature
Base fluid density
Free surface temperature
Similarity variable
Dimensional velocity profiles
Dimensional
volume fraction of and nanoparticles
Biot number
Dimensional heat profiles
Pressure
electrical conductivity of nanofluid
Prandtl number
Couple stress parameter
Local Reynolds number
Stefan Boltzmann constant
Stream function
Coefficient of mean absorption
Nusselt number
Skin friction coefficient
Specific heat of base fluid
Thermal conductivity ()
Subscripts
- Thnf
Tri-hybrid Nanofluid
- nf
Nanofluid
- f
Base fluid
References
1
AlgehyneE. A.WakifA.RasoolG.SaeedA.GhouliZ. (2022). Significance of Darcy-forchheimer and lorentz forces on radiative alumina-water nanofluid flows over a slippery curved geometry under multiple convective constraints: A renovated buongiorno’s model with validated thermophysical correlations. Waves Random Complex Media2022, 1–30. 10.1080/17455030.2022.2074570
2
AlghamdiM.WakifA.ThummaT.KhanU.BaleanuD.RasoolG. (2021). Significance of variability in magnetic field strength and heat source on the radiative-convective motion of sodium alginate-based nanofluid within a Darcy-Brinkman porous structure bounded vertically by an irregular slender surface. Case Stud. Therm. Eng.28, 101428. 10.1016/j.csite.2021.101428
3
Ali LundaL.OmaraZ.KhanI.SeikhA.El-SayedH.SherifM.et al (2020). Stability analysis and multiple solution of Cu–Al2O3/H2O nanofluid contains hybrid nanomaterials over a shrinking surface in the presence of viscous dissipation. J. Mat. Res. Technol.9 (1), 421–432. 10.1016/j.jmrt.2019.10.071
4
AzizA.JamshedW.AliY.ShamsM. (2020). Heat transfer and entropy analysis of Maxwell hybrid nanofluid including effects of inclined magnetic field, Joule heating and thermal radiation. Discrete Contin. Dyn. Syst. Ser. S13 (10), 101428. 10.3934/dcdss.20201.42
5
BilalM. (2020). Micropolar flow of EMHD nanofluid with nonlinear thermal radiation and slip effects. Alexandria Eng. J.59 (2), 965–976. 10.1016/j.aej.2020.03.023
6
ChoiU. S. (1995). Enhancing thermal conductivity of fluids with nanoparticles. AS-MEFED231, 99–103.
7
ForchheimerP. (1901). Wasserbewegung durch boden. Z. Des. Vereins Dtsch. Ingenieure45, 1782–1788.
8
GorlaR. S. R.SidawiI. (1994). Free convection on a vertical stretching surface with suction and blowing. Appl. Sci. Res.52 (3), 247–257. 10.1007/bf00853952
9
GulT.NomanW.SohailM.KhanM. A. (2019). Impact of the Marangoni and thermal radiation convection on the graphene-oxide-water-based and ethylene-glycol-based nanofluids. Adv. Mech. Eng.11 (6), 1687814019856773. 10.1177/1687814019856
10
HayatT.HaiderF.AlsaediA. (2020a). Darcy-Forchheimer flow with nonlinear mixed convection. Appl. Math. Mech.41 (11), 1685–1696. 10.1007/s10483-020-2680-8
11
HayatT.KhanS. A.AlsaediA.FardounH. M. (2020b). Heat transportation in electro-magnetohydrodynamic flow of Darcy-Forchheimer viscous fluid with irreversibility analysis. Phys. Scr.95 (10), 105214. 10.1088/1402-4896/abb7aa
12
HayatT.NadeemS. (2017). Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys.7, 2317–2324. 10.1016/j.rinp.2017.06.034
13
KhanA.SaeedA.TassaddiqA.GulT.MukhtarS.KumamP.et al (2021). Bio-convective micropolar nanofluid flow over thin moving needle subject to Arrhenius activation energy, viscous dissipation and binary chemical reaction. Case Stud. Therm. Eng.25, 100989. 10.1016/j.csite.2021.100989
14
KhanS. U.TliliI.WaqasH.ImranM. (2020). Effects of nonlinear thermal radiation and activation energy on modified second-grade nanofluid with Cattaneo–Christov expressions. J. Therm. Anal. Calorim.143 (2), 1175–1186. 10.1007/s10973-020-09392-6
15
KhanU.ZaibA.Mebarek-OudinaF. (2020). Mixed convective magneto flow of SiO2–MoS2/C2H6O2 hybrid nanoliquids through a vertical stretching/shrinking wedge: Stability analysis. Arab. J. Sci. Eng.45 (11), 9061–9073. 10.1007/s13369-020-04680-7
16
KhanU.AhmedN.Mohyud-DinS. T. (2017). Influence of the shape factor on the flow and heat transfer of a water-based nanofluid in a rotating system. Eur. Phys. J. Plus132 (4), 166–211. 10.1140/epjp/i2017-11410-4
17
KhanU.AhmedN.Mohyud-DinS. T. (2020). Surface thermal investigation in water functionalized Al2O3 and γAl2O3 nanomaterials-based nanofluid over a sensor surface. Appl. Nanosci., 1–11. 10.1007/s13204-020-01527-3
18
KhanU.AlkanhalT. A.AhmedN.KhanI.Mohyud-DinS. T. (2019). Stimulations of thermophysical characteristics of nano-diamond and silver nanoparticles for nonlinear radiative curved surface flow. IEEE Access7, 55509–55517. 10.1109/access.2019.2907304
19
KhanU.AsadullahM.AhmedN.Mohyud-DinS. T. (2017). Influence of Joule heating and viscous dissipation on MHD flow and heat transfer of viscous fluid in converging/diverging stretchable channels. J. nanofluids6 (2), 254–263. 10.1166/jon.2017.1327
20
KumarK. G.Rahimi-GorjiM.ReddyM. G.ChamkhaA. J.AlarifiI. M. (2020). Enhancement of heat transfer in a convergent/divergent channel by using carbon nanotubes in the presence of a Darcy–Forchheimer medium. Microsyst. Technol.26 (2), 323–332. 10.1007/s00542-019-04489-x
21
LiZ.SaleemS.ShafeeA.ChamkhaA. J.DuS. (2019). Analytical investigation of nanoparticle migration in a duct considering thermal radiation. J. Therm. Anal. Calorim.135 (3), 1629–1641. 10.1007/s10973-018-7517-z
22
Mebarek-OudinaF. (2019). Convective heat transfer of Titania nanofluids of different base fluids in cylindrical annulus with discrete heat source. Heat. Trans. Res.48 (1), 135–147. 10.1002/htj.21375
23
RasoolG.ShafiqA.KhaliqueC. M.ZhangT. (2019). Magnetohydrodynamic Darcy-Forchheimer nanofluid flow over a nonlinear stretching sheet. Phys. Scr.94, 105221. 10.1088/1402-4896/ab18c8
24
RasoolG.ShahN. A.El-ZaharE. R.WakifA. (2022). Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-forchheimer porous medium: Application of passive control strategy and generalized transfer laws. Waves Random Complex Media2022, 1–20. 10.1080/17455030.2022.2074571
25
ReddyP. S.SreedeviP.ChamkhaA. J. (2017). MHD boundary layer flow, heat and mass transfer analysis over a rotating disk through porous medium saturated by Cu-water and Ag-water nanofluid with chemical reaction. Powder Technol.307, 46–55. 10.1016/j.powtec.2016.11.017
26
SadiqM. A.HaiderF.HayatT.AlsaediA. (2020). Partial slip in Darcy-Forchheimer carbon nanotubes flow by rotating disk. Int. Commun. Heat Mass Transf.116, 104641. 10.1016/j.icheatmasstransfer.2020.104641
27
SaifR. S.HayatT.EllahiR.MuhammadT.AlsaediA. (2019). Darcy-Forchheimer flow of nanofluid due to a curved stretching surface. Int. J. Numer. Methods Heat. Fluid Flow.29, 2–20. 10.1108/hff-08-2017-0301
28
ShahN. A.WakifA.El-ZaharE. R.AhmadS.YookS. J. (2022). Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG),(40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng.35, 102046. 10.1016/j.csite.2022.102046
29
SheikholeslamiM.AbelmanS.GanjiD. D. (2014). Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation. Int. J. Heat. Mass Transf.79, 212–222. 10.1016/j.ijheatmasstransfer.2014.08.004
30
SheikholeslamiM.ArabkoohsarA.IsmailK. A. R. (2020). Entropy analysis for a nanofluid within a porous media with magnetic force impact using non-Darcy model. Int. Commun. Heat Mass Transf.112, 104488. 10.1016/j.icheatmasstransfer.2020.104488
31
SohailM.NazR.AbdelsalamS. I. (2020). On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Phys. Scr.95, 045206. 10.1088/1402-4896/ab3c3f
32
SundarL. S.SinghM. K.SousaA. C. M. (2020). Enhanced heat transfer and friction factor of MWCNT–Fe3O4/water hybrid nanofluids. Int. Commun. Heat Mass Transf.52, 73–83. 10.1016/j.icheatmasstransfer.2014.01.012
33
TahirF.GulT.IslamS.ShahZ.KhanA.KhanW.et al (2017). Flow of a nano-liquid film of Maxwell fluid with thermal radiation and magneto hydrodynamic properties on an unstable stretching sheet. J. nanofluids6 (6), 1021–1030. 10.1166/jon.2017.1400
34
WakifA.ZaydanM.AlshomraniA. S.MuhammadT.SehaquiR. (2022). New insights into the dynamics of alumina-(60% ethylene glycol+ 40% water) over an isothermal stretching sheet using a renovated buongiorno's approach: A numerical gdqllm analysis. Int. Commun. Heat Mass Transf.133, 105937. 10.1016/j.icheatmasstransfer.2022.105937
35
WangC. Y. (1989). Free convection on a vertical stretching surface. Z. Angew. Math. Mech.69 (11), 418–420. 10.1002/zamm.19890691115
36
XiaW. F.AnimasaunI. L.WakifA.ShahN. A.YookS. J. (2021). Gear-generalized differential quadrature analysis of oscillatory convective Taylor-Couette flows of second-grade fluids subject to Lorentz and Darcy-Forchheimer quadratic drag forces. Int. Commun. Heat Mass Transf.126, 105395. 10.1016/j.icheatmasstransfer.2021.105395
37
ZaimA.AissaA.Mebarek-OudinaF.MahantheshB.LorenziniG.SahnounM.et al (2020). Galerkin finite element analysis of magneto-hydrodynamic natural convection of Cu-water nanoliquid in a baffled U-shaped enclosure. Propuls. Power Res.9 (4), 383–393. 10.1016/j.jppr.2020.10.002
38
ZaydanM.HamadN. H.WakifA.DawarA.SehaquiR. (2022). Generalized differential quadrature analysis of electro‐magneto‐hydrodynamic dissipative flows over a heated riga plate in the presence of a space‐dependent heat source: The case for strong suction effect. Heat. Trans.51 (2), 2063–2078. 10.1002/htj.22388
Summary
Keywords
(Cu, CuO,) nanoparticles, thermal radiations, inclined plate, nonlinear convection, numerical RK-4 method
Citation
Gul T, Mukhtar S, Alghamdi W, Raizah Z, Alhazmi SE and ElDin ET (2022) Radiative couple stress Casson hybrid nanofluid flow over an inclined stretching surface due to nonlinear convection and slip boundaries. Front. Energy Res. 10:965309. doi: 10.3389/fenrg.2022.965309
Received
09 June 2022
Accepted
22 August 2022
Published
14 October 2022
Volume
10 - 2022
Edited by
Umar Khan, Hazara University, Pakistan
Reviewed by
Abderrahim Wakif, University of Hassan II Casablanca, Morocco
Md. Shafiqul Islam, Dhaka University, Bangladesh
Updates
Copyright
© 2022 Gul, Mukhtar, Alghamdi, Raizah, Alhazmi and ElDin.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Taza Gul, tazagul@cusit.edu.pk; ElSayed Tag ElDin, elsayed.tageldin@fue.edu.eg
This article was submitted to Process and Energy Systems Engineering, a section of the journal Frontiers in Energy Research
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.