Extracting Unknown Parameters of Proton Exchange Membrane Fuel Cells Using Quantum Encoded Pathfinder Algorithm

Proton exchange membrane fuel cell (PEMFC) is one of the most widely used fuel cell types. Accurate modeling of PEMFC can better facilitate the research of PEMFC and guide designers to design FC products that meet people’s needs. The modeling problem of PEMFC can be transformed into a parametric optimization problem. In order to improve the exploration capability of the pathfinder algorithm, the concept of quantum computing is introduced and a new quantum coded pathfinder optimization algorithm (QPFA) is proposed. QPFA was applied to the extraction of parameters of NedStackPS6, BCS500W and 250W FC, and these models of PEMFC have been applied for commercial use. The experimental results were compared with seven recently proposed metaheuristics and recently published literature, showing the accuracy and high precision of QPFA in extracting PEMFC parameters.

1 Introduction

Due to the air pollution and environmental changes caused by burning fossil fuels, green renewable energy is increasingly considered as an alternative energy source (Priya et al., 2018). The fuel cell is a new energy supply technology (Rezk et al., 2022). Several popular fuel cell products in the market can be divided into several types according to the type of electrolyte: proton exchange membrane FC (PEMFC) (Pourrahmani et al., 2019), alkaline FC (AFC) (Saebea et al., 2019), solid oxide FC (SOFC) (Chuahy and Kokjohn, 2019), phosphoric acid fuel cell (PAFC) (Guo et al., 2021), (Inci and Türksoy, 2019), and microbial fuel cell (MFC) (Sayed et al., 2021), (Ido and Kawase, 2020). PEMFC is the most widely used (Miao et al., 2020). A large number of PEMFCs use in transportation applications (Shaheen et al., 2021). These fuel cells have been used for a variety of purposes in power supply, the mathematical model of PEMFC accurately established to better promote the research of FC.

There are three main types of mathematical modeling for PEMFCs, theoretical (Ashraf et al., 2022), empirical (Busquet et al., 2004), and semi-empirical models (Amphlett et al., 1995). Accurate design and modeling of PEMFCs can help researchers design products that meet performance requirements and reduce production costs. Early researchers mainly used adaptive filters and black-box testing techniques to determine the parameters of PEMFC models. However, these methods have significant drawbacks, including poor accuracy and lack of flexibility. PFMFC has multi-variable and multi-peak nonlinear characteristics, and the operation of the PEMFC is accompanied by complex behavior of gas, liquid and heat conduction (Yang et al., 2020), which will lead to complex and labor time costly application of conventional technology (Abdel-Basset et al., 2021a). Therefore, a new technique is urgently needed to solve the PEMFC parameter extraction problem. With the development in the field of artificial intelligence, metaheuristic algorithms have achieved good results in nonlinear system optimization problems, and the problem of extracting PEMFC parameters can be seen as an optimization problem to be solved (Kandidayeni et al., 2019).

Many researchers have investigated the PEMFC parameter extraction problem using metaheuristic algorithms. GA was first used to extract the parameters of PEMFC (Priya et al., 2015), (Zhang and Wang, 2018), However, GA has the disadvantages of slow convergence speed and high parameter sensitivity, so a new optimization algorithm particle swarm optimization algorithm is applied to the PEMFC parameter extraction (Salim et al., 2015). Gong and Cai (2013) employed a named ranking-based differential evolution to find the parameters of the PEMFC model. El-Fergany (2018a) used Slap Algorithms to extract parameters of two PEMFC models that have been applied to commercial reality. Rao et al. (2019) modeled PEMFC using shark odor optimization and proved the reliability of shark odor optimization using statistical methods. Chen and Wang (2019) proposed a cuckoo search algorithm (CS-EO) with an explosion operator and applied it to the PEMFC parameter extraction problem with success on four models of fuel cell cases. Priya and Rajasekar (2019) used the flower pollination algorithm for PEMFC model parameter extraction. Selem et al. (2020) applied MRFO to the problem of accurate extraction of uncertain parameters of PEMFC models. Rizk-Allah and El-Fergany (2021) proposed an improved and developed AEO (IAEO) applying it to PEMFC modeling and optimization. Gouda et al. (2021a) used the jellyfish search algorithm to extract the exact parameters of the PEMFC and experimented on three test cases with success. Gouda et al. (2021b) investigated the dynamic performance of the fuel cell using the basic pathfinder algorithm. Several other optimization algorithms have been successfully applied to the PEMFC parameter extraction problem, such as ICHOA (Abdel-Basset et al., 2021a), MVO (Fathy and Rezk, 2018), IFSO (Qin et al., 2020), PO (Diab et al., 2020), JAYA (Xu et al., 2019), SMO (Gupta et al., 2021), EO (Seleem et al., 2021), GBO (Elsayed et al., 2021), BMO (Abdel-Basset et al., 2021a), and so on. Although many metaheuristic algorithms have been applied to extract unknown parameters of PEMFC, according to the No free lunch theorem (Wolpert and Macready, 1997), no single algorithm can solve all engineering optimization problems. There is still room to improve the extraction accuracy of PEMFC parameters, so it is necessary for researchers to improve the meta-heuristic algorithm and apply it in the extraction of PEMFC parameters.

Pathfinder optimization algorithm is a metaheuristic algorithm proposed by Yapici and Cetinkaya (2019). It is inspired by the principle that the group leader leads other individuals to the optimal future regional in nature. Pathfinder optimization algorithm has been applied to many complex practical engineering optimization problems and achieved success. In this paper, in order to solve the problem that the individual follower will easily fall into a local optimum in pathfinder algorithm, a quantum coded pathfinder optimization algorithm is proposed to solve continuous optimization problems. In QPFA, the probability amplitude is used to represent the probability of qubits two states, and the probability amplitude is mapped to the optimization problem interval to calculate the fitness value of individuals. Each individual corresponds to two solutions of the optimization space, which expands the diversity of the population, effectively avoids the problem of easily falling into a local optimum in PFA, and increases the exploration ability of the algorithm. The updating strategies of the PFA and the quantum revolving gate are used to update the probability amplitude for algorithm iteration. Then QPFA is applied to extract unknown parameters of PEMFC. This paper’s main contribution can be summarized as follows:

1) A novel quantum coding pathfinder optimization algorithm is proposed to extract unknown parameters of PEMFC.

2) Three real PEMFC cases, NedStackPS6, 500WFC and 250WFC, were solved successfully. The experimental results proving the superiority of QPFA in extracting unknown parameters of PEMFC.

3) The results extracted by QPFA were compared with the excellent metaheuristic algorithm. In order to improve the persuasion of this study, the parameter results extracted by QPFA were compared with the results of recently published literatures, and QPFA found the best results.

The structure of this article is as follows. Section 2 describes the fuel cell model. Section 3 explains the method of extracting unknown parameters of PEMFC by QPFA and an objective function of optimization. Section 4 introduces the basic pathfinder algorithm (PFA). Section 5 introduces the quantum coding pathfinder algorithm (QPFA). Section 6 introduces the experimental results and analysis of QPFA applied to three real cases, and compares the results with some powerful optimization algorithms. Section 7 is the summary of this paper and the prospect of the future work.

2 Proton Exchange Membrane Fuel Cell Model

This section introduces the semi-empirical model of PEMFC proposed by Mann et al. (2000). Its validity has been verified in many previous studies. The voltage output of PEMFC can be calculated using Eq. 1 (Mann et al., 2000).

$V_{o-cell}=E_{nernst}-V_{act}-V_{\mathrm{\Omega }}-V_{con}(1)$

where $V_{o-cell}$ represents the output voltage of PEMFC, its unit of measure is V. $E_{nernst}$ denotes the cell open circuit voltage in (V) that is derived from the Nernst equation. $V_{act}$ means a potential for activation in (V). $V_{\Omega }$ is the ohm voltage drop in the circuit and $V_{con}$ represents the concentration voltage loss in (V).

Assuming that all connected cells have the same polarization properties, when $N_s$ multiple cells are connected in series to form the stack, the stacks output voltage stack in (V) is described by Eq. 2.

$V_{o-\mathit{stack}}=N_s\cdot V_{o-cell}(2)$

Based on the Nernst equation and the magnitude of the change in temperature, $E_{nernst}$ can be calculated by Eq. 3.

$E_{nernst}=1.22-8.5\times \frac{\left(T-T^{\prime }\right)}{{10}^4}+4.3085\times \frac{T\left[\ln \left(P_{H_2}\cdot P_{O_2}^{0.5}\right)\right]}{{10}^5}(3)$

where T is the operating temperature of the cell in Kelvins and T $\le$ 100°C, $T^{\prime }$ = 273.15K. $P_{H_2}$ and $P_{O_2}$ are the hydrogen and oxygen partial regulating pressures in PFMFC, they use atm as the unit of measurement. Dynamic changes of external load will lead to changes in $P_{H_2}$ and $P_{O_2}$, and their numerical changes can be calculated by Eqs 4–6 respectively. When the fuel cell chooses natural air as oxidant for electrochemical reaction, $P_{O_2}$ will be calculated by Eq. 6.

$P_{H_2}=0.5\times F_{H_a}\times P_{H_{2}O}\times \left[\frac{P_a}{F_{H_a}\times P_{H_{2}O}\times \exp \left(\frac{4.192I_c}{A{T}^{0.832}}\right)}\right](4)$

$P_{O_2}=F_{H_a}\times P_{H_{2}O}\times \left[\frac{P_c}{F_{H_a}\times P_{H_{2}O}\times \exp \left(\frac{4.192I_c}{A{T}^{0.832}}\right)}\right](5)$

$P_{O_2}=P_c-F_{H_a}\times P_{H_{2}O}-\frac{0.79}{0.21}\times P_{O_2}\times \exp \left(\frac{4.192I_c}{A{T}^{0.832}}\right)(6)$

where $F_{H_a}$ and $F_{H_c}$ are the humidity of the steam at the anode and cathode of the fuel cell. $P_a$ and $P_c$ are the anode and cathode inlet pressures (atm). $I_c$ and A are the cell current in (A) and the membrane effective area in (cm²), respectively. Furthermore, $P_{H_{2}O}$ is the water vapor saturation pressure (atm), which is calculated by Eq. 7, its value is only affected by temperature T.

$\lg P_{H_{2}O}=2.95\times \frac{T-T^{\prime }}{100}-9.18\times \frac{{\left(T-T^{\prime }\right)}^2}{{10}^5}+1.44\times \frac{{\left(T-T^{\prime }\right)}^3}{{10}^7}-2.18(7)$

The electrochemical reaction in fuel cells is slow at the initial stage, and activation loss $V_{act}$ is used to describe the process, $V_{act}$ can be calculated from Eq. 8.

$V_{act}=-\left[{\mathrm{\omega }}_1+{\mathrm{\omega }}_{2}T+{\mathrm{\omega }}_{3}T{\log }_{10}\left(C_{O_2}\right)+{\mathrm{\omega }}_{4}T{\log }_{10}\left(I_c\right)\right](8)$

where ${\omega }_1$, ${\omega }_2$, ${\omega }_3$ and ${\omega }_4$ are the semi-empirical coefficient in the model, their units of measurement are $V$, $V{K}^{-1}$, $V{K}^{-1}$ and $V{K}^{-1}$. $C_{O_2}$ represents the oxygen concentration at the cathode catalytic layer in (mol/cm³), which is expressed by Eq. 9.

$C_{O_2}=\frac{P_{O_2}\times \exp \left(\frac{498}{T}\right)}{5.08\times {10}^6}(9)$

In addition, the concentration of hydrogen at the anode catalytic layer $C_{H_2}$ in (mol/cm3) is described by Eq. 10.

$C_{H_2}=\frac{P_{H_2}\times \exp \left(\frac{-77}{T}\right)}{10.9\times {10}^5}(10)$

The ohm voltage loss in the circuit is calculated by Eq. 11, in the polarization curve, it shows a linear relationship.

$V_{\mathrm{\Omega }}=I_c(R_W+R_I)(11)$

where $R_W$ in $\left(\mathrm{\Omega }\right)$ represents the resistance shown by electrons as they pass through the connections to the external circuit, which can be calculated from Eq. 12. $R_I$ in $\left(\mathrm{\Omega }\right)$ indicates the resistance shown by protons passing through membrane active area A (cm²).

$R_W={\mathrm{\eta }}_F\left(\frac{D}{A}\right)(12)$

where the thickness of the membrane is represented by D in (cm). The membrane’s specific resistivity is represented by ${\eta }_F$ in ($\mathrm{\Omega }$.cm), ${\eta }_F$ can be calculated by Eq. 13, $\lambda$ in Eq. 13 represents the amount of water in the membrane.

${\mathrm{\eta }}_F=\frac{181.6\times {\exp }^{-1}\left(\frac{4.18\times \left(T-303\right)}{T}\right)\times \left[1+0.03\left(\frac{I_c}{A}\right)+0.062{\left(\frac{T}{303}\right)}^2{\left(\frac{I_c}{A}\right)}^{2.5}\right]}{\left(\mathrm{\lambda }-0.634-\frac{3I_c}{A}\right)}(13)$

Finally, the concentration over-potential V con or mass transport losses will affect the I–V curve when the FC is overloaded, and this phenomenon can be calculated and described by Eq. 14.

$V_{con}=-\mathrm{\epsilon }{\log }_{10}\left(\frac{{\mathrm{\sigma }}_{\max }-\mathrm{\sigma }}{\mathrm{\sigma }}\right)(14)$

where $\epsilon$ is a parametric coefficient in (V), ${\sigma }_{\max }$ and $\sigma$ are represents the actual and maximum cell current density in (A.cm⁻²).

3 Proposed Identification Strategy

This section introduces a general framework for extracting PEMFC parameters using metaheuristic algorithm. The QPFA proposed in this paper will be applied to extracting PEMFC parameters. According to the semi-empirical PFMFC model introduced in the previous section, seven parameters in the equation are unknown, and there is a strong coupling between these parameters. For such an optimization problem with nonlinear constraints, the metaheuristic optimization algorithm is used to determine the best parameters. The objective function is of great significance for model parameter identification. In this paper, the sum of the squared error (SSE) between the actual output voltage and the estimated output voltage is chosen as the objective function. The optimal model parameters are extracted by minimizing the objective function. Objective function (SSE) can be calculated by Eq. 15.

$O{F}_{SSE}=\min \left\{{{\displaystyle \sum _{R=1}^{N_c}\left(V_{actual}\left(N_c\right)-V_{\text{simulation}}\left(N_c\right)\right)}}^2\right\}(15)$

where $V_{actual}$ and $V_{\text{simulation}}$ are the actual PFMFC data and simulation fuel cell voltage, $N_c$ is the number of data items retrieved.

The optimization variables are the unknown PEMFC parameters, which can be described as:

$x=\left[{\mathrm{\omega }}_1,{\mathrm{\omega }}_2,{\mathrm{\omega }}_3,{\mathrm{\omega }}_4,\mathrm{\lambda },\mathrm{\epsilon },{\mathrm{R}}_{\mathrm{I}}\right]$

Every variable has upper and lower bounds as follow:

$\begin{array}{l}{\mathrm{\omega }}_i^{\min }\le {\mathrm{\omega }}_i\ge {\mathrm{\omega }}_i^{\max }\left(i=\mathrm{1,2,3,4}\right)\\ {\mathrm{\lambda }}^{\min }\le \mathrm{\lambda }\ge {\mathrm{\lambda }}^{\max }\\ {\mathrm{\epsilon }}^{\min }\le \mathrm{\epsilon }\ge {\mathrm{\epsilon }}^{\max }\\ R_I^{\min }\le R_I\ge R_I^{\max }\end{array}$

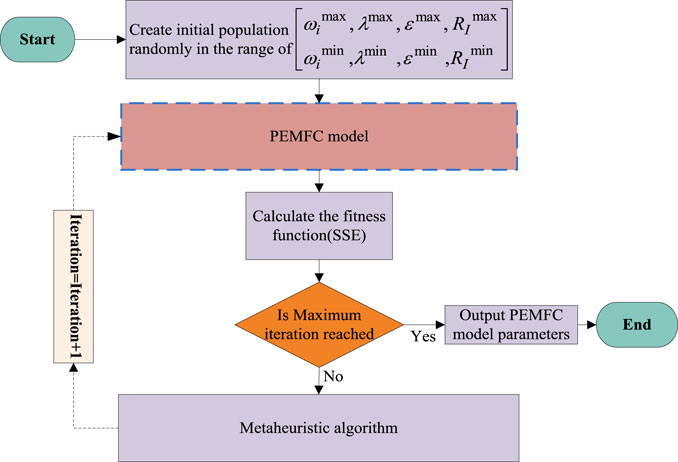
The specific values of upper and lower bounds of parameters are listed in Table 1. A general framework for PEMFC parameter extraction using metaheuristic optimization algorithm is shown in Figure 1.

TABLE 1

TABLE 1. Upper and lower bounds of parameters.

FIGURE 1

FIGURE 1. Process of extracting PEMFC parameters with metaheuristic optimization algorithm.

4 Basic Pathfinder Algorithm

In the PFA algorithm, each individual in the population will be placed in D - dimensional space. The individual in the most promising area is called the pathfinder, and the rest of the population will follow the pathfinder to search. This search model can be mathematically described by Eq. 16

$x_n^{i+1}=x_n^i+W_1\cdot \left(x_{n-1}^i-x_n^i\right)+W_2\cdot \left(x_p^i-x_n^i\right)+\epsilon n\in \left[\mathrm{2,3},\mathrm{...}N\right](16)$

where i represents the current iteration, $x_n$ represents the position of the follower of the population. $W_1$, $W_2$ are two randomly generated vectors calculated from Eqs 17, 18, $r_1$ and $r_2$ are a uniformly distributed random number generated randomly between (0, 1). $W_1$, $W_2$ can control the weight of the follower moving to the pathfinder and the neighboring individuals in the population. $\epsilon$ is the vibrancy vector, and its calculation can be obtained from Eq. 19, ${\mathrm{\Delta }}_{ij}$ is the distance between the i-th and the j-th position in population.

$W_1=\mathrm{\alpha }\cdot r_1(17)$

$W_2=\mathrm{\beta }\cdot r_2(18)$

$\mathrm{\epsilon }=\left(1-\frac{i}{i_{\max }}\right)\cdot u_1\cdot {\mathrm{\Delta }}_{ij},{\mathrm{\Delta }}_{ij}=\Vert x_i-x_{i-1}\Vert (19)$

The pathfinder updating position is obtained from Eq. 20

$x_p^{i+1}=x_p^i+2r_3\times \left(x_p^i-x_p^{i-1}\right)+\mathrm{\eta }(20)$

where $x_p^{i+1}$ represents the position of the i+1 generation pathfinder, $x_p^i$ is the location of the i-th pathfinder. $x_p^{i-1}$ is the location of the i-1 generation pathfinder, i represents the number of current iterations, $r_3$ represents a random number in a uniform distribution at [0,1]. $\eta$ is obtained from Eq. 21.

$\mathrm{\eta }=u_2\cdot e^{\frac{-2i}{i_{\max }}}(21)$

where $i_{\max }$ represents the maximum iteration number, $u_2$ is a random number evenly distributed within the range of [-1,1]. The pseudo-code of pathfinder algorithm is in Algorithm 1.

Algorithm 1. Pseudo-code of the Pathfinder algorithm.

5 Proposed Quantum Code Pathfinder Algorithm

A quantum coding method is proposed by Li et al. (Shiyong, 2007), this paper adopts the quantum coding method proposed by Li et al. The probability amplitude of qubit is used to encode the position vector of individual population in QPFA, quantum revolving gate updates the quantum bit rotation angle. In order to avoid premature convergence of PFA, quantum not gate is added into the algorithm as mutation behavior.

5.1 Quantum Theory

Since the concept of quantum mechanical systems was introduced, researchers in many fields have devoted themselves to the study of quantum mechanics (Benioff, 1982). Quantum physics is the theoretical root of quantum computing, and Schrödinger’s equation (SE) describes the intrinsic dynamics of quantum computing (Grover, 2001).

5.2 Qubit and Quantum Superposition

The smallest unit of information storage is called a qubit in quantum theory, qubits are the basic storage unit in quantum computing, and the Dirac symbol $|x\rangle$ is used to represent qubits. A qubit can have state $|0\rangle$ and state $|1\rangle$ or the linear combination of state $|0\rangle$ and state $|1\rangle$ (Shiyong, 2007), (Dey et al., 2014). The linear combination of state $|0\rangle$ and state $|1\rangle$ referred to as quantum superposition, this superposition is described by the wave function $|\mathrm{\Psi }\rangle$ in Hilbert space. The wave function is described as:

$|\mathrm{\Psi }\rangle =\mathrm{\omega }|0\rangle +\theta |1\rangle (22)$

where $\omega$ and $\theta$ are called the probability amplitude of the quantum state, $\omega$ and $\theta$ represents for when measuring a qubit, wave function $|\mathrm{\Psi }\rangle$ collapse to $|0\rangle$ with a probability ${\left|\omega \right|}^2$, collapse to $|1\rangle$ with a probability ${\left|\theta \right|}^2$. $\omega$ and $\theta$ satisfy the constraint of Eq. 23.

${\left|\mathrm{\omega }\right|}^2+{\left|\mathrm{\theta }\right|}^2=1(23)$

According to Eq. 23, use the coding method of Li et al. (Shiyong, 2007), $\omega =\cos \left(\phi \right),\theta =\sin \left(\phi \right)$, $\phi$ is the rotation angle of a qubit.

5.3 Initial Population

When the population is initialized, the probability amplitude of qubit is directly used as the position vector of the individual in PFA algorithm, the individual population can be initialized as:

$\left[P_m=\left[\begin{array}{l}\cos \left({\mathrm{\phi }}_{m,1}\right)\\ \sin \left({\mathrm{\phi }}_{m,1}\right)\end{array}|\begin{array}{l}\cos \left({\mathrm{\phi }}_{m,2}\right)\\ \cos \left({\mathrm{\phi }}_{m,2}\right)\end{array}|\begin{array}{l}\mathrm{...}\\ \mathrm{...}\end{array}|\begin{array}{l}\cos \left({\mathrm{\phi }}_{m,n}\right)\\ \sin \left({\mathrm{\phi }}_{m,n}\right)\end{array}|\right]\right](24)$

where n = 1,2,…,D represents the dimensions of the problem, m = 1,2, … , N represents the population number of individuals in PFA, ${\mathrm{\phi }}_{m,n}$ is the rotation angle of qubits, ${\mathrm{\phi }}_{m,n}$ is initialed by Eq. 25.

${\mathrm{\phi }}_{m,n}=2\mathrm{\pi }\cdot rand\left(\mathrm{0,1}\right)(25)$

Each individual in the QPFA corresponds to two positions in the problem space, they are calculated from the probability amplitude of qubits respectively, $P_{iC}$ is calculated by the probability amplitude of quantum bit $|0\rangle$, $P_{iS}$ is calculated by the probability amplitude of quantum bit $|1\rangle$.

$\begin{array}{l}{P}_{mC}=\left(\cos \left({\mathrm{\phi }}_{m,1}\right),\cos \left({\mathrm{\phi }}_{m,2}\right),\mathrm{...},\cos \left({\mathrm{\phi }}_{m,j}\right)\right)\\ P_{mS}=\left(\sin \left({\mathrm{\phi }}_{m,1}\right),\sin \left({\mathrm{\phi }}_{m,2}\right),\mathrm{...},\sin \left({\mathrm{\phi }}_{m,j}\right)\right)\end{array}(26)$

5.4 Solution Space Mapping

In QPFA, the search traversal space of the population individual is [−1,1] in every dimension. Since the form of qubit is used to represent the individual population in PFA, it is necessary to map the qubit to the optimization problem interval, the quantum bit’s probability $|0\rangle$ and $|1\rangle$ correspond to the two solutions of optimization problem. The mapping process is accomplished through Eqs 27, 28.

$Y_{mC}^n=\frac{1}{2}\left[Y_{\max }^n\left(1+{\omega }_N^n\right)+Y_{\min }^n\left(1-{\theta }_m^n\right)\right](27)$

$Y_{mS}^n=\frac{1}{2}\left[Y_{\max }^n\left(1+{\omega }_m^n\right)+Y_{\min }^n\left(1-{\theta }_m^n\right)\right](28)$

where $Y_{mC}^n$ and $Y_{mS}^n$ are calculated from the probabilities of qubits $|0\rangle$ and $|1\rangle$, respectively. Each qubit map to two positions in the solution space.

5.5 Individual Updates

In order to make use of the pathfinder search optimization algorithm to update rotation angle, the displacement difference of updating population individuals in the pathfinder search optimization algorithm is used to rewrite Eqs 16–30. In QPFA, the movement of individual population is carried out through the quantum revolving door, and the position update of individual population in PFA is transformed into the probability amplitude update of individual population qubit in QPFA.

5.5.1 Update of Qubit Angle on Individual

$\mathrm{\Delta }{\mathrm{\phi }}_{mn}^p\left(t+1\right)=\mathrm{\Delta }{\mathrm{\phi }}_{mn}^p\left(t\right)+\mathrm{\Delta }{\mathrm{\phi }}^p+\eta (29)$

$\mathrm{\Delta }{\mathrm{\phi }}_{mn}^F\left(t+1\right)=\mathrm{\Delta }{\mathrm{\phi }}_{mn}^F\left(t\right)+W_1\times \mathrm{\Delta }{\mathrm{\phi }}^F+W_2\times \mathrm{\Delta }{\mathrm{\phi }}_p^F+\epsilon (30)$

where t represents the current iteration, $\mathrm{\Delta }{\phi }^p$ represents the difference of the probability amplitude vector between the current pathfinder’s position and the previous pathfinder’s position. $\mathrm{\Delta }{\phi }^F$ represents the probability amplitude vector difference between the position of the current follower and the position of an adjacent follower. $\mathrm{\Delta }{\phi }_p^F$ represents the probability amplitude vector difference between the current follower position and the pathfinder position. $\mathrm{\Delta }{\phi }^p$, $\mathrm{\Delta }{\phi }_{ij}^F$ and $\mathrm{\Delta }{\phi }_p^F$ can be calculated as follows:

$\mathrm{\Delta }{\mathrm{\phi }}^p=\{\begin{array}{l}2\mathrm{\pi }+{\mathrm{\phi }}_p^n\left(t\right)-{\mathrm{\phi }}_p^n\left(t-1\right){\mathrm{\phi }}_p^n\left(t\right)-{\mathrm{\phi }}_p^n\left(t-1\right)<-\mathrm{\pi }\\ {\mathrm{\phi }}_p^n\left(t\right)-{\mathrm{\phi }}_p^n\left(t-1\right)-\mathrm{\pi }\le {\mathrm{\phi }}_p^n\left(t\right)-{\mathrm{\phi }}_p^n\left(t-1\right)\le \mathrm{\pi }\left(n=\mathrm{1,2},\mathrm{...},D\right)\\ {\mathrm{\phi }}_p^n\left(t\right)-{\mathrm{\phi }}_p^n\left(t-1\right)-2\mathrm{\pi }{\mathrm{\phi }}_p^n\left(t\right)-{\mathrm{\phi }}_p^n\left(t-1\right)>\mathrm{\pi }\end{array}(31)$

$\mathrm{\Delta }{\mathrm{\phi }}^F=\{\begin{array}{l}2\mathrm{\pi }+{\mathrm{\phi }}_m^n-{\mathrm{\phi }}_{m-1}^n{\mathrm{\phi }}_m^n-{\mathrm{\phi }}_{m-1}^n<-\mathrm{\pi }\\ {\mathrm{\phi }}_m^n-{\mathrm{\phi }}_{m-1}^n-\mathrm{\pi }\le {\mathrm{\phi }}_m^n-{\mathrm{\phi }}_{m-1}^n\le \mathrm{\pi }m=\mathrm{2,3},\mathrm{...},N.n=\mathrm{1,2},\mathrm{...},D\\ {\mathrm{\phi }}_m^n-{\mathrm{\phi }}_{m-1}^n-2\mathrm{\pi }{\mathrm{\phi }}_m^n-{\mathrm{\phi }}_{m-1}^n>\mathrm{\pi }\end{array}(32)$

$\mathrm{\Delta }{\mathrm{\phi }}_p^F=\{\begin{array}{l}2\mathrm{\pi }+{\mathrm{\phi }}_p^n-{\mathrm{\phi }}_m^n{\mathrm{\phi }}_p^n-{\mathrm{\phi }}_m^n<-\mathrm{\pi }\\ {\mathrm{\phi }}_p^n-{\mathrm{\phi }}_m^n-\mathrm{\pi }\le {\mathrm{\phi }}_p^n-{\mathrm{\phi }}_m^n\le \mathrm{\pi }\left(m=\mathrm{2,3},\mathrm{...},N.n=\mathrm{1,2},\mathrm{...},D\right)\\ {\mathrm{\phi }}_p^n-{\mathrm{\phi }}_m^n-2\mathrm{\pi }{\mathrm{\phi }}_p^n-{\mathrm{\phi }}_m^n>\mathrm{\pi }\end{array}(33)$

where ${\mathrm{\phi }}_p^n$ represents the angle of pathfinder individual in n-th dimension. ${\mathrm{\phi }}_m^n$ represents the angle of the follower individual in n-th dimension.

5.5.2 Update of Qubit Probability Amplitude of Individual

In the quantum optimization algorithm, the quantum revolving gate is used to update the probability amplitude of the qubit. The quantum revolving gate is set as Eq. 34, and the updating of the probability amplitude of the qubit is realized by Eq. 35.

$\kappa \left(\mathrm{\Delta \phi }\right)=\left[\begin{array}{cc}\cos \left(\mathrm{\Delta \phi }\right)& -\sin \left(\mathrm{\Delta \phi }\right)\\ \sin \left(\mathrm{\Delta \phi }\right)& \cos \left(\mathrm{\Delta \phi }\right)\end{array}\right](34)$

$\left[\begin{array}{l}\cos \left(\mathrm{\phi }\left(t+1\right)\right)\\ \sin \left(\mathrm{\phi }\left(t+1\right)\right)\end{array}\right]=\mathrm{\kappa }\left(\mathrm{\Delta \phi }\left(t+1\right)\right)\left[\begin{array}{l}\cos \left(\mathrm{\phi }\left(t\right)\right)\\ \sin \left(\mathrm{\phi }\left(t\right)\right)\end{array}\right](35)$

where ${\left[\cos \left(\mathrm{\phi }\left(t\right)\right),\sin \left(\mathrm{\phi }\left(t\right)\right)\right]}^T$ and ${\left[\cos \left(\mathrm{\phi }\left(t+1\right)\right),\sin \left(\mathrm{\phi }\left(t+1\right)\right)\right]}^T$ represents the probability amplitude before and after the update. $\mathrm{\phi }\left(t\right)$ and $\varphi (t+1)$ represents the rotation angle before and after the update. Through the Eq. 35, ${\left[\cos \left(\mathrm{\phi }\left(t+1\right)\right),\sin \left(\mathrm{\phi }\left(t+1\right)\right)\right]}^T$ can be calculated as Eq. 36. According to the trigonometric transformation formula Eq. 36 can be rewritten as Eq. 37.

$\{\begin{array}{l}\cos \left(\mathrm{\phi }\left(t+1\right)\right)=\cos \left(\mathrm{\Delta \phi }\right)\cos \left(\mathrm{\phi }\left(t\right)\right)-\sin \left(\mathrm{\Delta \phi }\right)\sin \left(\mathrm{\phi }\left(t\right)\right)\\ \sin \left(\mathrm{\phi }\left(t+1\right)\right)=\sin \left(\mathrm{\Delta \phi }\right)\cos \left(\mathrm{\phi }\left(t\right)\right)+\cos \left(\mathrm{\Delta \phi }\right)\sin \left(\mathrm{\phi }\left(t\right)\right)\end{array}(36)$

$\{\begin{array}{l}\cos \left(\mathrm{\phi }\left(t+1\right)\right)=\cos \left(\mathrm{\phi }+\mathrm{\Delta \phi }\right)\\ \sin \left(\mathrm{\phi }\left(t+1\right)\right)=\sin \left(\mathrm{\phi }+\mathrm{\Delta \phi }\right)\end{array}(37)$

when the update is complete, two new locations for the individual will be created:

$\begin{array}{l}{P}_{mC}=\left(\cos \left({\mathrm{\phi }}_{m,1}+\mathrm{\Delta }{\mathrm{\phi }}_{m,1}\left(t+1\right)\right),\mathrm{...},\cos \left({\mathrm{\phi }}_{m,n}+\mathrm{\Delta }{\mathrm{\phi }}_{m,n}\left(t+1\right)\right)\right)\\ P_{mS}=\left(\sin \left({\mathrm{\phi }}_{m,1}+\mathrm{\Delta }{\mathrm{\phi }}_{m,1}\left(t+1\right)\right),\mathrm{...},\sin \left({\mathrm{\phi }}_{m,n}+\mathrm{\Delta }{\mathrm{\phi }}_{m,n}\left(t+1\right)\right)\right)\end{array}(38)$

5.6 Mutation of Behavior

In PFA algorithm, pathfinder has a great influence on the follower. In the middle and late stage of algorithm execution, the follower will closely follow the pathfinder to search, which will increase the probability of the algorithm falling into the local optimal solution. Although quantum coding improves the diversity of the population, it is still possible to fall into the local optimal solution. In order to better jump out when the population falls into the local optimal solution, a quantum not gate is added to mutate the population qubit. Mutation behavior is carried out through quantum not gates, quantum not gates are described by Eq. 39. The mutation operation is described by Eq. 40.

$\left[\begin{array}{l}01\\ 10\end{array}\right]\left[\begin{array}{l}\mathrm{\omega }\\ \mathrm{\theta }\end{array}\right]=\left[\begin{array}{l}\mathrm{\theta }\\ \mathrm{\omega }\end{array}\right](39)$

$\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\left[\begin{array}{l}\cos \left({\mathrm{\phi }}_{mn}\right)\\ \sin \left({\mathrm{\phi }}_{mn}\right)\end{array}\right]=\left[\begin{array}{l}\sin \left({\mathrm{\phi }}_{mn}\right)\\ \cos \left({\mathrm{\phi }}_{mn}\right)\end{array}\right](40)$

5.7 Quantum Coding Pathfinder Algorithm Pseudo Code

The pseudo-code of the Quantum Pathfinder algorithm as in Algorithm 2.

Algorithm 2. Pseudo-code of the Quantum Pathfinder algorithm.

6 Results and Discussion

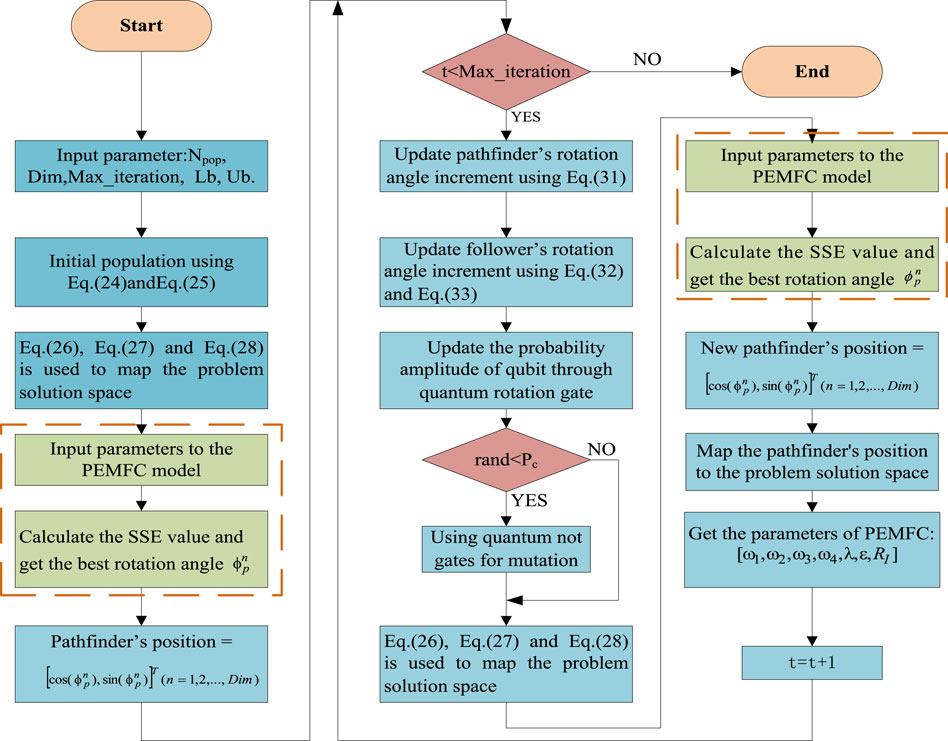
In this section, QPFA is applied to extract unknown parameters of three types of fuel cells, which are respectively NedStackPS6, BCS 500 and 250W FC. The objective function is to minimize the sum of squares of the difference between real data and simulation data, which can be obtained by Eq. 15. The simulations were performed on the MATLAB 2016b platform and run on a CPU Core i5-7100 v5 (3.80 GHz) with 16 GB RAM. The specific process of extracting fuel cell location parameters using QPFA algorithm is shown in Figure 2. Three types of fuel cell parameters, specific operating environments, and data sets are obtained in the Ref (Li et al., 2020a), the upper and lower bounds of the extracted unknown parameters are listed in Table 1.

FIGURE 2

FIGURE 2. Extracting PEMFC parameter flow chart using QPFA.

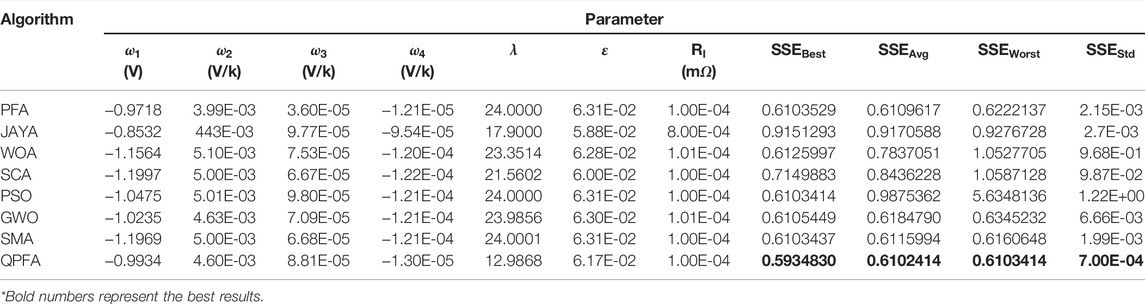
In order to better test the ability of QPFA to extract unknown parameters of fuel cells, it is compared with six other excellent meta-heuristic algorithms with the strong optimization ability, which are PFA (Yapici and Cetinkaya, 2019), JAYA (Rao, 2016), WOA (Mirjalili and Lewis, 2016), SCA (Mirjalili, 2016), PSO (Kennedy and Eberhart, 1995), GWO (Mirjalili et al., 2014), and SMA (Li et al., 2020b). Finally, the experimental results were compared with the recently published literature. Due to the execution characteristics of the metaheuristic algorithm, the results of each run are different. In order to better test the optimizing ability of the algorithm, the results of 30 runs are considered in the experimental verification. The population, number of all metaheuristic algorithms $N_{pop}$ = 30 and the number of iterations $Maxiteration$ = 1000. The specific parameter values of each metaheuristic algorithm are consistent with the settings of the original algorithm.

6.1 Case1: NedStackPS6

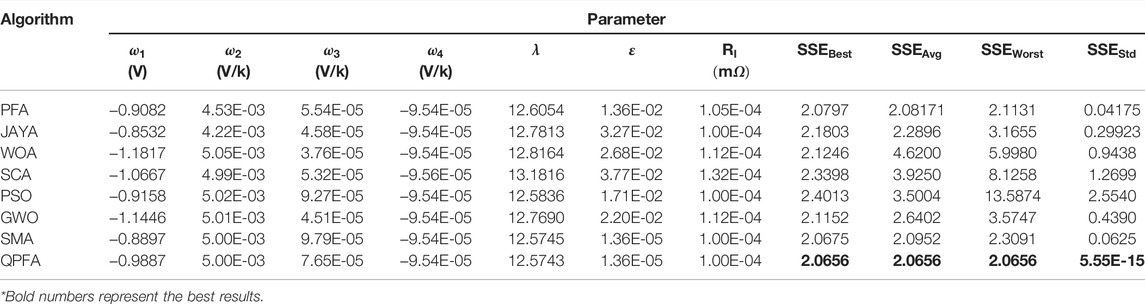
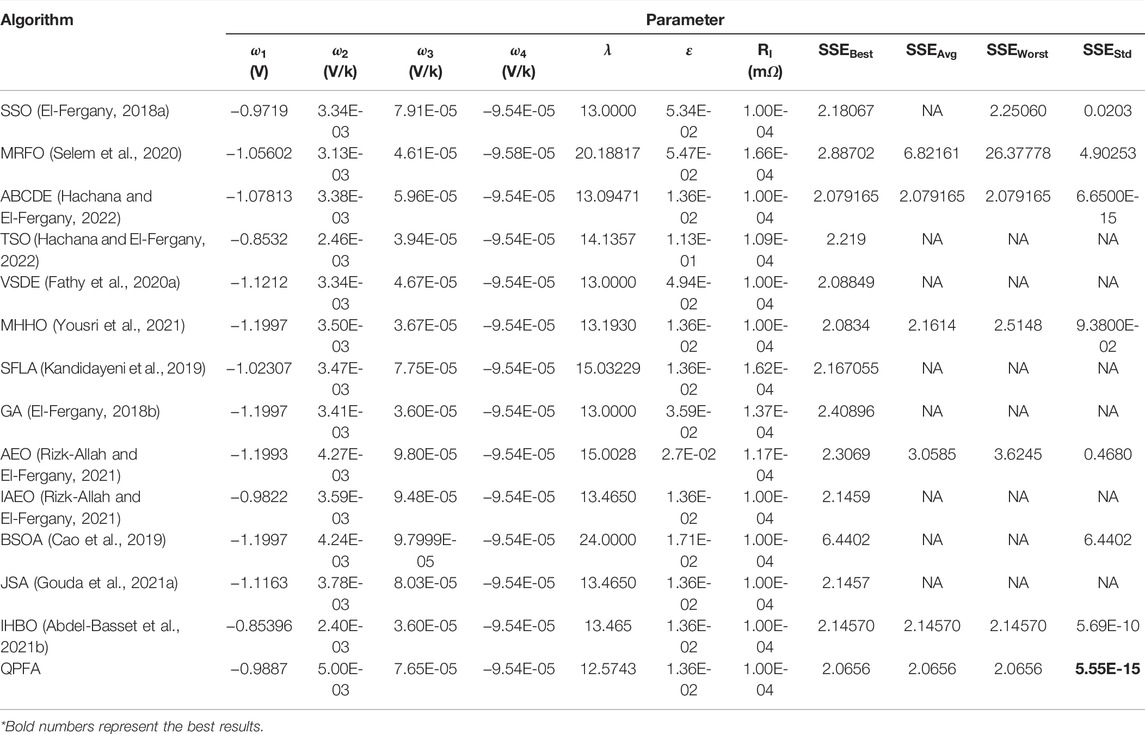
The technical parameters of NedStackPS6 are shown in the Table 2. According to the parameter extraction method as mentioned earlier, the parameter value of PEMFC obtained at the optimized minimum objective function will be the parameter to be extracted. Therefore, the performance of the optimization algorithm extracting PEMFC parameters can be judged by comparing the value of the objective function. After 30 runs, the experimental results obtained by QPFA and seven powerful optimization algorithms are shown in Table 3. Table 3 lists the minimum objective function value ($SS{E}_{Best}$), average objective function value ($SS{E}_{Avg}$), worst objective function value ($SS{E}_{Worst}$), variance value ($SS{E}_{Std}$), and best PEMFC parameters value obtained by the optimization algorithm used in the experiment after 30 runs. As can be seen from Table 3, QPFA has achieved the best average value, the best value and the worst value. QPFA ranks the first among the eight algorithms. The box plot of the 30 running results is shown in Figure 3A, which shows that QPFA has good stability. In order to intuitively see the convergence speed performance of the algorithm, the average convergence curve of 30 running results is drawn in Figure 3B. It can be seen that QPFA’s convergence speed is very fast, and its convergence curve is always at the bottom of the convergence curve of other algorithms, and finally achieves the best average objective function value in 1000 generations.

TABLE 2

TABLE 2. Specific parameters of the three PEMFCS.

TABLE 3

TABLE 3. SSE value obtained experimentally in Case1.

FIGURE 3

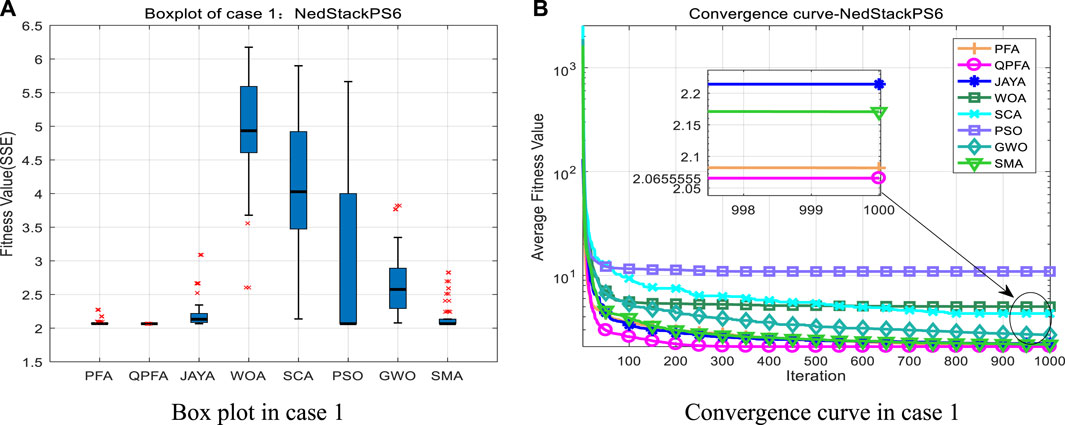
FIGURE 3. Box plot and convergence curve in case 1. (A) Box plot in case 1. (B) Convergence curve in case 1

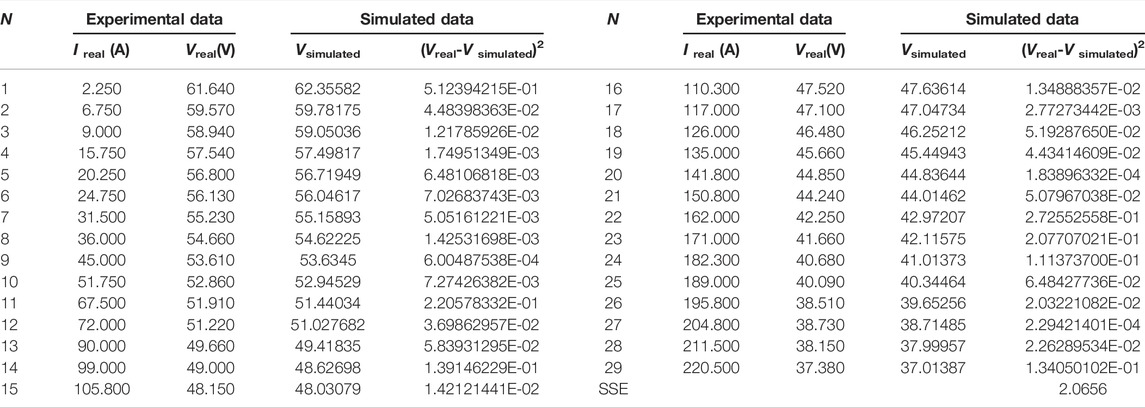
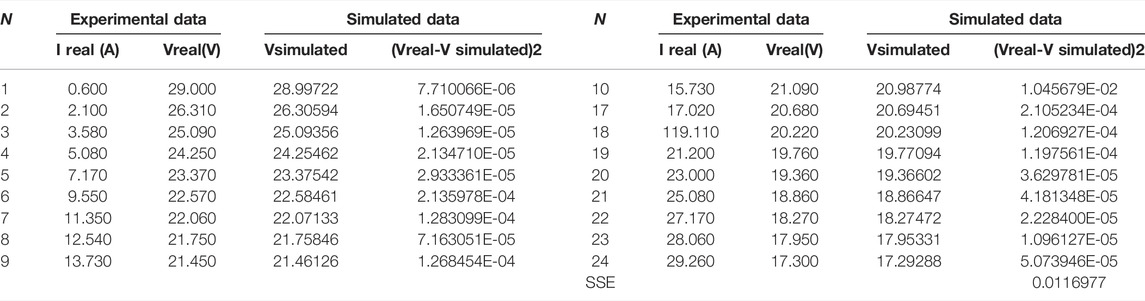
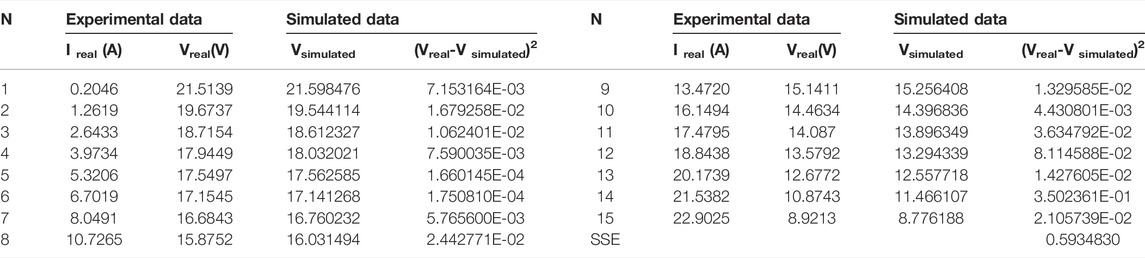
Table 4 shows each real data point and the simulated data point values calculated by the parameters extracted from QPFA, and the square of the difference between them (SSE) is also listed. PEMFC’s I-V curve and I-P curve obtained by QPFA is shown in the Figures 4A,B and . It can be seen from the simulated data curve and real discrete data points that the simulated data curve calculated by the parameter values given by QPFA fit the real discrete data points curve well. However, there are still some errors. In the activation and start-up stage of fuel cell, SSE reaches the maximum error: 5.12394215E-01, which may be because the output voltage PEMFC drops steeply and a lot of electrochemical reaction takes place in the initial stage. With the continuous output voltage of PEMFC, in the ohm region with linear voltage attenuation, their errors gradually decrease, and the minimum SSE value reaches 1.83896332E-04. In the third stage of PEMFC, concentration losses, SSE fluctuated with the increase of currency, but it was still within the acceptable range. In general, the NedstackPS6 parameter value extracted by QPFA well simulates the current-voltage polarization curve of NedstackPS6, and the error value is within an acceptable range. Based on the modeling PEMFC parameters extracted from QPFA, numerical simulation was carried out $P_{H_2}/P_{O_2}$= 1/1bar, 2/1.5 bar, 3/1.5 bar and 3/2 bar. The experimental results are consistent with the actual situation that the higher the pressure, the higher the output voltage of the battery stack. The I-V curve and I-P curve of the battery stack is shown in the Figures 4C,D. In order to better detect the optimization performance of QPFA, the Friedman test statistical analysis was conducted on the results of 30 times of optimization. As shown in the Figure 5, QPFA ranked first with the lowest rank value 1.35, proving that the optimum performance of QPFA ranked first. Table 5 lists parameters extracted by QPFA and parameters in recent published literature, comparing the SSE values obtained after optimization with the published literature in recent years, QPFA get a better result than these powerful optimizers.

TABLE 4

TABLE 4. Comparison of real data and simulated data in Case 1.

FIGURE 4

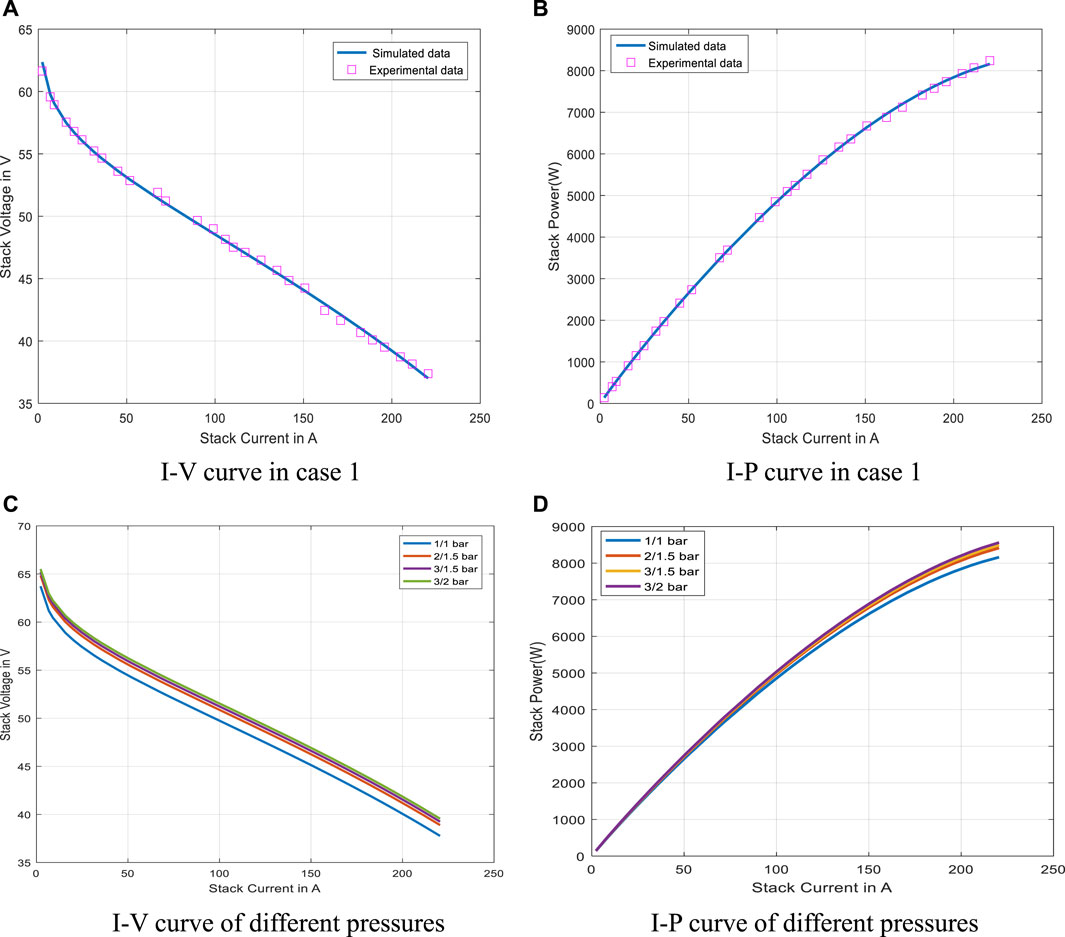
FIGURE 4. Electrical characteristics of parameters extracted by QPFA on Case 1. (A) I-V curve in case 1 (B) I-P curve in case 1 (C) I-V curve of different pressures (D) I-P curve of different pressures.

FIGURE 5

FIGURE 5. Friedman test on Case 1.

TABLE 5

TABLE 5. Compare the QPFA on case 1 with the reference paper.

6.2 Case2: BCS 500W

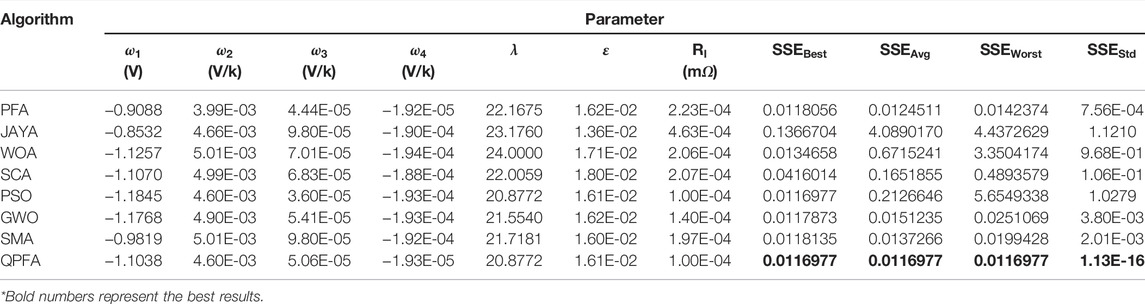
A named BCS 500W fuel cell is used in this case to extract parameters, Table 2 lists the specific parameters of this model. After 30 runs, the experimental results obtained by QPFA and seven powerful optimization algorithms are shown in Table 6, this table shows the fitness values obtained by each algorithm and lists the parameter values corresponding to the best fitness values, QPFA has achieved the best average value, the best value and the worst value. The box plot of the 30 running results is shown in the Figure 6A, which shows that QPFA has better stability than other algorithms. The average convergence curve of 30 running results is drawn in Figure 6B. It can be seen that QPFA’s convergence speed is very fast, and it converges to the minimum mean fitness at the end of the iteration.

TABLE 6

TABLE 6. SSE value obtained experimentally on Case2.

FIGURE 6

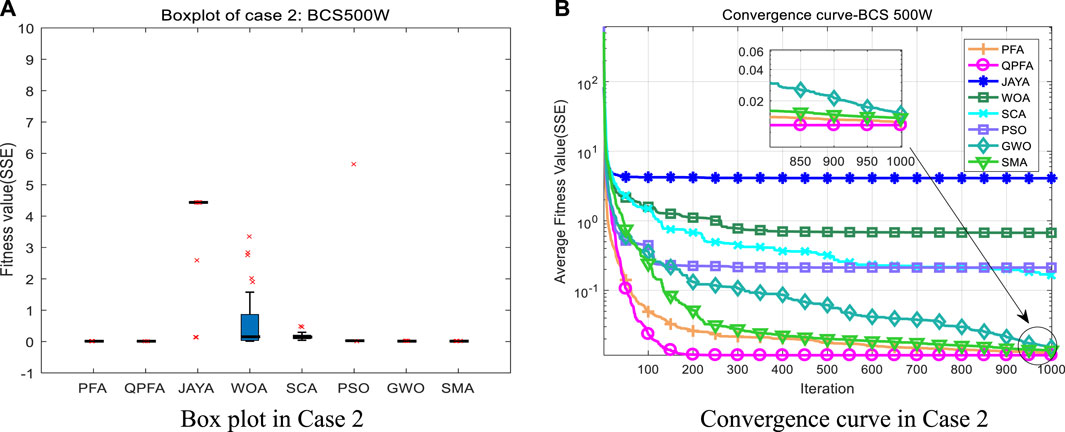
FIGURE 6. Box plot and convergence curve in Case 2. (A) Box plot in Case 2 (B) Convergence curve in Case 2.

Table 7 shows each real data point and the simulated data point values calculated by the parameters extracted from QPFA, and the square of the difference between them (SSE) is listed. PEMFC’s polarization curve obtained by QPFA is shown in Figure 7A, PEMFC’s I-P curve is also shown in Figure 7B. In order to better verify the correctness of PEMFC parameters extracted by QPFA, numerical simulation of the model was carried out under the condition of $P_{H_2}/P_{O_2}$ = 1/0.2075bar, 1.5/1bar, 2/1.25bar and 2.5/1.5 bar. I-V and I-P curves under different conditions are shown in Figures 7C,D. The results show that increasing the pressure of hydrogen and oxygen increases the output voltage and power of the battery stack. BCS500W models at different temperatures were also studied, I-V and I-P curves are shown in Figures 7E,F. The results show that improving the temperatures of battery stack can improve the output voltage and output power, which is consistent with the actual situation.

TABLE 7

TABLE 7. Comparison of real data and simulated data in Case 2.

FIGURE 7

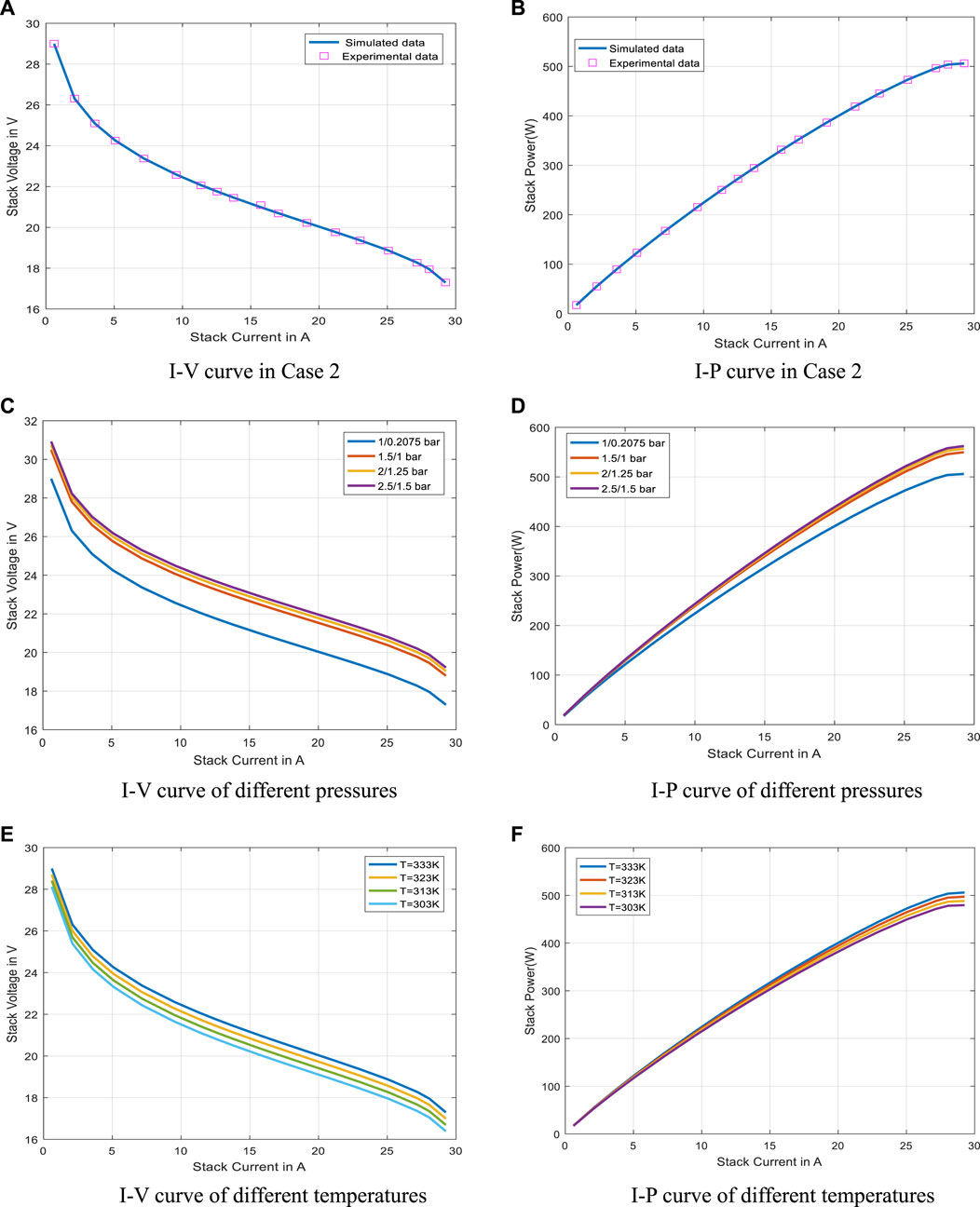
FIGURE 7. Electrical characteristics of parameters extracted by QPFA on Case 2 (A). I-V curve in Case 2 (B). I-P curve in Case 2 (C). I-V curve of different pressures (D). I-P curve of different pressures (E). I-V curve of different temperatures (F). I-P curve of different temperatures.

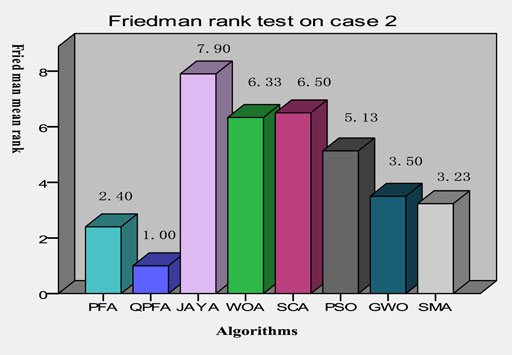
The Friedman test statistical analysis was conducted on the results of 30 times of optimization. As shown in Figure 8, QPFA ranked first with the lowest rank value 1.00, proving that the optimization performance of QPFA ranked first. Table.8 lists parameters extracted by QPFA and parameters in recent published literature, comparing the SSE values obtained after optimization with the published literature in recent years, QPFA get a better result than these powerful optimizers.

FIGURE 8

FIGURE 8. Friedman test on case 2.

TABLE 8

TABLE 8. Compare the QPFA on case 2 with the reference paper.

6.3 Case3: 250W PEMFC

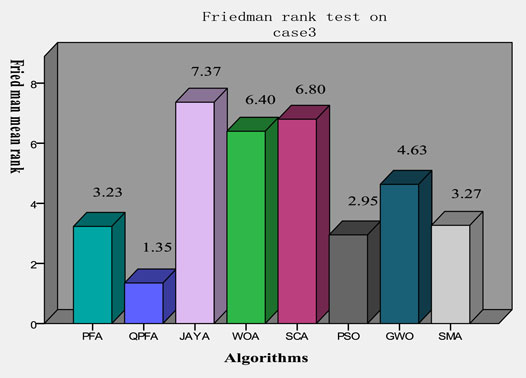
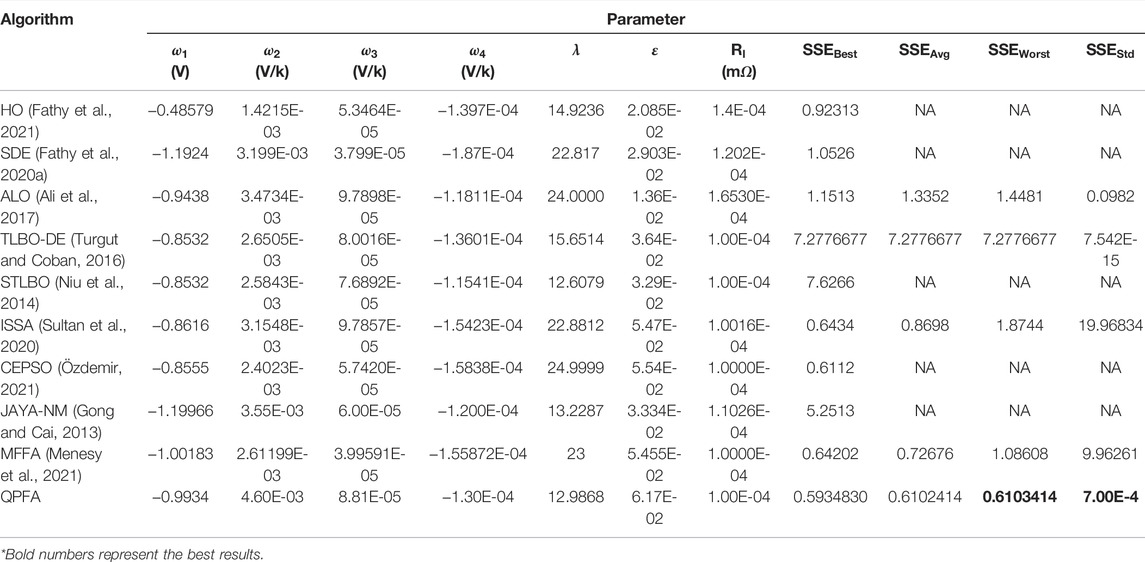
In order to better prove the excellent performance of QPFA in extracting PEMFC parameters, QPFA and other algorithms have been applied for extracting the model parameters of the 250W stack. The fitness function values after 30 runs are listed in Table 9, and the optimal parameter values found by each meta-heuristic algorithm are also given. After 30 times of running QPFA to extract the optimization problem of PEMFC parameters, QPFA obtained the minimum fitness function value, indicating that QPFA extracted the optimal PEMFC parameters. Figure 9A is the variance diagram of parameter extraction of 250W PEMFC. It can be seen that QPFA has very small variance and excellent stability. Figure 9B is the algorithms convergence diagram in the 250W PEMFC parameter extraction experiment. It can be seen that QPFA ranked first in the convergence speed at the beginning of iteration. As the algorithm continues to iterate, QPFA continues to search and optimize, and finally obtains the minimum average fitness function value at the end of iteration. Table. 10 lists the real values of 250W and the values obtained by numerical simulation after parameters were extracted from QPFA to establish the model. SSE is also calculated point by point in Table.10. Figures 10A,B are I-V and I-P curves drawn by the parameters obtained by QPFA. Experimental results at different pressures and temperatures are shown in Figures 10C–F, the results show that increasing pressure and temperature can result in higher voltage and higher power output of the battery stack. The Friedman test statistical analysis was conducted on the results of 30 times of optimization. As shown in Figure 11, QPFA ranked first with the lowest rank value 1.35. Table.11 lists parameters extracted by QPFA and parameters in recent published literature, comparing the SSE values obtained after optimization with the published literature in recent years, QPFA get a better result than these powerful optimizers.

TABLE 9

TABLE 9. SSE value obtained experimentally on case3.

FIGURE 9

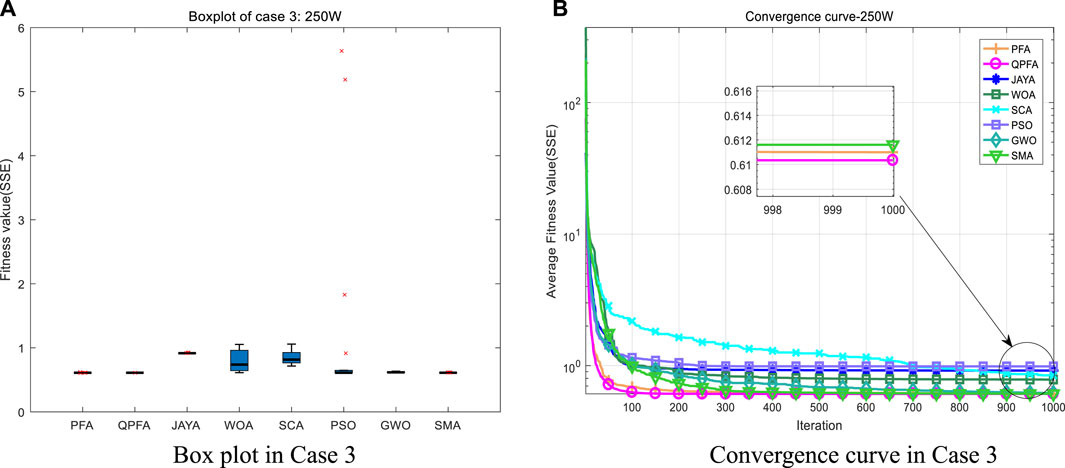
FIGURE 9. Box plot and convergence curve in Case 3. (A) Box plot in Case 3 (B) Convergence curve in Case 3.

TABLE 10

TABLE 10. Comparison of real data and simulated data in Case 3.

FIGURE 10

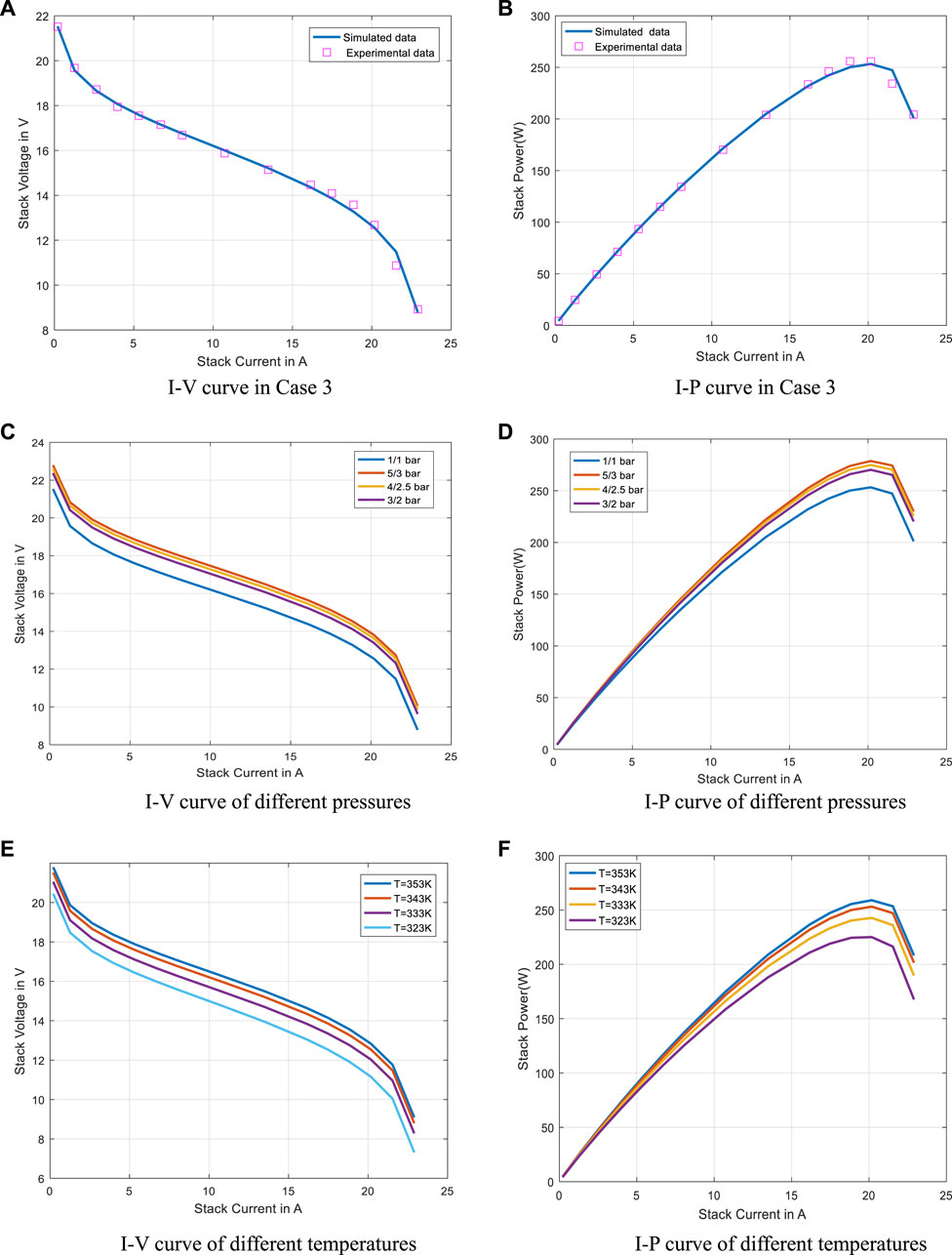
FIGURE 10. Electrical characteristics of parameters extracted by QPFA on Case 3 (A). I-V curve in Case 3 (B). I-P curve in Case 3 (C). I-V curve of different pressures (D). I-P curve of different pressures (E). I-V curve of different temperatures (F). I-P curve of different temperatures.

FIGURE 11

FIGURE 11. Friedman test on case 3.

TABLE 11

TABLE 11. Compare the QPFA on case 3 with the reference paper.

7 Conclusion and Future Work

In this paper, a new quantum coding pathfinder optimization algorithm is proposed, which uses probability angles to represent individuals and probability magnitudes to represent the probabilities of 1 and 0 in quantum computing, and maps them to the solution space of the optimization problem through mapping relations. The characteristics of quantum computing make one individual in QPFA correspond to two individuals in the solution space, which increases the population diversity and improves the exploration ability of PFA. Quantum revolving gate and pathfinder update strategies are used for iterative updates of probability angles, and quantum non-gates help QPFA to jump out of local optimal solutions. QPFA is applied to the determination of PEMFC location parameters, and three commercial types of PEMFC are studied. QPFA achieves the best results for all three PEMFC model parameter extraction, and the Friedman test also shows that the performance of QPFA ranks the first among all algorithms. The results obtained from QPFA search optimization were compared with those from published literature, and the results obtained by QPFA have higher stability and accuracy values. Various implementations of the group pathfinder algorithm will be considered in the future and applied to more types of PEMFC parameter extraction problems.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

NL: Investigation, experiment, writing—draft; GZ: experiment, formal analysis; YZ: supervision, writing—review and editing. WD: writing—review and editing. QL: supervision, writing—review and editing.

Funding

This work was supported by the National Science Foundation of China under Grant Nos. U21A20464, 62066005 and 61771087, and Program for Young Innovative Research Team in China University of Political Science and Law, under Grant No. 21CXTD02.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel-Basset, M., Mohamed, R., El-Fergany, A., Chakrabortty, R. K., and Ryan, M. J. (2021). Adaptive and efficient optimization model for optimal parameters of proton exchange membrane fuel cells: A comprehensive analysis. Energy 233, 121096. doi:10.1016/j.energy.2021.121096

CrossRef Full Text | Google Scholar

Abdel-Basset, M., Mohamed, R., Elhoseny, M., Chakrabortty, R. K., and Ryan, M. J. (2021). An efficient heap-based optimization algorithm for parameters identification of proton exchange membrane fuel cells model: Analysis and case studies. Int. J. Hydrogen Energy 46 (21), 11908–11925. doi:10.1016/j.ijhydene.2021.01.076

CrossRef Full Text | Google Scholar

Ali, M., El-Hameed, M., and Farahat, M. (2017). Effective parameters’ identification for polymer electrolyte membrane fuel cell models using grey wolf optimizer. Renew. Energy 111, 455–462. doi:10.1016/j.renene.2017.04.036

CrossRef Full Text | Google Scholar

Amphlett, J. C., Baumert, R. M., Mann, R. F., Peppley, B. A., Roberge, P. R., and Harris, T. J. (1995). Performance modeling of the ballard mark IV solid polymer electrolyte fuel cell: I. Mechanistic model development. J. Electrochem. Soc. 142 (1), 1–8. doi:10.1149/1.2043866

CrossRef Full Text | Google Scholar

Ashraf, H., Abdellatif, S. O., Elkholy, M. M., and El-Fergany, A. A. (2022). Computational techniques based on artificial intelligence for extracting optimal parameters of PEMFCs: Survey and insights. Arch. Comput. Methods Eng. 2022, 1–30. doi:10.1007/s11831-022-09721-y

CrossRef Full Text | Google Scholar

Ben Messaoud, R. (2021). Parameters determination of proton exchange membrane fuel cell stack electrical model by employing the hybrid water cycle moth‐flame optimization algorithm. Int. J. Energy Res. 45 (3), 4694–4708. doi:10.1002/er.6065

CrossRef Full Text | Google Scholar

Benioff, P. (1982). Quantum mechanical Hamiltonian models of Turing machines. J. Stat. Phys. 29 (3), 515–546. doi:10.1007/bf01342185

CrossRef Full Text | Google Scholar

Busquet, S., Hubert, C.-E., Labbé, J., Mayer, D., and Metkemeijer, R. (2004). A new approach to empirical electrical modelling of a fuel cell, an electrolyser or a regenerative fuel cell. J. Power sources 134 (1), 41–48. doi:10.1016/j.jpowsour.2004.02.018

CrossRef Full Text | Google Scholar

Cao, Y., Li, Y., Zhang, G., Jermsittiparsert, K., and Razmjooy, N. (2019). Experimental modeling of PEM fuel cells using a new improved seagull optimization algorithm. Energy Rep. 5, 1616–1625. doi:10.1016/j.egyr.2019.11.013

CrossRef Full Text | Google Scholar

Chen, Y., and Wang, N. (2019). Cuckoo search algorithm with explosion operator for modeling proton exchange membrane fuel cells. Int. J. Hydrogen Energy 44 (5), 3075–3087. doi:10.1016/j.ijhydene.2018.11.140

CrossRef Full Text | Google Scholar

Chuahy, F. D., and Kokjohn, S. L. (2019). Solid oxide fuel cell and advanced combustion engine combined cycle: A pathway to 70% electrical efficiency. Appl. Energy 235, 391–408. doi:10.1016/j.apenergy.2018.10.132

CrossRef Full Text | Google Scholar

Dey, S., Bhattacharyya, S., and Maulik, U. (2014). Quantum inspired genetic algorithm and particle swarm optimization using chaotic map model based interference for gray level image thresholding. Swarm Evol. Comput. 15, 38–57. doi:10.1016/j.swevo.2013.11.002

CrossRef Full Text | Google Scholar

Diab, A. A. Z., Ali, H., Abdul-Ghaffar, H., Abdelsalam, H. A., and Sattar, M. A. E. (2021). Accurate parameters extraction of PEMFC model based on metaheuristics algorithms. Energy Rep. 7, 6854–6867. doi:10.1016/j.egyr.2021.09.145

CrossRef Full Text | Google Scholar

Diab, A. A. Z., Tolba, M. A., El-Magd, A. G. A., Zaky, M. M., and El-Rifaie, A. M. (2020). Fuel cell parameters estimation via marine predators and political optimizers. IEEE Access 8, 166998–167018. doi:10.1109/access.2020.3021754

CrossRef Full Text | Google Scholar

El-Fergany, A. A. (2018). Electrical characterisation of proton exchange membrane fuel cells stack using grasshopper optimiser. IET Renew. Power Gener. 12 (1), 9–17. doi:10.1049/iet-rpg.2017.0232

CrossRef Full Text | Google Scholar

El-Fergany, A. A. (2018). Extracting optimal parameters of PEM fuel cells using Salp Swarm Optimizer. Renew. Energy 119, 641–648. doi:10.1016/j.renene.2017.12.051

CrossRef Full Text | Google Scholar

Elsayed, S. K., Agwa, A. M., Elattar, E. E., and El-Fergany, A. (2021). Steady-state modelling of PEM fuel cells using gradient-based optimizer. Dyna (Medellin). 96 (5), 520–527. doi:10.6036/10099

CrossRef Full Text | Google Scholar

Fathy, A., Abd Elaziz, M., and Alharbi, A. G. (2020). A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 146, 1833–1845. doi:10.1016/j.renene.2019.08.046

CrossRef Full Text | Google Scholar

Fathy, A., Abdel Aleem, S. H., and Rezk, H. (2021). A novel approach for PEM fuel cell parameter estimation using LSHADE‐EpSin optimization algorithm. Int. J. Energy Res. 45 (5), 6922–6942. doi:10.1002/er.6282

CrossRef Full Text | Google Scholar

Fathy, A., and Rezk, H. (2018). Multi-verse optimizer for identifying the optimal parameters of PEMFC model. Energy 143, 634–644. doi:10.1016/j.energy.2017.11.014

CrossRef Full Text | Google Scholar

Fathy, A., Rezk, H., and Ramadan, H. S. M. (2020). Recent moth-flame optimizer for enhanced solid oxide fuel cell output power via optimal parameters extraction process. Energy 207, 118326. doi:10.1016/j.energy.2020.118326

CrossRef Full Text | Google Scholar

Gong, W., and Cai, Z. (2013). Accelerating parameter identification of proton exchange membrane fuel cell model with ranking-based differential evolution. Energy 59, 356–364. doi:10.1016/j.energy.2013.07.005

CrossRef Full Text | Google Scholar

Gouda, E. A., Kotb, M. F., and El-Fergany, A. A. (2021). Investigating dynamic performances of fuel cells using pathfinder algorithm. Energy Convers. Manag. 237, 114099. doi:10.1016/j.enconman.2021.114099

CrossRef Full Text | Google Scholar

Gouda, E. A., Kotb, M. F., and El-Fergany, A. A. (2021). Jellyfish search algorithm for extracting unknown parameters of PEM fuel cell models: Steady-state performance and analysis. Energy 221, 119836. doi:10.1016/j.energy.2021.119836

CrossRef Full Text | Google Scholar

Grover, L. K. (2001). From Schrödinger’s equation to the quantum search algorithm. Pramana -. J. Phys. 56 (2), 333–348. doi:10.1007/s12043-001-0128-3

CrossRef Full Text | Google Scholar

Guo, X., Zhang, H., Hu, Z., Hou, S., Ni, M., and Liao, T. (2021). Energetic, exergetic and ecological evaluations of a hybrid system based on a phosphoric acid fuel cell and an organic Rankine cycle. Energy 217, 119365. doi:10.1016/j.energy.2020.119365

CrossRef Full Text | Google Scholar

Gupta, J., Nijhawan, P., and Ganguli, S. (2021). Optimal parameter estimation of PEM fuel cell using slime mould algorithm. Int. J. Energy Res. 45 (10), 14732–14744. doi:10.1002/er.6750

CrossRef Full Text | Google Scholar

Hachana, O., and El-Fergany, A. A. (2022). Efficient PEM fuel cells parameters identification using hybrid artificial bee colony differential evolution optimizer. Energy 250, 123830. doi:10.1016/j.energy.2022.123830

CrossRef Full Text | Google Scholar

Hasanien, H. M., Shaheen, M. A., Turky, R. A., Qais, M. H., Alghuwainem, S., Kamel, S., et al. (2022). Precise modeling of PEM fuel cell using a novel Enhanced Transient Search Optimization algorithm. Energy 247, 123530. doi:10.1016/j.energy.2022.123530

CrossRef Full Text | Google Scholar

Ido, A., and Kawase, M. (2020). Development of a tubular molten carbonate direct carbon fuel cell and basic cell performance. J. Power sources 449, 227483. doi:10.1016/j.jpowsour.2019.227483

CrossRef Full Text | Google Scholar

Inci, M., and Türksoy, Ö. (2019). Review of fuel cells to grid interface: Configurations, technical challenges and trends. J. Clean. Prod. 213, 1353–1370. doi:10.1016/j.jclepro.2018.12.281

CrossRef Full Text | Google Scholar

Kandidayeni, M., Macias, A., Khalatbarisoltani, A., Boulon, L., and Kelouwani, S. (2019). Benchmark of proton exchange membrane fuel cell parameters extraction with metaheuristic optimization algorithms. Energy 183, 912–925. doi:10.1016/j.energy.2019.06.152

CrossRef Full Text | Google Scholar

Kennedy, J., and Eberhart, R. (1995). “Particle swarm optimization,” in Proceedings of ICNN'95-international conference on neural networks (Perth, WA, Australia: IEEE), 1942–1948.

Google Scholar

Li, J., Gao, X., Cui, Y., Hu, J., Xu, G., and Zhang, Z. (2020). Accurate, efficient and reliable parameter extraction of PEM fuel cells using shuffled multi-simplexes search algorithm. Energy Convers. Manag. 206, 112501. doi:10.1016/j.enconman.2020.112501

CrossRef Full Text | Google Scholar

Li, S., Chen, H., Wang, M., Heidari, A. A., and Mirjalili, S. (2020). Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 111, 300–323. doi:10.1016/j.future.2020.03.055

CrossRef Full Text | Google Scholar

Mann, R. F., Amphlett, J. C., Hooper, M. A., Jensen, H. M., Peppley, B. A., and Roberge, P. R. (2000). Development and application of a generalised steady-state electrochemical model for a PEM fuel cell. J. Power sources 86 (1-2), 173–180. doi:10.1016/s0378-7753(99)00484-x

CrossRef Full Text | Google Scholar

Menesy, A. S., Sultan, H. M., Korashy, A., Kamel, S., and Jurado, F. (2021). A modified farmland fertility optimizer for parameters estimation of fuel cell models. Neural comput. Appl. 33 (18), 12169–12190. doi:10.1007/s00521-021-05821-1

CrossRef Full Text | Google Scholar

Miao, D., Chen, W., Zhao, W., and Demsas, T. (2020). Parameter estimation of PEM fuel cells employing the hybrid grey wolf optimization method. Energy 193, 116616. doi:10.1016/j.energy.2019.116616

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Mirjalili, S. (2016). Sca: A sine cosine algorithm for solving optimization problems. Knowledge-based Syst. 96, 120–133. doi:10.1016/j.knosys.2015.12.022

CrossRef Full Text | Google Scholar

Mossa, M. A., Kamel, O. M., Sultan, H. M., and Diab, A. A. Z. (2021). Parameter estimation of PEMFC model based on Harris Hawks’ optimization and atom search optimization algorithms. Neural comput. Appl. 33 (11), 5555–5570. doi:10.1007/s00521-020-05333-4

CrossRef Full Text | Google Scholar

Niu, Q., Zhang, H., and Li, K. (2014). An improved TLBO with elite strategy for parameters identification of PEM fuel cell and solar cell models. Int. J. Hydrogen Energy 39 (8), 3837–3854. doi:10.1016/j.ijhydene.2013.12.110

CrossRef Full Text | Google Scholar

Özdemir, M. T. (2021). Optimal parameter estimation of polymer electrolyte membrane fuel cells model with chaos embedded particle swarm optimization. Int. J. Hydrogen Energy 46 (30), 16465–16480. doi:10.1016/j.ijhydene.2020.12.203

CrossRef Full Text | Google Scholar

Pourrahmani, H., Siavashi, M., and Moghimi, M. (2019). Design optimization and thermal management of the PEMFC using artificial neural networks. Energy 182, 443–459. doi:10.1016/j.energy.2019.06.019

CrossRef Full Text | Google Scholar

Priya, K., Babu, T. S., Balasubramanian, K., Sathish Kumar, K., and Rajasekar, N. (2015). A novel approach for fuel cell parameter estimation using simple genetic algorithm. Sustain. Energy Technol. Assessments 12, 46–52. doi:10.1016/j.seta.2015.09.001

CrossRef Full Text | Google Scholar

Priya, K., and Rajasekar, N. (2019). Application of flower pollination algorithm for enhanced proton exchange membrane fuel cell modelling. Int. J. Hydrogen Energy 44 (33), 18438–18449. doi:10.1016/j.ijhydene.2019.05.022

CrossRef Full Text | Google Scholar

Priya, K., Sathishkumar, K., and Rajasekar, N. (2018). A comprehensive review on parameter estimation techniques for Proton Exchange Membrane fuel cell modelling. Renew. Sustain. Energy Rev. 93, 121–144.

CrossRef Full Text | Google Scholar

Qin, F., Liu, P., Niu, H., Song, H., and Yousefi, N. (2020). Parameter estimation of PEMFC based on improved fluid search optimization algorithm. Energy Rep. 6, 1224–1232. doi:10.1016/j.egyr.2020.05.006

CrossRef Full Text | Google Scholar

Rao, R. (2016). Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Industrial Eng. Comput. 7 (1), 19–34.

CrossRef Full Text | Google Scholar

Rao, Y., Shao, Z., Ahangarnejad, A. H., Gholamalizadeh, E., and Sobhani, B. (2019). Shark Smell Optimizer applied to identify the optimal parameters of the proton exchange membrane fuel cell model. Energy Convers. Manag. 182, 1–8. doi:10.1016/j.enconman.2018.12.057

CrossRef Full Text | Google Scholar

Rezk, H., Ferahtia, S., Djeroui, A., Chouder, A., Houari, A., Machmoum, M., et al. (2022). Optimal parameter estimation strategy of PEM fuel cell using gradient-based optimizer. Energy 239, 122096.

CrossRef Full Text | Google Scholar

Rizk-Allah, R. M., and El-Fergany, A. A. (2021). Artificial ecosystem optimizer for parameters identification of proton exchange membrane fuel cells model. Int. J. Hydrogen Energy 46 (75), 37612–37627. doi:10.1016/j.ijhydene.2020.06.256

CrossRef Full Text | Google Scholar

Saebea, D., Chaiburi, C., and Authayanun, S. (2019). Model based evaluation of alkaline anion exchange membrane fuel cells with water management. Chem. Eng. J. 374, 721–729. doi:10.1016/j.cej.2019.05.200

CrossRef Full Text | Google Scholar

Salim, R., Nabag, M., Noura, H., and Fardoun, A. (2015). The parameter identification of the Nexa 1.2 kW PEMFC's model using particle swarm optimization. Renew. Energy 82, 26–34. doi:10.1016/j.renene.2014.10.012

CrossRef Full Text | Google Scholar

Sayed, E. T., Abdelkareem, M. A., Alawadhi, H., Elsaid, K., Wilberforce, T., and Olabi, A. (2021). Graphitic carbon nitride/carbon brush composite as a novel anode for yeast-based microbial fuel cells. Energy 221, 119849. doi:10.1016/j.energy.2021.119849

CrossRef Full Text | Google Scholar

Seleem, S. I., Hasanien, H. M., and El-Fergany, A. A. (2021). Equilibrium optimizer for parameter extraction of a fuel cell dynamic model. Renew. Energy 169, 117–128. doi:10.1016/j.renene.2020.12.131

CrossRef Full Text | Google Scholar

Selem, S. I., Hasanien, H. M., and El‐Fergany, A. A. (2020). Parameters extraction of PEMFC's model using manta rays foraging optimizer. Int. J. Energy Res. 44 (6), 4629–4640. doi:10.1002/er.5244

CrossRef Full Text | Google Scholar

Shaheen, M. A., Hasanien, H. M., El Moursi, M., and El-Fergany, A. A. (2021). Precise modeling of PEM fuel cell using improved chaotic MayFly optimization algorithm. Int. J. Energy Res. 45 (13), 18754–18769. doi:10.1002/er.6987

CrossRef Full Text | Google Scholar

Shiyong, L. (2007). Quantum particle swarms algorithm for continuous space optimization. Chin. J. Quantum Electron. 24 (5), 569.

Google Scholar

Sultan, H. M., Menesy, A. S., Kamel, S., Selim, A., and Jurado, F. (2020). Parameter identification of proton exchange membrane fuel cells using an improved salp swarm algorithm. Energy Convers. Manag. 224, 113341. doi:10.1016/j.enconman.2020.113341

CrossRef Full Text | Google Scholar

Turgut, O. E., and Coban, M. T. (2016). Optimal proton exchange membrane fuel cell modelling based on hybrid Teaching Learning Based Optimization–Differential Evolution algorithm. Ain Shams Eng. J. 7 (1), 347–360. doi:10.1016/j.asej.2015.05.003

CrossRef Full Text | Google Scholar

Wolpert, D. H., and Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1 (1), 67–82. doi:10.1109/4235.585893

CrossRef Full Text | Google Scholar

Xu, S., Wang, Y., and Wang, Z. (2019). Parameter estimation of proton exchange membrane fuel cells using eagle strategy based on JAYA algorithm and Nelder-Mead simplex method. Energy 173, 457–467. doi:10.1016/j.energy.2019.02.106

CrossRef Full Text | Google Scholar

Yang, Z., Liu, Q., Zhang, L., Dai, J., and Razmjooy, N. (2020). Model parameter estimation of the PEMFCs using improved barnacles mating optimization algorithm. Energy 212, 118738. doi:10.1016/j.energy.2020.118738

CrossRef Full Text | Google Scholar

Yapici, H., and Cetinkaya, N. (2019). A new meta-heuristic optimizer: Pathfinder algorithm. Appl. soft Comput. 78, 545–568. doi:10.1016/j.asoc.2019.03.012

CrossRef Full Text | Google Scholar

Yousri, D., Mirjalili, S., Machado, J. T., Thanikanti, S. B., elbaksawi, O., and Fathy, A. (2021). Efficient fractional-order modified Harris Hawks optimizer for proton exchange membrane fuel cell modeling. Eng. Appl. Artif. Intell. 100, 104193. doi:10.1016/j.engappai.2021.104193

CrossRef Full Text | Google Scholar

Zhang, L., and Wang, N. (2018). Application of coRNA-GA based RBF-NN to model proton exchange membrane fuel cells. Int. J. Hydrogen Energy 43 (1), 329–340. doi:10.1016/j.ijhydene.2017.11.027

CrossRef Full Text | Google Scholar