Energy-efficient tram speed trajectory optimization considering the influence of the traffic light

The tram typically adopts the form of semi-independent right of way, which is affected by the traffic light at junctions. The parking and wait time of the tram due to red lights will increase the energy consumption and reduce the passenger comfort. This paper proposes a speed trajectory optimization approach for the tram without parking when encountering a red light. This approach is realized by reasonably adjusting the running time and speed of the tram between two adjacent sections bounded by the traffic light at the junction, on the premise that the total travel time of the whole section remains unchanged. In the model, the constraints of tram movement, speed limits, and line conditions are considered. Moreover, considering the influence of the traffic light, the comfort and traffic light constraints are added to establish the energy-efficient tram speed trajectory optimization model. The nonlinear constraints in the optimization model are converted to linear constraints using the segmental approximation method and adding constraints. As a result, the optimization model is reformulated into a mixed-integer linear programming model, which could be solved by a commercial solver like CPLEX. Numerical experiments are conducted with a 3,660 m long section of the tram line with the traffic light at the junction. The experimental results show that the speed trajectory optimization approach considering the influence of the traffic light proposed in this paper can reduce the total energy consumption by 23.46% and improve passenger comfort.

Introduction

The tram is a widely preferred transportation system in small and medium-sized cities due to its energy-efficient, comfortable, economic, and punctual characteristics (Gao and Yang, 2019). With the increase in the tram operating mileage, the tram energy consumption continues to grow. Due to the limited energy and the requirement for environmental protection, the energy conservation has become one of the issues that must be considered in the sustainable development of rail transportation (Tan et al., 2018).

At present, the newly-built tram system in China generally adopts the form of semi-independent right of way. Specifically, the tram has an independent right of way on the road section, and the right of way at the junction is determined by the traffic right (Luo et al., 2016). When the tram runs to the junction, it will be affected by the traffic light. If the tram encounters a red light, it must park and wait until the light turns green and then start to accelerate again. This process will increase the running energy consumption of the tram and reduce passenger comfort. To solve the problem, green wave control is usually used to coordinate the phase difference of each traffic light. Thus, the tram can be met with green light continuously when it operates between junctions according to the specified time (Chen and Wang, 2018). However, the tram will inevitably encounter a red light due to the uneven distribution of time margin between sections or failure to consider the starting and stopping maneuvering of the tram at the station in the green wave design. In addition, when the tram operates in a complex traffic environment, it will be disturbed by cars, non-motor vehicles, and pedestrians on the road (Shi et al., 2017). These are also the reasons why the tram encounters the red light under the green wave control. Therefore, it is exceedingly necessary to carry out energy-efficient optimization research on the case that the tram must park and wait when encountering a red light. The tram speed trajectory optimization is one of the effective ways. The traction energy consumption can be reduced by optimizing the tram speed trajectory, thus achieving energy savings in the system (Huang et al., 2018).

Hence, this paper considers the influence of the traffic light and proposes a speed trajectory optimization approach for the tram without parking when encountering a red light. This approach can be realized by reasonably adjusting the running time and speed of the tram between two adjacent sections bounded by the traffic light at the junction, on the premise that the total travel time of the whole section remains unchanged. In addition to the constraints in the classical speed trajectory optimization model, the comfort and traffic light constraints are also considered. Moreover, the energy-efficient optimization model of the tram speed trajectory considering the influence of the traffic light is established.

The remainder of this paper is structured as follows. The literature review of the speed trajectory optimization problem is provided in Section 2. Section 3 describes a speed trajectory optimization approach for the tram without parking when encountering a red light and the process of discretization of the tram running section. In Section 4, the energy-efficient optimization model of tram speed trajectory considering the influence of the traffic light is established based on the discrete space method. Furthermore, a mixed-integer programming method is used to solve the optimization problem. In Section 5, numerical experiments are carried out to verify the validity of the proposed approach. Finally, the conclusions of this paper are summarized in Section 6.

Literature review

High-speed rail and subway trains speed trajectory optimization

In recent years, there have been a large number of studies on the optimization of the train speed trajectory concerning subway and high-speed rail, which are similar to the tram. Moreover, most of these studies aim to minimize the energy consumption of trains. Ahmadi et al. (2018) put forward the approach for efficient utilization of regenerative braking energy with simultaneous optimization of speed trajectory and energy storage system. As a result, the goal of energy consumption minimization was achieved. The genetic algorithm was used to solve the problem, and the best speed trajectory and energy storage scheme was determined in the experiment. Ko et al. (Ko et al., 2004; Ko et al., 2005) transformed the optimization problem of the train speed trajectory into a multi-stage decision-making problem using the first-order Taylor formula and trapezoidal rules. The dynamic programming method was used to solve the optimal speed trajectory of the train. Zhou et al. (Zhou et al., 2016; Zhou et al., 2017)established the spatial network of the operation time, location, and speed to simplify the high-speed train’s operation process. Then dynamic programming was used to solve the speed trajectory and schedule of train energy-efficient optimization. Haahr J T et al. (Hayashi, 1989) put forward a method to seek the best speed trajectory, which used the space-time graph to describe the optimization problem and generated the energy-efficient train speed trajectory by the dynamic programming to reduce energy consumption. He et al. (2021) considered the actual line environment and uncertain trainload and established a multi-particle operation model. The model was solved using a mutation dichotomy and a differential evolution algorithm. Based on this model, the optimal energy-efficient train speed trajectory is determined. Wu et al. (2018) built a comprehensive optimization model to obtain the speed trajectory and minimize energy consumption. They considered the constraints of on-board energy storage device (ESD) characteristics. The mixed-integer linear programming model of the discrete distance was used to solve the optimization problem of speed trajectory.

Furthermore, some of the studies also considered passenger comfort and travel time in their objectives. Cao et al. (2022) proposed a method for optimizing the speed trajectory of the high-speed train. This optimization method defined the objective function as the trade-off function between energy consumption and passenger comfort. Besides the constraints in the classical train speed trajectory optimization model, the constraints also consider three new factors: discrete throttle setting, neutral zone, and segmented tunnel resistance. The mixed-integer linear programming method was used to address the speed trajectory optimization problem, thus reducing the difficulty of solving the problem. Jia et al. (2018) considered energy efficiency and service quality and established a dual-objective train speed trajectory optimization model with the minimum energy consumption and the shortest travel time. They reformulated the optimization objectives using a fuzzy linear programming method to obtain the optimal speed trajectory with equal satisfaction for both objectives. Besides, a genetic algorithm was used to address the problem of train speed trajectory optimization.

The above studies have achieved extensive results, which provide valuable references for the research in this paper, especially in the speed trajectory solution method. Classical mathematical planning methods such as dynamic programming, fuzzy linear and mixed-integer linear programming, and intelligent optimization algorithms such as genetic algorithms and differential evolutionary algorithms are used to solve the optimal speed trajectory of high-speed or subway trains. These methods can also be used to solve the tram speed trajectory. However, other research results are not fully applicable to the tram system because there are major differences in the operating environment of the tram compared to subway and high-speed trains. For example, the tram running between adjacent stations is affected by the junction speed limit and the traffic light, which are not considered in existing studies on the speed trajectory optimization of high-speed and subway trains.

Tram speed trajectory optimization

Compared with the studies on the speed trajectory optimization of high-speed and subway trains, there are few studies in the field of the tram. Zhang et al. (2021) proposed a sequential optimization structure to optimize speed trajectories and energy management strategies for tram operation to reduce tram operating costs. The optimization structure took the optimal solution of the speed trajectory as an input of the energy management strategy to realize the synchronization of the two optimizations. Xu et al. (2018) designed a coasting optimization algorithm considering the regenerative braking energy for energy storage trams and solved the energy-efficient speed trajectory and operating energy consumption at a given time. Yan et al. (2018) proposed a method to reduce the energy consumption of the tram operation and improve its operational stability. On the premise of ensuring that the running distance between stations remains equal, the running time between stations was within the feasible range, and the ability of the supercapacitor to absorb braking power was met. This method redistributes the running distance of the tram under traction, coasting, braking, and station parking conditions, as well as the magnitude of traction and braking force of the tram under traction and braking conditions. Thus, an optimal target operation curve of the tram was calculated. Enjalbert, S et al. (Enjalbert and Boukal, 2019) took the tram operating state, control input, and travel time as constraints and developed an optimization model for minimizing the energy consumption of the tram. Then, the nonlinear problem of speed trajectory optimization is converted into a linear problem based on space and distance formulations. The above studies aim to achieve energy-efficient operation of the tram and provide valuable references for this study, but none of them consider the influence of the traffic light.

However, the traffic light must be considered to seek an optimal speed trajectory that is closer to the actual running condition of the tram, thus achieving the goal of minimizing the energy consumption of the tram. Currently, only a few studies have considered the traffic light. Xiao et al. (Xiao et al., 2018; Xiao et al., 2020; Xiao et al., 2021) proposed a multi-stage integrated optimization approach considering signal control strategies for the cooperative optimization of tram speed trajectories and power allocation. A comprehensive optimization model was developed to minimize the total energy consumption, with running time, variable gradients and curves, speed limits, power balance, and signal timing at certain intersections as constraints. Moreover, the influences of green signal time windows on the optimized solution are investigated. Wu et al. (2020) put forward an optimal speed trajectory planning strategy based on terrain and traffic lights for the Autonomous-Rail Rapid Tram (ART). The speed trajectory optimization strategy based on the dynamic programming was constructed to pass the traffic light at the green time and reach the destination with minimum energy consumption within the predetermined time interval. Li et al. (2022) proposed an optimization model of two-stage stochastic for timetable and tram control to improve the reliability of Transit Signal Priority (TSP) considering uncertain dwell times. Compared with other methods, this method can reduce the energy consumption of trams and the number of stops of trams at junctions under the same travel time.

Several of the above studies considered the influence of the traffic light. It is mainly reflected in these aspects: the effects of the signal green time window and trip time are investigated by setting the traffic lights as constraints in the model; the tram is prevented from encountering a red light by green wave signal control; The number of the tram stops at junctions is reduced by signal priority strategies. Which have been conducted at the level of signal control to reduce the probability of the tram encountering a red light at the junction. They have the same objective as this study, i.e., to achieve the tram to cross the junction at a green light. However, the research in this paper focuses on how the tram can avoid a red light without parking when it encounters a red light. In addition, connected and automated buses running on dedicated car lanes are similar to trams and need to consider the influence of the traffic light. Thus, research in this field has laid the groundwork for this paper. Wang et al. (2019) proposed a trajectory planning strategy that considered traffic signal timings, bus schedules, and dynamic speeds for improving the fuel efficiency of connected and automated buses traveling on signal corridors. A Min-Sum-Min Model was constructed and solved using a Simultaneous Perturbation Stochastic Approximation (SPSA) and Pontryagin’s Maximum Principle, which guaranteed that the buses did not arrive at intersections at the red time. This study assumed that buses operate on dedicated car lanes, free from other vehicles, which is similar to the study in this paper and provides a lot of valuable references. However, the tram vehicles are heavier and have greater inertia, so the acceleration, deceleration rates, traction, and braking characteristics differ from those of connected and automated buses. More factors, such as passenger comfort, need to be considered.

To conclude, the main contributions of this paper can be summarized as follows.

1) In this paper, we propose a speed trajectory optimization approach for the tram without parking when encountering a red light. This approach is realized by reasonably adjusting the running time and speed of the tram between two adjacent sections bounded by the traffic light at the junction, on the premise that the total travel time of the whole section remains equal.

2) In addition to the tram movement equations, speed, and route constraints, we also consider the comfort and the traffic light constraints. An energy-efficient optimization model of tram speed trajectory considering the influence of the traffic light is established.

3) The nonlinear constraints in the optimization model are converted to linear constraints using the segmental approximation method and adding constraints. As a result, the optimization model is reformulated into a mixed-integer linear programming model to reduce the difficulty of solving the optimization model.

Problem statement

Analysis of the influence of the traffic light on tram operation

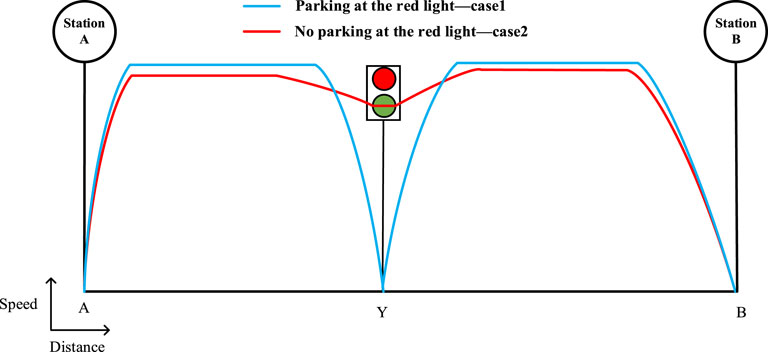
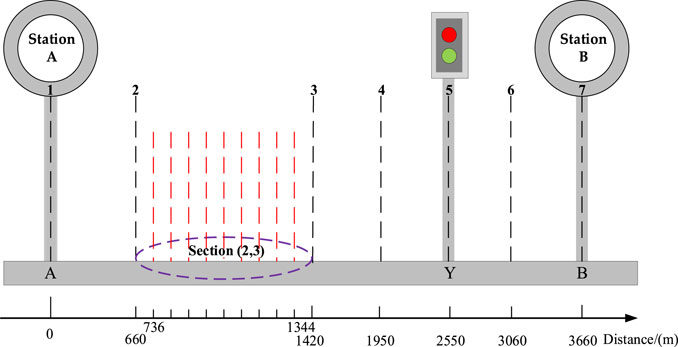
As shown in Figure 1, station A and station B on the tram line form section A-B, there is a junction in this section. With a parking point in front of the traffic light, which is denoted as point Y in this paper. This figure shows the schematic diagram of the two speed trajectories in two cases when the tram encounters a red light, which will be described below.

FIGURE 1

FIGURE 1. The schematic diagram of speed trajectories in two cases.

Case 1. Parking at the red light. In this case, we do not take any measures to avoid a red light. As shown in the blue curve in Figure 1, when the tram encounters a red light, it will park at point Y normally and start to accelerate after the traffic light turns green. The loss of energy consumption and reduced comfort caused by the red light is not considered.

Case 2. No parking at the red light. In this case, we consider the influence of the red light, as shown in the red curve in Figure 1. It is based on the optimization idea that the tram does not park at point Y and can pass through the junction at a relatively constant speed when the traffic light turns green. The purpose is to reduce the energy consumption loss of the tram due to the red light and ensure passenger comfort.After analyzing the two speed trajectories of the tram in the two cases described above, an optimization approach of the tram speed trajectory considering the influence of the red light is presented. Specifically, the optimization approach is to divide the tram running section A-B into two sections, A-Y and Y-B, with point Y as the boundary. When the tram is running in section A-Y, the tram driver knows in advance that a red light will be encountered and start to slow down until the tram can pass through the junction at a relatively constant speed just when the traffic signal turns green. During this period, the parking time of the tram at point Y affected by the red light will be changed into the running time. The total travel time of the tram, which is the sum of the running time and parking time in the whole section, is the same in case 1 and case 2. The case of no parking at the red light by adjusting the running speed and time of the tram in sections A-Y and Y-B, so that the tram does not park at point Y. As a result, to avoid the reduction of passenger comfort and the loss of energy consumption of tram caused by the situation that the tram decelerates from high speed to parking and then starts to accelerate.In the case of no parking at the red light, the tram does not park at point Y by adjusting the speed and time of tram operation in sections A-Y and Y-B. The situation that the tram decelerates from high speed to park and then starts to accelerate again no longer occurs, ensuring higher passenger comfort and lower energy consumption of the tram.

Discretization of tram the running section

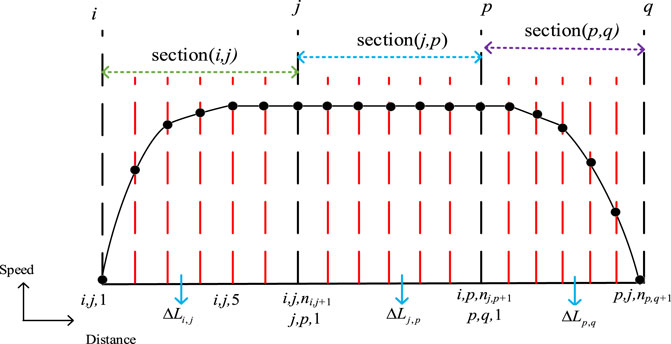
We use the discrete space method to disperse the tram running section. As a result, the tram speed trajectory optimization problem is converted into a multi-stage decision-making problem to reduce the difficulty of building and solving the tram speed trajectory optimization model (Tang and Feng, 2013).

The tram line is composed of a series of nodes, let $N$ be the set of all nodes, that is, $N=\left\{i,j,p,q,\dots \right\}$. First of all, we divide the whole running section of tram into multiple sections and set $U$ as the set of all the divided sections, that is, $U=\left\{\left(i,j\right),\left(j,p\right),\left(p,q\right),\dots \right\},i,j,p,q\in N$. Then, each section is again discretized into $n_{i,j},n_{j,p},n_{p,q},\dots$ small segments, and the discrete small segments on the same section have the same length. We take the section $\left(i,j\right)$ as an example. This section is discretized into $n_{i,j}$ small segments, and each small segment’s length is $\Delta L_{i,j}$. There will be $n_{i,j}+1$ speed points in this segment, and the position of each speed point can be expressed as $\left(i,j,k\right),k=1,\dots ,n_{i,j}+1$. The schematic diagram of discretization processing is shown in Figure 2.

FIGURE 2

FIGURE 2. Schematic diagram of discretization of tram running section.

Model formulation

Inputs, decision variables, outputs, and assumptions of the problem

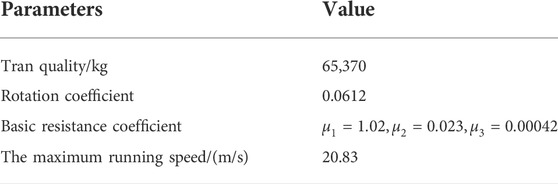
The input parameters of the energy-efficient optimization problem of the tram speed trajectory considering the influence of the traffic light include: 1) For the section with the traffic light on the tram line, the length, speed limit, curve, slope, fixed speed limit value, and the number of discrete segments of each section are known. 2) For the tram vehicle, the quality of the vehicle, rotation coefficient, parking time due to red light, running speed, upper and lower limits of acceleration, characteristics of train traction and braking force, and the calculation formulas of basic resistance and additional resistance are indicated.

The tram speed trajectory optimization problem considering the influence of the traffic light is identified for the tram, we need to determine the speed, acceleration, traction, and braking force at each discrete section node.

The output of the energy-efficient optimization problem of the tram speed trajectory considering the influence of the traffic light is the best energy-efficiency speed trajectory of the tram running in the whole section.

We make the following assumptions: 1) We do not consider the utilization and recovery of regenerative braking energy of the tram. 2) During the operation of the tram, the tram driver knows in advance that the traffic signal is red. 3) In the small discrete segment. The tram accelerates, decelerates, or runs at uniform speed with fixed acceleration or deceleration. The changes in acceleration and deceleration only occur in different discrete small segments. 4) The maximum speed limit of each section is given, and line conditions and tram vehicle characteristics determine the maximum speed.

Symbol definition

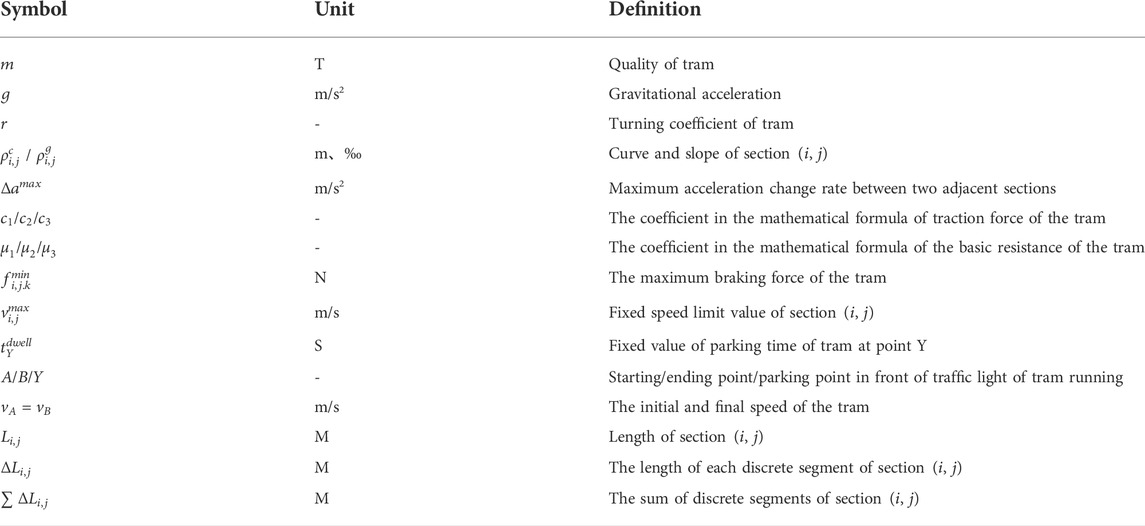
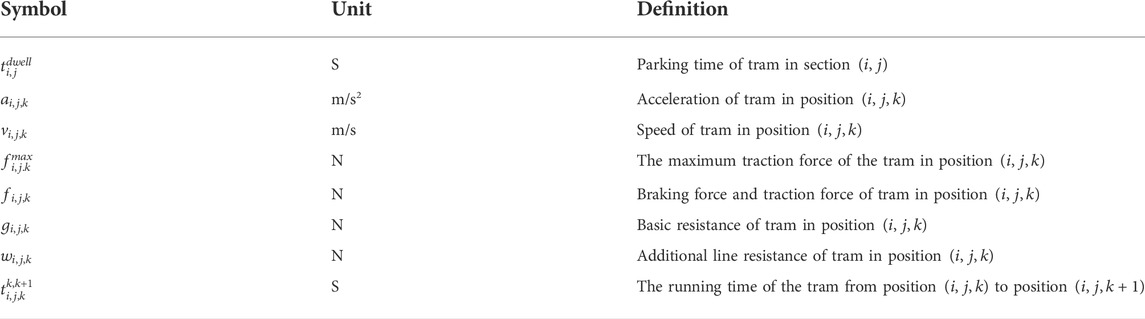
Tables 1–3 respectively list the symbols and definitions of corner markers and sets, input parameters, and decision variables in the model.

TABLE 1

TABLE 1. Corner markers and sets.

TABLE 2

TABLE 2. Input parameters.

TABLE 3

TABLE 3. Decision variables.

Objective function and constraints

The objective of the model is to minimize the energy consumption of tram operations.

$Z=\mathit{min}E=\mathit{min}{\displaystyle \sum }_0^{\left|L_{i,j}\right|}{f}_{i,j,k}\times \Delta L_{i,j}(1)$

Where $E$ is the traction energy consumption of tram (kwh); $f_{i,j,k}$ is the traction force of the tram at the position $\left(i,j,k\right)$ (N); $\left|L_{i,j}\right|$ is the total displacement length of the tram on the section $\left(i,j\right)$ (m); $\Delta L_{i,j}$ is the length of the discrete segment of section $\left(i,j\right)$ (m).

In this model, we make the following as constraints:

(1) Dynamic constraints of tram

1) Tram movement equations

This paper regards the tram as a point mass and the space of its operation is discretized. According to Newton’s second law, the movement equations of tram operations can be written as

$m(1+r)\cdot a=f_{i,j,k}-g_{i,j,k}-w_{i,j,k},\left(i,j\right)\in U;k=1,\dots ,n_{i,j}(2)$

$g_{i,j,k}=mg\left({\mu }_1+{\mu }_2{v}_{i,j,k}+{\mu }_3{v}_{i,j,k}^2\right),\left(i,j\right)\in U;k=1,\dots ,n_{i,j}(3)$

$w_{i,j,k}=mg\left(\frac{600}{{\rho }_{i,j}^c}+{\rho }_{i,j}^g\right),\left(i,j\right)\in U;k=1,\dots ,n_{i,j}(4)$

Constraint (2) represents the acceleration of the tram in position $\left(i,j,k\right)$, which is determined by the vehicle’s weight, traction or braking force, basic resistance, and additional resistance. Constraint (3) represents the basic resistance constraint when the tram runs to position $\left(i,j,k\right)$. Constraint (4) represents the additional resistance constraint during tram operation. Among them, the resistance generated when the tram passes through the curve and ramp is independent of the speed, which is expressed as $mg\times 600/p_{i,j}^c$ and $mg\times {\rho }_{i,j}^g$ respectively.

2) Tram traction and braking force constraints

Constraint (5) is used to restrain the upper and lower limits of the traction or braking force $f_{i,j,k}$ to which the tram is subjected during operation.

$f_{i,j,k}^{min}\le f\le f_{i,j,k}^{max},\forall \left(i,j\right)\in U;k=1,\cdots ,n_{i,j}(5)$

The upper limit, determined by constraint (6), is the maximum traction force $f_{i,j,k}^{max}$ of the tram, and the lower limit is the maximum braking force $f_{i,j,k}^{min}$ of the tram. The maximum traction force $f_{i,j,k}^{max}$ of the tram is related to the speed and is a piecewise function of the square of the speed.

$f_{i,j,k}^{max}=c_{1,m}+c_{2,m}{v}_{i,j,k}+c_{3,m}{v}_{i,j,k}^2,v_{i,j,k}\in \left[v_{r,}{v}_{r+1}\right],m=\mathrm{1,2}(6)$

3) The relationship between the running distance, running time, speed, and acceleration of the tram.

The relationship between running distance, running time, speed, and acceleration of the tram in discrete segments can be expressed as constraints (7) and (8). Among them, constraint (8) can be used to solve the running time of the tram passing through the kth discrete segment.

$a_{i,j,k}=\frac{v_{i,j,k+1}^2-v_{i,j,k}^2}{2\Delta L_{i,j}},\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(7)$

$\Delta L_{i,j}=\frac{\left(v_{i,j,k}+v_{i,j,k+1}\right)\times t_{i,j,k}^{k,k+1}}{2},\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(8)$

${{\displaystyle \sum }}^{\text{}}\Delta L_{i,j}=L_{i,j}(9)$

(2) Comfort constraint

During the tram running process, frequent changes in acceleration will reduce passenger comfort. Hence, the acceleration change rate is used to restrict the acceleration change. Constraint (10) is used to set the upper limit of the acceleration change rate on the two adjacent discrete segments to ensure passenger comfort (Li et al., 2019; Lin and Liu, 2021). $comfor{t}_{i,j}$ is used to express the comfort degree generated by the tram running in the section $\left(i,j\right)$, and its value is calculated by Eq. 11 (Liu et al., 2019), to evaluate the degree of comfort optimization more intuitively. The smaller the comfort value, the higher the comfort.

$\left|a_{i,j,k+1}-a_{i,j,k}\right|\le \Delta a^{max},\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(10)$

$comfor{t}_{i,j}={\displaystyle \sum }_{k=1}^{n_{i,j}}\left|a_{i,j,k+1}-a_{i,j,k}\right|,\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(11)$

(3) Tram speed constraints

1) The initial and final speed limit of the tram

Constraint (12) restricts the initial and final speed of the tram to ensure that the speed of the tram at the starting point and the terminal point is 0.

$v_A=v_B=0(12)$

2) Line fixed speed limit.

Generally speaking, each section of the tram line will be set with an allowed speed value. Constraint (13) is used to ensure that the running speed of the tram does not exceed the fixed speed limit given by the line.

$0<v_{i,j,k}<v_{i,j}^{max},\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(13)$

3) Speed continuity constraint of two adjacent sections.

For two adjacent sections, the speed at which the tram arrives in the previous section is the same as the departure speed of the latter section. That is, the speed of the two adjacent sections is continuous (Jin et al., 2018).

$v_{i,j,n_{i,j}+1}=v_{j,p,1},\forall \left(i,j\right)\in U;\left(j,p\right)\in U;j\in U-A-B(14)$

(4) Traffic light constraints

When the tram runs to the junction, the traffic signal is red. For case1, parking at the red light, after optimization, the total travel time of the tram in section A-B is expressed as $T_{A,B}$, the total running time is expressed as $t_{A,B}$, and the running time in section A-Y and section Y-B are expressed as $t_{A,Y}$ and $t_{Y,B}$, respectively. For case2, no parking at a red light, after optimization, the total travel time of the tram in section A-B is expressed as $T_{A,B}^{red}$, the total running time is expressed as $t_{A,B}^{red}$, and the running time in section A-Y and section Y-B are expressed as $t_{A,Y}^{red}$ and $t_{Y,B}^{red}$, respectively. Then, according to the description of the optimization approach proposed in this paper in Section 3.1, there can be constraints (15 to 19).

$T_{A,B}=t_{A,B}+t_{dwell}=t_{A,B}^{red}=T_{A,B}^{red}(15)$

$t_{A,Y}+t_{Y,B}=t_{A,B}(16)$

$t_{A,Y}^{red}+t_{Y,B}^{red}=t_{A,B}^{red}(17)$

$t_{A,Y}^{red}\ge t_{A,Y}(18)$

$v_Y>0(19)$

Constraint (15) is used to satisfy that the total travel time of the tram in section A-B is constant in case 1 and case 2. Constraint (16) and constraint (17) represent respectively that the sum of the running times of the tram in section A-Y and Y-B is equal to the running time of the tram in section A-B in case 1 and case 2. Case 2 is to change the parking time of the tram at point Y in case 1 to the running time of the tram in section A-Y. Therefore, in case 2, the running time of the tram in section A-Y is longer than in case 1, which is expressed by constraint 18). Constraint (19) is used to restrict the tram to not parking at point Y.

Solution approach

The discrete space method has been used to disperse the tram running section, which reduces the complexity of the optimization model to a certain extent. Due to the existence of square term, variable product term, and absolute value in the optimization model, the problem of tram speed trajectory optimization is still a nonlinear programming model subject to multiple constraints. It is more difficult to solve than the linear programming model (Long et al., 2019). Therefore, this paper uses the linear transformation idea proposed by Williams to linearize the square term, variable product term, and absolute value in the optimization model, respectively (Williams, 1985,2013). As a result, the nonlinear constraints in the optimization model are converted to linear constraints by using the segmental approximation method and adding constraints. The optimization model is reformulated into a mixed-integer linear programming model to solve the optimization model of tram energy-efficient speed trajectory considering the influence of the traffic light.

(1) Linearization of squared terms

The presence of the square term $v_{i,j,k}^2$ in the optimization model makes constraint (2) ∼ constraint (7) and constraint (10), i.e., the tram movement equations, the traction or braking force constraint, the basic resistance constraint, the relationship between acceleration and speed, and the comfort constraint are nonlinearly related. In this paper, the square term $v_{i,j,k}^2$ is linearly changed by the piecewise approximation (Long et al., 2020). The specific steps are as follows:

Step 1. Determination of the range of value of the variable in the squared term. In this paper, the lower limit of the variable $v_{i,j,k}^2$ of $v$ in this model is 0, and the upper limit is the speed limit value $v_{i,j}^{max}$ determined by the section and the characteristics of tram vehicles.

Step 2. The division of the range $\left[0,v_{i,j}^{max}\right]$ of value the variable in the square term. Within the range of value of $v_{i,j,k}^2$, divide the X-axis into $\omega$ small segments, and the length of each small segment is $v_{i,j}^{max}/\omega$.

Step 3. Introduction of variables. The logical variables $\tilde{\phi }$, ${\tilde{\phi }}_1$ 、 ${\tilde{\phi }}_2$ 、…… 、 ${\tilde{\phi }}_{\omega }$ are introduced to represent the proportion of line segments on the X-axis. Then the coefficients of ${\tilde{\phi }}_1$ 、 ${\tilde{\phi }}_2$ 、 …… 、 ${\tilde{\phi }}_{\omega }$ are $v_{i,j}^{max}/\omega$; The variable ${\tilde{y}}_{i,j,k}$ is introduced to represent $v_{i,j,k}^2$, that is, ${\tilde{y}}_{i,j,k}=v_{i,j,k}^2$.

Step 4. Using the variable $\widetilde{\phi }$ to represent the square term variable $v_{i,j,k}^2$ and the approximate variable ${\tilde{y}}_{i,j,k}$, as shown in Eqs 20–22.

${\tilde{v}}_{i,j,k}=\frac{v_{i,j}^{max}}{\omega }{\displaystyle \sum }_{x=1}^{\omega }{\tilde{\phi }}_{x,i,j,k},\forall \left(i,j\right)\in U,k=1,\dots ,n_{i,j}(20)$

${\tilde{y}}_{i,j,k}={\displaystyle \sum }_{x=1}^{\omega }\left[{\left(\frac{v_{i,j}^{max}}{\omega }\times x\right)}^2-{(\frac{v_{i,j}^{max}}{\omega }\times (x-1))}^2\right],\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(21)$

$0\le {\tilde{\phi }}_{x,i,j,k}\le 1,x=1,\dots ,\omega ;k=1,\dots ,n_{i,j}(22)$

Step 5. Introducing the 0–1 variable ${\tilde{\eta }}_{x,i,j,k}$ to represent the conditional expression ${\phi }_{x,i,j,k}>0\leftrightarrow {\eta }_{x,i,j,k}=1$, where ${\tilde{\eta }}_{x,i,j,k}$ and ${\phi }_{x,i,j,k}$ need to meet Eqs 23–26.

${\phi }_{x,i,j,k}-2{\eta }_{x,i,j,k}\le 0,k=1,\dots ,n_{i,j};x=1,\dots ,\omega (23)$

${\phi }_{x,i,j,k}-\epsilon \times {\eta }_{x,i,j,k}\ge 0,k=1,\dots ,n_{i,j};x=1,\dots ,\omega (24)$

${\displaystyle \sum }_{r=1}^{x-1}{\phi }_{x,i,j,k}\ge \left(x-1\right)\times {\eta }_{x,i,j,k},k=1,\dots ,n_{i,j};x=1,\dots ,\omega (25)$

${\displaystyle \sum }_{r=1}^{x-1}{\phi }_{x,i,j,k}\le \epsilon \times \left(1-{\eta }_{x,i,j,k}\right),k=1,\dots ,n_{i,j};x=1,\dots ,\omega (26)$

(2) Linearization of the equation for multiplying variables by variables

In the optimization model, the variable is multiplied by the variable to make Eq. 8 nonlinear constraint, which is linearized as follows:

Step 1. Representing the $\left(v_{i,j,k}+v_{i,j,k+1}\right)\times t_{i,j,k}^{k,k+1}$ in Eq. 8 as Eq. 27.

$\Delta L_{i,j}=\frac{1}{8}\left\{{\left[\left(v_{i,j,k}+v_{i,j,k+1}\right)+t_{i,j,k}^{k,k+1}\right]}^2-{\left[\left(v_{i,j,k}+v_{i,j,k+1}\right)+t_{i,j,k}^{k,k+1}\right]}^2\right\}\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(27)$

Step 2. Introducing 0–1 variables ${\psi }_{1,i,j,k}$ and ${\psi }_{2,i,j,k}$, and making them satisfy Eqs 28, 29, respectively.

${\psi }_{1,i,j,k}=\left(v_{i,j,k}+v_{i,j,k+1}\right)+t_{i,j,k}^{k,k+1},\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(28)$

${\psi }_{2,i,j,k}=\left(v_{i,j,k}+v_{i,j,k+1}\right)-t_{i,j,k}^{k,k+1},\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(29)$

Step 3. Representing the variable product $\left(v_{i,j,k}+v_{i,j,k+1}\right)\times t_{i,j,k}^{k,k+1}$ as a variable function, as shown in Eq. 30.

$\left(v_{i,j,k}+v_{i,j,k+1}\right)\times t_{i,j,k}^{k,k+1}={\psi }_{1,i,j,k}^2-{\psi }_{2,i,j,k}^2(30)$

Step 4. Linearizing ${\psi }_{1,i,j,k}^2$ and ${\psi }_{2,i,j,k}^2$ byEqs 20 –26, respectively.

(3) Linearization of absolute values

The presence of absolute value in the optimization model makes the comfort constraint of Eq. 10 nonlinear, and the constraints (31) and (32) can be added during linearization.

$a_{i,j,k+1}-a_{i,j,k}\le \Delta a^{max},\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(31)$

$a_{i,j,k}-a_{i,j,k+1}\le \Delta a^{max},\forall \left(i,j\right)\in U;k=1,\dots ,n_{i,j}(32)$

Numerical experiments

Experimental data

As shown in Figure 3, this paper takes a section with a length of 3660 m as an example. The section starts at A and ends at B, which is denoted as section A-B in this paper. The parking point Y in front of the traffic light at the junction is 2550 m away from station A. The duration time of the red light at the junction is the 30s, so in the numerical experiment we set $t_{dwell}$ in the model as 30s. In this paper, according to the slope and considering the location of point Y, section A-B is divided into six sections, expressed as $U=\left\{\left(\mathrm{1,2}\right),\left(\mathrm{2,3}\right),\left(\mathrm{3,4}\right)\mathrm{\dots }\dots \left(\mathrm{6,7}\right)\right\}$, and each section is discretized into ten small segments with equal length.

FIGURE 3

FIGURE 3. Section division and dispersion.

The information slope, curve and speed limit of each section is shown in Table 4. The parameters of the tram are shown in Table 5. The traction and braking characteristic fitting curve and the basic resistance curve of tram running are shown in Figure 4.

TABLE 4

TABLE 4. Slope, curve, and speed limit information of each section.

TABLE 5

TABLE 5. Parameters of the tram.

FIGURE 4

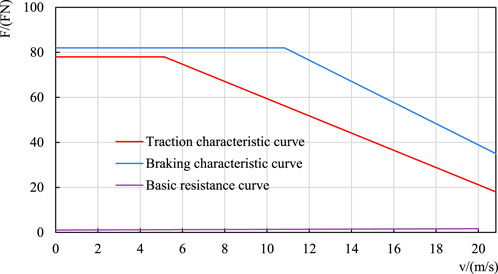
FIGURE 4. Traction characteristic, braking characteristic fitting curve, and running resistance curve.

Results and discussions

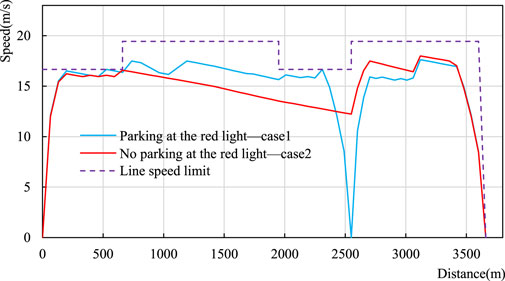
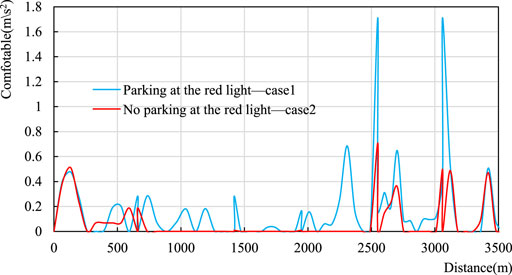
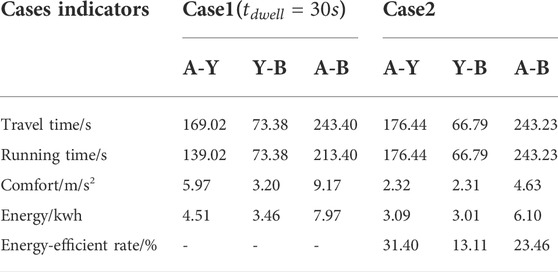
We use the optimization solver IBM ILOG CPLEX 12.7.1.0 to solve the MILP model. The CPLEX could obtain optimal solutions with the computational time of 46.34 and 67.36, respectively, for Cases 1 and 2, unit: second. According to the solving results of speed and acceleration at each position, the optimized speed trajectories and comfort curves of tram operations in the two cases are drawn, as shown in Figure 5; Figure 6, respectively. Table 6 shows the optimized tram running time, energy consumption, energy-efficient rate, comfort, and other indicators in the two cases.

FIGURE 5

FIGURE 5. Comparison after optimization of the tram speed trajectories in case 1 and case 2.

FIGURE 6

FIGURE 6. Comparison after optimization of the comfort curves in case 1 and case 2.

TABLE 6

TABLE 6. Comparison of the optimized indicators in case 1 and case 2 at.$t_{dwell}=30s$

As shown in Figure 5, In case1 and case2, the running speed of the tram fluctuated at different locations throughout the section, due to line conditions, vehicle characteristics, speed restrictions, and traffic light limitations. Moreover, the optimized speed trajectory in case 2 demonstrates that the speed oscillation of the tram at the junction is significantly smaller than that in case 1. Which is because in case 2, the tram avoids the red light by the speed trajectory optimization approach proposed in this paper. There is no deceleration from higher speed to park and restart back to higher speed operation. The optimization approach proposed in this paper can reduce the frequency of acceleration and deceleration of the tram, so that the speed of the tram will not fluctuate considerably. Figure 6 shows that in case 2, the values of the optimized comfort are significantly smaller than those in case 1, especially at the junction. In this paper, the acceleration change rate is used to express comfort. The smaller the value of comfort is, the smaller the acceleration change is, and the higher the comfort is. Therefore, in case 2, the tram operation comfort is higher.

Table 7 shows that the total travel time of the tram in section A-B remains unchanged in the two cases after optimization. Compared with case1, in case 2, the total running time of the tram in section A-B is increased by 30 s, the total running energy consumption is reduced by 1.87kwh, and the energy-efficient rate is 23.46%, comfort is 4.63 m/s², which increased by 49.50%. The running time in section A-Y is 176.44 s, which is an increase of 37.42 s. The running energy consumption is 3.09 kwh, representing a decrease of 1.42 kwh. The energy-efficient rate is 31.40%, and comfort is 2.32 m/s², which is increased by 61.14%. In section Y-B, the running time is 66.7 9s, which is reduced by 6.59s. The running energy consumption is 3.01 kwh, which is reduced by 0.45 kwh. The energy-efficient rate is 13.11%, and comfort is 2.31 m/s², which is increased by 27.81%. The comparison of running energy consumption and energy-efficient rate of the tram in sections A-B, A-Y, and Y-B after optimization in the two cases is shown in Figure 7.

TABLE 7

TABLE 7. Comparison of the optimized indicators in case 1 and case 2 at.$t_{dwell}=15\mathrm{s.}$

FIGURE 7

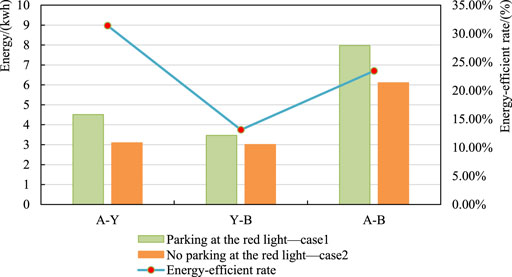
FIGURE 7. Comparison of energy consumption and energy-efficient rate of the tram in each section after optimization in case 1 and case 2.

The comparison of the tram running distance and energy consumption after optimization in the two cases is shown in Figure 8. This figure shows the changing trend of tram energy consumption in each section after optimization in the two cases. For case 2, the change of energy consumption of the tram running in section (2, 3) (3, 4) (4, 5) is close to 0. Compared with case 1, in case 2, the energy consumption of the tram operation in the whole section is less.

FIGURE 8

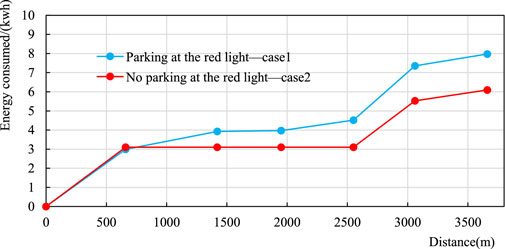
FIGURE 8. Comparison of the tram running distance and energy consumption after optimization in case 1 and case 2.

According to the experimental results, the speed trajectory optimization approach proposed in this paper is effective and can be used as a reference. When the tram meets the red light, the total travel time is guaranteed to be constant for the two cases. In the case of no parking at the red lightin the case of no parking at the red light, the tram can pass through the junction under the green light. The purpose of non-parking at point Y can be realized by adjusting the running time and speed of the tram between two adjacent sections bounded by the traffic light at the junction. It effectively prevents the tram’s energy consumption loss due to the influence of the red light and improves passenger comfort.

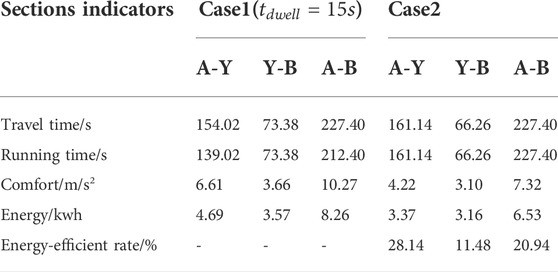
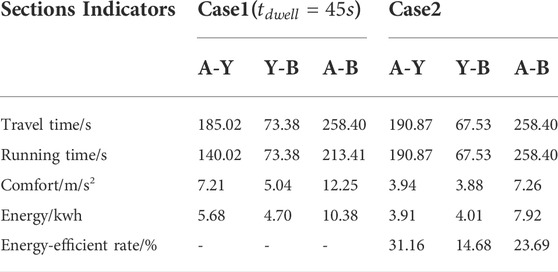
In case 1, this paper sets $t_{dwell}$ to 30 s based on the duration time of the red light at the junction and verifies the validity of the model under this condition. However, in this subsection, the parking time in case 1 is set to 15 and 45s for numerical experiments to verify that the model can still maintain good reliability under different parking times. The numerical experimental results are shown in Table 7 and Table8.

TABLE 8

TABLE 8. Comparison of the optimized indicators in case 1 and case 2 at.$t_{dwell}=45\mathrm{s.}$

As shown in Tables 7, 8, in case 1, when the parking time is set to 15 and 45s, the energy consumption of the tram and passenger comfort in case 2, i.e., no parking at the red light, still has a superiority than those in case 1 in sections A-Y, Y-B, and A-B. This result shows that the optimization approach and model proposed in this paper are still effective under different parking times.

Conclusion

This paper proposes a speed trajectory optimization approach for the tram without parking when encountering a red light. This approach is realized by reasonably adjusting the running time and speed of the tram between two adjacent sections bounded by the traffic light at the junction, on the premise that the total travel time of the whole section remains unchanged. The discrete space method is used to transform the tram speed trajectory optimization problem into a multi-stage decision-making problem. In addition to the tram movement equations, speed, and route constraints, the comfort and the traffic light constraints are also considered. An energy-efficient optimization model of tram speed trajectory considering the influence of the traffic light is established. The nonlinear constraints in the model are linearly transformed by adding constraints and the piecewise approximation method. As a result, the optimization model is reformulated into a mixed-integer programming model to reduce the complexity of the model solution. The experimental results show that the approach of the speed trajectory optimization considering the influence of the red light proposed in this paper can effectively reduce the total running energy consumption. The energy-efficient rate can reach 23.46% and improve passenger comfort significantly compared to the case of parking at the red light. This approach can provide an effective reference for the energy-efficient operation of tram drivers.

Specifically, this paper is focused on the speed trajectory optimization of a single section of the tram running. The research scope is small compared with the whole line or the whole network, and the effects on the tram by other vehicles and pedestrians at junctions will exist. Therefore, future research focuses on analyzing the speed trajectory optimization on the whole line under different degrees of interference. In addition, the comfort level in this paper is expressed in terms of the rate of change of acceleration. Passenger perception data can also be used in future studies to match comfort. Then, based on actual data to evaluate the comfort level from the passenger’s perspective.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors: conceptualization. JH, YL, SL, and YX: methodology. JH and YL: writing of the original draft. SL and YL: software. JH, YL, and SL: formal analysis, data curation, writing, reviewing, and language modification. JH: funding acquisition. All authors have read and agreed to the publication of the manuscript.

Funding

This research was funded by the Yunnan Provincial Department of Science and Technology, grant number 2019FB086, and Science and Technology Innovation and Demonstration Project of the Department of Transport of Yunnan Province, Yunnan Jiaotong Textbook Ben <2021> No. 85.

Acknowledgments

The authors are also grateful to the reviewers for their constructive comments.

Conflict of interest

JC are employed by the company China Railway Construction Yunnan Investment Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadi, S., Dastfan, A., and Assili, M. (2018). Energy saving in metro systems: Simultaneous optimization of stationary energy storage systems and speed profiles. J. rail Transp. Plan. Manag. 8 (1), 78–90. doi:10.1016/j.jrtpm.2018.03.003

CrossRef Full Text | Google Scholar

Cao, Y., Zhang, Z., Cheng, F., and Su, S. (2022). Trajectory optimization for high-speed trains via a mixed integer linear programming approach. IEEE Trans. Intelligent Transp. Syst., 1. doi:10.1109/TITS.2022.3155628

CrossRef Full Text | Google Scholar

Chen, Z., and Wang, H. (2018). Cictp 2017: Transportation reform and change—equity, inclusiveness, sharing, and innovation, Am. Soc. Civ. Eng. Rest. VA, 2761–.2772.

Google Scholar

Enjalbert, S., and Boukal, Y. (2019). On the eco-driving trajectory for tramway system. IFAC-PapersOnLine 52 (19), 115–120. doi:10.1016/j.ifacol.2019.12.121

CrossRef Full Text | Google Scholar

Gao, Z., and Yang, L. (2019). Energy-saving operation approaches for urban rail transit systems. Front. Eng. Manag. 6 (2), 139–151. doi:10.1007/s42524-019-0030-7

CrossRef Full Text | Google Scholar

Hayashi, Y. (1989). Issues in financing urban rail transit projects and value captures. Transp. Res. Part A General 23 (1), 35–44. doi:10.1016/0191-2607(89)90138-6

CrossRef Full Text | Google Scholar

He, D., Zhang, L., Guo, S., Chen, Y., Shan, S., Jian, H., et al. (2021). Energy-efficient train trajectory optimization based on improved differential evolution algorithm and multi-particle model. J. Clean. Prod. 304, 127163. doi:10.1016/j.jclepro.2021.127163

CrossRef Full Text | Google Scholar

Huang, Y., Yang, L., Tang, T., Gao, Z., Cao, F., Li, K., et al. (2018). Train speed profile optimization with on-board energy storage devices: A dynamic programming based approach. Comput. Industrial Eng. 126, 149–164. doi:10.1016/j.cie.2018.09.024

CrossRef Full Text | Google Scholar

Jia, J., Yang, K., Yang, L., Gao, Y., and Li, S. (2018). Designing train-speed trajectory with energy efficiency and service quality. Eng. Optim. 50 (5), 797–818. doi:10.1080/0305215x.2017.1358712

CrossRef Full Text | Google Scholar

Jin, B., Sun, P., Xu, M., and Wang, Q. (2018). Train timetable and trajectory optimization using improved state-space MILP. New york: IEEE, 7748–7753.

Google Scholar

Ko, H., Koseki, T., and Miyatake, M. (2004). Application of dynamic programming to the optimization of the running profile of a train. WIT Trans. Built Environ. 74, 10. doi:10.2495/CR040111

CrossRef Full Text | Google Scholar

Ko, H., Koseki, T., and Miyatake, M. (2005). Numerical study on dynamic programming applied to optimization of running profile of a train. IEEJ Trans. Ia. 125 (12), 1084–1092. doi:10.1541/ieejias.125.1084

CrossRef Full Text | Google Scholar

Li, J., Bai, Y., Chen, Y., Yang, L., and Wang, Q. A., 2022, Two-stage stochastic optimization model for integrated tram timetable and speed control with uncertain dwell times. Available at SSRN 4011129,

Google Scholar

Li, W., Li, X., Liu, Y., and Hua, C. (2019). Research on improved train automatic control strategy based on particle swarm optimization. New York: IEEE, 5867–5872.

Google Scholar

Lin, J., and Liu, X. (2021). Speed curve optimization of high-speed flying train based on improved genetic algorithm. New York: IEEE, 280–283.

Google Scholar

Liu, K-W., Wang, X-C., and Qu, Z-H. (2019). Research on multi-objective optimization and control algorithms for automatic train operation. Energies 12 (20), 3842. doi:10.3390/en12203842

CrossRef Full Text | Google Scholar

Long, S., Meng, L., Wang, Y., Luan, X., and Zhang, P. (2020). A bi-objective integrated optimization model of high-speed train rescheduling and train control. J. Transp. Syst. Eng. Inf. Technol. 20 (6), 163–169. doi:10.16097j/cnki.1009-6744.2020.06.021

CrossRef Full Text | Google Scholar

Long, S., Meng, L., Wang, Y., Miao, J., Li, T., and Corman, F. (2019). A train rescheduling optimization model with considering the train control for a high-speed railway line under temporary speed restriction. New York: IEEE, 2809–2816.

Google Scholar

Luo, M-Z., He, W., Chen, Y., and Gu, F. (2016). Research on control strategies of modern streetcar at intersection under semi-independent way condition. New York: IEEE, 1–6.

Google Scholar

Shi, J., Sun, Y., Schonfeld, P., and Qi, J. (2017). Joint optimization of tram timetables and signal timing adjustments at intersections. Transp. Res. Part C Emerg. Technol. 83, 104–119. doi:10.1016/j.trc.2017.07.014

CrossRef Full Text | Google Scholar

Tan, Z., Lu, S., Bao, K., Zhang, S., Wu, C., Yang, J., et al. (2018). Adaptive partial train speed trajectory optimization. Energies 11 (12), 3302. doi:10.3390/en11123302

CrossRef Full Text | Google Scholar

Tang, H., and Feng, X. (2013). Train running time allocation algorithm based on dynamic programming. New York: IEEE, 8157–8160.

Google Scholar

Wang, W., Hu, J., Ji, Y., and Du, Y. (2019). Improving fuel efficiency of connected and automated transit buses on signallised corridors. IET Intell. Transp. Syst. 13 (5), 870–879. doi:10.1049/iet-its.2018.5152

CrossRef Full Text | Google Scholar

Williams, H. P. (1985). Model building in linear and integer programming. Comput. Math. Program. 15, 25–53. doi:10.1007/978-3-642-82450-0_2

CrossRef Full Text | Google Scholar

Williams, H. P. (2013). Model building in mathematical programming. John Wiley & Sons.

Google Scholar

Wu, C., Zhang, W., Lu, S., Tan, Z., Xue, F., Yang, J., et al. (2018). Train speed trajectory optimization with on-board energy storage device. IEEE Trans. Intell. Transp. Syst. 20 (11), 4092–4102. doi:10.1109/tits.2018.2881156

CrossRef Full Text | Google Scholar

Wu, M., Wang, J., Yan, Y., Yin, G., and Ren, Z. (2020). Velocity trajectory planning of the autonomous-rail Rapid tram considering terrain and traffic lights. New York: IEEE, 1–6.

Google Scholar

Xiao, Z., Chen, H., Guo, J., Wang, Q., Sun, P., Feng, X., et al. (2021). Joint optimization of speed and voltage trajectories for hybrid electric trams. IEEE Trans. Ind. Appl. 57 (6), 6427–6439. doi:10.1109/tia.2021.3102881

CrossRef Full Text | Google Scholar

Xiao, Z., Feng, X., Wang, Q., and Sun, P. (2020). Eco‐driving control for hybrid electric trams on a signalised route. IET Intell. Transp. Syst. 14 (1), 36–44. doi:10.1049/iet-its.2019.0345

CrossRef Full Text | Google Scholar

Xiao, Z., Sun, P., Wang, Q., Zhu, Y., and Feng, X. (2018). Integrated optimization of speed profiles and power split for a tram with hybrid energy storage systems on a signalized route. Energies 11 (3), 478. doi:10.3390/en11030478

CrossRef Full Text | Google Scholar

Xu, M., Liu, Q., Mao, C., Wang, Q., and Sun, P. (2018). Energy-efficient control of energy storage tram with signaling constraints. New York: IEEE, 7742–7747.

Google Scholar

Yan, Y., Li, Q., Chen, W., Su, B., Liu, J., Ma, L., et al. (2018). Optimal energy management and control in multimode equivalent energy consumption of fuel cell/supercapacitor of hybrid electric tram. IEEE Trans. Ind. Electron. 66 (8), 6065–6076. doi:10.1109/tie.2018.2871792

CrossRef Full Text | Google Scholar

Zhang, H., Liu, B., Yang, J., and Zhang, J. (2021). Sequence optimization of target speed curve and energy management strategy for fuel cell hybrid tram. New York: Springer, 321–329.

Google Scholar

Zhou, L., Tong, L. C., Chen, J., Tang, J., and Zhou, X. (2017). Joint optimization of high-speed train timetables and speed profiles: A unified modeling approach using space-time-speed grid networks. Transp. Res. Part B Methodol. 97, 157–181. doi:10.1016/j.trb.2017.01.002

CrossRef Full Text | Google Scholar

Zhou, L., Zhou, X., Tang, J., and Tong, L. (2016). Jointly optimize high-speed train route, timetable and trajectories: A unified modeling approach using space-time-speed grid networks, Transp. Res. Part B Methodol., 97, 157. doi:10.1016/j.trb.2017.01.002

CrossRef Full Text | Google Scholar