Optimization and Control for Solid Oxide Fuel Cell System Hybrid DC Microgrids From the Perspective of High Efficiency, Thermal Safety, and Transient Response

Managing the power transients with both high efficiency and thermal management constraints is a difficult task in the solid oxide fuel cell (SOFC) hybrid direct-current (DC) microgrids. This article proposed a SOFC-based DC microgrid, which consists of the SOFC stand-alone system, DC microgrid network, and DC/DC boost converter, along with the associated DC/DC load. The control and optimization strategy of the SOFC-based DC microgrids has been designed, including the thermal and electrical characteristics analysis. First, the voltage and current regulator based on the proportional–integral (PI) is designed, which can maintain the voltage stability of the proposed SOFC system. In addition, the optimal regulator based on the optimal operating points (OOPs) is designed, which can realize high efficiency and steady-state thermal safety of the proposed SOFC system. Finally, the main performance, including the SOFC stack electrical characteristics verification, SOFC stand-alone system electrical and thermal response, load-tracking characteristics, and system efficiency is observed and discussed in the proposed control and optimization strategy. Experimental results verify the correctness of the theoretical analysis and the effectiveness of the proposed optimization and control strategy.

1 Introduction

In recent years, global energy demand is steadily increasing (Zhang et al., 2020a; Deng et al., 2021), which has made a great impact on various fields (Xie et al., 2020). Thus, the electric power generation, transmission, and distribution around the globe will be subjected to pre-eminent concern due to several reasons, such as the limited fossil fuel resources, incremental electric power consumption, global climatic change, legislation for integrating renewable energy sources (RESs), and stochastic properties of the RESs and their associated challenges (Zhang Y et al., 2019; Zhang et al., 2020b; Xu et al., 2022). Compared to the alternating-current (AC) microgrids, the direct-current (DC) microgrids have attracted both researchers and industrialists since it has many advantages, including the role to effectively solve the effects of the distributed generation accessing network to improve the power quality and transactive energy, and the elimination of the frequency and phase control (Eid, 2014; Srinivasan and Kwasinski, 2020). Among several novel propositions, the solid oxide fuel cell (SOFC) is one of the most effective and efficient RESs, which can generate electricity directly from the electrochemical reaction with the least spread of pollution, compared to the conventional energy production methods (Wang et al., 2022). The SOFCs are excellent regional power supply equipment applied to the power supply systems and will be widely used in the DC microgrids, due to the advantages of fuel adaptability, high efficiency, noiseless operation, and high reliability. The advantages of the SOFC generation in the microgrids can be summarized as follows:

• Improving system efficiency. Fuel utilization of the SOFC system is more than 60% and its energy storage systems (ESSs) sometimes reached 90% (Barnes, 2002). Its power generation efficiency can be 55%–65%, which is generally more efficient than the combustion engines (Singhal and Kendall, 2003). This is important in the DC microgrids needed for the combined heat and power systems.

• Cutting down expenditures. The wide varieties of fuel can be used in the SOFC system, and the DC microgrids based on the RES can be easily interfacing with the distribution generation without the interlinking AC/DC-and DC/AC-interfacing transformation stages, just by realizing the combined power supply through a variety of the new energy sources. Its implementation is simple and cost-effective. It shows a good application perspective in majority of the rural areas that do not have access to reliable electricity (Gandini and Almeida, 2017; Hirsch et al., 2018).

• Strengthening capability of the regulating peak. The SOFCs can serve as the independent power generation as well as the grid-connected system, and many SOFC power stations connected to the power grid can greatly enhance the peak regulation capability of the microgrids.

• Improving security. The worldwide power grids mostly use the high-voltage electricity for long distance transmission, which result in low reliability and serious losses caused by large area blackouts due to accidents. The SOFCs can go on the power supply for the basic load to support the power grid.

However, the researches on the SOFC are still in their beginning stage, with the lack of dynamic load following, the poor thermal response, and gas starvation being some of the drawbacks of SOFC systems that need to be addressed (Mumtaz et al., 2018; Pranita et al., 2022), which requires constant improvement and development to large-scale commercial applications, especially the fast load tracking on the premise of the high efficiency and operating safety under optimal working conditions should be discussed in the DC microgrids. For the SOFC-based DC microgrid development, safe operating, including thermal management and gas starvation, is an important control task, especially the high operating temperatures may lead to the thermal gradient and local hot spots (Zhang et al., 2010). Moreover, the optimal operation points and optimized power switching strategies are discussed to improve the system efficiency. In addition, the load transients often involve significant peaks in power relative to steady-state load (Li et al., 2015). Thus, load tracking is another important control task in the DC microgrids.

In recent years, diverse thermal safety has been focused and discussed to ensure the SOFC system operating in the proper temperature. When the SOFC system temperature has been recognized to have the significant impact on the cell lifespan and operating safety; in order to mitigate temperature excursion and ensure thermal safety, the excess air for the cooling SOFC system is controlled to maintain the SOFC system within a safe range (Sorrentino et al., 2008; Huo et al., 2010; Hajimolana et al., 2013), including a proportional–integral (PI) controller, a variable structure controller, or a neural network predictive controller, which are suitable for the thermal safety control. However, these control schemes had not considered the maximum electrical efficiency operations of the SOFC stand-alone system. Moreover, the gas starvation problem, considering the operating safety, is also discussed (Carré et al., 2015), by developing a feed-forward control for the SOFC system with anode-off gas recycle. The results show that the control scheme was sensitive to external disturbance and produced a steady-state error.

Many optimal control methods have been raised and developed, which can provide an important reference on the swift response and dynamic load variation issues of the SOFC-based DC microgrids. The load-tracking studies under both stand-alone and grid-connected conditions have been discussed, especially the load-tracking and small signal stability issues pertaining to grid-connection is investigated (Padulles et al., 2000; Zhu and Tomsovic, 2002; Li et al., 2005). An adaptive control paradigm is portrayed for the swift response of the SOFC in a grid-connected microgrid (Awais et al., 2021). The aforementioned control strategies are restricted to its constraints or unable to tackle the sudden and large load variations, and the cooperative thermo-electrical control strategy has been not considered, which further needs to be discussed and analyzed.

The main goal of this article was to design the optimization and control strategy to ensure fast load following by comprehensively considering the high efficiency, fuel exhaustion, and thermal safety in the SOFC-based hybrid DC microgrids. This article is organized as follows: Section 2 describes the hybrid power system architecture, including its essential operational requirements. Section 3 deals with the modeling and validation and optimization and control strategy of the SOFC-based hybrid DC microgrid. Finally, the article ends with a conclusion in Section 4.

2 Solid Oxide Fuel Cell Hybrid Direct-Current Microgrid System Layout

2.1 System Architecture

The overall block diagram of the SOFC-based hybrid DC microgrid system is shown in Figure 1. It includes the SOFC stand-alone system, commonly used DC/DC boost converters, whose controlled output voltage is greater than the input voltage, which can maintain the high reliability and load power supply (Ahmed and Blejis, 2013; Armghan et al., 2020; Liu et al., 2020). The investigated SOFC stand-alone system is shown in Figure 2. The system incorporates the stack and balance of plant (BOP), including the fuel feed pipes and valves, air feed pipes and valves, heat exchangers, SOFC stack, and tail-burner. The rated full power of the co-flow planar stack is 5 kW, which can provide the power to the external load through electrochemical reactions. Generally, a classic SOFC BOP includes the air/fuel feed pipes and valves, second air bypass manifold, fuel and air heat exchangers, and tail-burner. Then, the fuel and air heat exchangers are designed to minimize the inlet temperature difference of the SOFC stack. The tail-burner can promote the utility rate of the fuel by burning the tail gas. Meanwhile, its output hot gas is spilled into the heat exchanger as the heat source. Finally, the temperature of the SOFC system is convenient to control by adding the second air bypass manifold.

FIGURE 1

FIGURE 1. Schematic diagram of the SOFC-based hybrid DC microgrid.

FIGURE 2

FIGURE 2. Overall SOFC stand-alone system layout.

2.2 System Essential Operational Requirements

In addition to the fast power tracking, operating safety (including the thermal safety and avoiding fuel exhaustion) and high efficiency are the most important considerations for control and optimization. This article mainly discusses the thermal performance indices associated with thermal safety, fuel concentration indices associated with fuel exhaustion, and optimal operation points associated with high efficiency, which are depicted as follows:

2.2.1 Thermal Performance Indices

The high temperature or temperature gradient in the SOFC may cause material deformation or even damage, thus being the essential operational requirements. For example, as one of the most important components, the high temperature gradient in stack could result in large thermal stress and may cause stack deformation or even damage. In addition, stack temperature should be within the materials’ bearing range. Under the aforementioned assumption, the temperature constraints in the SOFC can be shown as follows:

(1) Burner temperature $T_B\le 1273K$.

(2) Maximum positive-electrode-electrolyte-negative (PEN) temperature $Max.T_{PEN}\in \left[873K,1173K\right]$.

(3) Maximum PEN temperature gradient $Max.\left|\mathrm{\Delta }{T}_{PEN}\right|\le 8Kc{m}^{-1}$.

(4) Stack inlet temperature difference $\mathrm{\Delta }{T}_{inlet}\le 200K$.

2.2.2 Fuel Concentration

The external load changes, ensuring that adequate fuel supply is one of the most important prerequisites for the safe operating. The primary cause of fuel exhaustion is identified as fuel delay due to the slow dynamics in the fuel and air supply path. To observe the fuel exhaustion condition, the fuel concentration in the stack must be observed in real time. For avoiding the fuel exhaustion, the fuel concentration in the stack must meet the basic requirements X_H2 > 0.

2.2.3 Optimal Operation Points

For the further analysis of SOFC system performance, considering the high efficiency of SOFC, the operating parameters, including the system inlet air and fuel flow rate and system current, are selected as the assemble-regulating variables in this article. The too low or high value of all these aforementioned operating parameters would lead to low efficiency or poor system performance, and they must be operated within their region under the different external load powers.

Based on the performance indices discussed previously, in addition to the thermal and electrical management and constraint enforcement, the optimal operating points (OOPs) are manipulated to achieve the optimal energy efficiency through the transverse optimization process, which have been conducted in our and other’s previous works (Zhang et al., 2015a; Zhang et al., 2015b; Zhang et al., 2018; Zhang L et al., 2019). The OOPs can ensure thermal safety, and high efficiency in static can be obtained, which is shown in Table 1.

TABLE 1

TABLE 1. OOPs of the SOFC stand-alone system.

3 Optimization and Control of Solid Oxide Fuel Cell-Based Direct-Current Microgrid

In the study of optimization and control of the hybrid SOFC system for the voltage stability, it is necessary to develop the full and quite accurate model of each subsystem component. This section first deals with the modeling of the system.

3.1 Mathematical Model

A lot of researches considering the SOFC stand-alone system model with the BOP were established for the simulation and optimization in our earlier works (Zhang et al., 2015a; Zhang et al., 2015b; Zhang et al., 2018; Zhang L et al., 2019), especially the exit temperatures, species molar fractions, and molar flow rates of each control volume, which can be divided into the gas phase and solid phase, as shown in Figure 3, have been obtained from the transient energy, species, and mass conservation equations, respectively. These conservation equations are of the same general form within various system components in Table 2. $\dot{Q}$ is the energy, T is the temperature, and V, ρ and C are the volume, density, and specific heat capacity of each control volume, respectively. W is the generating power, R_i is the reaction rate of the individual species i, U is the voltage, i is the current density, N is the molar flow rate, h is the gas enthalpy, S is the area, F is the gas flow rates or Faraday’s constant, X is the molar fraction, R is the universal gas constant, C_v is the constant volume-specific heat capacity, C_p is the constant pressure-specific heat capacity, h_gs is the convection heat transfer coefficient, λ_g is the gas thermal conductivity, d is the radius, u is the velocity, μ is gas viscosity, and L is the distance between the control volume. The subscript S represents the solid control volume, and in and out represent the inlet and outlet, respectively. Cell denotes the fuel cell, and ref represents reference. PEN is the positive electrode-electrolyte-negative electrode, and cond and conv represent the heat conduction and thermal conversion, respectively.

FIGURE 3

FIGURE 3. Nodes and control volumes of the 1D model.

TABLE 2

TABLE 2. Universal SOFC system building equations.

3.1.1 Burner

Burner is the main component for the off-gas recovery and recycle. To reduce the computational burden, the SOFC burner is assumed to operate adiabatically, and the fuel is oxidized completely. It is assumed as the 0D lumped parameter model, and the heat transfer with the external environment is ignored. Simultaneously, the catalytic combustion reaction time in the burner is in millisecond; thus, its reaction process can be neglected. The quasi-static model is selected to build the burner model. Its burning wall temperature can be determined according to (1), and its outlet molar flow rate, molar fractions, and outlet temperature can be computed by (5) and (7) to (12), respectively.

3.1.2 Fuel and Air Heat Exchangers

By introducing two heat exchangers in the SOFC system, the fuel and air can be preheated with the same hot stream from the burner at the same time. Thus, it can minimize the stack inlet temperature difference effectively. The structure of both the heat exchangers is assumed to be counter-current pipe heat exchangers. The integrated fuel and air heat exchangers are discretized into N nodes in the flow direction. As shown in Figure 3, each node includes the gas phase control volumes (air, fuel, and exhaust) and solid phase control volumes (the fuel tube, air tube, and exhaust tube). The temperature and species molar fractions of the gas phase control volumes are calculated by the conservation of the energy equation and the species conservation equation, respectively. The temperature of the solid phase control volumes is calculated from the dynamic solid-state energy conservation equation, as shown in (1), whereas the temperature of the gas phase control volumes can be calculated from (10).

3.1.3 Mass Flow Controllers

As shown in Figure 2, the air/fuel fed into the SOFC stack is manipulated by three pipes and valves, where the dynamics can be approximated by the first-order plus delay time, which is given by:

$G\left(s\right)=\frac{1}{Ts+1}{e}^{-T_{d}s},(16)$

where T is the inertia time constant; and T_d is delay time or dead time, in which the delay time have a direct effect on the dynamic response, especially during the load tracing.

3.1.4 Solid Oxide Fuel Cell Stack

In this article, each single cell unit in the SOFC stack is assumed to operate identically; thus, a single cell unit can be taken as a representative of the entire stack performance. In addition, as shown in Figure 3, the fuel cell can be quasi-dimensionally discretized into five nodes in this article.

Four temperature layers (such as fuel channel, air channel, interconnector, and PEN) are considered for the fuel cell in the SOFC stack model. The temperatures in the PEN and interconnect plates are determined using the energy conservation equation, as shown in (3) to (5). In addition, the temperatures and species mole fractions in the cathode and anode gas streams are calculated from the conservation of the energy equation and the species conservation equation, as shown in (5) to (12), respectively. Conduction of heat transfer between the solid phase control volumes is calculated based on the Fourier’s Law, as shown in (13). Finally, the convection heat transfer between each gas and solid phase control volume is determined according to (14) and (15).

As the polarization losses, ohmic loss and concentration loss are the function of the PEN temperature, gas pressure, and current density in the fuel cell. The fuel cell output voltage can be represented using a nonlinear algebraic equation, which is given by:

$U_{cell}=f\left(i,p_{H_2},p_{O_2},p_{H_{2}O},p_a,T_{PEN}\right),(17)$

where T_PEN represents the PEN temperature. For the accuracy of the model building, the electrical dynamic model of the fuel cell is obtained based on a lot of experimental data for the practical guidance. The equivalent resistance is shown using the partial derivative method, which is given by:

$R_{tot}=\frac{\partial \left(U_{ohm}+U_{act}+U_{con}\right)}{\partial I},(18)$

where I is the current; and U_ohm, U_act, and U_con represent the ohmic loss, activation loss, and concentration loss in the SOFC system, respectively, provided that:

$R_{tot}=a_0+a_{1}x+\cdots +a_n{x}^n;x=0.001T_{PEN}/I_s,(19)$

where a₀, ……a_n represent the polynomial coefficient. Then, we can have:

$\begin{array}{l}{U}_{cell}=U_{OCV}-I{R}_{tot},\\ =U_{OCV}-I\left(a_0+a_1\cdot \left(\frac{0.001T_{PEN}}{I_s}\right)+\cdots +a_n\cdot {\left(\frac{0.001T_{PEN}}{I_s}\right)}^n\right).\end{array}(20)$

The open circuit voltage can be adopted by the Nernst voltage, which is given by:

$U_{OCV}=E_0+\frac{R{T}_{PEN}}{2F}\ln \left(\frac{P_{H_2}{P}_{O_2}^{0.5}}{P_{H_{2}O}}\right),(21)$

$\begin{array}{l}{E}_0=-12.45058+26.3104\left(T_{PEN}/1000\right)\\ -12.4{\left(T_{PEN}/1000\right)}^2-\left(2.7645e-4\right)/T_{PEN}.\end{array}(22)$

To get the polynomial coefficient in (19), the electrical characteristics of the single cell (10*10 cm²) under the ideal conditions are conducted in an electrical furnace. As shown in Figures 4A,B, the voltage, current, and power density are investigated. The operating temperatures were set in the range from 923 to 973 K with the space of 50 K, especially the output power density and voltage are investigated under each temperature, and the open circuit voltage is calculated when the current is 0 A.

FIGURE 4

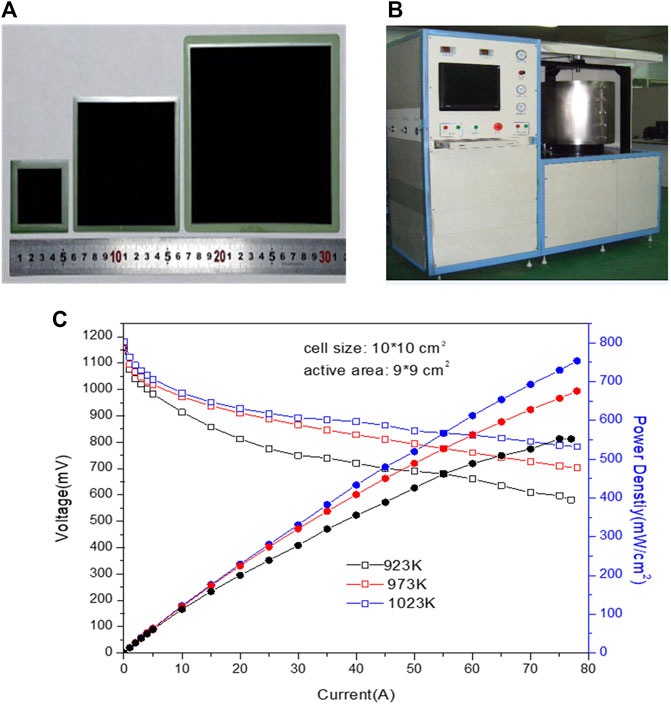
FIGURE 4. Test of the fuel cells. (A) Fuel cell; (B) test furnace; and (C) electrical characteristics.

Then, the electrical characteristics curves of the voltage–current–power density are shown in Figure 4C; it showed that the open circuit voltage is about 1.12–1.18 V, and the power density is about 550–770 mW/cm². Based on the value obtained in our test, referring to (20), the equivalent resistance can be calculated by the least square fitting; assuming the polynomial of order n = 4, the values of a₁-a₄ are shown in Table 3. Referring to our previous work, the Newton iteration algorithm is adopted to build the electrical characteristic model to ensure that the voltage of each fuel cell node is equal, which will not be addressed in this article. Moreover, the SOFC system structure parameters are confirmed by the physical facility in our group, and the physical parameters are determined by referring to the authoritative chemical handbook. More detail can be found in Zhang et al. (2015a) and Zhang et al. (2015b).

TABLE 3

TABLE 3. Parameter values of the equivalent resistance.

3.1.5 Blower

The blower supplies air to the SOFC system, which is the main parasitic losses in the SOFC stand-alone system; the output power of the different air flow can be expressed as:

$P_{bl}=-\frac{1}{{\mathit{\tau }}_{bl}}\ast \frac{\gamma R{T}_{amb}}{\gamma -1}\left[{\left(\frac{p_{out}}{p_{amb}}\right)}^{\left(\gamma -1\right)/\gamma }-1\right]F_{air},(23)$

where τ_bl is the effectiveness, γ is the specific heat ratio, and p is the pressure.

3.1.6 Solid Oxide Fuel Cell System Efficiency

The efficiency of the SOFC stand-alone system can be defined as:

${\eta }_{sys}=\frac{U_s\cdot I_s-P_{bl}}{F_{H2}\cdot LH{V}_{H2}}\times 100\%,(24)$

where U_s is the stack voltage and LHV_H2 is the low heating value of H₂.

3.2 Optimization and Control

As shown in Figure 5A, the SOFC stand-alone system is connected to the DC/DC converter of the boost type. The design of the two control loops is made considering the voltage stability and SOFC dynamics in the DC microgrids. The voltage and current regulator are shown in Figure 5B, which can allow voltage conversion as well as the full control of the fuel cell current and DC bus voltage. The average value of the DC/DC converter models can be referred to Zakzouk et al. (2019) for this study. The optimal regulator mainly controls the load demanded power by referring to OOPs. Figure 5C shows the high fuel utilization (FU) and low air excess ratio (AR) under the OOPs in the steady state, which can ensure high efficiency. Moreover, the PI regulator uses the control method, and the demanded voltage of the DC microgrid is 220 V in this study. The demanded load power change is given as 2.5 kW→3.5 kW→5 kW→1.5 kW→4.5 kW→5 kW. The efficiency of the DC/DC boost converter in this study is assumed to be 90%.

FIGURE 5

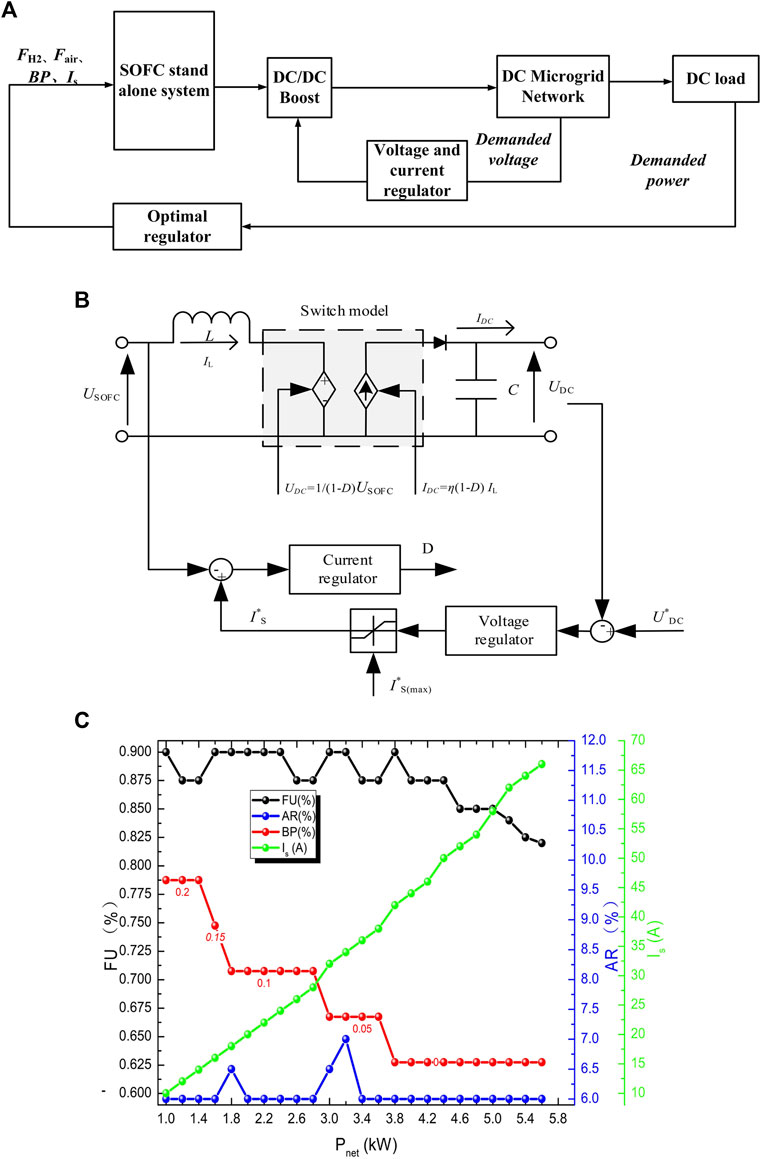
FIGURE 5. Control and optimization of the SOFC DC microgrid. (A) Overall control schemes; (B) boost-type DC/DC converter model; and (C) steady-state optimal points for the optimal regulator.

The proposed control and optimization scheme for the SOFC-based DC microgrids is implemented in the Simulink/SimPower systems, and the characteristics of the SOFC-based DC microgrid system are shown in Figure 6. Figure 6A shows the system input characteristics and stack remain H₂ molar flow fraction in the proposed SOFC system. It is worth pointing that our previous study (Zhang L et al., 2019) has revealed that safety operating, whether ensuring the thermal safety or avoiding fuel exhaustion, should be in the cost of the fast load tracing, namely, the SOFC system current that should slowly change. The SOFC system current slope limitation is adopted to deal with the problem of fuel exhaustion and thermal safety. By observing the H₂ molar flow fraction in the SOFC stack, the large amount of hydrogen is shown in stack (≥82%). The output electrical characteristics of the proposed SOFC system are shown in Figure 6C, and the response time of the output electrical variables, including the SOFC output net power and voltage, is within tens of seconds. In addition, by the proposed optimal regulator with the OOPs, considering the parasitic loss of the blower power, the SOFC system efficiency shows a high value (45%–65%). Due to the current slow switching and BP regulation, the output thermal characteristics of the proposed SOFC system shown in Figure 6D are all within their temperature constraints.

FIGURE 6

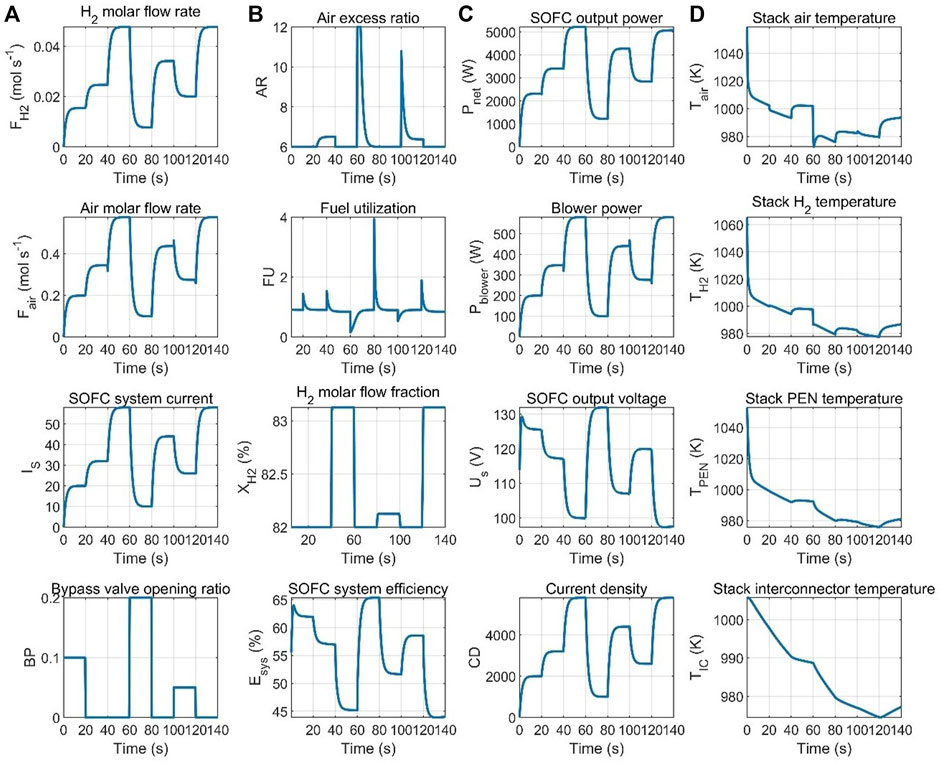
FIGURE 6. Characteristics of the SOFC-based DC microgrid system. (A) Input characteristic and stack remain H₂ molar flow fraction; (B) related outputs considering efficiency and fuel exhaustion; (C) output electrical characteristic; and (D) Output thermal characteristic.

The performances of the SOFC-based DC microgrid system is shown in Figure 7. The DC/DC inputs (Figure 7A) responses based on the SOFC system outputs and load changes, and the current is well limited to its maximum reference current (60 A). The DC/DC voltage outputs (Figure 7B) are well regulated at 220 V, and the power outputs can well meet the load requirements. Figure 7C shows the duty and efficiency to deal with voltage stability and the energy convert and transfer efficiency (40%–60%) in the proposed DC microgrid.

FIGURE 7

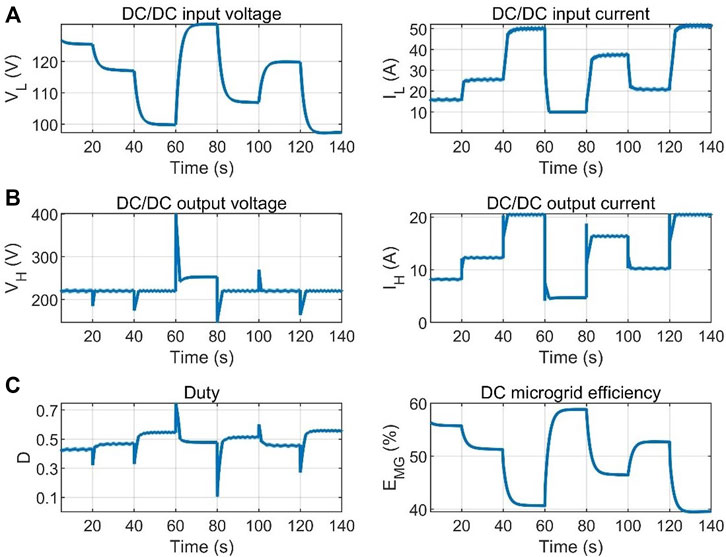
FIGURE 7. Performances of the SOFC-based hybrid DC microgrid system. (A) DC/DC inputs; (B) DC/DC outputs; and (C) Duty and DC microgrid efficiency.

4 Conclusion

This article presented the optimization and control strategy for the SOFC-based hybrid DC microgrids from the perspective of high efficiency, thermal safety fuel exhaustion, and transient response. The structure of the SOFC-based DC microgrid is first introduced. Moreover, the hybrid system has been modeled, especially the SOFC stand-alone system core part stack is validated with the experiments for the more precise corresponding electrical characteristics in the DC microgrid. Considering the high efficiency, steady-state thermal safety, and load tracing, the optimization and control strategy based on the voltage and current regulator and OOPs for the SOFC-based DC microgrid is implemented. The performance shows that the proposed DC microgrid has the large amount of hydrogen in stack (≥82%), thermal safety, voltage stability (220 V), and high efficiency (40%–60%). An alternative is to design the optimization, control, and energy management strategy to optimize all the performance of the SOFC-based DC microgrid, such as the SOFC/battery/supercapacitor-based DC microgrid, which is the next topic for our further studies.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

LZ: experiments, research methods, data processing, writing—original draft, and funding acquisition. HX: writing—original draft, resources, supervision, project administration, and funding acquisition. WT: experiment guidance. FW: experiment guidance. CX: performed writing—review. WZ: performed writing—review. All authors have contributed to the manuscript and approved the submitted version.

Funding

This work was co-supported by the Guangdong Basic and Applied Basic Research Foundation (No. 2021A1515010768), by the Science and Technology Talents Foundation Project of Air Force Early Warning Academy (No. 2021KJY11), by the Fundamental Research Funds for the Central Universities, Sun Yat-sen University (No. 2022ZZ028), by the National Natural Science Foundation of China (No. 61801510), and by the National Science Foundation of Hubei Province (No. 2019CFB263).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

All authors would like to thank the handling editors and reviewers for their very competent comments and constructive suggestions to improve this article.

References

Ahmed, O. A., and Bleijs, J. A. M. (2013). Power Flow Control Methods for an Ultracapacitor Bidirectional Converter in DC Microgrids-A Comparative Study. Renew. Sustain. Energy Rev. 26, 727–738. doi:10.1016/j.rser.2013.06.021

CrossRef Full Text | Google Scholar

Armghan, H., Yang, M., Wang, M. Q., Ali, N., and Armghan, A. (2020). Nonlinear Integral Backstepping Based Control of A DC Microgrid with Renewable Generation and Energy Storage Systems. Int. J. Electr. Power & Energy Syst. 117, 105613. doi:10.1016/j.ijepes.2019.105613

CrossRef Full Text | Google Scholar

Awais, M., Khan, L., Ahmad, S., and Jamil, M. (2021). Feedback-Linearization-Based Fuel-Cell Adaptive-Control Paradigm in a Microgrid Using a Wavelet-Entrenched NeuroFuzzy Framework. Energies 14 (71-17), 1850. doi:10.3390/en14071850

CrossRef Full Text | Google Scholar

Barnes, M. (2002). Fuel Cell System Explained. 2nd ed. New York, NY, USA: John Wiley.

Google Scholar

Carré, M., Brandenburger, R., Friede, W., Lapicque, F., Limbeck, U., and da Silva, P. (2015). Feed-Forward Control of A Solid Oxide Fuel Cell System with Anode Offgas Recycle. J. Power Sources 282 (15), 498–510. doi:10.1016/j.jpowsour.2015.02.053

CrossRef Full Text | Google Scholar

Deng, Y., Zhang, Y., Luo, F., and Mu, Y. (2021). Operational Planning of Centralized Charging Stations Utilizing Second-Life Battery Energy Storage Systems. IEEE Trans. Sustain. Energ. 12 (1), 387–399. doi:10.1109/TSTE.2020.3001015

CrossRef Full Text | Google Scholar

Eid, A. (2014). Utility Integration of PV-Wind-Fuel Cell Hybrid Distributed Generation Systems under Variable Load Demands. Int. J. Electr. Power & Energy Syst. 62 (11), 689–699. doi:10.1016/j.ijepes.2014.05.020

CrossRef Full Text | Google Scholar

Gandini, D., and de Almeida, A. T. (2017). Direct Current Microgrids Based on Solar Power Systems and Storage Optimization, as A Tool for Cost-Effective Rural Electrification. Renew. Energy 111, 275–283. doi:10.1016/j.renene.2017.04.009

CrossRef Full Text | Google Scholar

Hajimolana, S. A., Tonekabonimoghadam, S. M., Hussain, M. A., Chakrabarti, M. H., Jayakumar, N. S., and Hashim, M. A. (2013). Thermal Stress Management of A Solid Oxide Fuel Cell Using Neural Network Predictive Control. Energy 62 (1), 320–329. doi:10.1016/j.energy.2013.08.031

CrossRef Full Text | Google Scholar

Hirsch, A., Parag, Y., and Guerrero, J. (2018). Microgrids: A Review of Technologies, Key Drivers, and Outstanding Issues. Renew. Sustain. Energy Rev. 90, 402–411. doi:10.1016/j.rser.2018.03.040

CrossRef Full Text | Google Scholar

Huo, H.-B., Wu, Y.-X., Liu, Y.-Q., Gan, S.-H., and Kuang, X.-H. (2010). Control-oriented Nonlinear Modeling and Temperature Control for Solid Oxide Fuel Cell. J. Fuel Cell Sci. Technol. 7 (4), 0410051–0410059. doi:10.1115/1.3211101

CrossRef Full Text | Google Scholar

Li, Y. H., Choi, S. S., and Rajakaruna, S. (2005). An Analysis of the Control and Operation of A Solid Oxide Fuel-Cell Power Plant in an Isolated System. IEEE Trans. Energy Convers. 20 (2), 381–387. doi:10.1109/TEC.2005.847998

CrossRef Full Text | Google Scholar

Li, Y., Wu, Q., and Zhu, H. (2015). Hierarchical Load Tracking Control of a Grid-Connected Solid Oxide Fuel Cell for Maximum Electrical Efficiency Operation. Energies 8 (3), 1896–1916. doi:10.3390/en8031896

CrossRef Full Text | Google Scholar

Lingchong, X., Ibragimova, A. V., and Shilova, K. I. (2022). Analysis of International Practice in the Use of Renewable Energy Sources (RES). IOP Conf. Ser. Earth Environ. Sci. 979, 012188. doi:10.1088/1755-1315/979/1/012188

CrossRef Full Text | Google Scholar

Liu, Z., Zhao, J., and Zou, Z. (2020). Impedance Modeling, Dynamic Analysis and Damping Enhancement for DC Microgrid with Multiple Types of Loads. Int. J. Electr. Power & Energy Syst. 122 (1-12), 106183. doi:10.1016/j.ijepes.2020.106183

CrossRef Full Text | Google Scholar

Mumtaz, S., Khan, L., Ahmed, S., and Badar, R. (2018). Correction: Indirect Adaptive Soft Computing Based Wavelet-Embedded Control Paradigms for WT/PV/SOFC in A Grid/Charging Station Connected Hybrid Power System. PLoS ONE 13 (4), e0195914–17. doi:10.1371/journal.pone.0195914

PubMed Abstract | CrossRef Full Text | Google Scholar

Padulles, J., Ault, G. W., and McDonald, J. R. (2000). An Integrated SOFC Plant Dynamic Model for Power Systems Simulation. J. Power Sources 86 (1), 495–500. doi:10.1016/S0378-7753(99)00430-9

CrossRef Full Text | Google Scholar

Pranita, R., Sanjoy, K. M., and Sujit, K. B. (2022). Renewable Energy Generation System Connected to Micro Grid and Analysis of Energy Management: A Critical Review. Int. J. Power Electron. Drive Syst. 13 (1), 470–479. doi:10.11591/ijpeds.v13.i1

CrossRef Full Text | Google Scholar

Singhal, S. C., and Kendall, K. (2003). High Temperature Solid Oxide Fuel Cells: Fundamentals, Design, and Applications. New York, NY, USA: Elsevier.

Google Scholar

Sorrentino, M., Pianese, C., and Guezennec, Y. G. (2008). A Hierarchical Modeling Approach to the Simulation and Control of Planar Solid Oxide Fuel Cells. J. Power Sources 180 (1), 380–392. doi:10.1016/j.jpowsour.2008.02.021

CrossRef Full Text | Google Scholar

Srinivasan, M., and Kwasinski, A. (2020). Control Analysis of Parallel DC-DC Converters in A DC Microgrid with Constant Power Loads. Int. J. Electr. Power & Energy Syst. 122 (4), 106207. (1-9). doi:10.1016/j.ijepes.2020.106207

CrossRef Full Text | Google Scholar

Wang, Y., Li, S., Sun, H., Huang, C., and Youssefi, N. (2022). The Utilization of Adaptive African Vulture Optimizer for Optimal Parameter Identification of SOFC. Energy Rep. 8, 551–560. doi:10.1016/j.egyr.2021.11.257

CrossRef Full Text | Google Scholar

Xie, H., Hu, J., Duan, K., and Wang, G. (2020). High-Efficiency and High-Precision Reconstruction Strategy for P-Band Ultra-Wideband Bistatic Synthetic Aperture Radar Raw Data Including Motion Errors. IEEE Access 8, 31143–31158. doi:10.1109/ACCESS.2020.2971660

CrossRef Full Text | Google Scholar

Zakzouk, N. E., Khamis, A. K., Abdelsalam, A. K., and Williams, B. W. (2019). Continuous-Input Continuous-Output Current Buck-Boost DC/DC Converters for Renewable Energy Applications: Modelling and Performance Assessment. Energies 12 (11), 2208. doi:10.3390/en12112208

CrossRef Full Text | Google Scholar

Zhang, L., Jiang, J., Cheng, H., Deng, Z., and Li, X. (2015a). Control Strategy for Power Management, Efficiency-Optimization and Operating-Safety of a 5-kW Solid Oxide Fuel Cell System. Electrochimica Acta 177, 237–249. doi:10.1016/j.electacta.2015.02.045

CrossRef Full Text | Google Scholar

Zhang, L., Li, X., Jiang, J., Li, S., Yang, J., and Li, J. (2015b). Dynamic Modeling and Analysis of A 5-kW Solid Oxide Fuel Cell System from the Perspectives of Cooperative Control of Thermal Safety and High Efficiency. Int. J. Hydrogen Energy 40, 456–476. doi:10.1016/j.ijhydene.2014.10.149

CrossRef Full Text | Google Scholar

Zhang, L., Shi, S., Jiang, J., and Li, X. (2019). Current-based MPC for Operating-Safety Analysis of a Reduced-Order Solid Oxide Fuel Cell System. Ionics 25 (4), 1759–1772. doi:10.1007/s11581-018-2654-8

CrossRef Full Text | Google Scholar

Zhang, L., Shi, S., Jiang, J., Wang, F., Xie, H., Chen, H., et al. (2018). An Optimization and Fast Load-Oriented Control for Current-Based Solid Oxide Fuel Cell System. J. Solid State Electrochem 22 (18), 2863–2877. doi:10.1007/s10008-018-3996-x

CrossRef Full Text | Google Scholar

Zhang, X., Chan, S. H., Li, G., Ho, H. K., Li, J., and Feng, Z. (2010). A Review of Integration Strategies for Solid Oxide Fuel Cells. J. Power Sources 195 (3), 685–702. doi:10.1016/j.jpowsour.2009.07.045

CrossRef Full Text | Google Scholar

Zhang, Y., Meng, K., Luo, F., Yang, H., Zhu, J., and Dong, Z. Y. (2020a). Multi-agent-based Voltage Regulation Scheme for High Photovoltaic Penetrated Active Distribution Networks Using Battery Energy Storage Systems. IEEE Access 8, 7323–7333. doi:10.1109/ACCESS.2019.2962717

CrossRef Full Text | Google Scholar

Zhang, Y., Xu, Y., Yang, H., and Dong, Z. Y. (2019). Voltage Regulation-Oriented Co-planning of Distributed Generation and Battery Storage in Active Distribution Networks. Int. J. Electr. Power & Energy Syst. 105, 79–88. doi:10.1016/j.ijepes.2018.07.036

CrossRef Full Text | Google Scholar

Zhang, Y., Xu, Y., Yang, H., Dong, Z. Y., and Zhang, R. (2020b). Optimal Whole-Life-Cycle Planning of Battery Energy Storage for Multi-Functional Services in Power Systems. IEEE Trans. Sustain. Energy 11 (4), 2077–2086. doi:10.1109/TSTE.2019.2942066

CrossRef Full Text | Google Scholar

Zhu, Y., and Tomsovic, K. (2002). Development of Models for Analyzing the Load-Following Performance of Microturbines and Fuel Cells. Electr. Power Syst. Res. 62 (1), 1–11. doi:10.1016/S0378-7796(02)00033-0

CrossRef Full Text | Google Scholar