Data-Driven Optimization of Transmission Section Limits and Their Adaptability for New Power Systems With High Penetration of Renewable Energy

In traditional power systems, the transmission section limits are often set to predetermined values according to the typical peak-to-valley demand modes, which may be difficult to adapt to the complex and diverse operation modes of the new power systems with high penetration of renewable energy, and it cannot consider the coupling characteristics of AC and DC transmission sections also. In order to make better use of the efficiency of the transmission sections, a mathematical model for optimizing the adaptability of the transmission section limit is firstly proposed, in which a data-driven typical demand mode extraction method based on K-means clustering is proposed according to the load forecast, renewable energy forecast and market transaction data. Then, the adaptability assessment of the section limit and the transmission requirements are carried out. Finally, the power perturbation method is used to calculate the influence factor matrix of associated transmission section limit and stability margin of its dominant fault. And the influence factors are optimized according to section limit adaptability and stability margin influence, and the best adaptable limit of the associated transmission sections are obtained. The calculation and optimization results of the actual case of the interconnection corridor between Xinjiang and the northwest main power system of China verify the effectiveness and practicability of the proposed limit optimization model, which is able to improve the flexibility and adaptability of the actual power system operation.

1 Introduction

With the advancement of the new power systems, the development of renewable energy will be further accelerated, the operation mode of the power system with high penetration of renewable energy will become more and more complex and changeable, and the pressure of power supply guarantee and renewable energy consumption will increase significantly (Li, 2016). At the same time, the rapid development of ultra-high voltage direct current (UHVDC), the coupling degree of AC and DC power systems has been continuously improved. Thereafter, the correlation between associated transmission section limits and the complexity of power system control will also increase. In the actual operation of power systems, the operators usually select a number of transmission lines connecting the load center and the power generation center according to the geographical location, which are called transmission sections. The critical transmission section limits are of great significance to the secure and stable operation and control of the power systems. The traditional method of pre-setting transmission section limits based on extreme typical demand modes is often difficult to adapt to the complex and changeable characteristics of the new power systems, resulting in the system being unable to reliably balance the supply and demand. At present, it is urgent to carry out the adaptability evaluation and optimization of the associated transmission section limit, under the circumstances of complex and diverse operation modes of the new power systems.

During the traditional power system operation, the system operators can monitor the key transmission sections of the complex large power system, and form a set of secure operation knowledge base for the power system based on the section information and its control rules (Zhou et al., 2006). Ilic et al. (Ilic et al., 1998), obtain the transmission section limit through offline simulations under typical and extreme operation modes. On this basis, Zhao et al. (Zhao et al., 2015), ensure that the section power flow is less than the transmission section limit, and adjust the power system operation mode according to the operation experience by online monitoring the overloaded and over-limited sections of the above sections. Therefore, the current research on the associated transmission section limits mainly focuses on the identification method of the transmission section and the calculation method of the transmission section limit under various security constraints. In (Zhang and Liu, 2015; Fu, 2017; Wang et al., 2017), a model-driven online security analysis method driven is proposed, however, it is rather difficult to be implemented in actual large-scale power systems due to heavy computational burdens. In terms of off-line research, Jiang et al. (Jiang et al., 2008), propose a continuous power flow method to determine the extreme generation-load growth mode and obtain the transmission section limit, which combines the power flow sensitivity analysis for static security assessment and the transient energy function sensitivity analysis for transient stability assessment. Fang et al. (Fang et al., 2015), consider the transient stability limit coupling between different transmission sections of the power system, and aim to calculate the limit power of multiple transmission sections through iterative optimization, by obtaining the critical stable states of multiple sections that reach their the power limits simutaneously. An automatic search method for key transmission sections based on complex network theory is proposed in (Luo et al., 2013), which lays a foundation for real-time state monitoring and rapid analysis of power systems. Ejebe, et al. (Ejebe et al., 1998; Ejebe et al., 1999), propose a linear algorithm that can quickly calculate the available transmission capacity. In calculating the available transmission capacity, the sensitivity of the power transfer distribution factor and the branch disconnection distribution factor are used to perform the linear estimation of the changes of the available transmission capacity. Xu et al. (Xu et al., 2012), propose a parallel security check and search strategy of binning iteration, which effectively solves the problems of the large amount of calculation for associated transmission sections. Huo et al. (Huo et al., 2016), propose an AC cross-section identification method that is strongly correlated with DC transient stability, which is based on time-domain simulation, quantitative analysis and curve fitting, and it can only be used for offline analysis. Luo et al. (Luo et al., 2000), introduce the artificial intelligence technology to predict the available transmission capacity, and calculate the available transmission capacity based on the continuous power flow method as well as the adaptive positioning technology. The inputs are generator state parameters, line state parameters and load state parameters, and the authors have achieved reasonably good results considering the thermal stability, voltage stability and power angle stability.

In terms of typical operation modes extraction, Huang et al. (Huang et al., 2016), pointed out that there is a long tail effect in the sample set of actual operation data of the regional power system, and there are few unstable fault samples in the online data, and even in the offline data, the number is very small. Chen et al. (Chen et al., 2019), propose a method for generating power system simulation samples based on long short-term memory network algorithm, which collects and processes the user adjustment power flow behavior data in the process of offline data simulation of power system calculation. At present, the data improvement research based on data-driven transient stability assessment can be divided into two categories: under-sampling methods and over-sampling methods (Tan et al., 2018). The under-sampling method will lose most of the data information, so its application scope is limited. Ren et al. (Ren et al., 2022), start to investigate a new transmission mode extraction method, which is a useful exploration for the study of the clustering of complex operation modes of the power system with high proportion of renewable energy. Zhou et al. (Zhou et al., 2021), propose a double layer labeling (DLL) model based on two independent Bidirectional Encoder Representation from Transformers and Long Short-Term Memory and Conditional Random Fields networks (BERT-BiLSTM-CRF) to study the information extraction method to obtain grid operation rules. Cui et al. (Cui et al., 2020), propose a data-driven slow dynamic characteristic extraction and state estimation method to solve the computation speed problem of large power grid system state calculation by load prediction multiplied by jacobian inverse matrix. Mehmet et al. (Büyük et al., 2019), present a novel harmonic extraction method named as “virtual input signal based instantaneous power theory (VIS-IPT)” which is tested in a shunt active power filter (SAPF) for improving the performance under unbalanced electrical energy quality issues. Mohamed G et al. (Mohamed et al., 2018), propose an advanced strategy to synchronize the wind-driven Brushless Doubly-Fed Reluctance Generator (BDFRG) to the grid-side terminals.

The existing researches on the calculation of critical transmission section limit of complex power systems are mostly model-driven, and the results mainly focus on the optimization of the available transmission capacity of the power system and may not be able to be applied for online use. In addition, with the continuous growing of renewable energy sources such as wind and photovoltaic power, the uncertainty from both source and load sides has become increasingly prominent, and there are very few studies on the evaluation and optimization of transmission section limit adaptability to the new power systems. Moreover, UHV DC is gradually put into operation, thus the impact of large-capacity AC or DC faults and the multi-section coupling of AC and DC increase greatly, the combination and redistribution of power flow after faults will aggravate this impact on the system stability, and the correlation between associated transmission section limits will be more prominent. Therefore, a new method that fully considers the temporal and spatial distribution characteristics of renewable energy sources is needed. And the adaptability evaluation and coordinated optimization of the associated transmission section limits also need to be carried out, considering various types of uncertain factors.

This paper aims to propose a new data-driven optimization method of the transmission section limit and its adaptability for new power systems with high penetration of renewable energy. The method adopts the multi-dimensional K-means clustering method, and uses the renewable energy and load power forecast data to obtain the typical transmission demand modes of multiple associated transmission sections. Then the concept of influence factor of the section limit stability margin is constructed, and a coordinated optimization model of the transmission section limit is proposed, based on an iterative method to achieve the best match between the limit and the transmission demand. Finally, the proposed method is demonstrated on the case of the Northwest Power system of China.

2 Data-Driven Typical Demand Mode Extraction Method

In traditional power systems, the transmission section limits are often set to predetermined values according to the typical peak-to-valley demand modes, which may be difficult to adapt to the complex and diverse operation modes of the new power systems with high penetration of renewable energy. According to the day-ahead renewable energy forecast and the energy trading plan, it is possible to determine the demand of multiple transmission sections that are strongly associated to the critical fault stability margin at each moment, and integrate the values of multiple transmission sections at each moment into a multi-dimensional vector. Aiming at the complex and diverse transmission demand requirements of associated transmission sections, the K-means method is used to realize multi-dimensional vector clustering. After setting the number of cluster categories, the K-means clustering method can automatically calculate and find the optimal center point of each category, and then the Elbow Rule is used to obtain the optimal number of clusters of the assoicated sections, that is, calculate the sum of squared errors as follows:

$\mathit{SSE}={\displaystyle \sum _{\mathit{i}=1}^{\mathit{k}}{\displaystyle \sum _{\mathit{p}\in {\mathit{c}}_{\mathit{i}}}{\left|\mathit{p}-{\mathit{q}}_{\mathit{i}}\right|}^2}}(1)$

Where: $C_i$ is the $i$-th cluster; $p$ is the sample point in $C_i$; $q_i$ is the centroid of $C_i$, and $SSE$ is the clustering error of all samples, representing the performance of the clustering method.

As the number of clusters $k$ increases, the sample clustering will be more refined, and the aggregation degree of each cluster will gradually increase, so the $SSE$ will naturally become smaller. Moreover, when $k$ is smaller than the real number of clusters, the increase of $k$ will greatly increase the aggregation degree of each cluster, so the $SSE$ will be greatly decreased. When $k$ reaches the real number of clusters, the aggregation degree reward obtained by increasing $k$ will become smaller, so the decrease in $SSE$ will be smaller. Then, the $SSE$ tends to be flat with the continuous increase of $k$, that is, the relationship between $SSE$ and $k$ is an elbow shape, and the $k$ value corresponding to this elbow will be the optimal number of clusters. The flowchart for this clustering method is shown in Figure 1.

FIGURE 1

FIGURE 1. Flowchart of the data-driven clustering process.

After obtaining the optimal number of clusters, the Euclidean distance between each center point and the samples within this cluster can have the mean square error of about 2–14%. Considering the constraints of actual power system operation, it is recommended to multiply the value of the center point of each cluster by 1.15 as a typical demand mode, namely, using the equivalent maximum value of each cluster as the typical demand mode, so as to meet the power transmission requirements of all samples within this cluster.

The typical demand modes obtained by the proposed K-means clustering method can be compared with the initial stability limit to evaluate the adaptability of the initial limit, and the transmission section limit insufficieny index is defined in Eq. 2. This indicator reflects the shortage and optimization of the transmission section limit. When the indicator is greater than 1, it indicates that the section demand is greater than the limit, the limit is insufficient, and the optimization will be difficult. On the contrary, when the indicator is less than 1, it indicates that the limit is sufficient and the optimization will be easy to achieve.

$\mathit{\rho }=\frac{{\displaystyle \sum _{\mathit{i}=1}^{\mathit{l}}\frac{\left({\mathit{P}}_{\mathit{i},\mathit{demand}}-{\mathit{P}}_{\mathit{i},\mathit{limit}}\right)}{\mathit{l}\ast {\mathit{P}}_{\mathit{i},\mathit{limit}}}}}{{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}\frac{\left({\mathit{P}}_{\mathit{j},\mathit{limit}}-{\mathit{P}}_{\mathit{j},\mathit{demand}}\right)}{\mathit{m}\ast {\mathit{P}}_{\mathit{j},\mathit{limit}}}}}(2)$

Where: l is the number of transmision sections whose demand is greater than the initial limit of the section; m is the number of transmission sections whose demand is less than the initial limit of the section; $P_{i,demand}$ and $P_{i,limit}$ are the demand and limit of section i under the initial demand mode, respectively.

According to the sectioin limit insufficiency index $\mathit{\rho }$, if the initial pre-planned section limit cannot meet the typical demand mode, the overall optimization of the associated transmission section limit can be carried out according to the method proposed in the following .

3 Coordinated Optimization Model of Associated Transmission Section Limits

3.1 Mathematical Model

The post-fault stability of the power system is closely associated to the severity of the fault and the actual operating status of the power system. Under the same fault condition, the unit commitment mode, nodal voltage level and nodal/branch power flow will also affect the post-fault stability. A large number of simulation analyses show that the system stability level under critical dominant faults is negatively correlated with the transmission power of the relevant transmission sections. Generally, the higher the section power, the lower the post-fault stability level. During actual operating statuses, in order to facilitate monitoring and control for the system operators, the transmission section power is also used as a key characteristic quantity reflecting the system stability after certain faults, which is a practical engineering method (Tu et al., 2017; Fang et al., 2018; Qiu et al., 2019; Wang et al., 2020).

With the advancement of the construction of new power systems with high penetration rate of renewable energy, great changes have taken place in the traditional source side, grid side, and load side. On the one hand, the impact of UHV DC faults is much greater than traditional AC short circuit faults, which is highly associated to the coupling effect of the multi-section transmission power in the neighbouring area. On the other hand, the power generation of renewable energy sources is fluctuating and intermittent, so the power of each section fluctuates greatly in different time and space. The traditional fixed-value transmission section limits are difficult to adapt to the complex and changeable operation and control requirements of the new power system, because it is difficult to give full considerations of all possible operation statuses of the power system. Inappropriate section limits may even cause transmission congestion or renewable energy restrictions during actual system operations.

In the traditional power system, the stability level of the power system after a certain fault is mostly related to the power of a single section in the nearby area, and the correlation between sections is always weak. In a high proportion of renewable energy power systems, through a large number of calculations and analysis, it is found that for the same disturbance or fault, the stability of the power system can be related to the power of multiple sections, and these sections are highly correlated with the disturbances or faults. Different section power combinations also have different influences on the stability levels. According to the calculation standard of the power system stability guideline, the power limits of these sections have a trade-off relationship under a certain stability margin, and these sections are called associated transmission sections.

To ensure that the transmission capacity under different power system demand modes can meet the transmission of the fluctuating renewable energy, it is necessary to flexibly set the power stability limit of each transimission section according to the stability characteristics of the power system under different demand modes and various security constraints. The mathematical model for optimizing the adaptability of the transmission section limits can be described as follows.

$\{\begin{array}{c}\mathbf{min}{\displaystyle \sum _{\mathit{i}=1}^{\mathit{k}}{\displaystyle \underset{\mathit{t}0}{\overset{\mathit{t}}{\int }}\left({\mathit{P}}_{\mathit{i},\mathit{demand}}-{\mathit{P}}_{\mathit{i},\mathit{limit}}\right)}}\\ \mathbf{s}.\mathbf{t}. \begin{array}{c}\mathbf{g}\left({\mathit{P}}_{1,\mathit{limit}},{\mathit{P}}_{2,\mathit{limit}},\dots ,{\mathit{P}}_{\mathit{k},\mathit{limit}}\right)=\mathbf{0}\\ {\mathit{\eta }}_{\mathit{j}}\left({\mathit{P}}_{1,\mathit{limit}},{\mathit{P}}_{2,\mathit{limit}},\dots \mathrm{..},{\mathit{P}}_{\mathit{k},\mathit{limit}}\right)>\mathit{\epsilon }, \mathit{j}=\mathbf{1,2},\dots ,\mathit{m}\end{array}\end{array}(3)$

Where: $g$ is the power flow constraint of the power system; $\mathit{ }\epsilon$ is the minimum margin requirement for system stability; ${\eta }_j$ is the system stability margin under fault $j$. The adaptability of transmission section limits refer to the maximum active power that the section can transmit. And it is obtained by simulating and calculating a large number of section operating modes with the software PSASP.

Due to the nonlinear and time-varying characteristics of the power system stability problems, it is difficult to express the relationship between the stability margin and the section power in an explicit way. In this paper, by calculating the influence factors of the section power and dominant faults, and using the influence factors as adjustment reference, the “global-local” iterative method is used to solve the optimal power stability limit.

3.2 Solving Method

After establishing the mathematical model for optimizing the adaptability of the transmission section limits as shown in , it is necessary to solve the optimization problem according to the typical demand modes in Section 2. The optimal associated transmission section limits can be realized by setting the limit according to the real demand of the power system within a certain range, and the forecast data of fluctuating load and renewable energy. Based on the forecast data, the solving process can use the offline transient stability simulation software with models and parameters of the system dynamic components, i.e. PSS/E from Siemens or PSASP from CEPRI, and the key section data from the actual power system operations for analysis. The flowchart of the optimization solving process can be shown in Figure 2.

FIGURE 2

FIGURE 2. Flowchart of associated transmission section limits optimization method.

Step 1: According to the power system stability guideline, firstly select the $n$ associated transmission sections and $m$ dominant faults of the power system. Then determine the initial stability limit according to the time domain simulation and the system stability characteristics under the dominant fault. And then increase the section power gradually in a balanced manner, according to the section limit and stability margin influence factor (detailed description can be found in ); and take the power of each associated transmission section when the dominant fault stability margin meets the critical stability condition as the initial stability limit. When the initial limit is obtained, the stability margin of each dominant fault can be controlled to decrease synchronously, and each section limit can be increased in a balanced manner according to the influence factor matrix, so as to realize the global adjustment of the limit.

Step 2: Determine the transmission demand of each section at different times of the next day, according to the load and renewable energy forecast. In order to avoid inappropriate transmission section limits and difficult switching control during operation, the data-driven clustering method is used to determine the main typical demand modes.

Step 3: Compare the typical demand mode obtained by the K-means clustering method with the initial stability limit, and calculate the limit insufficiency index. When the initial limit meets the requirements of the typical demand mode, go to Step 5; otherwise, go to Step 4.

Step 4: When the initial limit does not meet the requirements of the typical demand mode, the power perturbation method is used to obtain the influence factor matrix of the section limit and the stability margin, according to the initial stability limit scheme.

Step 5: According to the influence factor matrix and stability margin obtained in Step 4, and the limit insufficiency index acquired in Step 3, heuristically increase the section limit that does not meet the transmission demand and reduce the section limit that exceeds the section demand and has the highest sensitivity, so that the difference between the section limit and its transmission demand can be minimized.

Step 6: Repeat Step 5 until the adjusted limit satisfies the transmission demand of the typical demand mode or the stability margin of the dominant fault reaches the critical value, then the section limit under the demand mode on the next day can be obtained.

The proposed transmission section limit optimization method has the following advantages:

(1) In the traditional method, it is assumed that the limits of the associated transmission sections are evenly distributed. But in the actual operation of a high-proportion renewable energy power system, due to the randomness of the renewable energy sources, the power transmission demand of each section is unbalanced, and the difference is sometimes very large. Therefore, the initial section limit of balanced distribution needs to be optimized according to actual demand mode. The proposed method is able to make the power of multiple associated transmission sections reach the critical stable operating point at the same time so as to obtain a stable limit combination. And then it can take a balanced distribution of the limit of each associated transmission section as the initial value to optimize and adjust the section limit, according to the real transmission demand.

(2) The proposed method is able to obtain the typical demand combinations through the data-driven clustering technique, and then calculate the influence factor matrix of the section power and stability margin, which guides the adjustment direction of the section limit in the iterative process and makes the iterative adjustment easier to converge.

(3) The proposed method is able to correct the influence factors of the section limit and stability margin at each step, which solves the strong nonlinearity and time-varying problem of power system stability and considers the stability mode change caused by the change of power flow. The stability margin influence factor is mainly used to guide the adjustment direction of the associated transmission section limits combination, and its accuracy will affect the algorithm efficiency, but will not affect the accuracy of the results and the level of system stability.

3.3 Calculation of Influence Factor Matrix

For different types of faults, different stability margin calculation methods are required. The commonly used methods include EEAC (extended equal area criterion), transient voltage margin, and other methods (Büyük et al., 2019; Cui et al., 2020). The quantitative indicators of the stability margin under different faults are always different. Taking the common transient voltage stability problem as an example, since the degree of voltage fluctuation after the fault often reflects the anti-disturbance capability of the power system (Xu et al., 2012), the stability margin after faults can be characterized by the integral value of voltage fluctuation, which is defined as follows.

${\mathit{\eta }}_{\mathit{j}}=\underset{{\mathit{t}}_{\mathit{c}}}{\overset{{\mathit{t}}_{\mathit{c}}+\mathbf{10}}{{\displaystyle \int }}}{\mathit{R}}_{\mathit{i},\mathit{j}}\left(\mathit{t}\right)\mathit{dt},{\mathit{R}}_{\mathit{i},\mathit{j}}\left(\mathit{t}\right)=\{\begin{array}{cc}\left|{\mathit{U}}_{\mathit{i},\mathit{j}}\left(\mathit{t}\right)-\mathbf{0.9}\right|& {\mathit{U}}_{\mathit{i},\mathit{j}}\left(\mathit{t}\right)\le \mathbf{0.9}\mathit{p}.\mathit{u}\\ \mathbf{0}& {\mathit{U}}_{\mathit{i},\mathit{j}}\left(\mathit{t}\right)>\mathbf{0.9}\mathit{p}.\mathit{u}\end{array}(4)$

Where: ${\eta }_j$ is the stability index after the occurrence of fault j; $t_c$ is the fault clearing time; $U_{i,j}\left(t\right)$ is the voltage amplitude of bus i at time t after fault j occurs.

The stability margin describes the area where the bus voltage is lower than 0.9 p. u. during the post-fault transient process, which can quantify the severity of the bus transient voltage drop. According to a large number of calculations, when the value of ${\eta }_j$ is less than 100, the voltage can remain stable; when the value is greater than 120, the voltage will be unstable. A practical stability index of $\left(100-{\eta }_j\right)$ is selected for calculation in this paper. During the iterative calculation process, it is necessary to ensure that $\left(100-{\eta }_j\right)$ needs to be greater than $\epsilon >0$, so as to ensure the system stability.

Because the power system is highly time-varing and nonlinear, it is difficult to express the relationship between the stability margin and characteristic quantity in an analytical way. Therefore, the concept of influence factor is proposed to quantify the influence of the characteristic quantity on the stability margin within a certain range. When analyzing the influence factors of multiple fault-dominated associated transmission sections, their relationship can be represented by Eq. 5, in which the stability margin influence factors of the section limit is a linear matrix as shown in Eq. 6.

$\mathit{\Delta \eta }=\mathit{J\Delta P}(5)$

$\mathit{J}=\left[\begin{array}{cccc}\frac{\mathit{\Delta }{\mathit{\eta }}_1}{\mathit{\Delta }{\mathit{p}}_1}& \frac{\mathit{\Delta }{\mathit{\eta }}_1}{\mathit{\Delta }{\mathit{p}}_2}& \dots & \frac{\mathit{\Delta }{\mathit{\eta }}_1}{\mathit{\Delta }{\mathit{p}}_{\mathit{n}}}\\ \frac{\mathit{\Delta }{\mathit{\eta }}_2}{\mathit{\Delta }{\mathit{p}}_1}& \frac{\mathit{\Delta }{\mathit{\eta }}_2}{\mathit{\Delta }{\mathit{p}}_2}& \dots & \frac{\mathit{\Delta }{\mathit{\eta }}_2}{\mathit{\Delta }{\mathit{p}}_{\mathit{n}}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\mathit{\Delta }{\mathit{\eta }}_{\mathit{m}}}{\mathit{\Delta }{\mathit{p}}_1}& \frac{\mathit{\Delta }{\mathit{\eta }}_{\mathit{m}}}{\mathit{\Delta }{\mathit{p}}_2}& \dots .& \frac{\mathit{\Delta }{\mathit{\eta }}_{\mathit{m}}}{\mathit{\Delta }{\mathit{p}}_{\mathit{n}}}\end{array}\right](6)$

Where: $\mathrm{\Delta }{p}_n$ is the adjustment change of section $n$; $\mathrm{\Delta }P$ is the section limit adjustment change vector composed; $\mathrm{\Delta }{\eta }_m$ is the stability margin change when fault $m$ occurs, and $\mathrm{\Delta }\eta$ is the stability margin vector; $J$ is the stability margin influence factor matrix.

The main constraint is that the stability margin after a certain fault can be related to the power of cascaded transmission sections, and different section powers may have different effects on the stability margin. The meaning of influencing factor matrix of stability margin is to express the relationship between the stability margin and characteristic quantity through the relationship between the section limit and the stability margin vector. After the above matrix is obtained, it can be used to guide the limit adjustment and evaluate the stability of the system.

4 Case Study

At present, the power generation of renewable energy in the Northwest Power system of China has exceeded 20%, and the installed capacity reaches about 45%. It has the characteristics of the primary form of the new power system. Taking the interconnection of the interconnection between the Xinjiang district power system and the Northwest main grid as an example, this transmission section carries three UHVDC lines, bringing together nearly 50 million kilowatts of renewable energy along the transmission corridor.

On the one hand, due to the characteristics of renewable energy power fluctuations, the transmission demand of each section is always different in different time periods, and the transmission capacity of multiple sections is often inversely proportional to each other. On the other hand, the unbalanced energy of AC and DC faults is often very large, resulting in intertwined stability issues such as voltage, angle and frequency stability, et al. The critical section limits are related to various factors, such as: renewable energy power generation output in different regions, different generator unit comittment, different transformer power, etc., and the associated transmission section limit under different demand modes are quite different. Considering the most severe faults under the typical demand mode, it is necessary to pre-set the power of the transmission sections within a certain range in advance. When the section limit is established under the typical demand mode, it is always difficult to meet the transmission demand of different renewable energy generation outputs in actual operation, and thus it might cause renewable energy curtailment due to insufficient power transmission capacity of the power system.

Due to the different temporal and spatial distribution of renewable energy, the output of different renewable energy stations in different regions has a certain complementarity. Taking the interconnection between the Xinjiang district power system and the Northwest main grid as an example, the Haixi region in Qinghai Province is dominated by solar power, and the Hexi region in Gansu Province is dominated by wind power. When the wind power in Hexi is small, the demand for renewable energy transmission will probably be small, but it will also be influenced by the actual solar outputs in Haixi. It is necessary to study the various demand combinations for different transmission sections, considering the random and intermittent renewable energy stations, and flexibly adjust the section stability limit to meet the demand for power transmission and consumption in a new power system with high proportion of renewable energy.

4.1 Cluster Analysis of Typical Demand Modes of Multiple Sections

The structure diagram of the interconnection network between Xinjiang and the Northwest main grid is shown in Figure 3. The Xinjiang-Northwest interconnection channel is a long-chain, cascaded power transmission channel, and the channel limit has a strong correlation with XJWS transmission section, DY section, GY section, QY section, HY section, and QHHX solar power output. The temporal and spatial distributions of Hexi wind power base and Haixi photovoltaic base are quite different. Therefore, the distribution of the transmission demand of the associated transmission sections is uneven.

FIGURE 3

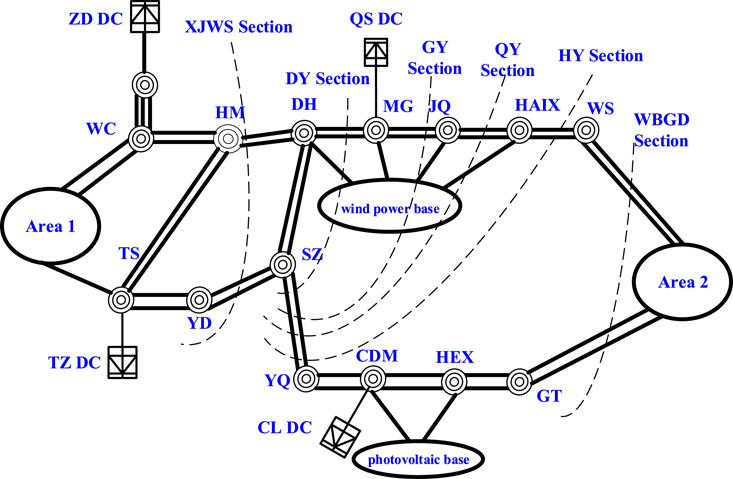
FIGURE 3. The structure diagram of the networked channel between Xinjiang district and Northwest main system.

To improve the overall transmission efficiency of the networking channels, it is necessary to obtain the typical transmission demand modes according to the power system operation conditions, and then carry out the overall optimization. Firstly, according to the load, renewable energy forecast, and the market transaction requirements, determine the transmission demand of XJWS section, DY section, GY section, QY section, HY section, and WBGD section, and use the clustering algorithm to obtain the typical demand mode for the system.

According to the typical day-ahead renewable energy forecast, load forecast and power transaction plan, the transmission demand of the above-mentioned sections in each time period of the objective day can be obtained. Using the K-means clustering method, the clustering results of a typical day can be divided into 4 categories with different colors, as shown in Figure 4. And the relationship between $SSE$ and the number of clusters is shown in Figure 5. It can be seen from Figure 4 that the traditional typical demand mode extraction method cannot obtain the regularity among various combinations of renewable energy stations. The clustering results obtained by the proposed K-means method are different from the traditional peak-to-valley demand modes. The method in this paper can better mine the random renewable energy and load data, and reflect the law of the demand mode of the power system.

FIGURE 4

FIGURE 4. Typical daily clustering results for the test system.

FIGURE 5

FIGURE 5. Relationship between the number of clusters and the $SSE$.

In order to further illustrate the advantages and practicability of the K-means clustering method, the clustering results of the three methods of K-means, DBSCAN and CLIQUE, which are showed in Figure 6, are compared. DBSCAN classifies the demand modes into three categories where there are still noise points that need to be excluded. If we want to continue to reduce the noise ratio, the lower limit of the density needs to be reduced, but at the same time, the clustering effect will be linked together into one category. Therefore, it is difficult to categorize the demand modes accordingly. CLIQUE also divides the demand mode into three categories, and its grid boundary can be divided by straight lines. But the divisions are irregular, it will be difficult to adjust the grid divisions in the actual power system, thus it is not suitable for the power system demand mode clustering. It can be seen from Figure 4 that the K-means clustering divides the demand modes into four categories, with clear boundaries between neibouring clusters, and the demand modes within each cluster have a high degree of similarity. And the boundaries can be described by fewer rules, and the corresponding rules can be easily formulated, which can well divide the areas with dense points together, thus it is suitable for the actual application of power system demand mode clustering.

FIGURE 6

FIGURE 6. DBSCAN and CLIQUE clustering effect.

There are certain differences in the shape and number of clusters generated by different clustering methods. However, considering the engineering practice, the most important purpose of dividing the power system demand modes is to formulate secure operation boundaries for the dispatch operations, as well as to provide support for the realization of power system economy, security, and renewable energy consumption goals. For the current power system operation and control applications, it is difficult to implement different control strategies for too many irregular demand modes in actual dispatch operation, because it will bring great trouble to the system operators in identifying and evaluating the demand modes. The K-means clustering method proposed in this paper can fully consider the current control technology level and divide the demand mode into several relatively regular clusters, which is convenient for dispatch operation and engineering realization. Therefore, the proposed K-means clustering method in this paper is more suitable for the classification of the demand mode of the power system.

4.2 Calculation and Verification of Section Limit Optimization and Adjustment

The center points of the four clusters in Figure 4 are then multiplied by a factor of 1.15 to generate the typical demand modes, which are shown Table 1. And the envelopes of the conventional section limit setting for the 4 typical demand modes are shown in Figure 7. It can be seen that in conventional transmission section limit analysis, only the cluster 4 fully satisfies the conventional mode classification, while the other three typical demand modes cannot be well satisfied. This is understandable since cluster 4 is equivalent to the typical peak-load demand mode in the conventional transmission section limits analysis. In order to meet the transmission demand, it is necessary to coordinate and optimize the conventional transmission section limits according to the actual data in the other three clusters.

TABLE 1

TABLE 1. Typical demand modes after K-means clustering (Unit:MW).

FIGURE 7

FIGURE 7. Envelope of the typical demand modes from conventional binning plan.

According to Eq. 6, the limit insufficiency indices of the 4 typical demand modes are calculated, which are 0, 0.29/2.5, 0.49/0.84, 0.34/0.48, respectively. It can be seen that demand modes 2, 3, and 4 still need to be optimized. For demand mode 2, the surplus part is large, and the insufficient part is small; therefore, it is easy to optimize. For demand mode 4, the proportion of the surplus part and the insufficient part is relatively coupled, and the optimization will be more difficult.

According to the proposed limit optimization method in , the limits of XJWS section, DY section, GY section, QY section, HY section and HXWS section can then be optimized. In the above test system, the main fault senarios are the commutation failure of Jiquan DC transmission line and the N-2 same-pole-different-phase short-circuit faults on the Hewu double-circuit lines (Xu et al., 2012). Taking the integral of post-fault transient voltage fluctuation as the quantitative index, and the matrices of the stability margin and the section power influence factor can be obtained, as shown in Table 2.

TABLE 2

TABLE 2. Key parameters during the iterative calculation process(Unit:MW).

Taking the optimization of demand mode 2 as an example, combined with the multiple section influence factor matrix and the transmission demand, the limit adjustment vector of each step can be obtained for the limit adaptability evaluation. It can be seen from Table 2 that, the optimization of demand mode 2 can be completed within three iterations. After the optimization, the demand insufficiency index of the typical mode 2 reaches 0, indicating that the optimized limit can meet the typical daily transmission demand during the relevant time period, which proves the effectiveness and practicability of the proposed method.

Moreover, according to the above method, the limit optimization for the clustered demand modes 3 and 4 are also carried out, and the optimized limits under various demand modes are shown in Table 3. In order to further verify the correctness and security of the optimized limit, the time-domain simulation verification is then carried out using the optimized stability limit to analyze the stability level of the power system under various faults. Figure 8 shows the post-fault voltage fluctuation curves of the weakest buses of the test system after the Jiquan DC commutation failure under the initial section limit and the other three optimized limits for the associated transmission sections. It can be seen that the voltage fluctuation curves under all the four limits are similar, and the stability margins are basically the same, which satisfies the power system operation requirements.

TABLE 3

TABLE 3. Optimized limits for the associated transmission sections(Unit:MW).

FIGURE 8

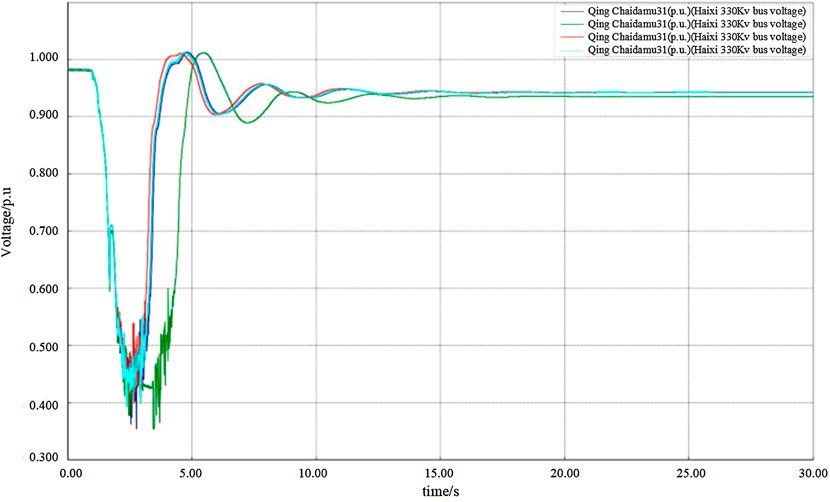
FIGURE 8. Voltage fluctuation curves under Jiquan DC commutation failure using the four section limits.

5 Conclusion

In the “double high” scenario with a high proportion of renewable energy sources and a high degree of power electronics integration, it is urgent to improve the power system control flexibility and satisfy the actual power system operation requirements to the greatest extent. In order to address the issue of adaptibility of the predetermined limits of the key transmission sections to the complex and diverse demand modes of the new power systems with high penetration of renewable energy, a novel data-driven method for optimizing the associated transmission section limit is proposed. The main conclusions are as follows.

(1) Aiming at the complex and changeable operation scenarios of high-proportion renewable energy power systems, considering the similarities and differences between the demand combinations of multiple associated transmission sections, a data-driven K-means method is used to extract the typical modes of transmission section demand and evaluate the adaptability of section limits.

(2) A concept of influence factor matrix of transmission section limit is presented, so as to quantify the stability margin of associated transmission section limits. Accordingly, a transmission section coordinated optimization model and solution method is proposed in this paper, which can adapt to the actual operation requirements of a high proportion of renewable energy power systems and improve the adaptability of associated transmission section limits.

(3) The northwest China power system is used to verify the proposed method, the optimized limits under various demand modes are tested using the time-domain analysis. The results have verified the correctness and security of the optimized limits, which demonstrates that the proposed method has both high computational efficiency and accuracy, and can meet the actual operation requirements of new power systems with high penetration of renewable energy.

In the follow-up research, the adjustment of the transmission section limits of the power system can be extended to various demand modes in modern smart distribution systems with more distributed generation and a variety of energy storage systems.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

MX proposes a mathematical model for optimizing the adaptability of the transmission section limit. KX proposes a data-driven typical demand mode extraction method based on K-means clustering. RC uses the power perturbation method to calculate the influence factor matrix of associated transmission section limit and stability margin of its dominant fault. WJ provides the load forecast, renewable energy forecast and market transaction data.

Conflict of Interest

Authors XM, XK, CR, and JW were employed by Northwest Branch of State Grid Co. Ltd.

This paper relies on the State Grid Corporation of China’s science and technology project “Research on Key Technologies of Frequency Correction Control in New Energy Field Cluster”.

The handling editor JL declared a shared affiliation with the author(s) MX at the time of review.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Büyük, M., İnci, M., Tan, A., and Tümay, M. (2019). Improved Instantaneous Power Theory Based Current Harmonic Extraction for Unbalanced Electrical Grid Conditions. Electr. Power Syst. Res. 177, 106014. doi:10.1016/j.epsr.2019.106014

CrossRef Full Text | Google Scholar

Chen, J., Chen, Y., and Tian, F. (2019). The Method of Sample Generation for Power Grid Simulation Based on LSTM. Proc. CSEE 39 (14), 4129–4134. doi:10.13334/j.0258-8013.pcsee.181622

CrossRef Full Text | Google Scholar

Cui, X., Ma, K., Meng, X., Zhang, X., Duan, F., Li, T., et al. (2020). “A Data-Driven Slow Dynamic Characteristic Extraction and State Estimation Method for Large Power Grid,” in 2020 IEEE student conference on electric machines and systems(SCEMS 2020), Jinan, China, 04-06 December 2020, 39–42. doi:10.1109/SCEMS48876.2020.9352371

CrossRef Full Text | Google Scholar

Ejebe, G. C., Tong, J., Waight, J. G., Frame, J. G., Wang, X., and Tinney, W. F. (1998). Available Transfer Capability Calculations. IEEE Trans. Power Syst. 13 (4), 1521–1527. doi:10.1109/59.736300

CrossRef Full Text | Google Scholar

Ejebe, G. C., Waight, J. G., Santos-Nieto, M., and Tinney, W. F. (1999). Fast Calculation of Linear Available Transfer Capability. IEEE Trans. Power Syst. 15 (3), 1112–1116. doi:10.1109/59.871741

CrossRef Full Text | Google Scholar

Fang, J., Su, C., Chen, Z., Sun, H., and Lund, P. (2018). Power System Structural Vulnerability Assessment Based on an Improved Maximum Flow Approach. IEEE Trans. Smart Grid 9 (2), 777–785. doi:10.1109/tsg.2016.2565619

CrossRef Full Text | Google Scholar

Fang, Y., Cui, X., Wang, S., and Huanf, Z. (2015). Coordinated Limit Power Calculation of Multi-Sections with Transient Stability Limit Coupling. Automation Electr. Power Syst. 39 (22), 53–58. doi:10.7500/AEPS20150205004

CrossRef Full Text | Google Scholar

Fu, X. (2017). Hybrid Control of Power System Static Security. Electr. Power Autom. Equip. 37 (1), 124–130. doi:10.16081/j.issn.1006-6047.2017.01.020

CrossRef Full Text | Google Scholar

Huang, Y., Yu, Z., Shi, D., and Zhou, X. (2016). Strategy of Huge Electric Power System Stability Quick Judgment Based on Massive Historical Online Data. Proc. CSEE 36 (3), 596–603. doi:10.13334/j.0258-8013.pcsee.2016.03.002

CrossRef Full Text | Google Scholar

Huo, C., Cui, X., and Niu, S. (2016). A Method for Identifying AC Cross-Sections Strongly Correlated with DC Transient Stability. Power Syst. Prot. Control 44 (17), 83–89. doi:10.7667/PSPC151614

CrossRef Full Text | Google Scholar

Ilic, M., Galiana, F., Fink, L., Bose, A., Mallete, P., and Othmanf, H. (1998). Transmission Capacity in Power Networks. Int. J. Electr. Power &Energy Syst. 20 (2), 99–110. doi:10.1016/s0142-0615(97)00074-4

CrossRef Full Text | Google Scholar

Jiang, W., Zhang, B., Wu, W., and Sun, H. (2008). A Total Transfer Capability Calculation Method for Power System Operation and Decision. Automation Electr. Power Syst. 32 (10), 12–17. doi:10.3321/j.issn:1000-1026.2008.10.003

CrossRef Full Text | Google Scholar

Li, M. (2016). Characteristic Analysis and Operational Control of Large-Scale Hybrid UHV AC/DC Power Grids. Power Syst. Technol. 27 (4), 985–991. doi:10.13335/j.1000-3673.pst.2016.04.001

CrossRef Full Text | Google Scholar

Luo, G., Chen, J., Shi, D., and Duan, X. (2013). Key Transmission Sections Analysis Based on Complex Network Theory. Proc. CSEE 33 (25), 147–155+22. doi:10.1007/s10354-003-0008-1

CrossRef Full Text | Google Scholar

Luo, X., Patton, A. D., and Singh, C. (2000). Real Power Transfer Capability Calculations Using Multi-Layer Feed-Forward Neural Networks. IEEE Trans. Power Syst. 15 (2), 903–908. doi:10.1109/59.867192

CrossRef Full Text | Google Scholar

Mohamed, G. M., Allam, S. M., and Essam, M. R. (2018). Maximum Power Extraction under Different Vector-Control Schemes and Grid-Synchronization Strategy of a Wind-Driven Brushless Doubly-Fed Reluctance Generator. ISA Trans. 72, 287–297. doi:10.1016/j.isatra.2017.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiu, W., He, J., and Yu, Z. (2019). Transient Voltage Stability Analysis of Hunan Power Grid with Infeed UHVDC. Electr. Power Autom. Equip. 39 (10), 168–177. doi:10.16081/j.epae.201909003

CrossRef Full Text | Google Scholar

Ren, C., Niu, S., and Ke, X. (2022). Clustering Analysis of Transmission Section Mode for Power Grid with Renewable Energy[J/OL]. Automation Electr. Power Syst. doi:10.7500/AEPS20210302008

CrossRef Full Text | Google Scholar

Tan, B., Yang, J., and Lai, Q. (2018). Data Augment Method for Power System Transient Stability Assessment Based on Improved Conditional Generative Adversarial Network. Automation Electr. Power Syst. 43 (1), 149–157. doi:10.7500/AEPS20180522004

CrossRef Full Text | Google Scholar

Tu, J., Zhang, J., Zeng, B., Pan, Y., Jia, J., and Yi, J. (2017). HVDC Transient Reactive Power Characteristics and Impact of Control System Parameters during Commutation Failure and Recovery. High. Volt. Eng. 43 (07), 2131–2139. doi:10.1049/joe.2017.0506

CrossRef Full Text | Google Scholar

Wang, F., Liu, W., Tian, H., and Liang, C. (2017). Fast Staticsecurity Calculation Based on Network Partition Algorithm. Electr. Power Autom. Equip. 37 (4), 203–209. doi:10.16081/j.issn.1006-6047.2017.04.031

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, Z., and Huang, M. (2020). Automatic Identification for Transmission Section Stability Rules and Adaptive Adjustment Technology for Stability Control Limits. Water Resour. Power 38 (06), 173–176.

Google Scholar

Xu, T., Peng, H., and Su, Y. (2012). Calculation of Ultimate Power of Interconnected Transmission Section Based on Parallel Mode. Automation Electr. Power Syst. 36 (07), 66–70.

Google Scholar

Zhang, L., and Liu, J. (2015). Static Security Risk Assessment of Power System Considering Wind Speed Correlation. Electr. Power Autom. Equip. 35 (4), 84–89. doi:10.16081/j.issn.1006-6047.2015.04.012

CrossRef Full Text | Google Scholar

Zhao, F., Huang, T., and Sun, H. (2015). Expression and Evolvement of Power System Security Operating Knowledge. Proc. CSEE 35 (20), 5117–5123. doi:10.13334/j.0258-8013.pcsee.2015.20.001

CrossRef Full Text | Google Scholar

Zhou, D., Zhang, B., Yao, F., and Wang, L.-Y. (2006). Fast Search Fortransmission Section Based on Graph Theory. Proc. CSEE 26 (12), 32–38. doi:10.1016/S0379-4172(06)60085-1

CrossRef Full Text | Google Scholar

Zhou, Z., Wang, B., and Gao, Z. (2021). “Information Extraction Method of Power Grid Operation Mode Based on Double Layer Labeling Model,” in 5th IEEE Conference on Energy Internet and Energy System Integration: Energy Internet for Carbon Neutrality, Taiyuan, China, 22-24 October 2021, 3256–3261. doi:10.1109/EI252483.2021.9713347

CrossRef Full Text | Google Scholar