- School of Renewable Energy, Shenyang Institute of Engineering, Shenyang, China
The prediction of photovoltaic power generation is helpful to the overall allocation of power planning departments and improves the utilization rate of photovoltaic power generation. Therefore, this study puts forward an ultra-short-term power forecasting model of a photovoltaic power station based on modal decomposition and deep learning. The methodology involved taking the data of a 50 MW photovoltaic power generation system in the Inner Mongolia Autonomous Region as a sample. Furthermore, the weather conditions were classified, and the historical power data were decomposed into multiple VMF subcomponents and residual terms by the VMD method. Then, the residual term was decomposed twice by the CEEMDAN method. All subcomponents were sent to the LSTM network for prediction, and the predicted value of the photovoltaic power station was obtained by superimposing the subcomponent prediction results. ARIMA, SVM, LSTM, and VMD-LSTM models were built to compare the accuracy with the proposed models. The results revealed that the prediction accuracy of a non-combination forecasting model was limited when the weather suddenly changed. The VMD method was used to decompose the residual term twice, which could fully extract the complex data information in the residual term, and when compared with the VMD-LSTM model, the eRMSE, eMAPE, and eTIC of the VMD-CEEMDAN-LSTM model were reduced by 0.104, 16.596, and 0.038, respectively. The second decomposition technology has obvious prediction advantages. The proposed quadratic modal decomposition model effectively improves the precision of ultra-short-term prediction of photovoltaic power plants.
1 Introduction
The increasing population and modern lifestyle are threatening the traditional energy sources such as coal, oil, and natural gas. In order to meet the world’s energy demand, renewable energy must be developed and utilized on a large scale (Wang H. et al., 2020; Sohani et al., 2021). In renewable energy, solar energy occupies a dominant position (Yuan et al., 2021). However, photovoltaic power generation is very sensitive to climate and seasonal factors (Meng et al., 2021). Small changes in photovoltaic power may affect the safe and stable operation of the power grid (Ding, 2021). In order to ensure the stability, reliability, and power dispatching ability of the power system, it is very important to design a true and accurate photovoltaic power forecasting method.
Photovoltaic power forecasting methods are generally divided into physical methods and statistical methods. Physical methods are not suitable in many cases because of their low prediction accuracy and high calculation cost (Ma et al., 2014; Yao, 2014; Hassan et al., 2021). The statistical method optimizes the mapping relationship between historical samples and actual photovoltaic power by minimizing the error, which is proved to be effective in the field of solar energy prediction. At present, the machine learning model (Chiteka and Enweremadu, 2016; Jang et al., 2016; Gao et al., 2019; Ghimire et al., 2019; Ye et al., 2021; Chiang and Young, 2022) has been successfully applied to photovoltaic power prediction. In order to improve the accuracy of power prediction, some combination models (Mellit et al., 2010; Mohammadi et al., 2015; Wang X. et al., 2020; Yang et al., 2020) have also been applied in the field of photovoltaic prediction. However, the prediction of photovoltaic power generation is not only related to the current weather conditions but also related to historical data. Machine learning belongs to the shallow network, which is more suitable for small batch data analysis. With the explosive growth of data, these methods cannot mine the most effective features from massive data, and there are problems such as gradient disappearance and explosion, so the prediction accuracy is limited (Changwei et al., 2019).
In recent years, the deep learning method has been successfully applied in the field of photovoltaic forecasting because of its strong ability of data feature extraction and fitting, which can independently mine the main learning features from massive data (Alzahrani et al., 2017; Abdel-Nasser and Mahmoud, 2019; Chang and Lu, 2018; Zang et al., 2018; Zhou et al., 2019). Zhou et al. (2019) adopted an attention mechanism, that adaptively focuses attention on two important input features, namely, temperature and irradiance, so that more relevant information can be mined. Alzahrani et al. (2017) proposed a recurrent neural network model to predict the solar irradiance level. Abdel-Nasser and Mahmoud (2019) compared long-term and short-term memory networks with three traditional methods: multiple linear regression, regression tree, and ANN. Chang and Lu (2018) compared the depth confidence network with SVR, back propagation neural network, and other methods, and the results show that DBN has the best prediction effect. In the work of Zang et al. (2018), the convolutional neural network is compared with BPNN and SVR models, and it is found that the CNN model has the lowest prediction accuracy.
The above research on photovoltaic power prediction has made some achievements, but the statistical model also has its own limitations. Compared with physical forecasting methods, statistical models are more concise in modeling, but there are also some problems in actual forecasting, such as difficulty in parameter adjustment, stagnation of convergence, etc., and the weather type has a great influence on photovoltaic forecasting, while most statistical models do not classify and analyze different weather conditions. At present, the existing literature uses the VMD decomposition method to decompose the photovoltaic power curve but ignores the important information in the residual term obtained by VMD decomposition. In order to further improve the accuracy of ultra-short-term prediction of photovoltaic power, this paper classified the weather conditions, used the VMD method to decompose the historical power, and used the adaptive noise complete empirical mode decomposition method to decompose the residual term for the second time. By making full use of the information in the residual term, VMF and IMF components were sent to the LSTM network, and the final prediction result was obtained by superimposing the prediction results of each subcomponent. The errors of ARIMA, SVM, LSTM, and VMD-LSTM models were compared, and the results showed the accuracy of the quadratic decomposition model proposed in this paper.
2 Influence of Weather Types on Photovoltaic Output
Photovoltaic power is affected by many factors such as meteorology, environment, and location. This paper selects the power data of a photovoltaic power station in the Inner Mongolia Autonomous Region from 1 January 2019 to 31 December 2020 as the sample. There are 52 sampling points in the power station, and the sampling interval is 15 min. As the photovoltaic power station only works in daytime, only the data from 08: 00 to 18: 00 are selected for analysis. When there is no sudden change in the weather (sunny, cloudy, rainy, and snowy), the photovoltaic output is relatively stable, and the output curve is approximately parabolic; However, when the weather suddenly changes during the day, the photovoltaic output curve fluctuates greatly, which affects the safe and stable operation of the power system. Therefore, it is necessary to distinguish between the weather types to study the photovoltaic output.
3 Description of the Model Concept and Mechanism
The photovoltaic power series is a non-stationary and nonlinear time series. The VMD method can decompose a photovoltaic series into several VMF components with low complexity and residual terms. In previous studies, only VMF components were studied and the residual terms were discarded, but the residual terms also contained a lot of useful information. If the residual term is discarded directly, the prediction accuracy of the model will be greatly affected. In order to improve the prediction accuracy, this study uses the CEEMDAN method to decompose the residual term after VMD decomposition for the second time and then sends both the VMF component and IMF component to the LSTM network (Li et al., 2021a; Li et al., 2021b; Le et al., 2021; Toyoda and Wu, 2021; Wu et al., 2021).
3.1 Variable Modal Decomposition
3.1.1 Variable Modal Decomposition Principle
The core of variable modal decomposition is to decompose signals by adaptive and completely non-recursive methods. This method can adaptively match the best frequency and bandwidth and then realize the effective decomposition of VMF components, thus solving the endpoint effect problem of the EMD method. The model expression is as shown in the following equation:
where k is the number of VMF components;
In order to obtain the optimal solution, the quadratic penalty factor
where Lagrange operator
1) Set the appropriate component number
2) Update
3) Update that
4) Judging the judgment precision.
When condition (6) is satisfied, the iteration stops, otherwise, the process returns to step 2.
In the abovementioned formula,
3.1.2 Variational Modal Decomposition Results
When the VMD method is used for modal decomposition of photovoltaic power, if there are many VMF components, modal aliasing will easily occur, but when there are few VMF components, the complexity of the photovoltaic power sequence cannot be effectively reduced, so the number of VMF components needs to be determined according to the change of instantaneous frequency before decomposition. When the number of VMF components is 7, the instantaneous frequency curve is obviously bent and over-decomposed. Therefore, this paper sets the number of VMF components to 6.
3.2 Complete Empirical Mode Decomposition of Adaptive Noise
3.2.1 Principle of Adaptive Noise Complete Empirical Mode Decomposition
Empirical decomposition can decompose a photovoltaic power sequence into several IMF components, but due to the non-stationary and nonlinear characteristics of the photovoltaic power curve, aliasing can easily appear in the decomposition process. The EEMD decomposition method adds white noise to the original sequence and makes use of the frequency equilibrium distribution characteristics of white noise to improve the mode aliasing problem, but the decomposition efficiency of this method is low. In this article, CEEMDAN method is chosen to decompose photovoltaic sequences, which adds white noise with different amplitudes to decompose the optimal IMF component and solves the problems of modal aliasing and low decomposition efficiency. CEEMDAN decomposition steps are as follows.
1) Add the white noise sequence
where,
2) Perform empirical mode decomposition on data sequence
In this formula,
3) Average
4) The final decomposition result of CEEMDAN is
where
3.3 Long-Term and Short-Term Memory Neural Network
3.3.1 Principle of Long-Term and Short-Term Memory Neural Network
By introducing a gating unit, the long-term memory neural network can selectively add or forget information, which keeps the feedback mechanism of the circulation neural network and solves the long-term dependence of the circulation neural network. A long-term memory neural network consists of input, output, and hidden layer containing a gated memory mechanism.
Data are memorized by controlling the forgetting gate, the input gate, and the output gate, and the calculation formulas are shown as follows:
where
The calculation of the state
where
3.3.2 Structure of Long-Term and Short-Term Memory Neural Network
The LSTM network model parameters are as follows: the dropout value is 0.2; the function is optimized to adam; the activation function takes tanh; the number of nodes is 50; training times are 1,000; batch size is 72, and the average absolute error function is selected as the loss function.
3.4 Construction of the VMD-EEMD-LSTM Model
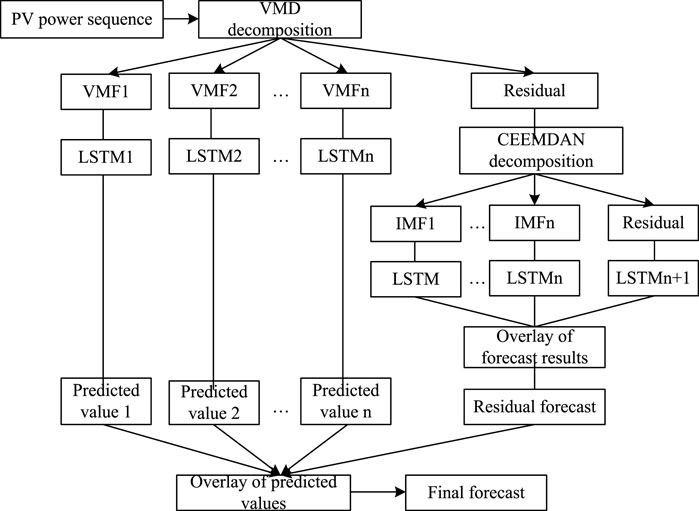
The modeling steps of the VMD-CEEMAN-LSTM model built in this study are as follows:
1) The PV power sequence is decomposed by the VMD method, which is divided into the VMF component and the residual term
2) Normalize each VMF component and send it to LSTM network to obtain the VMF subcomponent prediction result
3) The remaining residual term is decomposed twice by CEEMAN, and the IMF component obtained by decomposition is sent to the LSTM network
4) Superposing the IMF subcomponent prediction results to obtain the residual prediction results
5) Superposing the VMF subcomponent prediction result and the residual prediction result to obtain the final photovoltaic power prediction result
The modeling process of the VMD-CEEMAN-LSTM model is shown in Figure 1.
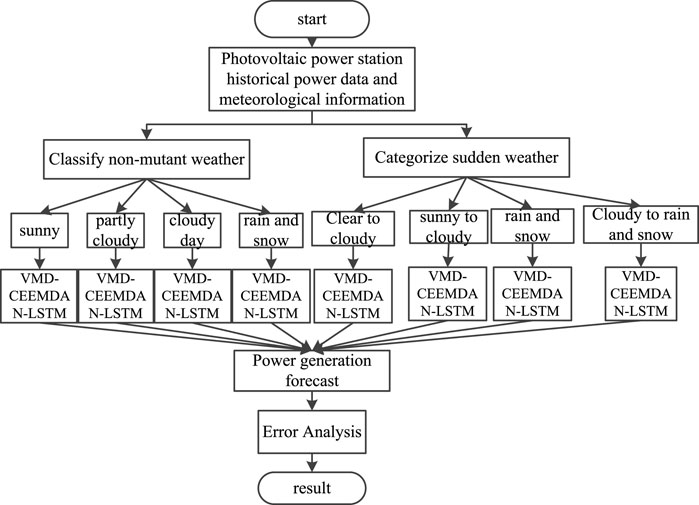
3.5 Modeling Classification
Because the weather type has a great influence on the photovoltaic output, in order to improve the prediction accuracy, this article separately predicts the abrupt weather (sunny, cloudy, rainy, and snowy) and the non-abrupt weather (sunny to cloudy, sunny to cloudy, etc.). In order to test the accuracy of the VMD-CEEMDAN-LSTM model, ARIMA, SVM, LSTM, and VMD-LSTM models are established and compared with the proposed models. When evaluating the accuracy of the model, the average absolute percentage error eMAPE, the root mean square error eRMSE, and the Hill inequality coefficient eTIC are selected, and the formula is as follows:
where Y is the true value of power; Y′ is the predicted value of power; and Z is for sample purpose.
4.2 Non-Abrupt Weather Forecast Model
The photovoltaic power of different weather types is predicted separately, and the prediction process is shown in Figure 2. In non-abrupt weather, the output data of historical photovoltaic power plants in sunny, rainy, or cloudy weather are decomposed by VMD, and the residual term generated by VMD decomposition is decomposed by CEEMDAN secondary mode, and all subcomponents are added to meteorological conditions and sent to the LSTM network for prediction. Photovoltaic output will fluctuate greatly in abrupt weather, so in abrupt weather forecast, the time of maximum output power in a day (2: 00 p.m.) is selected for decomposition, so that the original complex power sequence becomes a number of stable data sequences, and then meteorological factors are added and sent to LSTM network.
4 Example Analysis
4.1 Source of Examples
The historical power data from 2019 to 2020 of photovoltaic power stations with an installed capacity of 50 MW in the Inner Mongolia Autonomous Region are selected as samples to verify the validity of the VMD-CEEMDAN-LSTM model. The 71-day weather conditions are as follows: 265 days of sunny weather, 63 days of cloudy weather, 93 days of cloudy weather, 115 days of rain and snow, and 195 days of abrupt weather. Taking sunny, cloudy, and sunny-to-cloudy weather as examples, the days of training and testing samples are 221 and 44 days in sunny weather, 52 and 11 days in cloudy weather, and 21 and 4 days in sunny-to-cloudy weather.
4.2 Forecast Results
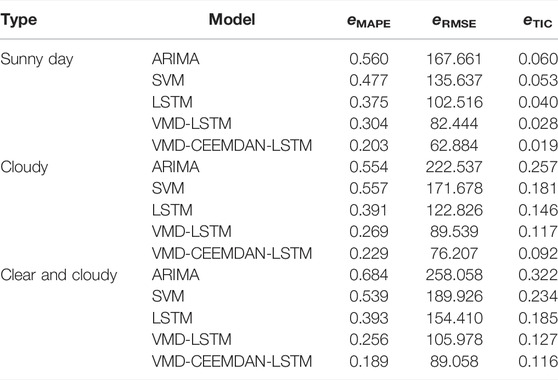
In sunny weather, the photovoltaic output prediction results are shown in Figure 3A, and the model evaluation results are shown in Table 1. In sunny weather, the fluctuation of photovoltaic output is small. In Figure 3A, it can be clearly observed that the prediction accuracy of the ARIMA model is insufficient, resulting in large errors, and the prediction effects of other models are better than those of the ARIMA model. Compared with ARIMA and SVM, the evaluation indexes of the three non-combination forecasting models show that the eMAPE value of the LSTM model decreases by 0.185 and 0.102 respectively, the eRMSE value decreases by 65.145 and 33.121, respectively, and the eTIC value decreases by 0.02 and 0.013, respectively. The evaluation index can clearly show that the deep learning method can mine more features of photovoltaic data and is more suitable for the prediction of nonlinear and non-stationary data. According to the data in Table 1, eMAPE, eRMSE, and eTIC of the VMD-CEEMDAN-LSTM prediction model are the smallest, and at noon, when the photovoltaic power curve fluctuates, the VMD-CEEMDAN-LSTM power prediction curve still keeps a high degree of fit with the real power curve.
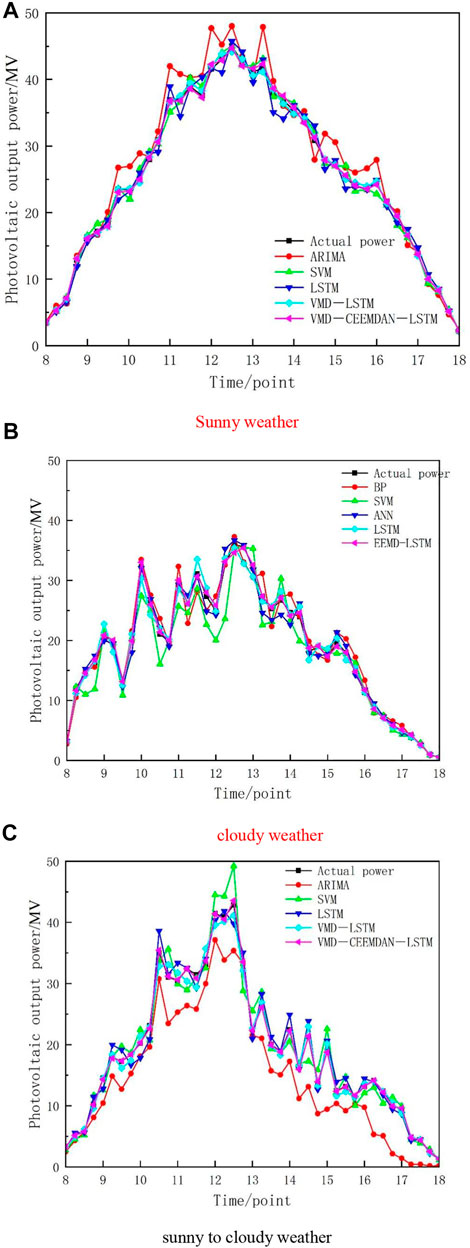
FIGURE 3. Prediction results of different weather power. (A) sunny weather. (B) cloudy weather. (C) sunny-to-cloudy weather.
In cloudy weather, the forecast results are shown in Figure 3B. Compared with sunny weather, cloudy weather reduces photovoltaic power due to the blocking effect of clouds on the Sun’s rays. Due to the change in cloud thickness, the photovoltaic power curve also fluctuates greatly. At this time, the predicted value of ARIMA model and SVM model has a big deviation from the real value, and the model accuracy decreases. On 4 May 2019 compared with ARIMA, SVM, and LSTM, the eMAPE value of VMD-LSTM model decreased by 0.285, 0.288, and 0.122 respectively, and that of VMD-CEEMDAN-LSTM model decreased by 0.325, 0.328, and 0.162 respectively. The VMD-LSTM model and the VMD-CEEMDAN-LSTM model reduces the complexity of data series and the influence of data fluctuation through variational modal decomposition.
The forecast result of photovoltaic output in sunny weather is shown in Figure 3C. When the weather suddenly changes, because the complexity of photovoltaic power series increases, the predicted values of ARIMA, SVM, and LSTM have a high degree of dispersion with the real values, so the prediction accuracy is limited and the accuracy is difficult to guarantee. Comparing the error evaluation indexes, it can be seen that the VMD-CEEMDAN-LSTM model still maintains the highest prediction accuracy. On 13 August 2020, its eMAPE value decreased by 0.204 and 0.067 compared with the LSTM and VMD-LSTM models.
In order to further highlight the accuracy of the proposed method, this article makes statistics on the test results of all test samples in the power station within 2 years. The errors of VMD-LSTM and VMD-CEEMD-LSTM were counted. Compared with the VMD-LSTM model, the eRMSE, eMAPE, and eTIC of the VMD-CEEMDAN-LSTM model decreased by 0.104, 16.596, and 0.038, respectively. The accuracy of the model is obviously improved after the second decomposition of the residual term obtained by VMD decomposition.
5 Conclusion
In order to further predict the accuracy of photovoltaic power, this article proposed a model combining modal decomposition with deep learning algorithm and built ARIMA, SVM, LSTM, and VMD-LSTM models to compare their errors with the proposed models. The main conclusions are as follows:
(1) In data processing, VMD decomposition and CEEMDAN secondary decomposition of residual terms greatly improve the prediction accuracy compared with the traditional non-combination prediction model
(2) The second CEEMDAN decomposition of the residual term obtained by VMD decomposition can fully improve the complex features of the residual term, which makes the eRMSE, eMAPE, and eTIC of the VMD-CEEMDAN-LSTM model lower than those of the VMD-LSTM model by 0.104, 16.596, and 0.038, respectively, and the prediction accuracy of the VMD-CEEMDAN-LSTM model is obviously higher than that of the VMD-LSTM model
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
SW and SL conceived the idea and designed the experiments. The experiments were led by XG, while SW contributed to data analysis and interpretation along with writing the manuscript. All authors read and approved the final manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
VMD, variational mode decomposition; VMF, Vienna mapping function; CEEMDAN, complete ensemble empirical mode decomposition with adaptive noise; IMF, intrinsic mode function; LSTM, long short-term memory; ADMM, alternating direction method of multipliers; EEMD, ensemble empirical mode decomposition; CEEMDAN, complete ensemble empirical mode decomposition with adaptive noise; ARIMA, autoregressive integrated moving average model; SVM, support vector machine.
References
Abdel-Nasser, M., and Mahmoud, K. (2019). Accurate Photovoltaic Power Forecasting Models Using Deep LSTM-RNN[J]. Neural Comput. Appl. 31 (7), 2727–2740. doi:10.1007/s00521-017-3225-z
Alzahrani, A., Shamsi, P., Dagli, C., and Ferdowsi, M. (2017). Solar Irradiance Forecasting Using Deep Neural Networks. Procedia Comput. Sci. 114, 304–313. doi:10.1016/j.procs.2017.09.045
Chang, G. W., and Lu, H. J. (2018). Integrating Grey Data Preprocessor and Deep Belief Network for Day-Ahead PV Power Output Forecast[J]. IEEE Trans. Sustain. Energy 11 (1), 185–194. doi:10.1109/tste.2018.2888548
Changwei, L., Jinghua, L., Bo, C., et al. (2019). Summary of Research on Photovoltaic Power Generation Output Prediction Technology[J]. J. Electrotech. Technol.,34 (06), 1201–1217.
Chiang, C-H., and Young, C-H. (2022). An Engineering Project for a Flood Detention Pond Surface-type Floating Photovoltaic Power Generation System with an Installed Capacity of 32,600.88 kWp. Energy Rep. 8, 2219–2232. doi:10.1016/j.egyr.2022.01.156
Chiteka, K., and Enweremadu, C. C. (2016). Prediction of Global Horizontal Solar Irradiance in Zimbabwe Using Artificial Neural Networks. J. Clean. Prod. 135 (Complete), 701–711. doi:10.1016/j.jclepro.2016.06.128
Ding, Y. (2021). Research on Microgrid System Optimization Considering Wind and Light Prediction [D]. Dissertaion. Beijing, China: Beijing Jiaotong University.
Gao, M., Li, J., Hong, F., and Long, D. (2019). Short-Term Forecasting of Power Production in a Large-Scale Photovoltaic Plant Based on LSTM. Appl. Sci. 9 (15), 3192. doi:10.3390/app9153192
Ghimire, S., Deo, R. C., Downs, N. J., and Raj, N. (2019). Global Solar Radiation Prediction by ANN Integrated with European Centre for Medium Range Weather Forecast Fields in Solar Rich Cities of Queensland Australia[J]. J. Clean. Prod. 216, 288–310. doi:10.1016/j.jclepro.2019.01.158
Hassan, M. A., Bailek, N., Bouchouicha, K., and Nwokolo, S. C. (2021). Ultra-short-term Exogenous Forecasting of Photovoltaic Power Production Using Genetically Optimized Non-linear Auto-Regressive Recurrent Neural Networks[J]. Renew. Energy 171, 191–209. doi:10.1016/j.renene.2021.02.103
Jang, H. S., Bae, K. Y., Park, H. S., and Sung, D. K. (2016). Solar Power Prediction Based on Satellite Images and Support Vector Machine[J]. IEEE Trans. Sustain. Energy 7 (3), 1255–1263. doi:10.1109/tste.2016.2535466
Le, S., Wu, Y., Guo, Y., and Vecchio, C. D. (2021). Game Theoretic Approach for a Service Function Chain Routing in NFV with Coupled Constraints. IEEE Trans. Circuits Syst. II 68, 3557–3561. Published online. doi:10.1109/TCSII.2021.3070025
Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D. K., and Cheng, Q. (2021). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energy Res. 9, 780928. doi:10.3389/fenrg.2021.780928
Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. D. K. (2021). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energy Res. 9, 799039. doi:10.3389/fenrg.2021.799039
Ma, T., Yang, H., and Lu, L. (2014). Solar Photovoltaic System Modeling and Performance Prediction. Renew. Sustain. Energy Rev. 36, 304–315. doi:10.1016/j.rser.2014.04.057
Mellit, A., Kalogirou, S. A., and Drif, M. (2010). Application of Neural Networks and Genetic Algorithms for Sizing of Photovoltaic Systems. Renew. Energy 35 (12), 2881–2893. doi:10.1016/j.renene.2010.04.017
Meng, A., Chen, J., Li, Z., et al. (2021). Short-Term Photovoltaic Power Prediction Based on Similar Day Theory and CSO-WGPR[J]. High. Volt. Technol. 47 (04), 1176–1184.
Mohammadi, K., Shamshirband, S., Tong, C. W., Arif, M., Petković, D., and Ch, S. (2015). A New Hybrid Support Vector Machine-Wavelet Transform Approach for Estimation of Horizontal Global Solar Radiation[J]. Energy Convers. Manag. 92 (Mar), 162–171. doi:10.1016/j.enconman.2014.12.050
Sohani, A., Shahverdian, M. H., Sayyaadi, H., Hoseinzadeh, S., and Memon, S. (2021). Enhancing the Renewable Energy Payback Period of a Photovoltaic Power Generation System by Water Flow Cooling. Int. J. Sol. Therm. Vac. Eng. 3 (1), 73–85. doi:10.37934/stve.3.1.7385
Toyoda, M., and Wu, Y. (2021). Mayer-type Optimal Control of Probabilistic Boolean Control Network with Uncertain Selection Probabilities. IEEE Trans. Cybern. 51, 3079–3092. (Regular Paper). doi:10.1109/tcyb.2019.2954849
Wang, H., Liu, Y., Zhou, B., Li, C., Cao, G., Voropai, N., et al. (2020). Taxonomy Research of Artificial Intelligence for Deterministic Solar Power Forecasting. Energy Convers. Manag. 214, 112909. doi:10.1016/j.enconman.2020.112909
Wang, X., Luo, D., Sun, Y., et al. (2020). Research on the Combination Forecasting Method of Daily Power Generation of Photovoltaic Microgrid Based on ABC-SVM and PSO-RF[J]. J. Sol. Energy 41 (03), 177–183.
Wu, Y., Guo, Y., and Toyoda, M. (2021). Policy Iteration Approach to the Infinite Horizon Average Optimal Control of Probabilistic Boolean Networks. IEEE Trans. Neural Netw. Learn Syst. 32 (6), 2910–2924. (Regular Paper). doi:10.1109/TNNLS.2020.3008960
Yang, L., Gao, X., Jiang, J., et al. (2020). Short-Term Power Prediction of Photovoltaic Power Station Based on Wavelet Transform and Neural Network[J]. J. Sol. Energy 41 (07), 152–157.
Yao, G. (2014). Design of Photovoltaic Grid-Connected Power Generation System and Research on MPPT Technology[D]. Dissertation. Hangzhou, China: Zhejiang University.
Ye, L., Ma, M., Jin, J., et al. (2021). Factor Analysis Considering the Correlation between Wind Power and Photovoltaic Power-Extreme Learning Machine Aggregation Method[J]. Power Syst. Autom. 45 (23), 31–40.
Yuan, Q., Zhao, B., Wang, L., et al. (2021). Photovoltaic Multi-Peak MPPT Control Based on TSA-P&O Hybrid Algorithm[J]. Power Syst. Acta AutomaticaSinica) 33 (12), 101–109.
Zang, H., Cheng, L., Ding, T., Cheung, K. W., Liang, Z., Wei, Z., et al. (2018). Hybrid Method for Short-Term Photovoltaic Power Forecasting Based on Deep Convolutional Neural Network[J].IET Generation,Transmission,Distribution 12 (20), 4557–4567. doi:10.1049/iet-gtd.2018.5847
Keywords: photovoltaic power station, quadratic modal decomposition, long-term memory neural network, ultra-short term, power prediction
Citation: Wang S, Liu S and Guan X (2022) Ultra-Short-Term Power Prediction of a Photovoltaic Power Station Based on the VMD-CEEMDAN-LSTM Model. Front. Energy Res. 10:945327. doi: 10.3389/fenrg.2022.945327
Received: 16 May 2022; Accepted: 30 May 2022;
Published: 08 July 2022.
Edited by:
Xun Shen, Tokyo Institute of Technology, JapanReviewed by:
Sandeep Kumar Duran, Lovely Professional University, IndiaVikram Kamboj, Lovely Professional University, India
Copyright © 2022 Wang, Liu and Guan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shuaijie Wang, RDExNDAyMDI3QG1haWwuZGx1dC5lZHUuY24=
 Shuaijie Wang
Shuaijie Wang Shu Liu
Shu Liu