- 1Academic Affairs Office, Guangdong University of Finance and Economics, Guangzhou, China
- 2School of Information Science, Guangdong University of Finance and Economics, Guangzhou, China
- 3School of Electric Power, South China University of Technology, Guangzhou, China
Transformer is one of the important equipment in the power grid, which helps to integrate renewable energy into the transmission and distribution network efficiently. The safe and stable operation of transformer is of great importance for the reliable transmission of electricity generated from renewable energy and for the reliable use of electricity by the end users. Therefore, it is important to assess the condition to avoid the faults of the transformer. In this paper, a variable weight synthesizing assessment model is presented that combines the G1 method, the entropy weight method, and a variable-weight method proposed in this paper to assess the condition of transformer based on the offset of the transformer equivalent circuit parameters. First, we propose deterioration indexes oriented to the maintenance management needs, which can well reflect the degree of deterioration of each transformer component. Second, the various defects of the transformer are used as the assessment indexes, and the initial weight is given to the assessment indexes according to the damage degree of the defect. The initial weight is calculated comprehensively by the G1 method and the entropy weight method. Then, each index is scored according to the offset of the equivalent circuit parameters, and the weights are adjusted appropriately according to the scores of the indicators using a variable weighting method to emphasize the severity of the defect or the “sub-health” condition of the transformer. Finally, the respective scores and combined weights of the assessment indexes are weighted to obtain a comprehensive score. The simulation shows that the model is more sensitive to abnormal and “subhealth” conditions of the transformer, which verifies the feasibility of the variable weight synthesizing model to assess the condtion of the transformer.
1 Introduction
For the power grid, renewable energy sources such as wind and solar are used on a large scale. They play an important role in reducing carbon emissions and reducing operating costs (Fu et al., 2020). A secure and stable power grid can reliably transmit electricity generated by renewable energy sources to end users. Whether it is a large main transformer or a small and medium-sized low-voltage distribution transformer of 35 kV and below, it has a wide distribution range and a large number, and occupies an important position in the power grid. Once a power transformer fails, it will have a hugeimpact on the power system, bring a great negative impact on industrial production and residential electricity consumption, and seriously endanger the safety of life and property (Kari et al., 2018). Therefore, only by accurately evaluating the status of transformers can we reliably develop low-carbon, digital, and intelligent renewable energy and achieve the goals of “carbon peak” and “carbon neutrality” (Long et al., 2022).
Due to the environment, service life and continuous use of the transformer, the health status of the transformer will naturally deteriorate day by day, sowing the seeds for the occurrence of faults. If the condition of the transformer can be accurately assessd, technicians will be able to detect defects in the transformer and take timely maintenance measures to ensure long-term healthy operation. Therefore, it is important to assess the condition of the transformer. However, from DL/T 1685-2017 Guide for condition assessment of oil-immersed power transformers (reactors) (NEA, 2017), it is known that there are many assessment condition quantities of transformers, and the changes of many condition quantities need to be considered in combination with various factors. In addition, there are ambiguous and uncertain relationships between different condition quantities. Therefore, the condition assessment is very difficult and the data is difficult to process.
In recent years, researchers have used intelligent techniques such as fuzzy theory (Rexhepi and Nakov, 2018), clustering (Eke et al., 2019), and neural networks (Islam et al., 2017) to fully combine and utilize the condition quantities of transformers, which can eventually assess the current health of transformers more accurately and thus avoid large-scale power accidents due to sudden failures. Many researchers have combined these intelligent techniques and their improved methods with the dissolved gas approach (DGA) for assessing the health of oil-immersed transformers. (Lin et al., 2017) pointed out that the traditional transformer condition assessment standards were single, and different types of condition information in power transformers gave different assessment results, which made it difficult for equipment managers to make decisions. To address these shortcomings, an artificial neural network model for transformer condition assessment based on Yager synthesis theory was proposed. (Yan et al., 2019) combined BP neural network with improved Adaboost algorithm, then combined PNN to form a series of diagnostic models for transformer faults. By connecting BP-Adaboost in series with PNN, it not only improves the defect of BP-Adaboost algorithm which does not diagnose samples, but also improves the defect of PNN model which has low diagnostic accuracy. (Arias Velásquez and Mejía Lara, 2020) proposed a new method with the lowest computational cost, using genetic algorithm to optimize ANN classifier, which was used to classify faults with genetic algorithm-based optimizer instead of the traditional RL action selection process. However, the DGA method is often limited to fault classification of transformer fault states. In fact, transformers are often in between normal and fault conditions (Tian et al., 2019). Therefore, the condition of the transformer cannot be accurately assessed by DGA alone.Many researchers also integrate multiple condition quantities in addition to dissolved gas data to assess the overall state of the transformer. Most of the currently used methods are data mining and intelligent algorithms such as combination of subjective and objective weights (Zhao et al., 2013), cloud models (Li et al., 2016; Du and Sun, 2020), fuzzy theory (Luo et al., 2007; Li et al., 2015), object element theory (Tan et al., 2020), set-pair analysis (Liao et al., 2010), association rules (Li et al., 2013) and their improvement algorithms. (Khalyasmaa et al., 2019) used random forest to solve the problem of actual technical status of operating power transformers. The initial dataset consisted of transformer oil analysis results, load conditions, infrared snapshots and integrated features of the technical state of the bushing, arrester and cooling system with a high accuracy of state identification. (Miao et al., 2014) developed a transformer state hierarchical assessment model incorporating a gray clustering approach and improved D-S evidence theory to evaluate the overall state of the transformer. The results showed that this artificial neural network model using Yager synthesis theory had better results than the traditional model. (Zhou and Hu, 2020) used DGA data, oil testing data, and electrical testing data as indicators to integrate condition information using a multi-factor condition assessment method based on fuzzy sets and factor spaces. In addition, an improved hierarchical analysis method is proposed to estimate the relative importance of attributes.
However, researchers mostly use artificial intelligence techniques to assess the condition of transformers, and the accuracy of condition assessment depends on the acquisition accuracy of data acquisition equipment to obtain characteristic quantities. The difference between the fault data and the data during normal operation is very small, and it is impossible for artificial intelligence technologies to make a completely accurate prediction. Second, researchers have also mostly assessed the condition of transformers using data such as dissolved gas ratios as indexes, i.e., diagnosing and assessing transformers based on their phenomena. Although the occurrence of abnormal phenomena is related to transformer defects to a certain extent, it cannot be directly inferred that the transformer is not working properly, and the specific fault location or type of fault cannot be accurately inferred. Moreover, these methods of assessment based on phenomena are not necessarily applicable to all transformers, such as oil chromatography for oil-immersed transformers but not for dry-type transformers.
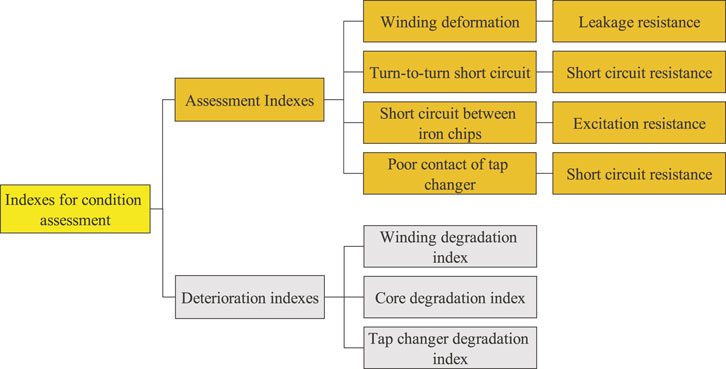
Many researchers found that transformer equivalent circuit parameters were closely related to transformer faults such as turn-to-turn short circuit, winding deformation, and core multipoint grounding. In addition, some standards (NDRC, 2008; NEA, 2010; AQSIQ, 2015a; AQSIQ, 2015b; NEA, 2021) also confirm this. The variation of leakage resistance correlates with the severity of winding deformation, the variation of short-circuit resistance correlates with the severity of turn-to-turn short circuit and poor contact, and the variation of excitation resistance correlates with the severity of multi-point grounding of the core or short circuit between the pieces. Therefore, using the leakage resistance, short-circuit resistance and excitation resistance as assessment indexes, the condition of the winding, core and tap changer of the transformer can be assessed, providing a reference for a comprehensive assessment of the transformer’s condition. Accurate identification of these parameters can accurately detect faulty components and helps to assess the condition of the transformer. Pan et al. (2017) proposed a method for online detection of short-circuit impedance of a three-phase transformer that allows online monitoring of transformer winding deformation independent of transformer three-phase load factor, three-phase load power factor, and three-phase load unbalance conditions. Ouyang et al. (2018) used online monitoring of the obtained transformer port information, combined with PSO to identify all parameters of the transformer T-equivalent circuit to improve the identification accuracy, and by comparing the changes of the equivalent parameters in real time, it can effectively determine whether there is an internal fault in the transformer. Wu et al. (2018) proposed an online identification method based upon the sudden short-circuit test to achieve the accurate calculation of short-circuit impedance and improve the testing capability and testing efficiency. Ecaterina and Ion (2019) proposed a transformer equivalent circuit parameter identification method for different equivalent circuits of double-winding transformers. Jiao et al. (2014) used least-squares method and time-domain fast algorithm to identify the excitation inductance of transformer T-equivalent circuit, and it is not affected by excitation inrush, system operation mode changes and system harmonics and can be used for testing. The transformer equivalent circuit parameter identification method performs fault diagnosis from the essence of the transformer rather than from the phenomena presented by the transformer like the DGA mentioned earlier to diagnose whether a fault will occur, so the method can reflect the severity of the transformer fault more accurately and has a wider range of application.
The only way to directly reflect whether a transformer is defective is to start with its function, i.e., to analyze whether the transformer is accurately completing its job of transforming voltage. And by starting from the function, we can determine the specific part of the transformer where the defect occurs, which is also more widely applicable. As mentioned above, transformer equivalent circuit parameters are closely related to transformer faults such as turn-to-turn short circuit, winding deformation, core multi-point grounding, etc. Accurate identification of these parameters can accurately identify faulty components and give maintenance recommendations. In this paper, leakage reactance, short-circuit resistance and excitation resistance are used as assessment indexes, which can assess the condition of the winding, core and tap changer, so as to comprehensively assess the condition of the transformer.
The main contributions of this paper are as follows:
• Most of the current researches assess the condition of transformers according to the parameters reflecting whether the phenomenon is abnormal or not. In contrast to these studies, we assess the condition of transformers based on its function, i.e., according to the deviation between the equivalent circuit parameters and the nominal value to assess the severity of each defect, and then assess the condition of transformers.
• The concept of deterioration indexes for maintenance management needs is presented. The deterioration indexes are used to reflect the deterioration level of windings, cores and tap changers and to assess the condition of transformer components.
• A variable weight synthesizing model is proposed. Different from the current research, the focus of this paper is on the innovation of the variable weight method. For the characteristics of transformers, this paper proposes a variable weight method and combines it with the G1 method and the entropy weight method to comprehensively assess the condition of transformers.
The rest of the paper is structured as follows: Section 2 presents the deterioration indexes of the transformer and describes the condition assessment for distribution operation and management. Section 3 presents the variable weight synthesizing model. Section 4 verifies the feasibility of the variable weight synthesizing model for different health conditions of transformers. Finally, conclusions are drawn in Section 5.
2 Transformer Deterioration Indexes and Condition Assessment
2.1 Deterioration Indexes for Maintenance Management Needs
Maintenance management is more focused on transformer components and requires diagnostic methods that point to the areas where problems occur. Therefore, the method designed in this subsection will ultimately give indexes of the degree of deterioration that can be reflected to the defective components to provide guidance for maintenance.
To reflect the degree of deterioration of each part of the transformer more precisely, the characteristic quantities of each part of the transformer need to be profiled. In general, the specific data of each part of the transformer cannot be obtained directly, and the corresponding parameters should be measured by transformer-related experiments to indirectly reflect the deterioration status of each part of the equipment. The physical quantities that can reflect the degree of deterioration of each part of the transformer are called deterioration indexes.
The transformer degradation indicator is defined as a vector:
where x1 indicates the degradation of the winding, x2 indicates the degradation of the core and x3 indicates the degradation of the tap changer.
The deterioration indexes of winding include winding deformation degree, winding insulation deterioration degree, winding resistance, winding insulation resistance to ground, winding capacitance and dielectric loss factor, short-circuit impedance and load loss, etc.
The deterioration indexes of core include no-load current and loss, no-load excitation characteristics, etc.
The deterioration indexes of the tap changer include tap changer contact pressure, contact resistance, rotational torque, etc.
The thresholds of each component of the deterioration indexes X are given: xi = 0 means intact, xi = 1 means very serious deterioration (i = 1, 2, 3). Taking winding deformation as an example, if the relative change in leakage resistance is greater than 2%, it can be determined that a winding deformation fault has occurred. Therefore, the winding degradation index of the transformer factory case can be defined as 0, and the winding degradation index of the relative change of leakage resistance reaching 2% is 1.
The deterioration indicators can reflect the severity of the deterioration of the transformer components more accurately and specifically, which in turn provides a basis for the diagnosis of transformer faults. According to the previous analysis, the transformer equivalent circuit parameters are associated with the fault and with some of the deterioration indexes, so the transformer equivalent circuit parameters can be used to analyze the degree of deterioration of the transformer components and the occurrence of the fault or not.
2.2 Condition Assessment for Distribution Operation Management
Distribution operation management is more concerned with the operation of transformers and requires assessment methods that point to the overall health of the transformers. Therefore, the method designed in this subsection will eventually give condition assessment indicators that can be reflected to transformers to provide guiding distribution operation management advice.
The change in the equivalent circuit parameters of a transformer can reflect whether a fault is imminent or not. Within the change threshold, the transformer is not faulty, but there is a high probability that a certain defect exists, and the deterioration of the defect will most likely lead to a fault. Therefore, assessing the severity of defects can prevent transformer faults.
There are several conditions of transformer as follows:
1) Transformer components are free of defects or the severity of defects is very low, when the transformer is very healthy.
2) “Sub-health” condition. Most of the components of the transformer are basically free of defects, and a few components have very serious defects, or multiple components are defective to some extent. Currently, the health status of the transformer is not optimistic, and it is in a “sub-health” condition.
3) At least one element of the transformer is on the verge of fault, at which point the transformer is about to fail and is in poor health.
3 Variable Weight Synthesizing Assessment Model
3.1 Assessment Process
Using the variable weight synthesizing assessment model, the transformer equivalent circuit parameters are compared to nominal values to assess the condition of the transformer and the degree of deterioration of each transformer component. The transformer condition assessment indexes are shown in Figure 1.
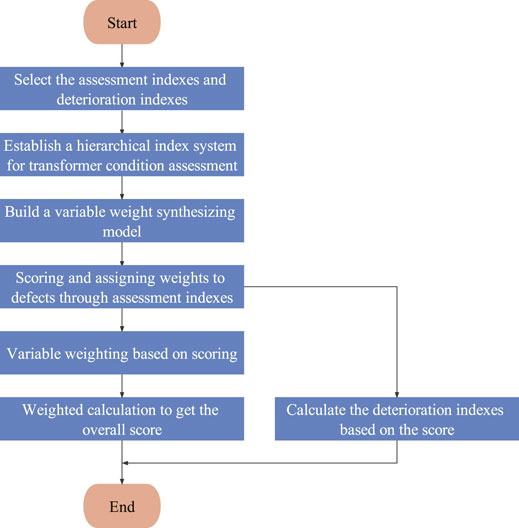
The process of condition assessment developed with the characteristics of the transformer is shown in Figure 2, and the specific process consists of the following steps.
1) Leakage resistance, short-circuit resistance and excitation resistance are used as assessment indexes to score the four defects of winding deformation, winding turn-to-turn short circuit, core chip-to-chip short circuit and poor tap changer contact according to the parameter offset of the transformer equivalent circuit. The score for each defect in the transformer of ex-factory is 100 points, and 60 points when the industry standard fault threshold is reached. The deterioration indexes are assessed comprehensively according to the part corresponding to the defect, with 0 being no deterioration and 1 being serious deterioration. For example, for windings, both winding deformation and winding turn-to-turn short circuit correspond to winding elements, and the deterioration indexes are obtained by imputing the lowest value of the scores of these two.
2) The G1 method and the entropy weight method are combined to assign weights to each defect index according to the degree of harm of the defect. For example, winding turn-to-turn short-circuit defects are more hazardous compared to core defects, so a greater weight needs to be assigned to the winding turn-to-turn short-circuit assessment index.
3) According to the scoring of each defect, a variable weight method is proposed to adjust the weight distribution of each index by the scoring situation to emphasize the severity of defects. The greater the weight, the more serious the defects. In addition, if the transformer is in a “sub-health” condition, the changed weights can reflect this condition. Finally, the weighting is calculated to obtain the overall rating of the transformer.
It should be noted that if the short-circuit resistance has changed, the presence of a defective tap changer contact cannot be fully judged, because a defect in the winding can lead to a change in short-circuit resistance and leakage resistance. If only the short-circuit resistance changes, the presence of a defective tap changer contact can be determined. Therefore, when it is not completely certain that poor tap changer contact occurs, the deterioration indicator of the tap changer is set to −1 and the fault type is also −1, indicating that a fault with poor tap changer contact may exist and alerting the staff to the tap changer condition.
3.2 Principle of G1 Method
Without loss of generality, let x1, x2, …, xm (m ≥ 2) be m maximal indexes that have been processed by index type consistency and dimensionlessness.
3.2.1 Determining Sequential Relationships
Definition 1. An index xi is denoted as xi ≥ xj if its importance relative to an evaluation criterion (or object) is not inferior to xi (the symbol
Definition 2. If the indexes x1, x2, …, xm have a relational expression with respect to an evaluation criterion (or object)
then the evaluation indexes x1, x2, …, xm are said to have established a sequential relationship with each other according to
3.2.2 Give the Ratio Judgment of the Relative Importance Between xk−1 and xk
Let the rational judgments of experts about the ratio wk−1/wk of the importance of evaluation index xk−1 to xk be respectively
Refer to Table 1 for the assignment of rk.
3.2.3 Calculation of the Weighting Factor wk
If the expert gives the rational assignment of rk, then wmis
3.3 Principle of Entropy Weight Method
The entropy weight method (EWM) is an objective assignment method that is stripped of the interpretation of the basic principles of information theory. It uses information entropy to measure the information utility value of each evaluation factor and determine the entropy weight (Tan et al., 2020). Information is a measure of the degree of order of the system, and entropy is a measure of the degree of disorder of the system. If the information entropy of the index is smaller, the more information the index provides, the greater the role it should play in the comprehensive evaluation, and the higher the weight should be.
3.3.1 Data Standardization
Firstly, each index is de-scaled. Assuming that m indexes X1, X2, …, Xm are given, where
3.3.2 Solve the Information Entropy of Each Index
From the definition of information entropy in information theory, the information entropy of a set of data is
where
If pij = 0, then define
3.3.3 Determine the Weights of Each Index
According to the formula of information entropy, the information entropies E1, E2, …, Em of each indicator are calculated. the weight of each indicator is calculated by information entropy.
where k refers to the number of indicators, i.e., k = m.
3.4 G1-Entropy Weight Method Combined Weighting
The subjective weights W1 calculated by the G1 method are obtained from Eqs 2–5, and the objective weights W2 calculated by EWM are obtained from Eqs 6–9. Using Eq. 10, the initial weight of the j-th index is calculated as
3.5 Variable Weight Method to Determine the Index Weights
In this subsection, a variable weight method is proposed to adjust the initial weights of each assessment index according to the scoring of each defect, emphasizing the severity of the defect. The larger the weight, the more serious the defect. In addition, if the transformer is in a “sub-health” condition, this condition can be reflected by the changed weights.
Let the weights of n defects be w1, w2, …, wn, and the scores of defects be x1, x2, …, xn. The steps of the variable weight method are as follows:
1) Highlighting the severity of defects that are about to turn into faults. If the minimum value of the score of each defect xmin < 60, the weight of the index corresponding to the score is set to wmin > 1. The weights of the other indexes are set as (1–wmin)/(n–1). In this paper, we take wmin = 1.2.
2) Highlighting the “sub-health” condition of the transformer. If the maximum mutual difference
3) Highlighting that the transformer is on the verge of fault. If the minimum value of the score of each defect is in the range of [60, 63], then the weight of the defect corresponding to the score is set to wmin, and 0.9 ≤ wmin ≤ 1. The weights of other defects are set to (1 − wmin)/(n − 1). In this paper, we take wmin = 0.95.
4) If the scores of the defects do not match the above, then the optimal value (100) is subtracted from each score and the resulting difference is added to the corresponding initial weight. The maximum weight is multiplied by a factor
4 Simulation and Validation
4.1 Judgment Standard for Condition Assessment
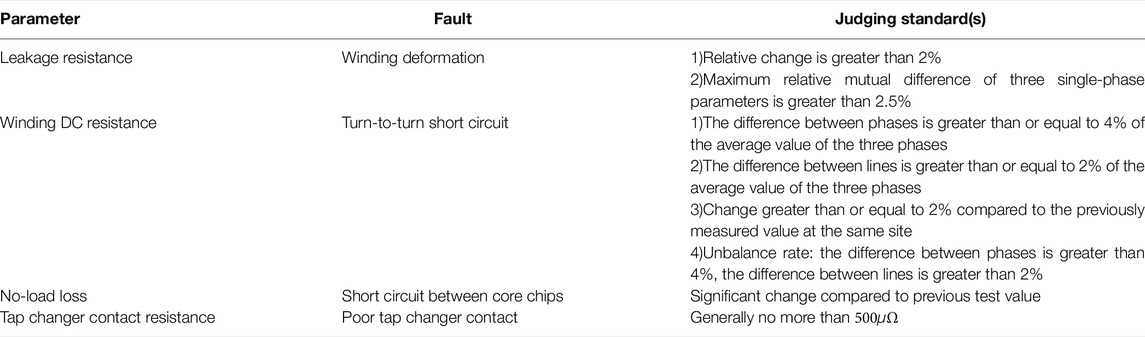
According to “DL/T 574-2010 Guide for reactance method to detect and diagnose winding deformation of power transformer”, “DL/T 596-2021 Preventive test code for electric power equipment” and other standards (NDRC, 2008; NEA, 2010; AQSIQ, 2015a; AQSIQ, 2015b; NEA, 2021), there are clear standard for judging four common faults, including winding deformation, turn-to-turn short circuit, short circuit between core chips and poor tap changer contact. The transformer fault judging standard summarized from these standards are shown in Table 2. It can be seen that these faults are closely related to the transformer equivalent circuit parameters.
As can be seen from Table 2, the changes in leakage resistance, winding DC resistance, no-load loss and tap changer contact resistance can reflect the defects of each transformer components and have clear numerical standards for fault diagnosis. The excitation resistance changes with the no-load loss, so the change in excitation resistance can be used to determine whether there is a short circuit between the core chips and its severity. However, there is still a coupling between transformer parameters and the fault connection, e.g., winding resistance and tap changer contact resistance are both considered as winding resistance in the transformer equivalent circuit. Therefore, the change in winding resistance cannot be accurately determined whether it is a short circuit between turns or a poor tap changer contact or both. The correspondence between transformer equivalent circuit parameters and faults is briefly summarized in Table 3.
4.2 Defect Simulation Results and Analysis
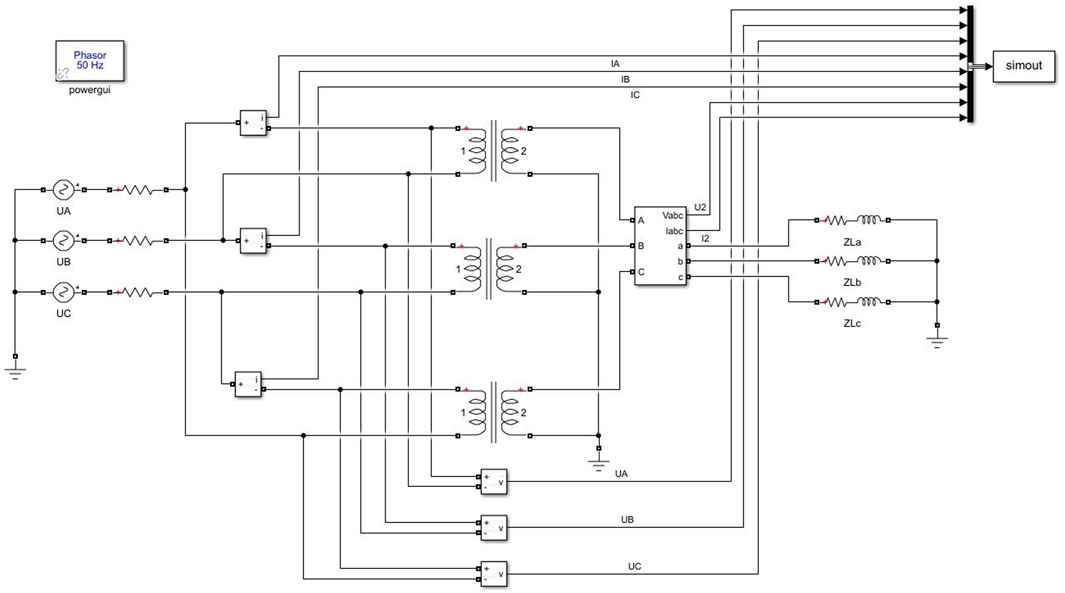
In this paper, a simulation model for the identification of short-circuit resistance, short-circuit reactance and excitation resistance of a three-phase variable power transformer is established based on the nameplate parameters of SG10-1000/10 dry-type power transformer of a water supply station, where the rated capacity SN = 1,000 kVA, frequency f = 50Hz, transformer high-voltage side line voltage U1 = 10 kV, transformer low-voltage side line voltage U2 = 0.4 kV, coupling group labeled Dyn11, no-load loss P0 = 1770W, load loss Pk = 8130 W, no-load current percentage I0 = 0.006, short-circuit impedance percentage Uk = 0.04, based on these data the parameters of the transformer γ-type equivalent circuit can be calculated, as shown in Table 4.
The Simulink transformer simulation circuit diagram is shown in Figure 3.
The RMS value of the three-phase externally applied voltage is set to 10 kV, and the three-phase voltage is symmetrical. The excitation resistance Rm = 1.6949 × 105 Ω, excitation inductance Lm = 166.5677H, and short-circuit impedance Zk = 2.4390 + j17.8340 Ω for each phase. The power factor is set to 0.9 and the load factor is 40%. In this case, the deterioration index of each component is 0, and the overall score of condition is 100.
4.2.1 Determine Initial Weights
4.2.1.1 Calculate the Index Weights W1 According to the G1 Method
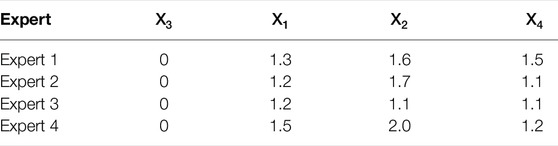
Four defect types of winding deformation X1, turn-to-turn short circuit X2, short circuit between core chips X3 and poor tap changer contact X4 are used as the assigned defects, and four experts based on their experience on these four indexes and give the relative importance between the indexes. The experts agreed on the importance ranking of X4 ≥ X2 ≥ X1 ≥ X3. The specific rank assessment is shown in Table 5.
The subjective weights W1 = [0.1853, 0.2867, 0.1544, 0.3735] are calculated according to Eqs. (2–5).
4.2.1.2 Calculate the Index Weights W2 According to the Entropy Weight Method
Experts assess the importance of the defects. Table 6 shows the importance levels of the four indexes assessed by the experts, where important = 1, slightly important = 3, significantly important = 5, strongly important = 7, and extremely important = 9, and the number in between is the level of importance between the two. The assessment of the importance of indexes is shown in Table 6.
The objective weights W2 = [0.2585, 0.2635, 0.2390, 0.2390] are calculated according to Eqs 6–9.
The initial weights of assessment indexes are obtained from Eq. 10 as W0 = [0.2223, 0.2791, 0.1951, 0.3034].
4.2.2 Based on the Variable Weight Method and Weighted Calculation to Obtain Comprehensive Evaluation Results
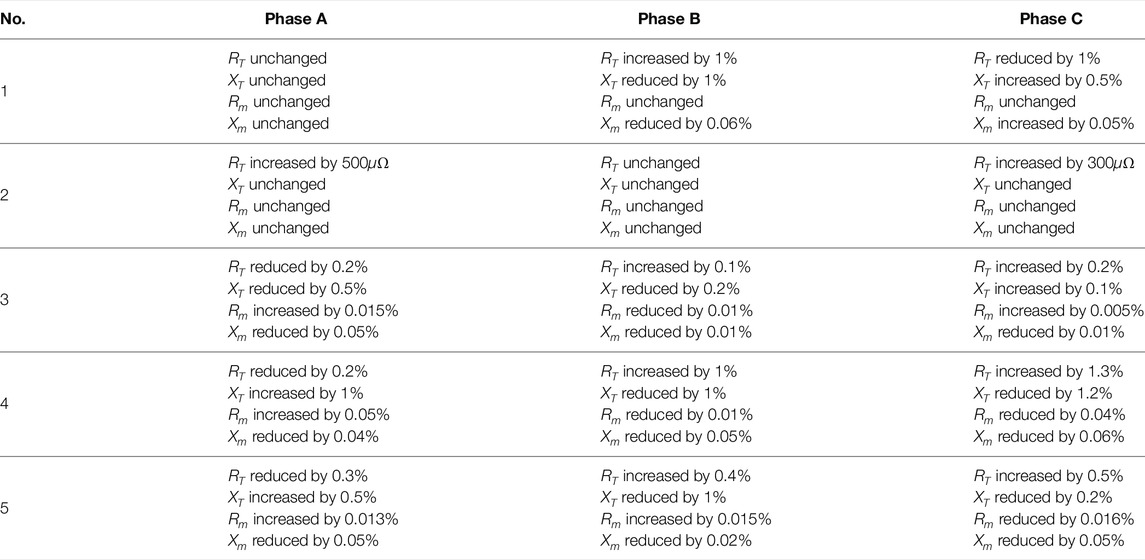
Table 7 shows the variation of the equivalent circuit parameters when the transformer is partially defective in the simulation. Table 8 shows the composite score of the transformer’s condition, as well as the values of the deterioration indexes, calculated by the variable weight synthesizing assessment model based on the parameter variations in Table 7. In Table 8, bold indicates scores that are worth paying attention to.
For case 1, the score of turn-to-turn short circuit has reached 60, and the winding deterioration index is 1. Because the inter-wire imbalance of DC resistance of the winding has reached 2%, it has reached the threshold of fault occurrence specified by the standard.
For case 2, the final tap changer score is 6.16 points lower than expected, the degree of deterioration is 0.15 higher, and the overall score is lower than expected. After examination, it is found that there is an error in converting the short-circuit resistance to winding DC resistance and converting it to operating temperature (75°C). However, since in practice this method is not used alone to determine the defective condition of the tap changer, the results of this evaluation can be used as a reference for the relevant personnel.
For case 3, in addition to the tap changer fault, the maximum mutual difference between the scores of the other three faults is less than or equal to 5 and the minimum score is 90, and the score of poor tap changer contact is −1. Therefore, the weight is changed according to point (2) of the variable weight method, and a comprehensive score is obtained.
For case 4, the transformer equivalent circuit parameters all have certain changes and two faults have scores lower than 70. The composite score obtained is as expected and reflects that the transformer is in a serious “subhealth” condition. Besides, each deterioration index also corresponds accurately to each fault score, which can reflect the severity of transformer winding and core deterioration.
For case 5, the defect situation satisfies point (4) of the variable weighting method, and the combined score is close to the lowest score for each fault, highlighting the most severe defect situation of the transformer. The deterioration index also corresponds accurately to each fault score.
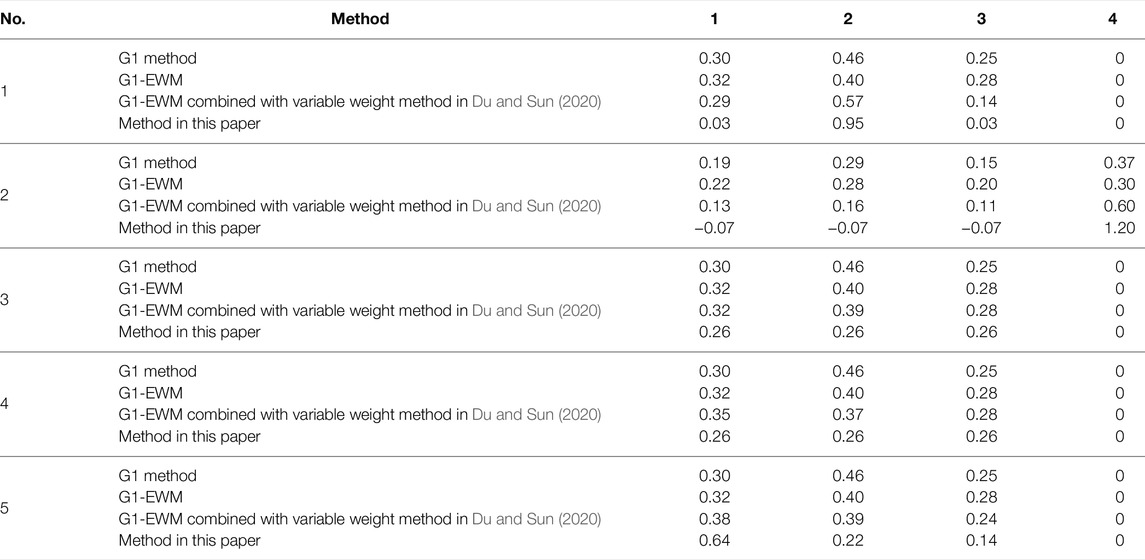
In order to further verify the effectiveness of the method proposed in this paper, the G1 method, G1-EWM method, and G1-EWM combined with variable weight method in (Du and Sun, 2020) are compared with the overall scores calculated by the method proposed in this paper. The weighting results are shown in Table 9, and the final assessment results are shown in Table 10.
A comparison of the weighting results and the assessment results shows that the score of 60 for the turn-to-turn short circuit in case 1 reaches the fault threshold. The score of less than 60 for the tap changer defect in case 2 indicates a fault in the tap changer. However, the assessment results of the first three methods in Table 10 fail to highlight their severity, and the method proposed in this paper has a higher sensitivity. As can be seen from the final weights, defects that reach or exceed the fault threshold are assigned significantly greater weights than the other weights, enabling the assessment results to more accurately reflect the severity of the defect. In cases 3 and 4, the scores of each defect show that the transformer is in “subhealth” condition, which is not reflected in the assessment results of the first three methods in Table 10. For case 5, the minimum value of each defect score is 75.76, which is more serious compared to the other defects scores. The assessment results of the first three methods in Table 10 also do not reflect this severity. The method proposed in this paper, by adjusting the weights, is able to assign the maximum weight to the defect corresponding to the lowest score, highlighting the severity of the defect.
5 Conclusion
In this paper, a variable weight synthesizing assessment model is proposed, which adopts the idea of weight assignment to make a comprehensive assessment of transformer based on the offset of transformer equivalent circuit parameters. In addition, deterioration indexes describing the degree of deterioration of transformer components are proposed from the perspective of maintenance management needs, so that the condition of each component of power transformers can be distinctly reflected in the form of data to provide guiding maintenance advice.
The model firstly uses leakage resistance, short-circuit resistance and short-circuit reactance as assessment indexes. The G1 method and the entropy weight method are used to assign the initial weight to the defects, and the defects are scored according to the deviation of the equivalent circuit parameters. Secondly, a variable weight method is proposed, which adjusts the weight of defects according to the severity of each defect of the transformer and the “sub-health” condition of the transformer, and obtains the final weight of each defect. Finally, the respective scores and comprehensive weights of the defects are weighted to obtain a comprehensive score.
In five simulation cases, the G1 assessment model, G1-EWM assessment model, G1-EWM combined with variable weight model in (Du and Sun, 2020) and the variable weight synthesizing model proposed in this paper are applied to assess the transformer. The variable weight synthesizing model proposed in this paper is more sensitive to the abnormal and “subhealthy” conditions of the transformer. For cases 1 and 2, the assessment results of the proposed model are close to the lowest value of each defect score, which does not exceed 10 points, while the assessmet results of other models differ from the lowest value by up to 32.17 points. In simulation cases 3 and 4, the scores of each defect show that the transformer is in a “subhealth” condition. The assessment result of the proposed model is lower than the minimum score of each defect, which can reflect this condition. The assessment results of other models are higher than the minimum score. For case 5, the minimum value of each defect score is 75.76. The assessment result of the proposed model is closest to this value, which is 3.76. But the assessment results of other models differ from this value by 6.41 at the minimum. It verifies the feasibility of the variable-right comprehensive assessment model for transformer condition assessment, and can provide guiding opinions in distribution operation management.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
Conceptualization: YZ, YL. Methodology: YT, ZL. Formal analysis and investigation: YT, ZL. Writing–original draft preparation: YT. Writing–review and editing: YZ, YL, ZL.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
AQSIQ (2015a). GB/T 10228-2015 Specification and Technical Requirements for Dry-type Power Transformers. Beijing: Standards Press of China.
AQSIQ (2015b). GB/T 6451-2015 Specification and Technical Requirements for Oil-Immersd Power Transformers. Beijing: Standards Press of China.
Arias Velásquez, R. M., and Mejía Lara, J. V. (2020). Root Cause Analysis Improved with Machine Learning for Failure Analysis in Power Transformers. Eng. Fail. Anal. 115, 104684. doi:10.1016/j.engfailanal.2020.104684
Du, J., and Sun, M. (2020). Hierarchical Assessment Method of Transformer Condition Based on Weight-Varying Grey Cloud Model. Trans. China Electrotech. Soc. 35, 4306–4316. doi:10.19595/j.cnki.1000-6753.tces.190827
Ecaterina, M., and Ion, S. (2019). “Parameter Identification for Two-Windings Power Transformers,” in 2019 International Conference on Electromechanical and Energy Systems (SIELMEN), Craiova, Romania, October 9–October 11, 2019 (IEEE), 1–6. doi:10.1109/sielmen.2019.8905914
Eke, S., Clerc, G., Aka-Ngnui, T., and Fofana, I. (2019). Transformer Condition Assessment Using Fuzzy C-Means Clustering Techniques. IEEE Electr. Insul. Mag. 35, 47–55. doi:10.1109/mei.2019.8636165
Fu, X., Guo, Q., and Sun, H. (2020). Statistical Machine Learning Model for Stochastic Optimal Planning of Distribution Networks Considering a Dynamic Correlation and Dimension Reduction. IEEE Trans. Smart Grid 11 (4), 2904–2917. doi:10.1109/tsg.2020.2974021
Islam, M. M., Lee, G., Hettiwatte, S. N., and Williams, K. (2017). Calculating a Health Index for Power Transformers Using a Subsystem-Based Grnn Approach. IEEE Trans. Power Deliv. 33 (4), 1903–1912. doi:10.1109/TPWRD.2017.2770166
Jiao, Z., Ma, T., Qu, Y., Zhang, M., and Suonan, J. (2014). A Novel Excitation Inductance-Based Power Transformer Protection Scheme. Proc. CSEE 34, 1658–1666. doi:10.13334/j.0258-8013.pcsee.2014.10.018
Kari, T., Gao, W., Zhao, D., Abiderexiti, K., Mo, W., Wang, Y., et al. (2018). Hybrid Feature Selection Approach for Power Transformer Fault Diagnosis Based on Support Vector Machine and Genetic Algorithm. IET Gener. Transm. Dis. 12, 5672–5680. doi:10.1049/iet-gtd.2018.5482
Khalyasmaa, A., Eroshenko, S. A., Tashchilin, V., Seguin, C., and Atluri, S. R. (2019). “Machine Learning Algorithms for Power Transformers Technical State Assessment,” in 2019 International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), Novosibirsk, Russia, October 21–October 27, 2019 (IEEE), 0601–0606.
Li, C., Li, X., and Gao, P. (2015). Real-Time Evaluation on Transformer State Based on Variable Weight Fuzzy Matter-Element Model. Guangdong Electr. Power 28, 8. doi:10.3969/j.issn.1007-290X.2015.11.014
Li, L., Longjun, X., Deng, Z., Bin, Y., Yafeng, G., and Fuchang, L. (2013). Condition Assessment of Power Transformers Using a Synthetic Analysis Method Based on Association Rule and Variable Weight Coefficients. IEEE Trans. Dielect. Electr. Insul. 20, 2052–2060. doi:10.1109/tdei.2013.6678853
Li, M., Li, S., Xian, X., Hao, C., Zheng, L., and Wu, G. (2016). Insulation Condition Assessment for Power Transformer Based on Intuitionistic Normal Cloud Model and Optimal Variable Weights. Electr. Meas. Instrum. 53, 9. doi:10.3969/j.issn.1001-1390.2016.06.009
Liao, R., Zheng, H., Yang, L., Zhang, Y., and Sun, C. (2010). A Power Transformer Insulation Condition Assessment Method Based on Set Pair Analysis. Automation Electr. Power Syst. 34, 55–60.
Lin, Z., Tang, S., Peng, G., Zhang, Y., and Zhong, Z. (2017). “An Artificial Neural Network Model with Yager Composition Theory for Transformer State Assessment,” in Advanced Information Technology, Electronic & Automation Control Conference, Chongqing, China, March 25–March 26, 2017 (IEEE), 652–655. doi:10.1109/iaeac.2017.8054097
Long, H., Fu, X., Kong, W., Chen, H., Zhou, Y., and Yang, F. (2022). Key Technologies and Applications of Rural Energy Internet in china. Inf. Process. Agric. (in press). doi:10.1016/j.inpa.2022.03.001
Luo, S., Liao, R., Wang, Y., and Liu, L. (2007). Fuzzy Synthetic Evaluation of Power Transformer Condition with Variable Weights. High. Volt. Eng. 33, 106–110. doi:10.3969/j.issn.1003-6520.2007.08.025
Miao, F., Ren, J. W., and Wei, J. J. (2014). Condition Assessment for Power Transformer Based on Improved Evidence Combination Rule. Adv. Mater. Res. 1003, 135–139. doi:10.4028/www.scientific.net/amr.1003.135
NDRC (2008). DL/T 1093-2008 Guide for Reactance Method to Detect and Diagnose Winding Deformation of Power Transformer. Beijing: China Electric Power Press.
NEA (2017). DL/T 1685-2017 Guide for Condition Assessment of Oil-Immersed Power Transformers (Reactors). Beijing: China Electric Power Press.
NEA (2010). DL/T 574-2010 Guide to the Operation and the Maintenance of Tap-Changers in the Transformer. Beijing: China Electric Power Press.
NEA (2021). DL/T 596-2021 Preventive Test Code for Electric Power Equipment. Beijing: China Electric Power Press.
Ouyang, F., Liu, Y., Liang, Z., Qiu, Z., and Yuan, B. (2018). “Parameter Identification of Transformer Based on Pso Algorithm,” in 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, November 6–November 8, 2018 (IEEE), 3864–3870. doi:10.1109/powercon.2018.8601728
Pan, J., Yan, X., and Zhou, H. (2017). “Research on On-Line Monitoring of Three-Phase Transformer Winding Deformation State Based on Short Circuit Reactance,” in 2017 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, June 18–June 20, 2017 (IEEE), 1558–1563. doi:10.1109/iciea.2017.8283086
Rexhepi, V., and Nakov, P. (2018). Condition Assessment of Power Transformers Status Based on Moisture Level Using Fuzzy Logic Techniques. J. Mechatron. Electr. Power Veh. Technol. 9, 17–24. doi:10.14203/j.mev.2018.v9.17-24
Tan, G., Liu, D., Shi, Y., and Yang, Z. (2020). “Condition Assessment Method for Power Transformers Based on Variable Weight Principle and Fuzzy Comprehensive Evaluation,” in 2020 7th International Forum on Electrical Engineering and Automation (IFEEA), Hefei, China, September 25–September 27, 2020 (IEEE), 883–888. doi:10.1109/ifeea51475.2020.00185
Tian, F., Jing, Z., Zhao, H., Zhang, E., and Liu, J. (2019). A Synthetic Condition Assessment Model for Power Transformers Using the Fuzzy Evidence Fusion Method. Energies 12 (5), 857. doi:10.3390/en12050857
Wu, Y., Gu, L., Zhang, X., and Wang, J. (2018). “An On-Line Identification Method for Short-Circuit Impedance of Transformer Winding Based on Sudden Short Circuit Test,” in Frontier Computing, Theory, Technologies and Applications (FC 2018). Editors J. Hung, N. Yen, and L. Hui (Singapore: Springer), 1365–1375.
Yan, C., Li, M., and Liu, W. (2019). Transformer Fault Diagnosis Based on Bp-Adaboost and Pnn Series Connection. Math. Problems Eng. 2019, 1–10. doi:10.1155/2019/1019845
Zhao, B. G., Zhao, X. H., Wang, C. Z., Tian, C., Zhao, X. L., and Li, K. J. (2013). A New Approach of Determination of Comprehensive Weight in Condition Assessment of Power Transformer. Appl. Mech. Mater. 273, 365–370. doi:10.4028/www.scientific.net/amm.273.365
Keywords: transformer condition assessment, variable weight synthesizing model, deterioration indexes, G1 method, entropy weight method
Citation: Zhang Y, Tang Y, Liu Y and Liang Z (2022) Research on Variable Weight Synthesizing Model for Transformer Condition Assessment. Front. Energy Res. 10:941985. doi: 10.3389/fenrg.2022.941985
Received: 12 May 2022; Accepted: 31 May 2022;
Published: 29 June 2022.
Edited by:
Dan Lu, Alfred University, United StatesCopyright © 2022 Zhang, Tang, Liu and Liang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yan Zhang, emhhbmd5YW5AZ2R1ZmUuZWR1LmNu
 Yan Zhang
Yan Zhang Yufeng Tang
Yufeng Tang Yongqiang Liu
Yongqiang Liu Zhaowen Liang
Zhaowen Liang