A Fundamental Moving Boundary Problem of 1D Commingled Preferential Darcian Flow and Non-Darcian Flow Through Dual-Layered Porous Media

In consideration of vertical formation heterogeneity, a basic nonlinear model of 1D commingled preferential Darcian flow and non-Darcian flow with the threshold pressure gradient (TPG) in a dual-layered formation is presented. Non-Darcian flow in consideration of the TPG happens in the low-permeability tight layer, and the Darcian kinematic equation holds in the other high-permeability layer. The similarity transformation method is applied to analytically solve the model. Moreover, the existence and uniqueness of the analytical solution are proved strictly. Through analytical solution results, some significant conclusions are obtained. The existence of the TPG in the low-permeability tight layer can intensify the preferential Darcian flow in the high-permeability layer, and the intensity of the preferential Darcian flow is very sensitive to the dimensionless layer thickness ratio. The effect of the layer permeability ratio and layer elastic storage ratio on the production sub-rate is more sensitive than that of the layer thickness ratio. In addition, it is strictly demonstrated that moving boundary conditions caused by the TPG should be incorporated into the model. When the moving boundary is neglected, the preferential Darcian flow in the high-permeability layer will be exaggerated. Eventually, solid theoretical foundations are provided here, which are very significant for solving non-Darcian seepage flow problems in engineering by numerical simulation validation and physical experiment design. Furthermore, they are very helpful for better understanding the preferential flow behavior through the high-permeability paths (such as fractures) in the water flooding development of heterogeneous low-permeability reservoirs; then, the efficient profile control technology can be further developed to improve oil recovery.

1 Introduction

Abundant physical experiments (Bear, 1972; Prada and Civan, 1999; Dou et al., 2014; Wang et al., 2016; Hu et al., 2018; Tian et al., 2018; Wang and Cheng, 2020; Chi and Wang, 2021; Zhao et al., 2021; Yin et al., 2022) and theoretical analysis (Cai, 2014; Wang et al., 2018; Zhang et al., 2018; Zhang et al., 2019a; Ye et al., 2019) have demonstrated when the formation permeability is low, the seepage flow in the formation will belong to the low-velocity non-Darcian flow with a threshold pressure gradient (TPG). The TPG can introduce additional formation energy consumption, which hinders the fluid flow ability through the formation. The low-velocity non-Darcian flow phenomena can be explained by the boundary layer theory and strong fluid–solid interaction (Xiong et al., 2009; Yang et al., 2016) in tiny micro-throats in low-permeability porous media. In addition, there also exists a TPG during the non-Newtonian Bingham fluid seepage flow process (Wang et al., 2006; Wang and Yu, 2011; Fusi and Farina, 2017; Bauer et al., 2019; Zhang et al., 2019b; Zhang et al., 2022). It can be explained by the existence of yield stress in the Bingham fluid. Many engineering problems relate to this non-Darcian flow behavior, such as low-permeability petroleum reservoir development, heavy oil reservoir development, water resource development, contaminant transport in porous media, and the consolidation of soils in hydrology. In fact, the resultant mathematical model is a strongly nonlinear moving boundary (MB) problem (Liu et al., 2012; Zhao et al., 2020; Jiao et al., 2021), owing to the effect of TPG. This threshold problem is really distinct from the classical Stefan MB problem (Voller et al., 2004; Olguín et al., 2007) in the heat conduction theory, although its governing equation has the same form as the heat conduction governing equation of the Stefan problem. Their main difference is that for the Stefan problem, the MB velocity is proportional to the first derivative of the potential (temperature) with respect to distance from the MB (Voller et al., 2004; Olguín et al., 2007). However, for the MB problem of the non-Darcian flow with the TPG, it has been proved theoretically that the MB velocity is proportional to the second derivative of the potential (pressure) with respect to distance from the MB (Liu et al., 2012; Liu et al., 2019a; Liu, 2019). Recently, for this type of MB problem, some exact analytical solutions (EASs) (Chen et al., 2004; Xie et al., 2010; Liu et al., 2012; Liu et al., 2019a; Liu, 2019; Zhou, 2019; Liu W. C., 2020; Liu W. C., 2020) have been presented, especially for the three basic cases of the 1D flow (Chen et al., 2004; Xie et al., 2010; Liu et al., 2012; Liu W. C., 2020; Wang et al., 2021; Zhou et al., 2021), the two-dimensional radial flow (Liu et al., 2019a; Zhou, 2019), and the three-dimensional spherical centripetal flow (Liu, 2019) in the homogenous porous media; both the existence and the uniqueness of the EASs are also strictly proved (Liu et al., 2012; Liu et al., 2019a; Liu, 2019; Liu W. C., 2020), respectively. Even more, the correctness of some numerical solutions (Yao et al., 2013; Li et al., 2016; Liu et al., 2019b) has been strictly verified by these EASs successfully, and they can also be applied to the inverse problems, such as the physical experiment design for testing the TPG.

Heterogeneity along the direction vertical to the flow (Shen and Reible, 2015; Song et al., 2015; Wu et al., 2016; Afshari et al., 2018; Gao et al., 2018; Swami et al., 2018; Li et al., 2019; Kaffel, 2019; Nijjer et al., 2019; Liu W. C., 2020; Ma et al., 2021; Shen et al., 2022), different from the heterogeneity along the flow direction (Liu et al., 2022), is a critical feature of the porous media in the real world. For example, the vertically stratified oil reservoirs (Song et al., 2015; Gao et al., 2018) with vertical permeability heterogeneity are commonly encountered in petroleum engineering, the contaminant transport (Shen et al., 2015; Swami et al., 2018) in vertically layered formations is frequently involved in environment engineering, and the rainfall infiltration into layered soils (Wu et al., 2016; Afshari et al., 2018; Kaffel, 2019; Nijjer et al., 2019) is very common in municipal engineering. Although the research area on the mass transfer through heterogeneous porous media is very challenging due to the involvement of the nonlinear flow process and complex flow situations in the actual engineering background, abundant research on the seepage flow problems in multi-layer porous media considering the heterogeneity has been carried out in recent years. In other words, through the separation of the variable technique, Shen and Reible (2015) obtained an EAS for a 1D solute transport model, which allowed an arbitrary number of layers, and the EAS was also verified through comparing with the numerical solution. Wu et al. (2016) conducted finite-element numerical solution research on a 1D water flow model in the unsaturated dual-layered porous media, and the rainfall infiltration process under different conditions was analyzed. Afshari et al. (2018) applied direct pore-level numerical simulations to modeling the dispersion and solute transport during the pore-scale miscible displacements in the heterogeneous layered formation, and it was demonstrated that the dispersion scale dependency was mainly affected by layering configuration. Gao et al. (2018) conducted numerical simulation research on the development of low-permeability multi-layer reservoirs, and a stratified hydraulic fracturing method was put forward for oil recovery enhancement. By employing the semi-analytical solution method, Swami et al. (2018) studied the asymptotic solute transport behavior in stratified porous media and also proposed an asymptotic relation that could provide valuable information on the mass transfer coefficient during solute transport. Li et al. (2019) defined a main flow channel index to identify the type of main flow channel in heterogenous petroleum reservoirs and put forward a quantitative classification method for the main flow channels. Through the numerical simulation method with high resolution, the permeability heterogeneity effect on the miscible displacement process in layered formation at three different flow times was analyzed by Nijjer et al. (2019). Liu W. C. (2020) focused on the exact analytical study on a generalized nonlinear MB problem of the 1D low-velocity non-Darcian flow in heterogeneous low-permeability multi-layered formation with the TPG; however, the Darcian flow is not involved in the flow behavior analysis, and the existence and the uniqueness of the EAS are not demonstrated in theory.

As far as we know, due to the strong nonlinearity, the studies on the EAS of low-velocity non-Darcian flow MB problems in heterogeneous layered formation are few at present, although they have been extensively involved in actual engineering problems (Song et al., 2015; Gao et al., 2018). In particular, the basic research topic on the preferential flow along the high-permeability porous media layer in the heterogeneous low-permeability reservoir is widely involved in the technical reservoir engineering problems for enhanced oil recovery, such as the high-permeability layer blocking by the in-depth profile control technology in the water flooding process (Zhou et al., 2017; Li et al., 2018; Zhao et al., 2018). Here, based on the concerns, considering the vertical permeability heterogeneity of porous media, a basic nonlinear model of the 1D commingled preferential Darcian flow and non-Darcian flow with the TPG in a dual-layered formation is studied. Although this commingled flow model can be considered as a partially degenerated case of the previously generalized MB model (Liu W. C., 2020), the mechanics of the high Darcian flow and non-Darcian flow happening simultaneously in each layer is first involved. For the commingled flow model, the non-Darcian flow in consideration of the TPG happens in the low-permeability tight layer (Liu et al., 2012; Dou et al., 2014), while the Darcian flow happens in the other high-permeability layer. The EAS of the nonlinear model is presented; moreover, both the existence and the uniqueness of the EAS are strictly proved. Consequently, some significant conclusions are obtained from the discussion of the EAS results.

2 Mathematical Modeling

The 1D commingled preferential Darcian flow and non-Darcian flow in a heterogeneous dual-layered rectangular formation is involved here, which is shown in Figure 1. The flow direction is parallel to the x coordinate. The upper tight layer (the thickness h₁ and the wideness L) has a very low permeability. The low-velocity non-Darcian flow with the TPG happens in the low-permeability tight layer (Dou et al., 2014); its kinematic equation is as follows (Liu et al., 2012; Dou et al., 2014) (Figure 1):

${\upsilon }_1=\{\begin{array}{cc}0& 0\le \frac{\partial p_1}{\partial x}\le \lambda ,\\ -\frac{k_1}{\mu }\cdot \left(\frac{\partial p_1}{\partial x}-\lambda \right)& \frac{\partial p_1}{\partial x}>\lambda ,\end{array}(1)$

FIGURE 1

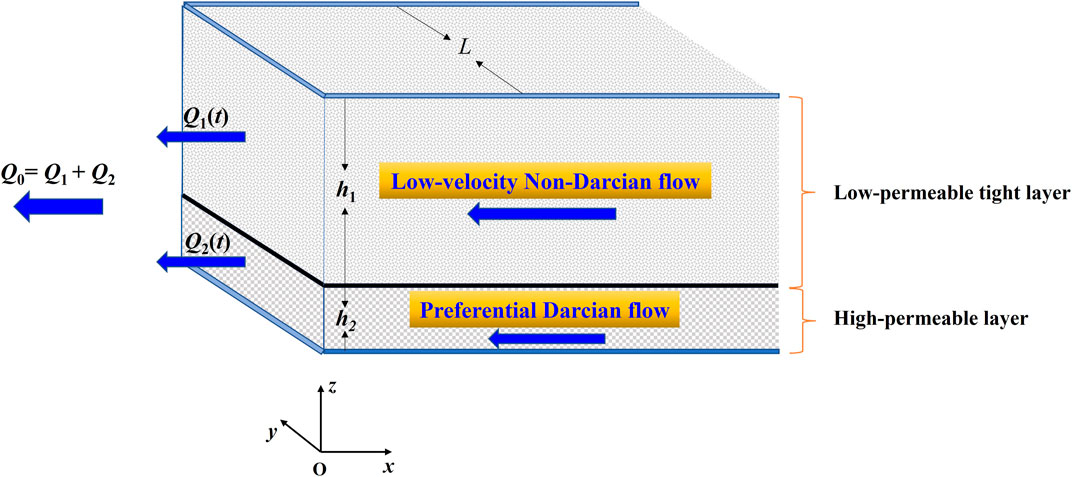
FIGURE 1. Schematics of the 1D commingled preferential Darcian flow and non-Darcian flow in a heterogeneous dual-layered rectangular formation.

where subscript 1 represents the low-permeability tight layer; k₁ is the tight layer permeability; λ is the TPG; υ₁ is the fluid velocity; μ is the fluid viscosity; and p₁ is the pressure.

However, the lower layer (the thickness h₂ and the wideness L) has a much higher permeability, and the preferential flow in the high-permeability layer obeys Darcy’s law. Darcy’s law for the flow in the high-permeability layer is as follows:

${\upsilon }_2=-\frac{k_2}{\mu }\cdot \frac{\partial p_2}{\partial x},(2)$

where subscript 2 represents the high-permeability tight layer; k₂ is the permeability; υ₂ is the fluid velocity; and p₂ is the pressure. It is worth mentioning that we assume the flow in the high-permeability layer is not fast enough to be affected by inertia and turbulence (Elkady et al., 2022), and thus, the flow obeys Darcy’s law.

In addition, there exists a very thin impermeable barrier layer (nearly zero thickness) between the low-permeability tight layer and the high-permeability layer; and then, there is no cross flow (Debbabi et al., 2017) in the z direction between the two different layers. At the outlet end, i. e., x = 0, the variable production rate from the low-permeability tight layer is noted as Q₁(t); and the variable production rate from the high-permeability layer is noted as Q₂(t). Furthermore, the total production rate Q₀ keeps constant, i. e., Q₁(t)+Q₂(t) = Q₀. t is the time.

Some assumptions are defined for mathematical modeling. The dual-layered porous medium is infinitely long, and the low-permeability tight layer and the high-permeability layer are both homogeneous, respectively. In the isothermal environment, the single-phase fluid flows in the dual-layered porous medium. Both the porous medium and the fluid are slightly compressible. The gravity effect is not considered. Initially, the pressure in the dual-layered porous medium stays constant as p_i. Both the liquid storage and the skin effect (Ehlig-Economides and Joseph, 1987; Liu and Wang, 1993) at the outlet end are not considered.

By applying a mathematical modeling method in the previous work (Liu W. C., 2020) for the fluid flow in multi-layered formation, a dimensionless mathematical model for the fundamental MB problem of the 1D commingled preferential Darcian flow and non-Darcian flow with the TPG in a dual-layered formation can be built. It is as follows:

$2{\alpha }_1\cdot \frac{{\partial }^2{U}_1}{\partial X^2}=\frac{\partial U_1}{\partial T},0\le X\le \delta \left(T\right),(3)$

$\delta \left(0\right)=0,(4)$

${U_1|}_{T=0}=0,(5)$

${U_1|}_{X=\delta \left(T\right)}=0,(6)$

${\frac{\partial U_1}{\partial X}|}_{X=\delta \left(T\right)}=-\mathrm{\Lambda },\mathrm{\Lambda }>0,(7)$

$2{\alpha }_2\cdot \frac{{\partial }^2{U}_2}{\partial X^2}=\frac{\partial U_2}{\partial T},0\le X<+\infty ,(8)$

${U_2|}_{T=0}=0,(9)$

${U_2|}_{X\to \infty }=0,(10)$

${{\beta }_1\cdot \frac{\partial U_1}{\partial X}|}_{X=0}+{\beta }_2\cdot {\frac{\partial U_2}{\partial X}|}_{X=0}=-\left(1+{\beta }_1\cdot \mathrm{\Lambda }\right),\mathrm{\Lambda }>0,(11)$

${U_1|}_{X=0}={U_2|}_{X=0},(12)$

where X is the dimensionless distance; U₁ and U₂ are the dimensionless pressures, respectively; T is dimensionless time; Λ is the dimensionless TPG; δ is the dimensionless MB distance; ω₁ and ω₂ are dimensionless layer elastic storage ratios (LESRs), respectively; H₁ and H₂ are dimensionless layer thickness ratios (LTRs); D₁ and D₂ are dimensionless layer permeability ratios (LPRs); α₁, α₂, β₁, and β₂ are defined parameters; υ_w0 is the flow velocity in average.

These dimensionless variables in the model are shown as follows:

$X=\frac{x}{L},(13)$

$T=\frac{k_1+k_2}{\mu \cdot \left({\varphi }_{\text{i}1}{C}_{\text{t}1}+{\varphi }_{\text{i}2}{C}_{\text{t}2}\right)\cdot L^2}t,(14)$

$\delta =\frac{s}{L},(15)$

$U_1=\frac{k_1+k_2}{{\upsilon }_{\text{w0}}L\mu }\left(p_{\text{i}}-p_1\right),(16)$

$U_2=\frac{k_1+k_2}{{\upsilon }_{\text{w0}}L\mu }\left(p_{\text{i}}-p_2\right),(17)$

$\mathrm{\Lambda }=\frac{\left(k_1+k_2\right)\lambda }{{\upsilon }_{\text{w0}}\mu },(18)$

${\omega }_1=\frac{{\varphi }_{\text{i}1}{C}_{\text{t}1}}{{\varphi }_{\text{i}1}{C}_{\text{t}1}+{\varphi }_{\text{i}2}{C}_{\text{t}2}},(19)$

${\omega }_2=\frac{{\varphi }_{\text{i}2}{C}_{\text{t}2}}{{\varphi }_{\text{i}1}{C}_{\text{t}1}+{\varphi }_{\text{i}2}{C}_{\text{t}2}},(20)$

$H_1=\frac{h_1}{h_1+h_2},(21)$

$H_2=\frac{h_2}{h_1+h_2},(22)$

$D_1=\frac{k_1}{k_1+k_2},(23)$

$D_2=\frac{k_2}{k_1+k_2},(24)$

${\alpha }_1=\frac{D_1}{2{\omega }_1},(25)$

${\alpha }_2=\frac{D_2}{2{\omega }_2},(26)$

${\beta }_1=H_1\cdot D_1,(27)$

${\beta }_2=H_2\cdot D_2,(28)$

${\upsilon }_{\text{w0}}=\frac{Q_0}{h_1\cdot L+h_2\cdot L},(29)$

where ϕ_i1 and ϕ_i2 are the initial porosity for the two layers, respectively; C_t1 and C_t2 are comprehensive compressibility coefficients for the two layers, respectively; s is the distance of the transient MB; t is time; Q₀ is the constant total production rate.

3 Exact Analytical Solutions

The model has a strong nonlinearity. It can be attributed to the existence of MB conditions, i. e., Eqs. 6, 7. However, the model can show a fully self-similarity property, which can be found by carrying out the stretching transform on the model (Ames, 1965). Then, some similarity transformations can be introduced as follows (Liu et al., 2012; Liu et al., 2019; Liu, 2019):

$\eta =\frac{U_1}{2T^{\frac{1}{2}}},(30)$

$\psi =\frac{U_2}{2T^{\frac{1}{2}}},(31)$

$\xi =\frac{X}{2T^{\frac{1}{2}}},(32)$

$\theta =\frac{\delta }{2T^{\frac{1}{2}}}.(33)$

Then, through Eqs. 30–33, the mathematical model, i. e., Eqs. 3–12 can be equivalently transformed as follows:

${\alpha }_1\cdot \frac{{\text{d}}^2\eta }{\text{d}{\xi }^2}+\xi \cdot \frac{\text{d}\eta }{\text{d}\xi }-\eta =0,0\le \xi \le \theta ,(34)$

${\eta |}_{\xi =\theta }=0,(35)$

${\frac{\text{d}\eta }{\text{d}\xi }|}_{\xi =\theta }=-\mathrm{\Lambda },\mathrm{\Lambda }>0,(36)$

${\alpha }_2\cdot \frac{{\text{d}}^2\psi }{\text{d}{\xi }^2}+\xi \cdot \frac{\text{d}\psi }{\text{d}\xi }-\psi =0,0\le \xi <+\infty ,(37)$

${\psi |}_{\xi \to +\infty }=0,(38)$

${{\beta }_1\cdot \frac{\text{d}\eta }{\text{d}\xi }|}_{\xi =0}+{{\beta }_2\cdot \frac{\text{d}\psi }{\text{d}\xi }|}_{\xi =0}=-\left(1+{\beta }_1\cdot \mathrm{\Lambda }\right),\mathrm{\Lambda }>0,(39)$

${\psi |}_{\xi =0}={\eta |}_{\xi =0}.(40)$

Equations 34–40 belong to an ordinary differential equation system. It is linear and closed, which means it can be analytically solved with ease. By using the similar solution procedures in the previous work (Liu W. C., 2020), the EAS of the model, i. e., Eq. 3 –Eq. 12 can be deduced as follows:

$\begin{array}{l}{U}_1\left(X,T\right)=-\mathrm{\Lambda }\cdot X-\frac{\sqrt{2}}{2}\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\text{π}}\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{X^2}{{\alpha }_1}}\\ +\mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \exp \left(-\frac{X^2}{8{\alpha }_{1}T}\right)\cdot 2T^{\frac{1}{2}}\\ +\frac{\sqrt{2}}{2}\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\text{π}}\cdot \text{erf}\left(\sqrt{\frac{X^2}{8{\alpha }_{1}T}}\right)\cdot \sqrt{\frac{X^2}{{\alpha }_1}},0\le X\le 2\theta \cdot T^{\frac{1}{2}},\end{array}(41)$

where erf is the error function (Liu, 2019).

$\begin{array}{l}{U}_2\left(X,T\right)=-\frac{\sqrt{2}}{2}\cdot \sqrt{\text{π}}\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_2}}\cdot X\\ +\mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \exp \left(-\frac{X^2}{8{\alpha }_{2}T}\right)\cdot 2T^{\frac{1}{2}}\\ +\frac{\sqrt{2}}{2}\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\text{π}}\cdot \text{erf}\left(\sqrt{\frac{X^2}{8{\alpha }_{2}T}}\right)\cdot \sqrt{\frac{X^2}{{\alpha }_2}},0\le X<+\infty ,\end{array}(42)$

where the value of θ can be determined for any given positive value of Λ by the following equation:

$\begin{array}{l}\sqrt{\text{π}}\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}\\ +\sqrt{\text{π}}\cdot {\beta }_2\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_2}}=\sqrt{2}.\end{array}(43)$

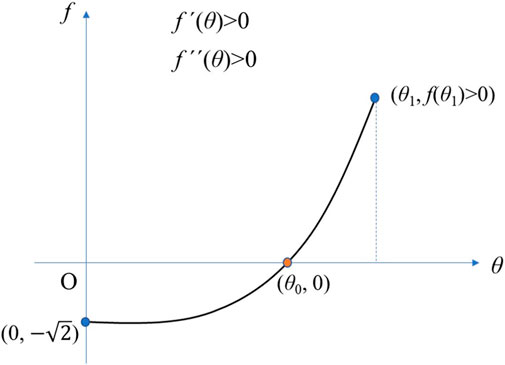
However, it is necessary to prove the existence and uniqueness of the positive solution of θ through Eq. 43. The following is the proof process.

By Eq. 43, a function f(θ) is defined:

$\begin{array}{l}f\left(\theta \right)=\sqrt{\text{π}}\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}\\ +\sqrt{\text{π}}\cdot {\beta }_2\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_2}}-\sqrt{2}.\end{array}(44)$

From Eq. 44, the following equations can be obtained:

$f\left(0\right)=-\sqrt{2},(45)$

$\underset{\theta \to +\infty }{\lim }f\left(\theta \right)=+\infty .(46)$

By using Eqs. 45, 46, it is obviously known that a positive value of θ noted as θ₁ exists, which satisfies f (θ₁) > 0.

Then, the derivative of f is deduced from Eq. 44:

$\begin{array}{l}{f}^{\prime }\left(\theta \right)=\sqrt{\text{π}}\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}\\ +\sqrt{\text{π}}\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot {\theta }^2\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1^3}}\\ +2\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot {\theta }^2\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{exp}\left(-\frac{1}{2}\cdot \frac{{\theta }^2}{{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}\cdot \frac{\sqrt{2}}{2}\cdot \sqrt{\frac{1}{{\alpha }_1}}\\ +\sqrt{\text{π}}\cdot {\beta }_2\cdot \mathrm{\Lambda }\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_2}}\\ +\sqrt{\text{π}}\cdot {\beta }_2\cdot \mathrm{\Lambda }\cdot {\theta }^2\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_2}}\cdot \frac{1}{{\alpha }_1}.\end{array}(47)$

From Eq. 47, the following equations can be obtained as follows:

$f^{\prime }\left(0\right)=\sqrt{\text{π}}\cdot {\beta }_2\cdot \mathrm{\Lambda }\cdot \sqrt{\frac{1}{{\alpha }_2}}>0,(48)$

$\begin{array}{l}{f}^{″}\left(\theta \right)=\sqrt{\text{π}}\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}\cdot \frac{\theta }{{\alpha }_1}\\ +2\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{exp}\left(-\frac{1}{2}\cdot \frac{{\theta }^2}{{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}\cdot \frac{\sqrt{2}}{2}\cdot \sqrt{\frac{1}{{\alpha }_1}}\\ +2\cdot \sqrt{\text{π}}\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1^3}}\\ +\sqrt{\text{π}}\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot {\theta }^3\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1^5}}\\ +2\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot {\theta }^2\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{exp}\left(-\frac{1}{2}\cdot \frac{{\theta }^2}{{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_1^3}}\cdot \frac{\sqrt{2}}{2}\cdot \sqrt{\frac{1}{{\alpha }_1}}\\ +4\cdot {\beta }_1\cdot \mathrm{\Lambda }\cdot \theta \cdot \sqrt{\frac{1}{{\alpha }_1}}\cdot \frac{\sqrt{2}}{2}\cdot \sqrt{\frac{1}{{\alpha }_1}}+\sqrt{\text{π}}\cdot {\beta }_2\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_2}}\cdot \frac{1}{{\alpha }_1}\\ +2\cdot \sqrt{\text{π}}\cdot {\beta }_2\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_2}}\cdot \frac{1}{{\alpha }_1}+\sqrt{\text{π}}\cdot {\beta }_2\cdot \mathrm{\Lambda }\cdot {\theta }^3\cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_2}}\cdot \frac{1}{{\alpha }_1^2}>0,\theta \ge 0.\end{array}(49)$

It is indicated from Eq. 49 that the derivative of f increases with the increment of θ ≥ 0. As a result, it is known from Eq. 48 that the derivative of f is larger than zero as θ ≥ 0. Consequently, it is shown that f is a strictly monotonically increasing function as θ ≥ 0. In consideration of the strict monotonicity of f, it can be known from Eqs. 45, 46 that there exists a unique positive value of θ noted as θ₀ that satisfies Eq. 43(Figure 2).

FIGURE 2

FIGURE 2. Schematics of the existence of a unique positive value of θ that satisfies f(θ) = 0.

4 Results and Discussion

In accordance with actual physical parameter values (Yao et al., 2013), the values of dimensionless variables are assigned appropriately: D₁ = 0.03, D₂ = 0.97, H₁ = 0.9, H₂ = 0.1, ω₁ = 0.85, and ω₂ = 0.15. From Eqs. 25–28, it can be calculated that α₁ = 0.0176, α₂ = 3.2333, β₁ = 0.0270, and β₂ = 0.097. It is worth mentioning that according to the assigned values of the dimensionless variables, thickness-weighted permeability k_avg for 1D flow in the whole formation (Zhang et al., 2015) can be calculated approximately as follows:

$\begin{array}{l}{k}_{\text{avg}}=\frac{D_1\cdot H_1+D_2\cdot H_2}{H_1+H_2}\cdot \left(k_1+k_2\right)\\ \approx 3.97\cdot k_1.\end{array}(50)$

Equation 50 is based on Darcy’s law, and thus, the weighted permeability must be overestimated. Therefore, it can be concluded from Eq. 50 that this permeability on average for the dual-layered formation and the low-permeability k₁ are on the same order of magnitude. Therefore, from the definition of the dimensionless TPG, i.e., Eq. 18, it can be deduced that its value for the commingled flow is much higher than the value (Liu et al., 2012; Yao et al., 2013; Liu W. C., 2020) that corresponds to the pure non-Darcian flow with the TPG in the low-permeability tight formation. It can be attributed to the reason that k₁+k₂ is much higher than the low permeability k₁, while their flow velocity υ_w0 is nearly of the same order of magnitude based on the aforementioned average permeability analysis. Here, the value of Λ is set as 20.0 appropriately. From Eq. 43, θ = 0.1297.

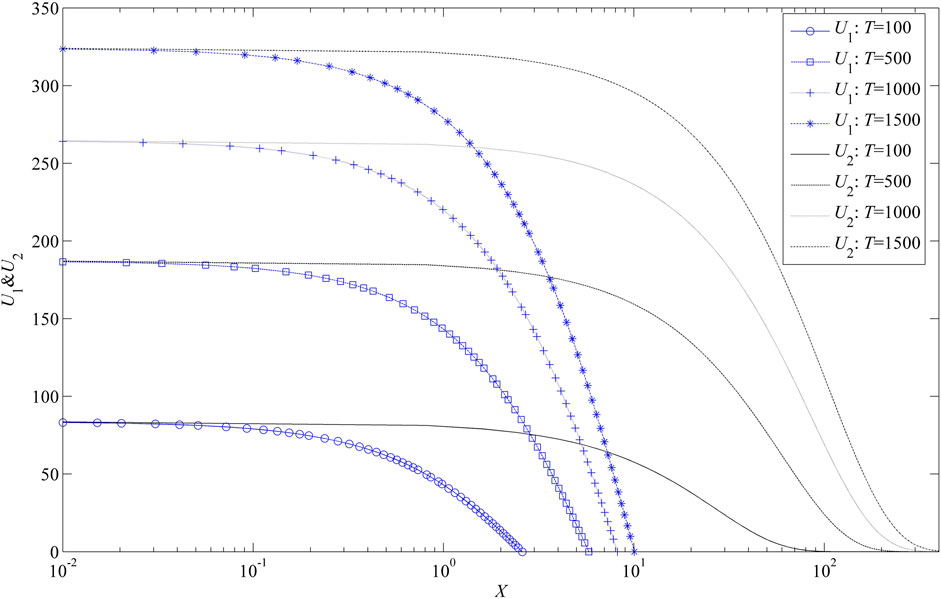
The dimensionless pressure distribution change in the two different layers under different dimensionless times is shown in Figure 3. It is indicated from Figure 3 that the pressure distribution curve corresponding to the Darcian flow in the high-permeability layer is much smoother than the one corresponding to the non-Darcian flow in the low-permeability tight layer. The pressure drop area in the high-permeability layer is much larger than that in the low-permeability tight layer (U₁ > 0). Furthermore, due to the existing TPG, there exists a large undisturbed area in the low-permeability tight layer (U₁ = 0); and the pressure distribution curves corresponding to the non-Darcian flow in the low-permeability tight layer with the TPG can show the characteristics of compact supports (Yao et al., 2013) (Figure 3).

FIGURE 3

FIGURE 3. Variation of dimensionless pressure distributions with dimensionless time.

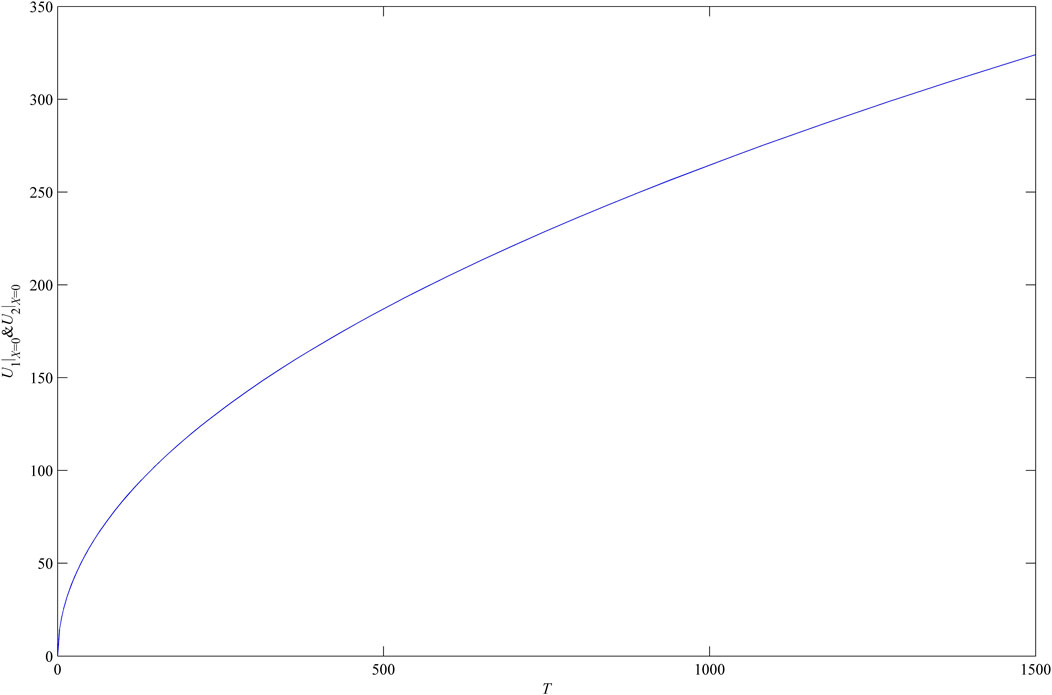
The change of the dimensionless transient pressure at X = 0 with dimensionless time is shown in Figure 4. It is indicated from Figure 4 that with dimensionless time increasing, the dimensionless transient pressure also increases gradually (Figure 4).

FIGURE 4

FIGURE 4. Variation of the dimensionless transient pressure with dimensionless time.

By using the model solution, from Eqs. 1, 2, and 11, the dimensionless production rate Q_1D from the low-permeability tight layer can be written as follows:

$\begin{array}{l}{Q}_{1\text{D}}=-{\beta }_1\cdot \left({\frac{\partial U_1}{\partial X}|}_{X=0}+\mathrm{\Lambda }\right)\\ ={\beta }_1\cdot \frac{\sqrt{2}}{2}\cdot \sqrt{\text{π}}\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}.\end{array}(51)$

The dimensionless production rate Q_2D from the high-permeability layer can be written as follows:

$\begin{array}{l}{Q}_{2\text{D}}=-{\beta }_2\cdot {\frac{\partial U_2}{\partial X}|}_{X=0}\\ ={\beta }_2\cdot \frac{\sqrt{2}}{2}\cdot \sqrt{\text{π}}\cdot \mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot \sqrt{\frac{1}{{\alpha }_2}}.\end{array}(\mathrm{52a})$

Through Eq. 43, it can be easily proven that Q_1D + Q_2D = 1.

For this case, Q_1D = 0.72, and Q_2D = 0.28.

Next, based on the basic case, the influences of the dimensionless TPG, dimensionless LTR, LPR, and dimensionless LESR are discussed, respectively, by using the EAS results. Moreover, the necessity that the MB should be incorporated in the mathematical modeling for describing the effect of the TPG is demonstrated.

4.1 Effect of the Dimensionless Threshold Pressure Gradient

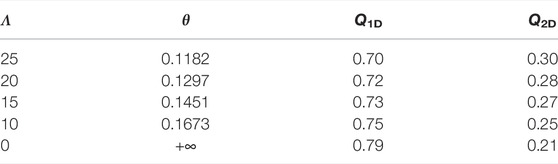
Here, the dimensionless TPG is assigned five different values, respectively: Λ = 0, Λ = 10, Λ = 15, Λ = 20, and Λ = 25. Correspondingly, by Eq. 43, θ can be calculated, as shown in Table 1. It is indicated from Table 1 that the larger dimensionless TPG corresponds to a smaller value of θ, which indicates a smaller dimensionless MB distance from Eq. 33. Figure 5A shows the influence of the dimensionless TPG on dimensionless pressure distributions. It is shown from Figure 5A that the dimensionless TPG affects not only the pressure distribution in the low-permeability tight layer but also the pressure distribution in the high-permeability layer. When the dimensionless distance from X = 0 is smaller, the influence becomes bigger. The TPG can decrease the pressure drop area in the low-permeability tight layer (U₁ > 0), and it can also increase the pressure drop in the high-permeability layer (the increment of formation energy consumption). As the dimensionless TPG increases, the sensitivity of the influence declines (Figure 5A). Under different values of the dimensionless TPG, some curves of the dimensionless transient pressure are plotted in Figure 5B. It is indicated from Figure 5B that the larger dimensionless TPG corresponds to a larger dimensionless transient pressure. Furthermore, when dimensionless time is longer, the influence of the TPG increases. However, as the dimensionless TPG increases, the sensitivity of the influence declines (Figure 5B). Table 1 also shows the influence of the dimensionless TPG on production rates from each layer. From Table 1, it is concluded that with the TPG increasing, less and less production rate comes from the low-permeability tight layer, and then, more and more production rates come from the high-permeability layer when the total production rate Q₀ is constant. Therefore, the existence of TPG in the low-permeability tight layer can intensify the preferential Darcian flow in the high-permeability layer.

TABLE 1

TABLE 1. Values of θ, Q_1D, and Q_2D corresponding to Λ.

FIGURE 5

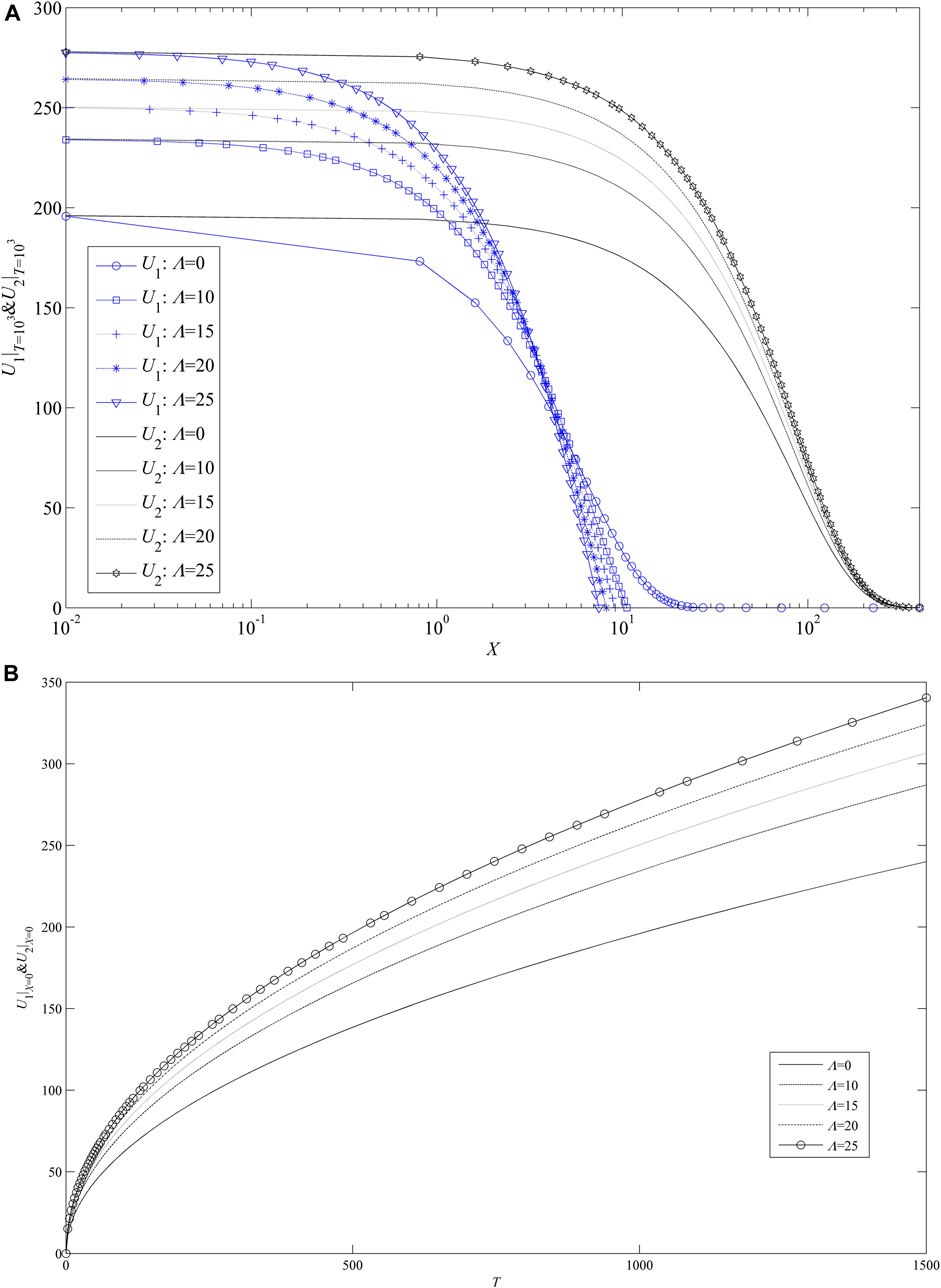
FIGURE 5. Effect of the dimensionless TPG. (A) On dimensionless pressure distributions; (B) on dimensionless transient pressure.

Physical interpretation: The larger TPG can reduce the flow ability in the low-permeability tight layer, which makes MB move more difficultly. As the total production rate is constant, the larger TPG can introduce a larger pressure drop (more energy consumption) in the layers, which also means less production rate from the low-permeability tight layer.

4.2 Effect of the Dimensionless Layer Thickness Ratio

The dimensionless LTR H₁ is assigned four different values, respectively: H₁ = 0.6 (H₂ = 0.4), H₁ = 0.8 (H₂ = 0.2), H₁ = 0.9 (H₂ = 0.1), and H₁ = 0.95 (H₂ = 0.05). Correspondingly, by Eq. 43, θ can be calculated, which is shown in Table 2. From Table 2, it is indicated that the dimensionless MB distance 2 $\sqrt{T}·\theta$ increases as the LTR of the low-permeability tight layer H₁ increases. The influence of the LTR on pressure distributions is shown in Figure 6A. It is indicated from Figure 6A that the bigger the LTR of the low-permeability tight layer, the larger is the pressure drop (U₁ and U₂) in both the layers. Moreover, when the dimensionless distance from X = 0 is smaller, the influence becomes bigger (Figure 6A). Under different values of the dimensionless LTR, some curves of the dimensionless transient pressure are plotted in Figure 6B. It is indicated from Figure 6B that the larger dimensionless LTR for the low-permeability layer corresponds to a greater dimensionless transient pressure (Figure 6B). Table 2 shows the influence of the dimensionless LTR on production rates from each layer. From Table 2, it is concluded that as H₁ increases, the production rate from the low-permeability tight layer becomes greater when the total production rate Q₀ is constant. Furthermore, the intensity of the preferential Darcian flow in the high-permeability layer is very sensitive to the LTR.

TABLE 2

TABLE 2. The value of θ, Q1D and Q2D corresponding to Λ.

FIGURE 6

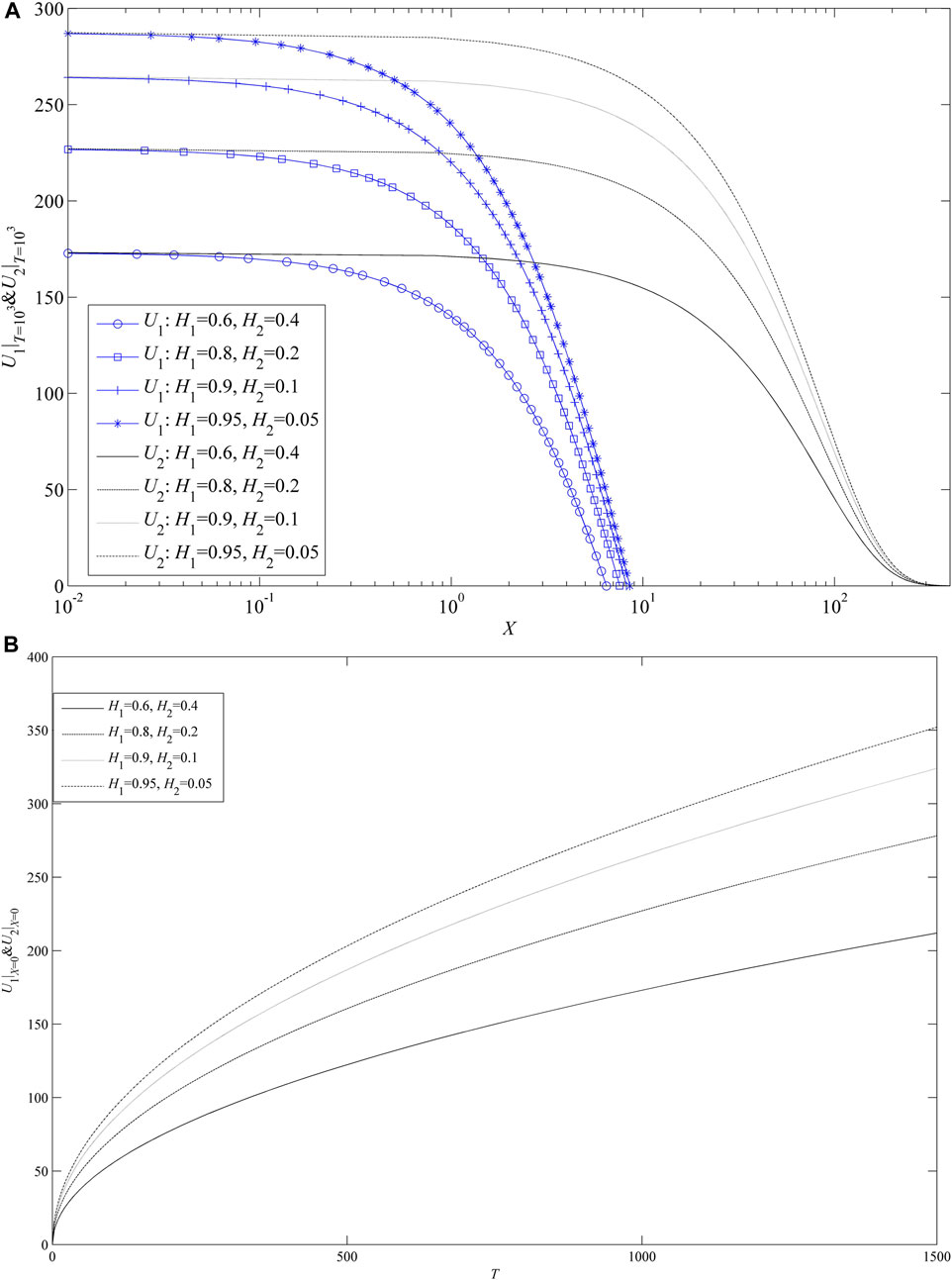
FIGURE 6. Effect of the dimensionless LTR. (A) On dimensionless pressure distributions (B) on dimensionless transient pressure.

Physical interpretation: The higher value of the LTR H₁ indicates a larger thickness of the low-permeability tight layer and a smaller thickness of the high-permeability layer (H₂ = 1.0-H₁). As the value of H₁ increases, due to the decrease in the average permeability of the layered porous media, more pressure drops will be generated in the layers in order to keep the production rate constant.

4.3 Effect of the Dimensionless Layer Permeability Ratio

The dimensionless LPR is assigned four different values, respectively: D₁ = 0.01 (D₂ = 0.99), D₁ = 0.03 (D₂ = 0.97), D₁ = 0.05 (D₂ = 0.95), and D₁ = 0.1 (D₂ = 0.9). Correspondingly, by Eq. (43), θ can be calculated, which is shown in Table 3. It is indicated from Table 3 that as the LPR of the low-permeability tight layer D₁ increases, the dimensionless MB distance 2 $\sqrt{T}·\theta$ increases. Figure 7A shows the effect of the LPR on pressure distributions. From Figure 7A, it is indicated that the bigger the value of D₁, the larger the pressure drop area in the low-permeability tight layer (U₁ > 0), and the smaller the pressure drop inside the pressure drop area in the low-permeability tight layer, the smaller is the pressure drop in the high-permeability layer when the LPR of the low-permeability tight layer increases. When the dimensionless distance from X = 0 is smaller, the influence becomes bigger (Figure 7A). Under different values of the dimensionless LPR, some curves of dimensionless transient pressure are plotted in Figure 7B. It is indicated from Figure 7B that the larger LPR for the low-permeability layer corresponds to a greater dimensionless transient pressure. Table 3 shows the influence of the LPR on production rates from each layer. From Table 3, it is concluded that as D₁ increases, the production rate from the low-permeability tight layer becomes greater, and the sensitivity of the influence of the LPR on the layer production sub-rate is not as much as that of the LTR (Figure 7B).

TABLE 3

TABLE 3. The value of θ, Q1D and Q2D corresponding to Λ.

FIGURE 7

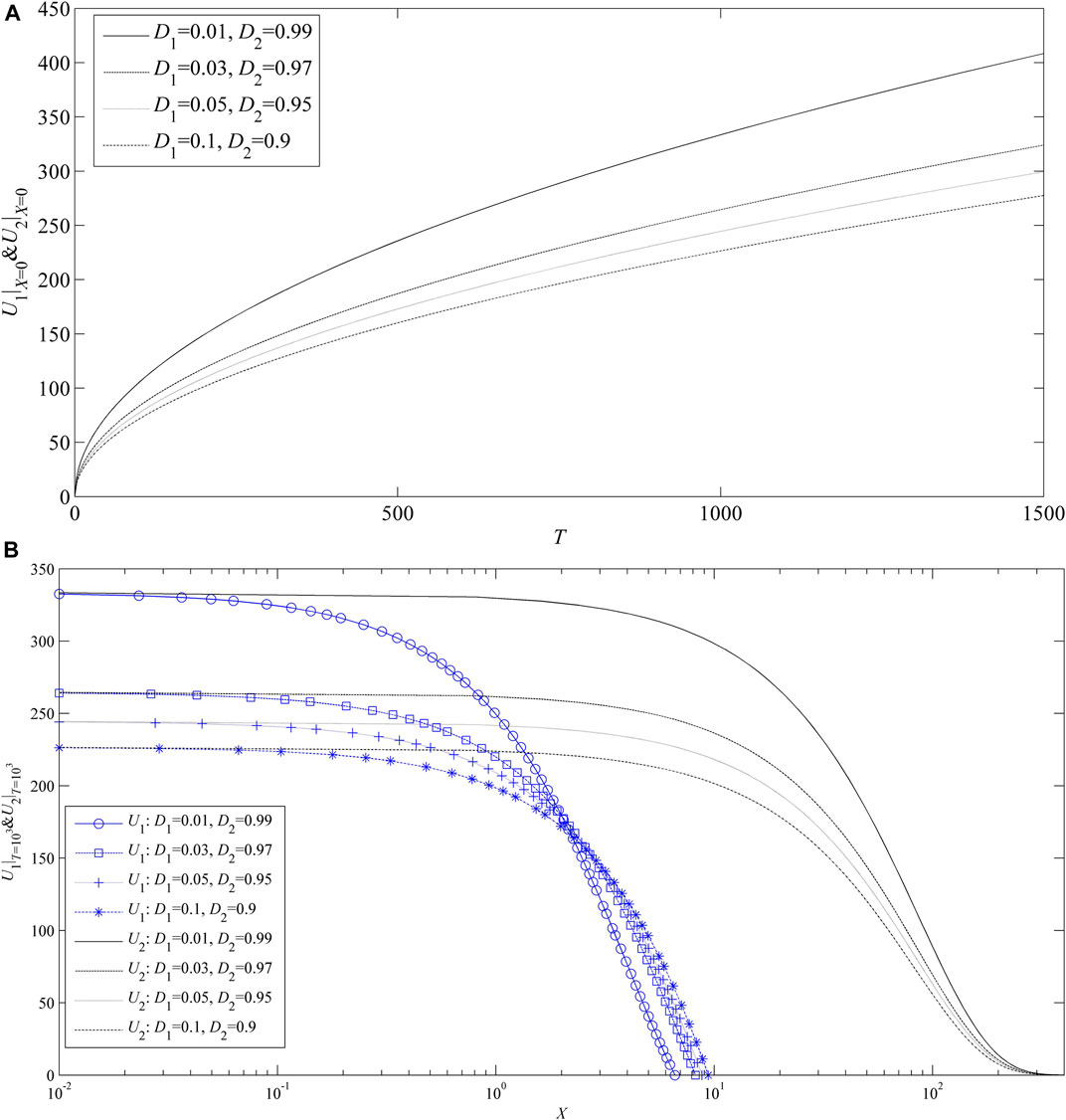
FIGURE 7. Effect of the dimensionless LPR. (A) On dimensionless pressure distributions; (B) on dimensionless transient pressure.

Physical interpretation: The higher value of D₁ directly reflects the enhancement of the flow ability in the low-permeability tight layer and, simultaneously, the reduction of the flow ability in the high-permeability layer (D₂ = 1.0-D₁). Furthermore, due to the reason that the thickness of the low-permeability tight layer is nine times that of the high-permeability layer (H₁ = 0.9), the influence of flow ability enhancement of the low-permeability tight layer is much larger than the influence of flow ability reduction of the high-permeability layer on the flow. Therefore, as the value of D₁ increases, the pressure drop in the layers decreases, and the production rate from the low-permeability tight layer increases.

4.4 Effect of Dimensionless Layer Elastic Storage Ratios

The dimensionless LESR is assigned four different values, respectively: ω₁ = 0.7 (ω₂ = 0.3), ω₁ = 0.8 (ω₂ = 0.2), ω₁ = 0.85 (ω₂ = 0.15), and ω₁ = 0.9 (ω₂ = 0.1). Correspondingly, by Eq. 43, θ can be calculated, which is shown in Table 4. It is indicated from Table 4 that the dimensionless LESR has little effect on θ. Figure 8A shows the effect of LESR on pressure distributions. It can be seen from Figure 8A that the LESR affects the pressure distribution of the low-permeability tight layer a little. However, it has a big effect on the pressure distribution of the high-permeability layer. Furthermore, the bigger the value of ω₁, the larger is the pressure drop in the high-permeability tight layer. When the dimensionless distance increases, the influence of the LESR becomes bigger (Figure 8A). Under different values of the dimensionless LESR, some curves of the dimensionless transient pressure are plotted in Figure 8B. It is indicated from Figure 8B that a larger LESR for the low-permeability layer corresponds to a bigger dimensionless transient pressure. As dimensionless time increases, the influence of the LESR becomes bigger (Figure 8B). Table 4 shows the influence of the LESR on production rates from each layer. From Table 4, it can be concluded that with ω₁ increasing, more and more production rates come from the low-permeability tight layer. The sensitivity of the influence of the LESR on the layer production sub-rate is also not as much as that of the LTR.

TABLE 4

TABLE 4. The value of θ, Q1D and Q2D corresponding to Λ.

FIGURE 8

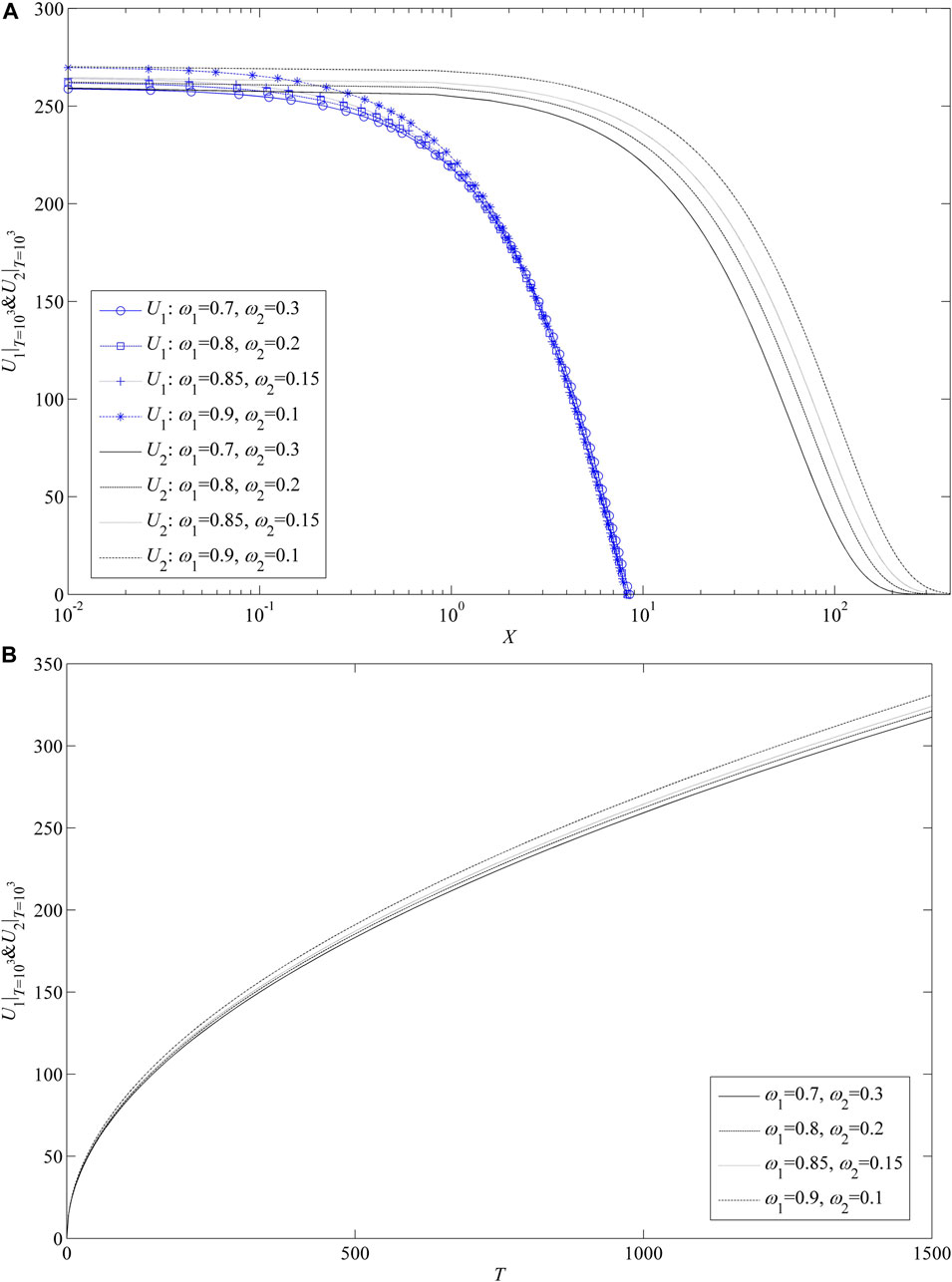
FIGURE 8. Effect of the dimensionless LESR. (A) On dimensionless pressure distributions; (B) on dimensionless transient pressure.

Physical interpretation: The higher value of the LESR ω₁ indicates more elastic energy from porous media and fluid in the low-permeability tight layer and, simultaneously, the less elastic energy in the high-permeability layer (ω₂ = 1.0-ω₁). When the pressure in the porous medium drops, more released elastic energy can cause more fluid to be produced. Therefore, as the value of ω₁ increases, the production rate from the low-permeability tight layer increases, but the production rate from the high-permeability layer decreases. In addition, with ω₁ increasing, it mainly has an effect on pressure drop in the high-permeability layer.

4.5 Effect of Considering Moving Boundary Conditions or Not

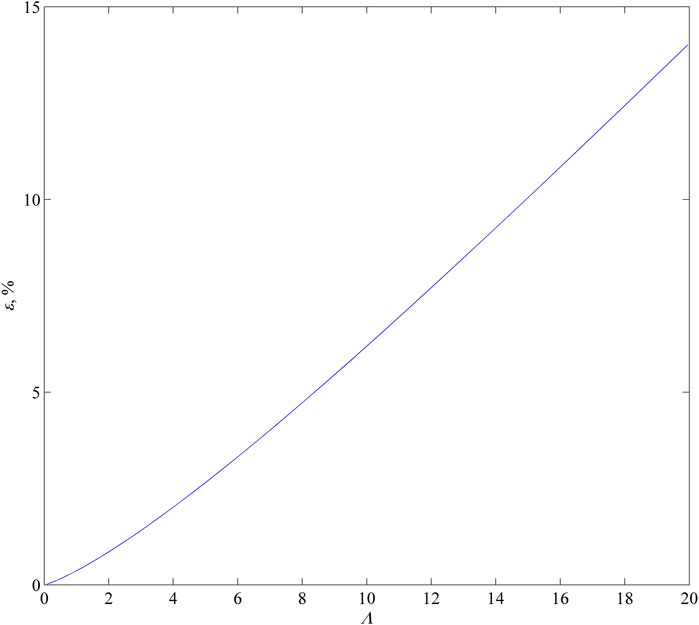
MB problems usually have a strong nonlinearity. In order to linearize the mathematical models for simplifying the model computation, MB conditions that describe the effect of TPG are not always taken into account in the relevant mathematical modeling in the previously published literature (Guo et al., 2012; Zeng et al., 2018; Wu et al., 2019). The TPG effect is just described through continuity equations or inner boundary conditions. However, this kind of linearization may introduce a lot of errors (Yao et al., 2013; Liu et al., 2019a). Here, without considering MB conditions (Guo et al., 2012; Zeng et al., 2018; Wu et al., 2019), a dimensionless mathematical model for this 1D commingled preferential Darcian flow and non-Darcian flow problem is presented, and its EAS is also presented. Please see Appendix A for the details of the mathematical model and its EAS process. Then, this EAS can be compared with the EAS for the model in consideration of MB conditions. As a result, the significance of considering MB conditions caused by the TPG can be demonstrated. Their dimensionless pressure distributions (U₁ and U₂) at T = 10³ are compared in Figure 9A under different values of Λ: Λ = 0, Λ = 10, Λ = 15, and Λ = 20. It can be seen from Figure 9A that when MB is not incorporated, dimensionless pressures U₁ and U₂ will be overestimated largely, and the pressure distribution corresponding to the non-Darcian flow in the low-permeability tight layer with the TPG becomes much smoother, and then, the characteristics of compact supports (Yao et al., 2013) for the pressure distribution corresponding to the non-Darcian flow in the low-permeability tight layer can be lost. A larger TPG can cause larger errors. Moreover, as dimensionless distance decreases, the errors become bigger. In addition, when the MB is not taken into account in the modeling, the pressure drop area (U₁ > 0) in the low-permeability tight layer will be largely overestimated (Figure 9A). Dimensionless transient pressures are compared in Figure 9B under different values of Λ: Λ = 0, Λ = 10, Λ = 15, and Λ = 20. It can be seen from Figure 9B that when the MB is not incorporated, the dimensionless transient pressure can be over-evaluated largely, especially when the dimensionless TPG is bigger, and errors also increase with dimensionless time. When the MB is not considered in the modeling, the relative error ε can be directly deduced through the two EASs, i. e., Eq. 41 and Eq. A9 (see Appendix B for the details) as follows (Figure 9B). The relative error affected by the dimensionless TPG Λ is directly shown in Figure 10. As Λ increases, relative error ε increases, and its increase rate also grows (Figure 10).

$\epsilon =\left|\frac{{\beta }_1\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}+{\beta }_2\cdot \sqrt{\frac{1}{{\alpha }_2}}}{{\beta }_1\cdot \sqrt{\frac{1}{{\alpha }_1}}+{\beta }_2\cdot \sqrt{\frac{1}{{\alpha }_2}}}\cdot \left(1+{\beta }_1\cdot \mathrm{\Lambda }\right)-1\right|\times 100\%.(\mathrm{52b})$

FIGURE 9

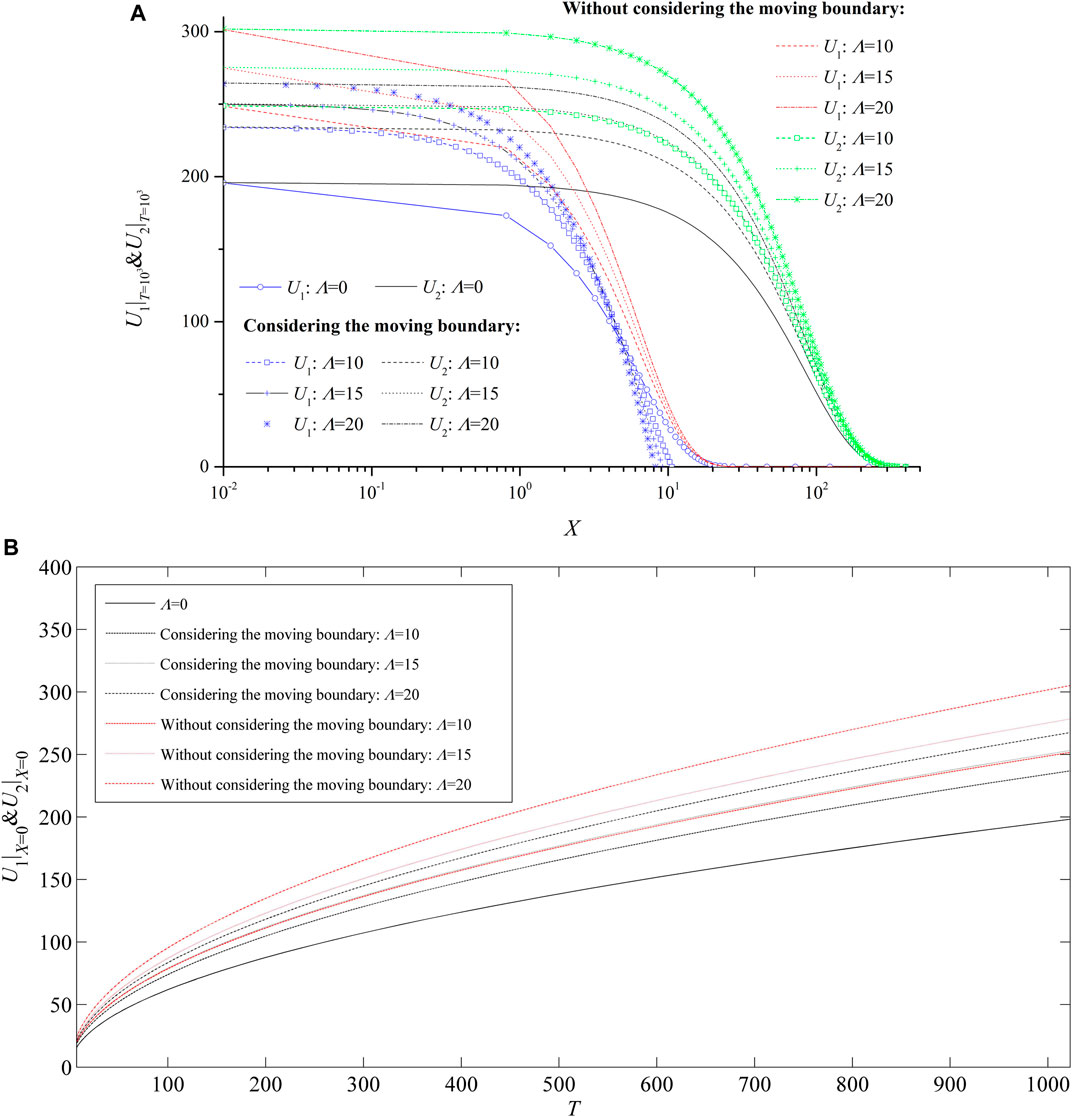
FIGURE 9. Comparison between two models with and without considering the MB. (A) Pressure distribution comparison; (B) transient pressure comparison.

FIGURE 10

FIGURE 10. Variation of the relative error ε with dimensionless TPG Λ.

Table 5 shows the effect of neglecting MB in the modeling on the dimensionless production rates from the two different layers. From Table 5, it can be concluded that as the MB caused by the TPG is neglected, the dimensionless production rate from the high-permeability layer can be overestimated. In other words, the preferential Darcian flow in the high-permeability layer can be exaggerated. A larger dimensionless TPG introduces a larger deviation. Therefore, MB conditions should be incorporated into the mathematical modeling of 1D commingled preferential Darcian flow and low-velocity non-Darcian flow problems.

TABLE 5

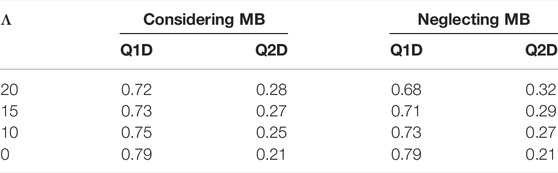
TABLE 5. Comparison of Q1D and Q2D corresponding to the two different models with and without considering the MB.

5 Conclusion

A basic nonlinear problem of the 1D commingled preferential Darcian flow and non-Darcian flow with the TPG in a dual-layered formation is studied. The flow in a low-permeability tight layer obeys the low-velocity non-Darcy kinematic equation with the TPG, while Darcy’s law holds for the flow in the high-permeability layer. Also, a nonlinear dimensionless mathematical model, incorporating MB conditions caused by the TPG, is presented. The EAS of this nonlinear model is obtained; in particular, its existence and uniqueness are both proved strictly. From the EAS results, the influences of the dimensionless TPG, dimensionless LTR, dimensionless LPR, and dimensionless LESR on pressure distribution, transient pressure, and layer production rate are discussed. It is found that the existence of the TPG in a low-permeability tight layer can intensify the preferential Darcian flow in the high-permeability layer; and the intensity of the preferential Darcian flow in the high-permeability layer is very sensitive to the LTR; however, the effect of LPR and LESR on the production sub-rate is more sensitive than that of LTR. Furthermore, it is strictly demonstrated that MB conditions caused by the TPG should be incorporated in the model. When the MB is neglected, the preferential Darcian flow into the high-permeability layer can be exaggerated. In addition, a relative error formula for calculating transient pressure, caused by neglecting MB in the model, is provided.

All in all, in the article, the major theoretical contributions are as follows: an EAS of a fundamental MB problem of the 1D commingled preferential Darcian flow and low-velocity non-Darcian flow in a dual-layered formation is presented; its existence and uniqueness are both strictly proved; then, the commingled flow behavior is analyzed. Therefore, solid theoretical foundations are provided here, which are very significant for solving non-Darcian seepage flow problems in engineering by numerical simulation validation and physical experiment design. Finally, it is worth mentioning that in the study, an impermeable barrier layer between the two layers exists, and thus, the cross flow between the layers is not involved. However, for the situation under consideration of the cross flow, the corresponding moving boundary problem will become more challenging and interesting. It will be our future research field.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

PW: conceptualization, writing, and editing; WL: methodology and literature survey; WD: literature survey and writing; XK: document arrangement and writing; HF: methodology and inspection.

Funding

This research was supported by the project (Grant Nos. FRF-TP-17–023A1) sponsored by the Fundamental Research Funds for Central Universities and CNPC Innovation Fund (Grant Nos. 2021DQ02–0901).

Conflict of Interest

HF was employed by China ZhenHuaOil Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afshari, S., Hejazi, S. H., and Kantzas, A. (2018). Longitudinal dispersion in heterogeneous layered porous media during stable and unstable pore-scale miscible displacements. Adv. Water Resour. 119, 125–141. doi:10.1016/j.advwatres.2018.06.005

CrossRef Full Text | Google Scholar

Ames, W. F. (1965). Nonlinear partial differential equations in engineering. New York: Academic.

Google Scholar

Bauer, D., Talon, L., Peysson, Y., Ly, H. B., Batôt, G., Chevalier, T., et al. (2019). Experimental and numerical determination of Darcy’s law for yield stress fluids in porous media. Phys. Rev. Fluids 4, 063301. doi:10.1103/physrevfluids.4.063301

CrossRef Full Text | Google Scholar

Bear, J. (1972). Dynamics of fluids in porous media. New York: American Elsevier.

Google Scholar

Cai, J. (2014). A fractal approach to low velocity non-Darcy flow in a low permeability porous medium. Chin. Phys. B 23, 044701. doi:10.1088/1674-1056/23/4/044701

CrossRef Full Text | Google Scholar

Chen, Y. M., Tang, X. W., and Wang, J. (2004). An analytical solution of one-dimensional consolidation for soft sensitive soil ground. Int. J. Numer. Anal. Methods Geomech. 28, 919–930. doi:10.1002/nag.353

CrossRef Full Text | Google Scholar

Chi, J., and Wang, J. (2021). A new calculation method on the critical well spacing of CO2 miscible flooding in ultra-low permeability reservoirs. J. Porous Media 24, 59–79. doi:10.1615/jpormedia.2020033488

CrossRef Full Text | Google Scholar

Debbabi, Y., Jackson, M. D., Hampson, G. J., Fitch, P. J. R., and Salinas, P. (2017). Viscous crossflow in layered porous media. Transp. Porous Media 117, 281–309. doi:10.1007/s11242-017-0834-z

CrossRef Full Text | Google Scholar

Dou, H., Ma, S., Zou, C., and Yao, S. (2014). Threshold pressure gradient of fluid flow through multi-porous media in low and extra-low permeability reservoirs. Sci. China Earth Sci. 57, 2808–2818. doi:10.1007/s11430-014-4933-1

CrossRef Full Text | Google Scholar

Ehlig-Economides, C. A., and Joseph, J. (1987). A new test for determination of individual layer properties in a multilayered reservoir. SPE Form. Eval. 2, 261–283. doi:10.2118/14167-PA

CrossRef Full Text | Google Scholar

Elkady, M. S., Abdelaziz, G. B., Sharshir, S. W., Mohamed, A. Y. A., Elsaid, A. M., El-Said, E. M. S., et al. (2022). Non-Darcian immiscible two-phase flow through porous materials (Darcy–Forchheimer–Brinkman Model). Therm. Sci. Eng. Prog. 29, 101204. doi:10.1016/j.tsep.2022.101204

CrossRef Full Text | Google Scholar

Fusi, L., and Farina, A. (2017). Peristaltic flow of a Bingham fluid in a channel. Int. J. Non. Linear. Mech. 97, 78–88. doi:10.1016/j.ijnonlinmec.2017.09.003

CrossRef Full Text | Google Scholar

Gao, D., Ye, J., Wang, T., Zhao, L., Pan, S., and Sun, Z. (2018). An independent fracturing water-flooding development method for shallow low-permeability thin oil layers in multi-layer sandstone reservoirs. J. Pet. Sci. Eng. 167, 877–889. doi:10.1016/j.petrol.2018.04.049

CrossRef Full Text | Google Scholar

Guo, J., Zhang, S., Zhang, L., Qing, H., and Liu, Q. (2012). Well testing analysis for horizontal well with consideration of threshold pressure gradient in tight gas reservoirs. J. Hydrodyn. 24, 561–568. doi:10.1016/s1001-6058(11)60278-3

CrossRef Full Text | Google Scholar

Hu, W., Wei, Y., and Bao, J. (2018). Development of the theory and technology for low permeability reservoirs in China. Petroleum Explor. Dev. 45, 685–697. doi:10.1016/s1876-3804(18)30072-7

CrossRef Full Text | Google Scholar

Jiao, X. R., Jiang, S., and Liu, H. (2021). Nonlinear moving boundary model of low-permeability reservoir. Energies 14, 8445. doi:10.3390/en14248445

CrossRef Full Text | Google Scholar

Kaffel, A. (2019). Rigorous derivation of a new macroscopic model for modeling partially-saturated flow of a liquid in multilayered thin swelling porous media. Int. J. Heat. Mass Transf. 129, 1274–1286. doi:10.1016/j.ijheatmasstransfer.2018.10.058

CrossRef Full Text | Google Scholar

Li, D., Zha, W., Liu, S., Wang, L., and Lu, D. (2016). Pressure transient analysis of low permeability reservoir with pseudo threshold pressure gradient. J. Pet. Sci. Eng. 147, 308–316. doi:10.1016/j.petrol.2016.05.036

CrossRef Full Text | Google Scholar

Li, J., Yang, H., Qiao, Y., Fan, Z., Chen, W., and Jiang, H. (2018). Laboratory evaluations of fiber-based treatment for in-depth profile control. J. Pet. Sci. Eng. 171, 271–288. doi:10.1016/j.petrol.2018.07.060

CrossRef Full Text | Google Scholar

Li, X., Lu, D., Luo, R., Sun, Y., Shen, W., Hu, Y., et al. (2019). Quantitative criteria for identifying main flow channels in complex porous media. Petroleum Explor. Dev. 46, 998–1005. doi:10.1016/s1876-3804(19)60256-9

CrossRef Full Text | Google Scholar

Liu, C., and Wang, X. (1993). Transient 2D flow in layered reservoirs with crossflow. SPE Form. Eval. 8, 287–291. doi:10.2118/25086-PA

CrossRef Full Text | Google Scholar

Liu, W. C. (2019). Analytical study on a moving boundary problem of semispherical centripetal seepage flow of Bingham fluid with threshold pressure gradient. Int. J. Non. Linear. Mech. 113, 17–30. doi:10.1016/j.ijnonlinmec.2019.03.011

CrossRef Full Text | Google Scholar

Liu, W. C., Duan, Y. Y., Zhang, Q. T., Chen, Z., Yan, X. M., Sun, H. D., et al. (2022). Analytical study on a one-dimensional model coupling both Darcy flow and low-velocity non-Darcy flow with threshold pressure gradient in heterogeneous composite reservoirs. J. Porous Med. 10, 1615.

CrossRef Full Text | Google Scholar

Liu, W. C. (2020a). Exact analytical solution of a generalized multiple moving boundary model of one-dimensional non-Darcy flow in heterogeneous multilayered low-permeability porous media with a threshold pressure gradient. Appl. Math. Model. 81, 931–953. doi:10.1016/j.apm.2020.01.028

CrossRef Full Text | Google Scholar

Liu, W. C. (2020b). Exact analytical solutions of non-Darcy seepage flow problems of one-dimensional Bingham fluid flow in finite long porous media with threshold pressure gradient. J. Pet. Sci. Eng. 184, 106475. doi:10.1016/j.petrol.2019.106475

CrossRef Full Text | Google Scholar

Liu, W. C., Yao, J., Chen, Z., and Zhu, W. Y. (2019a). An exact analytical solution of moving boundary problem of radial fluid flow in an infinite low-permeability reservoir with threshold pressure gradient. J. Pet. Sci. Eng. 175, 9–21. doi:10.1016/j.petrol.2018.12.025

CrossRef Full Text | Google Scholar

Liu, W. C., Yao, J., and Wang, Y. Y. (2012). Exact analytical solutions of moving boundary problems of one-dimensional flow in semi-infinite long porous media with threshold pressure gradient. Int. J. Heat. Mass Transf. 55, 6017–6022. doi:10.1016/j.ijheatmasstransfer.2012.06.012

CrossRef Full Text | Google Scholar

Liu, W. C., Zhang, Q. T., and Zhu, W. Y. (2019b). Numerical simulation of multi-stage fractured horizontal well in low-permeable oil reservoir with threshold pressure gradient with moving boundary. J. Pet. Sci. Eng. 178, 1112–1127. doi:10.1016/j.petrol.2019.04.033

CrossRef Full Text | Google Scholar

Ma, T. R., Zhang, K. N., Shen, W. J., Guo, C. B., and Xu, H. (2021). Discontinuous and continuous Galerkin methods for compressible single-phase and two-phase flow in fractured porous media. Adv. Water Resour. 156, 104039. doi:10.1016/j.advwatres.2021.104039

CrossRef Full Text | Google Scholar

Nijjer, J. S., Hewitt, D. R., and Neufeld, J. A. (2019). Stable and unstable miscible displacements in layered porous media. J. Fluid Mech. 869, 468–499. doi:10.1017/jfm.2019.190

PubMed Abstract | CrossRef Full Text | Google Scholar

Olguín, M. C., Medina, M. A., Sanziel, M. C., and Tarzia, D. A. (2007). Behavior of the solution of a stefan problem by changing thermal coefficients of the substance. Appl. Math. Comput. 190, 765–780. doi:10.1016/j.amc.2007.01.104

CrossRef Full Text | Google Scholar

Prada, A., and Civan, F. (1999). Modification of Darcy’s law for the threshold pressure gradient. J. Pet. Sci. Eng. 22, 237–240. doi:10.1016/s0920-4105(98)00083-7

CrossRef Full Text | Google Scholar

Shen, W., Ma, T., Li, X., Sun, B., Hu, Y., and Xu, J. (2022). Fully coupled modeling of two-phase fluid flow and geomechanics in ultra-deep natural gas reservoirs. Phys. Fluids. 34, 043101. doi:10.1063/5.0084975

CrossRef Full Text | Google Scholar

Shen, X., and Reible, D. (2015). An analytical solution for one-dimensional advective-dispersive solute equation in multilayered finite porous media. Transp. Porous Media 107, 657–666. doi:10.1007/s11242-015-0460-6

CrossRef Full Text | Google Scholar

Song, H., Cao, Y., Yu, M., Wang, Y., Killough, J. E., and Leung, J. (2015). Impact of permeability heterogeneity on production characteristics in water-bearing tight gas reservoirs with threshold pressure gradient. J. Nat. Gas. Sci. Eng. 22, 172–181. doi:10.1016/j.jngse.2014.11.028

CrossRef Full Text | Google Scholar

Swami, D., Sharma, P. K., Ojha, C. S. P., Guleria, A., and Sharma, A. (2018). Asymptotic behavior of mass transfer for solute transport through stratified porous medium. Transp. Porous Media 124, 699–721. doi:10.1007/s11242-018-1090-6

CrossRef Full Text | Google Scholar

Tian, W., Li, A., Ren, X., and Josephine, Y. (2018). The threshold pressure gradient effect in the tight sandstone gas reservoirs with high water saturation. Fuel 226, 221–229. doi:10.1016/j.fuel.2018.03.192

CrossRef Full Text | Google Scholar

Voller, V. R., Swenson, J. B., and Paola, C. (2004). An analytical solution for a stefan problem with variable latent heat. Int. J. Heat. Mass Transf. 47, 5387–5390. doi:10.1016/j.ijheatmasstransfer.2004.07.007

CrossRef Full Text | Google Scholar

Wang, F., and Cheng, H. (2020). Effect of tortuosity on the stress-dependent permeability of tight sandstones: Analytical modelling and experimentation. Mar. Pet. Geol. 120, 104524. doi:10.1016/j.marpetgeo.2020.104524

CrossRef Full Text | Google Scholar

Wang, F. Y., Liu, Z. C., Cai, J. C., and Gao, J. (2018). A fractal model for low-velocity non-Darcy flow in tight oil reservoirs considering boundary-layer effect. Fractals 26, 1850077. doi:10.1142/s0218348x18500779

CrossRef Full Text | Google Scholar

Wang, H. X., Xu, W., Zhang, Y. Y., and Sun, D. A. (2021). Simplified solution to one-dimensional consolidation with threshold gradient. Comput. Geotech. 131, 103943. doi:10.1016/j.compgeo.2020.103943

CrossRef Full Text | Google Scholar

Wang, S. F., and Yu, B. M. (2011). A fractal model for the starting pressure gradient for Bingham fluids in porous media embedded with fractal-like tree networks. Int. J. Heat. Mass Transf. 54, 4491–4494. doi:10.1016/j.ijheatmasstransfer.2011.06.031

CrossRef Full Text | Google Scholar

Wang, S. J., Huang, Y. Z., and Civan, F. (2006). Experimental and theoretical investigation of the Zaoyuan field heavy oil flow through porous media. J. Pet. Sci. Eng. 50, 83–101. doi:10.1016/j.petrol.2005.06.015

CrossRef Full Text | Google Scholar

Wang, S., Zhu, W., Qian, X., Xu, H., and Fan, X. (2016). Study of threshold gradient for compacted clays based on effective aperture. Environ. Earth Sci. 75, 693. doi:10.1007/s12665-016-5502-z

CrossRef Full Text | Google Scholar

Wu, L. Z., Liu, G. G., Wang, L. C., Zhang, L. M., Li, B. E., and Li, B. (2016). Numerical analysis of 1D coupled infiltration and deformation in layered unsaturated porous medium. Environ. Earth Sci. 75, 761. doi:10.1007/s12665-016-5579-4

CrossRef Full Text | Google Scholar

Wu, Z., Cui, C., Trivedi, J., Ai, N., and Tang, W. (2019). Pressure analysis for volume fracturing vertical well considering low-velocity non-Darcy flow and stress sensitivity. Geofluids 2019, 2046061. doi:10.1155/2019/2046061

CrossRef Full Text | Google Scholar

Xie, K. H., Wang, K., Wang, Y. L., and Li, C. X. (2010). Analytical solution for one-dimensional consolidation of clayey soils with a threshold gradient. Comput. Geotech. 37, 487–493. doi:10.1016/j.compgeo.2010.02.001

CrossRef Full Text | Google Scholar

Xiong, W., Lei, Q., Gao, S. S., Hu, Z. M., and Xue, H. (2009). Pseudo threshold pressure gradient to flow for low permeability reservoirs. Petroleum Explor. Dev. 36, 232–236. doi:10.1016/s1876-3804(09)60123-3

CrossRef Full Text | Google Scholar

Yang, L., Ge, H., Shi, X., Cheng, Y., Zhang, K., Chen, H., et al. (2016). The effect of microstructure and rock mineralogy on water imbibition characteristics in tight reservoirs. J. Nat. Gas. Sci. Eng. 34, 1461–1471. doi:10.1016/j.jngse.2016.01.002

CrossRef Full Text | Google Scholar

Yao, J., Liu, W. C., and Chen, Z. (2013). Numerical solution of a moving boundary problem of one-dimensional flow in semi-infinite long porous media with threshold pressure gradient. Math. Probl. Eng. 2013, 1–7. doi:10.1155/2013/384246

CrossRef Full Text | Google Scholar

Ye, W., Wang, X., Cao, C., and Yu, W. (2019). A fractal model for threshold pressure gradient of tight oil reservoirs. J. Pet. Sci. Eng. 179, 427–431. doi:10.1016/j.petrol.2019.04.039

CrossRef Full Text | Google Scholar

Yin, D. T., Li, C. G., Song, S., and Liu, K. (2022). Nonlinear seepage mathematical model of fractured tight stress sensitive reservoir and its application. Front. Energy Res. 10, 819430. doi:10.3389/fenrg.2022.819430

CrossRef Full Text | Google Scholar

Zeng, J., Wang, X., Guo, J., Zeng, F., and Zhang, Q. (2018). Composite linear flow model for multi-fractured horizontal wells in tight sand reservoirs with the threshold pressure gradient. J. Pet. Sci. Eng. 165, 890–912. doi:10.1016/j.petrol.2017.12.095

CrossRef Full Text | Google Scholar

Zhang, J. G., Du, D. F., Hou, J., Lei, G. L., and Lv, A. M. (2015). Seepage flow mechanics in oil and gas reservoi. Qingdao: China University of Petroleum Press.

Google Scholar

Zhang, Q., Liu, W., and Taleghani, A. D. (2022). Numerical study on non-Newtonian Bingham fluid flow in development of heavy oil reservoirs using radiofrequency heating method. Energy 239, 122385. doi:10.1016/j.energy.2021.122385

CrossRef Full Text | Google Scholar

Zhang, X., Kuang, S., Shi, Y., Wang, X., Zhu, W., Cai, Q., et al. (2019a). A new liquid transport model considering complex influencing factors for nano-to micro-sized circular tubes and porous media. Phys. Fluids 31, 112006. doi:10.1063/1.5126926

CrossRef Full Text | Google Scholar

Zhang, X., Shi, Y., Kuang, S., Zhu, W., Cai, Q., Wang, Y., et al. (2019b). A new liquid transport model considering complex influencing factors for nano- to micro-sized circular tubes and porous media. Phys. Fluids 31, 112006. doi:10.1063/1.5126926

CrossRef Full Text | Google Scholar

Zhang, X., Zhu, W., Cai, Q., Shi, Y., Wu, X., Jin, T., et al. (2018). Compressible liquid flow in nano- or micro-sized circular tubes considering wall-liquid lifshitz-van Der waals interaction. Phys. Fluids 30, 062002. doi:10.1063/1.5023291

CrossRef Full Text | Google Scholar

Zhao, G., You, Q., Tao, J., Gu, C., Aziz, H., Ma, L., et al. (2018). Preparation and application of a novel phenolic resin dispersed particle gel for in-depth profile control in low permeability reservoirs. J. Pet. Sci. Eng. 161, 703–714. doi:10.1016/j.petrol.2017.11.070

CrossRef Full Text | Google Scholar

Zhao, M. W., Cao, M. J., He, H. N., and Dai, C. L. (2020). Study on variation laws of fluid threshold pressure gradient in low permeable reservoir. Energies 13, 3704. doi:10.3390/en13143704

CrossRef Full Text | Google Scholar

Zhao, X., Liu, X., Yang, Z., Wang, F., Zhang, Y., Liu, G., et al. (2021). Experimental study on physical modeling of flow mechanism in volumetric fracturing of tight oil reservoir. Phys. Fluids 33, 107118. doi:10.1063/5.0068594

CrossRef Full Text | Google Scholar

Zhou, Y. (2019). Analytical solution for one-dimensional radial flow caused by line source in porous medium with threshold pressure gradient. Appl. Math. Model. 67, 151–158. doi:10.1016/j.apm.2018.10.024

CrossRef Full Text | Google Scholar

Zhou, Y., Zhang, L., and Wang, T. (2021). Analytical solution for one-dimensional non-Darcy flow with bilinear relation in porous medium caused by line source. Appl. Math. Comput. 392, 125674. doi:10.1016/j.amc.2020.125674

CrossRef Full Text | Google Scholar

Zhou, Z., Zhao, J., Zhou, T., and Huang, Y. (2017). Study on in-depth profile control system of low-permeability reservoir in block H of daqing oil field. J. Pet. Sci. Eng. 157, 1192–1196. doi:10.1016/j.petrol.2017.08.008

CrossRef Full Text | Google Scholar

Appendix A

As MB conditions caused by the TPG are neglected, an infinite outer boundary condition (Liu et al., 2019a; Liu, 2019; Liu W. C., 2020) has to be used instead. Then, without considering MB conditions, a dimensionless mathematical model for the 1D commingled preferential Darcian flow and non-Darcian flow in a dual-layered formation is built:

$2{\alpha }_1\cdot \frac{{\partial }^2{U}_1}{\partial X^2}=\frac{\partial U_1}{\partial T},0\le X<+\infty ,(\mathrm{A1})$

${U_1|}_{T=0}=0,(\mathrm{A2})$

${U_1|}_{X\to +\infty }=0,(\mathrm{A3})$

$2{\alpha }_2\cdot \frac{{\partial }^2{U}_2}{\partial X^2}=\frac{\partial U_2}{\partial T},0\le X<+\infty ,(\mathrm{A4})$

${U_2|}_{T=0}=0,(\mathrm{A5})$

${U_2|}_{X\to +\infty }=0,(\mathrm{A6})$

${{\beta }_1\cdot \frac{\partial U_1}{\partial X}|}_{X=0}+{\beta }_2{\cdot \frac{\partial U_2}{\partial X}|}_{X=0}=-\left(1+{\beta }_1\cdot \mathrm{\Lambda }\right),(\mathrm{A7})$

${U_2|}_{X=0}={U_1|}_{X=0}.(\mathrm{A8})$

Similarity transformations including Eqs. 30–32 can still be used here for the EAS of the self-similarity model formulated by Eqs. A1–A8. By using the similar solution procedures in the previous work (Liu W. C., 2020), the EAS of the model can be expressed as follows:

$U_1\left(X,T\right)=\left\{\begin{array}{l}-\sqrt{\frac{{\alpha }_2}{{\alpha }_1}}\cdot \frac{1}{{\beta }_1\cdot \sqrt{\frac{{\alpha }_2}{{\alpha }_1}}+{\beta }_2}\cdot X+\\ \frac{1}{{\beta }_1\cdot \sqrt{\frac{{\alpha }_2}{{\alpha }_1}}+{\beta }_2}\cdot \sqrt{\frac{2\cdot {\alpha }_2}{\text{π}}}\cdot \exp \left(-\frac{X^2}{8{\alpha }_{1}T}\right)\cdot 2T^{\frac{1}{2}}\\ +\frac{1}{{\beta }_1\cdot \sqrt{\frac{{\alpha }_2}{{\alpha }_1}}+{\beta }_2}\cdot \sqrt{{\alpha }_2}\cdot \text{erf}\left(\sqrt{\frac{X^2}{8{\alpha }_{1}T}}\right)\cdot \sqrt{\frac{X^2}{{\alpha }_1}}\end{array}\right\}\cdot \left(1+{\beta }_1\cdot \mathrm{\Lambda }\right),0\le X<+\infty ,(\mathrm{A9})$

$U_2\left(X,T\right)=\left\{\begin{array}{l}-\frac{X}{{\beta }_1\cdot \sqrt{\frac{{\alpha }_2}{{\alpha }_1}}+{\beta }_2}+\\ \frac{1}{{\beta }_1\cdot \sqrt{\frac{{\alpha }_2}{{\alpha }_1}}+{\beta }_2}\cdot \sqrt{\frac{2\cdot {\alpha }_2}{\text{π}}}\cdot \exp \left(-\frac{X^2}{8{\alpha }_{2}T}\right)\cdot 2T^{\frac{1}{2}}\\ +\frac{1}{{\beta }_1\cdot \sqrt{\frac{{\alpha }_2}{{\alpha }_1}}+{\beta }_2}\cdot \sqrt{{\alpha }_2}\cdot \text{erf}\left(\sqrt{\frac{X^2}{8{\alpha }_{2}T}}\right)\cdot \sqrt{\frac{X^2}{{\alpha }_2}}\end{array}\right\}\cdot \left(1+{\beta }_1\cdot \mathrm{\Lambda }\right),0\le X<+\infty .(\mathrm{A10})$

Appendix B

From Eq. 41, we have a dimensionless transient pressure (noted as $\stackrel{\sim }{U}$):

$\stackrel{\sim }{U}=U_1\left(0,T\right)=\mathrm{\Lambda }\cdot \theta \cdot \exp \left(\frac{{\theta }^2}{2{\alpha }_1}\right)\cdot 2T^{\frac{1}{2}}.(\mathrm{B1})$

$\stackrel{\sim }{U}$ corresponds to the model in consideration of the MB caused by the TPG.

By using Eq. 43, Eq. B1 can be equivalent to the following equation:

$\stackrel{\sim }{U}=\frac{\sqrt{2}\cdot 2T^{\frac{1}{2}}}{\sqrt{\text{π}}\cdot {\beta }_1\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}+\sqrt{\text{π}}\cdot {\beta }_2\cdot \sqrt{\frac{1}{{\alpha }_2}}}.(\mathrm{B2})$

From Eq. A9, we have another dimensionless transient pressure (noted as $\stackrel{-}{U}$):

$\stackrel{-}{U}=U_1\left(0,T\right)=\frac{1}{{\beta }_1\cdot \sqrt{\frac{1}{{\alpha }_1}}+{\beta }_2\cdot \sqrt{\frac{1}{{\alpha }_2}}}\cdot \sqrt{\frac{2}{\text{π}}}\cdot 2T^{\frac{1}{2}}\cdot \left(1+{\beta }_1\cdot \mathrm{\Lambda }\right).(\mathrm{B3})$

$\stackrel{-}{U}$ corresponds to the model without consideration of the MB caused by the TPG.

Then, when MB is not considered in the modeling, a relative error ε can be directly formulated by Eqs. B1 and B3:

$\epsilon =\left|\frac{\stackrel{-}{U}}{\stackrel{\sim }{U}}-1\right|=\left|\frac{{\beta }_1\cdot \text{erf}\left(\frac{\sqrt{2}}{2}\cdot \sqrt{\frac{{\theta }^2}{{\alpha }_1}}\right)\cdot \sqrt{\frac{1}{{\alpha }_1}}+{\beta }_2\cdot \sqrt{\frac{1}{{\alpha }_2}}}{{\beta }_1\cdot \sqrt{\frac{1}{{\alpha }_1}}+{\beta }_2\cdot \sqrt{\frac{1}{{\alpha }_2}}}\cdot \left(1+{\beta }_1\cdot \mathrm{\Lambda }\right)-1\right|\times 100\%.(\mathrm{B4})$

Nomenclature

C_t1 comprehensive compressibility coefficient of the low-permeability layer, (0.1 MPa)⁻¹

C_t2 comprehensive compressibility coefficient of the high-permeability layer, (0.1 MPa)⁻¹

D₁ LPR of the low-permeability tight layer, dimensionless

D₂ LPR of the high-permeability layer, dimensionless

F Function defined by Eq. 44, dimensionless

h₁ thickness of the low-permeability tight layer, cm

h₂ thickness of the high-permeability layer, cm

H₁ LTR of the low-permeability tight layer, dimensionless

H₂ LTR of the high-permeability layer, dimensionless

k₁ permeability of the low-permeability tight layer, μm²

k₂ permeability of the high-permeability layer, μm²

k_avg thickness-weighted formation permeability, μm²

L wideness of the low-permeability tight layer and high-permeability layer, cm

p₁ pressure in the low-permeability tight layer, 0.1 MPa

p₂ pressure in the high-permeability layer, 0.1 MPa

p_i initial pressure, 0.1 MPa

Q₀ total production rate, cm³·s⁻¹

Q_1D dimensionless production rate from the low-permeability tight layer, dimensionless

Q_2D dimensionless production rate from the high-permeability layer, dimensionless

S transient moving boundary distance, cm

t time, s

T dimensionless time, dimensionless

U₁ dimensionless pressure in the low-permeability tight layer, dimensionless

U₂ dimensionless pressure in the high-permeability layer, dimensionless

$\stackrel{\sim }{U}$ dimensionless transient pressure when the moving boundary is considered in the dimensionless model, dimensionless

$\stackrel{-}{U}$ dimensionless transient pressure when the moving boundary is not considered in the dimensionless model, dimensionless

x distance, cm

X dimensionless distance, dimensionless

x, y and z coordinate axes in rectangular coordinate systems, as shown in Figure 1

α₁ and α₂ defined parameters, dimensionless

β₁ and β₂ defined parameters, dimensionless

δ dimensionless moving boundary distance, dimensionless

ε relative error, dimensionless

η, θ, ξ and ψ relevant similarity transformation variables, dimensionless

θ₀ unique positive solution of Eq. 43, dimensionless

θ₁ positive value of θ which makes f(θ₁) > 0, dimensionless

λ threshold pressure gradient, 0.1 MPa cm⁻¹

Λ dimensionless threshold pressure gradient, dimensionless

μ fluid viscosity, mPa∙s

υ₁ fluid velocity in the low-permeability tight layer, cm·s⁻¹

υ₂ fluid velocity in the high-permeability layer, cm·s⁻¹

υ_w0 constant average flow velocity, cm·s⁻¹

φ_i1 initial porosity of the low-permeability tight layer, f

φ_i2 initial porosity of the high-permeability layer, f

ω₁ LESR of the low-permeability tight layer, dimensionless

ω₂ LESR of the high-permeability layer, dimensionless