
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 13 July 2022
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.935888
This article is part of the Research Topic Internal Flow Mechanism of Modern Hydraulic Machinery View all 20 articles
A vertical axial flow pump device has the characteristics of low head and large flow and has various forms, simple structure, and flexible installation. It is widely used in low-head pumping stations in plain areas. In order to explore the transient characteristics of the internal flow in the impeller and guide vane of the vertical axial flow pump at different flow rates, this article analyzes the internal flow field distribution on the surface of the impeller blade, the velocity and pressure distribution of the impeller inlet and outlet, and the pressure pulsation characteristics of the impeller. The flow field characteristics of the guide vane section, the entropy production loss, and the main frequency change of the pressure pulsation inside the guide vane are analyzed at different radii. The results show that under 0.8 Qbep condition, the streamline distortion area of the blade working face accounts for the largest part of the blade area, and the streamline distortion area of the blade surface decreases significantly at 1.2 Qbep. The circumferential pressure distribution at the impeller inlet presents four high-pressure regions and four low-pressure regions, and the number of regions is consistent with the number of impeller blades. The ratio of axial force to flow rate of 0.8Qbep, 1.0Qbep, and 1.2Qbep is approximately 11:10:9. The radial force on the impeller is the largest under the condition of 0.8 Qbep, and the radial force on the impeller is not significantly different between 1.0 Qbep and 1.2 Qbep. The pressure pulsation amplitude gradually decreases from the inlet to the outlet of the guide vane.
An axial flow pump has the characteristics of low head and large flow, which is widely used in inter-basin water transfer projects, plain municipal engineering, shipbuilding industry, military industry, and other important fields in China. With the development of social economy and the change in global climate and situation, China’s demand for efficient axial flow pumps is very urgent in the fields of military industry, nuclear energy development, municipal engineering, large-scale water diversion projects, and marine resources development (Shen et al., 2020).
A vertical axial flow pump device has the characteristics of various forms, simple structure, and flexible installation. In the first phase of the East Route Project of the South-to-North Water Diversion in China, 57% of the pumping stations are vertical axial flow pump stations (Yang et al., 2022a). During the operation of the vertical axial flow pump device, the internal flow is a complex three-dimensional unsteady turbulent flow, and the flow obtains energy through the impeller domain. In the process of flow out of the outlet channel through the guide vane rectifier, it is easy to produce unstable flow leading to flow separation due to the limitation and influence of boundary conditions such as tip clearance, blade root clearance, and hub rotation (Zhang et al., 2012). The complex flow phenomena such as vortex, impact, secondary flow, and tip clearance leakage lead to a significant reduction in the operation efficiency of the axial flow pump device and affect the efficient and stable operation of the pumping station. So far, many scholars have carried out a lot of research on axial flow pump devices. Zhang et al. (2022) used a physical model test to study the hydrodynamic characteristics and pressure fluctuation of bidirectional axial flow pump under forward and reverse conditions and revealed the energy characteristics and pressure fluctuation propagation law of a bidirectional axial flow pump under forward and reverse conditions. Kan et al. (2021a) used the SST k-ω turbulence model to simulate the stall condition of bidirectional axial flow pump and compared and analyzed the difference of torque and pressure pulsation of bidirectional axial flow pump under forward stall condition and reverse stall condition. Zhao et al. (2021) studied the dominant vortex structure in a diagonally separated flow in an axial flow pump impeller and obtained the average vortex intensity change, turbulent vortex dissipation change, and the evolution process of vortex in a life cycle under various working conditions. Meng et al. (2021) used entropy production theory as the evaluation criterion of energy dissipation, based on numerical simulation technology, to study the influence of backflow clearance on the energy characteristics of axial flow pump. It was found that the loss of impeller decreased first and then increased with the increase of clearance radius, and the other flow components decreased with the increase of clearance radius. Mu et al. (2020) proposed a flow control technology to improve the hydraulic performance of the axial flow pump when a rotating stall occurs in the saddle area. Shi et al. (2021) compared the structural mechanical properties of the full tubular pump and the axial flow pump. The results show that the maximum equivalent stress of the full tubular pump occurs at the outer edge of the blade, and the maximum equivalent stress of the axial flow pump occurs at the hub center of the blade. Yang et al. (2021a) revealed the phenomenon of flow deviation in the outlet channel of an axial flow pump and the influence of flow deviation on the pressure fluctuation distribution in the outlet channel by experimental research combined with CFD technology. Song and Liu (2021) studied the change process of FAV at the inlet of an axial flow pump and analyzed the energy change and velocity change of FAV combined with V3V. Yang W et al. (2022) used different flange load distribution types of axial flow pump impeller model based on CFD technology to study the influence of these three types of flange load distribution on the tip clearance leakage flow and leakage eddy current of axial flow pump. Zhou et al. (2022) designed a double-layer conduit structure to study the influence of different geometric parameters of the double-layer conduit structure on the external characteristics and internal flow field of the axial flow pump. Xie et al. (2022) studied the double hump characteristics of an axial flow pump under small flow conditions and explored the relationship between the head-flow curve of the axial flow pump and the characteristics of the internal flow field through an internal flow field test. Lin et al. (2021) simulated the influence of sediment concentration, particle size, and cavitation on the internal flow pressure fluctuation of axial flow pump under the combined action of clear water, sediment water, clear water cavitation, and cavitation and sediment wear based on CFD technology. Xu et al. (2021) studied the difference between the forward and reverse runaway transition process of axial flow pump, and calculated and analyzed the loss position and cause of loss in forward and reverse runaway transition process of axial flow pump based on entropy production theory.
The vertical axial flow pump device includes the pump and inlet and outlet conduits with good hydraulic performance. The impeller and guide vane are the core of the axial flow pump device, and their efficient and stable operation determines the operation state of the whole pump device. In actual operation, the internal flow field of the pump device is instantaneous change, and due to the influence of boundary conditions such as blade tip clearance, blade root clearance, and hub rotation, unstable flow is easily generated in the impeller domain. The internal flow of the guide vane becomes very complicated by the influence of the flow velocity loop at the outlet of the impeller, which is easy to induce the vibration of the axial flow pump device and affect the safe and stable operation of the pump station. In order to study the transient internal flow characteristics of the impeller and guide vane in vertical axial flow pump device, based on the theoretical basis and methods of previous research on axial flow pump devices, CFD technology is used to simulate the transient flow characteristics of vertical axial flow pump device under different flow conditions, and the distribution law and development mechanism of the transient flow of impeller and guide vane are clarified.
The vertical axial flow pump device consists of five flow passage components: campaniform inlet conduit, impeller, guide vane, 90°elbow, and straight outlet conduit. The three-dimensional model of the vertical axial flow pump device is shown in Figure 1. The geometric dimensions of the vertical axial flow pump device can be seen in the study by Yang et al. (2021b). The main parameters of the vertical axial flow pump device are shown in Table 1.
The internal flow medium of the vertical axial flow pump device studied in this research work is an incompressible viscous fluid, and the water flow obtains energy through the rotation of the pump impeller. There are some situations in which the swirling flow and some streamlines have a large bending degree. The RNG k-ε turbulence model considers this kind of rotation and swirling flow and can deal well with the flow with a high strain rate and large streamline bending degree. Based on the works of Mompean (1998), Fu et al. (2020), Wang et al. (2020), and Zhang et al. (2021), this study used the Reynolds time-averaged N-S (Navier-Stokes) equation and the RNG k-ε turbulence model to simulate and predict the flow field and hydraulic performance of the vertical axial flow pump device.
Commercial software ANSYS CFX was used to simulate the steady and unsteady numerical simulation of the vertical axial flow pump device under three working conditions of 0.8Qbep, 1.0Qbep, and 1.2Qbep. In order to avoid the influence of initial velocity distribution on the flow pattern of inlet and outlet channels, the inlet extension section and outlet extension section were added before the campaniform inlet conduit and after the straight outlet conduit. The boundary conditions in the calculation domain are set as shown in Table 2. The time parameter setting of unsteady numerical simulation of the vertical axial flow pump device can be used for the transient calculation of the axial flow pump device (Yang et al., 2021b).
ICEM CFD software was used to carry out the hexahedral structured grid for the pump device, and the grid quality was greater than 0.4. The grid number independence of the vertical axial flow pump device was analyzed when the rotational speed was 1433 r/min and the flow rate was 338 L/s. The seven groups of grids were numbered 1–7, and the corresponding number of grids were 2.84 million, 3.33 million, 3.6 million, 3.87 million, 4.1 million, 4.26 million, and 4.8 million, respectively. The efficiency comparison of different grid schemes is shown in Figure 2. The device efficiency of grid schemes 6 and 7 tended to be stable, and the absolute error of efficiency was controlled within 0.2%, which met the accuracy requirement of numerical simulation (Chalghoum et al., 2018).
Based on the works by Roache (1997), Celik et al. (2008), and Nandan Kumar and Govardhan (2014), we obtained grid error using the grid convergence index (GCI) criterion as the evaluation criteria, compared seven groups of different number of grids to solve the simulation value and extrapolation value, and selected a suitable number of grids, so that the solution of numerical simulation could achieve pseudo-steady-state conditions.
Based on the GCI calculation formula used by Celik et al. (2008), after calculation, GCI21 = 5.91%, GCI32 = 4.56%, GCI43 = 4.01%, GCI54 = 3.22%, GCI65 = 1.99%, and GCI76 = 1.14% and GCI65 and GCI76 were less than 3%, indicating that the discrete error was small (Liu et al., 2014; Kan et al., 2021b). Combined with the analysis of grid number independence, 4.26 million grids were finally used as the final number of grids. The structured grid of the vertical axial flow pump device is shown in Figure 3.
In order to ensure the influence of the grid on the calculation accuracy, the dimensionless parameter y + was introduced as the dimensionless number of the distance from the nearest grid node to the wall. At 1.0Qbep condition, the y+ value of the impeller was about 36, and the y+ value of the guide vane was about 78, which met the requirements of Wang (2020), Yang (2020), and Kan et al. (2021c).
The physical model test of the vertical axial flow pump device was carried out on the high-precision hydraulic mechanical test bench of the Hydrodynamic Engineering Laboratory of Jiangsu Province, China. The uncertainty of the test bench system was ±0.261%. The physical model test bench is shown in Figure 4. The parameters of the impeller and guide vane used in the physical model test can be referred to in Table 1. The pump device data from the physical model test are compared with the energy performance data from the numerical simulation, as shown in Figure 5. The maximum relative error between the predicted head by numerical simulation and the experimental value was 5.5%, and the minimum relative error was 0.2%. The maximum difference between the efficiency of the pump device by numerical simulation and the experimental value was 1.83%, and the minimum difference was 0.379%. The small error indicated that the numerical simulation of the vertical axial flow pump device had high accuracy.
The pressure and streamline distribution of the impeller blade surface are shown in Figure 6. Under the condition of 0.8 Qbep, streamline distortion occurred at the blade suction surface hub and pressure surface hub, and there was a small range of vortex at the blade suction surface inlet edge. The streamline distortion area of the suction surface accounted for 11.5% of the blade area, and the streamline distortion area of the pressure surface accounted for 14.4% of the blade area, which indicated that secondary flow occurred near the hub under small flow conditions. Under 1.0 Qbep and 1.2 Qbep conditions, the streamline allocation on the impeller blade pressure surface was uniform, and there was no reverse flow phenomenon. The local streamline distortion existed in the suction surface, and the streamline distortion area was reduced by 40 % and 73% compared with the 0.8 Qbep condition. The vortex at the rim disappeared at 1.2 Qbep condition, which indicated that the streamline allocation on the blade surface was straight, and the flow pattern was better in large flow. Under 0.8 Qbep and 1.0 Qbep, the blade inlet flow angle was negative, the local high-pressure area was formed at the pressure surface inlet edge, and the local low-pressure area was formed at the suction surface edge. Under 1.2 Qbep, the blade inlet flow angle was positive, forming a local low-pressure area at the pressure surface inlet of the blade and a small range of high-pressure area at the suction surface inlet. Under different flow conditions, the impeller head of the axial flow pump was also different, and the hydraulic work of the blade pressure surface and the suction surface of the impeller was also different, so the surface flow field of the blade pressure surface and suction surface were also different. When the flow changed from 0.8Qbep to 1.0Qbep, the flow increased by 25%, and when the flow changed from 1.0Qbep to 1.2Qbep, the flow increased by 20%. When the flow rate changed by more than 20%, there were obvious differences in the flow rate. The velocity distribution at the outlet edge of impeller blades with different flow rates (Figure 7) was different near the hub, especially 0.8Qbep, and the flow pattern had a significant impact on the velocity distribution.
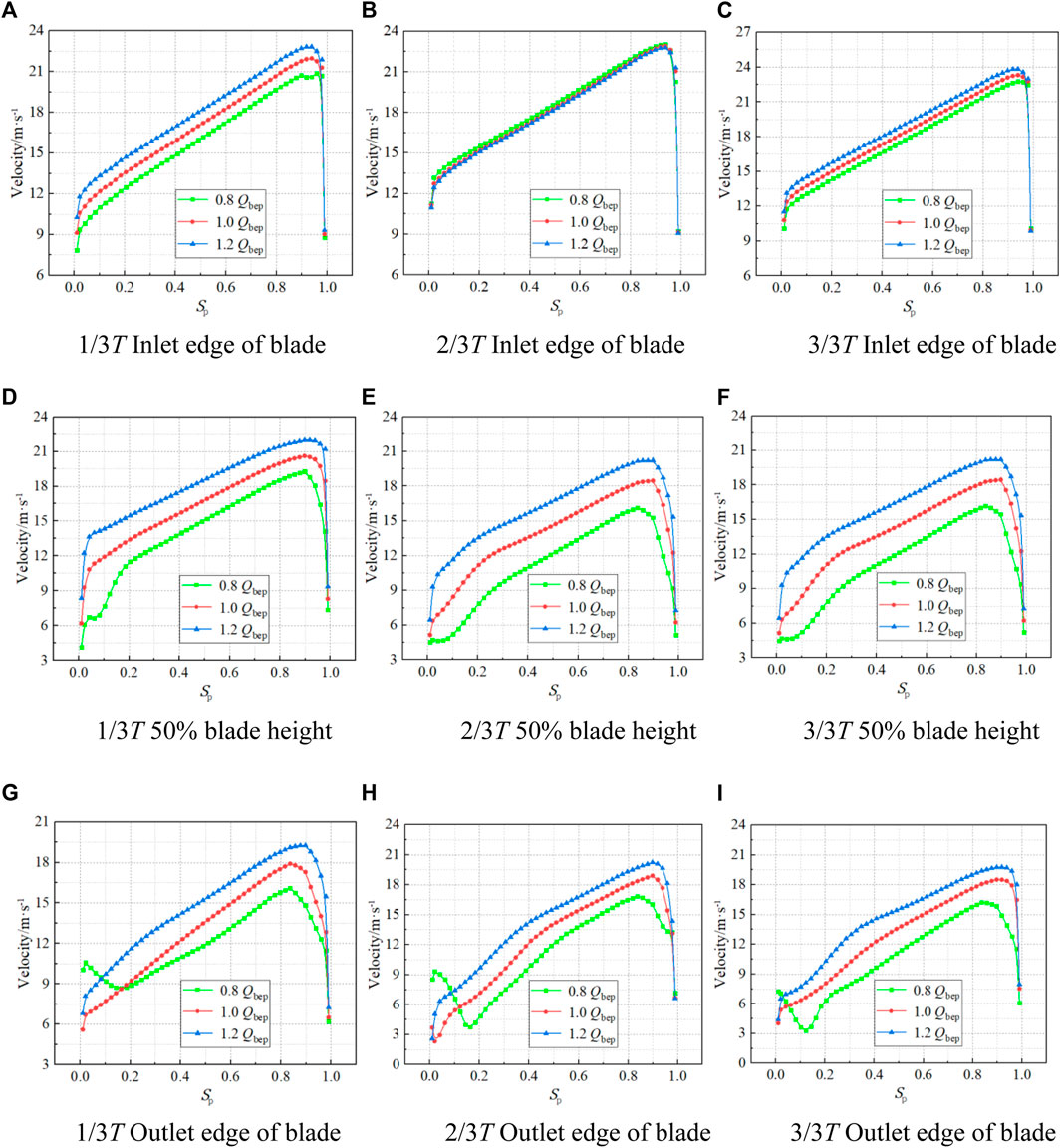
FIGURE 7. Velocity distribution of the impeller blade inlet and outlet edge and 50% blade height under different flow conditions at different times.
In this article, the blade radial coefficient Sp is defined to represent the dimensionless distance from the blade root to the blade tip of the pump device impeller. The expression of blade radial coefficient is as follows:
Figure 7 shows the velocity distribution at the inlet and outlet edges of impeller blades and at 50% of blade height. The flow velocity distribution at the impeller inlet increases gradually from the blade root to the blade tip. The flow is affected by the impeller hub wall and liquid viscous resistance, resulting in the decrease of flow velocity near the impeller hub. The sudden drop in the flow velocity near the tip of the blade is mainly due to the leakage of the tip clearance. In a rotating cycle, the velocity of the blade inlet side will change, and the maximum average velocity at the inlet edge of the blade is 17.68 m/s under 1.2Qbep at 1/3T. At the time of 2/3T, the inlet velocity of the blade at three working conditions decreases with the increase of flow rate, and the inlet velocity at each flow condition has little difference. At the time of 3/3T, the inlet velocity of the blade increases with the increase in flow rate, and the average inlet velocity of the blade is 17.47 m/s, 18.09 m/s, and 18.76 m/s, respectively. The velocity at 50% of blade height and at the outlet edge of the blade fluctuates to some extent near the blade root (Sp is 0–0.2), and the velocity at the outlet edge of the blade first decreases and then increases under 0.8Qbep. This is because the secondary flow and other adverse flow patterns near the hub are affected by the impeller blade root clearance, and the distortion of the airfoil blade at the hub position is large, resulting in local reverse flow and flow velocity fluctuation. The speed at the blade height of 50% and the outlet edge of the blade increases from the hub to the rim and reaches the maximum near Sp = 0.9, and the speed at the rim decreases sharply. The velocity at the blade height 50% and the outlet edge of the blade increases with the increase of flow rate. As the impeller rotates, the velocity changes at 50% of the blade height in a rotating cycle are not significant, and the velocity changes at the impeller outlet are mainly concentrated near the hub (Sp is 0–0.2). This is because the changes in adverse flow patterns, such as secondary flow near the hub in the rotating cycle, lead to the most obvious change, and the change regularity is not strong under the flow condition.
For the convenience of analysis, the pressure is dimensionless in this study. According to Zhang et al. (2019), the pressure is transformed into the pressure coefficient Cp. The formula is as follows:
Figure 8 shows the Cp distribution on the impeller inlet and outlet diameter of 0.725D at different times. The distribution of the Cp is relatively regular at the impeller inlet. The Cp distribution range of the impeller inlet is the largest at 0.8 Qbep, and the Cp allocation range of the impeller inlet is the smallest at 1.2 Qbep, showing four high-pressure regions and four low-pressure regions, the number of which corresponds to the number of blades. The water flows through the impeller, forming a low-pressure area at the head of the suction side of the impeller, and a high-pressure region at the head of the pressure side. As the position of the impeller blades changes, the angles corresponding to these high-pressure and low-pressure regions will change. Compared with the impeller inlet, the Cp allocation at the impeller outlet is less regular, indicating that the flow state of the impeller outlet is poor. The flow obtains energy through the rotation of the impeller, and the flow has a large circumferential speed at the impeller outlet. The moving flow is restrained by the solid wall of the guide vane itself, and the low-speed water flow on the pressure surface of the impeller blade and the high-speed water flow on the suction surface converge. This leads to the turbulence of the flow state of the impeller outlet, resulting in a significant change in the distribution of the Cp. At 0.8Qbep, the maximum Cp at the impeller outlet is 0.0546, and the angle distribution is around 250°at 2/3T. At 1.0Qbep and 1.2Qbep, the distribution of Cp fluctuates slightly, and the distribution trend at each time is similar.
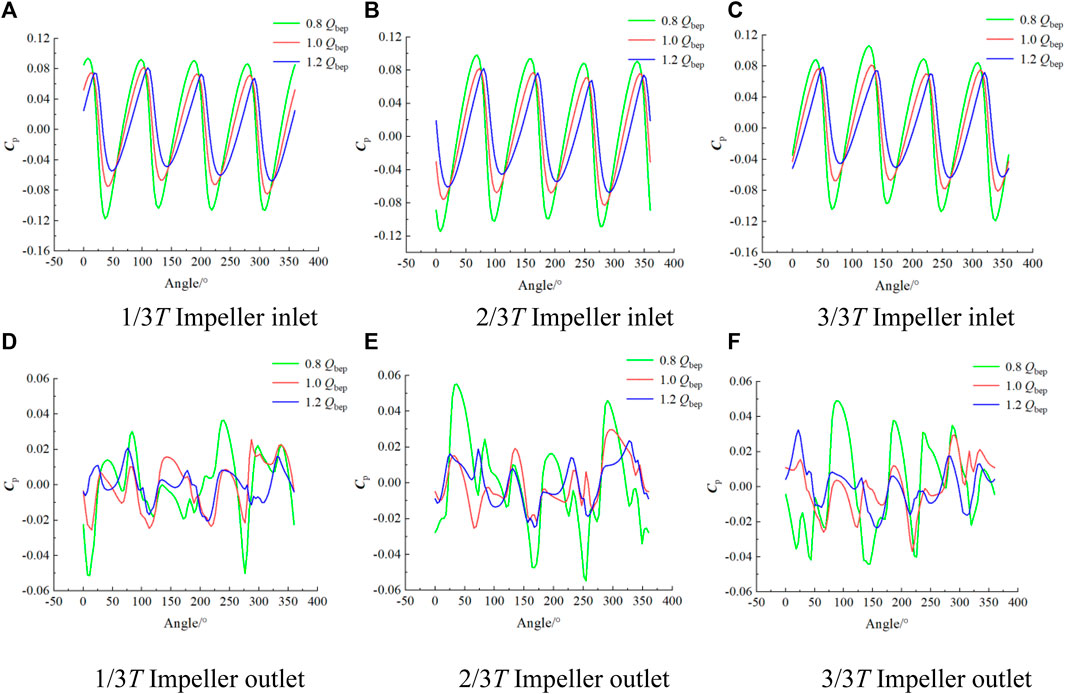
FIGURE 8. Distribution of circumferential pressure coefficient of the impeller inlet and outlet at different time.
In order to clarify the force variation of the impeller in the calculation condition, the axial force (FZ) and radial force (FR) of the impeller are calculated (Yang et al., 2022b). The calculation formulas of axial force and radial force are as follows:
The transient changes of axial force at various moments are shown in Figure 9. The axial force on the impeller of the pump device changes slightly at each time under three flow conditions of 0.8 Qbep, 1.0 Qbep, and 1.2 Qbep. The axial force on the impeller is greatly affected by the change of the flow rate. The larger the flow rate, the axial force get smaller. The ratio of the average FZ on the impeller in the calculation conditions of 0.8 Qbep, 1.0Qbep, and 1.2Qbep is about 11:10:9.
Figure 10 shows the radial force in the calculation condition. The FR is not significantly affected by the change in flow rate, and the FR is greatly affected by the change in the internal flow field of the pump device. Under 0.8 Qbep flow conditions, the large FR is the largest. The average FR is 249 N, and the fluctuation range of the FR is 60.2 %—127.7% of the average FR. The average FR under the calculation conditions of 1.0Qbep, and 1.2Qbep is similar. The average FR at 1.0Qbep is 89 N, respectively, and the average FR at 1.2Qbep is about 95.5% of that at 1.0Qbep. The fluctuation range of FR at each time under 1.0Qbep flow condition is 51.7 %–141.6% of the average FR, and the FR fluctuation range at each time under 1.2Qbep flow condition is 55.3 %—138.8% of the average FR. The FR on the impeller changes with no obvious regularity at each moment.
The impeller is the core component of the axial flow pump device, and its efficient and stable operation determines the operation stability of the whole pump device. The impeller produces obvious pressure pulsation when rotating. Three pressure pulsation monitoring points are set in the impeller domain to monitor the pressure pulsation in the impeller domain. Three monitoring points are P1, P2, and P3, respectively. Along the axial direction of the pump, P1 is set at the impeller domain inlet, P2 is set at the tip clearance at 50% of the blade height, and P3 is set at the impeller domain outlet. The location of monitoring points is shown in Figure 11.
Figure 12 shows the time-domain diagram of pressure pulsation at each monitoring point of the impeller. The Cp allocation at P1 is relatively regular and has obvious periodicity. In four cycles, there are 16 peaks and 16 valleys in total. The number of peaks and valleys in each cycle is equal, and the time of occurrence is roughly the same. The number of peaks and valleys in the interior corresponds to the number of blades, which is due to the periodic pressure fluctuations caused by the interaction between the two working surfaces of the impeller rotating. The Cp allocation in the tip clearance is not regular, and the Cp allocation in the tip clearance is unstable mainly due to the leakage of the tip clearance. The tip clearance leakage is mainly caused by the pressure difference between the pressure surface and the suction surface of the axial flow pump blade, and the tip clearance leakage becomes more serious in small flow. Therefore, the fluctuation of the pressure fluctuation coefficient of the tip clearance at 1.2Qbep is smaller than that at 0.8Qbep. The Cp allocation at P3 presents four peaks and four troughs, but the fluctuation law is unstable. The change of Cp is sometimes large and sometimes small, which is caused by static and dynamic interference. However, when the flow rate is 1.2 Qbep, the pressure pulsation at the impeller outlet has good regularity, and the fluctuation tends to be stable.
In this study, the time-domain signal of pressure pulsation was converted into the frequency-domain signal based on FFT (Fast Fourier Transform). As shown in Figure 13, the main frequency of P1 was 1 times the blade passing frequency (BPF), and the secondary main frequency was 2 times the BPF. The Cp amplitude of 1.0Qbep and 1.2Qbep was lower than that of 0.8Qbep, and the maximum Cp amplitude was 0.07113 at 0.8Qbep. The amplitude of Cp at 1.0Qbep was about 23.5% lower than that at 0.8Qbep, and the amplitude of Cp at 1.2Qbep was about 38.4% lower than that at 0.8Qbep. The pressure pulsation in the tip clearance was affected by the tip clearance leakage, and the main frequency distribution of pressure pulsation was irregular. The main frequency amplitude of Cp in 0.8Qbep blade tip clearance was 0.00869, and the main frequency amplitude of Cp in 1.2Qbep blade tip clearance was reduced by 63.1%, mainly because the pressure difference between the pressure surface and the suction surface of the impeller blade was reduced under the condition of large flow rate, which led to the decrease of tip clearance leakage. The pressure pulsation of P3 was still affected by the number of impeller blades, and the main frequency was the BPF. The Cp amplitude of the P3 was significantly lower than that of the P1, which was mainly due to the suction effect of the blade at the impeller inlet. There was a local impact between the flow and the blade, and a large pressure gradient was formed at the impeller inlet. There was dynamic and static interference at the impeller outlet, the flow at the impeller outlet was more complex, and the spectrum distribution area was more extensive than the P1.
In order to better analyze the internal flow field in the guide vane of the vertical axial flow pump device, three typical sections with different radii were selected from the hub to the rim to analyze the internal flow features of the pump. The radii of each section were 0.205D, 0.375D, and 0.495D, and they were numbered as 1–3, respectively. The selected sections are shown in Figure 14.
Figure 15 shows the flow field of the guide vane section. The entropy production loss calculation formula in the references (Li et al., 2017; Li et al., 2019; Li et al., 2020; Yang et al., 2022c) was used to calculate the entropy production loss of section 2 inside the guide vane, as shown in Figure 16. It can be seen from Figure 15 that there was a large range of reverse flow area on the guide vane back at 0.8Qbep condition. The reverse flow area of section 1 was the largest and was mainly located in the guide vane middle and lower section. The reverse flow area of section 2 was located in the guide vane middle and upper section, and the area of the reverse flow region decreased. The reverse flow area of section 3 was further reduced, mainly distributed near the guide vane trailing edge. Under 1.0Qbep condition, the reverse flow area in the guide vane was significantly reduced compared with 0.8Qbep condition. There was an obvious reverse flow area on the guide vane back of section 1, and the flow pattern in the guide vane of section 2 was better. Only a small range of reverse flow area existed on the back of the guide vane. Under 1.2 Qbep condition, the flow pattern in the guide vane was the best without obvious vortex and reverse flow. Under small flow condition, there was a wide range of recirculation zone and vortex motion in the guide vane, which led to the poor recovery effect of the guide vane on the flow velocity circulation and increased the hydraulic loss of the guide vane. When the flow increased, the flow pattern in the guide vane became better under the 1.0Qbep condition, and the decrease of the entropy production loss area was mainly concentrated in the guide vane back and the guide vane outlet. When the flow increased, the entropy production loss was further reduced in the guide vane, and the entropy production loss area was mainly concentrated on the trailing edge of the guide vane.
The design purpose of the guide vane is to recover the velocity circulation of the flow, correct the flow pattern of the flow, reduce the hydraulic loss of the flow in the radial direction, and enable the flow to enter the outlet conduit smoothly. This article studied the influence of the flow pattern inside the guide vane on the internal pressure pulsation. Therefore, nine monitoring points were set along the flow direction in the guide vane to explore the variation of pressure pulsation in the guide vane. Monitoring points P4, P5, and P6 were set at the guide vane inlet, P7, P8, and P9 were set at the guide vane middle, and P10, P11, and P12 were set at the guide vane outlet. The position of monitoring points is shown in Figure 17.
Figure 18 shows the frequency domain diagram of pressure pulsation in the guide vane. The pressure pulsation at the guide vane inlet was mainly affected by impeller rotation, and the main frequency was BPF. The flow at the guide vane inlet was affected by dynamic and static interference. It had a large velocity circulation, and with a large circumferential velocity was limited by the wall of the guide vane, which made the flow field at the guide vane inlet complicated, resulting in the Cp at the guide vane inlet being more complex and intense than that at the impeller inlet. Therefore, the peak number of the Cp amplitude at the guide vane inlet was more than that at the impeller inlet. When the flow increased, the Cp amplitude of the guide vane inlet decreased gradually. The main frequency of Cp in the middle and the guide vane outlet was not the BPF, indicating that the Cp amplitude at each monitoring point was less affected by the impeller rotation. At this time, the main excitation source of pressure pulsation was the velocity circulation of water flow. At small flow rate condition, the internal and outlet monitoring points of the guide vane were also affected by the local reverse flow. At 1.2 Qbep, the reverse flow area gradually disappeared, and the Cp in the guide vane decreased. The Cp amplitudes of P7, P8, and P9 were higher than those at each monitoring point at the guide vane outlet. At 0.8Qbep, the average Cp amplitude at the guide vane inlet was 1.33 times that at the guide vane middle, and the average Cp amplitude at the guide vane middle was 28.2% higher than that at the guide vane outlet. At 1.0Qbep, the average Cp amplitude at the guide vane inlet was 0.553 times that at the guide vane intermediate, and the average Cp amplitude at the guide vane intermediate was 17.5% higher than that at the guide vane outlet. At 1.2Qbep, the average Cp amplitude at the guide vane inlet was 6.46 times that at the guide vane intermediate, and the average Cp amplitude at the guide vane intermediate was 20.2% higher than that at the guide vane outlet.
In this article, the reliability of numerical simulation was verified by comparing the energy performance test of the pump device with the energy performance test of the numerical calculation of the pump device. The transient hydraulic characteristics of the impeller and the guide vane of the vertical axial flow pump device were studied, and the following three conclusions were obtained:
1) When the flow increases, the area of streamline distortion at the hub of the blade working face decreases. The velocity distribution on the impeller blade increases gradually from the blade root to the tip. The flow is affected by the viscous resistance of the impeller hub wall to the liquid and the leakage of the tip clearance, resulting in the decrease of the flow velocity near the impeller hub and the rim.
2) The ratio of the average FZ on the impeller under the three flow conditions of 0.8 Qbep, 1.0Qbep, and 1.2Qbep is about 11:10:9. Under 0.8 Qbep condition, the FR on the impeller is the largest, and the average FR is 249 N. The fluctuation range of FR is 60.2 %—127.7% of the average FR. Under different flow conditions, the main frequency of Cp at the impeller inlet and outlet is 1 times the BPF. When the flow increases, the Cp amplitude decreases. The pressure pulsation in the tip clearance is affected by the tip clearance leakage, and there is no obvious regularity.
3) The internal flow pattern of the guide vane is the worst at 0.8 Qbep, and the internal hydraulic loss is large. At 1.2 Qbep, the flow pattern is good, and the hydraulic loss caused by flow disorder is decreased. The pressure pulsation amplitude gradually decreases from the inlet to the outlet of the guide vane, and the main frequency of the pressure pulsation at the guide vane inlet is 1 times the BPF, while the guide vane outlet is not the BPF.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Conceptualization, FY; software and writing—original draft, PC; formal analysis, FY and PC; methodology, FY and PC; funding, FY and HJ; investigation, HJ and FT; resources, YJ and FT; supervision, FY and FT; visualization, PC and FY; and writing—review and editing, YL and YJ. All authors have read and agreed to the published version of the manuscript.
This research was funded by the National Natural Science Foundation of China (Grant No. 51609210), Major Projects of the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 20KJA570001), the Technology Project of the Water Resources Department of the Jiangsu Province (Grant No. 2020029), Open Project of Jiangxi Research Center on Hydraulic Structures (Grant No.2021SKSG06), the Scientific Research Program of Jiangsu Hydraulic Research Institute (Grant No. 2021), the Priority Academic Program Development of the Jiangsu Higher Education Institutions (Grant No. PAPD), and Postgraduate Research & Practice Innovation Program of Jiangsu Province-Yangzhou University (Grant No. SJCX21_1590).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Celik, I. B., Ghia, U., Roache, P. J., and Freitas, C. J. (2008). Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 130, 078001. doi:10.1115/1.2960953
Chalghoum, I., Elaoud, S., Kanfoudi, H., and Akrout, M. (2018). The Effects of the Rotor-Stator Interaction on Unsteady Pressure Pulsation and Radial Force in a Centrifugal Pump. J. Hydrodyn. 30 (4), 672–681. doi:10.1007/s42241-018-0073-y
Fu, S., Zheng, Y., Kan, K., Chen, H., Han, X., Liang, X., et al. (2020). Numerical Simulation and Experimental Study of Transient Characteristics in an Axial Flow Pump during Start-Up. Renew. Energy 146, 1879–1887. doi:10.1016/j.renene.2019.07.123
Jin, Y., He, X., Zhang, Y., Zhou, S., Chen, H., and Liu, C. (2019). Numerical and Experimental Investigation of External Characteristics and Pressure Fluctuation of a Submersible Tubular Pumping System. Processes 7 (12), 949. doi:10.3390/pr7120949
Kan, K., Zhang, Q., Xu, Z., Chen, H., Zheng, Y., Zhou, D., et al. (2021). Study on a Horizontal Axial Flow Pump during Runaway Process with Bidirectional Operating Conditions. Sci. Rep. 11 (1), 21834. doi:10.1038/s41598-021-01250-1
Kan, K., Chen, H., Zheng, Y., Zhou, D., Binama, M., and Dai, J. (2021b). Transient Characteristics during Power-Off Process in a Shaft Extension Tubular Pump by Using a Suitable Numerical Model. Renew. Energy 164, 109–121. doi:10.1016/j.renene.2020.09.001
Kan, K., Yang, Z., Lyu, P., Zheng, Y., and Shen, L. (2021). Numerical Study of Turbulent Flow Past a Rotating Axial-Flow Pump Based on a Level-Set Immersed Boundary Method. Renew. Energy 168, 960–971. doi:10.1016/j.renene.2020.12.103
Li, D., Wang, H., Qin, Y., Han, L., Wei, X., and Qin, D. (2017). Entropy Production Analysis of Hysteresis Characteristic of a Pump-Turbine Model. Energy Convers. Manag. 149, 175–191. doi:10.1016/j.enconman.2017.07.024
Li, D., Zuo, Z., Wang, H., Liu, S., Wei, X., and Qin, D. (2019). Review of Positive Slopes on Pump Performance Characteristics of Pump-Turbines. Renew. Sustain. Energy Rev. 112, 901–916. doi:10.1016/j.rser.2019.06.036
Li, Y., Zheng, Y., Meng, F., and Osman, M. K. (2020). The Effect of Root Clearance on Mechanical Energy Dissipation for Axial Flow Pump Device Based on Entropy Production. Processes 8 (11), 1506. doi:10.3390/pr8111506
Lin, P., Xiang, L., Hu, D., Zhai, S., Guo, P., and Wang, S. (2021). Effect of Cavitation on Pressure Pulsation Characteristics of an Axial-Flow Pump under Sand Conditions. J. Vib. Shock 40 (18), 140–147. doi:10.13465/j.cnki.jvs.2021.18.019
Liu, H., Liu, M., Bai, Yu., Du, H., and Dong, L. (2014). Grid Convergence Based on GCI for Centrifugal Pump. J. Jiangsu Univ. Nat. Sci. Ed. 35 (03), 279–283. doi:10.3969/j.issn1671-7775.2014.03.006
Meng, F., Li, Y., and Pei, J. (2021). Energy Characteristics of Full Tubular Pump Device with Different Backflow Clearances Based on Entropy Production. Appl. Sci. 11 (8), 3376. doi:10.3390/app11083376
Mompean, G. (1998). Numerical Simulation of a Turbulent Flow Near a Right-Angled Corner Using the Speziale Non-linear Model with RNG K–ε Equations. Comput. Fluids 27 (7), 847–859. doi:10.1016/s0045-7930(98)00004-8
Mu, T., Zhang, R., Xu, H., Zheng, Y., Fei, Z., and Li, J. (2020). Study on Improvement of Hydraulic Performance and Internal Flow Pattern of the Axial Flow Pump by Groove Flow Control Technology. Renew. Energy 160, 756–769. doi:10.1016/j.renene.2020.06.145
Nandan Kumar, K., and Govardhan, M. (2014). On Topology of Flow in a Turbine Cascade. J. Fluids Eng. 136 (8), 081201. doi:10.1115/1.4026056
Roache, P. J. (1997). Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 29, 123–160. doi:10.1146/annurev.fluid.29.1.123
Shen, X., Zhang, D., Xu, B., Jin, Y., and Shi, W. (2020). Experimental Investigation of the Transient Patterns and Pressure Evolution of Tip Leakage Vortex and Induced-Vortices Cavitation in an Axial Flow Pump. J. Fluids Eng. 142 (10), 101206. doi:10.1115/1.4047529
Shi, L., Zhu, J., Wang, L., Chu, S., Tang, F., and Jin, Y. (2021). Comparative Analysis of Strength and Modal Characteristics of a Full Tubular Pump and an Axial Flow Pump Impellers Based on Fluid-Structure Interaction. Energies 14 (19), 6395. doi:10.3390/en14196395
Song, X., and Liu, C. (2021). Experimental Study of the Floor-Attached Vortices in Pump Sump Using V3V. Renew. Energy 164, 752–766. doi:10.1016/j.renene.2020.09.088
Wang, Y., Yu, H., Guo, Y., Yan, M., Sui, H., Zhang, Y., et al. (2020). Numerical Study on Pressure Pulsation Characteristics of Liquid LBE Medium Axial-Flow Pump. Nucl. Power Eng. 41 (03), 202–207. doi:10.13832/j.jnpe.2020.03.0202
Wang, F. J. (2020). Analysis Method of Flow in Pumps and Pumping Stations. Beijing, China: China Water & Power Press.
Xie, R., Hua, E., Xu, G., Guo, X., Yang, F., and Tang, F. (2022). Research on Double Hump Phenomenon of Axial Flow Pump. Trans. Chin. Soc. Agric. Mach. 53 (01), 178–185. doi:10.6041/j.issn1000-1298.2022.01.019
Xu, Z., Zheng, Y., Kan, K., and Huang, J. (2021). Runaway Characteristics of Bidirectional Horizontal Axial Flow Pump with Super Low Head Based on Entropy Production Theory. Trans. Chin. Soc. Agric. Eng. 37 (17), 49–57. doi:10.11975/j.issn1002-6819.2021.17.006
Yang, F., Jiang, D., Wang, T., Chang, P., Liu, C., and Liu, D. (2021). Investigation into the Influence of Division Pier on the Internal Flow and Pulsation in the Outlet Conduit of an Axial-Flow Pump. Appl. Sci. 11 (15), 6774. doi:10.3390/app11156774
Yang, F., Chang, P., Yuan, Y., Li, N., Xie, R., Zhang, X., et al. (2021b). Analysis of Timing Effect on Flow Field and Pulsation in Vertical Axial Flow Pump. J. Marine Sci. Eng. 9 (12), 1429. doi:10.3390/jmse9121429
Yang, F., Li, Z., Fu, J., Lv, Y., Ji, Q., and Jian, H. (2022a). Numerical and Experimental Analysis of Transient Flow Field and Pressure Pulsations of an Axial-Flow Pump Considering the Pump-Pipeline Interaction. J. Marine Sci. Eng. 10 (2), 258. doi:10.3390/jmse10020258
Yang, F., Chang, P., Li, C., Shen, Q., Qian, J., and Li, J. (2022b). Numerical Analysis of Pressure Pulsation in Vertical Submersible Axial Flow Pump Device under Bidirectional Operation. AIP Adv. 12 (2), 025107. doi:10.1063/5.0063797
Yang, F., Li, Z., Hu, W., Liu, C., Jiang, D., Liu, D., et al. (2022). Analysis of Flow Loss Characteristics of Slanted Axial-Flow Pump Device Based on Entropy Production Theory. R. Soc. open Sci. 9 (1), 211208. doi:10.1098/rsos.211208
Yang, W., Yang, K., Fu, Z., and Wu, J. (2022). Numerical Study of Blade Loading Effects on Tip Leakage Flow in Axial Flow Pump. Trans. Chin. Soc. Agric. Mach. 1-12. [2022-03-23].
Yang, F. (2020). Internal Flow Characteristics and Hydraulic Stability of Low-Head Pump Device. Beijing, China: China Water & Power Press.
Zhang, D., Shi, W., Zhang, H., Yao, J., and Guan, X. (2012). Application of Different Turbulence Models for Predicting Performance of Axial Flow Pump. Trans. Chin. Soc. Agric. Eng. 28 (1), 6671+296. doi:10.3969/j.issn.1002-6819.2012.01.013
Zhang, Y., Xu, Y., Zheng, Y., Fernandez-Rodriguez, E., Sun, A., Yang, C., et al. (2019). Multiobjective Optimization Design and Experimental Investigation on the Axial Flow Pump with Orthogonal Test Approach. Complexity 2019, 1–14. doi:10.1155/2019/1467565
Zhang, X., Tang, F., Liu, C., Shi, L., Liu, H., Sun, Z., et al. (2021). Numerical Simulation of Transient Characteristics of Start-Up Transition Process of Large Vertical Siphon Axial Flow Pump Station. Front. Energy Res. 9, 382. doi:10.3389/fenrg.2021.706975
Zhang, X., Tang, F., Chen, Y., Huang, C., Chen, Y., Wang, L., et al. (2022). Experimental Study on the Internal Pressure Pulsation Characteristics of a Bidirectional Axial Flow Pump Operating in Forward and Reverse Directions. Machines 10 (3), 167. doi:10.3390/machines10030167
Zhao, H., Wang, F., Wang, C., Chen, W., Yao, Z., Shi, X., et al. (2021). Study on the Characteristics of Horn-like Vortices in an Axial Flow Pump Impeller under Off-Design Conditions. Eng. Appl. Comput. Fluid Mech. 15 (1), 1613–1628. doi:10.1080/19942060.2021.1985615
Zhou, Y., Chen, B., Zhang, D., Zhang, H., and Yang, C. (2022). Influence of Double-Layer Flow Passage Structure after Impeller on External Characteristics of Axial-Flow Pump. Trans. Chin. Soc. Agric. Mach. 53 (02), 149–157+176. doi:10.6041/j.issn.1000-1298.2022.02.15
Cp Pressure coefficient
D2 Exit diameter of shroud
D Impeller diameter
FR Radial force
Fx The radial force component on x axis
Fy The radial force component on y axis
FZ Axial force
GCI21 Grid convergence index of grid scheme 2 and grid scheme 1
GCI32 Grid convergence index of grid scheme 3 and grid scheme 2
GCI43 Grid convergence index of grid scheme 4 and grid scheme 3
GCI54 Grid convergence index of grid scheme 5 and grid scheme 4
GCI65 Grid convergence index of grid scheme 6 and grid scheme 5
GCI76 Grid convergence index of grid scheme 7 and grid scheme 6
Hy Working head of impeller
N The number of grid nodes on the coupling surface
P Instantaneous pressure
Pi The pressure at the ith grid node
Pzh The axial force generated by water flow on the hub
Pz The axial force on the blade
Qbep Design flow rate
R The radius of the impeller
r The radius from the measuring point to the hub
Rm Hub radius
Sp Blade radial coefficient
T Rotation cycle
ρ The density of water
V Circular velocity
CFD Computational fluid dynamics
FAV Floor-attached vortex
N-S Navier–Stokes
RNG Renormalization group
GCI Grid convergence index
FFT Fast Fourier transform
BPF Blade passing frequency
Keywords: vertical axial flow pump device, internal flow field, pressure pulsation, unsteady, numerical simulation
Citation: Yang F, Chang P, Jian H, Lv Y, Tang F and Jin Y (2022) Numerical Analysis of Unsteady Internal Flow Characteristics of Impeller-Guide Vane in a Vertical Axial Flow Pump Device. Front. Energy Res. 10:935888. doi: 10.3389/fenrg.2022.935888
Received: 04 May 2022; Accepted: 13 June 2022;
Published: 13 July 2022.
Edited by:
Kan Kan, College of Energy and Electrical Engineering, ChinaReviewed by:
Tianyi Li, University of Minnesota Twin Cities, United StatesCopyright © 2022 Yang, Chang, Jian, Lv, Tang and Jin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fan Yang, ZmFueWFuZ0B5enUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.