Route Stability in the Uncertain Capacitated Arc Routing Problem

Power line inspections in a microgrid can be modeled as the uncertain capacitated arc routing problem, which is a classic combinatorial optimization problem. As an evolutionary computation method, genetic programming is used as a hyper-heuristic method to automatically evolve routing policies that can make real-time decisions in an uncertain environment. Most existing research on genetic programming hyper-heuristic for the uncertain capacitated arc routing problem only focuses on optimizing the total cost of solutions. As a result, the actual routes directed by the routing policies evolved by genetic programming hyper-heuristic are usually not stable, i.e., the routes have large fluctuations in different uncertain environments. However, for marketing or considering the drivers’ and customers’ perspectives, the routes should not be changed too often or too much. Addressing this problem, this study first proposes a method to estimate the similarity between two routes and then extends it for evaluating the stability of the routes in uncertain environments. A novel genetic programming hyper-heuristic, which considers two objectives, i.e., the solution quality (total cost) and the stability of routes, was designed. Experimental studies demonstrate that the proposed genetic programming is hyper-heuristic with stability in consideration and can obtain more stable solutions than the traditional algorithm, without deteriorating the total cost. The approach provided in this study can be easily extended to solving other combinatorial optimization problems in the microgrid.

1 Introduction

With fossil fuel resources being rapidly depleting, conventional power plants becoming less efficient, and the environment becoming more polluted, a new grid architecture has emerged, dubbed the microgrid (Han et al., 2022b). In general, a microgrid is a hybrid electric system that combines distributed energy resources, local loads, and energy storage devices in order to supply power to specific regions or remote locations (Choudhury, 2020; Ma et al., 2021b). In addition to improving their energy stability and operations, microgrids can provide low-cost, clean energy to certain geographic regions. However, serious challenges are faced while implementing microgrids, such as architecture optimization, energy management, and fault inspection (Zhu et al., 2019; Cui et al., 2020; Tian et al., 2020). Although various approaches (e.g., the game theoretic approach) have been proposed to solve these challenges in microgrids, some shortcomings, for example, low robustness and high computational cost, restrict their extensive use in applications (Cui et al., 2019; Han et al., 2022a; Zhu et al., 2022). In recent years, some researchers have formulated these problems as the traditional combinatorial optimization problems and utilized heuristic or meta-heuristic (e.g., genetic algorithms and particle swarm optimization) approaches to solve them (Wang et al., 2019b; Ma et al., 2021a; Luo et al., 2021), since these approaches can provide approximate solutions with low computational cost. For example, Gao et al. (2017) transferred the load-shedding problem to the knapsack problem and proposed a Physarum-based ant colony optimization (PM-ACO) algorithm to solve it. Liu et al. (2019) modeled the problem of power line inspection using cooperated ground vehicle and drone as a two-layer-point arc routing problem and designed two constructive heuristics to solve it. Therefore, addressing such typical NP-complete problems can provide valuable solutions for many problems in the real world (Gao et al., 2021; Wang et al., 2021; Li et al., 2022), which has great practical and theoretical significance for solving existing challenges in the microgrid.

The capacitated arc routing problem (CARP) (Golden and Wong, 1981; Corberán et al., 2021) widely exists in smart transportation. It aims to find minimum-cost vehicle routes to serve arcs of a graph following some constraints, such as the total demands served by a vehicle cannot be larger than its capacity. During the past 60 years, this problem has attracted the attention of many researchers due to its great economic impact and the complexity of its mathematics (Corberán et al., 2021). Especially in recent years, drones equipped with cameras and sensors have been used to inspect power lines in a more efficient and cost-effective manner than traditional human inspection on site. The planning of network inspection operations naturally leads to CARP (Corberán et al., 2021).

Traditionally, CARP focuses on static environments, where all the details of the problems, such as the demands of tasks and the traversal costs of streets, can be precisely known beforehand (MacLachlan and Mei, 2021; Zhang et al., 2021). However, real-life often contradicts this assumption (Mei and Zhang, 2018; Zhu et al., 2018; Liu et al., 2020). In many cases, uncertainty widely exists. For example, in street sprinkling, the real-time temperature will influence the amount of water that should be sprinkled on the street, which is impossible to be known exactly beforehand. The traversing costs (such as the time taken traveling through the street) are also affected by the traffic conditions, and a street may also be temporarily inaccessible because of traffic accidents. In order to model reality more accurately, various uncertain CARP (UCARP) models (e.g., stochastic demands of tasks or stochastic traversal costs of edges) have been proposed (Mei et al., 2010; Liu et al., 2021) and become the hot research topic in most recent years.

Many researchers have proposed different kinds of approaches to solving the UCARP, which can be categorized into three groups (Ouelhadj and Petrovic, 2009; Nguyen et al., 2016): robust pro-active, completely reactive, and predictive-reactive. The robust pro-active approaches aim to produce a robust route for all possible environments and use recourse strategies to repair the route slightly when possible failures occur. And the predictive-reactive approaches not only generate a robust route but also use a re-optimization way to adapt the route when it is inefficient. It can be seen that the preplanned robust route restricts the flexibility of these two kinds of approaches (Liu et al., 2022). Hence, we focus on the completely reactive approaches in this study. In the completely reactive approaches, a rule or policy that is used to generate a route in real-time according to practical situations is evolved. Dynamic environments can be handled very efficiently due to the flexibility of rules (Wang et al., 2022a). Genetic programming (GP) is a kind of completely reactive approach, which has been demonstrated to be a powerful hyper-heuristic (also known as GPHH in short) capable of developing routing policies for UCARP automatically. Routing policies indicate to the vehicle the next task it should complete when it is idle. The decision is made online based on the current environment information and vehicle status. Hence, GPHH is good at handling dynamic and uncertain environments.

However, GPHH has the disadvantage that the actual traveling routes would be changed frequently in dynamic environments. There are many practical situations where this is not appropriate. First, it causes difficulty in planning and measuring the efficiency of routes in advance. Second, it has a negative effect on the psychology of drivers. For example, if the routes are changed frequently, it could lead to confusion among the drivers. As a result, there would be more errors and higher costs.

Hence, a certain degree of stability or robustness within the solution space is desirable in many real-world routing scenarios (Sörensen, 2006). For this issue, we first require a method to estimate the similarity between two given routes. Then, we need to measure the stability of routing policy in uncertain environments. Taking the stability of routes generated by GPHH into consideration, this study has the following research objectives:

• To develop a method to estimate the similarity between two routes and extend it for evaluating the stability of routes in uncertain environments.

• To develop a GPHH to evolve routing policies that can generate higher stability of routes as well as have a good quality of total travel cost.

• To verify the performance of the newly proposed GPHH (GPHH-αSta) in experiments from two aspects, i.e., stability and total cost.

• To analyze the routes obtained by GPHH-αSta and the traditional GPHH.

This study is organized in the following way: in Section 2, the background of the definition of UCARP and existing approaches for UCARP are presented. In Section 3, a way to measure the similarity between routes is developed first. Then, a new GPHH algorithm (GPHH-αSta) is designed to evolve routing policies for UCARP that can generate solutions with small travel costs and high stability simultaneously. In Section 4, the values of the parameter α are investigated, and the results of the compared algorithms on the typical data set are shown and analyzed. Finally, in Section 5, the conclusion and future work are discussed.

2 Background

Firstly, we will introduce the UCARP definition, then we will review the state-of-the-art approaches that are being used to solve it.

2.1 Uncertain Capacitated Arc Routing Problem

A CARP (Mei et al., 2010; Liu et al., 2020) is defined on a connected graph G=(V, E), where V denotes the vertex set and E denotes the edge set. The task is distributed alongside the edge, whose demand is denoted by d(e). Not all edges have demands, hence, when $d(e)>0$, the edge e is a task, otherwise, it represents a street without a task to serve. When a vehicle travels through the street, depending on whether it serves the tasks, it has two costs: serving cost sc(e) and traversal cost dc(e). In the beginning, all vehicles are located at the depot, which is usually represented by v0 in graph G. The vehicle has a capacity constraint, denoted by Q. The goal is to minimize the total cost of service of all tasks while adhering to the following restrictions:

1. Each route must start from v0 and end at v0.

2. An exact one-time service is provided in either direction for each task.

3. For each vehicle, the total demands on a single trip cannot exceed its capacity Q.

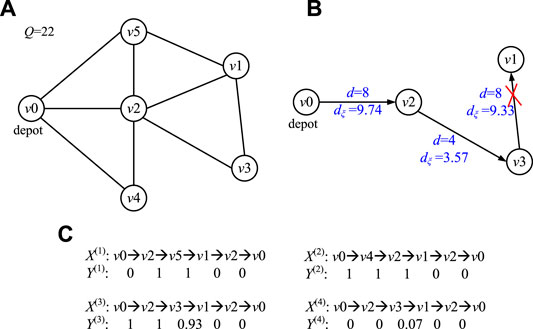
An example is given in Figure 1. In Figure 1, there are six vertices and nine edges in the graph, i.e., V = {v0, v1, v2, v3, v4, v5} and E = {(v0, v2), (v0, v4), (v0, v5), (v1, v2), (v1, v3), (v1, v5), (v2, v3), (v2, v4), (v2, v5)}. The vertex v0 represents the depot, and all the edges are required to be served. Suppose that the vehicle number is 3, whose capacities are all 22, i.e., Q = 22.

FIGURE 1

FIGURE 1. (A) CARP instance example, (B) possible route failure, and (C) possible solution.

In CARP, the three features associated with each edge, i.e., demand, serving cost, and traversal cost, are static and can be exactly known in advance. However, in UCARP, the demands and traversal costs are always seen as two uncertain variables. The actual demand of a task can only be known after the vehicle has completed the service of the task. The actual traversal cost of an edge can only be realized after the edge is traversed. To get a sample of a UCARP instance, the two variables are sampled random values for the corresponding UCARP instance. That is, a sample I_ξ of the UCARP instance I is constructed by sampling each random demand d_ξ(e) and each random traversal cost dc_ξ(e) under the environment (e.g., random seed) ξ. For example, in Table 1, the first three columns show the demand (d), serving cost (sc), and traversal cost (dc) of each edge of the graph, as shown in Figure 1, and the last two columns show the sampled demands (d_ξ) and traversal costs (dc_ξ). Due to the uncertainties of demands and traversal costs, route failure and edge failure are two unavoidable failures that may occur during the serving process.

TABLE 1

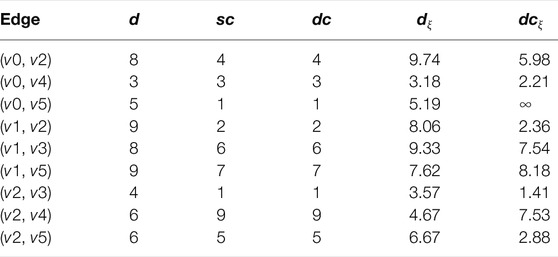
TABLE 1. The demands and costs of the instance in Figure 1.

When the actual demand of the task is larger than the vehicle’s remaining capacity, a route failure occurs. We use the example in Figure 1B to demonstrate this failure. For example, a vehicle has served the tasks (v0, v2) and (v2, v3) consequently, and its remaining capacity becomes 8.69 (i.e., 22 − 9.74 − 3.57 = 8.69). Then, the vehicle is allocated to serve the task (v3, v1), whose expected demand is 8, and 8 is less than the remaining capacity of 8.69. However, when the vehicle is conducting the service, it finds out that the actual demand of the task (v3, v1) is larger than 8. And when it is full, there are still unserved tasks in the street. The actual demand of the task (v3, v1) is 9.33. In this case, we can say that a route failure has occurred. Since the route failure always happens during the serving process, the failed vehicle can only choose to abandon the remaining parts of the task and return to the depot to refill. Then, who takes charge of the remaining tasks? The current recourse strategy can be divided into three categories. The first one is called the independent recourse strategy, which is widely used in the literature [18,27]. According to this recourse strategy, the remaining service of the failed task is finished by the same vehicle after it replenishes the capacity. In Figure 1B, the vehicle first abandons the remaining unserved tasks, goes back to v0 via v1 following the shortest path, and then comes back to the interrupted place via v3 to continue the service. The second one is called the pairing recourse strategy (Ak and Erera, 2007). This recourse strategy identifies the vehicles as Type I and Type II, and pairs them up to work. If the failure happens on the Type I vehicle, the unfinished tasks are attached to the end of the Type II vehicle’s route. Otherwise, if failure happens on the Type II vehicle, the unserved tasks are finished by themselves using the independent way. The third one is called the global recourse strategy [21,26], which aims to construct more collaborative forms of recourses. In this recourse strategy, the failure tasks can be reallocated to any potential vehicles that can reduce the expected costs caused by failure. Detailed strategies can be seen in [21,26].

When the edge ahead of a route suddenly becomes unfeasible, an edge failure occurs. For example, in Table 1, the actual traversal cost of the edge (v0, v5) is ∞, which means that the street is inaccessible. If a vehicle locates at v0 and wants to travel through v0 to v5, or it locates at v5 and wants to travel through v5 to v0, an edge failure occurs in this case. The recourse strategy to edge failure is relatively easy to cope with. The most common strategy is to find the shortest path from the current position to the destination under the current situation. If the edge is a task, the vehicle will abandon this task and go to the next task based on its routing plan.

A solution S to a UCARP instance sample can be presented by a combination of two components (X, Y), where X and Y represent the set of routes and the set of vectors with real values, respectively. For each route in X, $X^{(k)}=(x_1^{(k)},\dots ,x_{L_k}^{(k)})$ is a vertices sequence that begins and ends at the depot (i.e., $x_1^{(k)}$=$x_{L_k}^{(k)}$=v₀), where L_k represents the number of vertices within the k^th route. For each vector in Y, $Y^{(k)}=(y_1^{(k)},\dots ,y_{L_k-1}^{(k)})$, which means that the fraction of service of each edge is in X^(k). The value of $y_i^{(k)}$ is in [0, 1]. Specifically, $y_i^{(k)}=1$ represents that the task $(x_i^{(k)},x_{i+1}^{(k)})$ is served completely, $y_i^{(k)}=0$ represents that the vehicle traveled through the edge $(x_i^{(k)},x_{i+1}^{(k)})$ without serving it. For other values of $y_i^{(k)}$, it means that the edge $(x_i^{(k)},x_{i+1}^{(k)})$ is served partially at the current route. For example, Figure 1C shows a possible solution to the instance in Figure 1A with the data in Table 1. It can be seen that four routes are required to serve all the tasks. And a route failure occurs in X⁽³⁾. The independent recourse strategy is used, which generates the fourth route (i.e., X⁽⁴⁾ and Y⁽⁴⁾).

A solution’s total cost can be calculated as follows:

$\begin{array}{c}\hfill C\left(S_{\xi }\right)=\sum _{k=1}^m\sum _{i=1}^{L_k-1}\left(sc\left(S_{\xi }\left[x_i^{\left(k\right)}\right],S_{\xi }\left[x_{i+1}^{\left(k\right)}\right]\right)\times S_{\xi }\left[y_i^{\left(k\right)}\right]+\right.\\ \hfill \left.d{c}_{\xi }\left(S_{\xi }\left[x_i^{\left(k\right)}\right],S_{\xi }\left[x_{i+1}^{\left(k\right)}\right]\right)\times \left(1-S_{\xi }\left[y_i^{\left(k\right)}\right]\right)\right)\end{array}(1)$

In Eq. 1, $S_{\xi }[x_i^{(k)}]$ and $S_{\xi }[y_i^{(k)}]$ represent the $x_i^{(k)}$ and $y_i^{(k)}$ elements in the solution S_ξ on the environment ξ.

2.2 Related Work

The existing approaches for solving routing problems in uncertain environments can be divided into three categories according to the time when decisions are being made (Ouelhadj and Petrovic, 2009; Nguyen et al., 2016): 1) robust pro-active, 2) completely reactive, and 3) predictive-reactive.

Concerning the first category of approaches, the robust pro-active approaches focus on developing predictive solutions that can meet the needs of performance based on the prediction of the environment in the first step. In the second step, i.e., when applying the solutions to the actual environments, failures (e.g., route failure or edge failure) may occur, and carefully designed recourse strategies are used to repair the routes slightly. The optimization algorithms used for developing solutions are the tabu search (Mei et al., 2010), the estimation of the distribution algorithm (Wang et al., 2016), and the memetic algorithm (Fleury et al., 2004; Wang et al., 2013; Wang et al., 2022b).

In the new environment, proactive approaches can provide a solution with a high level of stability and predictability. From the perspective of drivers, this is very important because it is beneficial for them to be familiar with the routes quickly. However, it also brings some negative effects, i.e., the routes are inflexible and cannot be adapted to real-time conditions. When environments change greatly (e.g., the demands increase to a high degree), the actual routes must be adjusted accordingly.

In terms of the second category, the completely reactive approaches make decisions dynamically and locally in real-time. Its main idea is to design a routing policy, which can be used to generate routes step by step based on the real-time information in the environments. Since the routing policy is hard to design manually, GPHH (Koza, 1992) has been one of the hottest evolutionary computational methods that is good at evolving the routing policy automatically.

Weise et al. (2012) first proposed a GPHH to solve the static CARP. Experimental results show that most of the results on benchmark CARP instances are the same as the currently known lower bounds. Moreover, they have found that the evolved rules can still generate good results if the scenario has slight changes, such as a few tasks randomly disappearing. Since then, many researchers have extended the ability of GPHH for solving UCARP (Liu et al., 2017). For example, Mei and Zhang (2018) have designed a new meta-algorithm that can handle multiple vehicles for solving UCARP. MacLachlan et al. (2020) further proposed a GPHH with a collaborative multi-vehicle framework to UCARP. While Wang et al. (2019a), Wang et al. (2020), and Wang et al. (2022a) focused on improving the interpretability of rules evolved by GPHH to UCARP, their methods can evolve smaller and simpler rules. Ardeh et al. (2019), Ardeh et al. (2021a), and Ardeh et al. (2021b) devoted their study to detecting the reusability of rules by transfer learning.

The completely reactive approaches have the advantage of being able to easily generate routes online, which makes them very flexible and ideal for the uncertain environment (Nguyen et al., 2013). Moreover, the designing of rules is independent of the size of the problem (Weise et al., 2012), which can be very effective for solving large-scale problems. By contrast, their disadvantage is that no baseline solution (i.e., a set of routes) is generated, causing routes to be less stable and to be more difficult to plan and measure ahead of time (Nguyen et al., 2016). The stability of routes is an important aspect that should be paid attention to from a practical standpoint. For example, in express delivery, if the delivery route of a courier is relatively stable, then they can arrive at a community at a fixed time of the day. From the perspective of the courier, they are familiar with the driving environment and can be very relaxed at work. From the perspective of customers, they can consistently be visited by the same drivers and can expect to send or receive packages at a fixed time. Nevertheless, to the best of our knowledge, no completely reactive approaches for UCARP exist to optimize the total cost and stability simultaneously.

For the third category, the predictive-reactive can be seen as a hybridization of both pro-active and reactive approaches. They also generate a predictive solution using the robust proactive approaches first and then design a reoptimization strategy that reacts to changing conditions in real-time. A typical work can be seen in Liu et al. (2020), whose main idea was to use a new representation (i.e., the combination of a baseline task sequence and a recourse policy) to give the solutions. The baseline is generated by the estimation of the distribution algorithm, and the policy evolved by GPHH.

When using the predictive-reactive approaches, it is advantageous to take into account not only the quality of the predictive baseline solution (efficiency) but also the level of change to be introduced to the baseline solution to adapt to the new environment (stability) (Liu et al., 2020; MacLachlan et al., 2020).

3 Genetic Programming Hyper-Heuristic with Stability

Given a sampled UCARP instance I_ξ and a routing policy h(⋅), the meta-algorithm (Liu et al., 2017) can be used to generate a feasible solution. The traditional GPHH uses the average total cost of the solutions as the fitness function and tends to evolve a good routing policy with little total cost. In order to get a routing policy with not only little total cost but also high stability, we can revise the fitness function by considering these two factors. To this end, we first need a way to measure the similarity between two solutions, then extend it for evaluating the similarity between all solutions, which can be utilized to measure the stability of a routing policy. The overview of the proposed method can be seen in Figure 2.

FIGURE 2

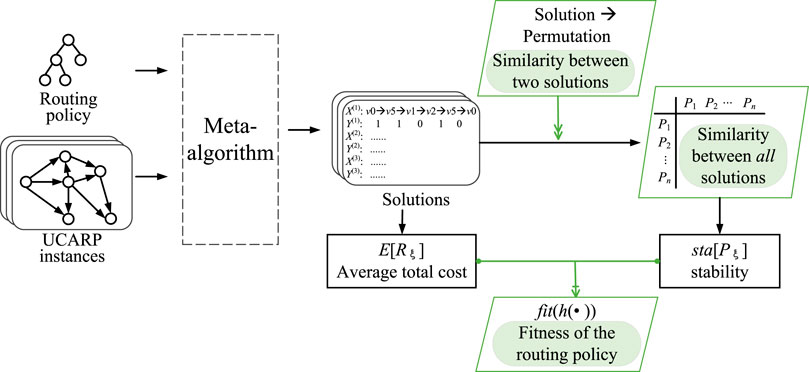
FIGURE 2. Overview of the proposed method. Given a sampled UCARP instance and routing policy, the meta-algorithm (Liu et al., 2017) can be used to generate a feasible solution. The proposed method revises the fitness function by considering the total cost and the stability simultaneously. To this end, we first propose a way to measure the similarity between two solutions, then extend it for evaluating the similarity between all solutions, which can be utilized to measure the stability of a routing policy.

3.1 The Similarity Between Two Routes

According to the previous description, we wanted to measure the stability of routes generated by a routing policy in uncertain environments. For this purpose, a way to measure the similarity between two routes is firstly required.

Combined with the characteristics of the arc routing problem, if a vehicle always serves the same next task y after it has served task x in uncertain environments, then these two tasks x and y are seen as stable in the process of being served. Otherwise, the service order of these two tasks x and y is unstable and changes in different environments. For two sequences that contain all the tasks, the larger the number of these kinds of tasks (i.e., two consecutive tasks are the same), the more similarities between these two sequences. Based on this idea, firstly, we propose that routes are represented by a permutation of tasks that are being served by all the vehicles in UCARP. In this sequence, the tasks are identified by their IDs, and 0 is used as the route delimiter. Two consecutive tasks mean that they are served by one another, and the shortest paths between the consecutive tasks are eliminated. We use an example of a UCARP instance in Figure 3 to show the route representation.

FIGURE 3

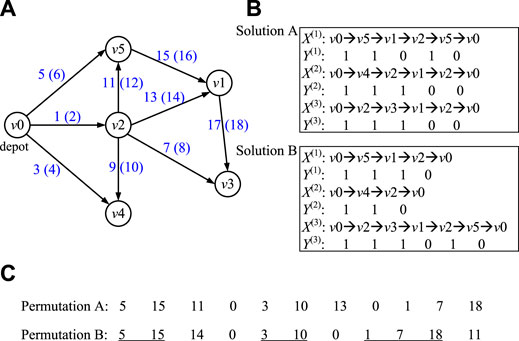
FIGURE 3. (A) UCARP instance example, (B) two possible solutions for the UCARP instance in (A), and (C) the corresponding two permutations of tasks based on the solutions A and B in (B).

Figure 3A illustrates an instance with nine edges (each edge is a task). The vertex v0 is the depot. Associated with each task are a pair of IDs, the one outside a parenthesis indicating the current direction and one inside a parenthesis indicating the opposite direction. Directing by the same routing policy, when the environments are changed (e.g., the demands of tasks being increased or decreased), two different feasible solutions are generated, as shown in Figure 3B. For comparing the similarity between the two solutions, they are transferred to the representation of two permutations of tasks, respectively, as shown in Figure 3C. For example, in the first route of solution A, (v0, v5) (its ID is 5) and (v5, v1) (its ID is 15) are tasks, they are served consequently. Hence, the first two elements of permutation A are 5 and 15.

Then, the similarity between the two permutations (denoted as s(A, B)) is measured by the percentage of the number of common consecutive tasks based on Eq. 2.

$s\left(A,B\right)=\frac{CNum\left(A\cap B\right)}{Num\left(B\right)}(2)$

where CNum(A ∩ B) means the number of common consecutive tasks, and Num(B) means the total number of consecutive tasks in permutation B. For example, by comparing the two permutations A and B in Figure 3C, there are four consecutive tasks which are the same, i.e., (5, 15), (3,10), (1,7), and (7, 18), and Num(B) is 6, i.e., (5, 15), (15, 14), (3, 10), (1, 7), (7, 18), and (18, 11). Hence, the similarity between B and A is 4/6, i.e., 66.67%.

Above all, the similarity between the two solutions is measured by the order of tasks being served in the sequence. In two routes generated in two different environments, the higher the same order of tasks being served, the higher the similarity between the two routes.

3.2 The Stability of Routes Generated by the Routing Policy

In order to measure the stability of routes generated by a routing policy in uncertain environments, we need to evaluate the similarity between all routes in all the possible uncertain environments. Addressing this problem, we propose that firstly, the similarities between any two routes are calculated based on Eq. 2 in Section 3.1, then the average value is counted as the stability.

We use a matrix in Figure 4 to describe further. Suppose Ξ(I) is the collection of all possible samples of a UCARP instance I, the size of Ξ(I) is n, and P_ξ represents the permutation of tasks transferred from solution R_ξ in the sampled instance ξ (ξ ∈ Ξ(I)). Each element in the matrix means the similarity between the two permutations in the corresponding column and row, and elements in the lower triangular are needed, as shown in Figure 4. The stability is calculated based on the following equation:

$sta\left(P_{\xi }\right)=\frac{n\left(n-1\right)}{2}\sum _{j=2}^n\sum _{i=1}^{j-1}s\left(P_i,P_j\right)(3)$

FIGURE 4

FIGURE 4. The matrix to show how to calculate the stability of routes. s(P_i, P_j) means the similarity between permutations P_i and P_j, which is calculated based on Eq. 2.

3.3 GPHH with the Stability in Consideration: GPHH-Sta

A routing policy in the GPHH is represented as a Lisp tree, which is used to select the next task to be served by vehicles according to their priorities on the list of unsettled tasks. The routing policy is composed of two sets, one is the state features in the environments (which we call terminals in GPHH), and the other are functions, such as +, −, ×, and /.

The traditional GPHH treats the UCARP as a single objective optimization problem that aims to minimize the total cost of routes. Since our purpose is to improve the stability of routes without decreasing the total cost, two objectives have to be optimized. One efficient way of solving this problem is to combine the two factors into one fitness function, which can be defined as follows:

$fit\left(h\left(\cdot \right)\right)=\alpha \times E\left[R_{\xi }\right]/E\left[sc\right]-sta\left(P_{\xi }\right)(4)$

where E[R_ξ] represents the average total cost of the routes obtained by using the policy with the training samples, i.e., $E[R_{\xi }]=\frac{1}{|{\mathrm{\Xi }}_{train}|}{\sum }_{I_{\xi }\in {\mathrm{\Xi }}_{train}}C(S_{\xi },h(\cdot ))$, in which C(S_ξ, h(⋅)) represents the total cost of the solution S_ξ under the routing policy h(⋅). E[sc] represents the total value of the serving costs of the tasks. sta(P_ξ) is the stability, which is calculated based on Eq. 3. Especially in Eq. 4, α is the parameter that controls the weight of the total cost. A high value for α means that the total cost is very important. In the experiments, we first investigate four α values, i.e., 2, 3, 4, and 5.

Note that the value of sta(P_ξ) is in the range of [0, 1], hence we let E[R_ξ]/E[sc] to make the two objectives (i.e., total cost and stability) fall on the same scale.

The standard GP process is used to train the proposed GPHH (denoted as GPHH-αSta), as shown in Algorithm 1. In our meta-algorithm, the independent recourse strategy is used to deal with route failure, and a detour is found by finding the shortest path under the new environment for edge failure. The special process to measure the stability of solutions and calculate the fitness of policies is underlined.

Algorithm 1. The training process of GPHH-αSta

4 Experimental Study

In order to examine the efficiency of GPHH-αSta in improving the stability of routes, we test the algorithms on benchmark UCARP instances ugdb (Liu et al., 2020). The traditional GPHH with the average total cost (i.e., E[R_ξ] in Eq. 4) as the fitness function is used for comparison, which is denoted as GPHH in order to distinguish with the proposed algorithms GPHH-αSta.

4.1 Experiment Setup

For the compared GPHH and GPHH-αSta, their population size is 1024, the maximum number of generations is set to 51, the tournament selection size is 7, and the maximal tree depth is 8. The crossover, mutation, and reproduction rates are 0.8, 0.15, and 0.05, respectively. Table 2 shows the 11 terminals used in GPHH and GPHH-αSta, and the function set is {+, −, ×, /, max, min}. “/” is protected, which returns 1 if divided by 0.

TABLE 2

TABLE 2. The terminal set.

The UCARP instance generator proposed in Mei et al. (2010) can be used to generate the training and test sets based on the static gdb instances. Five randomly generated instances are used to train each algorithm as per generation, and the best routing policy h*(⋅) in the final generation is tested on another 500 randomly generated instances. The average total cost and stability of routes over the 500 samples are used to evaluate the performance of GPHH and GPHH-αSta. For each algorithm, 30 independent runs are performed for each UCARP instance.

4.2 Parameter Analysis (α)

In this section, α = 2, 3, 4, and 5 are investigated on two representative instances, i.e., ugdb1 and ugdb8. ugdb1 represents the small instance with 22 tasks at the most, and ugdb8 represents the large instance with 46 tasks at the most. Figure 5 plots the box charts of the total cost and stability on the test sets. It shows a general pattern that by increasing the value of α, the total cost of GPHH-αSta becomes better, and the stability of GPHH-αSta becomes worse.

FIGURE 5

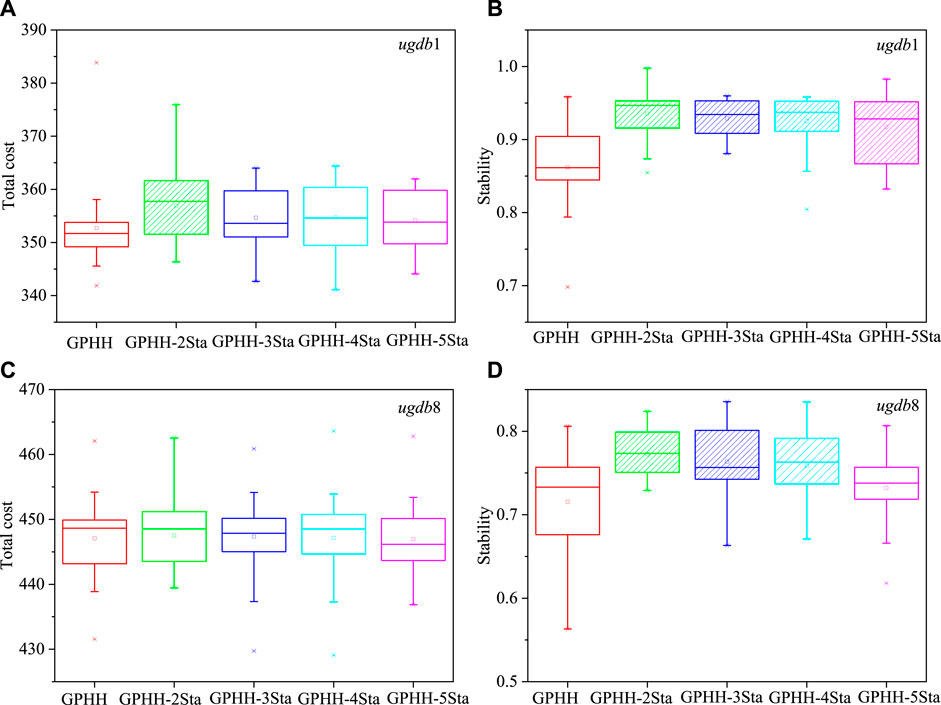
FIGURE 5. (A) and (B) show the box charts of the total cost and the stability of the compared GPHHs on the instances ugdb1, respectively. (C) and (D) show the box charts of the total cost and the stability of the compared GPHHs on the instances ugdb8, respectively.

We also use the Wilcoxon rank-sum test with a significance level of 0.05 to compare GPHH-αSta with the traditional GPHH. The box charts filled with lines in Figures 5A,C show that the total costs of GPHH-αSta are significantly worse than those of GPHH. And in Figures 5B,D, these line box charts show that the stabilities of GPHH-αSta are significantly better than those of GPHH. The results illustrate that when α = 2, although the stabilities of GPHH-2Sta are significantly better than those of GPHH in both instances, its total cost shows a significantly worse result than GPHH on ugdb1. This means that when the value of α is less than 2, GPHH-αSta tends to have high stability but a poor total cost, and when α = 5, both the total costs and stabilities of GPHH-5Sta have no significant difference with that of GPHH on ugdb8, which means that when the value of α is larger than 5, the weight of the total cost is too high that there is little difference between GPHH-αSta and the traditional GPHH. Hence, we test the performance of GPHH-αSta with α = 3 and 4 in the following experiments.

4.3 Results and Discussions

Table 3 shows the test performances (i.e., total cost and stability of solutions) of the compared algorithms, and the Wilcoxon rank-sum test with a significance level of 0.05 is also conducted. The (+) ((−)) represents that the proposed algorithms (i.e., GPHH-3Sta or GPHH-4Sta) perform significantly better (worse) than the traditional GPHH. (=) represents that the two algorithms have no significant difference.

TABLE 3

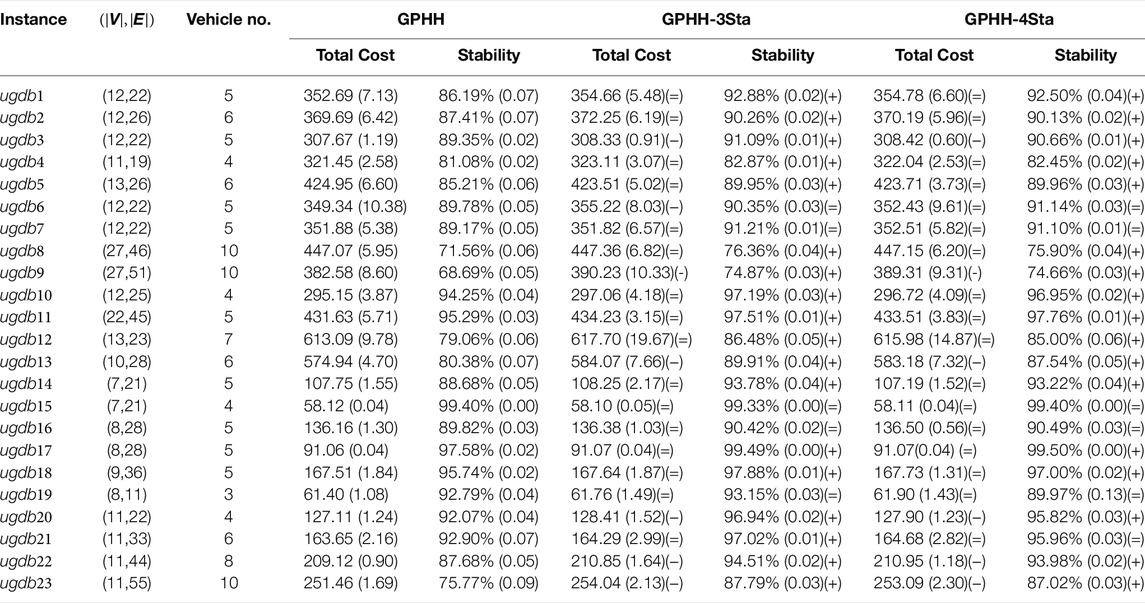
TABLE 3. The mean and standard deviation for the total cost and stability of the compared GPHHs on the test sets. (+), (−), and (=) mean that GPHH-αSta is significantly better than, worse than, and comparable with the traditional GPHH.

From the table, it can be found that the stabilities of GPHH-3Sta are significantly better than those of the traditional GPHH in 18 out of the 23 instances, and among the 18 instances, the total costs of GPHH-3Sta have no significant difference from those of GPHH on 12 instances, i.e., ugdb1, ugdb2, ugdb4, ugdb5, ugdb8, ugdb10, ugdb11, ugdb12, ugdb14, ugdb17, ugdb18, and ugdb21. This means that GPHH-3Sta can evolve much more stable routes without losing the test performance to a great extent. The performance of GPHH-4Sta shows almost the same pattern as GPHH-3Sta by comparing with the traditional GPHH. The only difference appears on the instance ugdb21. That is, the stability of GPHH-4Sta shows no further significantly better results than that of the traditional GPHH, which means that the stability of GPHH-αSta is very sensitive to the value of α on the instance ugdb21.

To make a further comparison, a pairwise comparison between the three algorithms is conducted, as shown in Tables 4, 5. Each entry in the table represents the result of comparing the column algorithm with the row algorithm in W-D-L format. W (L) refers to the number of instances in which the row algorithm performed significantly better (worse) than the column algorithm. D refers to the number of instances where the two algorithms do not show any significant difference. It can be seen that the total cost of GPHH-4Sta is significantly better than that of GPHH-3Sta on only one instance, i.e., ugdb14 actually, and the stabilities of GPHH-4Sta have no significant difference with those of GPHH-3Sta on all of the 23 instances. Hence, both the value of α = 3 and α = 4 is recommended, which can be determined based on the practical application, and if we focus more on the stability, then α = 3 is recommended; otherwise, we can let α = 4, ensuring that the total cost is not affected significantly.

TABLE 4

TABLE 4. The WDL table for the pairwise comparisons between GPHH algorithms in terms of the total cost.

TABLE 5

TABLE 5. The WDL table for the pairwise comparisons between GPHH algorithms in terms of the stability.

4.4 Further Analysis

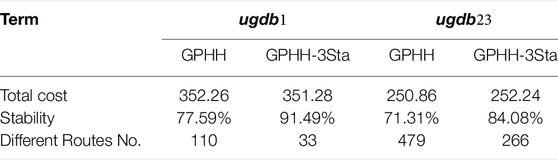
We randomly choose a rule evolved by the traditional GPHH and GPHH-3Sta on ugdb1 and ugdb23, respectively, and analyze the routes generated by each rule on the 500 test instances. The test instances are the same for rules on ugdb1, and also the same for rules on ugdb23. Comparable results can be seen in Table 6. It shows that there is little difference in the average total costs between the traditional GPHH and GPHH-3Sta. The stability of GPHH-3Sta is better than that of GPHH in both instances. Taking the 500 routes generated on the test instances in detail, we found that there are 110 different routes generated by the rule evolved by the traditional GPHH on ugdb1; however, GPHH-3Sta only generates 33 different routes on ugdb1. The same pattern shows on ugdb23. These further discover that along with the changes in the environments, the routes generated by the rules evolved by GPHH-3Sta have smaller volatility than those of traditional GPHH.

TABLE 6

TABLE 6. The comparable results between GPHH and GPHH-3Sta on ugdb1 and ugdb23, respectively.

5 Conclusion

This study aimed to improve the stability of routes generated by the routing policy evolved by GPHH to solve UCARP. At the same time, the solution quality should not decrease significantly. To this end, this study first showed that the stability of routes can be measured by counting the same order of tasks being served in the serving sequences of the tasks. Then, a novel GPHH-αSta approach was proposed to optimize the total cost and stability, simultaneously, with α as the weight of the total cost versus stability. Based on the compared experiments on benchmark UCARP instances, we showed that the proposed GPHH could evolve much more stable routes without losing the test performance. In the future, we will consider multi-objective approaches that optimize performance and stability simultaneously.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

YL and JW designed the main idea of the study. YL performed the experiments and analysis, and wrote the manuscript. JZ and XL revised the manuscript. All authors have read and approved the submitted version.

Funding

The work is sponsored by the National Key R&D Program of China (No. 2022YFE0112300), the Key Program for International Science and Technology Cooperation Projects of China (No. 2021YFE011201), the National Natural Science Foundation of China (Nos. 61976181, 11931015), and the Shanghai Sailing Program (No. 21YF1416700).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ak, A., and Erera, A. L. (2007). A Paired-Vehicle Recourse Strategy for the Vehicle-Routing Problem with Stochastic Demands. Transp. Sci. 41, 222–237. doi:10.1287/trsc.1060.0180

CrossRef Full Text | Google Scholar

Ardeh, M. A., Mei, Y., and Zhang, M. (2019). Genetic Programming Hyper-Heuristic with Knowledge Transfer for Uncertain Capacitated Arc Routing Problem. Proc. GECCO (ACM), 334–335. doi:10.1145/3319619.3321988

CrossRef Full Text | Google Scholar

Ardeh, M. A., Mei, Y., and Zhang, M. (2021). Genetic Programming with Knowledge Transfer and Guided Search for Uncertain Capacitated Arc Routing Problem. IEEE Trans. Evol. Comput., 1. doi:10.1109/TEVC.2021.3129278

CrossRef Full Text | Google Scholar

Ardeh, M. A., Mei, Y., and Zhang, M. (2021). “Surrogate-assisted Genetic Programming with Diverse Transfer for the Uncertain Capacitated Arc Routing Problem,” in 2021 IEEE Congress on Evolutionary Computation (CEC) (IEEE), 628–635. doi:10.1109/cec45853.2021.9504817

CrossRef Full Text | Google Scholar

Choudhury, S. (2020). A Comprehensive Review on Issues, Investigations, Control and Protection Trends, Technical Challenges and Future Directions for Microgrid Technology. Int. Trans. Electr. Energy Syst. 30, e12446. doi:10.1002/2050-7038.12446

CrossRef Full Text | Google Scholar

Corberán, Á., Eglese, R., Hasle, G., Plana, I., and Sanchis, J. M. (2021). Arc Routing Problems: A Review of the Past, Present, and Future. Networks. 77, 88–115. doi:10.1002/net.21965

CrossRef Full Text | Google Scholar

Cui, M., Han, D., and Wang, J. (2019). An Efficient and Safe Road Condition Monitoring Authentication Scheme Based on Fog Computing. IEEE Internet Things J. 6, 9076–9084. doi:10.1109/jiot.2019.2927497

CrossRef Full Text | Google Scholar

Cui, M., Han, D., Wang, J., Li, K.-C., and Chang, C.-C. (2020). Arfv: An Efficient Shared Data Auditing Scheme Supporting Revocation for Fog-Assisted Vehicular Ad-Hoc Networks. IEEE Trans. Veh. Technol. 69, 15815–15827. doi:10.1109/tvt.2020.3036631

CrossRef Full Text | Google Scholar

Fleury, G., Lacomme, P., and Prins, C. (2004). Evolutionary Algorithms for Stochastic Arc Routing Problems. Lect. Notes Comput. Science,Applications Evol. Comput., 501–512. doi:10.1007/978-3-540-24653-4_51

CrossRef Full Text | Google Scholar

Gao, C., Chen, S., Li, X., Huang, J., and Zhang, Z. (2017). A Physarum-Inspired Optimization Algorithm for Load-Shedding Problem. Appl. Soft Comput. 61, 239–255. doi:10.1016/j.asoc.2017.07.043

CrossRef Full Text | Google Scholar

Gao, C., Fan, Y., Jiang, S., Deng, Y., Liu, J., and Li, X. (2021). Dynamic Robustness Analysis of a Two-Layer Rail Transit Network Model. IEEE Trans. Intell. Transp. Syst., 1–16. doi:10.1109/TITS.2021.3058185

CrossRef Full Text | Google Scholar

Golden, B. L., and Wong, R. T. (1981). Capacitated Arc Routing Problems. Networks 11, 305–315. doi:10.1002/net.3230110308

CrossRef Full Text | Google Scholar

Han, D., Pan, N., and Li, K.-C. (2022). A Traceable and Revocable Ciphertext-Policy Attribute-Based Encryption Scheme Based on Privacy Protection. IEEE Trans. Dependable Secure Comput. 19, 316–327. doi:10.1109/tdsc.2020.2977646

CrossRef Full Text | Google Scholar

Han, D., Zhu, Y., Li, D., Liang, W., Souri, A., and Li, K.-C. (2022). A Blockchain-Based Auditable Access Control System for Private Data in Service-Centric Iot Environments. IEEE Trans. Ind. Inf. 18, 3530–3540. doi:10.1109/tii.2021.3114621

CrossRef Full Text | Google Scholar

Koza, J. R. (1992). Genetic Programming: On the Programming of Computers by Means of Natural Selection. Cambridge, MA, USA: MIT Press.

Google Scholar

Li, H., Han, D., and Tang, M. (2022). A Privacy-Preserving Storage Scheme for Logistics Data with Assistance of Blockchain. IEEE Internet Things J. 9, 4704–4720. doi:10.1109/jiot.2021.3107846

CrossRef Full Text | Google Scholar

Liu, J., Tang, K., and Yao, X. (2021). Robust Optimization in Uncertain Capacitated Arc Routing Problems: Progresses and Perspectives [Review Article]. IEEE Comput. Intell. Mag. 16, 63–82. doi:10.1109/mci.2020.3039069

CrossRef Full Text | Google Scholar

Liu, Y., Mei, Y., Zhang, M., and Zhang, Z. (2020). A Predictive-Reactive Approach with Genetic Programming and Cooperative Coevolution for the Uncertain Capacitated Arc Routing Problem. Evol. Comput. 28, 289–316. doi:10.1162/evco_a_00256

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Mei, Y., Zhang, M., and Zhang, Z. (2017). Automated Heuristic Design Using Genetic Programming Hyper-Heuristic for Uncertain Capacitated Arc Routing Problem. Proc. GECCO (ACM), 290–297. doi:10.1145/3071178.3071185

CrossRef Full Text | Google Scholar

Liu, Y., Shi, J., Liu, Z., Huang, J., and Zhou, T. (2019). Two-layer Routing for High-Voltage Powerline Inspection by Cooperated Ground Vehicle and Drone. Energies 12, 1385. doi:10.3390/en12071385

CrossRef Full Text | Google Scholar

Liu, Y., Wang, S., and Li, X. (2022). A New Cooperative Recourse Strategy for Emergency Material Allocation in Uncertain Environments. Front. Phys. 10, 835412. doi:10.3389/fphy.2022.835412

CrossRef Full Text | Google Scholar

Luo, X., Wu, H., Wang, Z., Wang, J., and Meng, D. (2021). A Novel Approach to Large-Scale Dynamically Weighted Directed Network Representation. IEEE Trans. Pattern Anal. Mach. Intell., 1. doi:10.1109/TPAMI.2021.3132503

CrossRef Full Text | Google Scholar

Ma, L., Cheng, S., and Shi, Y. (2021). Enhancing Learning Efficiency of Brain Storm Optimization via Orthogonal Learning Design. IEEE Trans. Syst. Man. Cybern. Syst. 51, 6723–6742. doi:10.1109/tsmc.2020.2963943

CrossRef Full Text | Google Scholar

Ma, L., Huang, M., Yang, S., Wang, R., and Wang, X. (2021). An Adaptive Localized Decision Variable Analysis Approach to Large-Scale Multiobjective and Many-Objective Optimization. IEEE Trans. Cybern., 1–13. doi:10.1109/TCYB.2020.3041212

CrossRef Full Text | Google Scholar

MacLachlan, J., Mei, Y., Branke, J., and Zhang, M. (2020). Genetic Programming Hyper-Heuristics with Vehicle Collaboration for Uncertain Capacitated Arc Routing Problems. Evol. Comput. 28, 563–593. doi:10.1162/evco_a_00267

PubMed Abstract | CrossRef Full Text | Google Scholar

MacLachlan, J., and Mei, Y. (2021). “Look-ahead Genetic Programming for Uncertain Capacitated Arc Routing Problem,” in 2021 IEEE Congress on Evolutionary Computation (CEC) (IEEE), 1872–1879. doi:10.1109/cec45853.2021.9504785

CrossRef Full Text | Google Scholar

Mei, Y., Tang, K., and Yao, X. (2010). “Capacitated Arc Routing Problem in Uncertain Environments,” in 2010 IEEE Congress on Evolutionary Computation (CEC) (IEEE), 1–8. doi:10.1109/cec.2010.5586031

CrossRef Full Text | Google Scholar

Mei, Y., and Zhang, M. (2018). Genetic Programming Hyper-Heuristics for Multi-Vehicle Uncertain Capacitated Arc Routing Problem. Proc. GECCO (ACM), 141–142.

Google Scholar

Nguyen, S., Mei, Y., Ma, H., Chen, A., and Zhang, M. (2016). “Evolutionary Scheduling and Combinatorial Optimisation: Applications, Challenges, and Future Directions,” in 2016 IEEE Congress on Evolutionary Computation (CEC) (IEEE), 3053–3060. doi:10.1109/cec.2016.7744175

CrossRef Full Text | Google Scholar

Nguyen, S., Zhang, M., Johnston, M., and Tan, K. C. (2013). A Computational Study of Representations in Genetic Programming to Evolve Dispatching Rules for the Job Shop Scheduling Problem. IEEE Trans. Evol. Comput. 17, 621–639. doi:10.1109/tevc.2012.2227326

CrossRef Full Text | Google Scholar

Ouelhadj, D., and Petrovic, S. (2009). A Survey of Dynamic Scheduling in Manufacturing Systems. J. Sched. 12, 417–431. doi:10.1007/s10951-008-0090-8

CrossRef Full Text | Google Scholar

Sörensen, K. (2006). Route Stability in Vehicle Routing Decisions: a Bi-objective Approach Using Metaheuristics. Cent. Eur. J. Oper. Res. 14, 193–207. doi:10.1007/s10100-006-0168-3

CrossRef Full Text | Google Scholar

Tian, Q., Han, D., Li, K.-C., Liu, X., Duan, L., and Castiglione, A. (2020). An Intrusion Detection Approach Based on Improved Deep Belief Network. Appl. Intell. 50, 3162–3178. doi:10.1007/s10489-020-01694-4

CrossRef Full Text | Google Scholar

Wang, J., Tang, K., Lozano, J. A., and Yao, X. (2016). Estimation of the Distribution Algorithm with a Stochastic Local Search for Uncertain Capacitated Arc Routing Problems. IEEE Trans. Evol. Comput. 20, 96–109. doi:10.1109/tevc.2015.2428616

CrossRef Full Text | Google Scholar

Wang, J., Tang, K., and Yao, X. (2013). “A Memetic Algorithm for Uncertain Capacitated Arc Routing Problems,” in 2013 IEEE Workshop on Memetic Computing, 72–79. doi:10.1109/mc.2013.6608210

CrossRef Full Text | Google Scholar

Wang, S., Mei, Y., and Zhang, M. (2020). “A Multi-Objective Genetic Programming Hyper-Heuristic Approach to Uncertain Capacitated Arc Routing Problems,” in 2020 IEEE Congress on Evolutionary Computation (CEC) (IEEE), 1–8. doi:10.1109/cec48606.2020.9185890

CrossRef Full Text | Google Scholar

Wang, S., Mei, Y., and Zhang, M. (2019). Novel Ensemble Genetic Programming Hyper-Heuristics for Uncertain Capacitated Arc Routing Problem. Proc. GECCO (ACM), 1093–1101. doi:10.1145/3321707.3321797

CrossRef Full Text | Google Scholar

Wang, S., Mei, Y., Zhang, M., and Yao, X. (2022). Genetic Programming with Niching for Uncertain Capacitated Arc Routing Problem. IEEE Trans. Evol. Comput. 26, 73–87. doi:10.1109/tevc.2021.3095261

CrossRef Full Text | Google Scholar

Wang, Z., Liu, Y., Luo, X., Wang, J., Gao, C., Peng, D., et al. (2021). Large-scale Affine Matrix Rank Minimization with a Novel Nonconvex Regularizer. IEEE Trans. Neural Netw. Learn. Syst., 1–15. doi:10.1109/TNNLS.2021.3059711

CrossRef Full Text | Google Scholar

Wang, Z., Wang, C., Li, X., Gao, C., Li, X., and Zhu, J. (2022). Evolutionary Markov Dynamics for Network Community Detection. IEEE Trans. Knowl. Data Eng. 34, 1206–1220. doi:10.1109/tkde.2020.2997043

CrossRef Full Text | Google Scholar

Wang, Z., Wang, W., Wang, J., and Chen, S. (2019). Fast and Efficient Algorithm for Matrix Completion via Closed-form 2/3-thresholding Operator. Neurocomputing 330, 212–222. doi:10.1016/j.neucom.2018.10.065

CrossRef Full Text | Google Scholar

Weise, T., Devert, A., and Tang, K. (2012). A Developmental Solution to (Dynamic) Capacitated Arc Routing Problems Using Genetic Programming. Proc. GECCO (ACM), 831–838. doi:10.1145/2330163.2330278

CrossRef Full Text | Google Scholar

Zhang, Y., Mei, Y., Zhang, B., and Jiang, K. (2021). Divide-and-conquer Large Scale Capacitated Arc Routing Problems with Route Cutting off Decomposition. Inf. Sci. 553, 208–224. doi:10.1016/j.ins.2020.11.011

CrossRef Full Text | Google Scholar

Zhu, P., Cheng, L., Gao, C., Wang, Z., and Li, X. (2022). Locating Multi-Sources in Social Networks with a Low Infection Rate. IEEE Trans. Netw. Sci. Eng. 9, 1853–1865. doi:10.1109/TNSE.2022.3153968

CrossRef Full Text | Google Scholar

Zhu, P., Dai, X., Li, X., Gao, C., Jusup, M., and Wang, Z. (2019). Community Detection in Temporal Networks via a Spreading Process. Epl 126, 48001. doi:10.1209/0295-5075/126/48001

CrossRef Full Text | Google Scholar

Zhu, P., Lv, R., Guo, Y., and Si, S. (2018). Optimal Design of Redundant Structures by Incorporating Various Costs. IEEE Trans. Rel. 67, 1084–1095. doi:10.1109/tr.2018.2843181

CrossRef Full Text | Google Scholar