Market-based hosting capacity maximization of renewable generation in power grids with energy storage integration

In an attempt to achieve net zero, the operation and planning of the energy system face techno-economic challenges brought by integrating large-scale distributed energy resources (DERs) with low carbon footprints. Previous work has analyzed the technical challenges including hosting capacity (HC) for DERs. In light of the deregulation of the power industry and the transition to power system with renewables at its center, this article takes the lead to maximizing renewable integration in power grids from a market viewpoint. It solves a significant problem brought forth by the fall in electricity prices, resulting from increasing renewable penetration that jeopardizes investment cost recovery and prevents sustainable grid integration of renewables. To this end, a novel bi-level optimization model is formulated, where the upper-level problem aims to maximize the HC of renewables ensuring the recovery of investment, and the lower-level problem describes the market clearing process considering network constraints. The optimal solution of devised bi-level problem can be found after reformulating it to a single-level mixed-integer linear problem (MILP) using the strong duality theorem and a special ordered set-type 1 (SOS1) founded linearization approach. Case studies confirm the significance of the devised model and quantitatively analyze the impact of different network capacities, renewable subsidies, and energy storage, respectively, on the market-based HC obeying its profitability constraint.

1 Introduction

It is an international scientific consensus that, in an attempt to prevent greenhouse effect and climate deterioration, net human-caused emissions of carbon dioxide should be necessarily reduced by approximately 45 percent from 2010 levels by 2030, achieving net-zero before 2050 (Bouckaert, 2021). The energy industry is the source of around three-quarters of greenhouse gas emissions today, so integrating renewable energy sources(RES) including wind and solar energy in the present power grid is an inevitable trend. In order to achieve net-zero greenhouse gas emissions target by the year 2060 (Qiu et al., 2021), China calls for realizing the transition to a new type of power system with renewables at its center, and it will account for nearly 80 percentages of its electric power generation by 2060. It also facilitates the utilization of energy storage (ES) technologies to cope with the intermittency of RES because it can provide flexibility to achieve system balance and restrict demand peaks, promoting the cost-effectiveness of power system with low carbon levels (Tan et al., 2021). In this context, the total installed capacity by the Chinese for power storing is expected to surpass 30 GW in 2025, about 10 times its present level. To promote the penetration of RES, an increasing level of distributed energy resources (DERs) is integrated in the distribution network, and the scale of new installed capacity of distributed photovoltaics in China far exceeds that of centralized ones (Fang et al., 2020).

Under these circumstances, significant technical challenges to the operation and planning of power systems emerge, owing to considerable DERs and ES penetration in distribution network (Husin et al., 2021). One aspect of relevant research lies in investigation of the acceptable level of DERs penetration under given circumstances, which is defined as hosting capacity (HC) for DERs (Al-Saadi et al., 2017). Besides, the technical impacts of DERs contribution on the distribution grid have been comprehensively studied including bus over-voltage (Divshali and Söder, 2019), power harmonic distortion (Santos et al., 2015), thermal overload, increased short-circuit current, and protection devices (Seuss et al., 2015) while maximizing DERs penetration (Mulenga et al., 2020) (Cicilio et al., 2021). However, a fundamental difference between these previous studies and this article is that the former did not take the price signal into consideration from a market perspective. Another drawback of aforementioned previous works on generation investment planning is that they are implemented for every time period separately, so ES cannot be considered for the reason that it is intrinsically related to time coupling influence brought by its charging and discharging cycles.

For the reason that ES is able to mitigate variability and uncertainty brought by RES, another aspect of research concentrates on evaluating the influence and capacity of ES in generation investment planning problems. Traditional works usually choose the minimal system cost as objective function and plan the capacity of ES and RES generation separately (Lakshminarayana et al., 2016) or simultaneously (Shi et al., 2022). In addition, many research have analyzed that how ES (Awad et al., 2014) (Virasjoki et al., 2016), electric vehicle (EV) (Philipp and Thomas, 2018), or other flexible resources (Ye et al., 2018) directly influence spot electricity prices. It can be found that they are able to smooth spot prices, leading to a notable electricity price increase during periods with off-peak demand and abundant RES, and a price decrease at times with peak demand and scarce RES, which facilitate the penetration of RES (Zhao et al., 2022). However, previous published work examined the impact of ES in generation investment planning using centralized models with the goal of minimizing costs retained from the period of regulated environment. To the best of our knowledge, no research had examined how ES influences the planning decisions of RES through price signals changed with different operating parameters of ES. Furthermore, to facilitate building a power system dominated by renewables in China, the main objective of this article is to maximize renewable generation capacity and quantitatively analyze the upper boundary from a market perspective.

Recognizing the shortcomings of the regulated price mechanism, China and many other countries have launched an unprecedented deregulation reform on its electricity market. In deregulation environment, electricity prices will be determined totally by supply and demand curve to reflect the real-time conditions (Liu et al., 2019). However, variable RES with negligible marginal prices (e.g., solar and wind power), change the supply curve because of the merit order influence and cause a reduction on electricity prices in many countries (e.g., Germany and Italy) (Brancucci Martinez-Anido et al., 2016), even to the extent that negative electricity prices occurred. Other types of electricity generation (e.g., nuclear power) with low marginal costs, impose less unpredictable and uncertain effect on the merit order than that of wind and solar power. To be specific, Kolb et al. (2020) analyzed previous German demand and supply curves in day-ahead market and reconstructed electricity prices with and without RES feed-in. Results found that RES forces electricity prices down by 2.89 ct/kWh in 2014 to 8.89 ct/kWh in 2017. So the penetration of RES largely affects the spot electricity prices, hence bringing significant changes in generation investment planning in power industry.

Nowadays, RES and other generation investment planning are driven by profit-motivated generation companies rather than by a central regulated utility in a more and more competitive electricity market (Bao et al., 2021). As a result of the large-scale penetration of RES, several fundamental problems associated with electricity market arise: Considering that the operation costs of RES are negligible and electricity prices are anticipated to fall and fluctuate, can potential RES investors recover investment fees and guarantee non-negative profitability? In addition, how to quantitatively analyze the upper boundary of integrated RES optimal capacity while adhering to operation limitations in power system and how will network constraints, subsides, and ES in power systems affect it?

This article employs an innovative multi-period bi-level optimization problem, modeling the decision-making process of RES generation investment to answer the aforementioned questions. The upper-level problem aims to find maximal renewable generation capacity defined as HC, maintaining its profit positive or equal to zero, while the lower-level problem represents endogenous market clearing process, minimizing the negative social welfare. Furthermore, to investigate and quantify about the impact of network and ES, a direct current optimal power flow (DCOPF) and time-coupling operational characteristics of ES are considered, in combination with locational marginal prices (LMP) to reflect the electricity prices and the influence of congestion. The solution to this problem involves reformulating it to a Mathematical Program with Equilibrium Constraints (MPEC) and applying a special ordered sets-type 1 (SOS1) based approach, as well as Karush–Kuhn–Tucker (KKT) optimality conditions to linearize the latter into a mixed-integer linear problem (MILP). Case studies are founded on a 6-node test system, and they illustrate first how network capacity and RES subsidy influence the siting and sizing decisions of RES. Moreover, an analysis is conducted on the HC of RES for different representative days in terms of different energy capacities of ES.

The organizations of the remaining part of this article are listed as following. Section 2 outlines devised bi-level optimization problem, expressing the optimal planning of RES investment capacity (subsection 2.1), corresponding MPEC (subsection 2.2) and MILP (subsection 2.3). Case studies and quantitative analysis are presented in Section 3. Finally, Section 4 draws the conclusions of this article.

2 Devised modeling framework

2.1 Bi-level optimization formulation

To conduct a quantitative analysis of the upper bounds of integrated RES optimal capacity obeying the allowable system operational performance boundaries, a complex multi-period bi-level optimization model, comprising of two coupled optimization problems, is used in this chapter. Specifically, the upper-level (UL) problem represents the decision-making problem of maximal generation capacity of RES and siting and sizing results, ensuring that the profit from selling wind or solar energy in a day-ahead spot electricity market can recover its investment, so RES investments are profitable. The lower-level (LL) problem represents the market clearing problem solved by the market operator that determines the dispatch of each participant that minimizes the negative social welfare.

Figure 1 demonstrates the framework for this bi-level optimization problem, whose formulation is given in (1)–(10). A yearly operation horizon is divided into discrete and representative hours in this suggested optimization approach. In addition, investment and profit are measured annually. These two optimization problems are interconnected that the UL’s solution to determine renewable energy capacity at different nodes affects the market clearing prices and generation dispatch in LL problem, and the latter also serves as feedback to revenues from selling RES in the electricity market in the UL problem.

FIGURE 1

FIGURE 1. Framework of the devised multi-period bi-level optimization model.

2.1.1 Upper-level problem

The devised multi-period bi-level optimization problem aims to find the HC of RES and ensure that RES investors can recover their investment. More importantly, the impacts of increased generation capacity on electricity prices are inconsistent at different nodes, places with higher electricity prices are more attractive to integrate RES than those with lower prices. In accordance with the purpose of the suggested model, it is crucial to determine favorable regions suitable for large-scale integration of renewables and optimize the HC of renewables in other areas. So the objective function of UL problem is listed as constraint (1) as follows.

$\max \sum _n{G}_n,(1)$

where n ∈ M denote the index and set of nodes and G_n represents the HC of RES generation at node n.

The UL problem should adhere to non-negative profitability constraint listed:

$\sum _{n,d,t}{w}_d\left({\lambda }_{n,d,t}+\gamma \right)r_{n,d,t}-\sum _{n}P{G}_n\ge 0,(2)$

where t ∈ T represent the index and set of steps, w_d denotes weighting factor of step t, λ_n,d,t represents the LMP at node n, day d, and step t, γ is the subsidy for selling renewable energy, r_n,d,t represents the dispatch of RES generation at node n, day d, and step t, P is the annual capital costs of RES.

2.1.2 Lower-level problem

Under the assumption that electricity market is an energy-only and pool-based market in the following devised model, the LL problem describes endogenously the market clearing process at every representative day and guarantees minimal negative social welfare (Constraint (3)), employing DCOPF model and deriving the LMP for each node n, day d, and step t so that the effect of network and ES can be analyzed quantitatively.

$\underset{D^{\text{LL}}}{\min }\sum _{i,d,t}\left(a_i{g}_{i,d,t}+b_i{g}_{i,d,t}^2\right)-\sum _{n,d,t}{b}_{n,d,t}{d}_{n,d,t},(3)$

where D^LL represents the LL problem’s decision variable set, d ∈ D are index and set of representative days, i ∈ I represent the index and set of thermal generation units, a_i and b_i denote the linear and quadratic coefficients of the thermal generation unit i’ cost functions, g_i,d,t is the actual production of thermal generation unit i produced at step t, b_n,d,t is the marginal benefit of demand at node n, day d, and step t, d_n,d,t is the power input at node n, day d, and step t.

$D^{\text{LL}}=\left\{g_{i\notin I^{MR},d,t},r_{n,d,t},{\theta }_{n,d,t},s_{j,d,t}^{\mathit{dis}},s_{j,d,t}^{ch},E_{j,d,t}\right\},(4)$

where θ_n,d,t is the voltage angle at node n, day d, and hour t.

The five aspect constraints (5)–(16) that the LL problem need to obey are listed as follows:

1) Demand-supply balance constraints: Constraint 5) describes that demand and supply need to be always balanced, the dual variables of which make up the LMPs.

$\begin{array}{ll}\hfill & d_{n,d,t}-\sum _{i\notin I^{MR}}{g}_{i,d,t}-\sum _{i\in I^{MR}}\overline{g_i}-r_{n,d,t}+\sum _{m\in M_n}\frac{{\theta }_{n,d,t}-{\theta }_{m,d,t}}{x_{n,m}}\hfill \\ \hfill & -\sum _{j\in J_n}\left(s_{j,d,t}^{\mathit{dis}}+s_{j,d,t}^{ch}\right)=0:{\lambda }_{n,d,t},\forall n,\forall d,\forall t,\hfill \end{array}(5)$

where I^MR ∈ I is the subset of must-run generation units, x_n,m is the reactance of line (n,m), m ∈ M_n are the index and set of nodes connected to node n through a line, j ∈ J_n are the index and set of ES units connected to node n, $s_{j,d,t}^{ch}$ and $s_{j,d,t}^{\mathit{dis}}$ are charging and discharging power of ES unit j at day d and step t.

2) Generation power limits: The operating constraints include thermal generators 6) and renewable generators 7).

${\underline{g}}_i\le g_{i,d,t}\le {\bar{g}}_i:{\zeta }_{i,d,t}^{-},{\zeta }_{i,d,t}^{+},\forall i\notin I^{MR},\forall d,\forall t,(6)$

$0\le r_{n,d,t}\le {\delta }_{n,d,t}{G}_n:{\varphi }_{n,d,t}^{-},{\varphi }_{n,d,t}^{+},\forall n,\forall d,\forall t,(7)$

where ${\bar{g}}_i$ and ${\underline{g}}_i$ are maximum and minimum output boundaries of thermal generation units, respectively, δ_n,d,t is the output of renewables at node n, day d, and step t after the normalizing process. However, following normalization, its output statistics are generally various across the network to account for regional and temporal diversity about renewables availability. Additionally, renewable energy is assumed to have negligible operating costs, and its output can be curtailed if necessary.

3) Demand power limits:

$0\le d_{n,d,t}\le {\bar{d}}_{n,d,t},:{\chi }_{n,d,t}^{-},{\chi }_{n,d,t}^{+}\forall n,\forall d,\forall t,(8)$

where ${\bar{d}}_{n,d,t}$ denotes maximum demand at node n, day d, and step t.

4) DCOPF-based network constraints: Constraints (9)–(10) represent power flow and nodal voltage angle limits. Node 1 is designated as the reference node by constraint (11).

$\begin{array}{c}-{\bar{P}}_{n,m}\le \frac{{\theta }_{n,d,t}-{\theta }_{m,d,t}}{x_{n,m}}\le {\bar{P}}_{n,m}:{\epsilon }_{n,m,d,t}^{-},{\epsilon }_{n,m,d,t}^{+},\\ \forall n,\forall m\in M_n,\forall d,\forall t\end{array},(9)$

$-\pi \le {\theta }_{n,d,t}\le \pi :{\kappa }_{n,d,t}^{-},{\kappa }_{n,d,t}^{+},\forall n,\forall d,\forall t,(10)$

${\theta }_{1,d,t}=0:\hspace{0.17em}{\phi }_t,\forall d,\forall t,(11)$

where ${\bar{P}}_{n,m}$ denotes the maximum power flow limit of line (n, m).

5) Inter-temporal constraints representing ES operation: Inter-temporal constraints 12) and 13) are applied to imply energy balance of ES and the assumption of energy neutrality in day-ahead market, respectively. Finally, constraints (14)–16) are applied to limit energy and power within minimum and maximum bounds.

$E_{j,d,t}=E_{j,d,t-1}+\tau {\eta }^{ch}{s}_{j,d,t}^{ch}-\frac{\tau s_{j,d,t}^{\mathit{dis}}}{{\eta }^{\mathit{dis}}}\hspace{0.17em}:\hspace{0.17em}{\nu }_{j,d,t},\forall j,\forall d,\forall t,(12)$

$E_0=E_{j,d,t}\hspace{0.17em}:\hspace{0.17em}{\beta }_{j,d},\forall j,\forall d,t=K^T,(13)$

$\underline{E}\le E_{j,d,t}\le \bar{E}\hspace{0.17em}:\hspace{0.17em}{\sigma }_{j,d,t}^{-},{\sigma }_{j,d,t}^{+},\forall j,\forall d,\forall t,(14)$

$0\le s_{j,d,t}^{ch}\le \bar{s}\hspace{0.17em}:\hspace{0.17em}{\rho }_{j,d,t}^{-},{\rho }_{j,d,t}^{+},\forall j,\forall d,\forall t,(15)$

$0\le s_{j,d,t}^{\mathit{dis}}\le \bar{s}\hspace{0.17em}:\hspace{0.17em}{\iota }_{j,d,t}^{-},{\iota }_{j,d,t}^{+},\forall j,\forall d,\forall t,(16)$

where E_j,d,t is the energy level of ES unit j at day d at the end of step t, τ and K^T are the temporal resolution and length of market horizon, η^ch and η^dis are the charging and discharging efficiency of ES, E₀ denotes initial energy level of ES, $\underline{E}$ and $\bar{E}$ are minimum and maximum energy limit of ES, $\bar{s}$ represents power capacity of ES.

2.2 MPEC formulation

Due to the continuous and convex characteristics of the LL problem, the multi-period bi-level optimization problem stated in Section 2.1 is converted into a single-level MPEC in the way of substituting the LL problem with corresponding KKT optimal conditions:

$\underset{D}{\max }\sum _n{G}_n(17)$

Among constraint (17), D is the decision variable set of the MPEC formulated in (18):

$\begin{array}{cc}\hfill D& =\left\{G_n,D^{\text{LL}},{\lambda }_{n,d,t},{\zeta }_{i,t}^{-},{\zeta }_{i,t}^{+},{\varphi }_{n,d,t}^{-},{\varphi }_{n,d,t}^{+},{\chi }_{n,d,t}^{-},{\chi }_{n,d,t}^{+},\right.\hfill \\ \hfill & {\epsilon }_{n,m,d,t}^{-},{\epsilon }_{n,m,d,t}^{+},{\kappa }_{n,d,t}^{-},{\kappa }_{n,d,t}^{+},{\phi }_t,{\nu }_{j,d,t},{\beta }_{j,d},{\sigma }_{j,d,t}^{-},\hfill \\ \hfill & \left.{\sigma }_{j,d,t}^{+}{\rho }_{j,d,t}^{-},{\rho }_{j,d,t}^{+},{\iota }_{j,d,t}^{-},{\iota }_{j,d,t}^{+}\right\}\hfill \end{array}.(18)$

The first-order KKT optimal conditions related to the LL problem (3)–(16) are derived as follows.

(2), (5), (11), (12), (13)

$a_i+2b_i{g}_{i,d,t}-{\lambda }_{\left(n:i\in I_n\right),t}-{\zeta }_{i,d,t}^{-}+{\zeta }_{i,d,t}^{+}=0,\forall i\notin I^{MR},\forall d,\forall t,(19)$

$-{\lambda }_{n,d,t}-{\varphi }_{n,d,t}^{-}+{\varphi }_{n,d,t}^{+}=0,\forall n,\forall d,\forall t,(20)$

${\lambda }_{n,d,t}-b_{n,d,t}-{\chi }_{n,d,t}^{-}+{\chi }_{n,d,t}^{+}=0,\forall n,\forall d,\forall t,(21)$

$\begin{array}{ll}\hfill & \sum _{m\in M_n}\frac{{\lambda }_{n,d,t}-{\lambda }_{m,d,t}}{x_{n,m}}+\sum _{m\in M_n}\frac{{\epsilon }_{n,m,d,t}^{+}-{\epsilon }_{m,n,d,t}^{+}}{x_{n,m}}\hfill \\ \hfill & -\sum _{m\in M_n}\frac{{\epsilon }_{n,m,d,t}^{-}-{\epsilon }_{m,n,d,t}^{-}}{x_{n,m}}+{\kappa }_{n,d,t}^{+}-{\kappa }_{n,d,t}^{-}+{\left({\phi }_t\right)}_{n=1}=0,\hfill \\ \hfill & \forall n,\forall d,\forall t,\hfill \end{array}(22)$

${\lambda }_{n,d,t}-\tau {\eta }^{ch}{s}_{j,d,t}^{ch}-{\rho }_{j,d,t}^{-}+{\rho }_{j,d,t}^{+}=0,\forall j,\forall d,\forall t,(23)$

$-{\lambda }_{n,d,t}+\frac{\tau s_{j,d,t}^{\mathit{dis}}}{{\eta }^{\mathit{dis}}}-{\iota }_{j,d,t}^{-}+{\iota }_{j,d,t}^{+}=0,\forall j,\forall d,\forall t,(24)$

$-{\sigma }_{j,d,t}^{-}-{\sigma }_{j,d,t}^{+}+{\nu }_{j,d,t}-{\nu }_{j,d,t+1}=0,\forall j,\forall d,\forall t<K^T,(25)$

$-{\sigma }_{j,d,t}^{-}-{\sigma }_{j,d,t}^{+}+{\nu }_{j,d,t}-{\beta }_{j,d}=0,\forall j,\forall d,\forall t=K^T,(26)$

$0\le {\zeta }_{i,d,t}^{-}\perp g_{i,d,t}\ge 0,\forall i,\forall d,\forall t,(27)$

$0\le {\zeta }_{i,d,t}^{+}\perp \left({\bar{g}}_i-g_{i,d,t}\right)\ge 0,\forall i,\forall d,\forall t,(28)$

$0\le {\varphi }_{n,d,t}^{-}\perp r_{n,d,t}\ge 0,\forall n,\forall d,\forall t,(29)$

$0\le {\varphi }_{n,d,t}^{+}\perp \left({\beta }_{n,d,t}{G}_n-r_{n,d,t}\right)\ge 0,\forall n,\forall d,\forall t,(30)$

$\begin{array}{c}0\le {\epsilon }_{n,m,d,t}^{-}\perp \left({\bar{P}}_{n,m}+\frac{{\theta }_{n,d,t}-{\theta }_{m,d,t}}{x_{n,m}}\right)\ge 0,\\ \forall n,\forall m\in M_n,\forall d,\forall t,\end{array}(31)$

$\begin{array}{c}0\le {\epsilon }_{n,m,d,t}^{+}\perp \left({\bar{P}}_{n,m}+\frac{{\theta }_{n,d,t}-{\theta }_{m,d,t}}{x_{n,m}}\right)\ge 0,\\ \forall n,\forall m\in M_n,\forall d,\forall t,\end{array}(32)$

$0\le {\kappa }_{n,t}^{-}\perp \left(\pi +{\theta }_{n,t}\right)\ge 0,\forall n,\forall t,(33)$

$0\le {\kappa }_{n,t}^{+}\perp \left(\pi -{\theta }_{n,t}\right)\ge 0,\forall n,\forall t,(34)$

$0\le {\sigma }_{j,d,t}^{-}\perp \left(E_{j,d,t}-\underline{E}\right)\ge 0,\forall j,\forall d,\forall t,(35)$

$0\le {\sigma }_{j,d,t}^{+}\perp \left(\bar{E}-E_{j,d,t}\right)\ge 0,\forall j,\forall d,\forall t,(36)$

$0\le {\rho }_{j,d,t}^{-}\perp \left(\bar{s}-s_{j,d,t}^{ch}\right)\ge 0,\forall j,\forall d,\forall t,(37)$

$0\le {\rho }_{j,d,t}^{+}\perp s_{j,d,t}^{ch}\ge 0,\forall j,\forall d,\forall t,(38)$

$0\le {\iota }_{j,d,t}^{-}\perp \left(\bar{s}-s_{j,d,t}^{\mathit{dis}}\right)\ge 0,\forall j,\forall d,\forall t,(39)$

$0\le {\iota }_{j,d,t}^{+}\perp s_{j,d,t}^{\mathit{dis}}\ge 0,\forall j,\forall d,\forall t,(40)$

The MPEC formulation retains not only the inequality constraint (2) in the UL problem but also primal equality constraints (5), (11), (12), and (13) in the LL problem. Moreover, equality constraints (19)–(26) are the stationary conditions derived from differentiating the Lagrangian function about the primal variables in set identified in (4). Related to the inequality constraints (6)–(10) and (14)–(16) in the LL problem, complementary slackness conditions are formulated in (27)–(40). The obtained KKT conditions (19)–(40) are first-order necessary optimality conditions.

2.3 MILP formulation

There are two types of non-linearities presented in the aforementioned MPEC model. The first type involves a bi-linear factor ∑_n,d,tλ_n,d,tr_n,d,t in the MPEC formulation. The product of the market clearing prices and renewable generation schedule variables is used to imply revenues of RES in electricity market. By adopting the linearization approach suggested in Ruiz and Conejo, (2009), which makes full use of all obtained KKT conditions (19)–(40), the bi-linear factor ∑_n,d,tλ_n,d,tr_n,d,t can be reformulated as the following linear expression (41):

$\begin{array}{ll}\hfill & \sum _{n,d,t}{\lambda }_{n,d,t}{r}_{n,d,t}\hfill \\ \hfill & =\sum _{d,t}{b}_{n,d,t}\hspace{0.17em}\ast \hspace{0.17em}{d}_{n,d,t}-\sum _{d,t}{\bar{d}}_{n,d,t}{\chi }_{n,d,t}^{+}\hfill \\ \hfill & -\sum _{i\notin I^{MR},d,t}\left(\left(a_i+2b_i{g}_{i,t}\right)g_{i,t}+{\zeta }_{i,t}^{+}{\bar{g}}_i\right)-\sum _{i\in I^{MR},d,t}{\bar{g}}_i{\lambda }_{n,d,t}\hfill \\ \hfill & -\sum _{n,\left(m\in M_n\right),t}\frac{\left({\epsilon }_{n,m,t}^{+}+{\epsilon }_{n,m,t}^{-}\right)}{x_{n,m}}{\bar{P}}_{n,m}-\sum _{n,t}\left({\kappa }_{n,t}^{+}+{\kappa }_{n,t}^{-}\right)\pi \hfill \\ \hfill & +\sum _{j\in J^n,n,t}\left({\sigma }_{j,d,t}^{+}\underline{E}-{\sigma }_{j,d,t}^{-}\bar{E}\right)+\sum _{j\in J^n,d}\left({\beta }_{j,d}-{\nu }_{j,d,1}\right)E_0.\hfill \end{array}(41)$

The next kind includes the bi-linear terms in the KKT complementary slackness conditions (27)–(40). One useful method to cope with this kind of non-linearity terms is the Big-M method using disjunctive constraints (Ye et al., 2016). However, choosing a sufficiently large number for a given parameter, for example, M, is extremely difficult. If M is too small, it may be unable to discover an accurate solution for imposing additional upper bounds on decision variables, while large M may result in ill-conditioned matrices where branch-and-cut solvers may fail to function (Ye et al., 2018). In addition, the disjunctive constraint method exhibits limited computational capabilities for large-scale problems. In this context, we use an alternative effective method based on special ordered set type 1 variable (SOS1) (Akbari-Dibavar et al., 2020) to perform the required linearization on the complementarity conditions. The linearized equations use SOS1 variables $s{o}_{i,d,t}^{+}$, $s{o}_{i,d,t}^{-}$ for positive and negative parts, respectively, and a consistent variable S_i,d,t. For example, constraint 27) can be replaced by its mixed-integer equivalence (42)–44) as follows. To be brief, the following description of the linearized constraints omits not only non-negativity limitations on primal and dual variables, but also the primal limitations.

$S_{i,d,t}-\left(s{o}_{i,d,t}^{+}+s{o}_{i,d,t}^{-}\right)=0\forall i,\forall d,\forall t,(42)$

$S_{i,d,t}=\frac{{\zeta }_{i,d,t}^{-}+g_{i,d,t}}{2}\forall i,\forall d,\forall t,(43)$

$s{o}_{i,d,t}^{+}-s{o}_{i,d,t}^{-}=\frac{{\zeta }_{i,d,t}^{-}-g_{i,d,t}}{2}\forall i,\forall d,\forall t.(44)$

3 Case studies

3.1 Analysis on the value of network capacity

3.1.1 Test system and implementation

In this section, a 6-node test system is used to confirm significance of the devised model and quantitatively analyze on the effects of RES integration with varying capacities of connection line (2.4) and (3.5). The results of case studies can answer a crucial question: will network reinforcement enable larger renewable energy volumes to be integrated? In addition, case studies will reveal the maximum capacity for RES integration, and the optimal siting and sizing decisions for the planning of RES capacity. The analyzed 6-node network is shown in Figure 2, along with related parameters in Table 1. The northern area is equipped with low electricity demand and abundant solar resources on average, while electricity demand is higher relatively in the southern area where solar resources are scarce. It is also worth mentioning that nodes in the north are characterized by lower variable cost of thermal generation with respect to nodes in the south, indicating a naturally occurring direction of power transfer from north to south. The key lines connecting the north and south regions are line (2, 4) and line (3, 5). The renewable generation capacity at each node is no more than 1800 kW for technical reasons.

FIGURE 2

FIGURE 2. Examined 6-node system.

TABLE 1

TABLE 1. Parameters of the 6-node system.

The devised optimization model was implemented in Python 3.9, and the globally optimum solution to the aforementioned MILP issue was successfully obtained using the Gurobi optimizer on a desktop computer equipped with an Intel(R) Core(TM) i5-10400 @2.90 GHz processor and 24 GB of RAM. It takes no more than 1 s to solve this MILP on average.

3.1.2 Validation of the devised model

This section begins with a case where the objective function of UL problem and non-negative profitability constraint are removed, by solving the conventional centralized market clearing process with different network capacities. Its aim lies in validating significance of considering the profitability of investing RES. For illustration, not only operating but also investment expenses are estimated hourly and we investigate 50 cases for various values of the total network capacity of line (2.4) and (3.5) ranging from 0 to 3,000 kW with a step of 60 kW, in which we keep all other lines uncongested and unchanged, as shown in Figure 3. For each of the cases, we seek to calculate the total optimal solar generation capacity and profit from day-ahead electricity market. It is notable that in many cases the solar generation profit illustrated in black point is negative in Figure 3. The reason behind is that large integration of solar energy causes a decline in the spot prices because of the merit order influence, so revenues from electricity market decrease and are unable to recover the considerable solar investment costs. The negative profitability of RES may be a disincentive to sustainable development of RES, so it is significant to take it into consideration and identify the HC of RES, which can be a reference for policymakers and RES investors.

FIGURE 3

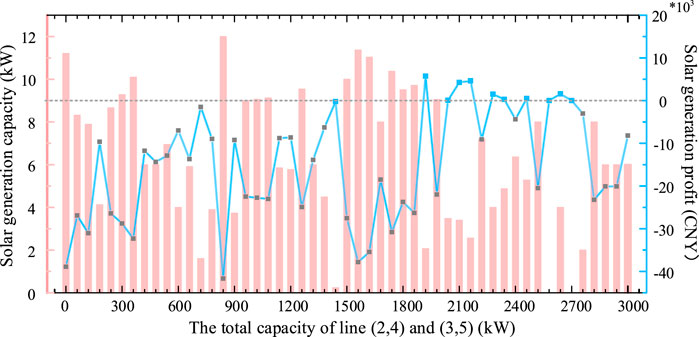
FIGURE 3. Total capacity and profit of solar generation for different values of the total capacity of lines (2.4) and (3.5).

3.1.3 Dependence of solar generation HC and network capacity

Furthermore, 50 unique examples are examined with the capacity of lines (2.4) and (3.5) varying from 0 to 3,000 kW with a 60 kW incremental step. Figure 4 shows the quantity and composition of the whole solar generation HC of the given network for different values of the total network capacity of line (2.4) and (3.5), while Figure 5 demonstrates the thermal and solar generation dispatch in two opposite areas, respectively, with the increasing level of certain line capacity.

Stage 1: when the total capacity of lines (2.4) and (3.5) varies from 0 to 600 kW.

FIGURE 4

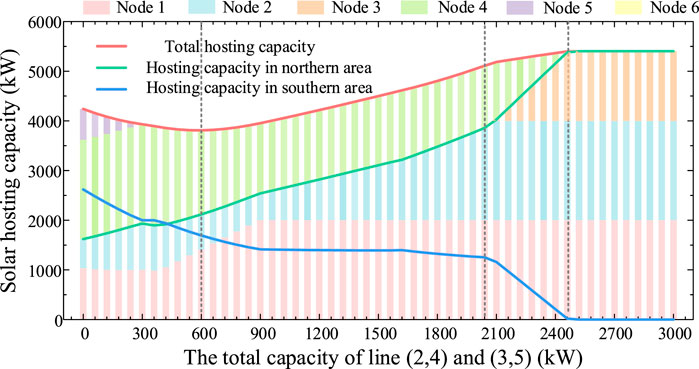
FIGURE 4. Total solar HC and its composition for different values of the total capacity of lines (2.4) and (3.5).

FIGURE 5

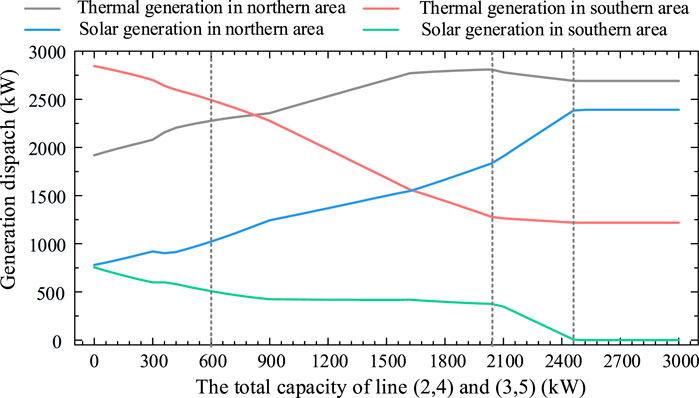
FIGURE 5. Total dispatch of thermal and solar generators for different values of the total capacity of lines (2.4) and (3.5).

The result that the total amount of HC presents a declining trend is seemingly counter-intuitive, which is usually expected to increase as the network expands in common sense. In fact, transmission expansion obviously impedes solar investment potential in the southern area, as the northern area is equipped with lower-cost thermal generation and more plentiful solar sources, making energy generation more advantageous than it is in the southern area. Furthermore, it can be noticed that the low levels of solar energy generation in the southern region are not being replaced by further investments in solar energy generation in the southern area totally, but rather by available low-cost thermal generation in the northern area that can be exported as a result of network expansions. This obviously decreases the overall market-based HC of solar energy, as exploitation of existing generation capacity is preferable to additional solar generation investments when network capacity is limited relatively. Figure 6 illustrates the average LMPs in the southern and northern areas, respectively, as the total capacity of line (2.4) and (3.5) increases. The quite difference in marginal cost of thermal plants between two areas and congestion in connecting line which creates an obvious price difference between the north and south.

Stage 2: when the total capacity of lines (2.4) and (3.5) varies from 600 to 2040 kW.

FIGURE 6

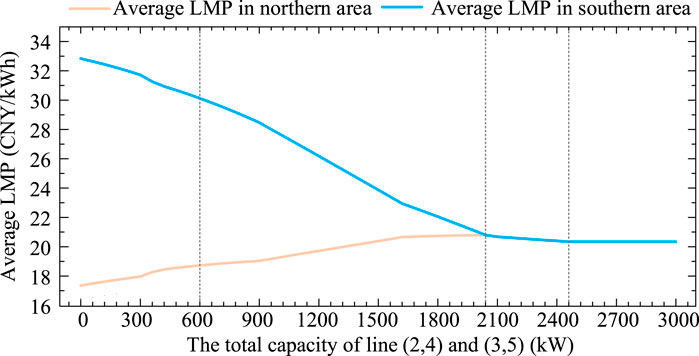
FIGURE 6. LMPs in the opposite area for different values of the total capacity of lines (2.4) and (3.5).

However, at the next stage, both solar and thermal power in the north becomes attractive than those in the south, contributing to a considerable increase in total solar HC and implying business opportunity in investment solar generation in the northern area. The reason accounting for this phenomenon is a combination of relatively more available solar resources and cheaper thermal operational cost in the northern area, while network capacity expansion enables more power to be transferable from north to south. So the gap between average LMPs in the northern or southern area gradually narrows as the congestion in two area relieves. Finally, not only the solar power investment and its output but also the production of the thermal generation in the southern area keeps considerably falling (Figures 4, 5). It is proved that expanding the network in this range releases substantial solar generation potential in the northern region, particularly at nodes 1 and 2, until they reach their maximum installed capacity.

Stage 3: When total capacity of lines (2.4) and (3.5) varies from 2040 to 2,460 kW.

At this stage, there has been a significant increase and decrease, respectively, in solar HC in northern and southern area, owing to the increased requirement to use nearly free solar output at node 1 and 2 to meet demand using the lowest cost. At this context, the network does not impose limitation on the solar generation export, so solar generation in the south loses competitiveness completely. As shown in Figure 6, the pricing gap between north and south are no longer existent as the congestion disappears.

Stage 4: When total capacity of lines (2.4) and (3.5) varies from 2,460 to 3,000 kW.

Finally, once the network capacity exceeds 2460kW, the aforementioned exploitation of solar power at node A reduces the uniform LMP, impeding the business case for solar generation investment at all nodes. As a result, investors abandon solar generation investment totally in the southern region, while their aggressive investment in the northern region eventually reaches a saturation value, due to the unappealing LMP caused by further penetration of solar generation.

According to the analysis mentioned earlier, increased network capacity does not always facilitate to invest larger total volumes of renewables in power grids. Increased network capacity, on the other hand, may impose limitations on the commercial potential for new RES generating development, particularly in locations near load centers and with higher power rates.

3.1.4 Combined impacts of distributed photovoltaic subsidies and network capacity on solar HC

In this section, we take potential subsidies into consideration and investigate that whether it can promote the level of RES penetration. As shown in Figure 7, we change the level of distributed photovoltaic subsidies γ upon the LMP for each kWh of distributed solar energy produced. An index is defined to quantitatively express the impact of subsidies on HC as Y-axis, expressing the increased percentage of solar generation HC resulting from various levels of subsidies.

FIGURE 7

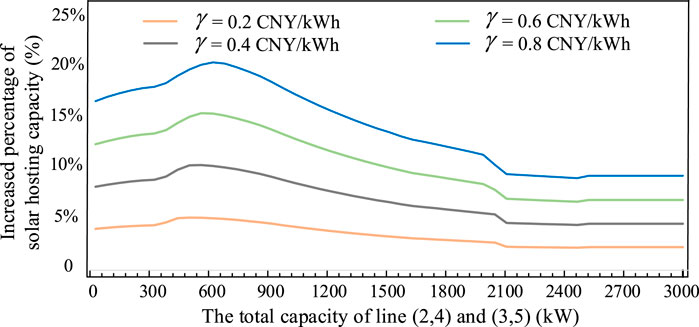
FIGURE 7. Impact of distributed photovoltaic subsidies on solar HC for different values of the total capacity of lines (2.4) and (3.5).

As expected, a higher level of subsidies facilitates larger amount of renewables integration in a profitable way. However, the growth rate of the HC shows a different tendency with increased network capacities. At the beginning, the growth rate shows an upward trend for the reason that it can facilitate investment of solar generation in both areas considerably instead of using existing thermal generation capacity, and the increased network capacity which makes this effect even greater. But at the next stage, the potential of solar energy in certain nodes where solar energy is relatively abundant has been realized generally under subsidies, so the growth rate slows down even if the network expands. Finally, economic favorability disappears and the growth rate keeps stable. It also demonstrates that higher level of subsidies sees an obvious increase in the solar HC and it fluctuates more heavily under the influence of network capacity when subsidies increase. This is critical information for policymakers since subsidies may not always have same beneficial influence on boosting renewables due to additional inefficiencies in network layout.

3.2 Analysis on the impact of ES

3.2.1 Test system and implementation

The purpose of this section is to examine that how the capacity of ES affects wind-generating HC in a day-ahead market with hourly resolution. The wind output profile after normalization and the temporal demand profile for five typical days in Nanjing are shown in Figure 8. Four of them represent the four seasons of a whole year, and the other day represents extreme conditions in the event of high temperature in certain summer days with statistics obtained from Li et al. (2021). In addition, the wind generation investment cost P is assumed as 13.7 CNY/kW/h. The assumed thermal generating units consist of four different technologies, each with its own installed capacity and marginal operating costs, as shown in Table 2. The assumed values of ES operational parameters except energy capacity are stated in Table 3. The devised optimization model was performed in the same environment as before. Solving this MILP needs about 2 s on average.

FIGURE 8

FIGURE 8. Normalized wind output and demand in five representative days.

TABLE 2

TABLE 2. Parameters of generation technology.

TABLE 3

TABLE 3. Parameters of ES.

3.2.2 Value of ES

We consider several scenarios about various energy capacities of ES and keep other parameters as their original value in Table 3. As a result, Figure 9 presents the impacts of several ES energy capacities on the wind HC and demonstrates that an increased capacity of ES can expand the wind HC consistently. To investigate the explanation for this positive effect of ES on the integration of renewable generation, Figure 10 presents the hourly market clearing prices in five considered representative days, it also can demonstrate net demand of the system including the charging and discharging power of ES for the different energy capacities of ES. Providing that the marginal cost of wind generation is inappreciable, ES reduces the demand peak by discharging in time period when wind sources is scarce (e.g., hours 8–11 and 18–20 in representative day 1) to minimize the negative social welfare. By contrast, ES increases the electricity prices hourly by the way of charging in periods with abundant wind sources and lower electrical load (e.g., hours 1–6 in representative day 1). With the increase of ES capacity, the effect of smoothing electricity prices becomes more and more obvious. Furthermore, Figure 11 presents impact of different ES energy capacities scenarios on hourly wind generation dispatch in five considered representative days. It should be noted that ES can force up wind production in valley time period with plentiful wind sources correspondingly (e.g., hours 1–6 in representative day 1), and the effect of which weakens when the corresponding demand is lower.

FIGURE 9

FIGURE 9. Impact of ES energy capacities on wind HC.

FIGURE 10

FIGURE 10. Impact of different ES energy capacity scenarios on hourly market clearing prices.

FIGURE 11

FIGURE 11. Impact of different ES energy capacity scenarios on hourly wind generation dispatch.

As a result, a combination of increased market prices and corresponding wind generation dispatch during periods of abundant wind resources consequently enhance revenues of wind generation, so the wind generation penetration can increase in a profitable way, hence enlarging wind HC.

4 Conclusion

In this article, we investigate the HC of renewable energy generation from a market perspective innovatively by formulating an innovative multi-period bi-level optimization problem. The main purpose of the upper-level problem is to maximize the HC and keep the profit non-negative, while the lower-level problem depicts the market clearing process including charging and discharging cycles of ES. The optimal result of this bi-level problem can be found by using appropriate techniques to convert it to a MILP problem. Case studies not only demonstrate the validity and significance of the devised model but also quantitatively analyze the impact of different network capacities, subsidies, and ES on the market-based HC without violating its profitability constrain.

Three key implications drawn from case studies are valuable and may be guidance for policy and regulation makers. 1) Enlarged network capacity does not always facilitate higher HC of RES. Increased network capacity may even impose limitations on the commercial potential for further RES generating investment, particularly in locations near load centers. 2) Subsidies for RES on top of electricity prices are conducive to higher HC of RES, but the rate of growth depends on network capacity. It is meaningful to identify up to which point subsidies can increase HC most effectively. 3) ES is able to facilitate RES integration and enlarge HC of RES for its ability to increase energy price and wind generation dispatch at times characterized by low electricity demand and abundant RES feed-in, consequently increasing income from investing RES. When the ES capacity is larger, the more obvious this effect is. Future work aims at considering the detailed representation of distribution network constraints including nonlinear AC power flow equations capturing losses, voltage limits, and current thermal limits. Furthermore, another meaningful work lies in considering a joint electricity and carbon market model and investigating the relationships between renewable generation capacity, electricity price, and carbon price.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

YY: conceptualization, methodology, supervision, and funding acquisition; WH: validation, visualization, and writing the original draft; TY: project administration and funding acquisition.

Funding

This work was supported by the Fundamental Research Funds for the Central Universities: 2242022k30038. This work was also supported by the 2021 Jiangsu Shuangchuang (Mass Innovation and Entrepreneurship) Talent Program, China (No. JSSCBS20210137).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akbari-Dibavar, A., Mohammadi-Ivatloo, B., and Zare, K. (2020). Optimal stochastic bilevel scheduling of pumped hydro storage systems in a pay-as-bid energy market environment. J. Energy Storage 31, 101608. doi:10.1016/j.est.2020.101608

CrossRef Full Text | Google Scholar

Al-Saadi, H., Zivanovic, R., and Al-Sarawi, S. F. (2017). Probabilistic hosting capacity for active distribution networks. IEEE Trans. Ind. Inf. 13, 2519–2532. doi:10.1109/TII.2017.2698505

CrossRef Full Text | Google Scholar

Awad, A. S. A., Fuller, J. D., El-Fouly, T. H. M., and Salama, M. M. A. (2014). Impact of energy storage systems on electricity market equilibrium. IEEE Trans. Sustain. Energy 5, 875–885. doi:10.1109/TSTE.2014.2309661

CrossRef Full Text | Google Scholar

Bao, M., Ding, Y., Zhou, X., Guo, C., and Shao, C. (2021). Risk assessment and management of electricity markets: A review with suggestions. Csee Jpes 7, 1322–1333. doi:10.17775/CSEEJPES.2020.04250

CrossRef Full Text | Google Scholar

Bouckaert (2021). Net zero by 2050: A roadmap for the global energy sector. France: International Energy Agency.

Google Scholar

Brancucci Martinez-Anido, C., Brinkman, G., and Hodge, B.-M. (2016). The impact of wind power on electricity prices. Renew. Energy 94, 474–487. doi:10.1016/j.renene.2016.03.053

CrossRef Full Text | Google Scholar

Cicilio, P., Cotilla-Sanchez, E., Vaagensmith, B., and Gentle, J. (2021). Transmission hosting capacity of distributed energy resources. IEEE Trans. Sustain. Energy 12, 794–801. doi:10.1109/TSTE.2020.3020295

CrossRef Full Text | Google Scholar

Divshali, P. H., and Söder, L. (2019). Improving pv dynamic hosting capacity using adaptive controller for statcoms. IEEE Trans. Energy Convers. 34, 415–425. doi:10.1109/tec.2018.2873057

CrossRef Full Text | Google Scholar

Fang, L., Honghua, X., and Yu, Y. (2020). National survey report of pv power applications in China. France: International Energy Agency, 1–45.

Google Scholar

Hanemann, P., and Bruckner, T. (2018). Effects of electric vehicles on the spot market price. Energy 162, 255–266. doi:10.1016/j.energy.2018.07.180

CrossRef Full Text | Google Scholar

Husin, H., Zaki, M., Erdiwansyah, , Mahidin, , Nasaruddin, , and Muhibbuddin, (2021). A critical review of the integration of renewable energy sources with various technologies. Prot. Control Mod. Power Syst. 6, 1–18. doi:10.1186/s41601-021-00181-3

CrossRef Full Text | Google Scholar

Kolb, S., Dillig, M., Plankenbühler, T., and Karl, J. (2020). The impact of renewables on electricity prices in Germany - an update for the years 2014-2018. Renew. Sustain. Energy Rev. 134, 110307. doi:10.1016/j.rser.2020.110307

CrossRef Full Text | Google Scholar

Lakshminarayana, S., Xu, Y., Poor, H. V., and Quek, T. Q. S. (2016). Cooperation of storage operation in a power network with renewable generation. IEEE Trans. Smart Grid 7, 2108–2122. doi:10.1109/TSG.2016.2542367

CrossRef Full Text | Google Scholar

Li, Y., Yu, J., and Cai, X. (2021). Characteristics of nanjing electric power load and relationship between extreme load and meteorological conditions in summer. Meteorological Sci. Technol. 49, 637–646.

Google Scholar

Liu, H., Zhang, Z., Chen, Z. M., and Dou, D. (2019). The impact of China's electricity price deregulation on coal and power industries: Two-stage game modeling. Energy Policy 134, 110957. doi:10.1016/j.enpol.2019.110957

CrossRef Full Text | Google Scholar

Mulenga, E., Bollen, M. H. J., and Etherden, N. (2020). A review of hosting capacity quantification methods for photovoltaics in low-voltage distribution grids. Int. J. Electr. Power & Energy Syst. 115, 105445. doi:10.1016/j.ijepes.2019.105445

CrossRef Full Text | Google Scholar

Qiu, S., Lei, T., Wu, J., and Bi, S. (2021). Energy demand and supply planning of China through 2060. Energy 234, 121193. doi:10.1016/j.energy.2021.121193

CrossRef Full Text | Google Scholar

Ruiz, C., and Conejo, A. J. (2009). Pool strategy of a producer with endogenous formation of locational marginal prices. IEEE Trans. Power Syst. 24, 1855–1866. doi:10.1109/TPWRS.2009.2030378

CrossRef Full Text | Google Scholar

Santos, I. N., Bollen, M. H. J., and Ribeiro, P. F. (2015). “Exploring the concept of hosting capacity for harmonic distortions assessment,” in 2015 IEEE Power Energy Society General Meeting, 1–5. doi:10.1109/PESGM.2015.7286552

CrossRef Full Text | Google Scholar

Seuss, J., Reno, M. J., Broderick, R. J., and Grijalva, S. (2015). “Maximum pv size limited by the impact to distribution protection,” in 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), 1–6. doi:10.1109/pvsc.2015.7356166

CrossRef Full Text | Google Scholar

Shi, Z., Wang, W., Huang, Y., Li, P., and Dong, L. (2022). Simultaneous optimization of renewable energy and energy storage capacity with the hierarchical control. CSEE J. Power Energy Syst. 8, 95–104. doi:10.17775/CSEEJPES.2019.01470

CrossRef Full Text | Google Scholar

Tan, K. M., Babu, T. S., Ramachandaramurthy, V. K., Kasinathan, P., Solanki, S. G., and Raveendran, S. K. (2021). Empowering smart grid: A comprehensive review of energy storage technology and application with renewable energy integration. J. Energy Storage 39, 102591. doi:10.1016/j.est.2021.102591

CrossRef Full Text | Google Scholar

Virasjoki, V., Rocha, P., Siddiqui, A. S., and Salo, A. (2016). Market impacts of energy storage in a transmission-constrained power system. IEEE Trans. Power Syst. 31, 4108–4117. doi:10.1109/tpwrs.2015.2489462

CrossRef Full Text | Google Scholar

Ye, Y., Papadaskalopoulos, D., and Strbac, G. (2016). “An mpec approach for analysing the impact of energy storage in imperfect electricity markets,” in 2016 13th International Conference on the European Energy Market (EEM) (Porto, Portugal: IEEE), 1–5. doi:10.1109/eem.2016.7521287

CrossRef Full Text | Google Scholar

Ye, Y., Papadaskalopoulos, D., and Strbac, G. (2018). Investigating the ability of demand shifting to mitigate electricity producers' market power. IEEE Trans. Power Syst. 33, 3800–3811. doi:10.1109/tpwrs.2017.2782703

CrossRef Full Text | Google Scholar

Zhao, D., Wang, H., Huang, J., and Lin, X. (2022). Time-of-use pricing for energy storage investment. IEEE Trans. Smart Grid 13, 1165–1177. doi:10.1109/tsg.2021.3136650

CrossRef Full Text | Google Scholar