High-Resistance Connection Diagnosis Considering Current Closed-Loop Effect for Permanent Magnet Machine

The permanent magnet (PM) machine has been widely applied in the areas of wind power and electric vehicles. As one of the most common electric faults, high-resistance connection (HRC) will induce 2nd-order components in the dq-axis current and voltage, which can be used for HRC diagnosis. However, these HRC-introduced 2nd-order components are also affected by the current closed-loop control, which ought to be taken into consideration for an accurate HRC diagnosis. In this study, a mathematical model of the 2nd-order components in the dq-axis current and voltage for the current closed-loop controlled PM machine is derived, and based on the model, a new HRC diagnosis method is proposed. In the proposed method, not only the location of HRC but also HRC severity can be accurately obtained. Simulations and experiments have been carried out to validate the effectiveness of the proposed method.

1 Introduction

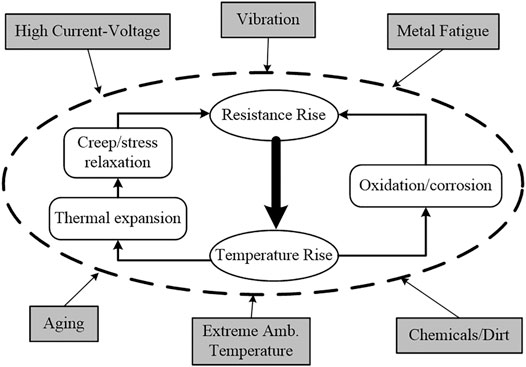
Recently, due to the advantages of high power density and high efficiency, the permanent magnet (PM) machine has been increasingly applied in the area of wind power and electric vehicles. The direct-driven permanent magnet synchronous generator is the most widely used scheme for high-power wind power generation, such as the large-scale intertidal and offshore wind turbines. However, the complex operating environment may cause unexpected faults to the machine. The high-resistance connection (HRC) (or called a resistance unbalance fault) is one of the common electrical faults for the PM machine (Hang et al., 2020a; Hang et al., 2021). Figure 1 (Braunovic et al., 2006) shows the failure mechanism of HRC. It is found that HRC can cause increased torque pulsation, decreased average torque, increased current, and voltage imbalance in the machine. The continuous HRC status of the PM machine may lead to excessive heating, which further increases the connection resistance. If these positive feedback loops are not broken, the HRC may propagate into uncontrolled consequences and even lead to catastrophic failure. Thus, it is of significant importance to detect the HRC fault and prevent potential severe damages (Gritli et al., 2013; Zarri et al., 2013).

FIGURE 1

FIGURE 1. Failure mechanism of HRC.

Many methods have been put forward to detect the HRC for induction machines, which are mainly based on stator current and voltage signals (Yun et al., 2007; Yun et al., 2009; Gritli et al., 2013; de la Barrera et al., 2014; de la Barrera et al., 2015; Mengoni et al., 2015; Antonino-Daviu et al., 2017; Hang et al., 2019; Hang et al., 2020b; Hang et al., 2020a; Hang et al., 2020c; Hang et al., 2021). In the study by Antonino-Daviu et al. (2017), the HRC of the wound rotor induction machine is detected by a series of frequency-domain characteristics of stator current. In the study by Yun et al. (2007), a dynamic model of the induction machine with HRC is established, and the negative-sequence current and the zero-sequence voltage are used for HRC diagnosis. An additional negative-sequence current controller is introduced by Mengoni et al., (2015) to compensate for the current imbalance caused by HRC and the output of the negative-sequence PI regulators is used to detect HRC. In the study by Yun et al. (2009), the negative-sequence current and zero-sequence voltage features are combined to realize the detection and classification of HRC and interturn fault. In the study by de la Barrera et al. (2014), the voltage between the machine’s neutral point and the dc-link negative terminal is measured to detect HRC. In the study de la Barrera et al. (2015), the improved dc signal injection is proposed to generate dc current components in the machine stator and the dc component in the line voltage is extracted online to calculate the HRC indicator. Recently, literature focusing on HRC detection for the PM machine has been put forward. In a study by (Hang et al. 2017; Hang et al. (2019); Hu et al. (2020); Hang et al. (2020b), the HRC is detected based on the zero-sequence voltage measured through a resistor network, where the faulty phase can be located and the fault severity can be estimated. In the study by Hang et al. (2020c), flux linkage biases are injected into the flux control loop to generate dc current in the stator. Then, the dc component in the measured zero-sequence voltage is extracted to estimate the resistance deviations. However, for all the fault diagnosis methods based on zero-sequence voltage, the neutral point of the machine must be accessible, which is not always available in real applications. In the study by Hang et al. (2020a), the HRC is detected by estimating the voltage distortions using the reference model. Similar to the idea of Hang et al. (2020b), high-order sliding mode controllers are proposed by Kommuri et al. (2020) to realize HRC-tolerant control and fault severity estimation. However, the dq-axis current of the faulty PM machine is assumed to be constant by Hang et al., (2020c), which may not be satisfied when the PI current controllers have relatively low control bandwidth or when the HRC resistance deviation is significant. In contrast, the bandwidth of the PI current controllers in the study by Kommuri et al., (2020) is set to be relatively low, which results in the apparent asymmetrics of the stator current when HRC occurs. In application, the current closed-loop control affects both the current and voltage fault features, but this effect has not been well-analyzed in previous works.

In this study, the mathematical model of the HRC-induced 2nd-order components in the dq-axis current and voltage is derived, where the current closed-loop effect is taken into consideration. Based on the established mathematical model, a new HRC diagnosis method is proposed. In the proposed method, not only the location of HRC can be identified but also the HRC severity can be accurately estimated.

The whole article is organized as follows: In Section 2, the model of the PM machine with HRC is established, and the current closed-loop effect is analyzed in Section 3. In Section 4, the proposed HRC diagnosis method is presented. Section 5 validates the proposed diagnosis method by simulations. In addition, experiment results are presented in Section 6 to show the effectiveness of the proposed method. Finally, conclusions are drawn in Section 7.

2 Permanent Magnet Machine With High-Resistance Connection

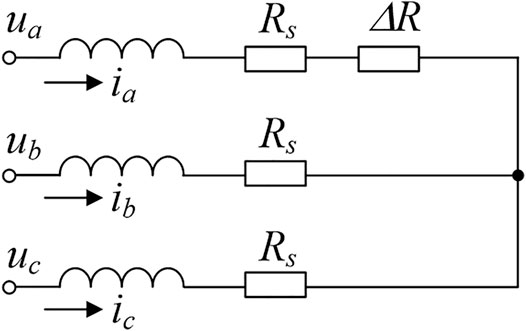
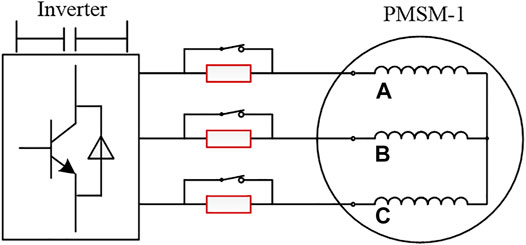
The HRC in the PM machine can be modeled by adding resistance in the faulty phase. Without loss of generality, the HRC is assumed in phase A, as shown in Figure 2, where the u_a, u_b, and u_c are the stator voltage, i_a, i_b, and i_c are the stator current, R_s is the stator phase resistance, and ΔR represents the resistance deviation in phase A. Then, the voltage equations of the PM machine under HRC conditions can be expressed as (Hang et al., 2017).

$\left[u_{abc}\right]=\left[R_s\right]\left[i_{abc}\right]+\frac{d}{dt}\left(\left[L_s\right]\left[i_{abc}\right]\right)+\left[e_{abc}\right],(1)$

where

$\left[u_{abc}\right]={\left[\begin{array}{ccc}{u}_a& u_b& u_c\end{array}\right]}^{\mathrm{T}},(2)$

$\left[i_{abc}\right]={\left[\begin{array}{ccc}{i}_a& i_b& i_c\end{array}\right]}^{\mathrm{T}},(3)$

$\left[e_{abc}\right]={\left[\begin{array}{ccc}{e}_a& e_b& e_c\end{array}\right]}^{\mathrm{T}},(4)$

$\left[R_s\right]=\left[\begin{array}{ccc}{R}_s+\mathrm{\Delta }{R}_a& 0& 0\\ 0& R_s& 0\\ 0& 0& R_s\end{array}\right],(5)$

$\left[L_s\right]=\left[\begin{array}{ccc}{L}_a& M_{ab}& M_{ac}\\ M_{ab}& L_b& M_{bc}\\ M_{ac}& M_{bc}& L_c\end{array}\right].(6)$

FIGURE 2

FIGURE 2. Equivalent circuit model of the PM machine with HRC in phase A.

The e_a, e_b, and e_c are the back-EMF of the PM machine. In the stator inductance matrix [L_s], the L_a, L_b, and L_c are the stator phase self-inductance and M_ac, M_bc, and M_ab are the mutual-inductance. The PM machine model in the synchronous frame can be obtained by applying Park’s transform to Eq. 1, and it yields.

$\{\begin{array}{l}{u}_d=R_c{i}_d+L_d\frac{d}{dt}{i}_d+e_d+e_{\text{HRC}d}\\ u_q=R_c{i}_q+L_q\frac{d}{dt}{i}_q+e_q+e_{\text{HRC}q}\end{array},(7)$

where u_d and u_q are the dq-axis voltages, i_d and i_q are the dq-axis current, and L_d and L_q are the dq-axis inductances of the PM machine. The e_d and e_q represent the coupling terms between the dq-axis voltage equations of the PM machine and can be expressed as

$\{\begin{array}{l}{e}_d=-{\omega }_e{L}_q{i}_q\\ e_q={\omega }_e\left(L_d{i}_d+{\psi }_f\right)\end{array},(8)$

where ω_e is the electrical angular speed and ψ_f is the PM flux linkage. The e_HRCd and e_HRCq are the terms introduced by the HRC and can be expressed as follows:

$\{\begin{array}{l}{e}_{\text{HRC}d}=\frac{1}{3}\mathrm{\Delta }R{i}_d+\frac{1}{3}\mathrm{\Delta }R\cos 2{\theta }_e{i}_d-\frac{1}{3}\mathrm{\Delta }R\sin 2{\theta }_e{i}_q\\ e_{\text{HRC}q}=\frac{1}{3}\mathrm{\Delta }R{i}_q-\frac{1}{3}\mathrm{\Delta }R\sin 2{\theta }_e{i}_d-\frac{1}{3}\mathrm{\Delta }R\cos 2{\theta }_e{i}_q\end{array},(9)$

where θ_e is the electrical angle of the PM machine rotor.

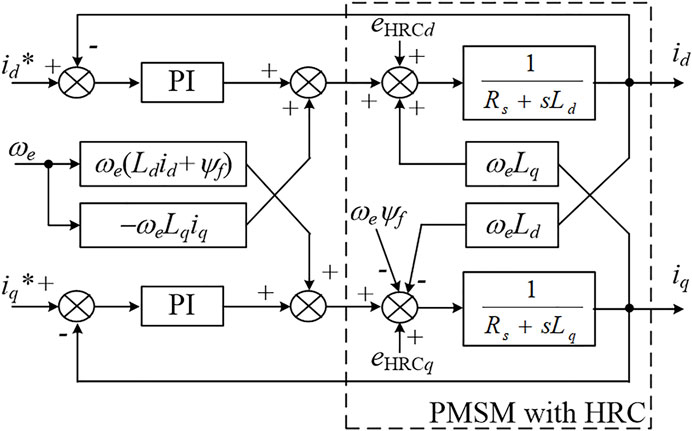
In the permanent magnet synchronous power generation (PMSG) and the PM machine drive system, the feed-forward compensation is commonly used to realize the dq-axis decoupling of the PM machine, as shown in Figure 3.

FIGURE 3

FIGURE 3. Dq-axis decoupling of the PM machine with HRC.

Then, the current controller diagram of the PM machine with HRC can be simplified after dq-axis decoupling, as shown in Figure 4.

FIGURE 4

FIGURE 4. Decoupled current control diagram of the PM machine with HRC. (A) q-axis; (B) d-axis.

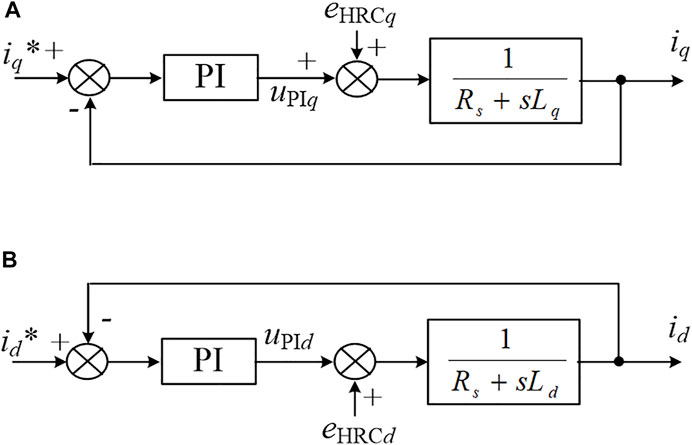
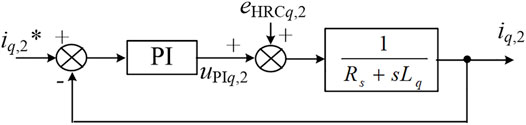
For a healthy PM machine, namely, the e_HRCd and e_HRCq equal 0 and the ideal dq-axis currents and voltages are of constant values. But, the e_HRCd and e_HRCq can induce harmonics in the dq-axis currents and voltages. According to Eq. 9, the e_HRCd and e_HRCq mainly comprise the 2nd-order and dc components. Thus, the 2nd-order component will appear in the dq-axis signals, such as current signals i_d and i_q, and the voltage signals u_PId and u_PIq. Figure 5 can be derived from Figure 4A, where only the 2nd-order components are considered (the subscript 2 represents the 2nd-order component). As the HRC can introduce 2nd-order torque to the PM machine (Braunovic et al., 2006), perturbation of the same frequency will be induced in the speed signal. Considering that the i_q* is the output of the speed closed-loop controller, the i_q* signal will also contain a 2nd-order component i_q,2*, which is significantly affected by the speed closed-loop controller and the mechanical parameters of the machine. Therefore, it can be drawn that the i_q,2 and u_PIq,2 are also affected by the speed closed-loop controller and the machine’s mechanical parameters.

FIGURE 5

FIGURE 5. 2nd-order components in q-axis current control diagram.

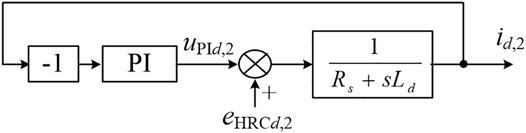
Similarly, the 2nd-order components in the d-axis current control diagram can be derived, as shown in Figure 6. For the commonly used i_d* = 0 method in the PM machine drive system, no 2nd-order component exists in the i_d* signal. It is apparent that the i_d,2 and u_PId,2 are generated only by the e_HRCd,2 and are independent of the mechanical-related parameters. Thus, the i_d,2 and u_PId,2 may be better signals for HRC diagnosis.

FIGURE 6

FIGURE 6. 2nd-order components in d-axis current control diagram.

3 Current Closed-Loop Effect

In this section, the expressions of the i_d,2 and u_PId,2 for the PM machine with HRC fault are derived in detail, where the current closed-loop effect is taken into consideration. It can be drawn from Figure 6 that the i_d,2 satisfies.

$\frac{e_{\text{HRC}d,2}-i_{d,2}\left(K_p+\frac{K_i}{2\text{j}{\omega }_e}\right)}{R_s+2\text{j}{\omega }_e{L}_d}=i_{d,2},(10)$

where K_p and K_i are the proportional and integral gains, respectively, and ω_e is the electric angular speed of the PM machine. Therefore, the i_d,2 and u_PId,2 satisfy.

$i_{d,2}=T_{id}{e}_{\text{HRC}d,2},(11)$

where T_id is

$T_{id}=\frac{2\mathrm{j}{\omega }_e}{\left(K_i-4{\omega }_e^2{L}_d\right)+2\mathrm{j}{\omega }_e\left(K_p+R_s\right)},(12)$

The i_d,2 and e_HRCd,2 can be expressed as

$i_{d,2}=I_{d,2}\cos \left(2{\theta }_e+{\theta }_{id,2}\right),(13)$

$e_{\text{HRC}d,2}=E_{\text{HRC}d,2}\cos \left(2{\theta }_e+{\theta }_{e\text{HRC}d,2}\right),(14)$

where the I_d,2 and θ_id,2 are the amplitude and initial phase angle of the i_d,2. The E_HRCd,2 and θ_eHRCd,2 are the amplitude and initial phase angle of the e_HRCd,2, respectively. Also, it has

$\{\begin{array}{l}{I}_{d,2}=\left|T_{id}\right|E_{\text{HRC}d,2}\\ {\theta }_{id,2}={\theta }_{e\text{HRC}d,2}+\arg \left(T_{id}\right)\end{array}.(15)$

Similarly, the u_PId,2 can be expressed as

$u_{\text{PI}d,2}=U_{\text{PI}d,2}\cos \left(2{\theta }_e+{\theta }_{u\text{PI}d,2}\right),(16)$

where the U_PId,2 and θ_uPId,2 are the amplitude and initial phase angle of the u_PId,2, respectively. Also, the u_PId,2 satisfies

$\begin{array}{l}{u}_{\text{PI}d,2}=-T_{\text{PI}}{i}_{d,2}=-T_{\text{PI}}{T}_{id}{e}_{\text{HRC}d,2}\\ =T_{ud}{e}_{\text{HRC}d,2},\end{array}(17)$

where

$T_{\mathrm{P}\mathrm{I}}=K_p+\frac{K_i}{2\mathrm{j}{\omega }_e},(18)$

$T_{ud}=-\frac{K_i+2j{\omega }_e{K}_p}{\left(K_i-4{\omega }_e^2{L}_d\right)+2\mathrm{j}{\omega }_e\left(K_p+R_s\right)},(19)$

where the ω_e is the electric angular speed of the PM machine. Thus, it has

$\{\begin{array}{l}{U}_{\text{PI}d,2}=\left|T_{\text{PI}}\right|I_{d,2}=\left|T_{ud}\right|E_{\text{HRC}d,2}\\ {\theta }_{u\text{PI}d,2}={\theta }_{id,2}+\arg \left(T_{\text{PI}}\right)+\pi ={\theta }_{e\text{HRC}d,2}+\arg \left(T_{ud}\right)\end{array}(20)$

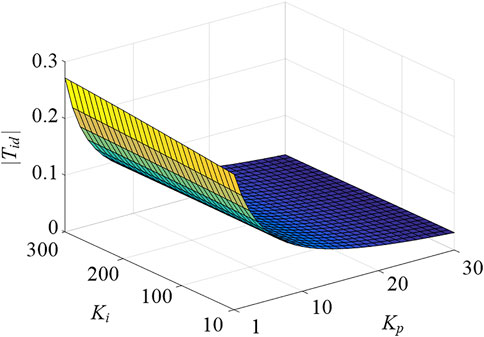
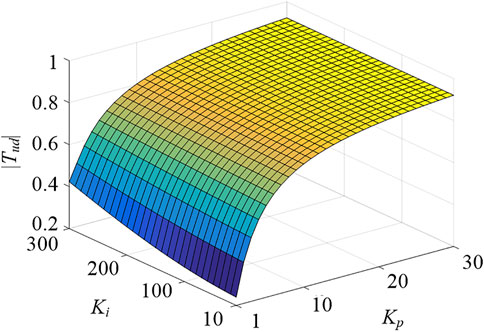
It is apparent that |T_id| and |T_ud | are greatly affected by the values of K_p and K_i. Figures 7, 8 show the |T_id| and |T_ud| versus different K_p and K_i values, where the PM machine operates at the speed of 300 r/min and its parameters are shown in Table 1. For the current closed-loop controller with high bandwidth, namely, when the K_p and K_i are relatively large, the amplitude of |T_id| is close to 0, while the |T_ud| is close to 1. Therefore, the i_d,2 is well-suppressed by the high bandwidth current closed-loop and only has quite a decreased amplitude. But the u_PId,2 has an increased amplitude under this condition. On the contrary, for the current closed-loop controller with low bandwidth, the amplitude of u_PId,2 may be small, while the i_d,2 may have a relatively larger amplitude.

FIGURE 7

FIGURE 7. |T_id| versus different K_p and K_i values.

FIGURE 8

FIGURE 8. |T_ud| versus different K_p and K_i values.

TABLE 1

TABLE 1. Machine parameters.

4 High-Resistance Connection Diagnosis

In industrial applications, it is preferred to design a high bandwidth current closed-loop to obtain better control performance of the PM machine. Therefore, the HRC induced u_PId,2 commonly has a relatively large amplitude and is more suitable for the diagnosis of HRC.

The frequency tracking algorithm (Hang et al., 2017) is used for online extraction of the 2nd-order component from the u_PId signal, and it has

$\{\begin{array}{c}{u}_{\text{PI}d,2x}=\text{LP}\left(2u_{\text{PI}d}\cdot \cos 2{\theta }_e\right)\\ u_{\text{PI}d,2y}=\text{LP}\left(2u_{\text{PI}d}\cdot \sin 2{\theta }_e\right)\end{array},(21)$

where LP represents the low-pass filter. Thus, the u_PId,2 can be written as

$u_{\text{PI}d,2}=u_{\text{PI}d,2x}\cos 2{\theta }_e+u_{\text{PI}d,2y}\sin 2{\theta }_e.(22)$

In addition, it has

$U_{\text{PI}d,2}=\sqrt{u_{\text{PI}d,2x}^2+u_{\text{PI}d,2y}^2},(23)$

${\theta }_{u\text{PI}d,2}=\{\begin{array}{ll}-\arctan \frac{u_{\text{PI}d,2y}}{u_{\text{PI}d,2x}}\hfill & \text{if}{u}_{\text{PI}d,2x}>0\hfill \\ \frac{\pi }{2}\hfill & \text{if}{u}_{\text{PI}d,2x}=0\hfill \\ -\arctan \frac{u_{\text{PI}d,2y}}{u_{\text{PI}d,2x}}+\pi \hfill & \text{if}{u}_{\text{PI}d,2x}<0\hfill \end{array}.(24)$

The amplitude U_PId,2 can be defined as the HRC detection indicator, which is 0 in theory for a healthy PM machine. According to (20), the amplitude and initial phase of i_d,2 and e_HRCd,2 can be calculated as

$\{\begin{array}{l}{I}_{d,2}=\frac{U_{\text{PI}d,2}}{\left|T_{\text{PI}}\right|}\\ {\theta }_{id,2}={\theta }_{u\text{PI}d,2}-\pi -\arg \left(T_{\text{PI}}\right)\end{array},(25)$

$\{\begin{array}{l}{E}_{\text{HRC}d,2}=\frac{U_{\text{PI}d,2}}{\left|T_{ud}\right|}\\ {\theta }_{e\text{HRC}d,2}={\theta }_{u\text{PI}d,2}-\arg \left(T_{ud}\right)\end{array},(26)$

where T_PI and T_ud can be easily calculated since the ω_e can be obtained through the encoder and the parameters of the current controller are known.

According to Eq. 9, for the case that the HRC occurs in phase A, the e_HRCd,2 can also be expressed as

$\begin{array}{l}{e}_{\text{HRC}d,2}=\frac{1}{3}\mathrm{\Delta }R{i}_{d,2}+\frac{1}{3}\mathrm{\Delta }R\cos 2{\theta }_e{i}_{d,0}-\frac{1}{3}\mathrm{\Delta }R\sin 2{\theta }_e{i}_{q,0}\\ =\frac{1}{3}\mathrm{\Delta }R\left(i_{d,2}+\cos 2{\theta }_e{i}_{d,0}-\sin 2{\theta }_e{i}_{q,0}\right)\\ =\frac{1}{3}\mathrm{\Delta }R{C}_a,\end{array}(27)$

where i_d,0 and i_q,0 are the dc components of i_d and i_q. The C_a is defined as the characteristic current of phase A and can be obtained by

$\begin{array}{l}{C}_a=i_{d,2}+\cos 2{\theta }_e{i}_{d,0}-\sin 2{\theta }_e{i}_{q,0}\\ =\left(I_{d,2}\cos {\theta }_{id,2}+i_{d,0}\right)\cos 2{\theta }_e-\left(I_{d,2}\sin {\theta }_{id,2}+i_{q,0}\right)\sin 2{\theta }_e\\ =I_{ca}\cos \left(2{\theta }_e+{\theta }_{ca}\right),\end{array}(28)$

where

$I_{ca}=\sqrt{{\left(I_{d,2}\cos {\theta }_{id,2}+i_{d,0}\right)}^2+{\left(I_{d,2}\sin {\theta }_{id,2}+i_{q,0}\right)}^2},(29)$

${\theta }_{ca}=\{\begin{array}{ll}\arctan \frac{I_{d,2}\sin {\theta }_{id,2}+i_{q,0}}{I_{d,2}\cos {\theta }_{id,2}+i_{d,0}}\hfill & \mathrm{i}\mathrm{f}{I}_{d,2}\cos {\theta }_{id,2}+i_{d,0}>0\hfill \\ \frac{\pi }{2}\hfill & \mathrm{i}\mathrm{f}{I}_{d,2}\sin {\theta }_{d,2}+i_{q,0}=0\hfill \\ \arctan \frac{I_{d,2}\sin {\theta }_{id,2}+i_{q,0}}{I_{d,2}\cos {\theta }_{id,2}+i_{d,0}}+\pi \hfill & \mathrm{i}\mathrm{f}{I}_{d,2}\cos {\theta }_{id,2}+i_{d,0}<0\hfill \end{array}.(30)$

Combining Eqs 14, 27, and 28 yields

$\{\begin{array}{l}{E}_{\text{HRC}d,2}=\frac{1}{3}\mathrm{\Delta }{R}_a{I}_{ca}\\ {\theta }_{e\text{HRC}d,2}={\theta }_{ca}\end{array}.(31)$

If the HRC occurs in phase B, the e_HRCd,2 can be written as

$e_{\text{HRC}d,2}=\frac{1}{3}\mathrm{\Delta }R{C}_b,(32)$

where

$\begin{array}{l}{C}_b=i_{d,2}+\cos \left(2{\theta }_e+\frac{2\pi }{3}\right)i_{d,0}-\sin \left(2{\theta }_e+\frac{2\pi }{3}\right)i_{q,0}\\ =I_{cb}\cos \left(2{\theta }_e+{\theta }_{cb}\right),\end{array}(33)$

Similarly, if the HRC occurs in phase C, the e_HRCd,2 can be written as

$e_{\text{HRC}d,2}=\frac{1}{3}\mathrm{\Delta }R{C}_c,(34)$

where

$\begin{array}{l}{C}_c=i_{d,2}+\cos \left(2{\theta }_e-\frac{2\pi }{3}\right)i_{d,0}-\sin \left(2{\theta }_e-\frac{2\pi }{3}\right)i_{q,0}\\ =I_{cc}\cos \left(2{\theta }_e+{\theta }_{cc}\right).\end{array}(35)$

The I_cb and θ_cb are the amplitude and initial phase angle of the C_b, and I_cc and θ_cc are the amplitude and initial phase angle of the C_c, respectively. If the HRC occurs in phase A, only the θ_ca equals θ_eHRCd,2, and the θ_cb and θ_cc will keep a distance to the θ_eHRCd,2. Therefore, the location of the HRC can be simply judged by respectively comparing the extracted θ_ca, θ_cb, and θ_cc with the calculated θ_eHRCd,2. Also, after the HRC is located in phase A, the resistance deviation in the faulty phase can be easily calculated according to Eq. 31, and it has

$\mathrm{\Delta }R=\frac{3E_{\text{HRC}d,2}}{I_{ca}}.(36)$

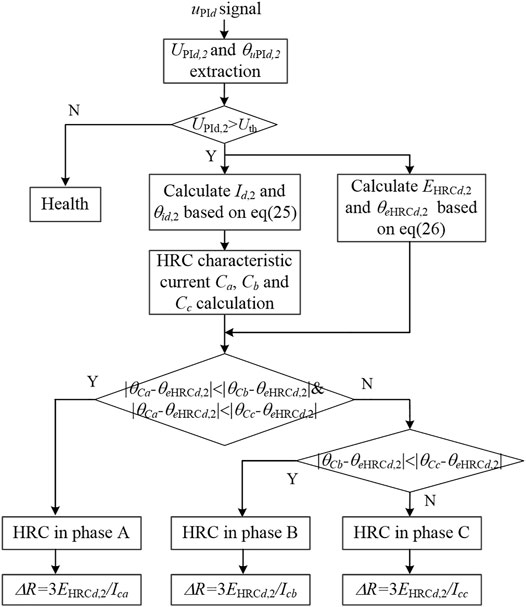
Figure 9 shows the flow chart of the HRC diagnosis process. The online HRC diagnosis process steps are summarized as follows:

FIGURE 9

FIGURE 9. Flow chart of HRC diagnosis.

Step 1. HRC detection. The 2nd-order component of u_PId is extracted online using the frequency tracking algorithm. Then, the HRC can be detected once the amplitude U_PId,2 is larger than the preset detection threshold U_th.

Step 2. HRC location. After the HRC is detected, the e_HRCd,2 and the three HRC characteristic current C_a, C_b, and C_c are calculated. The characteristic current for the faulty phase has the initial phase closest to the θ_eHRCd,2.

Step 3. HRC severity estimation. After the faulty phase is located, the resistance deviation ΔR can be calculated according to the Ε_HRCd,2 and the amplitude of the characteristic current of the faulty phase.

5 Simulations

The PM machine drive system with HRC is established in Matlab/Simulink, where the parameters of the PM machine are listed in Table 1.

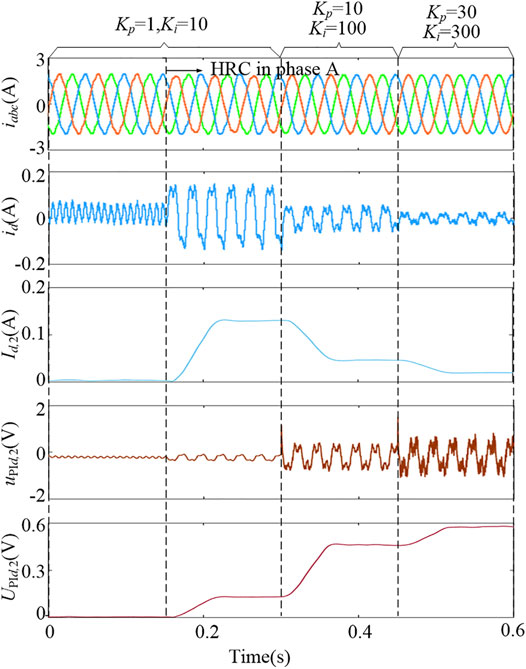
Figure 10 shows the simulation results of the PM machine with different K_p and K_i, where the PM machine operates with a rated load at a speed of 300 r/min. The K_p and K_i are, respectively, set to be 1 and 10 for t∈[0, 0.3]. Before t = 0.15 s, no HRC occurs to the PM machine, and the sinusoidal degree of the stator current is not high because of the low control bandwidth. The ripple in the d-axis current i_d is mainly made up of the 6th-order component, which is caused by the inverter nonlinearity, such as the dead-time effect. But, nearly no 2nd-order component exists in the i_d and u_PId. HRC (ΔR = 1Ω) is set in phase A at t = 0.15 s, and then the 2nd-order component appears in the i_d and u_PId signals. In addition, for the larger K_p and K_i (the higher control bandwidth), the harmonics in the stator current are well-suppressed by the current closed-loop controller. The I_d,2 decreases with the increase of control bandwidth, while the U_PId,2 increases with the increase of control bandwidth, which agrees well with the analysis in Section 3.

FIGURE 10

FIGURE 10. Waveforms of the PM machine with different current closed-loop controller parameters.

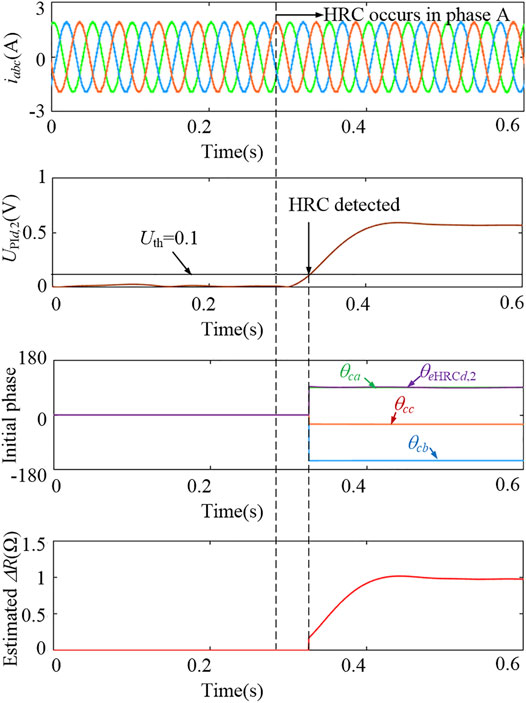
Considering that the high bandwidth current closed-loop is preferred in industry application, the case K_p = 30 and K_i = 300 is analyzed in the following part. Figure 11 shows the waveforms of the PM machine operating with rated load at a speed of 300 r/min, where the HRC (ΔR = 1Ω) occurs in phase A at t = 0.3 s. With the high bandwidth current closed-loop control, the stator current is well-controlled to be sinusoidal, and nearly no changes can be seen in the stator current after the HRC occurs. But when the HRC (ΔR = 1Ω) occurs in phase A at t = 0.3 s, the amplitude of U_PId,2 immediately increases, and the HRC can be detected when the U_PId,2 is larger than the preset detection threshold U_th. After the HRC is detected, the HRC location and severity estimation is activated. It can be seen in Figure 11 that the extracted θ_ca is quite closest to the θ_eHRCd,2. Thus, the HRC can be located in phase A. The calculated ΔR eventually converges to 0.98Ω, which agrees well with the real ΔR value.

FIGURE 11

FIGURE 11. Waveforms of the PM machine with HRC (ΔR = 1Ω) occur in phase A.

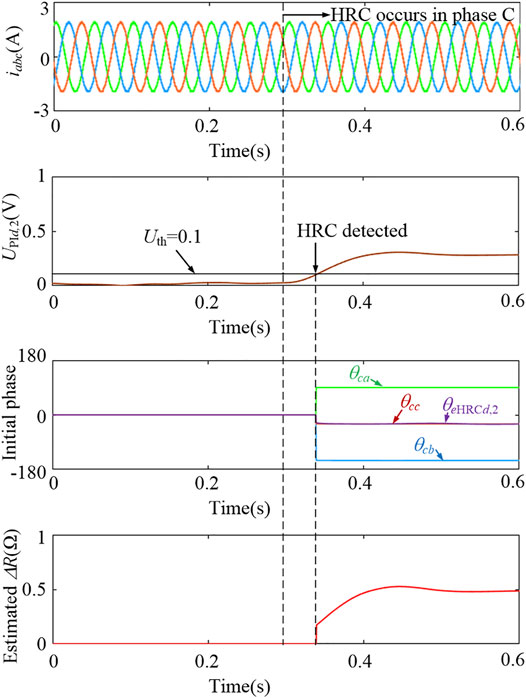
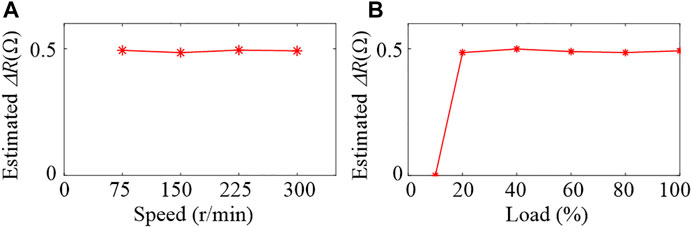
Figure 12 shows the waveforms of the PM machine operating with rated load at a speed of 300 r/min, where the HRC (ΔR = 0.5Ω) occurs in phase C at t = 0.3 s. The HRC can be quickly detected in less than 0.1 s, and the faulty phase can be accurately located in phase C. In addition, the estimated ΔR is 0.49Ω and is almost the same as the theoretical value. More simulations are conducted for the PM machine operating under different conditions, where the HRC (ΔR = 0.5Ω) is set in phase A. Figure 13A shows the estimated ΔR for the PM machine operating with rated load at different speeds. Also, Figure 13B shows the estimated ΔR for the PM machine operating with different loads at 300 r/min. It is shown in Figure 13 that the estimated ΔR is quite accurate under most operating conditions. But the ΔR cannot be directly estimated for the PM machine with a very light load. This is because the HRC-induced fault feature is dependent on the stator current, which only has small amplitude under light load. The d-axis current injection is used to solve this problem.

FIGURE 12

FIGURE 12. Waveforms of the PM machine with HRC (ΔR = 0.5Ω) occur in phase C.

FIGURE 13

FIGURE 13. Estimated ΔR. (A) Rated load at a different speed; (B) different loads at 300 r/min.

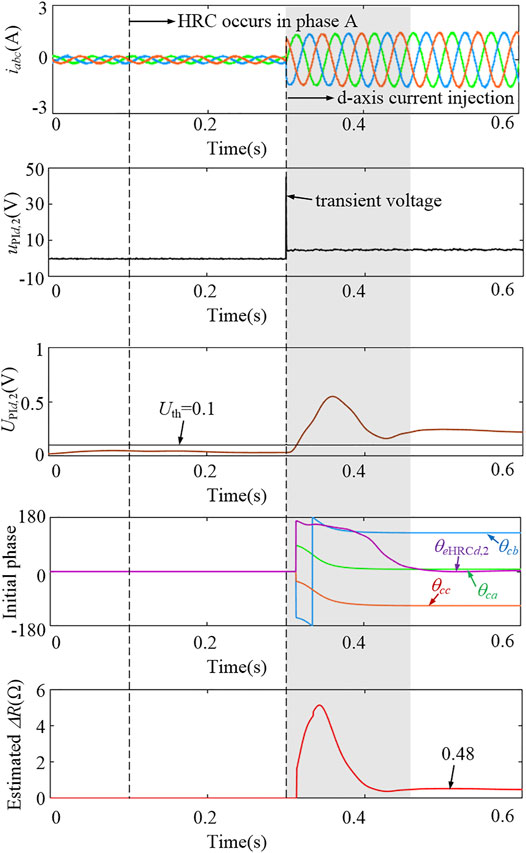
Figure 14 shows the waveforms of the HRC detection under 10% load at 300 r/min speed. After HRC (ΔR = 0.5Ω) occurs in phase A at t = 0.1 s, the extracted amplitude U_PId,2 remains smaller than the U_th, and the HRC may not be detected. With the d-axis current of 1.5 A injected into the machine, the stator current amplitude is immediately increased. However, the transient voltage in the u_PId signal can cause a large fluctuation to the extracted U_PId,2 and lead to a false diagnosis result, as shown in the shadow part in Figure 14. But a simple time delay can be inserted after the d-axis current injection to avoid the transient voltage effect. As shown in Figure 14, the estimated ΔR converges to 0.48Ω about 0.2 s after the d-axis current injection, and the faulty phase is located in phase A. It is worth mentioning that the interturn fault in the stator can also induce the 2nd-order component in the i_d and u_PId (Ebrahimi and Faiz, 2010), which might cause false detection for the proposed method. The d-axis current injection can also be used to realize the discrimination between the HRC and interturn fault since the HRC fault feature can be apparently enlarged, while the interturn fault feature may not vary obviously due to the d-axis current injection (Urresty et al., 2015).

FIGURE 14

FIGURE 14. Waveforms of 10% load PM machine INE with HRC (ΔR = 0.5Ω) occur in phase A.

6 Experiment

An experimental platform has been built to validate the proposed method, as shown in Figure 15. The PM machine-1 and PM machine-2 have the same parameters as presented in Table 1, and the PM machine-1 is used as a load, while PM machine-2 is used as the test machine. The HRC can be implemented by connecting an additional resistor in series with the phase winding, as shown in Figure 16. Also, the parallel switches are used to control whether the additional resistor is inserted.

FIGURE 15

FIGURE 15. Experimental platform.

FIGURE 16

FIGURE 16. HRC implementation.

Figure 17 shows the experimental waveforms of the PM machine operating at 300 r/min with rated load. Also, the HRC (ΔR = 1Ω) is set in phase A. In Figure 13A, the parameters of the current closed-loop controller are set as K_p = 1 and K_i = 10. After the occurrence of HRC, the u_PId,2x increases to 0.05 V and the u_PId,2y changes to −0.14 V. Thus, the amplitude of U_PId,2 can be obtained based on Eq. 23, and it is only around 0.15 V. In Figure 17B, the current closed-loop controller parameters are set as K_p = 30 and K_i = 300. After the same HRC occurs to phase A, the extracted u_PId,2x is 0.04V and the u_PId,2y is to −0.56 V. Therefore, the amplitude U_PId,2 is 0.56 V, and it is much larger than the case where K_p = 1 and K_i = 10, which agrees well with the analysis in Section 3. The experiment results considering different cases of HRC conditions are presented in Table 2, where the PM machine operates at 300 r/min with rated load. Also, the current closed-loop controller parameters are set as K_p = 30 and K_i = 300. It can be seen that the faulty phase can be accurately located, and the estimated ΔR values are quite close to the theoretical ones.

FIGURE 17

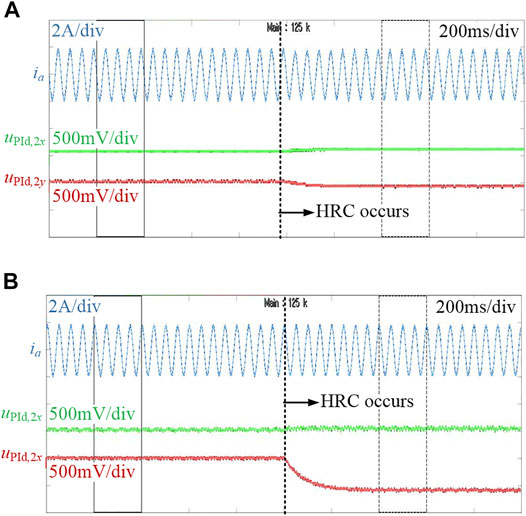
FIGURE 17. Stator current, extracted u_PId,2x, and u_PId,2y of the PM machine. (A) K_p = 1 and K_i = 10; (B) K_p = 30 and K_i = 300.

TABLE 2

TABLE 2. Experiment HRC diagnosis results.

To further validate the proposed method, more experiments are conducted under different operating conditions. The HRC (ΔR = 1Ω) is set in phase C. The K_p and K_i are set to be 30 and 300, respectively. It can be seen in Figure 18 that the ΔR can be accurately estimated at different operating conditions. In Figure 18B, the estimated ΔR is obtained with d-axis current injection. Also, the corresponding waveforms are shown in Figure 19. As the PM machine operates at 300 r/min with only 15% load, the extracted u_PId,2x and u_PId,2y are 0.06 V; thus, the U_PId,2 only has a value of 0.085 V, which is not larger than the detection threshold of 0.1 V, and the HRC fault may not be detected. By injecting the d-axis current of 1 A into the PM machine, the stator current is increased, and the fault feature is also enlarged as a result. It can be seen in Figure 15 that the u_PId,2x changes to −0.16 V and the u_PId,2y rises to −0.27 V after a short transient period. The expanded U_PId,2 is 0.31 V; thus, the HRC can be detected under the light load condition.

FIGURE 18

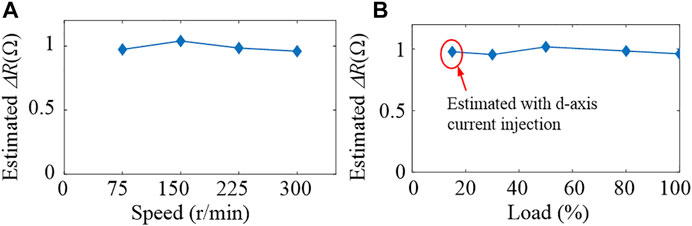
FIGURE 18. Experimental estimated ΔR. (A) Rated load at different speed; (B) different loads at 300 r/min.

FIGURE 19

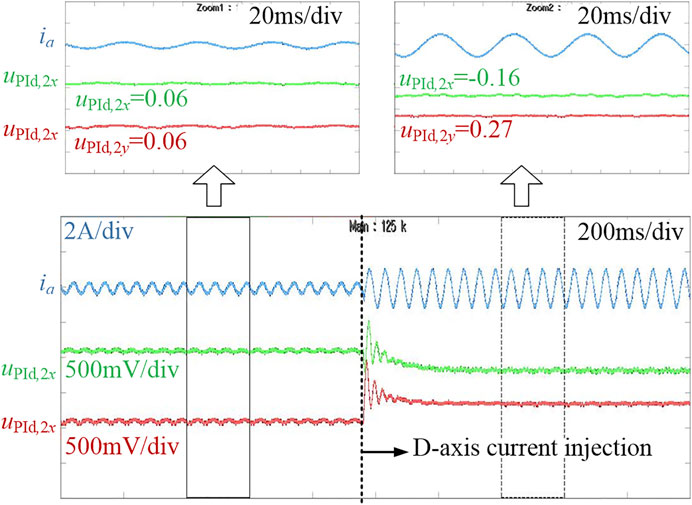
FIGURE 19. Stator current, extracted u_PId,2x, and u_PId,2y of the PM machine with d-axis current injection.

7 Conclusion

The HRC can induce a 2nd-order component in the dq-axis signals of the PM machine. However, as the current closed-loop bandwidth increases, the 2nd-order components in the dq-axis voltage increase. But, the 2nd-order components in the dq-axis current have an opposite trend. This study derives the mathematical model of the HRC-induced 2nd-order components in the dq-axis current and voltage. Also a new HRC diagnosis method is proposed based on the established mathematical model. In the proposed method, not only the location but also the resistance deviation ΔR can be accurately estimated. Also, the proposed method has been proven by the simulation and experiment results.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

ZX did the conceptual design, simulation analysis, and writing of the manuscript. ZD and YJ revised and improved the manuscript. KC, AM, and SA organized case studies.

Funding

This work was supported by the Natural Science Research Start-up Foundation of Recruiting Talents of Nanjing University of Posts and Telecommunications (Grant No. NY219154) and the Foundation of Jiangsu Provincial Double-Innovation Doctor Program under Grant (2020) 30639.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Antonino-Daviu, J., Quijano-Lopez, A., Climente-Alarcon, V., and Garin-Abellan, C. (2017). Reliable Detection of Rotor Winding Asymmetries in Wound Rotor Induction Motors via Integral Current Analysis. IEEE Trans. Ind. Appl. 53 (3), 2040–2048. doi:10.1109/tia.2017.2672524

CrossRef Full Text | Google Scholar

Braunovic, M., Myshkin, N., and Konchits, V. (2006). Electrical Contacts: Fundamentals, Applications and Technology. New York, NY, USA: Taylor & Francis.

Google Scholar

de la Barrera, P. M., Bossio, G. R., and Leidhold, R. (2015). Online Voltage Sensorless High-Resistance Connection Diagnosis in Induction Motor Drives. IEEE Trans. Ind. Electron. 62 (7), 4374–4384. doi:10.1109/tie.2014.2385038

CrossRef Full Text | Google Scholar

de la Barrera, P. M., Bossio, G. R., and Solsona, J. A. (2014). High-Resistance Connection Detection in Induction Motor Drives Using Signal Injection. IEEE Trans. Ind. Electron. 61 (7), 3563–3573. doi:10.1109/tie.2013.2278957

CrossRef Full Text | Google Scholar

Ebrahimi, B. M., and Faiz, J. (2010). Feature Extraction for Short-Circuit Fault Detection in Permanent-Magnet Synchronous Motors Using Stator-Current Monitoring. IEEE Trans. Power Electron. 25 (10), 2673–2682. doi:10.1109/tpel.2010.2050496

CrossRef Full Text | Google Scholar

Gritli, Y., Zarri, L., Rossi, C., Filippetti, F., Capolino, G.-A., and Casadei, D. (2013). Advanced Diagnosis of Electrical Faults in Wound-Rotor Induction Machines. IEEE Trans. Ind. Electron. 60 (9), 4012–4024. doi:10.1109/tie.2012.2236992

CrossRef Full Text | Google Scholar

Hang, S., Zhang, J., Ding, S., and Cheng, M. (2017). Online Diagnosis and Localization of High-Resistance Connection in PMSM with Improved Fault Indicator. IEEE Trans. Power Electron. 32, 3585–3594.

CrossRef Full Text | Google Scholar

Hang, J., Ren, X., Tang, C., Tong, M., and Ding, S. (2021). Fault-Tolerant Control Strategy for Five-phase PMSM Drive System with High-Resistance Connection. IEEE Trans. Transp. Electrific. 7 (3), 1390–1400. doi:10.1109/tte.2020.3037894

CrossRef Full Text | Google Scholar

Hang, J., Wu, H., Ding, S., Hua, W., and Wang, Q. (2020b). A DC-Flux-Injection Method for Fault Diagnosis of High-Resistance Connection in Direct-Torque-Controlled PMSM Drive System. IEEE Trans. Power Electron. 35 (3), 3029–3042. doi:10.1109/tpel.2019.2924929

CrossRef Full Text | Google Scholar

Hang, J., Xia, M., Ding, S., Li, Y., Sun, L., and Wang, Q. (2020a). Research on Vector Control Strategy of Surface-Mounted Permanent Magnet Synchronous Machine Drive System with High-Resistance Connection. IEEE Trans. Power Electron. 35 (2), 2023–2033. doi:10.1109/TPEL.2019.2918683

CrossRef Full Text | Google Scholar

Hang, J., Yan, D., Xia, M., Ding, S., and Wang, Q. (2019). Quantitative Fault Severity Estimation for High-Resistance Connection in PMSM Drive System. IEEE Access 7, 26855–26866. doi:10.1109/access.2019.2901121

CrossRef Full Text | Google Scholar

Hang, J., Zhang, J., Ding, S., Huang, Y., and Wang, Q. (2020c). A Model-Based Strategy with Robust Parameter Mismatch for Online HRC Diagnosis and Location in PMSM Drive System. IEEE Trans. Power Electron. 35 (10), 10917–10929. doi:10.1109/tpel.2020.2978139

CrossRef Full Text | Google Scholar

Hu, R., Wang, J., Mills, A. R., Chong, E., and Sun, Z. (2020). Detection and Classification of Turn Fault and High Resistance Connection Fault in Permanent Magnet Machines Based on Zero Sequence Voltage. IEEE Trans. Power Electron. 35 (2), 1922–1933. doi:10.1109/tpel.2019.2922114

CrossRef Full Text | Google Scholar

Kommuri, S. K., Park, Y., and Lee, S. B. (2020). High-Resistance Fault Control in Permanent Magnet Synchronous Motors. IEEE/ASME Trans. Mechatron. 25 (1), 271–281. doi:10.1109/tmech.2019.2951015

CrossRef Full Text | Google Scholar

Mengoni, M., Zarri, L., Gritli, Y., Tani, A., Filippetti, F., and Lee, S. B. (2015). Online Detection of High-Resistance Connections with Negative-Sequence Regulators in Three-phase Induction Motor Drives. IEEE Trans. Ind. Appl. 51 (2), 1579–1586. doi:10.1109/tia.2014.2360963

CrossRef Full Text | Google Scholar

Urresty, J.-C., Riba, J.-R., Romeral, L., and Ortega, J. A. (2015). Mixed Resistive Unbalance and Winding Inter-turn Faults Model of Permanent Magnet Synchronous Motors. Electr. Eng. 97 (1), 75–85. doi:10.1007/s00202-014-0316-z

CrossRef Full Text | Google Scholar

Yun, J., Cho, J., Lee, S. B., and Yoo, J. (2007). On-line Detection of High-Resistance Connections in the Incoming Electrical Circuit for Induction Motors. IEEE Int. Electr. Mach. Drives Conf., 583–589. doi:10.1109/IEMDC.2007.382732

CrossRef Full Text | Google Scholar

Yun, J., Lee, K., Lee, K.-W., Lee, S. B., and Yoo, J.-Y. (2009). Detection and Classification of Stator Turn Faults and High-Resistance Electrical Connections for Induction Machines. IEEE Trans. Ind. Appl. 45 (2), 666–675. doi:10.1109/tia.2009.2013557

CrossRef Full Text | Google Scholar

Zarri, L., Mengoni, M., Gritli, Y., Tani, A., Filippetti, F., Serra, G., et al. (2013). Detection and Localization of Stator Resistance Dissymmetry Based on Multiple Reference Frame Controllers in Multiphase Induction Motor Drives. IEEE Trans. Ind. Electron. 60 (8), 3506–3518. doi:10.1109/tie.2012.2235393

CrossRef Full Text | Google Scholar

Zhang, J., Hang, J., Ding, S., and Cheng, M. (2017). Online Diagnosis and Localization of High-Resistance Connection in PMSM with Improved Fault Indicator. IEEE Trans. Power Electron. 32 (5), 3585–3594. doi:10.1109/tpel.2016.2587670

CrossRef Full Text | Google Scholar