
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 12 October 2022
Sec. Solar Energy
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.933044
This article is part of the Research Topic Materials Design and Optimization for Next Generation Solar Cell and Light-Emitting Technologies View all 7 articles
The structural changes in the electronically excited state of tungsten oxide (WO3), a promising visible-light-responsive photocatalyst, are discussed from the viewpoint of carrier-phonon interactions using first-principles calculations. The increase in the pre-edge peak observed immediately after photoexcitation by high-speed time-resolved X-ray absorption spectroscopy is attributed to the local lattice distortion due to Fröhlich-Polaron generation by the interaction with optical longitudinal phonons. Bimolecular recombination could be suppressed by the formation of bipolaron states, and high internal quantum yields in photocatalysis are expected. The bipolaron states are unstable states in the electronically excited state, and relax to stable structures in the electronically excited state by phonon-phonon interaction. In the stable structure, the transition dipole moment is found to be nearly zero, suggesting a non-radiative transition to the electronic ground state and a long lifetime in the electronically excited state.
Photocatalysts, which utilize sunlight to extract hydrogen and oxygen from water, is an essential technology for realizing a sustainable and clean society (Kamat, 2007). In a photocatalytic reaction, when the photocatalyst absorbs light, the electrons are excited, and electron-hole pairs are generated; subsequently, they move away from each other and ultimately reach the surface to proceed with the reaction with the adsorbed substance (Kisch, 2015). This technology is one of the leading technologies in the development of renewable energy (Kudo and Miseki, 2009), and it is expected that the photocatalytic function will be improved by elucidating the reaction process. Thus far, research and development of photocatalysts were centered on titanium oxide (TiO2) that responds to ultraviolet light (Ameta and Ameta, 2017); however, the amount of ultraviolet light contained in sunlight is about 5% of the total, so it is essential to develop a catalytic material that absorbs visible light and promotes the reaction in order to ensure the effective use of sunlight (Maeda and Domen, 2010).
Tungsten trioxide (WO3), with a bandgap of 2.6–2.8 eV, has been noted as a visible light-responsive photocatalytic material (Kiu et al., 2012), and research has been conducted on the dynamics of photoexcited states and photocarriers. By light irradiation, electrons in the valence band of the 2p orbital of oxygen are excited to the conduction band of the 5 d orbital of Tungsten to generate optical carriers (Niklasson and Granqvist, 2007). Regarding the lifetime of optical carriers in WO3, it has been reported that more than 90% of photogenerated electron-holes recombine within 10 µs (Pesci et al., 2011). However, long-lived optical carriers with a lifetime of 100 μs or more have been observed in the WO3 fine particles, and it has been confirmed that they have important properties that cannot be ignored as a photocatalyst (Amano et al., 2013). Regarding the structure of the photocarrier and the size dependence of the material, a high photocurrent of ∼2.4 mA cm−2 was observed with the monoclinic nanoneedle WO3 (Fàbrega et al., 2016), and it has been reported that the life of charge carriers is longer in nano-sized powders compared to granular powders 390 ± 260 nm (Regan et al., 2016).
In contrast, there was a lack of information on the structural changes in the electronic excitation state generated by the WO3 photocatalyst under light irradiation. However, Asakura et al. followed the structural changes in the photoexcited state of WO3 by ultrafast time-resolved X-ray absorption spectroscopy at the W-LI, -LIII edges, and succeeded in observing local structural changes of photoexcited WO3 on an ultrafast atomic scale (Uemura et al., 2014; Uemura et al., 2016; Koide et al., 2020). At the W-LI end, a chemical shift in the absorption spectrum due to the decrease in the oxidation number of W associated with the electronic excitation from the oxygen 2p orbital to the W d(Eg) orbital in the valence band was observed with a time resolution of 0.5 ps in the experiment. The increase in the intensity of the W-LI pre-edge peak due to the p-d hybridization effect originating from the local structural distortion around W was observed to continue up to 150 ps, i.e., the fraction of sites where the local structural distortion occurs increased up to 150 ps. By full-potential multiple scattering calculation, the anisotropic and local distortion around the W atom reproduces the characteristics of the spectrum 150 ps after photoexcitation (Koide et al., 2020). In the future, it is expected that research will be developed to track the chemical state and the structural changes during the photocatalytic reaction under light irradiation.
In this study, the structural changes in the electronically excited state caused by the light irradiation of WO3 in relation to the femtosecond time-resolved X-ray absorption fine structure (XAFS) spectroscopy experiment by Asakura et al. are discussed, based on the first-principles calculation method on the density functional theory. In particular, the structural changes induced immediately after light irradiation are clarified from the viewpoint of electron-photon interaction, followed by a discussion of the relaxation process to a stable structure in the electronically excited state. This study provides insight into the dynamics of photogenerated carriers in WO3 and may contribute to the design of more efficient WO3-based photocatalysts.
The structure of the cubic phase Pm
Quantum ESPRESSO 6.3 (Giannozzi et al., 2009) and Yambo 4.2.5 (Marini et al., 2009; Sangalli et al., 2019) were used for first-principles calculations based on density functional theory. The exchange correlation energies were approximated by generalized-gradient approximation (GGA) (Hua et al., 1997) and the functional (Perdew et al., 1996) defined by Perdew, Burke & Ernzerhof was used. Optimized norm-conserving Vanderbilt pseudopotentials (Hamann, 2013; van Setten et al., 2018) was used as the pseudopotential. The fully relativistic pseudopotential was used only for the calculation of the effective mass, whereas the others used the scalar relativistic pseudopotential. Structural optimization was performed so that the force applied to the atom was 10−3 a. u. Or less and the stress was 0.1 kbar or less. The kinetic-energy cutoffs for the plane wave basis and charge density were 84 Ry and 336 Ry, respectively. VESTA (Momma and Izumi, 2011) and XCrySDen (Kokalj, 2003) were used to draw vectors such as structures and forces.
WO3 is known to be in the monoclinic phase P21/n at room temperature and not in the cubic phase Pm
From the band structure (Supplementary Figure S1), it was found that the CBM is Γ (X is almost the same energy level as Γ without SOC), VBM is M or R, and bandgap is indirect. The bandgap is 0.65 eV without SOC, and 0.47eV with SOC. For comparison we calculated the bandgap for the monoclinic phase P21/n and obtain 1.44eV without SOC and 1.34eV with SOC. The theoretical bandgaps are smaller than the experimental bandgap of 2.60–3.21 eV (González-Borrero et al., 2010; Migas et al., 2010; Zheng et al., 2011) for monoclinic phase P21/n. This can be attributed to the underestimation of the bandgap due to the use of the functional PBE and the fact that the bandgap by first principles calculation is larger for the monoclinic phase P21/n than for the cubic phase Pm
The band structure was fitted with the following equation to calculate the effective mass.
Recent studies have shown that the effective mass of Γ-X is a very small value, m* = 0.17, when calculated with spin-orbit coupling (SOC) (Wang et al., 2020). Therefore, in this study, SOC was considered for the calculation of effective mass. It can be seen that the effective mass is relatively large with the VB approximately 0.9–2.4 (Supplementary Table S1) and small with the CB approximately 0.2–0.4 (Table 1).
The phonon band and phonon DOS were calculated for the electron-phonon interaction analysis (Supplementary Figures S3, S4). The stable structure in the ground state is the monoclinic phase P21/n and not the cubic phase Pm
Electron-phonon spectral density α2F(ω) (Giustino, 2017) was calculated in order to confirm the magnitude of electron-phonon interaction in the VB and CB. It represents the scattering of an electron on the Fermi surface and cannot be applied to semiconductors with band gaps as is. Therefore, the Fermi energy of the electron-phonon spectral density was replaced with an arbitrary energy
where
Figure 1 shows the results of the calculation of α2F near the VBM and CBM, where εA is VBM or CBM. In both cases, the mode of ν = 9, 12 has a large peak. The electron-phonon matrix element in Figure 2A indicates that both ν = 9 and 12 become 0 at the Γ point, but increases while approaching q = Γ point. As the vicinity of the q = Γ point of ν = 9, 12 is LO1 and LO2, it can be seen that both vibrational modes are strongly coupling with the electrons near the q = Γ point. Therefore, we focus only on the electron-phonon coupling at the q = Γ point. Figures 2B,C shows the vibrational modes of LO1 and LO2 at the point q = Γ. As shown in phonon DOS, it can be seen that they both correspond to the vibration in the plane of the O atom.

FIGURE 1. Electron-phonon spectral density α2F of cubic phase Pm
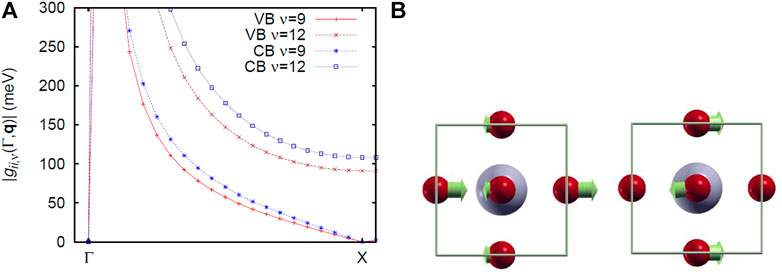
FIGURE 2. Cubic phase Pm
It is known that polar perovskite materials form Fröhlich polarons by the interaction of photogenerated carriers (electrons, holes) and longitudinal optical phonons (Fröhlich, 1954). It has been pointed out that polaron diffusion of photogenerated carriers is a factor contributing the high efficiency of methylammonium lead (MAPb) halide perovskite solar cells (Ghosh et al., 2020). Zhu et al. reported that Fröhlich polarons were generated at 0.3 ps in MAPbI3 (Miyata and Zhu, 2018), and 0.7 ps for CsPbBr3 after light irradiation (Cinquanta et al., 2019). The observed high defect tolerance is also explained by the formation of Fröhlich polarons (Miyata and Zhu, 2018). The interaction between electron and hole polarons is expected to be repulsive when the lattice distortion associated with polaron formation is large, because the Coulomb interaction between electrons and holes is shielded by the large dielectric constant of ferroelectric perovskites (Emin, 2018). Thus, the repulsive interaction between electron and hole polarons is thought to suppress bimolecular recombination and allow carriers to diffuse over long distances.
The Fröhlich constant αF, which indicates the coupling strength of Fröhlich polaron, is expressed by Feynman's Fröhlich-Hamiltonian-based path integral variational method (Feynman, 1955).
Here, ε∞ is the optical permittivity, ε0 is the electrostatic permittivity, m is the effective band mass, and ħω is the frequency of the LO phonon.
From the calculation result of electron-phonon spectral density for WO3 in the previous section, the photogenerated electrons and holes strongly interact with the longitudinal optical phonons (LO1, LO2) near the upper edge of the VB and the lower edge of the CB, respectively. Table 2 shows the Fröhlich constant αF calculated by Eq. 1. For the band effective mass, 0.216 (CBM) and 1.42 (VBM), which are the harmonic means of the electrons and hole effective masses in Table 1 and Supplementary Table S1, were used; for ε∞ and ε0, the theoretically calculated values [ (Ping et al., 2013), (Feynman et al., 1962)] were used. The Fröhlich constants of the electron-polaron by LO1 and LO2 were obtained as 0.68 and 1.02, and those of the hole-polaron as 1.74 and 2.62, respectively. Because the Fröhlich polaron generation conditions are 1< αF < 6, it is considered that the photogenerated electrons and holes could produce electrons-polarons and hole-polarons having distorted lattice deformation with locally shifted oxygen atoms. As described in Chapter III-1, it is believed that the formation of Fröhlich polarons suppresses electron-hole bimolecular recombination, and it is expected that a highly efficient internal quantum yield of photocatalysis for defect-free WO3.

TABLE 2. Fröhlich constant αF, effective mass mP, radius rp, lifetime τΚ, and mobility μΗ of electron- and hole-polarons.
The temperature dependence of the effective mass, radius, and mobility of the Fröhlich polaron is formulated by Feynman in a model of a simplified effective mass band structure that interacts with the continuum dielectric of the characteristic response frequency (Feynman, 1955; Feynman et al., 1962). Forst (Frost, 2017a) variationally solved the Feynman polaron model (Feynman, 1955) at a finite temperature (Feynman et al., 1962), and from the obtained variational parameters, developed a custom code to calculate the lifetime of polaron by Kadanoff's method (Kadanoff, 1963) and the mobility of polaron by Hellwarth et al. (Hellwarth and Biaggio, 1999); this is published in a GitHub repository (Frost, 2017b). Table 2 shows the effective mass mP of the polaron, radius rp, and Kadanoff lifetime τΚ and Hellwarth mobility μΗ at room temperature calculated by Forst's method (Frost, 2017a; Frost, 2017b). WO3 as a photocatalyst material is considered to be a promising material from the viewpoint of the mobility of the electron- and hole-polarons which are generated by interaction with LO1. In addition, W. Wang et al. predicted the electron mobility at room temperature by the first-principles calculation using the Boltzmann transport theory for the transport characteristics of WO3, and the same tendency as 485 cm2/Vs with 1,020 cm−3 doping (Wang et al., 2020). The very long electron mobility is expected to allow WO3 to be used effectively as an electron transport layer in high-efficiency solar cells.
Unfortunately, in the current first-principles calculation technology, and structural optimization of the bipolaron state (an electron-polaron and a hole-polaron coexist) with local lattice distortion is almost impossible even with the Bethe–Salpeter equation method considering the electron-hole interaction. Bousquet et al. calculated the self-trapped single-electron polaron in WO3 from density functional theory (Bousquet et al., 2020). The calculations concluded that the single polaron is at a higher energy than the fully delocalized solution and is an excited state of WO3. The shape of the density distribution corresponds to the shape of the W-dxy orbital with four lobes oriented towards the oxygen bond, consistent with the CBM of WO3. Moreover, because the dxy orbital extends in two directions (xy), the polaron formed by the entry of electrons into this dxy orbital shows a two-dimensional shape; and spin density showed that the charge of the polaron was localized in the xy plane of WO3 and did not spread to other atomic planes along the z direction. This disk-shaped electron density distribution has also been proposed from the ESR measurement of the single-electron polaron of WO3 (Salje, 1994).
Ultrahigh-speed time-resolved X-ray absorption spectra (Uemura et al., 2014; Uemura et al., 2016; Koide et al., 2020) by Asakura et al. have been interpreted as indicating that light irradiation induces local structural changes around W, with an increasing fraction of sites undergoing local structural distortion up to 150 ps. From the above calculation results, it is suggested that the local structural change after light irradiation is derived from the lattice distortion due to the formation of Fröhlich polaron.
The widely used method for describing the excited state of a solid by considering electron-hole interaction is a combination of the GW approximation (Hedin, 1965) and the Bethe-Salpeter equation (Salpeter and Bethe, 1951). However, this method is difficult to use in the calculation of large systems that may undergo localized structural changes, such as those used in this study. Therefore, we used the constrained occupation DFT method (Gali et al., 2009), which is a commonly used DFT-based method with low computational cost. In constrained occupied DFT, the total energy of the excited state configuration is approximated by the DFT total energy of the Kohn–Sham system. Where one of the occupied Kohn–Sham states drops out and a higher unoccupied Kohn–Sham state is occupied. In this study, an electron in the VBM was unoccupied and occupied by the CBM. During the self-consistent calculation of the Kohn–Sham equation, the constrained occupancy of the orbitals is fixed. In this method, the total energy is clearly defined, so that the structure of the system can be optimized.
First, the monoclinic P21/n (2 × 2 × 2 times cubic phase Pm
Observing the difference between the excited state configuration of ST2 and the charge density of the ground state (Figures 3A,B), it can be seen that the electron of one of O (p) atom on WO2 surface is excited to W (d). The charge densities of the CB and VB of ST1 (Supplementary Figures S5, S6) are both spread three-dimensionally throughout the crystal. This suggests that the electronic states of the CBM and VBM are separated into each surface due to the structural change in the excited state configuration.
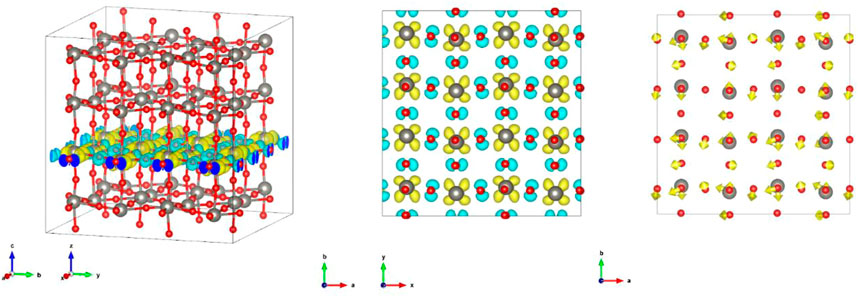
FIGURE 3. (Left) Panoramic view of the difference between the excited state configuration of ST2 and the charge density of the up spin in the ground state; (Middle) only the atomic surface of the excited surface; and (right) atomic displacement from ST1 to ST2.
Observing the displacement of atoms from ST1 to ST2 (Figure 3C), it can be seen that the W atom is displaced in the direction of the O atom in the excited state. This seems to correspond to the movement of the W atom in previous studies. In particular, the displacement of the W atom was moved in the direction of reducing the zigzag of the zigzag-W-O-W-O-chain. It was found that the O atom does not displace in the direction of the W atom. It can be seen from the distance between the W atom and the O atom near the n-th neighbor (Supplementary Table S2) that the W-O bonds near the 3rd and 4th neighborhood, which were originally almost equidistant, became shorter on one side and longer on the other side due to the structural change in the excited state. Similarly, when calculating the distance between W-O atoms for the structure shifted in the direction of force that was applied in the electronically excited state of ST1, it can be seen that, unlike the previous case, the W-O bond in the vicinity of the second neighborhood becomes longer, and the W-O bond in the vicinity of the 4th and 5th neighborhoods becomes shorter. In other words, it is suggested that the direction of the force that the atom receives are different at the beginning of the electronically excited state and when the structure finally becomes stable in the excited state configuration.
Figure 4 shows the force applied to the atom in the excited state configuration of ST1. Observing this, it can be seen that the W atom also tends to be displaced toward the O atom. As the displacement to the triclinic P1 in the excited state (Figure 3C) shows the same direction, it can be seen that the W atom continues to move to the O atom. In contrast, the O atom tries to displace in the direction of the W atom, but seems to move in the other direction from the middle.
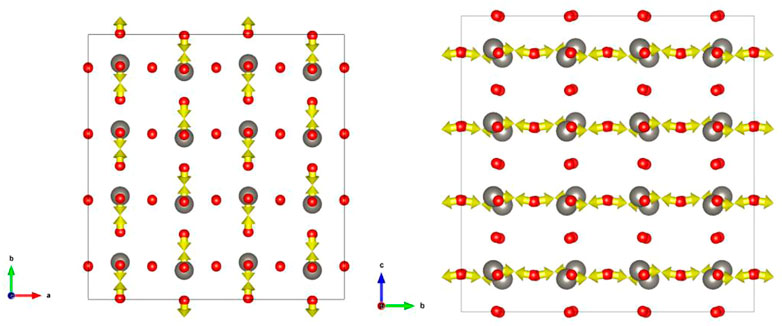
FIGURE 4. Force on atoms in ST1 excited state configuration: (Left) viewpoint in the c-axis direction; (Right) a viewpoint in the axial direction.
Figure 5 shows the band structure of ST1 and ST2 unfolded into the band structure of cubic phase Pm
An increase in pre-edge peak was observed immediately after photoexcitation in Asakura et al. The W-LI edge-time-resolved X-ray absorption spectroscopy (Koide et al., 2020) can be attributed to the increase in p-d hybrids due to orthorhombic local structural changes by Fröhlich polarons. In addition, the measured W-LI pre-edge peak intensity kinetics showed that the proportion of sites with orthorhombic local structure increased from the photoexcitation to 150 ps; and it can be understood that after 150 ps, we are observing a gradual return to the original monoclinic structure.
In this study, the structural change of WO3 in the electronic excited state was discussed by first-principles calculation from the viewpoint of carrier phonon interaction. The increase in pre-edge peaks immediately after photoexcitation observed by the ultrafast time-resolved X-ray absorption spectroscopy was discussed from the local structural changes due to Fröhlich polaron generation owing to their interaction with the optical vertical phonons. Therefore, in defect-free WO3, bimolecular recombination could be suppressed by the formation of bipolaron states, and high internal quantum yields in photocatalysis are expected. A detailed study of the defect structure is needed to further increase the quantum yield of WO3 in photocatalysis. The bipolaron state of the electronic polaron and hole polaron is an unstable state in the electronic excitation state, and is relaxed to a stable structure in the electronic excitation state by phonon-phonon interaction. The gradual increase in W-LI pre-edge peak intensity up to 150 ps indicates an increase in the proportion of sites with local structural changes due to Fröhlich polaron formation. In the stable structure, the electron and hole are delocalized at the top of the conduction band and the valence band, respectively. However, the transition dipole moment is indirectly transitional and almost zero. As observed by the ultra-high-speed time-resolved X-ray absorption spectroscopy experiment, it is considered that there is no radiation transition from the stable structure of the electronically excited state to the ground state with a relaxation time of 1800 ps.
However, the above discussion is based on the result of the electronic state theory in one electron approximation, and hence is quantitatively insufficient. In particular, the introduction of the Bethe-Salpeter method, which considers the electron-hole pair interaction, is indispensable for describing the excited state in which the electron-hole pair exists. Moreover, to describe the polaron state, band calculation in a very large supercell is required.
On the other hand, some important issues remain to be solved, such as the microscopic mechanism of hot excitons to Fröhlich polaron formation in the early stage of photoexcitation, the interaction between electron polaron and hole polaron, and the competitive mechanism between carrier conduction and local structural change, and theoretical studies to elucidate these issues are planned in the future.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
MK and KY performed the DFT calculation. All authors discussed the results and commented on the manuscript. KY supervised the project.
This research was supported by JSPS KAKENHI in Scientific Research on Innovative Areas “Innovations for Light-Energy Conversion (I4LEC)”, and by MEXT as “Program for Promoting Researches on the Supercomputer Fugaku” (Realization of innovative light energy conversion materials utilizing the supercomputer Fugaku, JPMXP1020210317) KY acknowledges the support from Toyota Physical and Chemical Research Institute. The computations were performed at the Research Center for Computational Science, Okazaki, Japan (Project: 22-IMS-C039).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.933044/full#supplementary-material
Cubic phase Pm
Cubic phase Pm
Phonon band.
Phonon DOS.
ST1 contribution of CB, CB+1, CB+2, CB+3 (1.442, 1.512, 1.512, 1.517 eV) wavefunctions to the charge density.
ST1 contribution of VB, VB+1, VB+2, VB+3 (0.000, -0.004, -0.004, -0.007 eV) wavefunctions to the charge density.
Effective mass of cubic phase Pm
Mean of distance between W atom and O atom near nth (Å).
Amano, F., Ishinaga, E., and Yamakata, A. (2013). Effect of particle size on the photocatalytic activity of WO3 particles for water oxidation. J. Phys. Chem. C 117, 22584–22590. doi:10.1021/jp408446u
Ameta, R., and Ameta, S. C. (2017). Photocatalysis: Principles and applications. Boca Raton: CRC Press.
Bousquet, E., Hamdi, H., Aguado-Puente, P., Salje, E. K. H., Artacho, E., and Ghosez, P. (2020). First-principles characterization of single-electron polaron in WO3. Phys. Rev. Res. 2, 012052. doi:10.1103/physrevresearch.2.012052
Cinquanta, E., Meggiolaro, D., Motti, S. G., Gandini, M., Alcocer, M. J. P., Akkerman, Q. A., et al. (2019). Ultrafast THz probe of photoinduced polarons in lead-halide perovskites. Phys. Rev. Lett. 122 (16), 166601. doi:10.1103/physrevlett.122.166601
Emin, D. (2018). Barrier to recombination of oppositely charged large polarons. J. Appl. Phys. 123, 055105. doi:10.1063/1.5019834
Fàbrega, C., Murcia-López, S., Monllor-Satocaa, D., Prades, J. D., Hernández-Alonsoc, M. D., Penelas, G., et al. (2016). Efficient WO3 photoanodes fabricated by pulsed laser deposition for photoelectrochemical water splitting with high faradaic efficiency. Appl. Catal. B Environ. 189, 133–140. doi:10.1016/j.apcatb.2016.02.047
Feynman, R. P., Hellwarth, R. W., Iddings, C. K., and Platzman, P. M. (1962). Mobility of slow electrons in a polar crystal. Phys. Rev. 127, 1004–1017. doi:10.1103/physrev.127.1004
Feynman, R. P. (1955). Slow electrons in a polar crystal. Phys. Rev. 97 (3), 660–665. doi:10.1103/physrev.97.660
Frost, J. M. (2017). Calculating polaron mobility in halide perovskites. Phys. Rev. B 96, 195202. doi:10.1103/physrevb.96.195202
Fröhlich, H. (1954). Electrons in lattice fields. Adv. Phys. X. 3 (11), 325–361. doi:10.1080/00018735400101213
Gali, A., Janzén, E., Deák, P., Kresse, G., and Kaxiras, E. (2009). Theory of spin-conserving excitation of theN−V−Center in diamond. Phys. Rev. Lett. 103, 186404. doi:10.1103/physrevlett.103.186404
Ghosh, D., Welch, E., Neukirch, A. J., Zakhidov, A., and Tretiak, S. (2020). Polarons in halide perovskites: A perspective. J. Phys. Chem. Lett. 11 (9), 3271–3286. doi:10.1021/acs.jpclett.0c00018
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502. doi:10.1088/0953-8984/21/39/395502
Giustino, F. (2017). Electron-phonon interactions from first principles. Rev. Mod. Phys. 89, 015003. doi:10.1103/revmodphys.89.015003
González-Borrero, P. P., Sato, F., Medina, A. N., Baesso, M. L., Bento, A. C., Baldissera, G., et al. (2010). Optical band-gap determination of nanostructured WO3 film. Appl. Phys. Lett. 96, 061909. doi:10.1063/1.3313945
Hamann, D. R. (2013). Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 88, 085117. doi:10.1103/physrevb.88.085117
Hamdi, H., Salje, E. K. H., Ghosez, P., and Bousquet, E. (2016). First-principles reinvestigation of bulk WO3. Phys. Rev. B 94, 245124. doi:10.1103/physrevb.94.245124
Hedin, L. (1965). New method for calculating the one-particle green’s function with application to the electron-gas problem. Phys. Rev. 139, A796–A823. doi:10.1103/physrev.139.a796
Hellwarth, R. W., and Biaggio, I. (1999). Mobility of an electron in a multimode polar lattice. Phys. Rev. B 60, 299–307. doi:10.1103/physrevb.60.299
Howard, C. J., Luca, V., and Knight, K. S. (2001). High-temperature phase transitions in tungsten trioxide - the last word? J. Phys. Condens. Matter 14, 377–387. doi:10.1088/0953-8984/14/3/308
Hua, X., Chen, X., and Goddard, W. A. (1997). Generalized generalized gradient approximation:an improved density-functional theory for accurate orbital eigenvalues. Phys. Rev. B 55, 16103–16109. doi:10.1103/physrevb.55.16103
Kadanoff, L. P. (1963). Boltzmann equation for polarons. Phys. Rev. 130, 1364–1369. doi:10.1103/physrev.130.1364
Kamat, P. V. (2007). Meeting the clean energy Demand: nanostructure architectures for solar energy conversion. J. Phys. Chem. C 111, 2834–2860. doi:10.1021/jp066952u
Kiu, X., Wang, F., and Wang, Q. (2012). Nanostructure-based WO3 photoanodes for photo-electrochemical water splitting. Phys. Chem. Chem. Phys. 14, 7894–7911. doi:10.1039/c2cp40976c
Koide, A., Uemura, Y., Kido, D., Wakisaka, Y., Takakusagi, S., Ohtani, B., et al. (2020). Photoinduced anisotropic distortion as the electron trapping site of tungsten trioxide by ultrafast W L1-edge X-ray absorption spectroscopy with full potential multiple scattering calculations. Phys. Chem. Chem. Phys. 22, 2615–2621. doi:10.1039/c9cp01332f
Kokalj, A. (2003). Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Comput. Mater. Sci. 28, 155–168. doi:10.1016/s0927-0256(03)00104-6
Kudo, A., and Miseki, Y. (2009). Heterogeneous photocatalyst materials for water splitting. Chem. Soc. Rev. 38, 253–278. doi:10.1039/b800489g
Locherer, K. R., Swainson, I. P., and Salje, E. K. H. (1999). Phase transitions in tungsten trioxide at high temperatures - a new look. J. Phys. Condens. Matter 11, 6737–6756. doi:10.1088/0953-8984/11/35/312
Maeda, K., and Domen, K. (2010). Photocatalytic water splitting: Recent progress and future challenges. J. Phys. Chem. Lett. 1, 2655–2661. doi:10.1021/jz1007966
Marini, A., Hogan, C., Grüning, M., and Varsano, D. (2009). Yambo: An ab initio tool for excited state calculations. Comput. Phys. Commun. 180, 1392–1403. doi:10.1016/j.cpc.2009.02.003
Medeiros, P. V. C., Stafström, S., and Björk, J. (2014). Effects of extrinsic and intrinsic perturbations on the electronic structure of graphene: Retaining an effective primitive cell band structure by band unfolding. Phys. Rev. B 89, 041407. doi:10.1103/physrevb.89.041407
Medeiros, P. V. C., Tsirkin, S. S., Stafström, S., and Björk, J. (2015). Unfolding spinor wave functions and expectation values of general operators: Introducing the unfolding-density operator. Phys. Rev. B 91, 041116. doi:10.1103/physrevb.91.041116
Migas, D. B., Shaposhnikov, V. L., Rodin, V. N., and Borisenko, V. E. (2010). Tungsten oxides. I. Effects of oxygen vacancies and doping on electronic and optical properties of different phases of WO3. J. Appl. Phys. 108, 093713. doi:10.1063/1.3505688
Miyata, K., and Zhu, X. Y. (2018). Ferroelectric large polarons. Nat. Mat. 17 (5), 379–381. doi:10.1038/s41563-018-0068-7
Momma, K., and Izumi, F. (2011). VESTA 3for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276. doi:10.1107/s0021889811038970
Niklasson, G. A., and Granqvist, C. G. (2007). Electrochromics for smart windows: Thin films of tungsten oxide and nickel oxide, and devices based on these. J. Mat. Chem. 17, 127–156. doi:10.1039/b612174h
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865
Pesci, F. M., Cowan, A. J., Alexander, B. D., Durrant, J. R., and Klug, D. R. (2011). Charge carrier dynamics on mesoporous WO3 during water splitting. J. Phys. Chem. Lett. 2, 1900–1903. doi:10.1021/jz200839n
Ping, Y., Rocca, D., and Galli1, G. (2013). Optical properties of tungsten trioxide from first-principles calculations. Phys. Rev. B 87, 165203. doi:10.1103/physrevb.87.165203
Regan, K. P., Koenigsmann, C., Sheehan, S. W., Konezny, S. J., and Schmuttenmaer, C. A. (2016). Size-dependent ultrafast charge carrier dynamics of WO3 for photoelectrochemical cells. J. Phys. Chem. C 120, 14926–14933. doi:10.1021/acs.jpcc.6b04390
Salpeter, E. E., and Bethe, H. A. (1951). A relativistic equation for bound-state problems. Phys. Rev. 84, 1232–1242. doi:10.1103/physrev.84.1232
Sangalli, D., Ferretti, A., Miranda, H., Attaccalite, C., Marri, I., Cannuccia, E., et al. (2019). Many-body perturbation theory calculations using the Yambo code. J. Phys. Condens. Matter 31, 325902. doi:10.1088/1361-648x/ab15d0
Uemura, Y., Kido, D., Wakisaka, Y., Uehara, H., Ohba, T., Niwa, Y., et al. (2016). Dynamics of photoelectrons and structural changes of tungsten trioxide observed by femtosecond transient XAFS. Angew. Chem. Int. Ed. 55, 1364–1367. doi:10.1002/anie.201509252
Uemura, Y., Uehara, H., Niwa, Y., Nozawa, S., Sato, T., Adachi, S., et al. (2014). In situ picosecond XAFS study of an excited state of tungsten oxide. Chem. Lett. 43, 977–979. doi:10.1246/cl.140144
van Setten, M. J., Giantomassi, M., Bousquet, E., Verstraete, M. J., Hamann, D. R., Gonze, X., et al. (2018). The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 226, 39–54. doi:10.1016/j.cpc.2018.01.012
Vogt, T., Woodward, P. M., and Hunter, B. A. (1999). The high-temperature phases of WO3. J. Solid State Chem. 144, 209–215. doi:10.1006/jssc.1999.8173
Wang, F., Di Valentin, C., and Pacchioni, G. (2011). Electronic and structural properties of WO3: A systematic hybrid DFT study. J. Phys. Chem. C 115, 8345–8353. doi:10.1021/jp201057m
Wang, W., Kang, Y., Peelaers, H., Krishnaswamy, K., and Van de Walle, C. G. (2020). 045116First-principles study of transport in WO3. Phys. Rev. B 101. doi:10.1103/physrevb.101.045116
Woodward, P. M., Sleight, A. W., and Vogt, T. (1995). Structure refinement of triclinic tungsten trioxide. J. Phys. Chem. Solids 56, 1305–1315. doi:10.1016/0022-3697(95)00063-1
Yang, H., Sun, H., Li, Q., Li, P., Song, K., Song, B., et al. (2019). Structural, electronic, optical and lattice dynamic properties of the different WO3 phases: First-principle calculation. Vacuum 164, 411–420. doi:10.1016/j.vacuum.2019.03.053
Keywords: electron-phonon interaction, Fröhlich-Polaron, electronically excited state, WO3 photocatalyst, density functional theory
Citation: Kaneko M, Nozawa S and Yamashita K (2022) Electron-phonon interaction and structural changes in the electronically excited state of WO3 photocatalyst. Front. Energy Res. 10:933044. doi: 10.3389/fenrg.2022.933044
Received: 30 April 2022; Accepted: 27 September 2022;
Published: 12 October 2022.
Edited by:
Sergei Manzhos, National University of Singapore, SingaporeReviewed by:
Minglei Sun, King Abdullah University of Science and Technology, Saudi ArabiaCopyright © 2022 Kaneko, Nozawa and Yamashita. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Koichi Yamashita, eWFtYXNpdGFAY2hlbXN5cy50LnUtdG9reW8uYWMuanA=
‡ORCID: Shunsuke Nozawa, orcid.org/org/0000-0003-4977-6849
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.