- 1School of Electrical Engineering, Southeast University, Nanjing, China
- 2College of Energy and Electrical Engineering, Hohai University, Nanjing, China
The high-penetrated renewables enable flexible and versatile dispatchable resources in power systems. As the digitalization process improves with the help of information and communication technology (ICT), a real-time online control framework is essential to regulate such a low-inertia power system dominated by renewables. To enable control practices, a control-oriented model is developed linking load increments to frequency dynamics. Based on such a control-oriented model, a model predictive control (MPC)–based online feedback algorithm is well designed by the virtue of rapid data transmission enabled by digitalization. The MPC optimization is a convex quadratic programming, where an objective function that balances frequency deviations and load increments is formulated and operational constraints are integrated into a matrix-type inequality. In the end, the proposed MPC-based load-frequency control framework is illustrated by several case studies, where validations and analyses of constraints inside the model are also included.
Introduction
Driven by the global climate change, renewables such as solar and wind are increasingly developed and connected to the current power system (Creutzig et al., 2014; Ge et al., 2022) using a concept of grid-forming (GFM) converter. Such renewables bring more dispatchable resources but also challenge the existing power system control framework due to the fact that most renewables have limited inertia support to the power system operation (Milano et al., 2018; Ratnam et al., 2020). To regulate such a low-inertia power system effectively and efficiently, a digitalization process has been conducted supported by information and communication technology (ICT) to enable rapid regulations in response to fast dynamics induced by low inertia (Ratnam et al., 2020; Di Silvestre et al., 2018). Such digitalization allows for high amounts of data, fast data transmission, and high-efficiency computation to further achieve a fully intelligent feedback control scheme in future power systems (Di Silvestre et al., 2018; Wu et al., 2021).
By the virtue of such a digitalization process, various control algorithms (Obaid et al., 2019; Fernández-Guillamón et al., 2019) have been investigated to maintain frequency stability (a priority in power system control). For example, Lyapunov-based stability analysis methods (Jin et al., 2019; Luo et al., 2020; Shang-Guan et al., 2020) are developed to guarantee frequency stability; the H2/H∞ controller (Zou et al., 2021) is designed to optimize the frequency dynamics performance; and a fuzzy event-triggered scheme (Shangguan et al., 2021) is employed to improve frequency control stability with limited communication expense. Moreover, different kinds of control properties can be satisfied in frequency control, that is, asymptotic (Guerrero et al., 2010; Xu et al., 2018; Singhal et al., 2022), finite-time (Zuo et al., 2016; Ge et al., 2020), and fixed-time (Ni et al., 2016), if we can model the system dynamics appropriately. However, many of these methods require full or partial models available at dispatchable points, which may not be feasible under the case where the load-frequency dynamics are aggregated by massive and small-capacity dispatchable loads such as residential PVs and electric vehicles.
On the other hand, owing to the fast response of feedback control methods (Zou et al., 2021; Shangguan et al., 2021; Zuo et al., 2016), control input saturations are considered in the actuation, which would not lead to optimized input sequences. Hence, practical operation constraints, for example, frequency nadir and RoCoF (rate of change of frequency), are essential to be considered in frequency regulation. If we cannot appropriately consider such constraints, the optimal operation would be degraded, or the system would face security issues. Such constraints have also been considered in the existing research work (Markovic et al., 2018; Stanojev et al., 2020). However, constrained load-frequency control regulation has not been fully investigated in terms of comprehensive constraints.
Therefore, to move forward even one step to cope with the aforementioned challenges, a real-time online control framework is proposed to regulate such a low-inertia power system frequency utilizing dispatchable load resources. The main contributions can be concluded as follows. To narrow down the gap between power-electronic dynamics and power flow models, we model the whole system dynamics by combining power-electronic–dominated dynamics and steady-state power flow–based Jacobian matrix. More specifically, GFM-inverter–based generator dynamics is unified in either a droop type or a VSG type. Based on such a control-oriented model concerning load increment and frequency dynamics, to fully consider the operational rules in practice, inspired by Stanojev et al. (2020) and Ge et al. (2021), we design a model predictive control (MPC)–based online feedback algorithm utilizing rapid sensing, computation, and actuation enabled by the power system digitalization trend. The constraints of frequency deviations, RoCoF, dispatchable load capacity, and load change ramping rate are integrated into a matrix-type inequality, which can be easily optimized subjected to an objective function that balances frequency deviations and load increments.
The rest of this article is organized as follows. Section 2 gives the model of GFM-inverter–involved power systems. In Section 3, an MPC-based control design is provided. Section 4 demonstrates the control performance, and Section 5 concludes this article.
Modeling for GFM-Based System
In this section, we will present the detailed modeling of an inverter-based power system. First, we start from a unified model of GFM inverters, where droop-based control and virtual synchronized generator–based control are included. Then, a control-oriented model of the whole system that considers the line impedance effect is proposed, which will bring the benefits in the grid-level control and operation.
System Description
A GFM inverter normally consists of three control loops, that is, power control loop, voltage control loop, and current control loop, as depicted in Figure 1. The power controller provides the reference for the voltage controller and the reference angular frequency for the whole inverter control system, while the voltage controller and current controller guarantee the non-steady-error–tracking performance of output voltage. Two mainstream power control loops of GFM inverters are VSG-based control and droop-based control, the dynamics of which can be, respectively, expressed as
where
A unified small-signal model that describes one inverter’s frequency dynamics can be expressed by
2.2 Control-Oriented Model of a Multi-GFM-Inverter–Penetrated Power System
Eq. 2 builds a relationship between the generator’s power output and system frequency dynamics, and it can be expanded to a multi-GFM system with appropriate stacking. However, in current power systems, massive load resources can also provide huge capability participating in frequency response. Compared to inverter-based generators, loads are owned by local aggregators who can use flexible loads to offer frequency regulation capability. Hence, it is of great importance to directly link the load change to the system’s frequency dynamics, further guiding the participation of load aggregators. The challenge is that the dynamics from flexible and massive loads are difficult to depict because aggregated and equivalent inertia and damping are not available directly. Hence, we hereafter build a control-oriented model, which utilizes the inverter’s dynamics and network topology, describing load-frequency dynamics.
For the sake of modeling multi-inverter systems, we generalize the model (2) with the subscript
For a multi-inverter system, the dynamics can be easily extended. Define a power system with m inverters:
with
The model (4) is developed from a generator perspective. However, a power grid also includes lines and loads. To involve such line impedance and load demand, we recall the power flow equation that has been widely investigated (Shen et al., 2020; Zimmerman et al., 2010), that is,
To form a control-oriented model of the whole power system, we split the power flow equation into generator nodes and load nodes, that is,
where the subscript G means the generator node, while the subscript L means the load node. From the second row of (5), we can obtain
where
3 Modeling Application: Model Predictive Control Design
In this section, based on the previous model, we proposed a secondary frequency control method based on the MPC algorithm.
Currently, the digitalization in the power system leads to a digital control mode; hence, we need to form the system in a discrete-time way that is more practical in the real world. Based on the continuous model (6), the discrete-time state-space model using the sampling time
where
MPC is an optimal control that can fully consider state, output, and input constraints. Such constraints are useful in frequency control because the load increment and output frequency have intrinsic limits. The first thing to form predictive control is to form a model-based prediction system based on (7), that is,
where N denotes the prediction horizon and “
with
Then, we can use the prediction model (8) to form the objective as follows:
with
It should be noted that the matrices
Throughout the load-frequency control of demand response, there are four classes of constraints, that is, frequency security limits, RoCoF (rate of change of frequency) limits, dispatchable load capacity limits, and load change ramping limits. For the frequency security limits, we should guarantee the generator frequency inside the valid operation limits, that os,
where
where
where
As a result, combining all objective function and constraints from (10) to (15), we can obtain the MPC optimization problem in a compact matrix form:
where
It should be noted that the objective function is simplified from (11) by reducing the constant term
The proposed MPC-based secondary frequency control has two main advantages compared to conventional methods such as PI controllers. More specifically, the PI controller is a non-constrained control method, while the proposed MPC method can handle frequency constraints, which will be investigated comprehensively in. On the other side, the MPC method can even give sequential control commands in the presence of random packet loss due to its prediction horizon mechanism, although the tolerant packet loss length is limited by the prediction horizon. The fault tolerance capability is obvious because the system operator can use the sequential control commands of
Due to the modeling of the whole power system based on the small-signal model (6), we need to update the Jacobian matrix
provides a solution to regulate system frequency dynamics using dispatchable loads. However, the MPC algorithm itself would not be feasible if system constraints such as the load change ramping rate and load change capability have strict limits. To handle this problem, we should evaluate and then relax the constraints firstly. Then, if the constraints cannot make the MPC optimization feasible, we should combine the generator’s capability and load-shedding operation to guarantee frequency stability. This topic is out of this article’s scope and will be considered in our future work.
Simulation Results
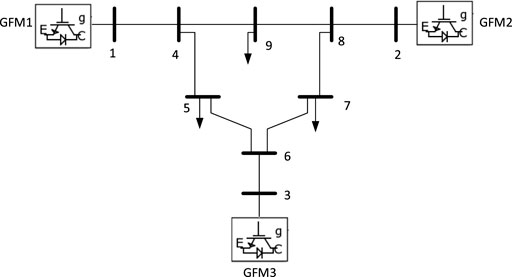
In this section, we will establish a modified IEEE 9 bus system (Zimmerman et al., 2010) with three GFM inverters to illustrate the effectiveness of the propose MPC optimization–based secondary load-frequency control using a control-oriented model. The topology and the parameter of the system are detailed in Figure 2 and Table 2, respectively.
General Frequency Control Performance
In the first case study, we evaluate the control performance of the proposed MPC-based frequency regulation algorithm. The system is operating under the situation where there exist small frequency deviations initially. At t = 4 s, the proposed MPC optimization is activated, and a load increase of 0.02 p.u. and a load decrease of 0.025 p.u. occur at node 7, t = 7 s and node 9, t = 10 s, respectively. As shown in Figure 3, the frequency deviations can be restored to the reference value with appropriate load change, and all constraints are fully satisfied.
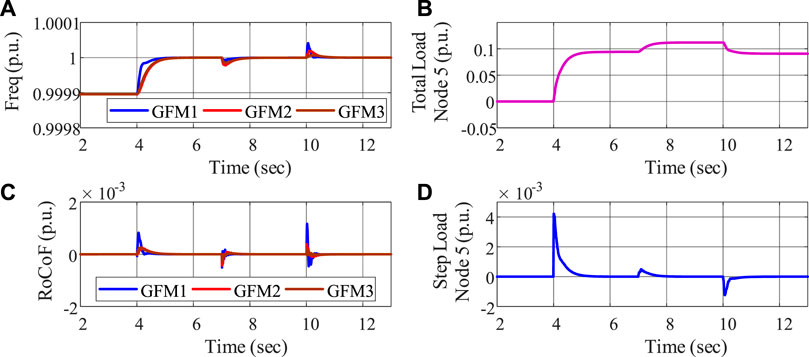
FIGURE 3. Load-frequency response: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.
Validation and Analysis of Constraints
To validate the constraint implementation, the case in is seen as the baseline case. We first set the dispatchable load capacity
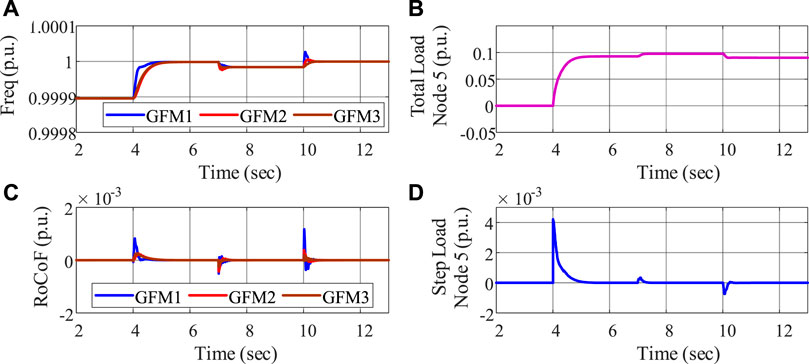
FIGURE 4. Dispatchable load capacity constraint evaluation: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.
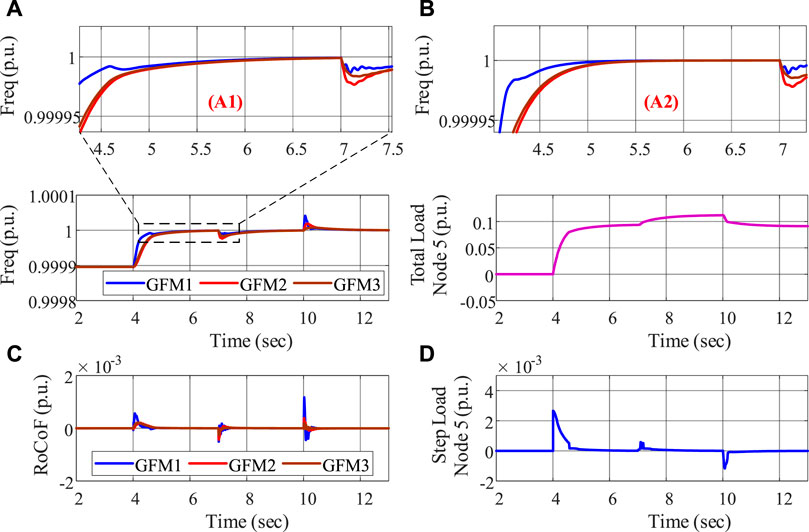
FIGURE 5. Load ramping rate constraint evaluation: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.
Then, we turn to frequency constraints, for which we first double the loads on all nodes to enlarge the frequency deviations and set
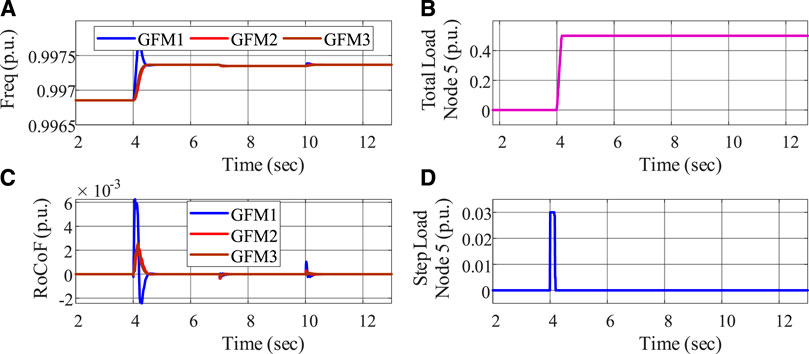
FIGURE 6. Frequency constraint evaluation with tight input constraints: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.
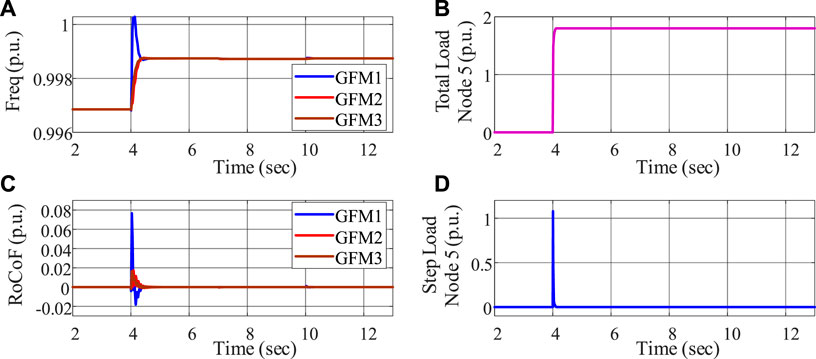
FIGURE 7. Frequency constraint evaluation with relaxed input constraints: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.
Conclusion
This article proposed a control-oriented model to link the load increment to the frequency dynamics of the GFM-based generator. This model combines the well-developed power flow analysis to obtain the steady-state Jacobian matrix and state-space dynamic models of GFM generators, to formulate the simplified and linearized power system model. Based on this model, though there exists some modeling uncertainty due to the linearization process, we can design the control algorithm to enable rapid load-frequency regulations. To fully consider constraints in frequency regulation, the MPC optimization algorithm is utilized to form an online feedback control that satisfies frequency security limits, RoCoF limits, dispatchable load capacity limits, and load change ramping limits. The constraints normally come from the practical operational rules, which can be easily integrated into convex quadratic programming and solved using well-developed tools. The effectiveness of the proposed frequency regulation algorithm is finally validated by comprehensive simulations and analyses based on a modified IEEE 9 bus system using MATLAB/Simulink.
However, the proposed method is based on the small-signal analysis, which limits the model applicability near the equilibrium point of the power system. In the future, to fully depict the system operation dynamics, large-signal methods should be further involved, and we will consider this in our following research.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
XQ: establishing the model, running the simulation, and writing the paper. JZ: advising and revising the paper. FM: advising and revising the paper.
Funding
This work was funded by the Key R&D Plan of Jiangsu Province (BE2020027) and Jiangsu International Science and Technology Cooperation Project (BZ2021012).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Creutzig, F., Goldschmidt, J. C., Lehmann, P., Schmid, E., von Blücher, F., Breyer, C., Fernandez, B., Jakob, M., Knopf, B., Lohrey, S., Susca, T., and Wiegandt, K. (2014). Catching Two European Birds with One Renewable Stone: Mitigating Climate Change and Eurozone Crisis by an Energy Transition. Renew. Sustain. Energy Rev. 38, 1015–1028. doi:10.1016/j.rser.2014.07.028
Di Silvestre, M. L., Favuzza, S., Riva Sanseverino, E., and Zizzo, G. (2018). How Decarbonization, Digitalization and Decentralization Are Changing Key Power Infrastructures. Renew. Sustain. Energy Rev. 93, 483–498. doi:10.1016/j.rser.2018.05.068
Fernández-Guillamón, A., Gómez-Lázaro, E., Muljadi, E., and Molina-García, Á. (2019). Power Systems with High Renewable Energy Sources: A Review of Inertia and Frequency Control Strategies over Time. Renew. Sustain. Energy Rev. 115, 109369. doi:10.1016/j.rser.2019.109369
Ge, P., Chen, B., and Teng, F. (2021). Event‐triggered Distributed Model Predictive Control for Resilient Voltage Control of an Islanded Microgrid. Int. J. Robust Nonlinear Control 31 (6), 1979–2000. doi:10.1002/rnc.5238
Ge, P., Dou, X., Quan, X., Hu, Q., Sheng, W., Wu, Z., et al. (2020). Extended-state-observer-based Distributed Robust Secondary Voltage and Frequency Control for an Autonomous Microgrid. IEEE Trans. Sustain. Energy 11 (1), 195–205. doi:10.1109/tste.2018.2888562
Ge, P., Teng, F., Konstantinou, C., and Hu, S. (2022). A Resilience-Oriented Centralised-To-Decentralised Framework for Networked Microgrids Management. Appl. Energy 308, 118234. doi:10.1016/j.apenergy.2021.118234
Guerrero, J. M., Vasquez, J. C., Matas, J., De Vicuña, L. G., and Castilla, M. (2010). Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach toward Standardization. IEEE Trans. industrial Electron. 58 (1), 158–172. doi:10.1109/TIE.2010.2066534
Jin, L., Zhang, C.-K., He, Y., Jiang, L., and Wu, M. (2019). Delay-dependent Stability Analysis of Multi-Area Load Frequency Control with Enhanced Accuracy and Computation Efficiency. IEEE Trans. Power Syst. 34 (5), 3687–3696. doi:10.1109/tpwrs.2019.2902373
Luo, H., Hiskens, I. A., and Hu, Z. (2020). Stability Analysis of Load Frequency Control Systems with Sampling and Transmission Delay. IEEE Trans. Power Syst. 35 (5), 3603–3615. doi:10.1109/tpwrs.2020.2980883
Markovic, U., Chu, Z., Aristidou, P., and Hug, G. (2018). LQR-Based Adaptive Virtual Synchronous Machine for Power Systems with High Inverter Penetration. IEEE Trans. Sustain. Energy 10 (3), 1501–1512. doi:10.1109/TSTE.2018.2887147
Markovic, U., Stanojev, O., Aristidou, P., Vrettos, E., Callaway, D., and Hug, G. (2021). Understanding Small-Signal Stability of Low-Inertia Systems. IEEE Trans. Power Syst. 36 (5), 3997–4017. doi:10.1109/tpwrs.2021.3061434
Milano, F., Dörfler, F., Hug, G., Hill, D. J., and Verbič, G. (2018). “Foundations and Challenges of Low-Inertia Systems,” in 2018 Power Systems Computation Conference (PSCC) (New York: IEEE), 1–25.
Ni, J., Liu, L., Liu, C., Hu, X., and Li, S. (2016). Fast Fixed-Time Nonsingular Terminal Sliding Mode Control and its Application to Chaos Suppression in Power System. IEEE Trans. Circuits Syst. II Express Briefs 64 (2), 151–155. doi:10.1109/TCSII.2016.2551539
Obaid, Z. A., Cipcigan, L. M., Abrahim, L., and Muhssin, M. T. (2019). Frequency Control of Future Power Systems: Reviewing and Evaluating Challenges and New Control Methods. J. Mod. Power Syst. Clean. Energy 7 (1), 9–25. doi:10.1007/s40565-018-0441-1
Ratnam, K. S., Palanisamy, K., and Yang, G. (2020). Future Low-Inertia Power Systems: Requirements, Issues, and Solutions - A Review. Renew. Sustain. Energy Rev. 124, 109773. doi:10.1016/j.rser.2020.109773
Shang-Guan, X., He, Y., Zhang, C., Jiang, L., Spencer, J. W., and Wu, M. (2020). Sampled-data Based Discrete and Fast Load Frequency Control for Power Systems with Wind Power. Appl. Energy 259, 114202. doi:10.1016/j.apenergy.2019.114202
Shangguan, X. C., He, Y., Zhang, C. K., Jiang, L., and Wu, M. (2021). Adjustable Event-Triggered Load Frequency Control of Power Systems Using Control Performance Standard-Based Fuzzy Logic. IEEE Trans. Fuzzy Syst. 30 (8), 3297–3311. doi:10.1109/tfuzz.2021.3112232
Shen, J., Li, W., Liu, L., Jin, C., Wen, K., and Wang, X. (2020). Frequency Response Model and its Closed-form Solution of Two-Machine Equivalent Power System. IEEE Trans. Power Syst. 36 (3), 2162–2173. doi:10.1109/TPWRS.2020.3037695
Singhal, A., Vu, T. L., and Du, W. (2022). Consensus Control for Coordinating Grid-Forming and Grid-Following Inverters in Microgrids. IEEE Trans. Smart Grid, 1. doi:10.1109/tsg.2022.3158254
Stanojev, O., Markovic, U., Aristidou, P., Hug, G., Callaway, D. S., and Vrettos, E. (2020). MPC-Based Fast Frequency Control of Voltage Source Converters in Low-Inertia Power Systems. IEEE Trans. Power Syst. 37, 3209–3220. doi:10.1109/TPWRS.2020.2999652
Tøndel, P., Johansen, T. A., and Bemporad, A. (2003). An Algorithm for Multi-Parametric Quadratic Programming and Explicit MPC Solutions[J]. Automatica 39 (3), 489–497. doi:10.1016/S0005-1098(02)00250-9
Wu, Y., Wu, Y., Guerrero, J. M., and Vasquez, J. C. (2021). Digitalization and Decentralization Driving Transactive Energy Internet: Key Technologies and Infrastructures. Int. J. Electr. Power & Energy Syst. 126, 106593. doi:10.1016/j.ijepes.2020.106593
Xu, Y., Sun, H., Gu, W., Xu, Y., and Li, Z. (2018). Optimal Distributed Control for Secondary Frequency and Voltage Regulation in an Islanded Microgrid. IEEE Trans. Industrial Inf. 15 (1), 225–235.
Zimmerman, R. D., Murillo-Sánchez, C. E., and Thomas, R. J. (2010). MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. power Syst. 26 (1), 12–19. doi:10.1109/TPWRS.2010.2051168
Zou, Y., Qian, J., Zeng, Y., Ismail, S., Dao, F., Feng, Z., Nie, C., and Mei, H. (2021). Optimized Robust Controller Design Based on CPSOGSA Optimization Algorithm and H 2/H ∞ Weights Distribution Method for Load Frequency Control of Micro-grid. IEEE Access 9, 162093–162107. doi:10.1109/access.2021.3132729
Keywords: load-frequency regulation, grid-forming inverter, model predictive control, demand response, power system digitalization
Citation: Qi X, Zheng J and Mei F (2022) Model Predictive Control–Based Load-Frequency Regulation of Grid-Forming Inverter–Based Power Systems. Front. Energy Res. 10:932788. doi: 10.3389/fenrg.2022.932788
Received: 30 April 2022; Accepted: 23 June 2022;
Published: 24 August 2022.
Edited by:
Mingyu Yan, Imperial College London, United KingdomCopyright © 2022 Qi, Zheng and Mei. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianyong Zheng, anlfemhlbmdAc2V1LmVkdS5jbg==
 Xiaojing Qi
Xiaojing Qi Jianyong Zheng
Jianyong Zheng Fei Mei
Fei Mei