An Investment Efficiency Evaluation Model for Distribution Network With Distributed Renewable Energy Resources

Introduction

Power grid investment is a crucial part of power grid operation and management, which has the characteristics of a high investment amount and a long payback period (Li et al., 2021). Under the intricate internal and external investment environment, investment efficiency becomes the key orientation and basic criterion for power grid investment decision-making. However, the investment profit is gradually declining under the massive power grid investment demand and scale (Lv and Yang, 2020; Sha et al., 2021). And, the operation pressure on the power grid is increasingly severe. Therefore, the improvement of investment efficiency has become the focus of power grid planning.

With the acceleration of global energy transition, renewable energy is an extremely crucial stage in the energy development process. Considering the long-distance electricity interconnection of centralized generation, distributed renewable energy generation, which reduces the transmission line construction costs, decreases carbon dioxide emissions, and enhances the benefits to society, has become the focus of modern power systems (Olujobi, 2020; Wu et al., 2021). However, the inherent intermittency and volatility of renewable energy increase the uncontrollability of the power grid, which can affect the safety and stability of the power system and improve the system maintenance costs. In addition, the investment costs increase due to the massive renewable energy equipment (Olujobi, 2020; Zhong et al., 2020; Zhang et al., 2022). Consequently, considering the uncertainty of the benefits brought about by the grid connection of distributed renewable energy sources, it is extremely vital to construct a scientific evaluation model for the investment efficiency of the distribution network, which improves the quality of power grid investment.

The Evaluation Indicator System of Investment Benefit

Accurately evaluating the changes in the investment benefit of the power grid after the integration of distributed renewable energy is the basis for calculating investment efficiency. The traditional investment benefit refers to the achievement of investment activities, that is, the economic benefit obtained through investment (Wang et al., 2019; Erdiwansyah et al., 2021; Wu et al., 2021). Based on the clean, low-carbon, and sustainable characteristics of renewable energy, investing in it will produce not only economic benefits but also environmental and social benefits. The social benefits of investment refer to the impact of the construction and operation of investment projects on social development, employment, and technological innovation, which have a positive effect on improving the social image of the power grid. The environmental benefits of investment refer to the improvement of resources and ecology through the construction and operation of investment projects (Lv and Yang, 2020; Wang, 2020; Padhy and Panda, 2021).

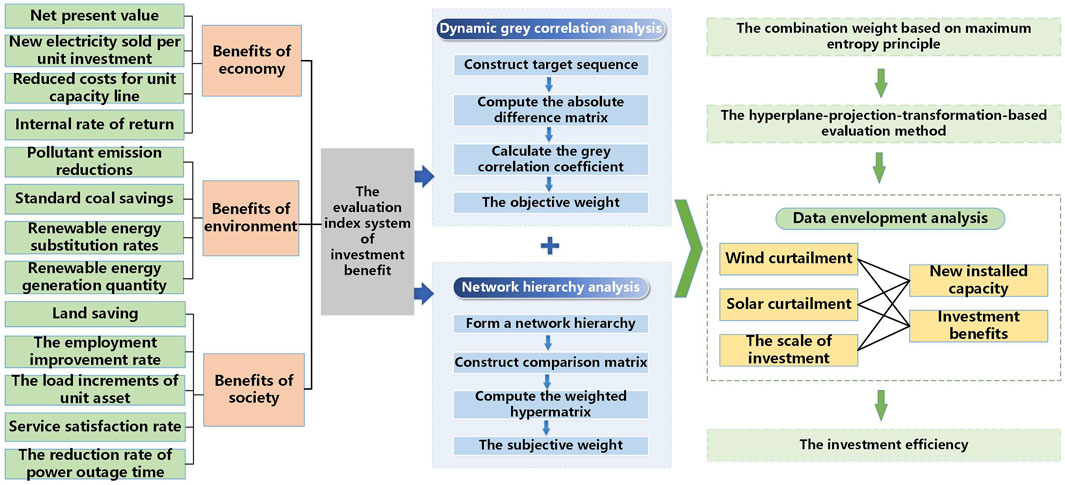
To comprehensively evaluate the changes of the benefits brought about by the grid connection of distributed renewable energy sources, an investment benefit evaluation indicator system including economic benefits, environmental benefits, and social benefits is established in this paper. Due to the cheap price of renewable energy electricity, electricity consumption is increased. Furthermore, the line construction costs are reduced due to the characteristic of nearby users. Thus, the economic benefits are reflected by net present value (NPV), internal rate of return (IRR), new electricity sold per unit investment, and savings in line construction costs. The damage to the environment is greatly reduced by using clean energy. Therefore, the environmental benefits are reflected by pollutant emission reductions, renewable energy generation quantity, standard coal savings, and renewable energy substitution rates. The social benefits are reflected by the amount of land saved, the employment improvement rate, the service satisfaction rate, the average household income, the load increments of unit assets, and the reduction rate of power outage time. Based on the above analysis, a comprehensive evaluation indicator system of investment benefit is formed.

The Hyperplane-Projection-Transformation-Based Evaluation Method

A combination weight calculation method based on the analytic network process and dynamic gray relational analysis is proposed in this paper. The subjective weight is obtained by establishing the network relationship model and constructing the super-matrix. The objective weight is calculated by determining the resolution coefficient under different smoothnesses of sequence. The combination weight is calculated based on the maximum entropy principle. The Technique for Order Preference by Similarity to an Ideal Solution is the most widespread evaluation method but comes with a serious drawback, that is, the balance between investment benefits cannot be identified (Alhabo and Zhang, 2018; Li and Zhao, 2020). Therefore, the investment evaluation method based on the hyperplane projection transformation is used to consider the quality and balance of investment in this paper. The origin is transformed into a global optimal solution by the normalization method. The investment benefit $d_{benefit}$ is expressed as the distance from the origin to the project point. The equilibrium of the benefits $d_{balance}$ is expressed as the distance that is projected on the hyperplane. The distance weight is determined based on investment preferences. The final comprehensive distance $d_{finally}$ is calculated by the normalized investment benefit $d_{benefit}^{\prime }$ and the normalized benefit equilibrium $d_{balance}^{\prime }$ (Chen et al., 2020; Zhou et al., 2020).

Investment Efficiency Evaluation Model Based on Data Envelopment Analysis

Data envelopment analysis (DEA) is a technical efficiency method based on relative comparisons between evaluated subjects (Olfati et al., 2020; Zhong et al., 2020). The core idea of the model is to determine the effective production frontier which is formed by mathematical programming and statistical data. The relative effectiveness is evaluated by comparing the degree of deviation of the unit from the frontier. This method has special advantages in analyzing the research objects with multiple inputs and outputs. Specifically, the simultaneous performance is effectively improved while evaluating the relative efficiency of multiple inputs and outputs. Fewer parameter estimation and preset functions are required. In addition, a uniform dimension is not required due to its own characteristics.

The investment efficiency of renewable energy power systems is a complicated problem with multiple inputs, multiple outputs, and complex coupling relationships, which has a certain impact on the efficient and stable development of the power grid. Based on the above research, DEA is an effective method to evaluate the input–output efficiency. Thus, this paper proposes an investment efficiency evaluation model based on data envelopment analysis. The indicators selected when evaluating the input–output efficiency of the power grid are comprehensive, comparable, and important. Considering the intuitive feedback of investing in renewable energy projects, installed capacity and comprehensive investment efficiency are selected as output indicators. The scale of investment, the amount of solar curtailment, and the amount of wind curtailment are determined as input indicators. The model for constant returns to scale (CRS) is as follows:

$\{\begin{array}{l}\max \frac{{\nu }_1{G}_{energy,j_0}+{\nu }_2{d}_{finally,j_0}}{{\mu }_1{T}_{total,j_0}+{\mu }_2{C}_{wind,j_0}+{\mu }_3{C}_{solar,j_0}}\\ \text{s}.\text{t}.\frac{{\nu }_1{G}_{energy,j}+{\nu }_2{d}_{finally,j}}{{\mu }_1{T}_{total,j}+{\mu }_2{C}_{wind,j}+{\mu }_3{C}_{solar,j}}\le 1,\\ {\nu }_1,{\nu }_2,{\mu }_1,{\mu }_2,{\mu }_3\ge 0,\end{array}(1)$

where $G_{energy,j}$ is the new installed capacity at project j, $T_{total,j}$ is the investment scale at project j, $C_{wind,j}$ and $C_{solar,j}$ are the wind curtailment volume and solar curtailment volume at project j, ${\nu }_1$ and ${\nu }_2$ are the weights of new installed capacity and comprehensive investment efficiency, and ${\mu }_1$, ${\mu }_2$, and ${\mu }_3$ represent the weights of the scale of investment, wind curtailment volume, and solar curtailment volume.

Considering the difficulty of fractional optimization, the model constructed above is converted to linear based on Charnes–Cooper transformation. Furthermore, the non-Archimedean infinitesimal ɛ and slack variables s are introduced to convert the inequality constraints into equations and identify the effectiveness of the model. Based on duality theorem, a computable and concise model is established, as follows:

$\{\begin{array}{l}\min \theta -\epsilon \left(s_T^{-}+s_{c_1}^{-}+s_{c_2}^{-}+s_G^{+}+s_d^{+}\right)\\ {\displaystyle \sum _{j=1}^n{\lambda }_j{G}_{energy,j}-s_G^{+}=G_{energy,j_0},}\\ {\displaystyle \sum _{j=1}^n{\lambda }_j{d}_{finally,j}-s_d^{+}=d_{finally,j_0},}\\ \text{s}.\text{t}.{\displaystyle \sum _{j=1}^n{\lambda }_j{T}_{total,j}+s_T^{-}=\theta T_{total,j_0},}\\ {\displaystyle \sum _{j=1}^n{\lambda }_j{C}_{wind,j}+s_{c_1}^{-}=\theta C_{wind,j_0},}\\ {\displaystyle \sum _{j=1}^n{\lambda }_j{C}_{solar,j}+s_{c_2}^{-}=\theta C_{solar,j_0},}\\ {\lambda }_j,s_T^{-},s_{c_1}^{-},s_{c_2}^{-},s_G^{+},s_d^{+}\ge 0,\end{array}(2)$

where θ is the relative efficiency at project $j_0$, ${\lambda }_j$ is the elastic coefficient at project j, ɛ is the non-Archimedean infinitesimal, s represents the slack variable, and n is the number of investment projects.

As shown in Figure 1, an investment efficiency evaluation framework for distribution networks considering the integration of distributed renewable energy sources is formed. A renewable energy investment benefit evaluation indicator system is established around economic, societal, and environmental factors. The analytic network process and dynamic gray relational analysis are used to calculate the subjective and objective weights of indicators, respectively, and the combined weights are obtained based on the maximum entropy principle. The investment benefit is comprehensively evaluated by hyperplane projection transformation. Considering the uncertainty of distributed renewable energy, an investment efficiency evaluation model based on DEA is constructed, which lays the foundation for improving the quality of power grid investment.

FIGURE 1

FIGURE 1. An investment efficiency evaluation framework.

Discussion and Conclusion

Under the trend of renewable energy generation, investment efficiency is increasingly valued due to the emergence of a large number of renewable energy projects. The investment efficiency of the power grid with distributed renewable energy is scientifically and reasonably calculated through the investment efficiency evaluation model constructed in this paper, which has a guiding significance for the subsequent distribution network planning and construction. Based on the changes in investment efficiency, it is the key to formulate the investment strategy in subsequent research. Also, it is a research direction to enrich the indicator system from other aspects and improve the scientificity of the weight calculation method.

Author Contributions

QY wrote the original draft and edited the paper. ZL conceptualized the research idea. YC was involved in formal analysis. YZ and QD contributed to visualization and discussion of the topic.

Funding

This work was supported by the Hunan Natural Science Foundation of China under Grant No. 2021JJ10019.

Conflict of Interest

ZL was employed by State Grid Zhangjiajie Electric Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alhabo, M., and Zhang, L. (2018). Multi-Criteria Handover Using Modified Weighted TOPSIS Methods for Heterogeneous Networks. IEEE Access 6, 40547–40558. doi:10.1109/ACCESS.2018.2846045

CrossRef Full Text | Google Scholar

Chen, Y., Li, J., Sheng, K., Yang, T., Xu, X., Han, Z., et al. (2020). Many-criteria Evaluation of Infrastructure Investment Priorities for Distribution Network Planning. IEEE Access 8, 221111–221118. doi:10.1109/ACCESS.2020.3043248

CrossRef Full Text | Google Scholar

Erdiwansyah, E., Mahidin, M., Husin, H., Nasaruddin, M. Z., Zaki, M., and Muhibbuddin, M. (2021). A Critical Review of the Integration of Renewable Energy Sources with Various Technologies. Prot. Control Mod. Power Syst. 6 (1), 37–54. doi:10.1186/s41601-021-00181-3

CrossRef Full Text | Google Scholar

Li, J., Chen, W., Chen, Y., Sheng, K., Du, S., Zhang, Y., et al. (2021). A Survey on Investment Demand Assessment Models for Power Grid Infrastructure. IEEE Access 9, 9048–9054. doi:10.1109/ACCESS.2021.3049601

CrossRef Full Text | Google Scholar

Li, J., and Zhao, H. (2020). “Power Efficiency Evaluation Model for Industrial Users Based on Improved TOPSIS,” in 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), 1764–1768. doi:10.1109/ITAIC49862.2020.9338785

CrossRef Full Text | Google Scholar

Lv, Y., and Yang, X. (2020). “Research on Grid Precision Investment Strategy of Grid Companies Considering Multidimensional Economic and Social Factors,” in 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), 128–132. doi:10.1109/ITAIC49862.2020.9339176

CrossRef Full Text | Google Scholar

Olfati, M., Yuan, W., Khan, A., and Nasseri, S. H. (2020). A New Approach to Solve Fuzzy Data Envelopment Analysis Model Based on Uncertainty. IEEE Access 8, 167300–167307. doi:10.1109/ACCESS.2020.3022158

CrossRef Full Text | Google Scholar

Olujobi, O. J. (2020). The Legal Sustainability of Energy Substitution in Nigeria’s Electric Power Sector: Renewable Energy as Alternative. Prot. Control Mod. Power Syst. 5 (4), 358–369. doi:10.1186/s41601-020-00179-3

CrossRef Full Text | Google Scholar

Padhy, S., and Panda, S. (2021). Application of a Simplified Grey Wolf Optimization Technique for Adaptive Fuzzy PID Controller Design for Frequency Regulation of a Distributed Power Generation System. Prot. Control Mod. Power Syst. 6 (1), 21–36. doi:10.1186/s41601-021-00180-4

CrossRef Full Text | Google Scholar

Sha, Y., Li, W., Yan, J., Li, W., and Huang, X. (2021). Research on Investment Scale Calculation and Accurate Management of Power Grid Projects Based on Three-Level Strategy. IEEE Access 9, 67176–67185. doi:10.1109/ACCESS.2021.3077481

CrossRef Full Text | Google Scholar

Wang, H. (2020). “Investment Efficiency and Cost Analysis of New Renewable Energy Sources,” in 2020 IEEE Sustainable Power and Energy Conference (ISPEC), 1082–1087. doi:10.1109/iSPEC50848.2020.9351110

CrossRef Full Text | Google Scholar

Wang, S., Liu, Q., Yuksel, S., and Dincer, H. (2019). Hesitant Linguistic Term Sets-Based Hybrid Analysis for Renewable Energy Investments. IEEE Access 7, 114223–114235. doi:10.1109/ACCESS.2019.2935427

CrossRef Full Text | Google Scholar

Wu, C., Zhang, X. P., and Sterling, M. J. H. (2021). Global Electricity Interconnection with 100% Renewable Energy Generation. IEEE Access 9, 113169–113186. doi:10.1109/ACCESS.2021.3104167

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, B., Chung, C. Y., Bu, S., Wang, Q., and Voropai, N. (2022). A Coordinated Multi-Energy Trading Framework for Strategic Hydrogen Provider in Electricity and Hydrogen Markets. IEEE Trans. Smart Grid 2022, 1. doi:10.1109/TSG.2022.3154611

CrossRef Full Text | Google Scholar

Zhong, J., Hu, X., Yuksel, S., Dincer, H., and Ubay, G. G. (2020). Analyzing the Investments Strategies for Renewable Energies Based on Multi-Criteria Decision Model. IEEE Access 8, 118818–118840. doi:10.1109/ACCESS.2020.3005064

CrossRef Full Text | Google Scholar

Zhou, B., Cao, Y., Li, C., Wu, Q., Liu, N., Huang, S., et al. (2020). Many-criteria Optimality of Coordinated Demand Response with Heterogeneous Households. Energy 207, 118267. doi:10.1016/j.energy.2020.118267

CrossRef Full Text | Google Scholar