A half-bridge distributed static compensator with a DC-link filter capacitor of a reduced size LCL filter

Distributed static compensators (DSTATCOMs), composed of power converters and passive filters, have been extensively utilized in distribution systems to improve their power quality. For the selection of passive filters, LCL filters with smaller sizes and lower costs are increasingly being adopted to replace the conventional L filters. However, the filter components of LCL filters are normally designed for the application of grid-connected inverters, and therefore, these passive components can be further optimized when applied to the DSTATCOM, where the grid-injected current is mainly capacitive. In this study, the novel LCL-filtered half-bridge DSTATCOM topology is proposed, where the conventional filter capacitor of the LCL filter is replaced by the DC-link capacitors with relatively larger capacitances. As a consequence, the grid-side inductance can be dramatically reduced from the order of millihenry to several microhenries. Furthermore, the current stress of semiconductor switches can be decreased. In addition, the power flow analysis and filter design procedure are presented in this study. It is revealed that a constant DC-link voltage can always be maintained, and the voltage variation across each capacitor can be well regulated with properly designed filters and controllers. Experiments were carried out on a down-scaled laboratory prototype, and simulation and experimental results are presented to verify the effectiveness of the proposed DSTATCOM topology.

1 Introduction

Reactive power compensation has been one of the major solutions to resolve power quality (PQ)-related issues caused by the large-scale deployment of induction motors, arc furnaces, and other inductive loads in the distribution system [1]. Traditionally, the static VAR compensator (SVC), such as the thyristor-switched capacitor (TSC) and thyristor-controlled reactance (TCR), served as a simple and straightforward measure for reducing the reactive currents flowing through the transmission lines and regulating the voltages at the point of common coupling. Although being extensively utilized, these reactive power compensators have relatively slow dynamic responses, inflexible reactive power compensation, and may introduce resonances when interacting with the system impedance [1].

Ever since the appearance of the distributed static compensator (DSTATCOM), it has been one of the research focuses in modern power systems and has received increasing attention worldwide due to its advantages such as flexible reactive power compensation, multifunctionality, and elimination of resonances (Dugan et al., 2004). Although different in details, the topologies of DSTATCOM are basically similar structures composed of two parts, namely, power converters and passive filters. It should be noted that transformers can also be involved in the DSTATCOM configuration and considered a part of passive filters (Singh et al., 2014). Passive filters are essential for attenuating high-frequency harmonics introduced by the modulation of power converters. For selection of passive filters, single inductor L filters, which are normally utilized at the medium or high voltage level for applications of the STATCOM and modular multilevel cascade converter (MMCC) (Peng et al., 1996; Liang and Nwankpa, 1999; Akagi, 2011), have been gradually replaced by third-order LCL filters, whose sizes and costs are much reduced, at the low voltage level (Liserre et al., 2005; Kumar and Mishra, 2014a; Fang et al., 2017a).

For DSTATCOM applications, the grid-injected current is mainly capacitive. This characteristic has been widely utilized to optimize the DSTATCOM system to improve its efficiency, compensation ability, and the reduction of system rating (Inzunza and Akagi, 2005; Karanki et al., 2012; Wang et al., 2015). In Inzunza and Akagi (2005), an extra capacitor connected in series with the conventional filter inductor that served as a series LC passive filter has been utilized in the active power filter (APF) application. This extra capacitor exhibits high impedance at the fundamental frequency so that much of the grid voltage appears across this capacitor, resulting in lower output voltage and power rating of the power converter. However, the reactive power compensation ability of this system remains fixed, which is limited by the filter parameters of passive components (Wang et al., 2015). When the same series LC passive filter is applied to the DSTATCOM, the reactive power required by the load can be partly compensated by the filter capacitor while the remaining reactive power is still supplied by the power converter, and therefore, the DC-link voltage of the DSTATCOM can be reduced (Karanki et al., 2012). However, a prominent disadvantage of this series LC topology is the inevitable series resonance, leading to zero impedance at the resonant frequency. Therefore, care must be taken to ensure a zero-converter output voltage near the resonant frequency; otherwise, the output current would become very large. Moreover, the capacitive impedance of this passive filter below the resonance frequency challenges the controller design (Wang et al., 2015). It should be noted that this extra capacitor can also be connected in series with the LCL filter. However, multiple resonances further complicate the aforementioned problems (Kumar and Mishra, 2014a). In Wang et al. (2016a), this series capacitor is replaced by a thyristor-controlled LC reactance, achieving a wide compensation range and low DC-link voltage simultaneously, however, at the expense of increased passive components and system complexity.

In contrast, a filter capacitor shunted with the DSTATCOM can be used to reduce the current stress of semiconductor switches of power converters. In previous references, the shunt capacitor together with the DSTATCOM essentially forms a hybrid filter, and therefore, the design of the whole system becomes much more complicated (Solanki et al., 2015). For another interesting topology proposed in Kumar and Mishra (2014b), an extra inductor is inserted between the shunt capacitor and the power grid. By regulating the voltage across the shunt capacitor, the grid-injected current can be indirectly controlled, and in this case, the DSTATCOM system is actually operated in the voltage control mode. In this case, the shunt capacitor, conventional interfacing inductor, and additional inductor essentially form an LCL filter (Kumar and Mishra, 2015). Indeed, the well-known LCL filter inherently contains a shunt capacitor, which has not been fully utilized for DSTATCOM applications. For all the aforementioned topologies, the filter capacitors of the LCL filters are always designed based on the application of grid-connected inverters (GCIs) (Liserre et al., 2005). As a consequence, the range of capacitances is typically from several to tens of microfarads for limiting the converter reactive current. However, it should be noted that the converter current and, thus, the current stress of semiconductor switches can be decreased with larger filter capacitances of LCL filters in DSTATCOM applications because the capacitor branch loop can bypass much more grid-injected current. Another prominent advantage of using larger filter capacitances is the reduced filter inductance when the resonant frequency of the LCL filter is fixed (Fang et al., 2017a). Furthermore, if the filter capacitor could also serve as the DC-link capacitor, the filter components could be further reduced.

The single-phase pulse-width-modulated (PWM) converters have inherent second-order voltage harmonics in the DC link introduced by the unbalanced instantaneous power between their input and output (Tang et al., 2015a), (Shimizu et al., 1997). These AC voltage components in the DC link distort the compensation current reference and therefore deteriorate the system performance (Tang et al., 2015b; Farivar et al., 2015; Tang and Blaabjerg, 2015). This issue can be solved by either installing large capacitors in the DC link or utilizing active power decoupling strategies (Shimizu et al., 1997; Tang et al., 2015a; Tang et al., 2015b; Farivar et al., 2015; Tang and Blaabjerg, 2015). With the former solution, the voltage fluctuations in the DC link can be decreased. In contrast, the DC-link voltage can be maintained as a constant value using active power decoupling strategies (Tang et al., 2015a), (Shimizu et al., 1997), (Tang et al., 2015b), and (Tang and Blaabjerg, 2015). In Tang et al. (2015a), an additional half-bridge active power decoupling circuit was involved in the DC link to greatly reduce DC-link capacitances. The idea behind this power decoupling circuit is to make the voltage across individual capacitors fluctuate while maintaining a constant DC-link voltage. For single-phase DSTATCOMs, the same issue exists, and the DC-link voltage fluctuations can be reduced using large capacitances, as suggested in Peng et al. (1996), Liang and Nwankpa (1999), Akagi (2011), and Kumar and Mishra (2014a) (Peng et al., 1996; Liang and Nwankpa, 1999; Akagi, 2011; Kumar and Mishra, 2014a). Alternatively, as will be analyzed later, for the single-phase half-bridge DSTATCOM, it is possible to decouple the reactive power completely based on the same principle, as proposed in Tang et al. (2015a). However, the voltage fluctuation across each capacitor is uncontrollable and may far exceed the permitted values, resulting in the overmodulation of power converters (Isobe et al., 2016). Fortunately, with the proposed DSTATCOM topology and filter design method, reactive power decoupling can be achieved, and the capacitor voltage fluctuations can be maintained within the limits, leading to a constant DC-link voltage and undistorted grid current.

In this study, the novel LCL-filtered single-phase half-bridge DSTATCOM topology is proposed to reduce the filter components and current stresses of semiconductor switches while combining filter capacitors with DC-link capacitors. In Section 2, the analysis of the single-phase H-bridge DSTATCOM is provided first to explain the mechanism of DC-link voltage fluctuations. Furthermore, the power flow analysis of the single-phase half-bridge DSTATCOM is presented in Section 3 (A) to illustrate the feasibility of reactive power decoupling. Moreover, the operating principles and advantages of the proposed half-bridge DSTATCOM are extensively analyzed in Section 3. The filter design procedure is then given in Section 4 with a design example provided. Simulation and experimental results are shown in Section 5 to validate the theoretical analysis. Finally, Section 6 concludes the main contribution of the study.

2 Analysis of single-phase H-bridge distributed static compensators

2.1 Operation principle of single-phase H-bridge distributed static compensators

Figure 1A shows the circuit diagram of a single-phase H-bridge DSTATCOM connected to the power grid through an LCL filter. The filter components of the LCL filter are denoted as L_i, L_g, and C_f, respectively. The equivalent series resistances (ESRs) of the filter are ignored here to obtain the worst stability condition. The major objective of the DSTATCOM is to compensate for the reactive power consumed by the load, resulting in the grid current i_s in phase with the grid voltage v_g. In other words, a unity power factor can be observed from the power grid.

FIGURE 1

FIGURE 1. Circuit diagrams of single-phase (A) H-bridge and (B) half-bridge DSTATCOMs.

Assuming that the waveform of v_g is an ideal sinusoidal with fundamental frequency f_o and angular frequency ω_o, it can be represented as

${\mathit{v}}_{\mathit{g}}\mathit{=}\sqrt{\mathbf{2}}{\mathit{V}}_{\mathit{g}}\mathit{sin}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right),(1)$

where V_g stands for the root-mean-square (rms) value of v_g. In most cases, DSTATCOMs are employed to compensate for the reactive power absorbed by inductive or resistive-inductive loads. Under such conditions, the load current i_l lags v_g by an angle θ, and it can be expressed as

${\mathit{i}}_{\mathit{l}}\mathit{=}\sqrt{\mathbf{2}}{\mathit{I}}_{\mathit{l}}\mathit{sin}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t-\theta }\right)\mathit{=}{\mathit{i}}_{\mathit{lp}}\mathit{+}{\mathit{i}}_{\mathit{lq}}\mathit{=}\sqrt{\mathbf{2}}{\mathit{I}}_{\mathit{lp}}\mathit{sin}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right)\mathit{-}\sqrt{\mathbf{2}}{\mathit{I}}_{\mathit{lq}}\mathit{cos}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right),(2)$

where I_l stands for the rms value of i_l, and I_lp and I_lq can be, respectively, derived as

${\mathrm{I}}_{\mathrm{lp}}\mathrm{=}{\mathrm{I}}_{\mathrm{l}}\mathrm{cos\theta ; }{\mathrm{I}}_{\mathrm{lq}}\mathrm{=}{\mathrm{I}}_{\mathrm{l}}\mathrm{sin\theta }\mathrm{.}(3)$

From the equation (Singh et al., 2014), it can be observed that i_lp is the active current component of i_l which is in phase with v_g, and i_lq denotes the reactive current component of i_l which is orthogonal to v_g. In theory, i_g should be equivalent to −i_lq when the power losses in the DSTATCOM system are neglected, which can be represented as

${\mathit{i}}_{\mathit{g}}\mathit{=-}{\mathit{i}}_{\mathit{lq}}\mathit{=}\sqrt{\mathrm{2}}{\mathit{I}}_{\mathit{lq}}\mathit{cos}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right).(4)$

Power flow analysis of single-phase H-bridge DSTATCOMs

The instantaneous power absorbed by the DSTATCOM can be calculated as

${\mathit{p}}_{\mathit{ac}}\mathit{=}{\mathit{v}}_{\mathit{g}}{\mathit{i}}_{\mathit{g}}\mathit{=}{\mathit{V}}_{\mathit{g}}{\mathit{I}}_{\mathit{lq}}\mathit{sin}\left(\mathbf{2}{\mathit{\omega }}_{\mathit{o}}\mathit{t}\right).(5)$

Normally, for LCL filters, the reactive power consumed by the filter inductors and capacitors is designed to be small enough as compared with the equipment rated power (Liserre et al., 2005; Fang et al., 2017a). Assuming that the power losses of these filter elements can be ignored, the instantaneous power absorbed by the DC-link capacitors p_dc should be the same as p_ac, which can be expressed as

${\mathit{P}}_{\mathit{dc}}\mathit{=}{\mathit{P}}_{\mathit{ac}}\mathit{=}{\mathit{V}}_{\mathit{g}}{\mathit{I}}_{\mathit{lq}}\mathit{sin}\left(\mathbf{2}{\mathit{\omega }}_{\mathit{o}}\mathit{t}\right).(6)$

In order to absorb the fluctuating power p_dc, the DC-link voltage v_dc contains both a DC component and an AC component, which can be represented as

${\mathit{v}}_{\mathit{dc}}\mathit{=}{\mathit{V}}_{\mathit{dc}}\mathit{+}{\tilde{\mathit{v}}}_{\mathit{dc}},(7)$

where V_dc and ${\tilde{v}}_{dc}$ stand for the DC and AC components of v_dc, respectively. The dominating voltage harmonic of ${\tilde{v}}_{dc}$ is the second-order harmonic, with its rms value denoted as V_dch, and can be expressed as

${\tilde{\mathit{v}}}_{\mathit{dc}}\mathit{=}\sqrt{\mathbf{2}}{\mathit{V}}_{\mathit{dch}}\mathit{sin}\left(\mathbf{2}{\mathit{\omega }}_{\mathit{o}}\mathit{t+\alpha }\right).(8)$

Under this condition, the relevant power absorbed in the DC link, denoted as p_dch, can be derived as

${\mathit{P}}_{\mathit{dch}}\mathit{=}\left({\mathit{V}}_{\mathit{dc}}\mathit{+}{\tilde{\mathit{v}}}_{\mathit{dc}}\right)\frac{{\mathit{C}}_{\mathit{dc}}}{\mathbf{2}}\frac{\mathit{d}{\tilde{\mathit{v}}}_{\mathit{dc}}}{\mathit{dt}}\mathit{=}{\mathit{C}}_{\mathit{dc}}{\mathit{\omega }}_{\mathit{o}}{\mathit{V}}_{\mathit{dch}}\left[\sqrt{\mathbf{2}}{\mathit{V}}_{\mathit{dc}}\mathit{cos}\left(\mathbf{2}{\mathit{\omega }}_{\mathit{o}}\mathit{t+\alpha }\right)\mathit{+}{\mathit{V}}_{\mathit{dch}}\mathit{sin}\left(\mathrm{4}{\mathit{\omega }}_{\mathit{o}}\mathit{t+2\alpha }\right)\right],(9)$

where the DC-link capacitances C_dc1 and C_dc2 in Figure 1 are chosen to be identical and denoted as C_dc. Comparing the equations by (Inzunza and Akagi, 2005) and (Kumar and Mishra, 2014a), α = −90° can be obtained. Furthermore, it is clear that p_dch and p_dc are not equal due to the additional fluctuating power of frequency 4f_o in p_dch caused by the interaction between ${\tilde{v}}_{dc}$ and ${\tilde{i}}_{dc}$. Consequently, the DC-link voltage of the single-phase H-bridge DSTATCOM is mixed with DC components, second-order voltage harmonic, and other voltage harmonics. These harmonics will give rise to a distorted current reference defined by the production of voltage-loop controller output and sin (ω₀t) obtained from the phase-locked loop (PLL) (Wu et al., 2012; Farivar et al., 2015). Therefore, the grid current i_g will be distorted by ${\tilde{v}}_{dc}$, provided that C_dc is not large enough. Consequently, large capacitors should be adopted in the DC link as a solution to the instantaneous power imbalance problem.

3 Proposed LCL-filtered single-phase half-bridge distributed static compensators

3.1 Power flow analysis of half-bridge distributed static compensators

Figure 1B shows the circuit diagram of a conventional single-phase half-bridge DSTATCOM. In comparison with the single-phase H-bridge DSTATCOM, two semiconductor switches can be saved for the half-bridge DSTATCOM. As shown in Figure 1B, the power absorbed by the half-bridge DSTATCOM can be represented as that of the H-bridge DSTATCOM expressed in the equation by Akagi (2011) and the equation by Kumar and Mishra (2014a) due to the same reactive power compensation requirement.

In Figure 2, the DC-link voltage v_dc is composed of both the upper arm capacitor voltage v_dc1 and lower arm capacitor voltage v_dc2, and it can be expressed as

${\mathit{v}}_{\mathit{dc}}\mathit{=}{\mathit{v}}_{\mathit{dc1}}\mathit{+}{\mathit{v}}_{\mathit{dc2}}\mathit{=}{\mathit{V}}_{\mathit{dc1}}\mathit{+}{\tilde{\mathit{v}}}_{\mathit{dc1}}\mathit{+}{\mathit{V}}_{\mathit{dc2}}\mathit{+}{\tilde{\mathit{v}}}_{\mathit{dc2}},(10)$

where V_dci and ${\tilde{v}}_{dci}$ stand for the DC and AC components of v_dci (i = 1, 2), respectively. The currents flowing through the DC-link capacitors, denoted as i_dc1 and i_dc2, are correlated with each other according to the Kirchhoff’s current law, and their relationship can be expressed as

${\mathit{i}}_{\mathit{dc1}}\mathit{-}{\mathit{i}}_{\mathit{dc2}}\mathit{=}{\mathit{i}}_{\mathit{i}}\mathit{\approx }{\mathit{i}}_{\mathit{g}}\mathit{=}\sqrt{\mathit{2}}{\mathit{I}}_{\mathit{lq}}\mathit{cos}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right).(11)$

FIGURE 2

FIGURE 2. C_dc1 as a function of V_g and P_ac under the reactive power decoupling operating condition.

It should be noted that the filter capacitor current i_c is assumed to be zero in the equation by Karanki et al. (2012) to simplify the analysis. Based on the equation by Karanki et al. (2012), the difference between v_dc1 and v_dc2 can be derived as

${\mathit{v}}_{\mathit{dc1}}\mathit{-}{\mathit{v}}_{\mathit{dc2}}\mathit{=}{\tilde{v}}_{\mathit{dc2}}\mathit{-}{\tilde{v}}_{\mathit{dc1}}\mathit{=}\frac{\mathit{1}}{{\mathit{C}}_{\mathit{dc1}}}{\displaystyle \int \left({\mathit{i}}_{\mathit{dc1}}\mathit{-}{\mathit{i}}_{\mathit{dc2}}\right)}\mathit{dt=}\frac{\sqrt{\mathit{2}}{\mathit{I}}_{\mathit{lq}}}{{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}}\mathit{sin}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right),(12)$

where the DC-link capacitances C_dc1 and C_dc2 in Figure 2 are chosen to be identical and denoted as C_dc1. Furthermore, if the DC-link voltage v_dc can be maintained as a constant DC value, the following equation can be satisfied:

${\tilde{\mathit{v}}}_{\mathit{dc1}}\mathit{=-}{\tilde{\mathit{v}}}_{\mathit{dc2}}\mathit{=}\frac{\sqrt{\mathit{2}}{\mathit{I}}_{\mathit{lq}}}{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}}\mathit{sin}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right)\mathit{,}{\mathit{i}}_{\mathit{dc1}}\mathit{=-}{\mathit{i}}_{\mathit{dc2}}\mathit{=}\frac{\sqrt{\mathit{2}}{\mathit{I}}_{\mathit{lq}}}{\mathit{2}}\mathit{cos}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right).(13)$

Under this condition, the power absorbed in the DC link, denoted as p_dcf, can be derived as

${\mathit{p}}_{\mathit{dcf}}\mathit{=}{\mathit{v}}_{\mathit{dc1}}{\mathit{i}}_{\mathit{dc1}}\mathit{+}{\mathit{v}}_{\mathit{dc2}}{\mathit{i}}_{\mathit{dc2}}\mathit{=}\frac{{\mathit{I}}_{\mathit{lq}}^2}{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}}\mathit{sin}\left(\mathit{2}{\mathit{\omega }}_{\mathit{o}}\mathit{t}\right).(14)$

Under the condition that p_dcf = p_dc, the DC-link capacitance can be derived as

${\mathit{C}}_{\mathit{dc1}}\mathit{=}\frac{{\mathit{I}}_{\mathit{lq}}}{\mathit{2}{\mathit{\omega }}_{\mathit{o}}{\mathit{V}}_{\mathit{g}}}\mathrm{.}(15)$

From the aforementioned analysis, for single-phase half-bridge DSTATCOMs, it is possible to regulate the DC-link voltage v_dc to be constant and free of voltage harmonics under the rated operating condition by selecting C_dc1 properly. However, the fundamental voltage components in v_dc1 and v_dc2 may lead to overmodulation, and they can only be reduced with a larger C_dc1, according to the equation by Solanki et al. (2015). Therefore, it can be concluded that a constant DC-link voltage requires additional capacitors inserted in the individual arm to maintain the power balance between the DSTATCOM and the power grid. C_dc1 as a function of V_g and P_ac under the reactive power decoupling operating condition is shown in Figure 2. As shown, C_dc1 under the complete power decoupling condition increases with the increase of P_ac and decrease of V_g.

3.2 Proposed LCL-filtered half-bridge distributed static compensators

The circuit diagram of the proposed LCL-filtered half-bridge DSTATCOM is shown in Figure 3A. As can be observed, two additional capacitors C_dc3 and C_dc4 are adopted in the DC link to counteract voltage fluctuation. Furthermore, the filter capacitor C_f shown in Figure 2 is saved. The power absorbed by this novel half-bridge DSTATCOM can also be represented by the equation by Akagi (2011) and Kumar and Mishra (2014a). Furthermore, equation (Karanki et al., 2012)-(14) still holds true.

FIGURE 3

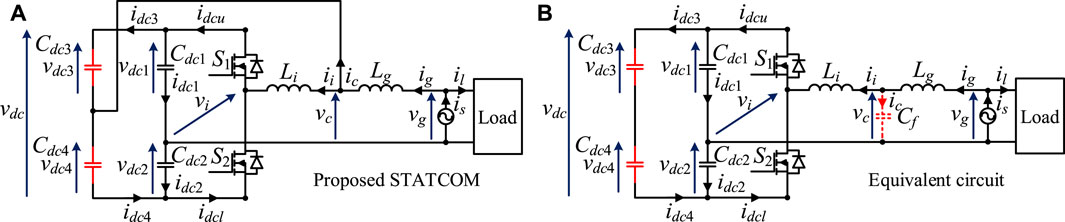
FIGURE 3. Circuit diagrams of (A) the proposed LCL-filtered half-bridge DSTATCOM and (B) its equivalent circuit.

Different from the conventional half-bridge DSTATCOM, C_dc3 and C_dc4 shown in Figure 4 can further absorb the reactive power, represented as

${\mathit{p}}_{\mathit{dca}}\mathit{=}{\mathit{p}}_{\mathit{dc}}\mathit{-}{\mathit{p}}_{\mathit{dcf}}\mathit{=}{\mathit{v}}_{\mathit{dc3}}{\mathit{i}}_{\mathit{dc3}}\mathit{+}{\mathit{v}}_{\mathit{dc4}}{\mathit{i}}_{\mathit{dc4}}\mathit{=}\frac{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}{\mathit{V}}_{\mathit{g}}{\mathit{I}}_{\mathit{lq}}\mathit{-}{\mathit{I}}_{\mathit{lq}}^2}{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}}\mathit{sin}\left(\mathit{2}{\mathit{\omega }}_{\mathit{o}}\mathit{t}\right),(16)$

where p_dca denotes the reactive power absorbed by C_dc3 and C_dc4.

FIGURE 4

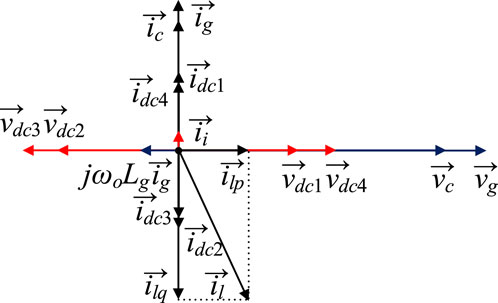
FIGURE 4. Vector diagram of the proposed half-bridge DSTATCOM. Equivalent LCL filter and the controller structure of the proposed half-bridge DSTATCOM.

The AC voltage components across C_dc3 and C_dc4 can be derived from Figure 3A and (Solanki et al., 2015), which can be described as

${\tilde{\mathit{v}}}_{\mathit{dc3}}\mathit{=-}{\mathit{v}}_{\mathit{c}}\mathit{+}{\tilde{\mathit{v}}}_{\mathit{dc1}}\mathit{\approx }\sqrt{\mathit{2}}\left(\mathit{-}{\mathit{V}}_{\mathit{g}}\mathit{+}\frac{{\mathit{I}}_{\mathit{lq}}}{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}}\right)\mathit{sin}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right)\mathit{,}{\tilde{\mathit{v}}}_{\mathit{dc4}}\mathit{=}{\mathit{v}}_{\mathit{c}}\mathit{+}{\tilde{\mathit{v}}}_{\mathit{dc2}}\mathit{\approx }\sqrt{\mathit{2}}\left({\mathit{V}}_{\mathit{g}}\mathit{-}\frac{{\mathit{I}}_{\mathit{lq}}}{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}}\right)\mathit{sin}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right)\mathrm{.}(17)$

The currents flowing through C_dc3 and C_dc4, denoted as i_dc3 and i_dc4, respectively, can be derived based on the derivation relationship between the capacitor voltages and capacitor currents, which can be expressed as

${\mathit{i}}_{\mathit{dc3}}\mathit{=}{\mathit{C}}_{\mathit{dc3}}\frac{\mathit{d}{\tilde{\mathit{v}}}_{\mathit{dc3}}}{\mathit{dt}}\mathit{=}\sqrt{\mathit{2}}{\mathit{C}}_{\mathit{dc3}}{\mathit{\omega }}_{\mathit{o}}\left(\mathit{-}{\mathit{V}}_{\mathit{g}}\mathit{+}\frac{{\mathit{I}}_{\mathit{lq}}}{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}}\right)\mathit{cos}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right),{\mathit{i}}_{\mathit{dc4}}\mathit{=}{\mathit{C}}_{\mathit{dc3}}\frac{\mathit{d}{\tilde{\mathit{v}}}_{\mathit{dc4}}}{\mathit{dt}}\mathit{=}\sqrt{\mathit{2}}{\mathit{C}}_{\mathit{dc3}}{\mathit{\omega }}_{\mathit{o}}\left({\mathit{V}}_{\mathit{g}}\mathit{-}\frac{{\mathit{I}}_{\mathit{lq}}}{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}}\right)\mathit{cos}\left({\mathit{\omega }}_{\mathit{o}}\mathit{t}\right),(18)$

where the additional capacitances C_dc3 and C_dc4 are chosen to be identical and denoted as C_dc3. It should be noted that the DC components V_dc3 of v_dc3 and V_dc4 of v_dc4 have no contribution to i_dc3 and i_dc4. Furthermore, p_dca shown in the equation by Tang et al. (2015a) will not be influenced by V_dc3 and V_dc4 due to the opposite directions of i_dc3 and i_dc4. Substituting the equations by Shimizu et al. (1997) and Farivar et al. (2015) into the equation by Tang et al. (2015a) and solving for C_dc3,

${\mathit{C}}_{\mathit{dc3}}\mathit{=}\frac{{\mathit{C}}_{\mathit{dc1}}{\mathit{I}}_{\mathit{lq}}}{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{\omega }}_{\mathit{o}}{\mathit{V}}_{\mathit{g}}\mathit{-}{\mathit{I}}_{\mathit{lq}}}.(19)$

From the equation by Tang et al. (2015b), C_dc3 can be calculated based on C_dc1 and the rated operating point of DSTATCOM systems. The system vector diagram is shown in Figure 4 to illustrate the relationships among all the voltage vectors and current vectors. As can be observed, $\overrightarrow{vc}$ approximates the grid voltage $\overrightarrow{vg}$, equivalent to the difference between $\overrightarrow{vdc1}$ and $\overrightarrow{vdc3}$ or $\overrightarrow{vdc4}$ and $\overrightarrow{vdc2}$. Therefore, the required reactive power represented in the equation by Kumar and Mishra (2014a) can be shared by all the four capacitors C_dc1, C_dc2, C_dc3, and C_dc4, reducing the voltage stress across C_dc1 or C_dc2. In addition, $\overrightarrow{ic}$ is in phase with $\overrightarrow{ig}$, resulting in a smaller magnitude of the converter current $\overrightarrow{ii}$, and thus, the reduced current stress of semiconductor switches.

The equivalent LCL filter of the proposed half-bridge DSTATCOM is shown in Figure 3B. Based on Figure 3, the equivalent filter capacitance C_f can be derived as

${\mathit{C}}_{\mathit{f}}\mathit{=}\frac{{\mathit{C}}_{\mathit{dc1}}{\mathit{C}}_{\mathit{dc3}}}{{\mathit{C}}_{\mathit{dc1}}\mathit{+}{\mathit{C}}_{\mathit{dc3}}}\mathit{+}\frac{{\mathit{C}}_{\mathit{dc2}}{\mathit{C}}_{\mathit{dc4}}}{{\mathit{C}}_{\mathit{dc2}}\mathit{+}{\mathit{C}}_{\mathit{dc4}}}\mathit{=}\frac{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{C}}_{\mathit{dc3}}}{{\mathit{C}}_{\mathit{dc1}}\mathit{+}{\mathit{C}}_{\mathit{dc3}}},(20)$

where C_dc2 and C_dc4 are selected to be the same as C_dc1 and C_dc3, respectively.

The resonant frequency f_r of the equivalent LCL filter can be derived as

${\mathit{f}}_{\mathit{r}}\mathit{=}\frac{\mathit{1}}{\mathit{2\pi }}\sqrt{\frac{\left({\mathit{L}}_{\mathit{i}}\mathit{+}{\mathit{L}}_{\mathit{g}}\right)\left({\mathit{C}}_{\mathit{dc1}}\mathit{+}{\mathit{C}}_{\mathit{dc3}}\right)}{\mathit{2}{\mathit{C}}_{\mathit{dc1}}{\mathit{C}}_{\mathit{dc3}}{\mathit{L}}_{\mathit{i}}{\mathit{L}}_{\mathit{g}}}}.(21)$

Normally, for LCL filters, the filter capacitance C_f is selected to be several µF (6–8). The reason for choosing such small values is that larger capacitances increase the reactive component of the converter current i_i and the system costs and volumes. However, for the proposed half-bridge DSTATCOM, the magnitude of i_i can be reduced with a larger C_f, as shown in Figure 4, and C_f composed of C_dc1, C_dc2, C_dc3, and C_dc4 can be a relatively large value. When f_r remains fixed, one direct advantage of using a larger C_f is the reduction in filter inductances. The inductance L_i should be determined by the converter ripple current requirement (Wu et al., 2012), which can be represented as

$\frac{\mathit{\Delta }{\mathit{I}}_{\mathit{i}}}{{\mathit{I}}_{\mathit{lq}}}\mathit{=}\frac{{\mathit{V}}_{\mathit{dc}}}{\mathit{4}{\mathit{L}}_{\mathit{i}}{\mathit{f}}_{\mathit{sw}}{\mathit{I}}_{\mathit{lq}}}\mathit{\le 40\%,}(22)$

where ΔI_i denotes the peak value of the current ripple flowing through the inductor L_i. Consequently, the grid-side inductance L_g can be greatly reduced to maintain a fixed f_r (Jalili and Bernet, 2006; Tang et al., 2012).

The control block diagram of the proposed half-bridge DSTATCOM is shown in Figure 5. Figure 5A shows the reactive current detection and voltage-loop controller. A phase-locked loop (PLL) is utilized to synchronize the phase of v_g for d-q transformation (Blaabjerg et al., 2006; Singh and Solanki, 2009). The fundamental active component of i_l is extracted first by multiplying sin ωt with i_l and then filtered through a low-pass filter (LPF) with a gain of 2. v_dc^* represents the reference voltage of v_dc, which is regulated by a voltage-loop proportional-integral (PI) controller. It should be noted that i_gref would contain a considerable third-order harmonic, provided that the second-order voltage harmonic in v_dc is large (Tang et al., 2015a; Tang et al., 2015b). The z-domain control block diagram of the current-loop controller can be observed from Figure 5B. In Figure 5B, G_i(z) denotes the z-domain current-loop controller, and z⁻¹ is introduced by the computational delay of digital microprocessors (Pan et al., 2014; Parker et al., 2014; Van de Sype et al., 2016).

FIGURE 5

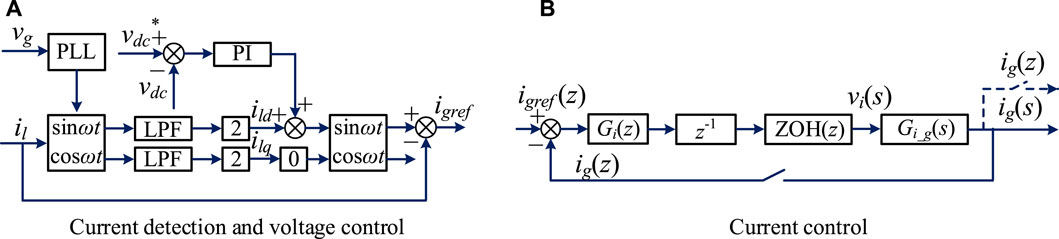
FIGURE 5. Control block diagrams of the proposed half-bridge DSTATCOM. (A) Current detection and voltage control and (B) Current control.

The transfer function ZOH(z) represents the effect of zero-order hold (ZOH), and the converter output voltage v_i(s) can be obtained after the ZOH. G_{i_g}(s) stands for the transfer function from v_i(s) to i_g(s), as shown in Figure 5B, which can be derived as

${\mathit{G}}_{\mathit{i\_g}}\left(\mathit{S}\right)\mathit{=}\frac{{\mathit{C}}_{\mathit{dc1}}\mathit{+}{\mathit{C}}_{\mathit{dc3}}}{\mathit{2s}{\mathit{C}}_{\mathit{dc1}}{\mathit{C}}_{\mathit{dc3}}{\mathit{L}}_{\mathit{i}}{\mathit{L}}_{\mathit{g}}\left({\mathit{s}}^{\mathit{2}}\mathit{+}{\mathit{\omega }}_r^2\right)},(23)$

where ω_r = 2π f_r represents the resonant angular frequency. The z domain transfer function G_{i_g}(z) can be derived from the equation by Tang et al. (2012) using the z transform with ZOH, and G_{i_g}(z) can be expressed as

${\mathit{G}}_{\mathit{i\_g}}\left(\mathit{z}\right)\mathit{=ZOH}\left[{\mathit{G}}_{\mathit{i\_g}}\left(\mathit{s}\right)\right]\mathit{=}\frac{{\mathit{T}}_{\mathit{s}}}{{\mathit{L}}_{\mathit{t}}\left(\mathit{z-1}\right)}\mathit{-}\frac{\mathit{(z-1)sin(}{\mathit{\omega }}_{\mathit{r}}{\mathit{T}}_{\mathit{s}}\mathit{)}}{{\mathit{L}}_{\mathit{t}}{\mathit{\omega }}_{\mathit{r}}\left[{\mathit{z}}^{\mathit{2}}\mathit{-2zcos}\left({\mathit{\omega }}_{\mathit{r}}{\mathit{T}}_{\mathit{s}}\right)\mathit{+1}\right]},(24)$

where T_s = 1/f_s denotes the sampling period, and L_t stands for the sum of L_i and L_g. Based on the equation by Jalili and Bernet (2006) and Figure 5, the z domain loop gains of the current-loop can be derived as

${\mathit{T}}_{\mathit{i}}\left(\mathit{z}\right)\mathit{=}{\mathit{G}}_{\mathit{i}}\left(\mathit{z}\right){\mathit{z}}^{\mathit{-1}}{\mathit{G}}_{\mathit{i\_g}}\left(\mathit{z}\right)\mathit{=}\frac{{\mathit{T}}_{\mathit{s}}{\mathit{G}}_{\mathit{i}}\left(\mathit{z}\right)}{{\mathit{L}}_{\mathit{t}}\mathit{z}\left(\mathit{z-1}\right)}\mathit{-}\frac{\left(\mathit{z-1}\right)\mathit{sin}\left({\mathit{\omega }}_{\mathit{r}}{\mathit{T}}_{\mathit{s}}\right){\mathit{G}}_{\mathit{i}}\left(\mathit{Z}\right)}{{\mathit{L}}_{\mathit{t}}{\mathit{\omega }}_{\mathit{r}}\mathit{z}\left({\mathit{z}}^{\mathit{2}}\mathit{-2zcos}\left({\mathit{\omega }}_{\mathit{r}}{\mathit{T}}_{\mathit{s}}\right)\mathit{+1}\right)}.(25)$

It can be observed that the system mathematical model derived previously is similar to that of grid-current feedback LCL-filtered grid-connected converters (Wang et al., 2016b). Therefore, the controllers shown in Figure 7 can be designed based on the existing design methods, as provided in Bao et al. (2014), Zou et al. (2014), and Wang et al. (2016b). A proportional gain K_p is used as G_i (z) in the following section for simplifying the analysis.

4 Passive component design procedure

The passive components shown in Figure 3, including the filter inductances L_i and L_g and DC-link capacitances C_dc1–C_dc4 will be designed in this section. Before designing these parameters, the DSTATCOM system parameters should be provided, which include the fundamental frequency f_o, sampling frequency f_s, switching frequency f_sw, grid voltage rms value V_g, rated reactive current rms value I_lq, and DC-link voltage reference v_dc^*.

With the system parameter values given, a step-by-step passive component design flowchart is shown in Figure 6. As can be observed, the first step is to specify $\left|{\tilde{v}}_{dc1}\right|$ and $\left|{\tilde{v}}_{dc2}\right|$. It should be kept in mind that a large magnitude of ${\tilde{v}}_{dc1}$ (${\tilde{v}}_{dc2}$) may lead to overmodulation of PWM converters. In contrast, a small value results in a large capacitance C_dc1 (C_dc2) and higher costs. With selected $\left|{\tilde{v}}_{dc1}\right|$ and $\left|{\tilde{v}}_{dc2}\right|$, the second step is to derive C_dc1 and C_dc2 based on the equation in Solanki et al. (2015). Furthermore, the third step is to calculate C_dc3 and C_dc4 based on Tang et al. (2015b), and the relevant voltages $\left|{\tilde{v}}_{dc3}\right|$ and $\left|{\tilde{v}}_{dc4}\right|$ can be obtained from the equation by Shimizu et al. (1997). If $\left|{\tilde{v}}_{dc3}\right|$ or $\left|{\tilde{v}}_{dc4}\right|$ exceeds v_dc/2, $\left|{\tilde{v}}_{dc1}\right|$ and $\left|{\tilde{v}}_{dc2}\right|$ should be redesigned. Alternatively, the equivalent filter capacitance C_f shown in Figure 4 can be derived based on the equation by Tang and Blaabjerg (2015). After the derivation of C_f, the remaining design steps are similar to those of the LCL filter parameter design. Therefore, the fourth step is the selection of L_i based on the ripple current requirement equation (Wu et al., 2012). Followed by the resonant frequency requirement, f_r > f_s/6 should be guaranteed for system stability (Parker et al., 2014; Wang et al., 2016b), and f_r < f_s/2 is recommended for system controllability (27). With an appropriate f_r, the fifth step is to derive L_g based on the equation by Isobe et al. (2016). With all the parameter values of passive components, the sixth step is to validate whether the current harmonics at multiple switching frequencies can be attenuated to the limited values according to IEEE standard 519–1992 (IEEE, 1992). If the current harmonics exceed these limitations, f_r, L_i, or C_dc1 (C_dc2) should be redesigned. Alternatively, if the current harmonics can comply with the grid code, the design procedure is completed. With these straightforward design steps, a design example is listed in Table 1.

FIGURE 6

FIGURE 6. Passive components’ design flowchart.

TABLE 1

TABLE 1. System parameter values for the experiments.

As can be obtained from Table 1, the grid-side filter inductance L_g is much smaller than that of the conventional LCL filter (Liserre et al., 2005; Jalili and Bernet, 2006; Channegowda and John, 2010; Bao et al., 2012; Liu et al., 2014; Fang et al., 2017b), leading to lower costs and power losses. In addition, it should be noted that capacitances C_dc1–C_dc4 listed in Table 1 are slightly different from theoretical calculated values, considering that the DSTATCOM system is implemented with standard capacitances; however, the differences are maintained within 10%. In Table 1, K_pv and K_iv represent the proportional gain and integral gain of the voltage-loop controller, respectively.

The Bode diagram and root locus of T_i(z) with the parameter values listed in Table 1 are shown in Figure 7. As can be observed from Figures 7A, the gain margin (GM) of 4.63 dB and phase margins (PM) greater than 40° can be obtained with a 700-Hz current-loop crossover frequency, indicating the satisfactory dynamic response of the current-loop controller (Bao et al., 2012; Pan et al., 2014). Furthermore, as verified by the locations of closed-loop poles shown in Figure 7B, the system stable margin is large enough to tackle the uncertainties introduced by component tolerance (Dannehl et al., 2010a; Dannehl et al., 2010b).

FIGURE 7

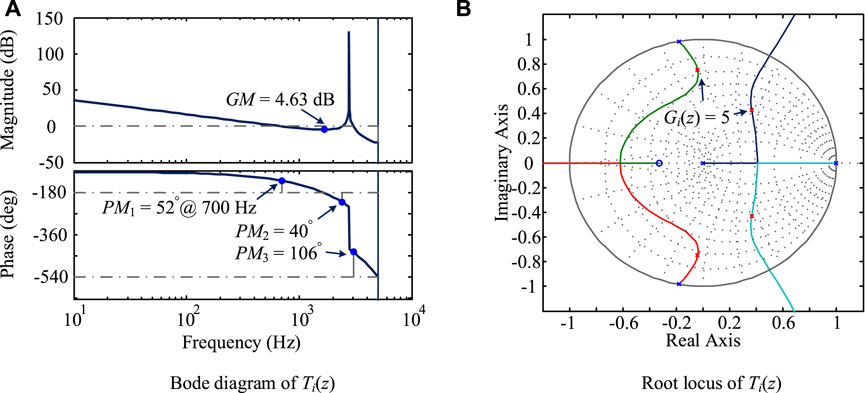
FIGURE 7. Bode diagram and root locus of T_i(z) with system parameters listed in Table 1. (A) Bode diagram T_i(z). (B) Root locus of T_i(z).

5 Simulations and experiment results

The simulation models of the conventional single-phase half-bridge DSTATCOM, single-phase H-bridge DSTATCOM, and proposed single-phase half-bridge DSTATCOM were constructed based on the MATLAB/Simulink software, and the relevant simulation parameter values are listed in Table 2. In Table 2, the DC-link capacitances of conventional and proposed half-bridge DSTATCOMs are selected using the equation by Kumar and Mishra (2015) and Figure 6, respectively. Moreover, the DC-link equivalent capacitance of the H-bridge DSTATCOM is chosen to be equivalent to that of the proposed DSTATCOM.

TABLE 2

TABLE 2. Simulation parameter values.

The simulation results of the conventional half-bridge DSTATCOM are shown in Figure 8A. As shown, although the DC-link capacitances of the conventional half-bridge DSTATCOM are smaller, the voltage across each DC-link capacitor, namely, v_dc1 and v_dc2, varies in a wide range. At its minimum value, v_dc1 or v_dc2 may drop below 200 V, which is lower than 2/3 of the peak value of v_g, leading to overmodulation of the PWM converter. Furthermore, the distorted waveforms of the compensating current i_g and source current i_s can be observed from Figures 10A,B; 6.26% THD of i_s can be obtained (through FFT analysis), which obviously violates the grid code (IEEE, 1992).

FIGURE 8

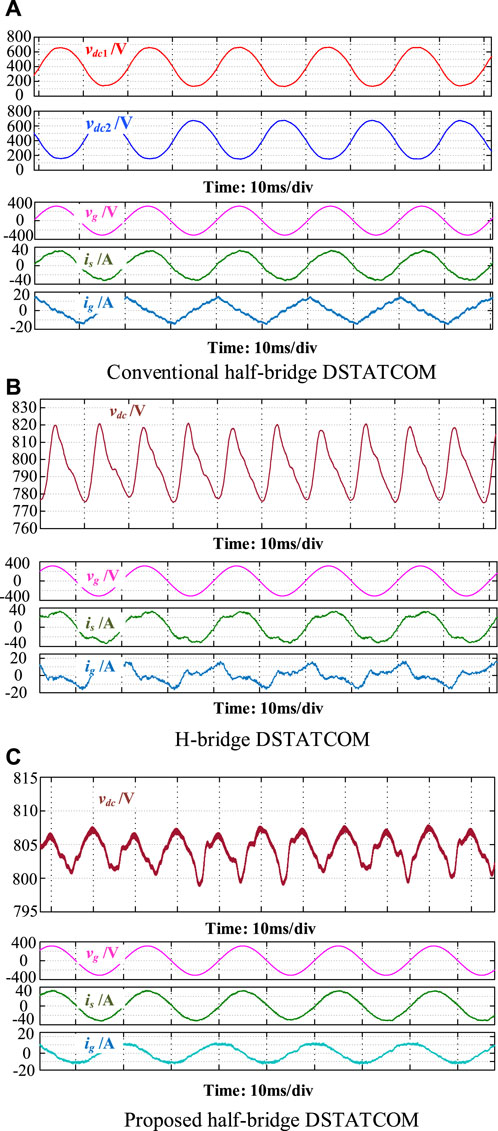
FIGURE 8. Simulation waveforms of the conventional half-bridge, H-bridge, and proposed half-bridge DSTATCOMs. (A) Conventional half-bridge DSTATCOM. (B) H-bridge DSTATCOM. (C) Proposed half-bridge DSTATCOM.

The simulation waveforms of the conventional H-bridge DSTATCOM are illustrated in Figure 8B. As shown in Figure 8B, the DC-link voltage v_dc fluctuates with considerable second-order harmonics and other even-order harmonics. These voltage harmonics deteriorate the grid current. As a consequence, the THD of i_s was found to be 17.04%, which is far from satisfactory levels of the grid code.

The simulation waveforms of the proposed half-bridge DSTATCOM are shown in Figure 8C. With carefully designed DC-link capacitances, the variation of v_dc is maintained within 10 V. The waveform of i_s becomes sinusoidal with a THD of 3.88%, indicating compliance with the grid code.

A single-phase half-bridge DSTATCOM experimental prototype was built and tested in the laboratory, whose schematic diagram is depicted in Figure 3. The system parameters used in the experiments are listed in Table 3, and the relevant controller structures are shown in Figure 5. The control algorithm was executed on a dSPACE control platform (DS1103). Litz wires were utilized for filter inductor windings to minimize their ESRs. Filter capacitors are film capacitors instead of electrolytic capacitors, which are combined with DC-link capacitors. It is clear from the experimental parameters (listed in Table 3) that capacitances are small, which is only 470 μF. The power grid was emulated by a programmable AC power supply (Chroma 61,502), and all the experimental waveforms were captured from a digital oscilloscope (MSO 44MXs-B). SiC MOSFETs (C3M0065090D) with low power losses were employed as S₁ and S₂ switched complementarily with a 1-µs dead time inserted.

TABLE 3

TABLE 3. Parameter values of the conventional LCL filtered half-bridge DSTATCOM.

Before enabling the proposed half-bridge DSTATCOM, a 22-mH inductance L_l connected in parallel with a 10 Ω resistance R_l served as the load. The load current lags the grid voltage by 75° approximately.

Figure 9 shows the experimental waveforms with the reactive power compensated by the proposed half-bridge DSTATCOM. As can be observed, the DC-link voltage v_dc has been regulated to the reference value of 200 V. In addition, i_g leads v_g about 90°, indicating that i_g is mainly composed of the capacitive reactive current. It should be noted that i_g also contains an active current component, whose magnitude is much smaller than that of the capacitive reactive current. The active current component is necessary to maintain a constant DC-link voltage and compensate for the power losses. After the reactive power compensation, the source current i_s comes in phase with v_g, indicating that the power factor observed from the power grid has been improved to unity. Furthermore, as verified by Figure 9, the converter current i_i is much lower than i_g, as has been discussed in Section 3 B. Figure 9 also shows the experimental waveforms of capacitor voltages v_dc1–v_dc4 with the proposed half-bridge DSTATCOM enabled. As can be noticed, the DC components of v_dc1–v_dc4 are the same and equals to 100 V. The AC components of v_dc1, v_dc4, and i_s are all in phase, as proved by Figure 4. Moreover, the AC components of v_dc2 and v_dc3 are in the opposite direction to v_dc1 and v_dc4, respectively, which proves that the required reactive power is compensated by all the four capacitors.

FIGURE 9

FIGURE 9. Experimental waveforms with reactive power compensated by the proposed DSTATCOM.

Figure 10 illustrates the experimental waveforms when the proposed half-bridge DSTATCOM is enabled with a light load, composed of a 22-mH inductance L_l connected in series with a 10 Ω resistance R_l. Before compensation, i_s is a resistive–capacitive current that leads v_g by approximately 60°, which is mainly composed of the reactive current absorbed by C_dc1–C_dc4. After the proposed half-bridge DSTATCOM is put into operation under the light load condition, the reactive current absorbed by the proposed DSTATCOM can be regulated to the reference value, and as a result i_s comes in phase with v_g. Once again, the DC-link voltage v_dc can be maintained as a reference value of 200 V.

FIGURE 10

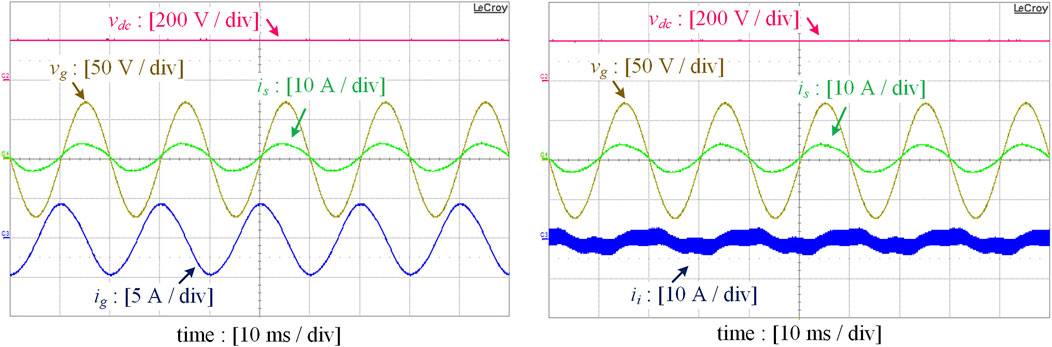
FIGURE 10. Experimental waveforms with reactive power compensated by the proposed DSTATCOM under light load condition.

Figure 11 shows the experimental waveforms when the reactive power is compensated by a conventional LCL-filtered half-bridge DSTATCOM. All the DC-link capacitances remain the same as those listed in Table 1, and parameter values of the LCL filter are provided in Table 2.

FIGURE 11

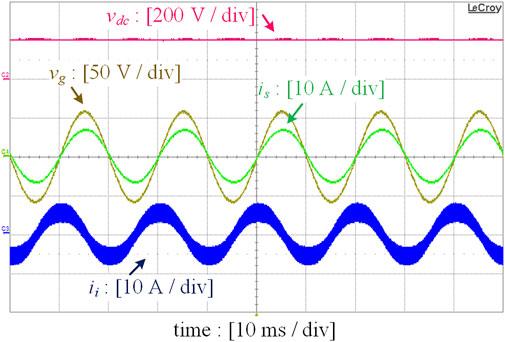
FIGURE 11. Experimental waveforms with reactive power compensated by the conventional LCL-filtered half-bridge DSTATCOM.

It can be observed that a larger inductor L_g and an additional capacitor C_f are added to form the LCL filter, as shown in Figure 2. Furthermore, the load inductance L_l has been intentionally reduced from 22 to 12 mH in order to decrease the magnitude of reactive current i_g. The reason is that i_s and v_g may have a phase difference due to the limited compensation ability of controllers provided that the same load as that adopted in Figure 10 is used. As can be observed from Figure 11, the magnitude of i_i becomes larger than that of i_g and i_s, leading to increased current stress and power losses. In this case, the overmodulation of power converters will not be observed due to small power ratings. In addition, the third-order current harmonic can be attenuated to be less than 3% of I_lp with an additional 100 Hz second-order notch filter inserted into the voltage-loop PI controller.

The experimental results of the dynamic response of the proposed half-bridge DSTATCOM are provided in Figure 12. As can be observed, i_g can be stabilized after 2–3 cycles of the sudden load change, indicating that the dynamic performance of the proposed controllers is satisfactory. The aforementioned experimental results agree well with the theoretical analysis.

FIGURE 12

FIGURE 12. Experimental waveforms of the dynamic response of the proposed half-bridge DSTATCOM.

6 Conclusion

In this study, the novel LCL-filtered half-bridge DSTATCOM topology has been proposed. With the proposed half-bridge DSTATCOM, it is possible to regulate the DC-link voltage as a constant DC value without any fluctuations. Furthermore, the filter capacitor of the LCL filter can be replaced by the DC-link capacitors and hence be saved. Moreover, the currents flowing through the converter side inductance and semiconductor switches can be dramatically decreased, leading to lower power losses and current stresses of the switching devices. Another prominent advantage of the proposed half-bridge DSTATCOM is that its grid-side inductance can be greatly reduced from the order of millihenry to several microhenries. Following the passive component design procedure introduced in this study, the voltage fluctuation across each DC-link capacitor can be maintained within the predetermined limitation values, preventing the overmodulation caused by uncontrollable DC-link voltage fluctuations. A down-scaled prototype of the proposed half-bridge DSTATCOM was built and tested in the laboratory, and the experimental results are provided to validate the feasibility and correctness of the theoretical analysis.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

JF came up with the raw idea of this novel LCL-filtered half-bridge DSTATCOM topology and instructed the simulations and the experiments. XM carried out the detailed analysis on this proposed topology and finished simulation and experiment verification.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akagi, H. (2011). Classification, terminology, and application of the modular multilevel cascade converter (MMCC). IEEE Trans. Power Electron. 26, 3119–3130. doi:10.1109/IPEC.2010.5543243

CrossRef Full Text | Google Scholar

Bao, C., Ruan, X., Wang, X., Li, W., Pan, D., Weng, K., et al. (2012). Design of injected grid current regulator and capacitor-current-feedback active- damping for LCL-type grid-connected inverter. Proc. IEEE Energy Conver. Congr. Expo. 29, 579–586. doi:10.1109/ECCE.2012.6342769

CrossRef Full Text | Google Scholar

Bao, C., Ruan, X., Wang, X., Li, W., Pan, D., Weng, K., et al. (2014). Step-by-step controller design for LCL-type grid-connected inverter with capacitor-current-feedback active-damping. IEEE Trans. Power Electron. 29, 1239–1253. doi:10.1109/TPEL.2013.2262378

CrossRef Full Text | Google Scholar

Blaabjerg, F., Teodorescu, R., Liserre, M., and Timbus, A. (2006). Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 53, 1398–1409. doi:10.1109/TIE.2006.881997

CrossRef Full Text | Google Scholar

Channegowda, P., and John, V. (2010). Filter optimization for grid interactive voltage source inverters. IEEE Trans. Ind. Electron. 57, 4106–4114. doi:10.1109/tie.2010.2042421

CrossRef Full Text | Google Scholar

Dannehl, J., Fuchs, F., Hansen, S., and Thøgersen, P. (2010). Investigation of active damping approaches for PI-based current control of grid-connected pulse width modulation converters with LCL filters. IEEE Trans. Ind. Appl. 46, 1509–1517. doi:10.1109/TIA.2010.2049974

CrossRef Full Text | Google Scholar

Dannehl, J., Fuchs, F., and Thøgersen, P. (2010). PI state space current control of grid-connected PWM converters with LCL filters. IEEE Trans. Power Electron. 25, 2320–2330. doi:10.1109/TPEL.2010.2047408

CrossRef Full Text | Google Scholar

Dugan, R., McGranaghan, M., Santoso, S., and Beaty, H. (2004). Electrical power systems quality. USA: McGraw-Hill.

Google Scholar

Fang, J., Li, H., and Tang, Y. (2017). A magnetic integrated LLCL filter for grid-connected voltage source converters. IEEE Trans. Power Electron. 32, 1725–1730. doi:10.1109/TPEL.2016.2613578

CrossRef Full Text | Google Scholar

Fang, J., Xiao, G., Yang, X., and Tang, Y. (2017). Parameter design of a novel Series-Parallel-Resonant LCL filter for single-phase half-bridge active power filters. IEEE Trans. Power Electron. 32, 200–217. doi:10.1109/TPEL.2016.2532961

CrossRef Full Text | Google Scholar

Farivar, G., Hredzak, B., and Agelidis, V. (2015). Reduced-capacitance thin-film H-bridge multilevel STATCOM control utilizing an analytic filtering scheme. IEEE Trans. Ind. Electron. 62, 6457–6468. doi:10.1109/tie.2015.2420675

CrossRef Full Text | Google Scholar

IEEE (1992). IEEE recommended practices and requirements for harmonic control in electric power systems. IEEE Stand. 1992, 519. doi:10.1109/IEEESTD.1993.114370

CrossRef Full Text | Google Scholar

Inzunza, R., and Akagi, H. (2005). A 6.6-kV transformerless shunt hybrid active filter for installation on a power distribution system. IEEE Trans. Power Electron. 20, 893–900. doi:10.1109/TPEL.2005.850951

CrossRef Full Text | Google Scholar

Isobe, T., Shiojima, D., Kato, K., Hernandez, Y., and Shimada, R. (2016). Full-bridge reactive power compensator with minimized-equipped capacitor and its application to static var compensator. IEEE Trans. Power Electron. 31, 224–234. doi:10.1109/TPEL.2015.2412954

CrossRef Full Text | Google Scholar

Jalili, K., and Bernet, S. (2006). Design of LCL filters of active-front-end two level voltage-source converters. IEEE Trans. Ind. Electron. 56, 1674–1689. doi:10.1109/TIE.2008.2011251

CrossRef Full Text | Google Scholar

Karanki, S., Geddada, N., Mishra, M., and Kumar, B. (2012). A DSTATCOM topology with reduced DC-link voltage rating for load compensation with nonstiff source. IEEE Trans. Power Electron. 27, 1201–1211. doi:10.1109/TPEL.2011.2163946

CrossRef Full Text | Google Scholar

Kumar, C., and Mishra, M. (2014). A multifunctional DSTATCOM operating under stiff source. IEEE Trans. Ind. Electron. 61, 3131–3136. doi:10.1109/TIE.2013.2276778

CrossRef Full Text | Google Scholar

Kumar, C., and Mishra, M. (2014). An improved hybrid DSTATCOM topology to compensate reactive and nonlinear loads. IEEE Trans. Ind. Electron. 61, 6517–6527. doi:10.1109/TIE.2014.2321355

CrossRef Full Text | Google Scholar

Kumar, C., and Mishra, M. (2015). Operation and control of an improved performance interactive DSTATCOM. IEEE Trans. Ind. Electron. 62, 6024–6034. doi:10.1109/TIE.2015.2420635

CrossRef Full Text | Google Scholar

Liang, Y., and Nwankpa, C. (1999). A new type of STATCOM based on cascading voltage-source inverters with phase-shifted unipolar SPWM. IEEE Trans. Ind. Appl. 35, 1118–1123. doi:10.1109/28.793373

CrossRef Full Text | Google Scholar

Liserre, M., Blaabjerg, F., and Hansen, S. (2005). Design and control of an LCL filter-based three-phase active rectifier. IEEE Trans. Ind. Appl. 41, 1281–1291. doi:10.1109/TIA.2005.853373

CrossRef Full Text | Google Scholar

Liu, Q., Peng, L., Kang, Y., Tang, S., Wu, D., Qi, Y., et al. (2014). A novel design and optimization method of an LCL filter for a shunt active power filter. IEEE Trans. Ind. Electron. 61, 4000–4010. doi:10.1109/TIE.2013.2282592

CrossRef Full Text | Google Scholar

Pan, D., Ruan, X., Bao, C., Li, W., and Wang, X. (2014). Capacitor-current-feedback active damping with reduced computation delay for improving robustness of LCL-type grid-connected inverter. IEEE Trans. Power Electron. 29, 3414–3427. doi:10.1109/TPEL.2013.2279206

CrossRef Full Text | Google Scholar

Parker, S., McGrath, B., and Holmes, D. (2014). Regions of active damping control for LCL filters. IEEE Trans. Ind. Appl. 50, 424–432. doi:10.1109/TIA.2013.2266892

CrossRef Full Text | Google Scholar

Peng, F., Lai, J., McKeever, J., and VanCoevering, J. (1996). A multilevel voltage-source inverter with separate DC sources for static var generation. IEEE Trans. Ind. Appl. 32, 1130–1138. doi:10.1109/IAS.1995.530626

CrossRef Full Text | Google Scholar

Shimizu, T., Fujita, T., Kimura, G., and Hirose, J. (1997). A unity power factor PWM rectifier with DC ripple compensation. IEEE Trans. Ind. Electron. 44, 447–455. doi:10.1109/41.605618

CrossRef Full Text | Google Scholar

Singh, B., Jayaprakash, P., Kothari, D., Chandra, A., and Haddad, K. (2014). Comprehensive study of DSTATCOM configurations. IEEE Trans. Ind. Inf. 10, 854–870. doi:10.1109/tii.2014.2308437

CrossRef Full Text | Google Scholar

Singh, B., and Solanki, J. (2009). A comparison of control algorithms for DSTATCOM. IEEE Trans. Ind. Electron. 56, 2738–2745. doi:10.1109/TIE.2009.2021596

CrossRef Full Text | Google Scholar

Solanki, J., Fröhleke, N., and Böcker, J. (2015). Implementation of hybrid filter for 12-Pulse thyristor rectifier supplying high-current variable-voltage DC load. IEEE Trans. Ind. Electron. 62, 4691–4701. doi:10.1109/TIE.2015.2393833

CrossRef Full Text | Google Scholar

Tang, Y., and Blaabjerg, F. (2015). A component-minimized single-phase active power decoupling circuit with reduced current stress to semiconductor switches. IEEE Trans. Power Electron. 30, 2905–2910. doi:10.1109/TPEL.2014.2369959

CrossRef Full Text | Google Scholar

Tang, Y., Blaabjerg, F., Loh, P., Jin, C., and Wang, P. (2015). Decoupling of fluctuating power in single-phase systems through a symmetrical half-bridge circuit. IEEE Trans. Power Electron. 30, 1855–1865. doi:10.1109/TPEL.2014.2327134

CrossRef Full Text | Google Scholar

Tang, Y., Loh, P., Wang, P., Choo, F., Gao, F., Blaabjerg, F., et al. (2012). Generalized design of high performance shunt active power filter with output LCL filter. IEEE Trans. Ind. Electron. 59, 1443–1452. doi:10.1109/TIE.2011.2167117

CrossRef Full Text | Google Scholar

Tang, Y., Qin, Z., Blaabjerg, F., and Loh, P. (2015). A dual voltage control strategy for single-phase PWM converters with power decoupling function. IEEE Trans. Power Electron. 30, 7060–7071. doi:10.1109/tpel.2014.2385032

CrossRef Full Text | Google Scholar

Van de Sype, D., Gusseme, K., De Belie, F., Bossche, A., and Melkebeek, J. (2016). Small-signal z-domain analysis of digitally controlled converters. IEEE Trans. Power Electron. 21, 470–478. doi:10.1109/TPEL.2005.869758

CrossRef Full Text | Google Scholar

Wang, J., Yan, J., Jiang, L., and Zou, J. (2016). Delay-dependent stability of single-loop controlled grid-connected inverters with LCL Filters. IEEE Trans. Power Electron. 31, 743–757. doi:10.1109/TPEL.2015.2401612

CrossRef Full Text | Google Scholar

Wang, L., Lam, C., and Wong, M. (2016). A hybrid-STATCOM with wide compensation range and low DC-link voltage. IEEE Trans. Ind. Electron. 63, 3333–3343. doi:10.1109/TIE.2016.2523922

CrossRef Full Text | Google Scholar

Wang, X., Pang, Y., Loh, P., and Blaabjerg, F. (2015). A series-LC-filtered active damper with grid disturbance rejection for ac power-electronics-based power systems. IEEE Trans. Power Electron. 30, 4037–4041. doi:10.1109/TPEL.2014.2382477

CrossRef Full Text | Google Scholar

Wu, W., He, Y., and Blaabjerg, F. (2012). An LLCL power filter for single-phase grid-tied inverter. IEEE Trans. Power Electron. 27, 782–789. doi:10.1109/TPEL.2011.2161337

CrossRef Full Text | Google Scholar

Zou, C., Liu, B., Duan, S., and Li, R. (2014). Influence of delay on system stability and delay optimization of grid-connected inverters with LCL filter. IEEE Trans. Ind. Inf. 10, 1775–1784. doi:10.1109/TII.2014.2324492

CrossRef Full Text | Google Scholar