Frequency regulation in adaptive virtual inertia and power reserve control with high PV penetration by probabilistic forecasting

The large-scale deployment of sustainable energy sources has become a mandatory goal to reduce pollution from electricity production. As photovoltaic (PV) plants replace conventional synchronous generators (SGs), their significant inherent rotational inertia characteristics are reduced. The high penetration of PV results in reduced system inertia, leading to system frequency instability. Virtual inertial control (VIC) technology has attracted increasing interest because of its ability to mimic inertia. Adoption of the energy storage system (ESS) is hindered by the high cost, although it can be used to provide virtual inertia. The determined forecast gives PVs the ability to reserve power before shading and compensate the power when a system power drop occurs, which can increase system inertia. Nevertheless, it has forecast errors and energy waste in a stable state. To improve the stability of the microgrid and improve the ESS efficiency, this study proposes an adaptive forecasting-based (AFB) VIC method using probabilistic forecasts. The adaptive power reserve and virtual inertia control are proposed to reduce energy waste and increase system inertia. The simulation results reveal that the proposed method has adaptive system inertia to reduce the reserved power, required ESS power capacity, and battery aging.

1 Introduction

Local loads, energy storage systems (ESS), and distributed generators (DGs) comprise a micro-grid. Due to the clean, sustainable, and environmentally friendly nature of solar energy sources, photovoltaic power generation has seen rapid growth in remote areas as one of the most promising renewable energy sources (Woodhouse et al., 2011). The amount of energy obtained from renewable energy has increased exponentially over the last decade, making distributed generation a viable scheme for mainstream power generation (Askarian et al., 2018). The evolution of the global power generation mode has changed and will continue to change the prospects of the power system. The adaptability of micro-grids allows for rapid tracking of fluctuations in renewable energy power generation. It has the potential to reduce demand from large grid power systems (Zhang et al., 2020a).

For the 2030 scenario, the Australian Energy Market Operator (AEMO) has proposed a 100% renewable power system (RPS) composition (Gu et al., 2018). The RPS of the national electricity market (NEM) generation mix projection is expected. The PV power ratio accounts for 22% of total power while providing 51% of the peak demand power. Thus, with the increasing PV penetration level, the intermittent nature of solar energy poses new challenges for the conventional grid. Non-dispatchable PV power may result in a loss of system inertia and increased frequency deviation. Mararakanye and Bekker (2019) specified two conditions for frequency control in the NEM: ±0.5 Hz/s RoCoF and ±0.15 Hz frequency deviations.

Because of the high penetration of PVs, system inertia is reduced, resulting in an unstable system frequency in micro-grids (Dreidy et al., 2017). Due to the high penetration of PVs, many researchers have considered the impact of low inertia on the stability and operation of grid systems (Gu et al. 2018; Tielens and Van Hertem, 2016; Ulbig et al. 2014). For the response to system contingencies, frequency regulation actions must be implemented multiple times. The problem of reducing system inertia and the challenges of system operation are investigated in Tielens and Van Hertem (2016). The main challenge for Australia is to maintain enough inertia in the system to ensure safe operation (Gu et al., 2018). Ulbig et al. (2014) investigates the impact of low inertia on the operation and stability of micro-grids at high PV penetration levels. It is demonstrated that in a micro-grid with low inertia, it may result in rapid frequency changes and overshoot the frequency policy limitations. Because of the high penetration of PVs in the micro-grid, the generator may not increase power in time to regulate frequency when the frequency drops. As a result, the low inertia issues are widely acknowledged.

The low inertia issues in a micro-grid system can be improved by virtual inertial control (VIC). In Tielens and Van Hertem (2016), the rate of change of frequency (RoCoF) is increased to a higher level. Iit uses the VIC technique to increase system inertia by simulating the properties of traditional synchronous generators (SGs). Most VIC strategies necessitate the use of additional ESS energy, such as a battery or super capacitor. Hammad et al. (2019) proposed an efficient virtual inertial measurement method. It is suitable for actuated ESS. Although the ESS efficiently provides enough power for VIC, it results in higher capital and operating costs.

The PV-based VIC method is comparable to other ESS-VIC technologies. A sufficient power supply for the VIC can be provided by reserving PV power (Crăciun et al., 2014; Hua et al., 2017; Yan et al., 2018). This approach is provided by the development of active power reserves (Hoke and Maksimović, 2013; Yang et al. 2016). However, to provide sufficient power buffers to the VIC when frequency deviations occur, the aforementioned method usually necessitates a constant power reduction, such as 10% of the maximum available power. This study describes the process of modeling the PV small signal with VIC and implements the details of simulating the dynamic properties of SGs (Li et al., 2019). As a result, once the micro-grid system is stabilized, there is a constant waste of energy.

Algorithms for determining forecasting PV power using historical solar irradiance data are proposed in the literature reports (Chen et al., 2019; Mahmud et al., 2021; da Luz et al., 2020; Han et al., 2019; Wang et al., 2020). The impact of data normalization on forecast performance is introduced in Mahmud et al. (2021) using a variety of performance indicators. Han et al. (2019) proposed a reserve method in which the optimal operation plan of a controllable generator is used to deal with the forecast error uncertainty. The methods described earlier typically require forecast information about the PV power drop. The reserve method, known as local curtailment (LC), is used at the local PV power station. Forecasting errors are unavoidable. With forecast errors, PV may not provide the required virtual inertia. It may cause a frequency deviation that exceeds the grid limit.

Coordinate control is proposed in Chang et al. (2021) to reduce the effect of forecast error. In a large distributed area, the PV stations have a geographical distance. When power is changed at one local PV station, using other remote PV station’s reserve power can provide constant virtual inertia. The remote reserve has improved frequency stability via probabilistic forecasting. However, it works in a transient state with constant virtual inertia and cannot limit the frequency deviation in policy. As a result, it is challenging to limit frequency deviations in any limitations. Given the policy constraints in continuous operation, an adaptive virtual inertia parameter and a power reserve control strategy are required.

The contribution of this study is listed as follows:

1) The proposed reserve strategy is capable of filtering and determining the working point in quantile regression results. It reduces reserve power in stable irradiance and improves the efficiency of reserved power in the regulating frequency.

2) The ESS capacity and charge/discharge times are reduced by improved virtual inertia control for the remote reserve using adaptive inertia parameters. The virtual inertia is changed to be suitable for different scenarios of the PV power drop. The system frequency and RoCoF variation are reduced in the continuous control throughout the single daytime.

3) Considering the policy of RoCoF and frequency nadir limitation to the virtual inertia control, coordinated control of PV and ESS helps micro-grids improve the system stability.

The remainder of this study is structured as follows. The framework and islanded micro-grid components are described in Section 2. The system inertia and control strategies are defined in Section 3. The simulation results are presented and discussed in Section 4. Conclusion is provided in Section 5.

2 System configuration

The proposed framework of the AFB-VIC strategy, including PV, load, SG, and ESS connected to a micro-grid controlled by a micro-grid control center, is depicted in Figure 1. There is a geographical distance between PV stations where the irradiance changes asynchronously. The forecast information from the shaded PV station is used to generate reserve power demand in the stable station, shown as the orange arrow. When one of the PV stations is expected to be shaded, the other stable PV begins to reserve power. Following a power drop in a shaded PV station, the ESS and reserved power can be released to provide VIC. For load frequency control (LFC), SG provides constant inertia. Figure 2 shows a simple mathematical schematic representation of an islanded micro-grid. The system’s inertia is divided into two parts. The governor (GOV) of the power plant provides the constant inertia. The virtual inertia is controlled by PV and ESS. The parameters of virtual inertia can be adaptively changed according to the forecasting information. The RoCoF and frequency nadir methods are used to control the value of virtual inertia. The following sections follow the specifics of the proposed control strategy.

FIGURE 1

FIGURE 1. Framework of the islanded micro-grid.

FIGURE 2

FIGURE 2. Schematic representation of the micro-grid plant model.

2.1 Synchronous generators

An SG module to regulate the system frequency with feedback control is proposed in Liu et al. (2016). The constant inertia is provided by SGs in the micro-grid. The control system of the SG is shown in Figure 2; the GOV is used to change the shaft power P_m when angular frequency deviation occurs. The difference between the SG output angular frequency ω₀ and the rated angular frequency ω_r is the angular frequency deviation. The GOV droop coefficient is k_p. In control, a first-order equation is added to represent inertia, where t_d is the inertial response of the governor. The automatic voltage regulator (AVR) is shown in Figure 3. It consists of a power calculation, root-mean-square (RMS), and proportional–integral (PI) control. The excitation system provides the DC to regulate the SG voltage, where k_q is the AVR droop coefficient.

FIGURE 3

FIGURE 3. Control system of the automatic voltage regulator.

2.2 Photovoltaic

A maximum power point (MPP) estimation method for PV power sources is proposed in Belhachat and Larbes (2019). The maximum available power is estimated by irradiance G and temperature T, which is represented as

$P_{mp}=\frac{25°\mathrm{C}\cdot G}{T}\cdot \frac{K}{\frac{\sqrt{A}}{2\pi \cdot 0.02}s+1},(1)$

where K is a constant parameter and A is the PV panel area. Here, s represents the continuous domain. As shown in Figure 4, PV reserve power means changing the working point from A to B. V_cmd is the reserved voltage to regulate the PV voltage. Figure 5 depicts the PV power control strategy that employs MPP estimation and reserve control. P_r is the PV working away from the MPP to reserve power for VIC. The controlled power is limited to less than the reserve power. It ensures PV will not over-regulate. The control strategy of VIC is shown in the PV-controlled power in Figure 2. PVs can compensate the power with virtual inertia when frequency deviation occurs. The VIC function is determined by

$D_p\cdot \mathrm{\Delta }\omega =\left(2H_{pv}s+D_{pv}\right)\cdot P_c,(2)$

where D_p is p_ω droop coefficient, H_pv is the virtual inertia, and D_pv is the virtual damping. The ramp-rate violations are considered in power-reserved processing. The PV power change rate should be suitable for the forecast horizon. The ramp rate limits R_s will help grid stability in the reserve strategy. It limits the reserve speed before the stable PV provides the virtual inertia.

$R_s=|\frac{d{P}_{PV}}{dt}|.(3)$

FIGURE 4

FIGURE 4. Movement of PV power reserves by the operating point away from the MPP.

FIGURE 5

FIGURE 5. Power reserve and the VIC strategy of the PV.

2.3 Energy storage system

The frequency deviation in the power system is caused by a mismatch between supply and demand as a result of a generator fault. Furthermore, frequency deviation exists in the forecasting system as a result of forecasting errors. Keeping the ESS state of charge (SOC) in the middle of its capacity can increase delivered energy while decreasing its capacity. Figure 6 illustrates the ESS charge and discharge control strategy. It is stable in the middle of the SOC and is only affected by minor frequency deviations.

FIGURE 6

FIGURE 6. SOC control and limitation to charging.

The virtual inertia and damping components of the ESS recovery control are similar to the grid forming control for VIC of PVs. When there is a frequency deviation, the ESS compensates the power to the system except for the no-action region. The following Figure 2 illustrates ESS control, which consists of energy recovery control and virtual inertia-damping emulation. It is similar to the VIC of the PV. The ESS virtual inertia is H_e, and damping is D_e.

3 Proposed control strategy

For the evaluated adaptive virtual inertia, forecasting results must be transformed into system inertia demand. As a result, the PV and ESS can share the inertia demand with their respective energy capacities. For frequency regulation, the control strategy employs a two-part strategy that includes forecasted reserve control and inertia control.

3.1 Inertia

A sudden change in irradiance causes PV power deviations, which may lead to a generation-demand disequilibrium. Initially, the inertia prevents the system’s frequency drop. The primary control is to operate the output power of generators to compensate for the frequency deviations. The inertia could be provided by SG, ESS, and reserved power in the PV.

The instantaneous RoCoF is determined by system inertia, and the power of contingency size is expressed by

${RoCoF}_{\max }=\frac{f_0{P}_d}{2H_{\mathit{sys}}},(4)$

where P_d is the contingency size, f₀ is the nominal system frequency, and H_sys is the total system inertia. If the permissible RoCoF is determined, the required minimum system inertia can be formulated as

$H_{\min }=\frac{f_0{P}_d}{2{RoCoF}_{\max }}.(5)$

Figure 7 shows the relationship between the contingency size, maximum RoCoF, and minimum system inertia. It can be seen that the minimum system inertia and contingency size have a positive relationship. On the contrary, there is an inverse relationship between minimum system inertia and maximum RoCoF. When the maximum RoCoF is determined, the contingency size determines the minimum system inertia.

FIGURE 7

FIGURE 7. Relationships of inertia and power in different RoCoF limitations.

Another critical indicator of frequency control is the frequency nadir. Chávez et al. (2014) proposed the overall generator power response in the event of a sudden loss of generation. Figure 8 depicts the relationship between the frequency nadir and drop power. It uses a simplified dynamic model that approximation underestimates the actual response and validates the assumption.

where f₀ is the nominal frequency and G_sys is the approximation-aggregated ramp rate limit of the system primary reserve. Re-arranging the integral limits leads to a lower limit equal to zero so that the integral of Eq. 5 between time 0 and t_nadir of the frequency nadir can be formulated by

${\int }_0^{t_{\mathit{nadir}}}\frac{df\left(t\right)}{dt}dt=\frac{f_0}{2H_{\mathit{sys}}}{\int }_0^{t_{\mathit{nadir}}}{P}_{d}dt.(6)$

FIGURE 8

FIGURE 8. Relationship of the frequency nadir and drop power in primary control.

An approximation ramp rate G_sys of total governor responses is assumed (Chávez et al., 2014) to facilitate the definite integral calculation of power imbalance, as shown in Figure 8.

$f_{\mathit{nadir}}-f_0=-\frac{f_0}{2H_{\mathit{sys}}}\cdot \frac{P_d^2}{2G_{\mathit{sys}}},(7)$

where t_nadir is the time frequency it takes to reach the nadir, and it can be represented by

$t_{\mathit{nadir}}=\frac{P_d}{G_{\mathit{sys}}}.(8)$

In Liu et al. (2020), it establishes a frequency nadir prediction model (FNP) and predicts the time required to reach the maximum frequency deviation, following a major disturbance. The analytical FNP model has a simple structure to the polynomial fitting step response for each governor. The minimum-squared-error method for governors in the islanded model is used to solve the coefficient vector P_i = [p_r0, i, p_r1, i, …p_rn, i,]. Here, α_i is the transfer coefficient per unit; the time of maximum frequency deviation can also be represented by

$t_{\mathit{nadir}}=\frac{\left[-\frac{1}{2}A+\sqrt{\frac{1}{4}{A}^2+\frac{16}{3}B{H}_{\mathit{sys}}}\right]}{\frac{4}{3}B},(9)$

where

$\left\{\begin{array}{c}\hfill A={\sum }_{i=1}^{N_G}{\alpha }_i{p}_{r1},i\hfill \\ \hfill B={\sum }_{i=1}^{N_G}{\alpha }_i{p}_{r2},i\hfill \end{array}\right.(10)$

3.2 Forecasted reserve control

A lasso-based short-term forecasting model for a PV system is proposed in Zhao et al. (2019) and Wang et al. (2022). It constructs a penalty function that allows it to compress some regression coefficients to obtain a refined model. Zhang et al. (2020b) proposed a hybrid forecasting framework based on the LSTM model. The quantile regression architecture for deep learning is probabilistic forecasting.

In this work, the forecast model is trained on a publicly available dataset obtained on Oahu Island, Hawaii, installed by the National Renewable Energy Laboratory (NREL). The details of the dataset are recorded in Sengupta and Andreas (2014). The results of single-daytime forecasting are shown in Figure 9, with cloudy conditions, resulting in significant forecast errors. The blue line is the actual PV power. The orange line represents the determined forecast information. The red line represents the quantile results of the probabilistic forecast. A deeper red color indicates that the results are closer to 50%. The gray area depicts the ability of SGs to compensate for power using Eq. 5 and Eq. 7. If the PV power fluctuated between gray areas, the frequency deviations could adhere to the NEM limitations by only using SGs to regulate the frequency. When PV power fluctuates dramatically, the determined forecast has lower accuracy. For probabilistic forecasting, lower quantile results perform better in terms of accuracy at unstable states. However, in a stable irradiance state, it wastes power.

FIGURE 9

FIGURE 9. Single daytime forecasting results.

The proposed reserve strategy is to add the filter and determine quantile processing. The SG boundary, as shown in Figure 9, can cover a portion of the forecasting results. The SG boundary primarily coincides with 15% quantile results. As a result, the quantile can be calculated. The reserve strategy is illustrated in Figure 10. The blue line represents the actual power drop, while the yellow line represents the determined forecasted power. Forecasted results may not equal actual power at the start of the operation. Thus, even if the calculated forecasted drop power results are equal to the actual drop power, the LC reserve strategy wastes energy due to initial errors. The AFB-VIC was more concerned with the power shift. It has reduced the amount of energy wasted due to initial errors. Furthermore, Eq. 5 and Eq. 7 show that the constant inertia of SG results in a limited boundary of power change. This portion of the power can also be reduced to reduce the energy waste. The power drop can be handled by the sum of virtual inertia in the PV and constant inertia in the SG.

FIGURE 10

FIGURE 10. Reserved power control using forecasting results.

3.3 Inertia control strategy

Inertia has a relationship with RoCoF and the frequency nadir. Thus, the system inertia demand can be calculated by the normalized forecasting results. The system inertia demand, according to Eq. 5 and Eq. 7, is the sum of H_rocof and H_nadir. The system inertia distribution of SG, PV, and ESS is expressed by

$H_{\mathit{sys}}=\sum _{i\in \varphi SG}^{N_G}{H}_i{x}_i+\sum _{i\in \varphi PV}^{N_G}{H}_j{x}_j+\sum _{i\in \varphi ESS}^{N_G}{H}_k{x}_k,(11)$

where ϕSG, ϕPV, and ϕESS are sets of SGs, PVs, and ESSs in the islanded micro-grid, and the SG has constant inertia. The requirement for minimum system inertia can be evaluated by the adaptive virtual inertia of the PV and ESS.

The SG maintains constant inertia. If the stable PV is working at the MPP, it cannot provide virtual inertia to the micro-grid. When the rapid power drops from the shaded PV, the SG may not be able to compensate for the total system inertia demand. The remaining virtual inertia must be distributed adaptively by reserve power at the stable PV and ESS. Figure 11 depicts the inertia demand when PV power is reduced in a single day. The actual power drop at the shaded PV station is depicted by the blue line. The orange line depicts the LC strategy. It reserves power at the shaded PV by determined forecasting. The red line represents the virtual inertia supplied by the remote stable PV via AFB-VIC. The gray portion represents the constant inertia provided by the SG. The remainder of the inertia demand needs to be compensated by the PV and ESS. As a result, SG inertia reduces the power demand in a remote stable PV. The PV reserve power can be used to charge the ESS when considering the ESS recovery process. As a result, the PV and ESS have distributed virtual inertia, and the parameters of H_pv are governed by the NEM guideline limitation.

Algorithm 1

Algorithm 1. LC – pseudo code.

FIGURE 11

FIGURE 11. Inertia demand and distribution.

Maximum power point tracking (MPPT) control, local curtailment (LC), determined region reserve (DRR), and AFB-VIC are the four PV power control strategies. The MPPT control is defined as the PV operating at the MPP at all times. It does not require any forecasting data. Based on forecast information, LC is the reserved power in the local PV station. It has a ramp limit to reserve power before the PV power drops. As a result, the reserved processing avoids frequency deviation. Algorithm 1—Local curtailment—Pseudo Code depicts the control strategy. The DRR is comparable to LC control. It uses the determined forecast result at PV1 but reserves power at a stable PV station.

Based on probabilistic forecast data, AFB-VIC is a method of reserving power at geographically separated, stable PV stations. It also has a ramp limit for power reserves. When the other PV station is shaded, the reserved power at the stable PV station can be released to compensate for the loss of power. The system inertia consists of SG, PV, and ESS. SG has constant inertia. The required virtual inertia is provided by the PV and ESS. The value of virtual inertia is thus adaptively changed for different forecasted PV power levels, according to Eq. 7. Within the limits of RoCoF and the frequency nadir, the SG can compensate for a constant power deficit. The PV and ESS must supply the remainder of the predicted power and inertia demand. As a result, the power reserved in the PV can be calculated using the Algorithm 2-AFB-VIC-pseudo code.

Algorithm 2

Algorithm 2. AFB-VIC – pseudo code

4 Simulation results

As shown in Figure 1, an islanded micro-grid with the SG, PV, ESS, and load has been modeled using MATLAB/Simulink. The actual power change in a single day (36000s, 7:30–19:30) is depicted in Figure 12. PVs, ESS, and SG supply load demand in this islanded micro-grid system. The AFB-VIC strategy employs two PVs to simulate the frequency variation. According to the forecasting results, one of the PV stations will be shaded. The other has consistent irradiance. Table 1 shows the corresponding parameters of the tested system.

FIGURE 12

FIGURE 12. Basic output power and load demand in 36,000 s of a single daytime.

TABLE 1

TABLE 1. Corresponding parameters of the tested system.

To validate the effectiveness of the proposed AFB-VIC strategy, the other three cases, including traditional MPPT, DRR, and LC strategies, are simulated and compared. Podder et al. (2019) used a traditional MPPT control strategy that employs a fixed-step-size perturb and observed the algorithm (P&O). Single-day forecasting results, including spot and probabilistic methods, are used for power reservation purposes. LC uses determined forecast results of PV1 and makes PV1 reserve power before shading and lets PV2 always work at its MPP. The DRR uses a determined forecast to reserve power at PV2 and then releases it to provide VIC, which performs PV1 work at the MPP. AFB-VIC reserves power in stable PV2 by probabilistic forecasting while allowing shaded PV1 to operate at the MPP. The ESS is configured to compensate power only when frequency deviations exceed ±0.05 Hz. It is designed with infinite capacity and no constraints to ignore the effect of the energy capacity that could show the different rated energy capacities controlled with four strategies.

4.1 Photovoltaic reserved power

Using the forecast information in Figures 9, Figure 13 depicts the reserved power change for LC, DRR, and AFB-VIC. The orange zone denotes reserved power via LC and DRR control. The reserved power was shown in red using AFB-VIC. At a stable state, LC control has reserved power ranging from t₁ to t₂. AFB-VIC reduced the reserved power between t₁ and t₂. Furthermore, in an unstable state, it reserves more power. The LC Algorithm 1 obtains the new working point to reserve power in shaded PV1. When shading arrives, ESS and the reserved power in PV1 should compensate for PV1 power loss. However, if the determined forecast is incorrect, the actual power drop will exceed the calculated forecast. It leads to PV1 becoming a burden in this islanded micro-grid system. More power is required from the SG and ESS to regulate the frequency. AFB-VIC uses PV2 to reserve power and employs probabilistic forecast results from PV1. If there is a forecast error in PV1, PV2 can continue to provide power indefinitely. It has the advantage of the structural parameter variety for AFB-VIC. A probabilistic forecast can accommodate a higher power change than a determined forecast. As a result, AFB-VIC can mitigate some of the effects of forecast errors in PV1. Compared to these two methods, AFB-VIC has a higher maximum reserve power than LC. Furthermore, as shown in Figure 14, AFB-VIC has provided adaptive virtual inertia in the PV to limit frequency deviation.

FIGURE 13

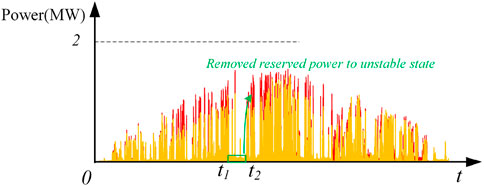
FIGURE 13. Reserved power of the determined forecast and AFB-VIC probabilistic forecast reserve strategy.

FIGURE 14

FIGURE 14. Value of virtual inertia in the PV using AFB-VIC.

4.2 Frequency response

We simulated the single daytime frequency deviations of MPPT, LC, DRR, and AFB-VIC strategies in Figure 15 using the irradiance results in Figure 9. In NEM, the frequency nadir is represented by the black dashed line. The frequency limit is 49.85 Hz. The MPPT control strategy is represented by the blue line. It has a frequency nadir of 49.826 Hz. Moreover, there are four ways to exceed the frequency nadir limitation. The orange line represents the frequency response of the LC control strategy. The frequency nadir falls below the limitation once during a single daytime simulation, reaching 49.833 Hz, and it has three chances to shoot over the frequency limitation. The gray line depicts the DRR results. The frequency nadir is 49.536 Hz, and it has three points above the frequency nadir. The ESS and SG cannot compensate for the power and inertia caused by the determined forecast error. The red line represents the AFB-VIC strategy. There is only one instance of the over-frequency nadir during the single daytime simulation. It has the lowest nadir frequency of 49.84 Hz. The SG provides the majority of the inertia. AFB-VIC has lower frequency deviations and times of the over-frequency nadir when compared to these methods.

FIGURE 15

FIGURE 15. Micro-grid frequency response with different control strategies.

Figure 16 shows a close-up of the frequency response at 3.58 h. The black dashed line represents a SOC constraint. When the frequency falls below 49.95 Hz, the ESS is discharged. The PV, ESS, and SG all worked together to control the frequency in the first 3 s. Only the ESS and SG are used in the MPPT control strategy to compensate for power and provide inertia. As a result, the frequency nadir is lower, and the recovery time is longer. Due to the MPPT and LC not having any reserve power after the first 3 s, the frequency regulation has only relied on the SG after that. The DRR can provide VIC using reserved power, but it has a lower reserve capacity than AFB, so it takes longer to reach 50 Hz. In comparison to these methods, AFB-VIC limits frequency deviation to a narrower range and reduces more subtle oscillations. Furthermore, AFB-VIC only uses 10 s to restore the frequency.

FIGURE 16

FIGURE 16. Close-up view of the frequency deviation.

Accordingly, the RoCoF limitation is another condition in the micro-grid of NEM. Figure 17 shows the RoCoF response of these methods. The RoCoF change is mainly concentrated because irradiance rapidly changes. The blue line shows the RoCoF change region of the MPPT. It is −1.3 ˜1.4 Hz/s. With the power being reserved in PV1 using LC, the PV power drop is reduced. Therefore, the RoCoF change region is −1.2 ˜1.3 Hz/s of local curtailment. Because the DRR reserve power in stable PV2 uses determined forecasting results, it provides power and virtual inertia when irradiance changes in PV1, and the RoCoF deviation region is −1.0 ˜1.3 Hz/s. The AFB-VIC using probabilistic forecasting results has reduced the RoCoF change region to −0.6 ˜1.2 Hz/s. For the RoCoF, AFB-VIC has reduced 21.7%, 28%, and 33%, compared to DRR, LC, and the MPPT strategies, respectively. Moreover, the times over the RoCoF limitation using MPPT, LC, DRR, and the AFB-VIC strategy are 137, 52, 45, and 28, respectively.

FIGURE 17

FIGURE 17. RoCoF response.

The mean absolute percentage error (MAPE) and root mean squared error (RMSE) are considered. The MAPE and RMSE are standard criteria to evaluate the accuracy of frequency or RoCoF.

$MAPE=\frac{100\%}{n}\sum _{i=1}^n\left|\frac{{\widehat{y}}_i-y_i}{y_i}\right|,(12)$

$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left({\widehat{y}}_i-y_i\right)}^2}.(13)$

${\widehat{y}}_i$ denotes the frequency or RoCoF value, while y_i denotes the reference value of frequency and RoCoF. Although the maximum range of deviations and times over frequency or the RoCoF limitation can offer a comparison of the control strategies, the accuracy of deviations is still an essential result of the model.

4.3 Energy storage system

The ESS is programmed to operate at 50% SOC and has an infinite power capacity. It clearly shows the maximum ESS power used for frequency regulation. The charge and discharge power capacity of these methods is depicted in Figure 18. As shown in Table 2, the times of charge and discharge of MPPT, local curtailment, DRR, and AFB-VIC are 287, 183, 156, and 120, respectively. Thus, the AFB-VIC has the potential to reduce costs by extending the life cycle. The MPPT control has a maximum ESS capacity of 3.7 p.u. in the 36000 s daytime simulation due to PV being continuously operated at the MPP. The local curtailment reduces the ESS power capacity to 2.4 p.u. The DRR requires 1. p.u. of the ESS capacity. The AFB-VIC strategy has a minimum power capacity of the ESS. It only requires 1.7 p.u.

FIGURE 18

FIGURE 18. ESS power provided to the micro-grid.

TABLE 2

TABLE 2. Results of the MAPE and RMSE.

5 Conclusion

The AFB-VIC method is proposed in this study to improve the system stability caused by the irradiance drop. It simulates a daytime of continuous operations. With the high penetration of the PV and the geographical distance between the PVs, we proposed a power reserve strategy based on probabilistic forecasting results to reduce the reserved power with stable irradiance and increase the power reserve with unstable irradiance. Using the stable PV station generates VIC. The adaptive virtual inertia and power reserve are controlled by the NEM RoCoF and frequency nadir limitation. The proposed AFB-VIC offers advantages in the following areas:

The RoCoF and frequency nadir can both be restricted. The virtual inertia is changed adaptively based on the forecasted PV power drop. It continuously provides virtual inertia, even with an initial forecast error in shaded PV stations. Furthermore, it shortens the time required for frequency regulation.

The AFB-VIC proposed a method for calculating and filtering quantile regression from probabilistic forecasting results. It reduces the power waste in a stable state and increases reserve power in a large range of areas. It improves the reserved power efficiency in the frequency nadir and RoCoF limitation.

The ESS power capacity has been reduced due to the proposed AFB-VIC. Furthermore, it extends ESS aging by reducing charge and discharge times.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All the authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the Xi’an Jiaotong-Liverpool University, Research Development Fund of XJTLU (RDF-17-01-28); and the AI University Research Centre (AI-URC) through the XJTLU Key Programme Special Fund (KSF-P-02).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Askarian, I., Eren, S., Pahlevani, M., and Knight, A. M. (2018). Digital real-time harmonic estimator for power converters in future micro-grids. IEEE Trans. Smart Grid 9 (6), 6398–6407. doi:10.1109/tsg.2017.2711016

CrossRef Full Text | Google Scholar

Belhachat, F., and Larbes, C. (2019). Comprehensive review on global maximum power point tracking techniques for pv systems subjected to partial shading conditions. Sol. Energy 183, 476–500. doi:10.1016/j.solener.2019.03.045

CrossRef Full Text | Google Scholar

Chang, J., Du, Y., Lim, E. G., Wen, H., Li, X., and Jiang, L. (2021). Coordinated frequency regulation using solar forecasting based virtual inertia control for islanded microgrids. IEEE Trans. Sustain. Energy 12 (4), 2393–2403. doi:10.1109/tste.2021.3095928

CrossRef Full Text | Google Scholar

Chávez, H., Baldick, R., and Sharma, S. (2014). Governor rate-constrained opf for primary frequency control adequacy. IEEE Trans. Power Syst. 29 (3), 1473–1480. doi:10.1109/tpwrs.2014.2298838

CrossRef Full Text | Google Scholar

Chen, X., Du, Y., Wen, H., Jiang, L., and Xiao, W. (2019). Forecasting-based power ramp-rate control strategies for utility-scale pv systems. IEEE Trans. Ind. Electron. 66 (3), 1862–1871. doi:10.1109/tie.2018.2840490

CrossRef Full Text | Google Scholar

Crăciun, B.-I., Kerekes, T., Séra, D., and Teodorescu, R. (2014). Frequency support functions in large pv power plants with active power reserves. IEEE J. Emerg. Sel. Top. Power Electron. 2 (4), 849–858. doi:10.1109/jestpe.2014.2344176

CrossRef Full Text | Google Scholar

da Luz, C. M. A., Vicente, E. M., and Tofoli, F. L. (2020). Experimental evaluation of global maximum power point techniques under partial shading conditions. Sol. Energy 196, 49–73. doi:10.1016/j.solener.2019.11.099

CrossRef Full Text | Google Scholar

Dreidy, M., Mokhlis, H., and Mekhilef, S. (2017). Inertia response and frequency control techniques for renewable energy sources: A review. Renew. Sustain. Energy Rev. 69, 144–155. doi:10.1016/j.rser.2016.11.170

CrossRef Full Text | Google Scholar

Gu, H., Yan, R., and Saha, T. K. (2018). Minimum synchronous inertia requirement of renewable power systems. IEEE Trans. Power Syst. 33 (2), 1533–1543. doi:10.1109/tpwrs.2017.2720621

CrossRef Full Text | Google Scholar

Hammad, E., Farraj, A., and Kundur, D. (2019). On effective virtual inertia of storage-based distributed control for transient stability. IEEE Trans. Smart Grid 10 (1), 327–336. doi:10.1109/tsg.2017.2738633

CrossRef Full Text | Google Scholar

Han, Y., Wang, N., Ma, M., Zhou, H., Dai, S., and Zhu, H. (2019). A pv power interval forecasting based on seasonal model and nonparametric estimation algorithm. Sol. Energy 184, 515–526. doi:10.1016/j.solener.2019.04.025

CrossRef Full Text | Google Scholar

Hoke, A., and Maksimović, D., “Active power control of photovoltaic power systems,” in 2013 1st IEEE Conference on Technologies for Sustainability (SusTech), 01-02 August 2013, Portland, 2013, pp. 70–77.

CrossRef Full Text | Google Scholar

Hua, T., Yan, X., and Fan, W., “Research on power point tracking algorithm considered spinning reserve capacity in gird-connected photovoltaic system based on vsg control strategy,” in 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017 - ECCE Asia), 03-07 June 2017, Kaohsiung, Taiwan, 2017, pp. 2059–2063.

CrossRef Full Text | Google Scholar

Li, X., Wen, H., Zhu, Y., Jiang, L., Hu, Y., and Xiao, W. (2019). A novel sensorless photovoltaic power reserve control with simple real-time mpp estimation. IEEE Trans. Power Electron. 34 (8), 7521–7531. doi:10.1109/tpel.2018.2880461

CrossRef Full Text | Google Scholar

Liu, J., Yushi, M., Ise, T., Yoshizawa, J., and Watanabe, K., “Parallel operation of a synchronous generator and a virtual synchronous generator under unbalanced loading condition in microgrids,” in 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), 22-26 May 2016, Hefei, China, 2016, pp. 3741–3748.

CrossRef Full Text | Google Scholar

Liu, L., Li, W., Ba, Y., Shen, J., Jin, C., and Wen, K. (2020). An analytical model for frequency nadir prediction following a major disturbance. IEEE Trans. Power Syst. 35 (4), 2527–2536. doi:10.1109/tpwrs.2019.2963706

CrossRef Full Text | Google Scholar

Mahmud, K., Azam, S., Karim, A., Zobaed, S., Shanmugam, B., and Mathur, D. (2021). Machine learning based pv power generation forecasting in alice springs. IEEE Access 9 (46 117), 46117–46146 128. doi:10.1109/access.2021.3066494

CrossRef Full Text | Google Scholar

Mararakanye, N., and Bekker, B. (2019). Renewable energy integration impacts within the context of generator type, penetration level and grid characteristics. Renew. Sustain. Energy Rev. 108, 441–451. doi:10.1016/j.rser.2019.03.045

CrossRef Full Text | Google Scholar

Podder, A., Roy, N., and Pota, H. (2019). Mppt methods for solar pv systems: A critical review based on tracking nature. IET Renew. Power Gener. 13, 1615–1632. doi:10.1049/iet-rpg.2018.5946

CrossRef Full Text | Google Scholar

Sengupta, M., and Andreas, A. (2014). Oahu solar measurement grid (1-year archive): 1-second solar irradiance; oahu Hawaii(data). Colorado: Nrel.

Google Scholar

Tielens, P., and Van Hertem, D. (2016). The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 55, 999–1009. doi:10.1016/j.rser.2015.11.016

CrossRef Full Text | Google Scholar

Ulbig, A., Borsche, T. S., and Andersson, G. (2014). Impact of low rotational inertia on power system stability and operation. IFAC Proc. Vol. 47 (3), 7290–7297. 19th IFAC World Congress. doi:10.3182/20140824-6-za-1003.02615

CrossRef Full Text | Google Scholar

Wang, F., Lu, X., Mei, S., Su, Y., Zhen, Z., Zou, Z., et al. (2022). A satellite image data based ultra-short-term solar pv power forecasting method considering cloud information from neighboring plant. Energy 238, 121946. doi:10.1016/j.energy.2021.121946

CrossRef Full Text | Google Scholar

Wang, F., Xuan, Z., Zhen, Z., Li, Y., Li, K., Zhao, L., et al. (2020). A minutely solar irradiance forecasting method based on real-time sky image-irradiance mapping model. Energy Convers. Manag. 220, 113075. doi:10.1016/j.enconman.2020.113075

CrossRef Full Text | Google Scholar

Woodhouse, M., Jones-Albertus, R., Feldman, D., Fu, R., Horowitz, K., Chung, D., et al. (2011). On the path to sunshot - the role of advancements in solar photovoltaic efficiency, reliability, and costs. Seattle: Semanticscholar.

Google Scholar

Yan, X., Li, J., Wang, L., Zhao, S., Li, T., Lv, Z., et al. (2018). Adaptive-MPPT-based control of improved photovoltaic virtual synchronous generators. Energies 11 (7), 1834–1918. doi:10.3390/en11071834

CrossRef Full Text | Google Scholar

Yang, Y., Blaabjerg, F., Wang, H., and Simões, M. G. (2016). Power control flexibilities for grid-connected multi-functional photovoltaic inverters. IET Renew. Power Gener. 10 (4), 504–513. doi:10.1049/iet-rpg.2015.0133

CrossRef Full Text | Google Scholar

Zhang, C., Xu, Y., and Dong, Z. Y. (2020). Robustly coordinated operation of a multi-energy micro-grid in grid-connected and islanded modes under uncertainties. IEEE Trans. Sustain. Energy 11 (2), 640–651. doi:10.1109/tste.2019.2900082

CrossRef Full Text | Google Scholar

Zhang, H., Wang, J., Sun, Z., Zurada, J. M., and Pal, N. R. (2020). Feature selection for neural networks using group lasso regularization. IEEE Trans. Knowl. Data Eng. 32 (4), 659–673. doi:10.1109/tkde.2019.2893266

CrossRef Full Text | Google Scholar

Zhao, Y., Xu, K., Zhu, E., Liu, X., Zhu, X., and Yin, J. (2019). Triangle lasso for simultaneous clustering and optimization in graph datasets. IEEE Trans. Knowl. Data Eng. 31 (8), 1610–1623. doi:10.1109/tkde.2018.2865342

CrossRef Full Text | Google Scholar