Distributionally Robust Capacity Configuration for Energy Storage in Microgrid Considering Renewable Utilization

The energy storage plays an important role in the operation safety of the microgrid system. Appropriate capacity configuration of energy storage can improve the economy, safety, and renewable energy utilization of the microgrid. This study considers the uncertainty of renewable energy, and builds an energy storage capacity configuration (ESCC) in microgrid by using the distributionally robust optimization (DRO). This model co-optimizes energy storage planning, day-ahead scheduling, and renewable energy utilization of the microgrid, which derives the energy storage configuration strategy, balancing renewable energy utilization and operation economics of microgrid. The proposed model is a two-stage model with distributionally robust chance constrains. By applying decision rules, variable substitution, and duality techniques, this model is approximately transformed into a mixed integer programming problem with a second-order cone constraint, which can be directly solved. Experiments on the IEEE 33-bus system are carried out to verify the effectiveness and advantages of the proposed model.

1 Introduction

In recent years, renewable energy (e.g., wind and solar power) power generation has developed rapidly (Zhou et al., 2020; Li Y. et al., 2020; Chen et al., 2021), and its proportion in energy consumption continues to increase. Renewable energy power generation has the advantages of clean, pollution-free, and low power generation cost. However, the random and fluctuating characteristics of renewable generation (Miao, 2016) will affect the dispatching accuracy of the power system when it is connected to the grid and may also cause operation safety and power quality problems (Zhu et al., 2020). The proposal of microgrid technology can not only effectively solve these problems but also integrate the advantages of distributed energy. With the development of microgrid technology, the economics of system safety operation and renewable utilization issues and challenges have always been faced by the microgrid. The vigorous development of energy storage technology has further matured the microgrid technology. In the microgrid system, the energy storage system (ESS) can not only improve the flexibility of the power system and maintain the stability of the microgrid operation but also participate in peak shaving and effectively reduce the phenomenon of wind abandonment.

For the microgrid system, the capacity configuration of the ESS has a great impact on the overall economy and operational safety (Li et al., 2012; Guo et al., 2021), and some achievements on energy storage capacity configuration (ESCC) in microgrid have been made in academic. Brekken et al. (2011) added large-scale energy storage to the output of wind farms to improve the predictability of wind power generation, thereby improving the predictability of wind farm output, but did not consider the cost of energy storage, which may lead to excessive scale. The grid-connected PV system was studied by Ru et al. (2013), and the optimal size for battery storage was determined. In Brekken et al. (2011) and Ru et al. (2013), only the ESS to promote the integration of renewable energy is considered, and the operation of other resources in the grid is not considered. Nguyen et al. (2015) established the optimal size of the ESS by considering different loads and sunshine duration. Masaud and El-Saadany (2020) established the optimal size and service life of energy storage capacity, but did not consider the uncertainty of renewable energy. Hu et al. (2015) proposed a capacity configuration optimization model of island microgrid considering demand response and uses the particle swarm algorithm to minimize system life cycle cost. Zhu et al. (2019) comprehensively considered the electricity cost, photovoltaic power generation, and energy storage cost, and established an optimization model for photovoltaic power generation and ESCC. Li and Xu (2017) and Wang et al. (2017) configured the capacity of the ESS in the grid-connected microgrid system and considered the time-of-use electricity price, and made the overall benefit higher through the “low storage and multiple discharge” of the energy storage equipment. Wang et al. (2018) proposed a statistical method for the optimal configuration of the capacity of the hybrid energy storage system. Monte Carlo simulation was performed on the statistical model to determine the appropriate energy storage capacity to improve the economy of the system. He et al. (2022) established a two-layer optimization model of the hybrid ESS and realized the optimization of the hybrid energy storage capacity through parameter transmission.

The microgrid ESCC models established previously are all based on deterministic analysis, ignoring the uncertain factors of wind and solar outputs, so the ESCC results do not consider the system’s ability to withstand renewable energy fluctuations, which is not conducive to the safe operation of the system. There are mainly two methods to deal with the uncertainty in the power system, namely, stochastic programming and robust optimization. Stochastic programming uses random variables to describe uncertain information and optimizes the scheduling scheme with the smallest expected cost. Shen et al. (2021) proved that thermal inertia in multi-energy systems can reduce the investment cost of hybrid energy storage systems. Jooshaki et al. (2020) proposed a stochastic model for expansion planning of multi-level distribution systems to improve network flexibility through optimal installation of energy storage systems. Alharbi and Bhattacharya (2018) proposed a stochastic optimization model, considering the uncertainty of solar radiation and wind speed and determined the sizing of the battery energy storage system, with a decomposition-based method in isolated microgrid. The stochastic programming method is based on accurate probability distributions, which however in practice are usually difficult to accurately obtain. The robust optimization method characterizes the uncertainty of the variable with the variable range and does not require an accurate probability distribution function, which has advantages for the optimization decision of continuous uncertain variables. Yi et al. (2018) proposed a new method of utilizing multi-type demand response resources to smooth fluctuations in renewable energy on different timescales and establishes a multi-objective robust scheduling model considering renewable energy and demand response uncertainty. Li P. et al. (2020) proposed a robust configuration method for integrated energy system energy storage, considering renewable energy and electric/heating/cooling load uncertainties. Fang et al. (2021) considered the uncertainty of renewable energy output, established a two-layer game model, and obtained the optimal capacity of energy storage. The distributionally robust optimization (DRO) method combines the advantages of stochastic programming and robust optimization (Liu et al., 2016), and considers the uncertainty of the probability distribution function of random variables, which can reasonably model the uncertainty. The DRO method can reduce the conservatism of the traditional robust optimization method and improve the robustness of the stochastic programming method. It has been widely used in power system optimization problems with uncertain parameters. Zhou et al. (2019) established a distributionally robust chance constrained (DRCC) model for the integrated heat and electricity system and transformed the DRCC model into a second-order cone programming model using the conditional value at the risk approximation method and duality theorem; Zhou et al. (2021) proposed a DRO model and used a modified column and constraint generation algorithm to solve. Yang et al. (2020) presented a two-stage DRO economic dispatch model, considering the renewable energy resource generation uncertainty, and proposed a stochastic dual dynamic programming algorithm to solve the robust counterpart problem. However, studies on DRO-based energy storage capacity allocation are still relatively few. Xie et al. (2022) co-optimized the sizes of renewable generation and energy storage based on the DRO method in stand-alone microgrids, considering shortfall risk of load shedding, which minimizes the investment cost and the load shedding risk. Different with it, our work focuses on the balance between energy storage investment and renewable energy utilization capability. In the microgrid, although energy storage can increase the capability of renewable admission, the cost of energy storage is still relatively expensive. If we require full utilization, the investment cost will be very high. Therefore, a trade-off between energy storage investment cost and renewable energy utilization is required. For this purpose, this work studies the energy storage configuration issue by applying a moment-based DRO method to evaluate renewable energy utilization probability and make a trade-off.

In this article, we propose a microgrid system ESCC model, considering renewable utilization based on the DRO method. The main contributions are: 1) propose a DRO-based microgrid ESCC model, which can balance the ability of withstanding renewable energy fluctuations and investment and operation economics of the microgrid, and establish adjustable distributionally robust joint chance constraints to measure the renewable utilization capability; 2) establish the appropriate affine decision rules for ESS operation equations, present the transformation of constraints containing distributionally robust probability of random variables with adjustable boundaries, and approximately transform the proposed model to a mixed integer programming problem with second-order cone constraints through variable substitution and duality techniques. The model can be directly solved by commercial optimization software such as Gurobi; and 3) the numeral experiments are carried out based on the IEEE 33-bus system to verify the validity and advantage of the proposed model, and the impact of ESCC on the renewable energy utilization is analyzed.

The rest of this article is organized as follows: Section 2 establishes the mathematical formulation, Section 3 presents the solution methodology, Section 4 performs the case study, and finally, Section 5 concludes this article.

2 Mathematical Model

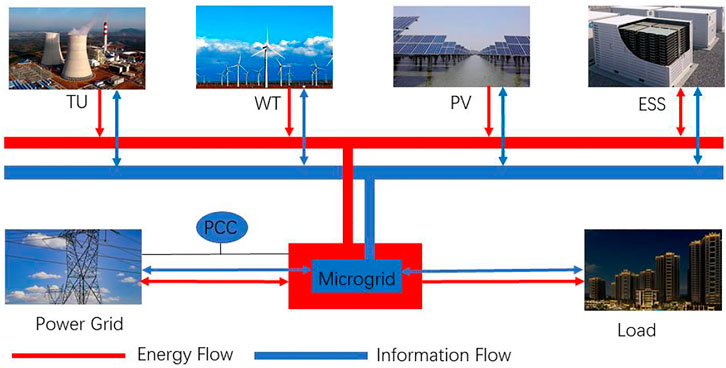
Microgrid can fully promote the large-scale access of distributed power and renewable energy and achieve highly reliable supply of various energy forms to loads, which is an effective way to realize an active distribution network. Figure 1 is a schematic diagram of the structure of the microgrid, which is composed of thermal units, renewable distributed power sources, loads, and energy storage systems. In the microgrid, photovoltaics (PV), wind turbines (WT), and thermal units (TU) are the main sources to supply power to the load. The energy of the energy storage system (ESS) flows in both directions, which plays an important role in regulation. The microgrid and power grid are connected by the point of common coupling (PCC). The interactive power between the microgrid and power grid, the charging and discharging of ESS, and the output of WT, PV, and TU are controlled by the microgrid through information flow, which are all transmitted through two-way channels. Based on such microgrid structure, we build the ESCC model as follows.

FIGURE 1

FIGURE 1. Structure of microgrid.

2.1 Objective Function

This study considers the impact of three factors on the decision-making of ESCC in the microgrid, namely, energy storage investment cost, system dispatch cost, and the admission on renewable energy fluctuations. The goal is to reduce the energy storage investment cost and the system dispatch cost as much as possible, while improves the admissible range of renewable energy. Therefore, the objective function consists of three parts as shown in (1)–(3). In this article, the capability of renewable utilization is represented by the probability that the system can withstand the actual fluctuation of renewable energy.

$\min C_{\text{sto}}\left({{\displaystyle P}}_s^{\max },{{\displaystyle S}}_s^{\max }\right)+C_{\text{disp}}\left({{\displaystyle \widehat{P}}}_{gt},{{\displaystyle \widehat{P}}}_{qt}^{\text{buy}},{{\displaystyle \widehat{P}}}_{qt}^{\text{sell}}\right)-\delta a,(1)$

$C_{\text{sto}}\left({{\displaystyle P}}_s^{\max },{{\displaystyle S}}_s^{\max }\right)=\frac{{\displaystyle \sum _{s\in \left[S\right]}\left({\text{C}}_{\text{p}}{{\displaystyle P}}_s^{\max }+{\text{C}}_{\text{s}}{{\displaystyle S}}_s^{\max }\right)}}{{\text{T}}_{\text{s}}}+\text{M,}(2)$

$C_{\text{disp}}\left({{\displaystyle \widehat{P}}}_{gt},{{\displaystyle \widehat{P}}}_{qt}^{\text{buy}},{{\displaystyle \widehat{P}}}_{qt}^{\text{sell}}\right)={\displaystyle \sum _{t\in \left[T\right]}{\displaystyle \sum _{g\in \left[G\right]}{F}_g\left({{\displaystyle \widehat{P}}}_{gt}\right)}}+{\displaystyle \sum _{t\in \left[T\right]}{\displaystyle \sum _{g\in \left[G\right]}\left({\text{NL}}_g{x}_{gt}+{\text{SU}}_g{u}_{gt}+{\text{SD}}_g{v}_{gt}\right)}}+{\displaystyle \sum _{t\in \left[T\right]}{\displaystyle \sum _{q\in \left[Q\right]}\left({\text{C}}_{\text{buy}}{{\displaystyle \widehat{P}}}_{qt}^{\text{buy}}-{\text{C}}_{\text{sell}}{{\displaystyle \widehat{P}}}_{qt}^{\text{sell}}\right)}},(3)$

where $C_{\text{sto}}$ represents the investment cost of ESS and $C_{\text{disp}}$ represents the dispatch cost of the system. The investment cost of ESS is related to ${{\displaystyle P}}_s^{\max }$ and ${{\displaystyle S}}_s^{\max }$ of ESS. The dispatch cost $C_{\text{disp}}$ includes the operating cost and start–stop cost of thermal units, as well as the cost of power transaction between the microgrid and power grid. $F_g(.)$ is the fuel cost function of thermal unit $g$, which is generally represented by a quadratic function, and can also be approximated by a piecewise linear function. $x_{gt}$, $u_{gt}$, and $v_{gt}$ are both binary variables, respectively, that represent the on–off state (1 is on and 0 is off), starting state (1 is start and 0 is no-start), and shutdown state (1 is stop and 0 is no-stop) of thermal unit $g$ during time period $t$. $\delta$ is a weight coefficient related to renewable utilization, and its numeral represents the additional economic cost of renewable utilization.

2.2 Constraints of Energy Storage System Configuration

The energy and power of the configured energy storage devices should be positive values, and the constraints of the site- and grid-connected power should be considered. The constraints are as follows.

$0\le {{\displaystyle P}}_s^{\max }\le {{\displaystyle \text{P}}}_{\text{M}},(4)$

$0\le {{\displaystyle S}}_s^{\max }\le {{\displaystyle \text{S}}}_{\text{M}},(5)$

where ${{\displaystyle \text{P}}}_{\text{M}}$ and ${{\displaystyle \text{S}}}_{\text{M}}$ represent the maximum power capacity and maximum energy capacity of the ESS allowed by the conditions of site- and grid-connected power, respectively.

2.3 Constraints During Pre-Dispatch

2.3.1 System Operating Constraints

In the microgrid, the power demand should be balanced by the output of the thermal power units, the power of renewable energy (including wind and solar power), the power of charging and discharging of ESS, and the power purchased from and sold to the grid. The power flow on lines should not exceed the limits. Therefore, for any time period $t$, the balancing and line power flow constraints of the microgrid are as follows:

${\displaystyle \sum _{g\in \left[G\right]}{{\displaystyle \widehat{P}}}_{gt}+}{\displaystyle \sum _{k\in \left[K\right]}{{\displaystyle \widehat{R}}}_{kt}}-{\displaystyle \sum _{s\in \left[S\right]}{{\displaystyle \widehat{P}}}_{st}^{\text{cha}}}+{\displaystyle \sum _{s\in \left[S\right]}{{\displaystyle \widehat{P}}}_{st}^{\text{dis}}}-{\displaystyle \sum _{q\in \left[Q\right]}{{\displaystyle \widehat{P}}}_{qt}^{\text{sell}}}+{\displaystyle \sum _{q\in \left[Q\right]}{{\displaystyle \widehat{P}}}_{qt}^{\text{buy}}}={\displaystyle \sum _{n\in \left[N\right]}{d}_{nt}},\forall t\in \left[T\right],(6)$

$-F_l\le {\displaystyle \sum _{n\in \left[N\right]}S{F}_{nl}\left({\displaystyle \sum _{g\in g_n}{{\displaystyle \widehat{P}}}_{gt}+}{\displaystyle \sum _{k\in k_n}{{\displaystyle \widehat{R}}}_{kt}}-{\displaystyle \sum _{s\in s_n}{{\displaystyle \widehat{P}}}_{st}^{\text{cha}}}+{\displaystyle \sum _{s\in s_n}{{\displaystyle \widehat{P}}}_{st}^{\text{dis}}}-{\displaystyle \sum _{q\in q_n}{{\displaystyle \widehat{P}}}_{qt}^{\text{sell}}}+{\displaystyle \sum _{q\in q_n}{{\displaystyle \widehat{P}}}_{qt}^{\text{buy}}}-d_{nt}\right)}\le F_l,\forall t\in \left[T\right],\forall l\in \left[L\right],(7)$

where (6) represents the balancing constraint and (7) represents the line capacity restrictions based on the dc approximation of the power flow equations.

2.3.2 Constraints of Thermal Units

The on–off state, start-up state, and shutdown state of thermal units are all 0–1 binary variables, and these three variables should satisfy the following constraints:

$\forall t\in \left[T\right],\forall g\in \left[G\right]$

$-x_{gt-1}+x_{gt}-x_{gi}\le \mathrm{0,1}\le i-\left(t-1\right)\le {\text{UT}}_g,(8)$

$x_{gt-1}-x_{gt}+x_{gi}\le \mathrm{1,1}\le i-\left(t-1\right)\le {\text{DT}}_g,(9)$

$-x_{gt-1}+x_{gt}-u_{gt}\le 0,(10)$

$x_{gt-1}-x_{gt}-v_{gt}\le 0,(11)$

$x_{gt},u_{gt},v_{gt}\in \left\{\mathrm{0,1}\right\},(12)$

where (8)–(9) represent the minimum start-up time constraint and the minimum shutdown time constraint of thermal units; constraints (10)–(11) represent the logical relationship between the three variables.

The constraints of upper and lower limit and the ramp-rate of thermal units are as follows:

${{\displaystyle P}}_g^{\min }{x}_{gt}\le {{\displaystyle \widehat{P}}}_{gt}\le {{\displaystyle P}}_g^{\max }{x}_{gt},\forall t\in \left[T\right],g\in \left[G\right](13)$

$-\left({{\displaystyle \tilde{\text{W}}}}_g^{\text{dn}}{v}_{gt}+{{\displaystyle \text{W}}}_g^{\text{dn}}{x}_{gt}\right){\Delta }_{\text{d}}\le {{\displaystyle \widehat{P}}}_{gt}-{{\displaystyle \widehat{P}}}_{gt-1}\le ({{\displaystyle \tilde{\text{W}}}}_g^{\text{up}}{u}_{gt}+{{\displaystyle \text{W}}}_g^{\text{up}}{x}_{gt-1}){\Delta }_{\text{d}},\forall t\in \left[T\right],g\in \left[G\right].(14)$

2.3.3 Operating Constraints of Energy Storage System

The ESS can be charged or discharged during operation, and constraints are as follows:

$\forall t\in \left[T\right],\forall s\in \left[S\right]$

$0\le {{\displaystyle \widehat{P}}}_{st}^{\text{dis}},{{\displaystyle \widehat{P}}}_{st}^{\text{cha}}\le {{\displaystyle P}}_s^{\text{max}},(15)$

$0\le S_{st}\le {{\displaystyle S}}_t^{\max },(16)$

${\widehat{S}}_{s\left(t+1\right)}=\left(1-\beta \right){\widehat{S}}_{st}-\frac{{{\displaystyle \widehat{P}}}_{st}^{\text{dis}}}{{\text{η}}_{\text{d}}}.{\Delta }_{\text{ds}}+{\text{η}}_{\text{c}}.{{\displaystyle \widehat{P}}}_{st}^{\text{cha}}.{\Delta }_{\text{ds}},(17)$

$S_0={\widehat{S}}_T,(18)$

where (15)–(16) represent the capacity limits of ESS; (17) represents the relationship between the amount of energy and power of ESS; (18) represents that the ESS has the same amount of energy at the beginning and end of the dispatch cycle, which ensures the sustainable operation of the ESS, which is beneficial to cyclic dispatching and prolong the service life of ESS.

2.3.4 Constraints of Interactive Power With Grid

The microgrid can purchase energy from the power grid when the system output is insufficient, or sell electricity to the power grid when the system output is surplus. The power purchased or sold should not exceed the transmission power of PCC as the following.

$0\le {{\displaystyle \widehat{P}}}_{qt}^{\text{buy}},{{\displaystyle \widehat{P}}}_{qt}^{\text{sell}}\le {{\displaystyle \text{P}}}_{\text{line}}^{\text{max}},\forall t\in \left[T\right].(19)$

2.4 Constraints Related to Renewable Energy Utilization

Considering the uncertainty of renewable generation in real-time operation, the system may not maintain power balance due to lack of sufficient regulation capability, resulting in the risk of curtailment of renewable energy or load shedding. This article evaluates the capability of renewable admission of microgrid by the distributionally robust probability that the system can withstand the fluctuation of renewable energy. Let ${\xi }_{kt}$ represent the actual output deviation of renewable resource $k$ from its forecasting value during time period $t$. Let $\left[{{\displaystyle \xi }}_{kt}^{\text{L}},{{\displaystyle \xi }}_{kt}^{\text{U}}\right]$ represent the admissible fluctuation range of ${\xi }_{kt}$. That is to say, if ${\xi }_t$ exceeds the range $\left[{{\displaystyle \xi }}_t^{\text{L}},{{\displaystyle \xi }}_t^{\text{U}}\right]$, the system under a certain operating condition will face risks of load shedding or renewable curtailment. Based on the DRO method, the following constraints can be established.

$\underset{\text{P}\in D}{\inf }\text{P}\left({\xi }_t\in \left[{{\displaystyle \xi }}_t^{\text{L}},{{\displaystyle \xi }}_t^{\text{U}}\right]\right)\ge a,\forall t\in \left[T\right],(20)$

$a_0\le a\le 1,(21)$

where $a$ is renewable utilization probability, decision variable, not greater than 1 and $a_0$ represents a lower bound of $a$. In this article, we assume that $a_0\ge 2/3$, this assumption is not very restrictive because power system operators often desire high utilization of renewable energy in the actual operation of the power system. In addition, we consider an ambiguity set $D$ consisting of probability distributions $\text{P}$ that (i) match the empirical mean ${\mu }_{kt}$ and empirical variance ${\sigma }_{kt}$ of each ${\xi }_{kt}$ and (ii) ${\xi }_{kt}$ is unimodal about ${\mu }_{kt}$, that is,

$D:=\left\{\begin{array}{l}\text{P}:{\text{E}}_{\text{P}}\left[{\xi }_{kt}\right]={\mu }_{kt},\text{Var}\left[{\xi }_{kt}\right]={{\displaystyle \sigma }}_{kt}^2,\\ {\xi }_{kt}\text{ is unimodal about }{\mu }_{kt},\forall t\in \left[T\right],k\in \left[K\right]\end{array}\right\},(22)$

where ${\mu }_{kt}$ indicates that the probability density function of ${\xi }_{kt}$, if exists, is non-decreasing from 0 to ${\mu }_{kt}$ and is non-increasing afterward.

Furthermore, when renewable generation deviation ${\xi }_t$ is within the range $\left[{{\displaystyle \xi }}_t^{\text{L}},{{\displaystyle \xi }}_t^{\text{U}}\right]$, the system must have the corresponding dispatch scheme which satisfies all operating and safety constraints. Thus, constraints for $\left[{{\displaystyle \xi }}_t^{\text{L}},{{\displaystyle \xi }}_t^{\text{U}}\right]$ are as follows:

$\forall {\xi }_t\in \left[{{\displaystyle \xi }}_t^{\text{L}},{{\displaystyle \xi }}_t^{\text{U}}\right],\forall t\in \left[T\right],\forall s\in \left[S\right],\forall g\in \left[G\right],\forall k\in \left[K\right],\forall l\in \left[L\right],\forall q\in \left[Q\right]$

${\displaystyle \sum _{g\in \left[G\right]}{{\displaystyle P}}_{gt}\left({\xi }_{kt}\right)+}{\displaystyle \sum _{k\in \left[K\right]}\left({{\displaystyle \widehat{R}}}_{kt}+{\xi }_{kt}\right)}-{\displaystyle \sum _{s\in \left[S\right]}{{\displaystyle P}}_{st}^{\text{cha}}\left({\xi }_{kt}\right)}+{\displaystyle \sum _{s\in \left[S\right]}{{\displaystyle P}}_{st}^{\text{dis}}\left({\xi }_{kt}\right)}-{\displaystyle \sum _{q\in \left[Q\right]}{{\displaystyle P}}_{qt}^{\text{sell}}\left({\xi }_{kt}\right)}+{\displaystyle \sum _{q\in \left[Q\right]}{{\displaystyle P}}_{qt}^{\text{buy}}\left({\xi }_{kt}\right)}={\displaystyle \sum _{n\in \left[N\right]}{d}_{nt}},(23)$

${{\displaystyle P}}_g^{\min }{x}_{gt}\le {{\displaystyle P}}_{gt}\left({\xi }_{kt}\right)\le {{\displaystyle P}}_g^{\max }{x}_{gt},(24)$

$-F_l\le {\displaystyle \sum _{n\in \left[N\right]}S{F}_{nl}\left({\displaystyle \sum _{g\in g_n}{{\displaystyle \widehat{P}}}_{gt}+}{\displaystyle \sum _{k\in k_n}\left({{\displaystyle \widehat{R}}}_{kt}+{\xi }_{kt}\right)}-{\displaystyle \sum _{s\in s_n}{{\displaystyle \widehat{P}}}_{st}^{\text{cha}}}+{\displaystyle \sum _{s\in s_n}{{\displaystyle \widehat{P}}}_{st}^{\text{dis}}}-{\displaystyle \sum _{q\in q_n}{{\displaystyle \widehat{P}}}_{qt}^{\text{sell}}}+{\displaystyle \sum _{q\in q_n}{{\displaystyle \widehat{P}}}_{qt}^{\text{buy}}}-d_{nt}\right)}\le F_l,(25)$

$-\left({{\displaystyle \tilde{\text{W}}}}_g^{\text{dn}}{v}_{gt}+{{\displaystyle \text{W}}}_g^{\text{dn}}{x}_{gt}\right){\Delta }_{\text{t}}\le {{\displaystyle P}}_{gt}\left({\xi }_{kt}\right)-{{\displaystyle \widehat{P}}}_{gt}\le \left({{\displaystyle \tilde{\text{W}}}}_g^{\text{up}}{u}_{gt}+{{\displaystyle \text{W}}}_g^{\text{up}}{x}_{gt-1}\right){\Delta }_{\text{t}},(26)$

$-\left({{\displaystyle \tilde{\text{W}}}}_g^{\text{dn}}{v}_{gt}+{{\displaystyle \text{W}}}_g^{\text{dn}}{x}_{gt}\right){\Delta }_{\text{d}}\le {{\displaystyle P}}_{gt}\left({\xi }_{kt}\right)-{{\displaystyle P}}_{g\left(t-1\right)}\left({\xi }_{kt}\right)\le \left({{\displaystyle \tilde{\text{W}}}}_g^{\text{up}}{u}_{gt}+{{\displaystyle \text{W}}}_g^{\text{up}}{x}_{g\left(t-1\right)}\right){\Delta }_{\text{d}},(27)$

$0\le {{\displaystyle P}}_{st}^{\text{cha}}\left({\xi }_{kt}\right),{{\displaystyle P}}_{st}^{\text{dis}}\left({\xi }_{kt}\right)\le {{\displaystyle P}}_s^{\max },(28)$

$0\le {{\displaystyle P}}_{qt}^{\text{buy}}\left({\xi }_{kt}\right),{{\displaystyle P}}_{qt}^{\text{sell}}\left({\xi }_{kt}\right)\le {{\displaystyle \text{P}}}_{\text{line}}^{\text{max}},(29)$

$0\le S_{st}\left({\xi }_{kt}\right)\le {{\displaystyle S}}_s^{\max },(30)$

$S_{s\left(t+1\right)}\left({\xi }_{kt}\right)=\left(1-\beta \right)S_{st}\left({\xi }_{kt}\right)-\frac{{{\displaystyle P}}_{st}^{\text{dis}}\left({\xi }_{kt}\right)}{{\text{η}}_{\text{d}}}.{\Delta }_{\text{ds}}+{\text{η}}_{\text{c}}.{{\displaystyle P}}_{st}^{\text{cha}}\left({\xi }_{kt}\right).{\Delta }_{\text{ds}},(31)$

${{\displaystyle R}}_k^{\min }\le {{\displaystyle \widehat{R}}}_{kt}+{{\displaystyle \xi }}_{kt}^{\text{L}}\le {{\displaystyle \widehat{R}}}_{kt}\le {{\displaystyle \widehat{R}}}_{kt}+{{\displaystyle \xi }}_{kt}^{\text{U}}\le {{\displaystyle R}}_k^{\max },(32)$

where (23) and (25) represent the balancing constraint and line capacity constraints during actual operation; (24) and (27) are the capacity and ramp-rate constraint of thermal units during actual operation, respectively; (26) is the ramp-rate constraint of thermal units at response time window; (28)–(30) represent the ESS capacity limits and the transmission capacity constraint of the PCC during actual operation; (31) represents the relationship between the amount of energy and the power of the ESS during actual operation; (32) indicates that the upper and lower bounds of renewable energy utilization need to include its predicted generation, and it is limited by the maximum and minimum output of renewable generation.

In a nutshell, the established microgrid ESCC model is shown in constraints (1)–(32), which is a two-stage DRO model with adjustable chance constraints. By solving such model, the system operator can obtain the ESCC strategy and the corresponding renewable energy utilization capability.

3 Solution

The proposed microgrid ESCC model is a two-stage model with distributionally robust chance constraints, and the boundaries of random variables are adjustable, which cannot be solved directly. In this section, the model is further transformed.

3.1 Affine Decision Rule

In the second stage of the aforementioned model, ${{\displaystyle P}}_{gt}\left({\xi }_{kt}\right)$, ${{\displaystyle P}}_{st}^{\text{dis}}\left({\xi }_{kt}\right)$, ${{\displaystyle P}}_{st}^{\text{cha}}\left({\xi }_{kt}\right)$, ${{\displaystyle P}}_{qt}^{\text{buy}}\left({\xi }_{kt}\right)$, ${{\displaystyle P}}_{qt}^{\text{sell}}\left({\xi }_{kt}\right)$, and $S_{st}\left({\xi }_{kt}\right)$ are recourse variables, which are decided by the random variable ${\xi }_t$. In order to facilitate the solution of the problem, we first assume the following affine decision rules:

$\forall g\in \left[G\right],\forall t\in \left[T\right],\forall s\in \left[S\right],\forall q\in \left[Q\right]$

${{\displaystyle P}}_{gt}\left({\xi }_{kt}\right)={{\displaystyle \widehat{P}}}_{gt}+{\displaystyle \sum _{k\in K}\left(B_{gkt}{\xi }_{kt}+b_{gkt}\right)},(33)$

${{\displaystyle P}}_{qt}^{\text{buy}}\left({\xi }_{kt}\right)={{\displaystyle \widehat{P}}}_{qt}^{\text{buy}}+{\displaystyle \sum _{k\in K}\left({{\displaystyle B}}_{qkt}^{\text{buy}}{\xi }_{kt}+{{\displaystyle b}}_{qkt}^{\text{buy}}\right)},(34)$

${{\displaystyle P}}_{qt}^{\text{sell}}\left({\xi }_{kt}\right)={{\displaystyle \widehat{P}}}_{qt}^{\text{sell}}+{\displaystyle \sum _{k\in K}\left({{\displaystyle B}}_{qkt}^{\text{sell}}{\xi }_{kt}+{{\displaystyle b}}_{qkt}^{\text{sell}}\right)},(35)$

${{\displaystyle P}}_{st}^{\text{dis}}\left({\xi }_{kt}\right)={{\displaystyle \widehat{P}}}_{st}^{\text{dis}}+{\displaystyle \sum _{k\in K}\left({{\displaystyle B}}_{skt}^{\text{dis}}{\xi }_{kt}+{{\displaystyle b}}_{skt}^{\text{dis}}\right)},(36)$

${{\displaystyle P}}_{st}^{\text{cha}}\left({\xi }_{kt}\right)={{\displaystyle \widehat{P}}}_{st}^{\text{cha}}+{\displaystyle \sum _{k\in K}\left({{\displaystyle B}}_{skt}^{\text{cha}}{\xi }_{kt}+{{\displaystyle b}}_{skt}^{\text{cha}}\right)},(37)$

where $B$ and $b$ are the coefficients of the decision rule to be optimized, which represent the response of the re-dispatch decisions ${{\displaystyle P}}_{gt}\left({\xi }_{kt}\right)$, ${{\displaystyle P}}_{st}^{\text{dis}}\left({\xi }_{kt}\right)$, ${{\displaystyle P}}_{st}^{\text{cha}}\left({\xi }_{kt}\right)$, ${{\displaystyle P}}_{qt}^{\text{buy}}\left({\xi }_{kt}\right)$, and ${{\displaystyle P}}_{qt}^{\text{sell}}\left({\xi }_{kt}\right)$ to the forecast deviation ${\xi }_t$. It should be noted that the assumption of affine decision rules will reduce the search space of solution and obtain conservative approximation.

However, $S_{st}\left({\xi }_{kt}\right)$ is different from the aforementioned variables. If we assume that $S_t\left({\xi }_{kt}\right)$ is only determined by the deviation ${\xi }_t$ at time $t$, the result will lead to a non-negligible error. According to the equality (31), the expression of the ESS energy can be translated into the following:

$S_{s\left(t+1\right)}=S_0+{\displaystyle \sum _{\tau =1,\mathrm{...}t}{(1-\beta )}^{t-\tau }\left(-\frac{{{\displaystyle P}}_{s\tau }^{\text{dis}}}{{\text{η}}_{\text{d}}}.{\Delta }_{\text{ds}}+{\text{η}}_{\text{c}}.{{\displaystyle P}}_{s\tau }^{\text{cha}}.{\mathrm{\Delta }}_{\text{ds}}\right)},\forall t\in \left[T\right],\forall s\in \left[S\right],(38)$

where we can see that ESS energy at $t+1$ $\left(S_{s\left(t+1\right)}\right)$ is decided by all the discharge power and charge power before time $t+1$, that is, ${{\displaystyle P}}_{s\tau }^{\text{cha}}$ and ${{\displaystyle P}}_{s\tau }^{\text{dis}}$ $\left(\forall \tau =1,\mathrm{...}t\right)$ , and the relationship is linear. According to the assumed affine decision rules of ${{\displaystyle P}}_{st}^{\text{dis}}\left({\xi }_{kt}\right)$ and ${{\displaystyle P}}_{st}^{\text{cha}}\left({\xi }_{kt}\right)$, we can conclude that the actual $S_{s\left(t+1\right)}$ under uncertainty is affected by all fluctuation deviations at time before $t+1$. Therefore, we assume that $S_{s\left(t+1\right)}\left(\mathit{\xi }\right)$ follows such decision rule:

$S_{s\left(t+1\right)}\left(\mathit{\xi }\right)={\widehat{S}}_{s\left(t+1\right)}+{\left(1-\beta \right)}^t{\displaystyle \sum _{\tau =1,\mathrm{...}t}{\displaystyle \sum _{k\in \left[K\right]}\left({{\displaystyle B}}_{sk\tau }^S{\xi }_{k\tau }+{{\displaystyle b}}_{sk\tau }^S\right)}},\forall t\in \left[T\right],\forall s\in \left[S\right].(39)$

This rule conforms to the general law of ESS energy variation. Moreover, it makes constraints (30)–(31) easier to transform and solve.

3.2 Adjustable Robust Constraints

For adjustable robust constraints (23)–(32) equality constraints and inequalities are handled differently, they are transformed separately.

3.2.1 Equality

By applying decision rules (33)–(37), constraint (23) is equivalent to:

$\forall {\xi }_{kt}\in \left[{{\displaystyle \xi }}_{kt}^{\text{L}},{{\displaystyle \xi }}_{kt}^{\text{U}}\right],\forall t\in \left[T\right]$

$\begin{array}{l}{\displaystyle \sum _{g\in \left[G\right]}{\displaystyle \sum _{k\in \left[K\right]}\left(B_{gkt}{\xi }_{kt}+b_{gkt}\right)}}-{\displaystyle \sum _{s\in \left[S\right]}{\displaystyle \sum _{k\in \left[K\right]}\left({{\displaystyle B}}_{skt}^{\text{cha}}{\xi }_{kt}+{{\displaystyle b}}_{skt}^{\text{cha}}\right)}}+{\displaystyle \sum _{s\in \left[S\right]}{\displaystyle \sum _{k\in \left[K\right]}\left({{\displaystyle B}}_{skt}^{\text{dis}}{\xi }_{kt}+{{\displaystyle b}}_{skt}^{\text{dis}}\right)}}-\\ {\displaystyle \sum _{q\in \left[Q\right]}{\displaystyle \sum _{k\in \left[K\right]}\left({{\displaystyle B}}_{qkt}^{\text{sell}}{\xi }_{kt}+{{\displaystyle b}}_{qkt}^{\text{sell}}\right)}}+{\displaystyle \sum _{k\in \left[K\right]}{\xi }_{kt}}+{\displaystyle \sum _{q\in \left[Q\right]}{\displaystyle \sum _{k\in \left[K\right]}\left({{\displaystyle B}}_{qkt}^{\text{buy}}{\xi }_{kt}+{{\displaystyle b}}_{qkt}^{\text{buy}}\right)}}=0.\end{array}(40)$

Since the aforementioned formula holds $\forall {\xi }_{kt}\in \left[{{\displaystyle \xi }}_{kt}^{\text{L}},{{\displaystyle \xi }}_{kt}^{\text{U}}\right]$ , it is further equivalent to the following linear equations without random variables:

${\displaystyle \sum _{g\in \left[G\right]}{b}_{gt}}-{\displaystyle \sum _{s\in \left[S\right]}{{\displaystyle b}}_{st}^{\text{cha}}}+{\displaystyle \sum _{s\in \left[S\right]}{{\displaystyle b}}_{st}^{\text{dis}}}-{\displaystyle \sum _{q\in \left[Q\right]}{{\displaystyle b}}_{qt}^{\text{sell}}}+{\displaystyle \sum _{q\in \left[Q\right]}{{\displaystyle b}}_{qt}^{\text{buy}}}=0,\forall t\in \left[T\right],(41)$

${\displaystyle \sum _{g\in \left[G\right]}{B}_{gkt}}+I_{kt}-{\displaystyle \sum _{s\in \left[S\right]}{{\displaystyle B}}_{skt}^{\text{cha}}}+{\displaystyle \sum _{s\in \left[S\right]}{{\displaystyle B}}_{skt}^{\text{dis}}}-{\displaystyle \sum _{q\in \left[Q\right]}{{\displaystyle B}}_{qkt}^{\text{sell}}}+{\displaystyle \sum _{q\in \left[Q\right]}{{\displaystyle B}}_{qkt}^{\text{buy}}}=0,\forall t\in \left[T\right],\forall k\in \left[K\right],(42)$

where, $I_{kt}$ represents a matrix of all ones.

For constraint (31), substitute recourse variables by (36)–(39) and obtain:

$\begin{array}{l}{\widehat{S}}_{s\left(t+1\right)}-\left(1-\beta \right){\widehat{S}}_{st}+{\left(1-\beta \right)}^t{\displaystyle \sum _{k\in \left[K\right]}\left({{\displaystyle B}}_{skt}^S{\xi }_{kt}+{{\displaystyle b}}_{skt}^S\right)}=-\left({{\displaystyle \widehat{P}}}_{st}^{\text{dis}}+{\displaystyle \sum _{k\in \left[K\right]}\left({{\displaystyle B}}_{skt}^{\text{dis}}{\xi }_{kt}+{{\displaystyle b}}_{skt}^{\text{dis}}\right)}\right)\frac{{\Delta }_{\text{ds}}}{{\text{η}}_{\text{d}}}+\\ {\text{η}}_{\text{c}}.\left({{\displaystyle \widehat{P}}}_{st}^{\text{cha}}+{\displaystyle \sum _{k\in \left[K\right]}\left({{\displaystyle B}}_{skt}^{\text{cha}}{\xi }_{kt}+{{\displaystyle b}}_{skt}^{\text{cha}}\right)}\right).{\Delta }_{\text{ds}},\forall {\xi }_{kt}\in \left[{{\displaystyle \xi }}_{kt}^{\text{L}},{{\displaystyle \xi }}_{kt}^{\text{U}}\right],\forall k\in \left[K\right],\forall t\in \left[T\right],\forall s\in \left[S\right],\end{array}(43)$

where, similarly, it can also be equivalent to the following linear equation:

$\forall k\in \left[K\right],\forall t\in \left[T\right],\forall s\in \left[S\right]$

${\left(1-\beta \right)}^t{{\displaystyle B}}_{skt}^S=-\frac{{{\displaystyle B}}_{skt}^{\text{dis}}}{{\text{η}}_{\text{d}}}.{\Delta }_{\text{ds}}+{\text{η}}_{\text{c}}.{{\displaystyle B}}_{skt}^{\text{cha}}.{\Delta }_{\text{ds}}(44)$

${\left(1-\beta \right)}^t{\displaystyle \sum _{k\in \left[K\right]}{{\displaystyle b}}_{skt}^S}=-\frac{{\Delta }_{\text{ds}}}{{\text{η}}_{\text{d}}}.{\displaystyle \sum _{k\in \left[K\right]}{{\displaystyle b}}_{skt}^{\text{dis}}}+{\text{η}}_{\text{c}}.{\displaystyle \sum _{k\in \left[K\right]}{{\displaystyle b}}_{skt}^{\text{cha}}}.{\Delta }_{\text{ds}}.(45)$

3.2.2 Inequality

For convenience, rewrite constraints (24)–(29) as the following abstract form:

$\mathit{T}\left(\mathit{x}\right)+\mathit{Wy}\left(\mathit{\xi }\right)\le \mathit{V\xi },\mathit{\xi }\in \left[{\mathit{\xi }}^{\mathbf{L}},{\mathit{\xi }}^{\mathbf{U}}\right],(46)$

where the matrix $\mathit{T}$, $\mathit{W}$, and $\mathit{V}$ denote the parameter matrix in the second-stage constraints; $\mathit{x}$ denote the decision variables of this model; $\mathit{y}\left(\mathit{\xi }\right)$ denote the re-dispatch variables in the second stage, and it can be substituted by decision rules (33)–(37) which are represented by the following abstract equation: $\mathit{y}\left(\mathit{\xi }\right)=\mathit{B\xi }+\mathit{b}$.

First, (46) can be transformed into a standard robust optimization form by variable substitution. Letting $\mathit{E}:=\text{diag}\left({\mathit{\xi }}^{\mathbf{U}}-{\mathit{\xi }}^{\mathbf{L}}\right)$, we represent the hypercube $\left[{\mathit{\xi }}^{\mathbf{L}},{\mathit{\xi }}^{\mathbf{U}}\right]$ as $\left\{{\mathit{\xi }}^{\mathbf{L}}+\mathit{Ev}:\mathit{v}\in \left[\mathbf{0}\text{,}\mathbf{e}\right]\right\}$, where $\mathbf{e}$ denotes the vector of all ones. Then, the random variable $\mathit{\xi }$ bounded by $\left[{\mathit{\xi }}^{\mathbf{L}},{\mathit{\xi }}^{\mathbf{U}}\right]$ can be replaced by the random variable $\mathit{v}$ bounded by $\left[\mathbf{0}\text{,}\mathbf{e}\right]$, as follows:

$\mathit{\xi }={\mathit{\xi }}^{\mathbf{L}}+\mathit{Ev},\mathit{v}\in \left[\mathbf{0},\mathbf{e}\right].(47)$

By variable substitution, (46) can be transformed into:

$\mathit{T}\left(\mathit{x}\right)+\mathit{W}\left(\mathit{BEv}+B{\mathit{\xi }}^{\mathbf{L}}+\mathit{b}\right)\le \mathit{V}{\mathit{\xi }}^{\mathbf{L}}+\mathit{VEv},\mathit{v}\in \left[\mathbf{0},\mathbf{e}\right].(48)$

There exist quadratic terms in the aforementioned formula. Letting $\mathit{h}=\mathit{B}{\mathit{\xi }}^{\mathbf{L}}+\mathit{b}$, $\mathit{H}=\mathit{BE}$,we recast (48) as:

$\mathit{T}\left(\mathit{x}\right)+\mathit{W}\left(\mathit{Hv}+\mathit{h}\right)\le \mathit{V}{\mathit{\xi }}^{\mathbf{L}}+\mathit{VEv},\mathit{v}\in \left[\mathbf{0},\mathbf{e}\right].(49)$

which can also be equivalent to the following linear equation:

$\underset{\mathit{v}\in \left[\mathbf{0}\text{,}\mathbf{e}\right]}{{\displaystyle \sup }}\left(\mathit{WH}-\mathit{VE}\right)\mathit{v}\le \mathit{V}{\mathit{\xi }}^{\mathbf{L}}-\mathit{T}\left(\mathit{x}\right)-\mathit{Wh}\mathit{.}(50)$

Furthermore, using standard technique in robust optimization, (50) is equivalent to:

$\mathit{R}\mathbf{e}\le \mathit{V}{\mathit{\xi }}^{\mathbf{L}}-\mathit{T}\left(\mathit{x}\right)-\mathit{Wh,}(51)$

$\mathit{R}\ge \mathit{WH}-\mathit{VE},\mathit{R}\ge \mathbf{0}\mathbf{,}(52)$

where R denotes a dual variable.

Therefore, using the aforementioned method, Eqs (24)–(29) can be transformed into linear inequalities that are easy to solve. Take an example, (24) can be transformed to:

$\forall t\in \left[T\right],\forall g\in \left[G\right],\forall k\in \left[K\right]$

${\displaystyle \sum _{k\in \left[K\right]}{{\displaystyle \lambda }}_{gkt}^{\text{R}}}+{{\displaystyle h}}_{gt}+{{\displaystyle \widehat{P}}}_{gt}\ge {{\displaystyle P}}_g^{\min }{x}_{gt},(53)$

${\displaystyle \sum _{k\in \left[K\right]}{{\displaystyle \gamma }}_{gkt}^{\text{R}}}+{{\displaystyle h}}_{gt}+{{\displaystyle \widehat{P}}}_{gt}\le {{\displaystyle P}}_g^{\max }{x}_{gt},(54)$

${{\displaystyle \lambda }}_{gkt}^{\text{R}}\le H_{gkt},{{\displaystyle \lambda }}_{gkt}^{\text{R}}\le 0,{{\displaystyle \gamma }}_{gkt}^{\text{R}}\ge H_{gkt},{{\displaystyle \gamma }}_{gkt}^{\text{R}}\ge 0,(55)$

where ${{\displaystyle \lambda }}_{gkt}^{\text{R}}$ and ${{\displaystyle \gamma }}_{gkt}^{\text{R}}$ are auxiliary variables. The transformations of constraints (25)–(29) are detailed in Supplementary Appendix A.

For the inequality constraint (30), substitute $S_t\left({\xi }_{kt}\right)$ by (39) and the subsequent transformation process is similar. However, $S_t\left({\xi }_{kt}\right)$ is jointly affected by the fluctuation deviations of multiple time intervals. As a result, the dimensions of the random variables contained in constraint (30) are different at different time intervals. Thus, it is necessary to transform at different times one by one, and the equations can be further simplified by making a difference between the formulas at adjacent times. The final transformation is as follows:

$\forall k\in \left[K\right],\forall t=[\mathrm{2,3},\mathrm{...},T],\forall s\in \left[S\right]$

$\{\begin{array}{c}{\widehat{S}}_{st}-\left(1-\beta \right){\widehat{S}}_{s\left(t-1\right)}+{\left(1-\beta \right)}^{\left(t-1\right)}{{\displaystyle h}}_{s\left(t-1\right)}^{\text{S}}+{\displaystyle \sum _{k\in \left[K\right]}{{\displaystyle \lambda }}_{sk\left(t-1\right)}^{\text{S}}}\ge -\left(1-\beta \right){{\displaystyle S}}_s^{\max }\\ {\widehat{S}}_{st}-\left(1-\beta \right){\widehat{S}}_{s\left(t-1\right)}+{\left(1-\beta \right)}^{\left(t-1\right)}{{\displaystyle h}}_{s\left(t-1\right)}^{\text{S}}+{\displaystyle \sum _{k\in \left[K\right]}{{\displaystyle \gamma }}_{sk\left(t-1\right)}^{\text{S}}}\le {{\displaystyle S}}_s^{\max }\\ {{\displaystyle \lambda }}_{sk\left(t-1\right)}^{\text{S}}\le 0,{{\displaystyle \lambda }}_{sk\left(t-1\right)}^{\text{S}}\le {\left(1-\beta \right)}^{\left(t-1\right)}{{\displaystyle H}}_{sk\left(t-1\right)}^{\text{S}}\\ {{\displaystyle \gamma }}_{sk\left(t-1\right)}^{\text{S}}\ge 0,{{\displaystyle \gamma }}_{sk\left(t-1\right)}^{\text{S}}\ge {\left(1-\beta \right)}^{\left(t-1\right)}{{\displaystyle H}}_{sk\left(t-1\right)}^{\text{S}}\end{array},(56)$

where ${{\displaystyle \lambda }}_{skt}^{\text{S}}$ and ${{\displaystyle \gamma }}_{skt}^{\text{S}}$ are auxiliary variables.

3.3 Distributionally Robust Joint Chance Constraints

For all $t\in \left[T\right]$, the distributionally robust joint chance constraint (20) can be equivalent to the following second-order conic constraint for solving:

${\Vert \left[\begin{array}{c}\sqrt{\frac{8}{3}}\\ r_{kt}-z_{kt}\end{array}\right]\Vert }_2\le r_{kt}+z_{kt},\forall t\in \left[T\right],\forall k\in \left[K\right],(57)$

${\Vert \left[\begin{array}{c}{s}_{kt}-1\\ 2z_{kt}\end{array}\right]\Vert }_2\le s_{kt}+1,\forall t\in \left[T\right],\forall k\in \left[K\right],(58)$

${\sigma }_{kt}{r}_{kt}\le {\mu }_{kt}-{{\displaystyle \xi }}_{kt}^{\text{L}},\forall t\in \left[T\right],\forall k\in \left[K\right],(59)$

${\sigma }_{kt}{r}_{kt}\le {{\displaystyle \xi }}_{kt}^{\text{U}}-{\mu }_{kt},\forall t\in \left[T\right],\forall k\in \left[K\right],(60)$

${\displaystyle \sum _{k\in \left[K\right]}{s}_{kt}}\le 1-a,\forall t\in \left[T\right],(61)$

$s_{kt},r_{kt},z_{kt}\ge 0,\forall t\in \left[T\right],\forall k\in \left[K\right],(62)$

where $s_{kt},r_{kt},z_{kt}$ represent auxiliary variables [see, e.g., Ma et al. (2020)].

To summarize, the final model easily to be solved is as follows:

$\{\begin{array}{l}\text{obj}\text{. }\left(1\right)\\ \text{s}\text{.t}\text{. }\left(2\right)-\left(19\right),\left(21\right),\left(32\right),\left(41\right)-\left(42\right),\left(44\right)-\left(45\right),\left(47\right),\left(53\right)-\left(62\right),\left(a1\right)-\left(a26\right)\end{array}.(63)$

4 Case Study

In this study, we conducted simulation analysis based on the IEEE 33-bus system to verify the effectiveness of the established model. The platform used for the test is Matlab 2018b, the model is solved based on Gurobi, and the processor of the test computer is Intel Core i5-7200U CPU, running at 2.50 GHz with 12 GB of RAM.

4.1 Data Settings

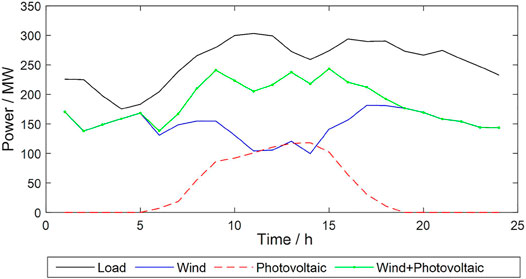
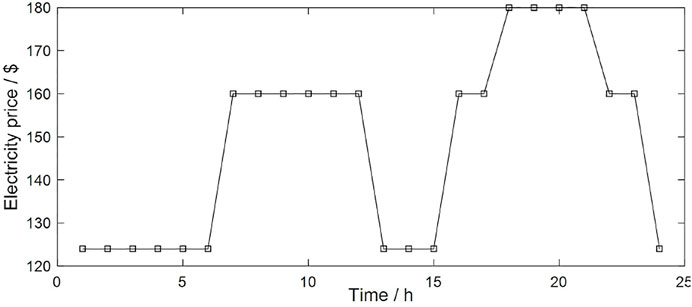
A microgrid system is constructed based on the IEEE 33-bus system for simulation, and 2 WT and 1 PV are added to nodes 5, 28, and 14 of the system, respectively. According to Xiao et al. (2015), we set ESS at node 17. The typical daily forecast load curve of the microgrid and the forecast output of renewable energy (wind plus solar power) are shown in Figure 2. ESS parameters are set as Table 1; the transaction price between microgrid and power grid is shown in Figure 3. The upper limit of the PCC power between the microgrid and the power grid is set to 60 MW, and PCC is set at node 1. We consider T = 24 h and set ${\Delta }_{\text{d}}=60\min$, ${\text{Δ}}_{\text{t}}=5\min$.

FIGURE 2

FIGURE 2. Renewable energy forecast output and load curve.

TABLE 1

TABLE 1. Energy storage device parameters.

FIGURE 3

FIGURE 3. Day-ahead transaction price between microgrid and power grid.

We assume that the actual output error of renewable energy follows a Gaussian distribution with a mean value of 0, where the wind power output variance gradually increases over time (increase from 10% step by step 0.1%), and the photovoltaic power output variance is 10% of the predicted output. According to the assumed probability distribution, a large amount of historical data is generated and divided into two groups for sample training and out-of-sample testing separately.

4.2 Energy Storage Capacity Configuration Simulation Results

By setting $\delta =350000$, we solve the proposed ESCC model and obtain the optimal allocation results that the maximum energy and maximum power of ESS are 65.2 MWh and 72.4 MW separately, and total investment cost is 74,700.8$. The corresponding day-ahead dispatch results (output of thermal units, the power transaction between microgrid and power grid, the charging and discharging results of the ESS) are shown in Figure 4, where the net load is equal to load minus renewable energy predictive power generation.

FIGURE 4

FIGURE 4. Day-ahead scheduling strategy.

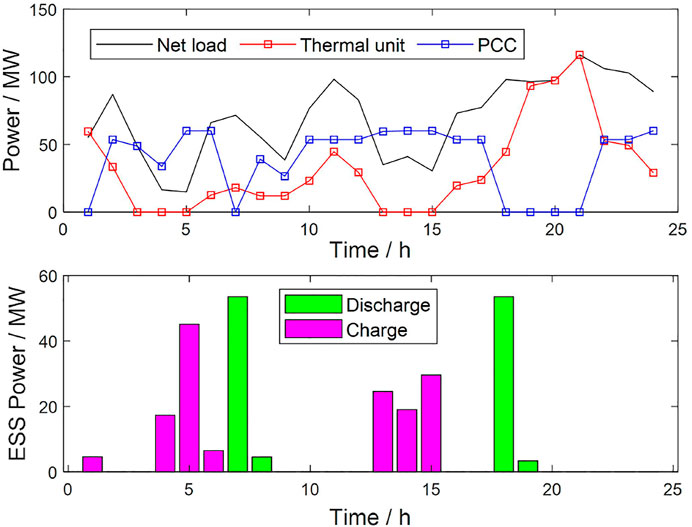
Figure 4 shows that a large portion of the load in this microgrid can be met by the renewable energy generation, and the remaining load (net load) is matched by thermal units, power grids, or ESS, according to the principle of economy. For example, during time period 18–21 h, the electricity price of power grid is higher than the thermal power generation, so the output of the thermal unit is higher, while the system preferentially purchases electricity from the power grid when the electricity price is low. The charging and discharging of ESS comprehensively considers the net load demand and the electricity price. For example, during time period 4–5 h, net load and electricity prices are low so that ESS is charged, and ESS discharges when the net load and electricity price are high. It is verified that the proposed model can effectively derive the energy storage configuration scheme, which adapts to the regulation needs of the microgrid.

4.3 Impact of Energy Storage Capacity Configuration Strategy on Renewable Utilization

Configuration of energy storage can improve the renewable utilization capability of microgrid. In this section, we set different weight coefficients $\delta$ and analyze their influences. By gradually increasing $\delta$ and solving the corresponding model, we can obtain different ESCC schemes and the corresponding renewable admission capability. According to our actual tests, the simulation step size of the weight coefficient $\delta$ is set as follows: $\delta$ varies in the range [90,000, 1,200,000], the step size is 5,000 at $\delta \in \left[\mathrm{90000,100000}\right]$ , and the step size increases as $\delta$ increases, until $\delta \in \left(\mathrm{700000,1200000}\right]$ the step size is 100,000.

By increasing $\delta$ sequentially and solving the corresponding models, we obtain 28 groups of simulation results, including ESCC schemes, investment costs, renewable admissible ranges, and renewable utilization probabilities. Based on this, Figure 5 show the variation of renewable utilization capability with ESCC schemes. In Figure 5D, the upper and lower bands of renewable utilization and the renewable output all are the average values within a day. From Figure 5, we can easily see that with the increase of energy storage investment cost and its capacity, the admissible range of renewable energy gradually widens, and renewable utilization probability also increases. This means that increasing the investment cost of ESS can improve the flexibility of the system, thereby increase the capability of renewable admission.

FIGURE 5

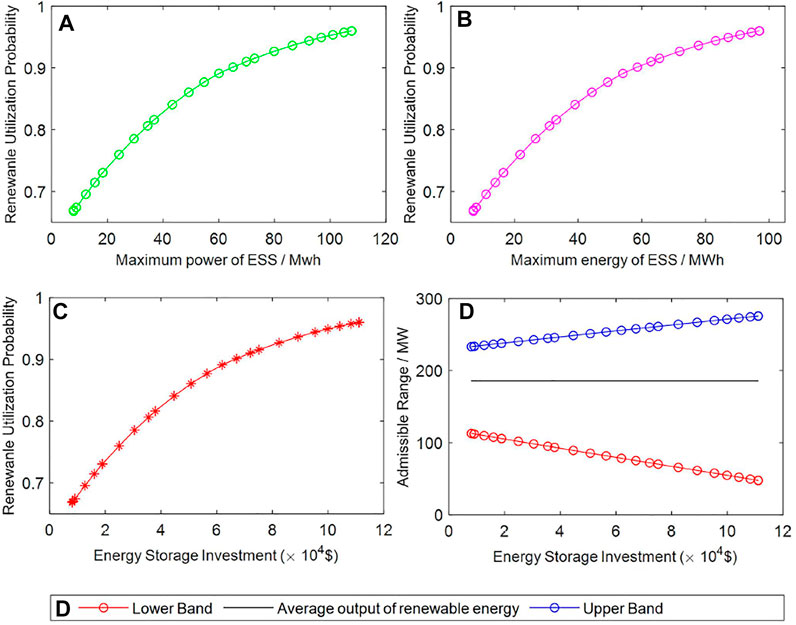
FIGURE 5. Relationship between ESCC strategy and renewable utilization. (A) Relationship between maximum power of ESS and renewable utilization. (B) Relationship between maximum energy of ESS and renewable utilization. (C) Relationship between Energy Storage investment and renewable utilization. (D) Relationship between energy storage investment and admissible range.

In addition, Figures 5A∼C also show that the increase rate of renewable utilization probability gradually decreases with the increase of energy storage investment cost. From the simulation results, the investment cost of ESS and renewable utilization probability increase very little when $\delta >800000$, which indicates that as the investment cost increases, the benefits of renewable energy utilization gradually decrease, and there is a limit. System operators can adjust $\delta$, according to the required renewable utilization probability and the cost they are willing to pay.

4.4 Comparison of Different Energy Storage Capacity Configuration Methods

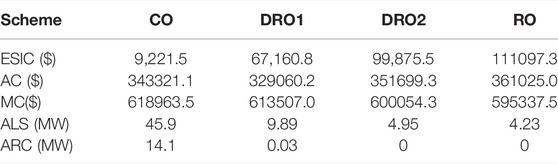
In order to analyze the advantages of the proposed distributionally robust ESCC model considering renewable utilization in this article, we compare the proposed ESCC model with an ESCC model without considering the renewable utilization. For convenience, the former method is abbreviated as DRO scheme and the latter as CO scheme. In DRO scheme, we set $\delta$ as 350,000 and 600,000, abbreviated as DRO1 and DRO2, respectively.

First, we solve these three ESCC models separately to obtain the corresponding ESCC schemes and pre-dispatch schemes. Second, according to 5,000 groups of randomly generated out-of-sample scenarios for renewable energy forecast errors, we calculate the actual operating results for each of the three schemes under all 5,000 random scenarios. We evaluate the results by the average values of 5,000 times of tests, including renewable admissible range and the actual economic cost which contains energy storage investment cost, pre-dispatch cost, and re-dispatch cost considering risk and penalty cost. In order to simulate the actual scenario, we set the real-time power purchase price to 1.5 times the day-ahead price, and the real-time power sale price is 0.6 times the day-ahead price. The penalty cost mainly includes the cost of load shedding and the cost of renewable curtailment. The price of load shedding is set at 2,000 $/MW, and the price of renewable curtailment is 100 $/MW.

Figure 6 and Table 2 show the comparison of the evaluation results of different schemes. Figure 6 shows the difference of the daily renewable admission ranges between different schemes. We can clearly see that the admissible ranges of PV, WTs, and total renewable energy under DRO scheme are all wider than those under CO scheme in each time period, which shows that the proposed method can better deal with the deviation of renewable energy output through the introduction of distributionally robust probability of renewable admission, and then improve the renewable utilization capability in the microgrid. We also see that the larger $\delta$ is, the wider the admissible range of renewable energy is, that is, by using the proposed DRO-based method, the microgrid operator can design different admissible ranges by changing $\delta$.

FIGURE 6

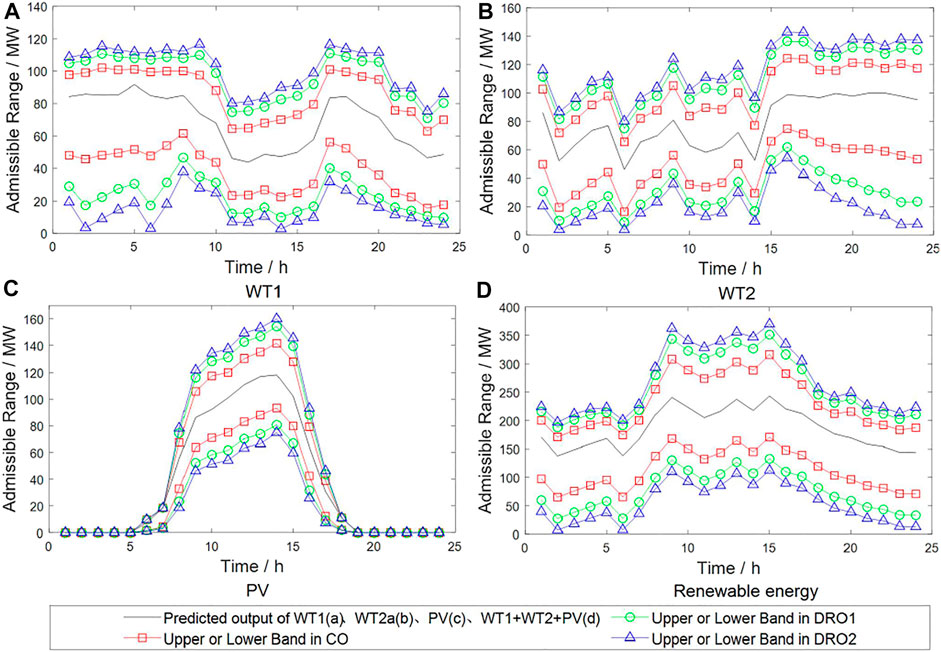
FIGURE 6. Comparison of different schemes on renewable utilization ranges of (A) WT1, (B) WT2, (C) PV and (D) total renewable energy.

TABLE 2

TABLE 2. Comparison on out-of-sample result of different schemes.

Table 2 compares the differences of economic costs and operational risks under different schemes. With comparison to CO scheme, DRO1 scheme increases the energy storage investment cost (ESIC) by 57,939.3$, while its average actual cost (AC) and the maximum actual cost (MC) in out-of-sample tests are all reduced. In addition, DRO1 significantly reduces the average load shedding (ALS) and average renewable curtailment (ARC), which effectively improves the system operation safety and reduce the waste of renewable energy and is overall better than CO scheme. In DRO2, although ALS and ARC have been further reduced, investment in energy storage has further been increased, so the operator can take the scheme according to the expected comprehensive benefits. Thus, through the comprehensive comparison of the three schemes, appropriate energy storage investment can improve the safety and economy of system operation, as well as the capability of renewable utilization. In addition, Table 2 also gives the operation results of the robust optimization (RO) method. We can see that under RO scheme, ALS is low, but ESIC and AC are very high, which shows the results under RO are more conservative than DRO-based method. All these conclusions further verify the effectiveness and advantages of the proposed DRO-based ESCC model.

5 Conclusion

In this article, we propose a distributionally robust ESCC model for microgrid by considering renewable energy utilization, and apply affine decision rules to approximately transform the two-stage model with distributionally robust adjustable chance constraints into a mixed integer programming problem. The proposed model can help the microgrid operator to make decisions on ESCC while making a trade-off between energy storage investment and renewable energy utilization. We apply the proposed DRO-based ESCC model on the IEEE 33-bus system and verify its effectiveness and advantages. From the simulation results, we conclude that proper ESCC can improve the safety of system operation and the capability of renewable admission. The connecting point of the energy storage device in this article is considered briefly but not treated as a decision variable. In future work, we will further explore the optimal connecting point. In addition, more security constraints, including voltage stability, inertia, and frequency stability will be considered in future work.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

XD and HM contributed to the methodology. HM, ZY, and JS contributed to the validation and review and editing. XD, JX, and HM analyzed the data and carried out the simulation. ZY, JS, and JX contributed to the supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the National Key Research and Development Program of China (2019YFE012784), the Fundamental Research Funds for the Central Universities, China (2232020D-53), and the Shanghai Sailing Program, China (21YF1400200).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alharbi, H., and Bhattacharya, K. (2018). Stochastic Optimal Planning of Battery Energy Storage Systems for Isolated Microgrids. IEEE Trans. Sustain. Energy 9 (1), 211–227. doi:10.1109/tste.2017.2724514

CrossRef Full Text | Google Scholar

Brekken, T. K. A., Yokochi, A., von Jouanne, A., Yen, Z. Z., Hapke, H. M., and Halamay, D. A. (2010). Optimal Energy Storage Sizing and Control for Wind Power Applications. IEEE Trans. Sustain. Energy 2 (1), 69–77. doi:10.1109/TSTE.2010.2066294

CrossRef Full Text | Google Scholar

Chen, Q., Xie, R., Chen, Y., Liu, H., Zhang, S., Wang, F., et al. (2021). Power Configuration Scheme for Battery Energy Storage Systems Considering the Renewable Energy Penetration Level. Front. Energy Res. 9, 718019. doi:10.3389/fenrg.2021.718019

CrossRef Full Text | Google Scholar

Fang, F., Zhu, Z., Jin, S., and Hu, S. (2021). Two-Layer Game Theoretic Microgrid Capacity Optimization Considering Uncertainty of Renewable Energy. IEEE Syst. J. 15 (3), 4260–4271. doi:10.1109/JSYST.2020.3008316

CrossRef Full Text | Google Scholar

Guo, Z., Wei, W., Chen, L., Dong, Z. Y., and Mei, S. (2021). Impact of Energy Storage on Renewable Energy Utilization: A Geometric Description. IEEE Trans. Sustain. Energy 12 (2), 874–885. doi:10.1109/TSTE.2020.3023498.6

CrossRef Full Text | Google Scholar

He, J., Shi, C., Wu, Q., Zhang, W., and Gao, Y. (2022). Capacity Configuration Method of Hybrid Energy Storage Participating in AGC Based on Improved Meta-Model Optimization Algorithm. Front. Energy Res. 10, 828913. doi:10.3389/fenrg.2022.828913

CrossRef Full Text | Google Scholar

Hu, R. X., He, X. Y., Jing, Z. X., Yuan, Z. X., and Wu, Q. H. (2015). “Capacity Configuration Optimization for Island Microgrid with Wind/solar/pumped Storage Considering Demand Response,” in IEEE Innovative Smart Grid Technologies - Asia (ISGT ASIA) (Bangkok, Thailand: IEEE), 1–6. doi:10.1109/ISGT-Asia.2015.7387085

CrossRef Full Text | Google Scholar

Jooshaki, M., Fattaheian-Dehkordi, S., Fotuhi-Firuzabad, M., and Lehtonen, M. (2020). “Planning a Flexible Distribution Network with Energy Storage Systems Considering the Uncertainty of Renewable Sources and Demand,” in CIRED 2020 Berlin Workshop (Online Conference: IEEE), 132–135. doi:10.1049/oap-cired.2021.0288

CrossRef Full Text | Google Scholar

Li, J., Yan, G., Xie, G., Mu, G., Feng, X., Liu, Y., et al. (2012). Research on Energy Storage System Capacity Allocation to Improve Wind Power Integration Capability. IEEE PES Innov. Smart Grid Technol. 2012, 1–6. doi:10.1109/ISGT-Asia.2012.6303280

CrossRef Full Text | Google Scholar

Li, P., Diao, H., Xue, W., and Wang, J. (2020). “Robust Energy Storage Configuration of Integrated Energy System Considering Multiple Uncertainties,” in 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC) (Nanjing, China: IEEE), 1–5. doi:10.1109/APPEEC48164.2020.9220394

CrossRef Full Text | Google Scholar

Li, Y., Wang, C., and Li, G. (2020). A Mini-Review on High-Penetration Renewable Integration into a Smarter Grid. Front. Energy Res. 8, 84. doi:10.3389/fenrg.2020.00084

CrossRef Full Text | Google Scholar

Li, Z., and Xu, Y. (2017). “Dynamic Dispatch of Gridconnected Multi-Energy Microgrids Considering Opportunity Profit,” in IEEE Power & Energy Society General Meeting (Chicago, USA: IEEE).

CrossRef Full Text | Google Scholar

Liu, C., Lee, C., Chen, H., and Mehrotra, S. (2016). Stochastic Robust Mathematical Programming Model for Power System Optimization. IEEE Trans. Power Syst. 31 (1), 821–822. doi:10.1109/TPWRS.2015.2394320

CrossRef Full Text | Google Scholar

Ma, H., Jiang, R., and Yan, Z. (2020). Distributionally Robust Co-optimization of Power Dispatch and Do-Not-Exceed Limits. IEEE Trans. Power Syst. 35 (2). doi:10.1109/tpwrs.2019.2941635

CrossRef Full Text | Google Scholar

Masaud, T. M., and El-Saadany, E. F. (2020). Correlating Optimal Size, Cycle Life Estimation, and Technology Selection of Batteries: A Two-Stage Approach for Microgrid Applications. IEEE Trans. Sustain. Energy 11 (3), 1257–1267. doi:10.1109/TSTE.2019.2921804

CrossRef Full Text | Google Scholar

Miao Fan, F. (2016). “A Novel Optimal Generation Dispatch Algorithm to Reduce the Uncertainty Impact of Renewable Energy,” in IEEE Power and Energy Society General Meeting (PESGM) (Boston, MA: IEEE), 1–5. doi:10.1109/PESGM.2016.7741737

CrossRef Full Text | Google Scholar

Nguyen, T. A., Crow, M. L., and Elmore, A. C. (2015). Optimal Sizing of a Vanadium Redox Battery System for Microgrid Systems. IEEE Trans. Sustain. Energy 6 (3), 729–737. doi:10.1109/TSTE.2015.2404780

CrossRef Full Text | Google Scholar

Ru, Y., Kleissl, J., and Martinez, S. (2013). Storage Size Determination for Grid-Connected Photovoltaic Systems. IEEE Trans. Sustain. Energy 4 (1), 68–81. doi:10.1109/TSTE.2012.2199339

CrossRef Full Text | Google Scholar

Shen, X., Luo, Z., Xiong, J., Liu, H., Lv, X., Tan, T., et al. (2021). Optimal Hybrid Energy Storage System Planning of Community Multi-Energy System Based on Two-Stage Stochastic Programming. IEEE Access 9, 61035–61047. doi:10.1109/ACCESS.2021.3074151

CrossRef Full Text | Google Scholar

Wang, L., Li, Q., Ding, R., Sun, M., and Wang, G. (2017). Integrated Scheduling of Energy Supply and Demand in Microgrids under Uncertainty: a Robust Multi-Objective Optimization Approach. Energy 130, 1–14. doi:10.1016/j.energy.2017.04.115

CrossRef Full Text | Google Scholar

Wang, L., Liu, J., Tian, C., Li, G., and Wei, W. (2018). Optimal Configuration of Microgrid Hybrid Energy Storage Capacity Based on Statistical Methods. Power Syst. Technol. 42 (01), 187–194. doi:10.13335/j.1000-3673.pst.2017.0852

CrossRef Full Text | Google Scholar

Xiao, J., Zhang, Z., and Liang, H. (2015). Optimization Method for Location and Capacity of Public Energy Storage in Distribution Network. Automation Electr. Power Syst. 39 (19), 54–60+67.

Google Scholar

Xie, R., Wei, W., Shahidehpour, M., Wu, Q., and Mei, S. (2022). Sizing Renewable Generation and Energy Storage in Stand-Alone Microgrids Considering Distributionally Robust Shortfall Risk. IEEE Trans. Power Syst. 1, 1. doi:10.1109/TPWRS.2022.3142006

CrossRef Full Text | Google Scholar

Yang, C., Sun, W., Yang, J., and Han, D. (2022). “Risk-averse Two-Stage Distributionally Robust Economic Dispatch Model under Uncertain Renewable Energy,” in CSEE Journal of Power and Energy Systems (Macao, China: IEEE). doi:10.17775/CSEEJPES.2020.03430

CrossRef Full Text | Google Scholar

Yi, W., Zhang, Y., Zhao, Z., and Huang, Y. (2018). Multiobjective Robust Scheduling for Smart Distribution Grids: Considering Renewable Energy and Demand Response Uncertainty. IEEE Access 6, 45715–45724. doi:10.1109/ACCESS.2018.2865598

CrossRef Full Text | Google Scholar

Zhou, J., Liu, W., Chen, X., Sun, M., Mei, C., He, S., et al. (2019). “A Distributionally Robust Chance Constrained Planning Method for Integrated Energy Systems,” in IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC) (Macao, China: IEEE), 1–5. doi:10.1109/APPEEC45492.2019.8994548

CrossRef Full Text | Google Scholar

Zhou, Q., Shahidehpour, M., Paaso, A., Bahramirad, S., Alabdulwahab, A., and Abusorrah, A. (2020). Distributed Control and Communication Strategies in Networked Microgrids. IEEE Commun. Surv. Tutorials 22 (4), 2586–2633. doi:10.1109/COMST.2020.3023963

CrossRef Full Text | Google Scholar

Zhou, Y., Wei, Z., Shahidehpour, M., and Chen, S. (2021). Distributionally Robust Resilient Operation of Integrated Energy Systems Using Moment and Wasserstein Metric for Contingencies. IEEE Trans. Power Syst. 36 (4), 3574–3584. doi:10.1109/TPWRS.2021.3049717

CrossRef Full Text | Google Scholar

Zhu, H., Shi, L., and Wu, F. (2020). “Optimal Allocation of Energy Storage Capacity for Stabilizing Wind Power Fluctuation,” in 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC) (Nanjing, China: IEEE), 1–5. doi:10.1109/APPEEC48164.2020.9220356

CrossRef Full Text | Google Scholar

Zhu, Y., Zhang, Q., Liu, K., Han, M., Chen, Q., and Liu, Y. (2019). “Optimized Capacity Configuration of Photovoltaic Generation and Energy Storage for Residential Microgrid,” in IEEE Innovative Smart Grid Technologies - Asia (ISGT Asia) (Chengdu, China: IEEE), 1751–1755. doi:10.1109/ISGT-Asia.2019.8881525

CrossRef Full Text | Google Scholar

Nomenclature

${\mathbf{C}}_{\mathbf{buy}}$ ${\text{C}}_{\text{sell}}$ Price of purchase and sale between microgrid and power grid, respectively

${\mathbf{C}}_{\mathbf{p}}$ ${\text{C}}_{\text{s}}$ Power cost and energy cost of the ESS, respectively

${\mathbf{T}}_{\text{s}}$ $\text{M}$ Service life and average daily maintenance cost of the ESS, respectively

$\beta$ Self-discharge rate of the energy storage battery

${\text{η}}_{\text{c}}$ ${\text{η}}_{\text{d}}$ Charging and discharging efficiency of the ESS, respectively

${\mathbf{NL}}_g$ ${\text{SU}}_g$, ${\text{SD}}_g$ No-load cost, start-up cost, and shutdown cost of thermal unit $g$, respectively.

${\mathbf{UT}}_g$ ${\text{DT}}_g$ Minimum start-up time and shutdown time of thermal unit $g$, respectively.

${\Delta }_{\mathbf{d}}$ ${\text{Δ}}_{\text{t}}$ Dispatch interval and response time window, respectively

${\Delta }_{\mathbf{ds}}$ Charging and discharging interval of ESS

${{\displaystyle P}}_s^{\max }$ ${{\displaystyle S}}_s^{\max }$ Maximum power and energy of ESS, respectively

$a_0$ Lower bound of $a$

$S{F}_{nl}$ Power transfer distribution factors of node $n$ relative to line $l$

$d_{nt}$ Load of node $n$ during time period $t$

${{\displaystyle \widehat{R}}}_{kt}$ Forecasted output of renewable resource $k$ during time period $t$

${{\displaystyle \tilde{\mathbf{W}}}}_g^{\mathbf{dn}}$ Downward ramp-rate during shutting-down of thermal unit

${{\displaystyle \tilde{\mathbf{W}}}}_g^{\mathbf{up}}$ Upward ramp-rate during starting-up of thermal unit $g$

${{\displaystyle \mathbf{W}}}_g^{\mathbf{dn}}$ ${{\displaystyle \text{W}}}_g^{\text{up}}$ Downward and upward ramp-rate of thermal unit $g$ while on, respectively

${{\displaystyle P}}_g^{\max }$ ${{\displaystyle P}}_g^{\min }$ Minimum and maximum generation capacity of thermal unit $g$, respectively

${{\displaystyle R}}_k^{\min }$ ${{\displaystyle R}}_k^{\max }$ Minimum and maximum generation capacity of renewable resource $k$, respectively

$F_l$ Transmission capacity limit of line $l$

${{\displaystyle \mathbf{P}}}_{\mathbf{line}}^{\mathbf{max}}$ Maximum transmission power of the PCC

$S_0$ ${\widehat{S}}_T$ Beginning and end states in one dispatch cycle of ESS, respectively

${\xi }_{kt}$ Actual output deviation of renewable resource $k$ from its forecasting value during time period $t$

$\delta$ Weight coefficient between power dispatch and renewable utilization

${{\displaystyle \widehat{P}}}_{gt}$ ${{\displaystyle P}}_{gt}$ Scheduled and actual generation amount of thermal unit $g$ during time period $t$, respectively

${{\displaystyle \widehat{P}}}_{st}^{\mathbf{cha}}$ ${{\displaystyle P}}_{st}^{\text{cha}}$ Forecasted and actual charging power of energy storage device $s$ during time period $t$, respectively

${{\displaystyle \widehat{P}}}_{st}^{\mathbf{dis}}$ ${{\displaystyle P}}_{st}^{\text{dis}}$ Forecasted and actual discharging power of energy storage device $s$ during time period $t$, respectively

${\widehat{S}}_{st}$ $S_{st}$ Forecasted and actual energy of energy storage device $s$ during time period $t$, respectively

${{\displaystyle \widehat{P}}}_{qt}^{\mathbf{sell}}$ ${{\displaystyle P}}_{qt}^{\text{sell}}$ Scheduled and actual power amount of sale between microgrid and power grid, respectively

${{\displaystyle \widehat{P}}}_{qt}^{\mathbf{buy}}$ ${{\displaystyle P}}_{qt}^{\text{buy}}$ Scheduled and actual power amount of purchase between microgrid and power grid, respectively

$a$ Renewable utilization probability

${{\displaystyle \xi }}_{kt}^{\mathbf{L}}$ ${{\displaystyle \xi }}_{kt}^{\text{U}}$ Lower and upper limits of ${\xi }_{kt}$, respectively

$r_{kt}$ $s_{kt}$, $z_{kt}$ Auxiliary dual variables in the reformulation of the adjustable joint chance constraint

$B$ $b$ Coefficients of the affine decision rule

$x_{gt}$ $u_{gt}$, $v_{gt}$ binary variables

$g$ $k$, $s$, $n$, $l$, $q$, $t$ Index of thermal unit, renewable resource, ESS, node, transmission line, PCC, and time period, respectively

$\left[G\right]$ $\left[K\right]$, $\left[S\right]$, $\left[N\right]$, $\left[L\right]$, $\left[Q\right]$, $\left[T\right]$ Set of thermal units, renewable resources, ESSs, nodes, transmission line, PCC, and time periods, respectively

$g_n$ $k_n$, $s_n$, $q_n$ Sets of thermal units, renewable resources, ESSs, and PCC at node $n$, respectively