
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 05 July 2022
Sec. Smart Grids
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.921426
 CH. Naga Sai Kalyan1
CH. Naga Sai Kalyan1 B. Srikanth Goud2
B. Srikanth Goud2 Ch. Rami Reddy3
Ch. Rami Reddy3 Ramanjaneya Reddy Udumula4
Ramanjaneya Reddy Udumula4 Mohit Bajaj5
Mohit Bajaj5 Naveen Kumar Sharma6
Naveen Kumar Sharma6 Elmazeg Elgamli7*
Elmazeg Elgamli7* Mokhtar Shouran7
Mokhtar Shouran7 Salah Kamel8
Salah Kamel8This study initiates the implementation of fractional-order (FO) fuzzy (F) PID (FOFPID) controller fine-tuned using a seagull optimization algorithm (SOA) for the study of load frequency control (LFC). Initially, the SOA-tuned FOFPID regulator is implemented on the widely utilized model of dual-area reheat-thermal system (DARTS), named test system-1 in this work for a perturbation of 10% step load (10% SLP) on area-1. Dynamical analysis of the DARTS system reveals the viability of the SOA-tuned FOFPID control scheme in regulating frequency deviations effectively compared to other control schemes covered in the literature. Later, the presented regulator is implemented on the multi-area diverse sources (MADS) system possessing realistic constraints in this study, termed test system-2. The sovereignty of the presented FOFPID controller is once again evidenced with controllers of PID/FOPID/FPID fine-tuned with the SOA approach. Moreover, the effect of considering practical realistic nonlinearity constraints such as communication time delays (CTDs) on MADS system performance is visualized and the necessity of its consideration is demonstrated. Furthermore, AC-DC lines are incorporated with the MADS system to enhance the performance under heavy-load disturbances and the robustness of the proposed regulatory mechanism is deliberated.
In modern days, the most powerful ancillary service is the LFC, especially for the control and operation of interconnected power system networks. The electrical system is becoming more complex due to the integration of several diverse sources of generating units to meet the variable load demand. The operating point of the generation unit must be altered to keep the real power mismatch (RPM) as minimum as possible. RPM is the exact difference between the amount of real power generated by the generation units and the existing load demand. This RPM is the direct analogy to one of the powerful parameters in the interconnected network, which is frequency. Thus, the minimization of RPM should be monitored continuously, as there will be continuous fluctuations in load demand. This must be done automatically; otherwise, the real power mismatch may become worse and affect the power system frequency. Frequency regulation must be done with the utmost care; if not, it adversely affects the power system stability. This task can be easily and automatically accomplished by LFC.
Researchers have put forward several control techniques in the LFC domain, and their performance was tested on numerous test system models that were elaborated by Tungadio and Sun (2019). Regardless of considering the power system networks, numerous techniques have been administered by the researchers of which standard PI, PID, PID plus filter (F), and PIDF regulators (Madasu et al., 2018; Arya, 2019a) are utilized extensively due to design simplicity. However, the performance efficacy of classical controllers is more likely to be dependent upon the optimization algorithms that have been deployed to optimize the controller gains. Several population- and stochastic-based searching algorithms reported in domain of LFC in optimizing classical controllers are chaotic atom search optimization (CASO) (Irudayaraj et al., 2022), many-objective optimization approach (MOOA) (Hajiakbari Fini et al., 2016), chaotic crow search (CCS) algorithm (Khokhar et al., 2021), gray wolf optimizer (GWO) (Sharma and Saikia, 2015), quadratic approach with pole compensator (QAWPC) (Hanwate and Hote, 2018), marine predator algorithm (MPA) (Yakout et al., 2021), Hooke–Jeeve’s optimizer (HJO) (Chatterjee, 2010), quasi-oppositional harmony search algorithm (QOHSA) (Shankar and Mukherjee, 2016), chemical reaction optimizer (CRO) (Mohanty and Hota, 2018), hybrid artificial electric field algorithm (HAEFA) (Sai Kalyan et al., 2020), bacteria foraging optimization (BFOA) (Ali and Elazim, 2015), mine blast optimizer (MBO) (Alattar et al., 2019), particle swarm optimizer (PSO) (Magid and Abido, 2003), differential evolution (DE) (Kalyan and Suresh, 2021), combination of DE with pattern search (Sahu et al., 2015a) and AEFA (DE-AEFA) (Kalyan and Rao, 2021a), grasshopper optimizer (GHO), and cuckoo search approach (CSA) (Latif et al., 2018). Moreover, the conventional controllers exhibit efficacy in linearized models and could not maintain the stability of nonlinear interconnected power systems (IPS).
In contrast to classical regulators, model predictive controllers (MPC) (Zhang et al., 2020) are widely implemented by researchers. Moreover, the researchers adopted algorithms to train the model predictive network such as multiverse optimizer (MVO) (Ali et al., 2020), adaptive distributed auction algorithm (ADAA) (Zhang et al., 2021), and GHO (Nosratabadi et al., 2019). However, the design of MPC involves many control parameters, large load complexity, huge algorithmic complexity, and more computational burden. Thus, complex IPS models adapting MPC as a secondary regulator become more complex and thereby affect the automatic functioning and stability of IPS.
Owing to the advantage of possessing additional knobs in fractional order (FO)–type regulators (Delassi et al., 2018) they are also used by the researchers extensively in the LFC study. However, the uncertainty in FO parameters diluted the regulator sensitivity, thereby greatly influencing the robustness of system performance which led researchers to focus on the degree of freedom (DOF) controllers (Kalyan, 2021). Moreover, the performances of DOF regulators are also limited to only a certain extent, especially to IPS models with practical constraints such as communication time delays (CTDs), governor dead band (GDB), and generation rate constraint (GRC) (Arya, 2019b). Contrary to the aforementioned, fuzzy-logic controllers (FLC) exhibit more efficacy in handling nonlinearized models. Thus, FLC is suitable for IPS with practical constraints. FLC in conjunction with traditional controllers is successfully implemented in the LFC study with different optimization algorithms such as an imperialist competitive algorithm (ICA) (Arya, 2020), DE (Sahu et al., 2015b), water cycle algorithm (WCA) (Kalyan et al., 2021), sine–cosine approach (SCA) (Khezri et al., 2019), and ant lion optimizer (ALO) (Fathy and Kassem, 2019). To further enhance the ability of FLC in governing the IPS models toward stability effectively, FO nature is imparted to the FPID regulator in this work and is termed as the FOFPID regulator. From the literature on LFC, it is apparent that LFC performance is greatly handled by the optimization-based controllers. Hence, applications of new optimization algorithms for solving realistic power system problems are always welcome. In this regard, a new nature-inspired algorithm of the seagull optimization approach (SOA) is implemented in this study and is a maiden attempt, especially for power system operation and control of IPS with practical constraints. Until now, the regulators presented by the researchers so far were tested on linearized and nonlinearized power system models with and without integrating renewable energy units. To authenticate the investigative analysis of LFC closer to the nature of realistic practice, the researchers must adopt the nonlinearity constraints with power system models. Constraints of nonlinearity such as GRC and GDB are widely considered by the researchers, and less attention is given to other constraints of CTDs. In realistic practice, IPSs are widely spread and employ numerous sensing and phasor measurement devices. The measured data will be transmitted and received among different devices located in distant places via communication peripherals. The exchange of information will not be done instantly, and there exists a certain time delay. The delay might affect the IPS performance, and hence, this study tried to investigate the predominance of time delays in coordination with the constraint of GRC. Limited work is available on LFC with CTDs and is restricted to the implementation of traditional regulators (Kalyan and Rao, 2021b; Kalyan and Rao, 2021c). Thus, this study addresses the impact of the realistic constraint parameter, that is, CTDs on IPS performance in coordination with GRC under a fuzzy-aided FO-based regulator based on the newest optimization algorithm.
The following are the research contributions:
1) The SOA-optimized FOFPID controller is designed and implemented for the study of LFC for the first time.
2) Supremacy of the SOA-tuned FOFPID controller is established with PSO-based PI, PID tuned with HAEFA and BFOA, GA-based FOPID, and DE-based FPID techniques available in the literature by implementing it on the test system-1 model.
3) Presented controller performance is tested on a nonlinear MADS system (test system-2) and efficacy is revealed with controllers of PID/FOPID/FPID.
4) The impact of CTDs on the performance of the MADS system is demonstrated.
5) Further AC-DC lines are enacted to enhance MADS system performance.
6) Sensitivity analysis is conducted to showcase the secondary and territorial control schemes’ robustness.
This work considered two different power system networks to assess the FOFPID controller performance. One is DARTS termed as test system-1 and the other is MADS termed as test system-2. The DARTS model incorporates thermal units of reheat-type turbines in both areas with equal generation capacities. On the other hand, the MADS system that tests system-2 consists of two areas in area-1 and area-2 comprising thermal-hydro-wind units. The participation factor for each source of generation unit is allocated to achieve smooth load distribution and is considered as 0.6225 for thermal, 0.3 for hydro unit, and a factor of 0.075 for gas/wind unit. The required data to build the DARTS system depicted in Figure 1 and MADS system model depicted in Figure 2 are considered from Sai Kalyan et al. (2020) and Sahu et al. (2020), respectively. The power system models are designed in the (R2016a) version of MATLAB/SIMULINK. The mathematical modeling of MADS system is as follows:
Thermal unit:
Hydro unit:
Gas unit:
Wind unit:
Furthermore, MADS system is employed with an additional DC line with an AC line in parallel for performance boost up. The modeling of the DC line (Kalyan and Rao, 2020) employed in this work is expressed in Eq. 11.
Acquainted with the complexity of the modern power system, many measuring sensors which are located at remote terminal units (RTUs) are used to transmit data to the control center. Generally, information from sensors or measuring apparatus is transmitted to the control center where the command signals have been generated. Command signals are transmitted to the plant location to shift the generating unit operating point so that the real power mismatch gets minimized. Transmitting and receiving signals among measurement devices at RTUs and command centers in plant locations can be done only via communication channels. Inherently, these communication channels possess the feature of time delays which distinctly affect the power system performance. Designing secondary regulators for large power system networks without taking these CTDs with the system may yield unsatisfactory performance. Moreover, in the event of large CTDs the system may become unstable. Considering the aforementioned aspects, this study addresses the LFC of interconnected power systems with CTDs as expressed in Eq. 12 (Kalyan and Rao, 2021a).
Implementation of traditional PID controllers in the domain of LFC has been reported extensively because of its robustness, simplicity in design, and efficiency, especially for linear systems. Despite that, traditional PID regulators are not suitable for the system with time delays and nonlinear features of uncertainties. On the contrary, fuzzy-logic controllers (FLC) are one of the finest regulators and are best suitable for obtaining the performance of nonlinear control systems optimally. Researchers proved that FLC systems can effectively change the system operating point compared to many classical controllers like PI/PID/PIDD to sustain stability. FLC has been provided with input as area control error (ACE) and its derivative. During the phase of transients, the FPI regulator exhibited low performance due to the internal integrator for the higher-order process. This motivated the authors in this study to implement FPID, and to further enhance the performance of FLC in a closed-loop system where the FO gains are incorporated (Sharma et al., 2021). Thus, FOFPID is designed, whose architecture is shown in Figure 3, and implemented for the stability of the interconnected power systems. The membership functions (MFs) perceived in this work for both error and change in error are five linguistic variables termed as (BP) big positive, (SP) small positive, (Z) zero, (BN) big negative, and (SN) small negative, as depicted in Figure 4. Mamdani type of fuzzy engine has been perceived, and the FLC output is calculated by employing the defuzzification method of the center of gravity. FLC rule base in two dimensional is noted in Table 1. Moreover, a time domain–based integral square error (ISE) index is enacted to optimize the FOFPID controller gains in this work as given in Eqn. 13. The framework of FOFPID based on SOA is depicted in Figure 5.
Seagulls are intelligent and are technically called Laridae, normally living on the banks of seas and oceans all over the globe. The species of seagulls can be differentiated based on their length and mass. Usually, seagulls come under the food chain of omnivorous and are likely to feed on amphibians, reptiles, earthworms, fish, and insects. The body of seagulls is covered with feathers of white color and possesses specialized glands at the bottom of their neck. Seagulls possess the ability to feed on saltwater and by making use of the glands behind the neck, the excess salt in the body can be flushed out. This is the unique ability of these birds, something that no other bird can do. Seagulls are very clever and make raining sounds through their feet to trap the prey that hide underwater. Moreover, seagulls sprinkle the bread crumbs that have been collected from nearby neighborhoods for catching fish.
Depending on attacking prey and the migration nature of seagulls, the SOA was put forward by the authors Dhiman and Kumar (2019). The coding of this algorithm has been carried out based on a group of seagulls shifting from one place to another during the migration phase, and the strategies that are implemented by them while attacking the prey. In SOA, collision avoidance among searching agents can be achieved by employing an additional parameter “N” to find the position of the new search agent
The current position of the seagull is represented with
The value of the collision avoidance parameter is chosen as “2” in this work to govern the change in a variable that can be reduced linearly from Ec to 0. Upon finishing the phenomena of avoidance in the collision mechanism, the search agents try to move closer to the position of the best individual using
The parameter “A” is randomized to achieve the tendency of equilibrium among the phases of exploitation and exploration and can be calculated as
Later, the position of each search agent will be updated as follows:
While migrating, seagulls regularly change their speed and attacking angle based on experience. In the plane of three dimensions, the behavior of seagull’s migration can be modeled as
“r” indicates the radius of seagulls’ movement in spiral, and “j” is the randomized number chosen in the range of (0–2). After saving the best solution, the remaining searching agent’s positions will be updated as
The procedure involved in SOA optimization is pictorially represented in Figure 6. SOA is implemented for other engineering optimization problems and no literature has been reported so far in the domain of LFC to the best of the authors’ knowledge. The intelligent behavior of seagulls motivated the authors to implement the searching strategy of SOA for the LFC study.
Evidently, the supremacy of the proposed FOFPID controller optimized with the SOA approach, a rigorously utilized model of the DARTS system in the literature, is considered and the analysis is carried out upon laying 10% SLP in area-1. In addition to the proposed control scheme, other control approaches that are listed in the literature such as PSO-based PI (Magid and Abido, 2003), BFOA-optimized PID (Ali and Elazim, 2015), FOPID (PIλDμ) fine-tuned with GA (Delassi et al., 2018), HAEFA-based PID (Sai Kalyan et al., 2020), and FPID rendered with DE (Sahu et al., 2015b) are used as regulators one after the other. System responses under various approaches to the same disturbance are displayed in Figure 7 to obtain a comparative analysis. Responses are numerically interpolated because of settling time and the optimal controller gains are placed in Table 2. Observing Figure 7 and explaining the numerical results in Table 2 exposed the dominance of the presented SOA-based FOFPID controller in minimizing the response deviations and also the time taken to reach a steady condition. This is possible only because the SOA searching mechanism that inherits the potentiality of keeping equilibrium between exploration and exploitation facilitates optimally locating the parameters of FOFPID in reducing control error. The objective value with the presented searching scheme is also greatly enhanced by 56.23% with PSO, 43.5% with BFOA, 27.3% with GA, 23.4% with HAEFA, and 16.5% with DE approaches available in the literature.
Later, the implementation of the proposed SOA-tuned FOFPID controller is assessed on another realistic test system model of MADS system, the practical constraint of GRCs is considered, and the CTDs are not perceived for this case. Controllers such as PID/FOPID/FPID/FOFPID are consecrated as regulators in every area one after the other, and the parameters are optimally located with the SOA searching strategy. The dynamical analysis is conducted by applying MADS system with 10% SLP on area-1, and the responses are comparatively rendered in Figure 8. Noting the MADS system dynamical behavior displayed in Figure 8, that the FOFPID regulator outperforms PID/FOPID/FPID controllers is visualized and is more dominant in regulating system dynamical behavior in aspects of settling time noted in Table 3. Moreover, the responses peak undershoots are improvised with FOFPID (∆f1 = 0.0041 Hz, ∆Ptie12 = 0.0009 Pu.MW, ∆f2 = 0.0019 Hz) compared to those of FPID (∆f1 = 0.0051 Hz, ∆Ptie12 = 0.0016 Pu.MW, and ∆f2 = 0.0024 Hz), FOPID (∆f1 = 0.0087 Hz, ∆Ptie12 = 0.00285 Pu.MW, and ∆f2 = 0.0043 Hz), and traditional PID (∆f1 = 0.0123 Hz, ∆Ptie12 = 0.00537 Pu.MW, and ∆f2 = 0.0054 Hz).
The MADS system is considered with CTDs along with another nonlinear feature of GRCs, for analysis purposes in this case. Variations of MADS system responses under different controllers optimized with SOA strategy are shown in Figure 9, and the employed gains are displayed in Table 4. Responses are interpreted numerically from a settling time point of view and are placed in Table 3. Observing Figure 9 and Table 3, we concluded that under the situations of nonlinearity also, the proposed controller exhibits superior performance in damping out the oscillations that are induced in the system responses due to CTDs consideration. Moreover, the proposed controller drags down the system response deviations to a steady-state position quickly compared to other methodologies. Furthermore, the peak undershoots of the responses are improvised with FOFPID (∆f1 = 0.0099 Hz, ∆Ptie12 = 0.0040 Pu.MW, and ∆f2 = 0.0036 Hz) compared to those of FPID (∆f1 = 0.0193 Hz, ∆Ptie12 = 0.0089 Pu.MW, and ∆f2 = 0.0095 Hz), FOPID (∆f1 = 0.022 Hz, ∆Ptie12 = 0.0094 Pu.MW, and ∆f2 = 0.01373 Hz), and traditional PID (∆f1 = 0.0212 Hz, ∆Ptie12 = 0.0088 Pu.MW, and ∆f2 = 0.0144 Hz).
To visualize the constraint CTD’s impact on system performance, MADS system responses under the supervision of the FOFPID regulator, which was already established as the best from the aforementioned analysis, are compared in Figure 10 for the same disturbance conditions. From Figure 10, it is revealed that the CTDs have a significant impact on frequency fluctuations and deviations in power flow through the tie-line in the LFC problem. Because considering CTDs means a delay in signal reception and transmission between different devices at various locations. CTDs delay the sending of area control error signal (ACE) to the secondary controller, resulting in the shift of the power system operating point with some delay. This results in more deviations in the frequency and tie-line power of the system. Even though the responses of the system are more deviated while perceiving CTDs, it is very much recommended to adopt the nonlinear features of CTDs in the course of designing secondary regulators. Because considering CTDs while designing a secondary controller can regulate the system dynamics to maintain stability. In this work, the parameter of CTDs is deliberated as 0.25 sec of real value. The designed regulator without considering CTDs may not be robust and cannot maintain stability in case of any unpredicted delays induce with the network.
To suppress fluctuations in the power flow of interconnected lines further and to damp out the variations in area frequency, an additional DC is installed with the existing AC line in parallel. During sudden heavy load disturbances, the demand for exchange of power via intralines is more and the secondary regulator alone is not adequate to govern frequency deviations. Therefore, a territorial control strategy needs to be employed with the system. Simulation results depicted in Figure 11 reveal that with the incorporation of the DC line, the fluctuations in system dynamical behavior are damped and undergo steady position in less time compared to the case of employing only the AC line. The settling time of MADS responses with AC and AC-DC lines is indicated in the bar chart in Figure 12.
System parameters have been subjected to deviations in ± 50% from nominal parametric values to manifest the robustness of implemented secondary and territorial control schemes. Responses of the system under the control of SOA-tuned FOFPID along with the territorial scheme of AC-DC lines for variations in loading and tie-line coefficient are displayed, respectively, in Figure 13 and Figure 14. The responses are shown in Figure 13 and Figure 14, which conclude that the deviations in responses for wide range loadings do not affect the system performance much. Furthermore, the system is subjugated with a pattern of random loading, and the responses are shown in Figure 15. It has been deliberated that the oscillations are supposed to be more damped with the AC-DC line rather than only the AC line. Hence, the presented secondary and territorial control schemes are robust.
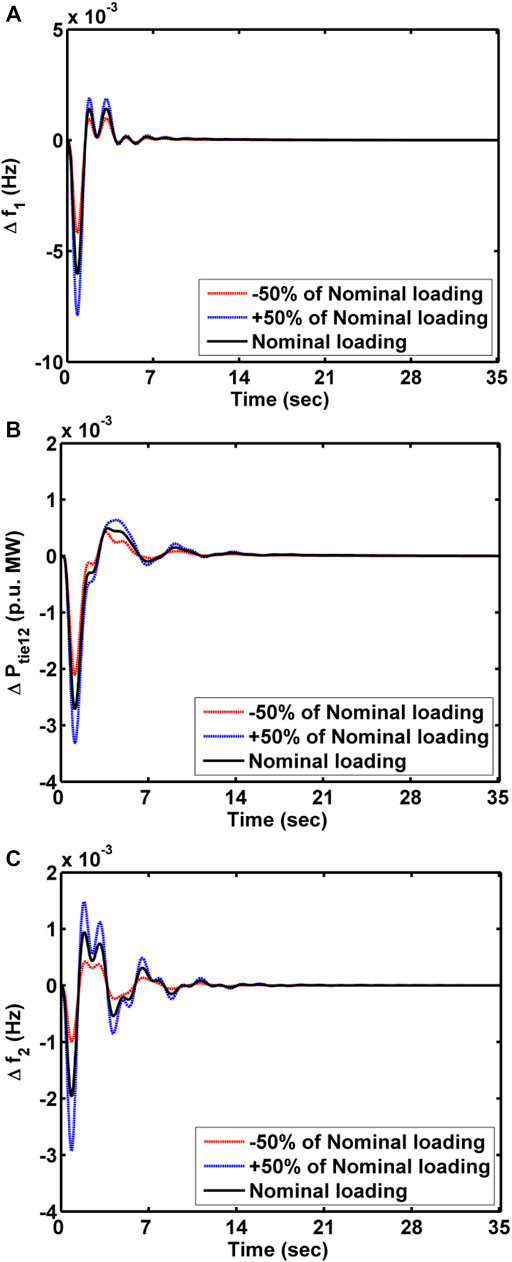
FIGURE 13. Sensitivity analysis of MADS with CTDs and AC-DC lines for a wide range of load variations. (A) ∆f1, (B) ∆Ptie12, and (C) ∆f2.
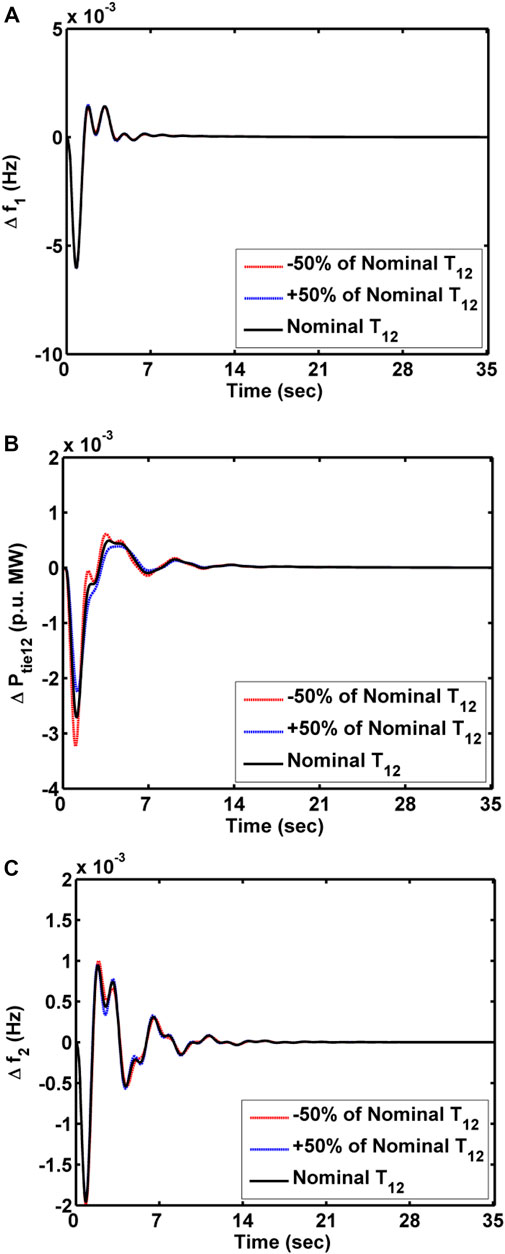
FIGURE 14. Sensitivity analysis of MADS with CTDs and AC-DC lines for a wide range of tie-line coefficients. (A) ∆f1, (B) ∆Ptie12, and (C) ∆f2.
A novel control scheme of SOA tuned FOFPID is designed and implemented successfully for regulating the frequency of interconnected power system networks. However, the supremacy of the presented control schema is established with other controllers that are implemented on the same power system model of the test system-1 available in recent literature. Moreover, the presented SOA-based FOFPID controller shows remarkable performance in damping out oscillation in tie-line power and frequency of MADS effectively even though the system is perceived with realistic constraints. Moreover, the minimization of the objective function is very finely performed under the presented controller and is enhanced by 70.40, 59.56, and 44.11% with PID, FOPID, and FPID for the case of the MADS system not conceiving CTDs. For the case of conceiving CTDs, the improvisation in objective function minimization was 50.18, 37.06, and 27.28%, respectively. The CTDs’ impact on the performance of MADS is demonstrated clearly and the necessity of perceiving CTDs is justified and convinced. Furthermore, AC-DC tie-lines are established with the MADS system and the performance is enhanced especially due to the ability of the DC line in transferring bulk power during heavy load disturbances. Finally, robustness is validated by conducting the sensitivity test. In the future, there is a lot of scope for assessing the effect of CTDs on LFC performance and the implementation of SOA-based FOFPID for the optimization of IPS in the restructured environment.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
The authors have contributed the same in producing this manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alattar, A. H., Selem, S. I., Metwally, H. M. B., Ibrahim, A., Aboelsaud, R., Tolba, M. A., et al. (2019). Performance Enhancement of Micro Grid System with SMES Storage System Based on Mine Blast Optimization Algorithm. Energies 12 (16), 3110. doi:10.3390/en12163110
Ali, E. S., and Elazim, S. M. A. (2015). BFOA Based Design of PID Controller for Two Area Load Frequency Control with Nonlinearities. Int. J. Electr. Power Energy Syst. 51, 224–231. doi:10.1016/j.ijepes.2013.02.030
Ali, H. H., Kassem, A. M., Al-Dhaifallah, M., and Fathy, A. (2020). Multi-verse Optimizer for Model Predictive Load Frequency Control of Hybrid Multi-Interconnected Plants Comprising Renewable Energy. IEEE Access 8, 114623–114642. doi:10.1109/access.2020.3004299
Arya, Y. (2020). A Novel CFFOPI-FOPID Controller for AGC Performance Enhancement of Single and Multi-Area Electric Power Systems. ISA Trans. 100, 126–135. doi:10.1016/j.isatra.2019.11.025
Arya, Y. (2019). AGC of PV-Thermal and Hydro-Thermal Power Systems Using CES and a New Multi-Stage FPIDF-(1+PI) Controller. Renew. Energy 134, 796–806. doi:10.1016/j.renene.2018.11.071
Arya, Y. (2019). Impact of Hydrogen Aqua Electrolyzer-Fuel Cell Units on Automatic Generation Control of Power Systems with a New Optimal Fuzzy TIDF-II Controller. Renew. Energy 139, 468–482. doi:10.1016/j.renene.2019.02.038
Chatterjee, K. (2010). Design of Dual Mode PI Controller for Load Frequency Control. Int. J. Emerg. Electr. Power Syst. 11. doi:10.2202/1553-779x.2452
Delassi, A., Arif, S., and Mokrani, L. (2018). Load Frequency Control Problem in Interconnected Power Systems Using Robust Fractional PI λ D Controller. Ain Shams Eng. J. 9, 77–88. doi:10.1016/j.asej.2015.10.004
Dhiman, G., and kumar, V. (2019). Seagull Optimization Algorithm: Theory and its Applications for Large-Scale Industrial Engineering Problems. Knowledge-Based Syst. 165, 169–196. doi:10.1016/j.knosys.2018.11.024
Fathy, A., and Kassem, A. M. (2019). Antlion Optimizer-ANFIS Load Frequency Control for Multi-Interconnected Plants Comprising Photovoltaic and Wind Turbine. ISA Trans. 87, 282–296. doi:10.1016/j.isatra.2018.11.035
Hajiakbari Fini, M., Yousefi, G. R., and Alhelou, H. (2016). Comparative Study on the Performance of Many‐objective and Single‐objective Optimisation Algorithms in Tuning Load Frequency Controllers of Multi‐area Power Systems. IET Gener. Transm. & Distrib. 10, 2915–2923. doi:10.1049/iet-gtd.2015.1334
Hanwate, S. D., and Hote, Y. V. (2018). Optimal PID Design for Load Frequency Control Using QRAWCP Approach. IFAC-PapersOnline. 51, 651–656. doi:10.1016/j.ifacol.2018.06.170
Irudayaraj, A. X. R., Wahab, N. I. A., Premkumar, M., Radzi, M. A. M., Sulaiman, N. B., Veerasamy, V., et al. (2022). Renewable Sources-Based Automatic Load Frequency Control of Interconnected Systems Using Chaotic Atom Search Optimization. Appl. Soft Comput. 119, 108574. doi:10.1016/j.asoc.2022.108574
Kalyan, C., Goud, B., Reddy, C., Ramadan, H., Bajaj, M., and Ali, Z. (2021). Water Cycle Algorithm Optimized Type II Fuzzy Controller for Load Frequency Control of a Multi-Area, Multi-Fuel System with Communication Time Delays. Energies 14, 5387. doi:10.3390/en14175387
Kalyan, C. H. N. S., and Rao, G. S. (2021). Impact of Communication Time Delays on Combined LFC and AVR of a Multi-Area Hybrid System with IPFC-RFBs Coordinated Control Strategy. Prot. Control Mod. Power Syst. 6. doi:10.1186/s41601-021-00185-z
Kalyan, C. N. S. (2021). “Determination of Appropriate GRC Modelling for Optimal LFC of Multi Area Thermal System,” in 2021 IEEE International Power and Renewable Energy Conference (IPRECON), Kollam, India, 24-26 Sept. 2021 (IEEE), 1–6. doi:10.1109/IPRECON52453.2021.9640892
Kalyan, C. N. S., and Rao, G. S. (2021). “Demonstarting the Effect of Excitation Cross Coupling and Communication Time Delays on Automatic Generation Control,” in 2021 4th Biennial International Conference on Nascent Technologies in Engineering (ICNTE), NaviMumbai, India, 15-16 Jan. 2021 (IEEE), 1–6. doi:10.1109/ICNTE51185.2021.9487779
Kalyan, C. N. S., and Rao, S. G. (2021c). Coordinated Control Strategy for Simultaneous Frequency and Voltage Stabilisation of the Multi-Area Interconnected System Considering Communication Time Delays. Int. J. Ambient Energy 1, 13. doi:10.1080/01430750.2021.1967192
Kalyan, C. N. s., and Suresh, C. V. (2021). “Differential Evolution Based Intelligent Control Approach for LFC of Multiarea Power System with Communication Time Delays,” in 2021 International conference on Computing, Communication, and intelligent Systems (ICCCIS), Greater Noida, India, 19-20 Feb. 2021 (IEEE), 868–873. doi:10.1109/ICCCIS51004.2021.9397112
Kalyan, N. S. C., and Rao, S. G. (2020). Frequency and Voltage Stabilisation in Combined Load Frequency Control and Automatic Voltage Regulation of Multiarea System with Hybrid Generation Utilities by AC/DC Links. Int. J. Sustain. Energy 39, 1009–1029. doi:10.1080/14786451.2020.1797740
Khezri, R., Oshnoei, A., Oshnoei, S., Bevrani, H., and Muyeen, S. M. (2019). An Intelligent Coordinator Design for GCSC and AGC in a Two-Area Hybrid Power System. Appl. Soft Comput. 76, 491–504. doi:10.1016/j.asoc.2018.12.026
Khokhar, B., Dahiya, S., and Parmar, K. P. S. (2021). A Novel Hybrid Fuzzy PD-TID Controller for Load Frequency Control of a Standalone Microgrid. Arab. J. Sci. Eng. 46, 1053–1065. doi:10.1007/s13369-020-04761-7
Latif, A., Pramanik, A., Das, D. C., Hussain, I., and Ranjan, S. (2018). Plug in Hybrid Vehicle-Wind-Diesel Autonomous Hybrid Power System: Frequency Control Using FA and CSA Optimized Controller. Int. J. Syst. Assur Eng. Manag. 9, 1147–1158. doi:10.1007/s13198-018-0721-1
Madasu, S. D., Kumar, M. L. S. S., and Singh, A. K. (2018). A Flower Pollination Algorithm Based Automatic Generation Control of Interconnected Power System. Ain Shams Eng. J. 09 (04), 1215–1224. doi:10.1016/j.asej.2016.06.003
Magid, Y. L. A., and Abido, M. A. (2003). “AGC Tuning of Interconnected Reheat Thermal Systems with Particle Swarm Optimization,” in 10th IEEE International conference on Electronics, Circuits and Systems., Sharjah, United Arab Emirates, 14-17 Dec. 2003 (IEEE), 376–379. doi:10.1109/ICECS.2003.1302055
Mohanty, B., and Hota, P. K. (2018). A Hybrid Chemical Reaction-Particle Swarm Optimisation Technique for Automatic Generation Control. J. Electr. Syst. Inf. Technol. 5, 229–244. doi:10.1016/J.JESIT.2017.04.001
Nosratabadi, S. M., Bornapour, M., and Gharaei, M. A. (2019). Grasshopper Optimization Algorithm for Optimal Load Frequency Control Considering Predictive Functional Modified PID Controller in Restructured Multi-Resource Multi-Area Power System with Redox Flow Battery Units. Control Eng. Pract. 89, 204–227. doi:10.1016/j.conengprac.2019.06.002
Sahu, P. C., Prusty, R. C., and Panda, S. (2020). Approaching Hybridized GWO-SCA Based Type-II Fuzzy Controller in AGC of Diverse Energy Source Multi Area Power System. J. King Saud Univ. - Eng. Sci. 32, 186–197. doi:10.1016/j.jksues.2019.01.004
Sahu, R. K., Chandra Sekhar, G. T., and Panda, S. (2015). DE Optimized Fuzzy PID Controller with Derivative Filter for LFC of Multi Source Power System in Deregulated Environment. Ain Shams Eng. J. 6, 511–530. doi:10.1016/j.asej.2014.12.009
Sahu, R. K., Gorripotu, T. S., and Panda, S. (2015). A Hybrid DE-PS Algorithm for Load Frequency Control under Deregulated Power System with UPFC and RFB. Ain Shams Eng. J. 6, 893–911. doi:10.1016/j.asej.2015.03.011
Sai Kalyan, C. N., Rao, G. S., and Rao, G. S. (2020). Coordinated SMES and TCSC Damping Controller for Load Frequency Control of Multi Area Power System with Diverse Sources. ijeei 12, 747–769. doi:10.15676/ijeei.2020.12.4.4
Shankar, G., and Mukherjee, V. (2016). Load Frequency Control of an Autonomous Hybrid Power System by Quasi-Oppositional Harmony Search Algorithm. Int. J. Electr. Power & Energy Syst. 78, 715–734. doi:10.1016/j.ijepes.2015.11.091
Sharma, M., Dhundhara, S., Arya, Y., and Prakash, S. (2021). Frequency Stabilization in Deregulated Energy System Using Coordinated Operation of Fuzzy Controller and Redox Flow Battery. Int. J. Energy Res. 45 (2), 7457–7475. doi:10.1002/er.6328
Sharma, Y., and Saikia, L. C. (2015). Automatic Generation Control of a Multi-Area ST - Thermal Power System Using Grey Wolf Optimizer Algorithm Based Classical Controllers. Int. J. Electr. Power & Energy Syst. 73, 853–862. doi:10.1016/j.ijepes.2015.06.005
Tungadio, D. H., and Sun, Y. (2019). Load Frequency Controllers Considering Renewable Energy Integration in Power System. Energy Rep. 5, 436–453. doi:10.1016/j.egyr.2019.04.003
Yakout, A. H., Attia, M. A., and Kotb, H. (2021). Marine Predator Algorithm Based Cascaded PIDA Load Frequency Controller for Electric Power Systems with Wave Energy Conversion Systems. Alexandria Eng. J. 60, 4213–4222. doi:10.1016/j.aej.2021.03.011
Zhang, X., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021). Adaptive Distributed Auction-Based Algorithm for Optimal Mileage Based AGC Dispatch with High Participation of Renewable Energy. Int. J. Electr. Power & Energy Syst. 124, 106371. doi:10.1016/j.ijepes.2020.106371
Keywords: load frequency control, seagull optimization algorithm, FOFPID controller, 10% SLP, AC-DC lines
Citation: Naga Sai Kalyan C, Goud BS, Reddy CR, Udumula RR, Bajaj M, Sharma NK, Elgamli E, Shouran M and Kamel S (2022) Seagull Optimization Algorithm–Based Fractional-Order Fuzzy Controller for LFC of Multi-Area Diverse Source System With Realistic Constraints. Front. Energy Res. 10:921426. doi: 10.3389/fenrg.2022.921426
Received: 15 April 2022; Accepted: 26 May 2022;
Published: 05 July 2022.
Edited by:
Bo Yang, Kunming University of Science and Technology, ChinaReviewed by:
Jingbo Wang, Kunming University of Science and Technology, ChinaCopyright © 2022 Naga Sai Kalyan, Goud, Reddy, Udumula, Bajaj, Sharma, Elgamli, Shouran and Kamel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elmazeg Elgamli, RWxnYW1saWVzQGNhcmRpZmYuYWMudWs=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.