Coupled Dynamic Response of an Offshore Multi-Purpose Floating Structure Suitable for Wind and Wave Energy Exploitation

This paper presents the coupled analysis performed in the frequency and time domain, considering a multi-purpose floating structure suitable for offshore wind and wave energy source exploitation. The floating structure encompasses an array of hydrodynamically interacting Oscillating Water Column (OWC) devices, moored through tensioned tethers as a Tension Leg Platform (TLP), and supports a 10 MW Wind Turbine (WT). The analysis is built to incorporate properly the solutions of the diffraction and the pressure- and motion-dependent radiation problems around the floating structure, the mooring lines characteristics, the OWCs characteristics, and the aerodynamics of the WT by accounting for the aerodynamic modelling of the rotor, the elastic modelling of the turbine components, namely the blades, the drive train, and the tower. Numerical results are obtained through the developed analysis methods, presenting the fundamental hydrodynamic properties of the platform, as well as the ultimate and fatigue loads at several locations on the structure expected to be imposed on it over its lifetime. The effect of the installation sites (i.e., environmental excitation) on the lifetime loads is investigated by comparing the estimated loads at various Mediterranean Sea and North Sea locations. Finally, the OWC effect, due to the air pressure oscillation inside the wave energy converters, is discussed, highlighting its significant influence on the hybrid system’s loading conditions.

1 Introduction

In the first half of 2021, Europe’s grid connected 1.3 GW of new offshore wind turbines (WT) across five wind farms. Consequently, Europe has a total offshore installed wind capacity of 26 GW, which translates to 5,566 WT and 120 wind farms. The average size of offshore WT amounts to 8–10 MW, whereas concerning their foundation type, 80% of them stand on monopiles (Wind Europe, 2021). According to Wind Europe (2020), 29 GW of new offshore wind will be installed in the EU by 2025, which corresponds to a doubling of the annual installation rate from 3 to 5.8 GW. These trends show that the number of offshore farms will increase rapidly. In addition, offshore wind costs continue to fall significantly. Specifically, last year’s actions (i.e., 2021) delivered a process for consumers of 44 €/MWh (Energy, 2021).

In recoverable wave energy exploitation, the cumulative global installed capacity of ocean energy is 534.7 MW, which is dominated by tidal barrage with around 521.5 MW, while the remaining capacity of around 13.2 MW is shared between tidal stream, wave energy, thermal energy, and salinity gradient (IRENA 2020). Nevertheless, due to tidal and wave projects currently under construction, 2.9 GW can be deployed globally by 2030, while 92% of this will be on the European coastline. These deployments will reduce the cost of tidal energy to 90 €/MWh,, whilst wave will sit at approximately 110 €/MWh (Ocean Energy Europe, 2020). However, when compared to offshore wind energy, the cost of wave and tidal energy is high, leading many to proclaim it is not worth pursuing.

Offshore wind and wave energy are expected to satisfy 15% of EU electricity demand by 2050 (Perez-Collazo et al., 2013). The investigation of the technological and economic feasibility of multi-purpose floating structures, which combine offshore wind turbines with wave energy converters, is one promising alternative for reducing the levelized cost of energy and increasing the performance of renewable technologies. In addition, the hybrid exploitation of offshore wind and wave energy resources on a common platform enables maintenance and grid connections to be streamlined as compared with two separate technologies, also providing improvements for both capital expenditure (CAPEX) and operational expenditure (OPEX), as well as for substructure or foundation costs. Furthermore, the ecological footprint of a co-located wind and wave energy exploitation system is expected to be lower than the separate alternative due to the lower affected area, which leads to increased public acceptance for offshore renewables (Karimirad, 2014). Although offshore multi-purpose floating systems have not yet achieved commercial maturity, apart from a few concepts, namely Pelagic Power AS (2010), DualSub (2019), and Floating Power Plant (2021), the feasibility of combining a floating wind turbine and a wave energy converter has already been investigated by numerous authors. Specifically, several wave energy absorption technologies, namely point absorbers, attenuators, and flap type converters, have been coupled with offshore floating structures supporting a WT. Indicative studies are Bachynski and Moan (2013), Muliawan et al. (2013a), Muliawan et al. (2013b), Veigas and Iglesias (2015), Gao et al. (2016), Michailides et al. (2016a), Michailides et al. (2016b), Karimirad and Koushan (2016), Wang et al. (2020), to name only a few.

In addition to the aforementioned wave energy absorption technologies, the Oscillating Water Column (OWC) systems are among the most credited solutions for wave energy conversion. Although OWCs dominate today’s installed capacity, they account for only three projects, i.e., Voith Hydro (2009), REWEC3 (2019), Ocean Energy Ltd (2020), and (IRENA 2020). Nevertheless, numerous studies on hybrid systems based on the oscillating water column principle have been reported in the literature in recent years. Aubault et al. (2011) developed a numerical model, which was also verified experimentally, to account for the effect of power-take-off (PTO) on the inner free surface of an OWC device when the latter is considered as a part of a multi-megawatt WT floating foundation. Mazarakos et al. (2015) studied a multi-purpose tension leg platform which encompasses three hydrodynamically interacting OWCs and a 5 MW WT. They present a coupled-hydro-aero-elastic formulation in the frequency and time domain, to incorporate properly the solutions of the diffraction and radiation problems around the structure and the aerodynamics of the WT. The analysis has been further extended by Mazarakos et al. (2019a) concerning numerical validations with corresponding scaled down tank tests to extrapolate the effect of the air pressure inside the OWCs on the structure’s seakeeping. A hybrid wind-wave system that integrates an OWC converter with a WT on a jacket-frame substructure has been experimentally studied by Perez-Collazo et al. (2018). The latter hybrid system has been upgraded by Perez-Collazo et al. (2019), integrating an OWC device with an offshore wind substructure of the monopile type. Sarmiento et al. (2019) presented experimental scaled down tests of a hybrid structure, moored with conventional mooring lines, which combines three OWC devices and a 5 MW WT under wind, wave, and current effects. In addition, Zhou et al. (2020) investigated numerically and experimentally the hydrodynamic performance of an OWC converter integrated into a monopile-mounted WT. Herein, a 3D time-domain numerical model was developed to examine the effect of the OWC on the structure’s wave loads. A similar concept was also studied by Cong et al. (2021), in which a detailed numerical analysis was conducted for the case of an OWC integrated into a 5 MW WT in regular and irregular wave trains. Recently, Konispoliatis et al. (2021) presented a multi-purpose floating TLP concept for the combined wind and wave energy resource exploitation that consists of a triangular platform supported by three OWC devices, with a 10 MW WT mounted at the deck’s center. The paper focused on the description of the environmental conditions for three candidate installation locations (i.e., two in the Mediterranean Sea and one in the North Sea), as well as on the presentation of the conducted experimental campaign with a scaled-down physical model in order to compare the numerical results with the corresponding experimental outcomes. However, the hydro-servo-aero-elastic coupled modeling of the applied numerical formulation was set aside.

The present paper extends the work from Konispoliatis et al. (2021) by presenting the coupled analysis performed in the frequency and time domain, considering a multi-purpose floating structure. The analysis is designed to properly incorporate, the solutions to the diffraction and pressure- and motion-dependent radiation problems around the floating structure, the mooring characteristics (stiffness, pretension level), the OWCs characteristics (dynamic pressure fluctuation in the chamber, air flow rate to the air turbine) and the aerodynamics of the WT taking into consideration the aerodynamic modelling of the rotor, the elastic modelling of the turbine components, namely the blades, the drive train and the tower. Furthermore, in the present work, the extreme (ultimate) and fatigue loads (forces and moments) of the system’s main components expected to be imposed on them over their lifetime are determined through time-domain hydro-servo-aero-elastic simulations for various design load cases (DLCs). The effect of the installation location (i.e., environmental excitation) on the lifetime loads is investigated, by comparing the estimated loads at various Mediterranean Sea and North Sea locations.

The manuscript is structured as follows: in Section 2 the characteristics of the multi-purpose floating structure are given, whereas in Section 3 the applied hydrodynamic formulation in the frequency domain through the proper solution of the diffraction and radiation problems under the action of regular wave trains is presented. Furthermore, it envelops the formulation of the servo-aero-elasto-dynamic problem due to the WT and the solution of the coupled hydro-aero-elastic problem of the hybrid structure (i.e., floater, WT, OWC, and mooring system). Section 4 is dedicated to the presentation of numerical results, whereas the conclusions are drawn in Section 5.

2 Description of the Hybrid Floating Structure

The considered hybrid structure encompasses a triangular floater with three hydrodynamically interacting OWC converters located at its corners, whereas, at the deck’s center, a vertical truncated cylinder supports a 10 MW horizontal axis WT (see Figure 1). The wave energy converters comprises of an internal truncated cylinder and an external coaxial cylindrical shell. In the annular fluid area formed between the solids’ vertical walls, oscillations of the enclosed water column are developed, compressing, and decompressing the air above the water surface. Consequently, there is an air volume flow through an air turbine located at each chamber’s top and coupled to an electric generator. The key components of the structure are: a) rotor-nacelle-assembly system (RNA), b) tower structure, c) floating structure, consisting of three OWCs and a solid cylindrical body supporting the WT, and d) mooring system consisting of tendon pipes.

FIGURE 1

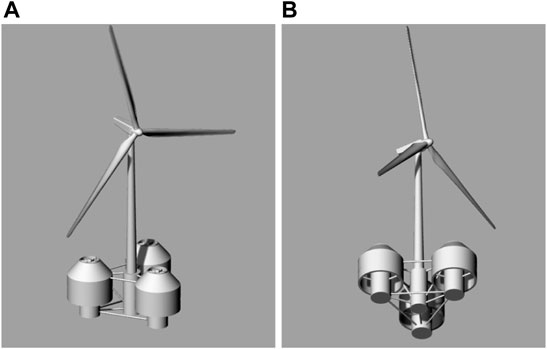
FIGURE 1. 3-D representation of the multi-purpose floating structure suitable for offshore wind and wave energy exploitation: (A) above (left), (B) below (right) sea water level (SWL) (Konispoliatis et al., 2021)

The floating system has been defined to support the DTU 10 MW reference WT (Bak et al., 2013). Regarding the three OWC devices, a Wells type air turbine is considered placed at the top of each device’s chamber, which is a bidirectional turbine designed for directional changing flows, like the ones produced in the air chamber. It is assumed that each OWC uses the same air turbine regardless of its position in relation to the wave impact. The characteristics of the air turbine can be represented by a complex pneumatic admittance Λ (Falnes, 2002), whereas in the present contribution the thermodynamic effects have not been taken into consideration. Hence Λ is considered as a real number.

Since wind and wave climate analysis has been performed (Konispoliatis et al., 2021) for three candidate installation locations, i.e., two in the Mediterranean Sea (with coordinates 35.34oN, 26.80oE and 37.30oN, 12.69oE) and one in the North Sea (with coordinates 59.42oN, 3.40oE), two turbines’ pneumatic admittances $\text{Λ}$ were considered, i.e., $\text{Λ}=343.848 {\text{m}}^5/(\text{kN}.\text{s})$ for the Mediterranean Sea; whilst $\text{Λ}=125.115{\text{ m}}^5/(\text{kN}.\text{s})$ for the North Sea site. An analytical description of the air turbine design is presented in Konispoliatis et al. (2019).

To secure the hybrid platform, the floater is moored through a TLP mooring system of three tendons spread symmetrically about the platform’s vertical axis. The tendon system provides a structural link between the seabed and the floater’s fairleads, which are located at the bottom of the OWCs’ offset columns (i.e., at 20 m below the sea water level -SWL).

Table 1 summarizes the geometric characteristics of the examined floater, whereas in Table 2 the mooring properties are presented. Nevertheless, a detailed presentation of the selection of the floater’s specifications as well as of the design of the hybrid structure can be found in Mazarakos et al. (2018, 2019b) and Konispoliatis et al. (2021).

TABLE 1

TABLE 1. Geometric characteristics of the hybrid structure.

TABLE 2

TABLE 2. Mooring properties of the hybrid structure.

3 Materials and Methods

3.1 Formulation of the Hydrodynamic Problem

The group of four bodies of the multi-purpose floating structure (i.e., three OWCs and one central truncated cylindrical body) are excited by a plane periodic wave of amplitude $H/2$, frequency $\omega$, and wave number $k$. In the present formulation, viscous effects are neglected, whereas the fluid is assumed incompressible and the flow irrotational. In addition, the fluid’s motions are assumed to be small, so that the linearized diffracted and radiated problems can be considered. The fluid flow around each body $q=1,\dots ,4$ of the arrangement can be described by the velocity potential ${\Phi }^q\left(r_q,{\theta }_q,z;t\right)=\text{Re}\left\{{\phi }^q\left(r_q,{\theta }_q,z\right)e^{-i\omega t}\right\}$ where:

${\phi }^q={\phi }_0^q+{\phi }_7^q+{\displaystyle \sum }_{p=1}^4{\displaystyle \sum }_{j=1}^6{\dot{\xi }}_{j0}^p{\phi }_j^{qp}+{\displaystyle \sum }_{p=1}^3{p}_{in0}^p{\phi }_{\text{P}}^{qp}.(1)$

In Eq. 1 the velocity potential of the undisturbed incident harmonic wave is denoted by ${\phi }_0^q$, whereas ${\phi }_7^q$ is the scattered potential around the body $q$ when it is considered fixed in waves, with atmospheric inner air pressure (i.e., for the three OWCs). The term ${\phi }_j^{qp}$ stands for the motion radiation velocity potential around the body $q$ due to forced oscillations of the body $p=1,\dots ,4$ in the $j$ th direction due to unit time harmonic velocity amplitude, ${\dot{\xi }}_{j0}^p$. Herein, the air pressure inside the OWCs is considered equal to the atmospheric pressure. The term ${\phi }_{\text{P}}^{qp}$ denotes the pressure radiation velocity potential around the body $q$ with a zero air pressure head, due to unit time harmonic air pressure, $p_{in0}^p$, inside the body $p=1,\dots ,3$. Here, the bodies of the arrangement are considered fixed in waves. It should be also noted that $\left(r_q,{\theta }_q,z\right), q=1,\mathrm{...},4$ are local cylindrical coordinates located at the sea bottom, with their $z$ axis pointing upwards and coinciding with the vertical axis of symmetry of each body $q$. Furthermore, apart from four local coordinate systems, a global Cartesian coordinate system O-XYZ is considered, with its origin on the sea bottom and its vertical axis Oz directed positive upwards, which coincides with the local coordinate system of the central truncated cylindrical body, $q=4$, i.e., the vertical axis Oz is located at the vertical axis of symmetry of the cylinder (see Figure 2).

FIGURE 2

FIGURE 2. Definition sketch of the selected global- and local-coordinate systems.

The potentials ${\phi }_j^q, j=\mathrm{0,7};q=1,\mathrm{..},4$, ${\phi }_j^{qp}, j=1,\dots ,6;q,p=1,\dots ,4$, and ${\phi }_{\text{P}}^{qp},q=1,\dots ,4;p=\mathrm{1,2,3}$ are solutions of the Laplace equation in the entire fluid domain and satisfy appropriate boundary conditions on the sea bottom ($z=0$), at the outer and inner free surface of each body, and the mean body’s wetted surface. An analytical representation of the imposed boundary conditions can be found in Supplementary Appendix A. Furthermore, a radiation condition is fulfilled, stating the outgoing propagating disturbances.

The velocity potential of the undisturbed incident harmonic wave train propagating at an angle $\beta ,$ with respect to the positive X-axis, expressed in the local cylindrical coordinate frame of the $q=1,\dots ,4$ body, can be written as:

${\phi }_0^q\left(r_q,{\theta }_q,z\right)=-i\omega \frac{H}{2}{\displaystyle \sum }_{m=-\infty }^{\infty }{i}^m{\Psi }_{0,m}^q\left(r_q,z\right)e^{im{\theta }_q}.(2)$

Here,

${\Psi }_{0,m}^q\left(r_q,z\right)=e^{ik{l}_{0q}\cos \left({\theta }_{0q}-\beta \right)}\frac{{{\rm Z}}_0\left(z\right)}{d{{{\rm Z}}^{\prime }}_0\left(d\right)}{J}_m\left(k{r}_q\right)e^{-im\beta }.(3)$

In Eq. 3, $d$ stands for the water depth, $J_m$ is the $m$ th order Bessel function of first kind, $l_{0q}$ is the distance of the global coordinate system origin from the $q$ body’s local coordinate system, and ${\theta }_{0q}$ is the formed angle between $l_{0q}$ and the horizontal axis X (see Figure 2). The ${{\rm Z}}_0$ is defined by:

${{\rm Z}}_0\left(z\right)={\left[\frac{1}{2}\left[1+\frac{\text{sinh}\left(2kd\right)}{2kd}\right]\right]}^{-1/2}\text{cosh}\left(kz\right).(4)$

With ${{{\rm Z}}^{\prime }}_0\left(d\right)$ being its derivative at $z=$ d.

The diffraction velocity potential around the body $q$, which equals to ${\phi }_D^q={\phi }_0^q+{\phi }_7^q$, expressed in its coordinate system, can be written as:

${\phi }_D^q\left(r_q,{\theta }_q,z\right)=-i\omega \frac{H}{2}{\displaystyle \sum }_{m=-\infty }^{\infty }{i}^m{\Psi }_{D,m}^q\left(r_q,z\right)e^{im{\theta }_q}.(5)$

Similar, the motion- and pressure-radiation potentials, ${\phi }_j^{qp}$ and ${\phi }_{\text{P}}^{qp}$, respectively can be expressed by:

${\phi }_j^{qp}\left(r_q,{\theta }_q,z\right)=-i\omega {\displaystyle \sum }_{m=-\infty }^{\infty }{\Psi }_{j,m}^{qp}\left(r_q,z\right)e^{im{\theta }_q},(6)$

${\phi }_{\text{P}}^{qp}\left(r_q,{\theta }_q,z\right)=\frac{1}{i\omega \rho }{\displaystyle \sum }_{m=-\infty }^{\infty }{\Psi }_{\text{P},m}^{qp}\left(r_q,z\right)e^{im{\theta }_q},(7)$

In Eqs. 5–7, the functions ${\Psi }_{D,m}^q,{\Psi }_{j,m}^{qp},{\Psi }_{\text{P},m}^{qp}$ denote the principal unknowns of the hydrodynamic problem. These can be established through the method of matched axisymmetric eigenfunction expansions and the multiple scattering approach. Specifically, the flow field around each body of the hybrid structure is subdivided into coaxial ring-shaped regions in which different series of expansions of the functions ${\Psi }_{D,m}^q,{\Psi }_{j,m}^{qq},{\Psi }_{\text{P},m}^{qq}$ can be established. These functions are solutions of the Laplace equation and satisfy the kinematic boundary conditions at the bodies’ horizontal walls and on the sea bottom, the linearized condition on the free surface, as well as the kinematic condition at infinity. The various potential solutions are matched by the continuity requirements of the hydrodynamic pressure and radial velocity along the vertical boundaries of adjacent fluid regions, and the satisfaction of the kinematic boundary condition at the bodies’ vertical walls. Subsequently, a linear system of equations is obtained for the determination of the functions ${\Psi }_{D,m}^q,{\Psi }_{j,m}^{qq},{\Psi }_{\text{P},m}^{qq}$ in each fluid region. It should be noted that the advantage of using these functions in the solution procedure is that they can be described by simple Fourier series for all the types of ring elements. Nevertheless, when examining an array of bodies, the hydrodynamic interaction phenomena between the array’s members should also be taken into consideration. According to the multiple scattering approach each body of the hybrid structure (i.e., three OWCs and one solid cylinder) scatters waves towards the others, which in turn scatter waves towards the initial device. By superposing the incident wave potential and various orders of propagating and evanescent modes that are scattered and radiated by the array members, exact representations of the functions ${\Psi }_{D,m}^q,{\Psi }_{j,m}^{qp},{\Psi }_{\text{P},m}^{qp}$ in each fluid region can be obtained. The method achieves a considerable reduction in the storage requirements in computer applications since the boundary conditions on each body of the array are satisfied successfully, without simultaneously retaining the partial amplitudes around all the bodies of the array. The methods of matched axisymmetric eigenfunction expansions as well as multiple scattering have been thoroughly presented by Mavrakos and Koumoutsakos (1987), Mavrakos (1991), and Konispoliatis and Mavrakos (2016), hence they are not further elaborated herein.

The first-order exciting wave forces acting on each body $q=1,\dots ,4$ of the hybrid structure (i.e., three OWCs and one vertical, solid cylinder) are determined by the integration of the first-order hydrodynamic pressure due to the incident and diffracted wave fields on each solid’s mean wetted surface $S$. Thus, it holds:

$F_i^q=-i\omega \rho \underset{S}{{\displaystyle \mathrm{\iint }}}({\phi }_0^q+{\phi }_7^q)n_{i}dS, i=1,\dots ,6.(8)$

Here $n_i$ are the components of the generalized unit normal vector to the wetted surface $S$, defined in Supplementary Appendix A.

The total exciting forces and moments, $F_i^T, i=1,\dots , 6$, acting on the structure are evaluated by reducing the corresponding exciting forces on each body of the array with respect to the platform’s reference point of motion. Thus, the total exciting forces can be written in a matrix form as:

$\left[F^T\right]=\left[B\right]\left[F^q\right].(9)$

In Eq. 9 $\left[F^T\right]$ is a column matrix ($6\times 1$) containing the total exciting forces and moments on the hybrid structure, whereas $\left[F^q\right]$ is a column matrix ($24\times 1$) containing the exciting forces and moments on each body of the array, i.e., four bodies. $\left[B\right]$ is a ($6\times 24$) matrix defined in Supplementary Appendix B.

The hydrodynamic reaction forces and moments $F_{ij}^{qp}, i,j=1,\dots ,6;q,p=1,\dots ,4$ of the body $q$ in the $i$ th direction due to forced oscillation of the body $p$ in the $j$ th direction with amplitude ${\xi }_{j0}^p$ are evaluated by:

$F_{ij}^{qp}=-{\omega }^2\rho {\xi }_{j0}^p\underset{S}{{\displaystyle \mathrm{\iint }}}{\phi }_j^{qp}{n}_{i}dS, i,j=1,\dots ,6.(10)$

The complex force $F_{ij}^{qp}$ can also be written in the form:

$F_{ij}^{qp}={\omega }^2\left(a_{ij}^{qp}+\frac{1}{\omega }{b}_{ij}^{qp}\right){\xi }_{j0}^p={\omega }^2{\pi }_{ij}^{qp}{\xi }_{j0}^p, i,j=1,\dots ,6.(11)$

In Eq. 11 $a_{ij}^{qp},b_{ij}^{qp},$ stand for the hydrodynamic added mass and damping coefficients, respectively, both real and dependent on wave frequency $\omega$.

In order to evaluate the hydrodynamic coefficients of the hybrid structure, the hydrodynamic reaction forces $F_{ij}^{qp}$ expressed with respect to each body’s reference point of motion have to be rewritten with respect to the platform’s reference point of motion. Hence, the hydrodynamic masses, $A_{ij}$, and potential damping, $B_{ij}$, coefficients of the hybrid structure are obtained by:

$A_{ij}+\frac{1}{\omega }{B}_{ij}={\displaystyle \sum }_{q=1}^4{\displaystyle \sum }_{p=1}^4{\Pi }_{ij}^{qp}, i,j=1,\dots ,6.(12)$

Here, the terms ${\Pi }_{ij}^{qp}$ are elements of the ($6\times 6$) square matrix $\left[{\Pi }^{qp}\right]$ which is defined by:

$\left[{\Pi }^{qp}\right]=\left[B\right] \left[{\pi }^{qp}\right] {\left[B\right]}^T.(13)$

In Eq. 13 $\left[{\pi }^{qp}\right]$ is a ($24\times 24$) square matrix whose elements are the terms ${\pi }_{ij}^{qp}$ , defined in Eq. 11. The transformation matrix $\left[B\right]$ is defined in Supplementary Appendix B and ${\left[B\right]}^T$ is its transpose matrix.

The pressure-dependent hydrodynamic forces and moments, $F_{\text{P}j}^{qp},$ acting on the body $q, q=1,\dots ,4$ in the $j$ th direction due to air pressure oscillation in the $p$ device $, p=\mathrm{1,2,3}$ can be written in the form of Equation 14, i.e.,

$F_{\text{P}j}^{qp}={\lambda }_{\text{P}j}^{qp}{p}_{in0}^p, j=1,\dots ,6.(14)$

Here the complex term ${\lambda }_{\text{P}j}^{qp}$ represents the hydrodynamic coupling between the oscillating devices and the pressure oscillation.

The pressure-dependent hydrodynamic forces and moments, $F_{\text{P},i}^T$, on the hybrid structure due to air pressure inside the three OWC devices can be expressed in matrix form as:

$\left[F_{\text{P}}^T\right]=\left[B\right]\left[F_{\text{P}}^q\right].(15)$

Here $\left[F_{\text{P}}^T\right]$ is a column matrix ($6\times 1$) containing the total hydrodynamic forces and moments on the hybrid structure, $F_{\text{P},i}^T$, whereas $\left[F_{\text{P}}^q\right]$ is a column matrix ($24\times 1$) containing the pressure-dependent hydrodynamic forces and moments, $F_{\text{P}j}^{qp},$ acting on the body $q$, i.e., four bodies. $\left[B\right]$ is a ($6\times 24$) matrix defined in Supplementary Appendix B.

3.2 Coupled Hydro-Aero-Dynamic Formulation in the Frequency Domain

The translational and rotational motions of the hybrid floating structure can be evaluated by the following system of differential equations, which describes the coupled hydro-aero-dynamic problem in the frequency domain.

${\displaystyle \sum }_{j=1}^6\left[-{\omega }^2\left({{\rm M}}_{ij}+M_{ij}^{WT}+A_{ij}+\frac{i}{\omega }{{\rm B}}_{ij}+\frac{i}{\omega }{{\rm B}}_{ij}^{WT}\right)+C_{ij}+C_{ij}^{WT}\right]{\Xi }_{j0}-F_{\text{P},i}^T=F_i^T, i=1,\dots ,6.(16)$

In Eq. 16, ${{\rm M}}_{ij}$ are the structure’s mass coefficients, including the mass of the system and the structure’s moment of inertia. the terms $A_{ij},B_{ij}$ are the floater’s hydrodynamic mass and potential damping coefficients, as presented in Eq. 12, whereas $M_{ij}^{WT},B_{ij}^{WT},C_{ij}^{WT}$ denote the additional, linearized mass, damping, and stiffness matrices, contributed by the WT to the floater dynamic equations. They derive from a Hamiltonian based dynamic model of the WT combined with Blade Element Momentum theory that accounts for aerodynamic, gravitational, and inertial-gyroscopic loading provided for various reference states (wind speed, rotational speed, and blade pitch) (Mazarakos et al., 2019a; Konispoliatis et al., 2021). In addition, $C_{ij}$ stands for the restoring coefficients of the structure, which consist of three parts, namely, the conventional mooring line stiffness, the platform hydrostatic restoring stiffness, and the tendon geometric stiffness (Konispoliatis et al., 2021). The terms $F_{\text{P},i}^T$ and $F_i^T$ are the pressure hydrodynamic- and the wave exciting-forces, respectively, acting on the floater. Also, ${\Xi }_{j0}$ is the structure’s motion component in the $j$ th direction with respect to the global coordinate system.

It should be noted that the structure’s motion components can be expressed through the translational and angular motions, ${\xi }_{j0}^p,$ of each body $p, p=1,\dots ,4$ of the array, which in turn are coupled with the inner air pressure head, $p_{in0}^p$, of the $p, p=\mathrm{1,2,3}$ OWC device of the array. The translational and angular motions, as well as the inner air pressure head, are also linked with the volume flux equation, produced by the oscillating internal water surface in each OWC. Hence the solution of two differential equations (i.e., motion- and volume flux-equation) is required. For more details on the methodology followed, we refer the reader to Konispoliatis et al. (2016).

3.3 Coupled Servo-Hydro-Aero-Elasto-Dynamic Formulation in the Time Domain.

Nonlinear time domain simulations of the coupled floating wind turbine are performed using the in-house servo-hydro-aero-elastic solver hGAST (Riziotis and Voutsinas, 1997; Manolas, 2015; Manolas et al., 2015; Manolas et al., 2020), developed at the National Technical University of Athens (NTUA). It is an integrated software for the design and verification of wind turbines, used for performing nonlinear time domain simulations as well as eigen-value and stability analysis (Chaviaropoulos, 1999; Riziotis et al., 2004). The solver has been extensively used in numerous (national and EU-funded) research projects over the last 30 years, as well as by the industry. Its predictions in offshore applications have been verified through code-to-code comparison in the OC4 annex (Popko et al., 2014; Robertson et al., 2014). Its modular form comprises:

• the “dynamic module” that defines the dynamics of the whole system.

• the “structural module” that provides the deformed shape and the associated kinematics defined for each separate component of the structure (including the mooring lines).

• the “aerodynamic module” that provides the aerodynamic loads along the rotor blades.

• the “hydrodynamic module” that provides the wave and current loading on the support structure.

• the “control module” that provides the operational conditions for the wind turbine (blades’ pitch angle and generator torque demand), regulating the power output.

A fully coupled nonlinear solution procedure is adopted. At every discrete time step, convergence is ensured not only within each separate module but also for the entire hydro-servo-aero-elastic coupled system, taking into account the nonlinear couplings between the modules. The modular definition in hGAST accommodates various options (related to the fidelity but also to the computational cost) for the physical modeling associated with a specific module. For a detailed description of the solver, the reader is directed to (Manolas et al., 2020), whereas a brief description of the options considered in the present work is given next.

3.4 Dynamic Module

In the multibody context, a local coordinate system (Figure 3A) is assigned to each component body with respect to which local elastic displacements are defined. In hGAST, the local frame of each body is subjected to rigid body and elastic motions communicated by preceding bodies as kinematic conditions imposed at their connection points. Rigid body motions can be either prescribed or controlled, while elastic motions consist of the total deflection of the previous components “transferred” to the current component. For example, the blades are subjected to elastic translational and rotational motions of the drive train and the tower (Figure 3B) as well as to rigid body motions such as the pitch motion and teetering motion of two-bladed rotors (directly imposed on the blades), azimuthal rotation, yaw rotation (indirectly imposed on the blades through the drive train and the nacelle), foundation motions or motions of the supporting structure in case of floating wind turbines (indirectly imposed to the blades through the tower) (Figure 3C). In addition to the kinematic conditions imposed at the connection points, loading conditions must also be satisfied. In particular, at each connection point, one of the connected bodies contributes the displacements and rotations to all the others, which in turn contribute their internal (reaction) loads.

FIGURE 3

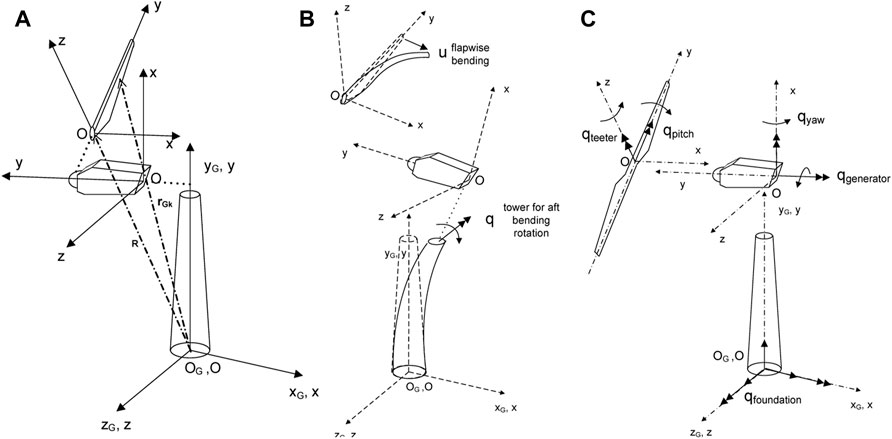
FIGURE 3. (A) Wind turbine inertial frame and local component local frames, (B) multibody kinematics realization, examples of elastic q DOFs, (C) multibody kinematics realization, examples of controlled or free motion q DOF.

The advantage of the above formulation in comparison to other multibody formulations applying the Lagrange multipliers approach is that the resulting dynamic equations of motion can be easily linearized analytically and, thereafter, linear eigenvalue stability analysis can be performed with respect to a highly deflected steady or periodic state.

3.5 Structural Module

The structural modeling is based on either linear Timoshenko beam theory or truss elements (1D structural elements only transferring axial loads) and FEM approximation. All flexible components of the wind turbine (blades, drive train, tower, members of the jacket support structure) are modeled by one or several beams with appropriate connections. Bending in two directions, including shear, tension, and torsion, is included as degrees of freedom.

The mooring lines (catenary or TLP) are modeled using the so called “dynamic modeling” with truss elements following a nonlinear, co-rotational formulation. Inertial, gravitational, and hydrodynamic loads through Morison’s equation are taken into account. The interaction with the seabed is modelled by a series of springs that are activated once the mooring line approaches the seabed surface. In addition, this formulation is able to capture non-linear geometric coupling effects, as e.g., between surge-heave and sway-heave motions that appear in TLPs.

The multibody formulation is also extended to the component level in hGAST. Highly flexible components, such as the blades, can be divided into a number of interconnected “sub-bodies,” each considered as an assembly of linear beam elements. Large deflections and rotations gradually build up and nonlinear dynamics are introduced by imposing on each sub-body the deflections and rotations of the preceding sub-body as rigid body nonlinear motions. This approach allows capturing the geometrical nonlinear effects due to large deflections and rotations using linear beam theory at the element level but considering nonlinear effects at the sub-body level (Manolas et al., 2015).

The beam model has been re-formulated to account for full stiffness matrix cross-sectional input (fully populated stiffness matrix) in order to simulate structural couplings for blade load alleviation (i.e., through bend-twist structural coupling) (Bagherpour et al., 2018).

3.6 Aerodynamic Module

Rotor aerodynamics in hGAST is simulated using an elaborated Blade Element Momentum model that accounts for dynamic inflow, yaw misalignment, and unsteady aerodynamics and dynamic stall effect through the ONERA (Petot, 1989) or the Beddoes-Leishman model (Leishman and Crouse, 1989; Hansen et al., 2004).

3.7 Hydrodynamic Module

Hydrodynamic loading for bottom-based support structures is added based on Morison’s semi-empirical equation. The relative form of Morison’s equation is adopted, considering wave kinematics (velocity and acceleration) and elastic and/or rigid body velocity and acceleration. Wave kinematics for highly nonlinear waves are defined based on stream function theory, while for irregular waves they are based on provided wave spectra (i.e., Pierson-Moskowitz or Jonswap) and linear Airy theory.

Hydrodynamic loading for floating support structures is added based on linear potential theory by solving in the frequency domain the diffraction and radiation problems and thereby obtaining the hydrodynamic mass, damping, and forcing operators needed in the dynamic equations of the floater rigid body degrees of freedom (i.e., terms $A_{ij},B_{ij}$ and $F_i^T, i=1,\dots ,6$—see Section 3.1). As far as the OWC contribution is concerned, its effect can be taken into account through the provided hydrodynamic operators, $F_{\text{P},i}^T, i=1,\dots ,6$, estimated in the frequency domain (see also Section 3.1).

3.8 Control Module

The control module implements a baseline power controller that is a variable speed and variable pitch controller, based on linear PI elements. The controller ensures, on the one hand, operation at optimum c_p maximizing power production below rated wind speed by controlling the generator torque demand, and on the other hand, speed regulation above rated wind speed by controlling the blade pitch angle and, in turn, the generated electrical power.

4 Results

4.1 Frequency Domain Analysis

The coupled hydro-aero-elastic analysis in the frequency domain, described in Sections 3.1 and 3.2, is applied for the determination of the fundamental hydrodynamic properties of the hybrid platform. In the below plots, the exciting forces and moments imposed on the entire hybrid structure are presented against the wave frequency. It should be noted that since it was assumed that the wind propagates along the positive X axis (see Figure 4), the examined angles of wave impact are in the range of $\beta \in \left[-60\text{o}, 60\text{o}\right]$. Figure 5 depicts the Response Amplitude Operator (RAOs) of the exciting forces and moments, $F_i, i=\mathrm{1,2},\dots ,6$, defined as the modulus of $F_i^T, i=\mathrm{1,2},\dots ,6$ (see Eq. (9)), in terms of wave frequency $\omega \in \left[0, 3\right]$ rad/s. It can be seen that the horizontal exciting forces attain an oscillatory variation pattern regardless of the wave angle. Specifically, for $\beta =0\text{o}$, the values of $F_1$ are generally greater than those for $\beta =30\text{o}, 60\text{o}$. On the other hand, $F_2$ zeros for $\beta =0\text{o}$ and maximizes for $\beta =60\text{o}.$ In addition, the wave heading angle does not seem to affect $F_3$, since the vertical force attains comparable results for the three examined angles of wave incidence, $\beta$. Regarding the overturning exciting moments, $F_4,F_5$, they attain a reverse variation pattern since $F_4$ presents maximum values for $\beta =60\text{o}$, whereas $F_5$ maximizes for $\beta =0\text{o}.$ Finally, concerning the yaw exciting moment, $F_6$ , a tense oscillatory behavior is depicted, which is maximized for $\beta =30\text{o}$.

FIGURE 4

FIGURE 4. 3D definition sketch of the examined wind and wave heading angles.

FIGURE 5

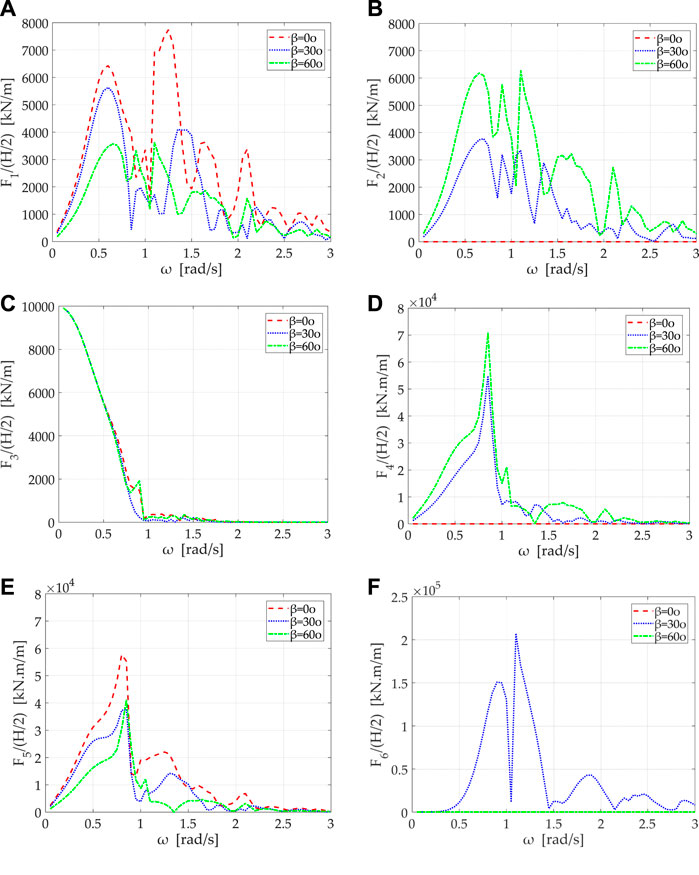
FIGURE 5. Exciting forces and moments on the hybrid structure for wave angles 0, 30, and 60 degree versus wave frequency: (A) $F_1$/(H/2), (B) $F_2$/(H/2), (C) $F_3$/(H/2), (D) $F_4$/(H/2), (E) $F_5$, (F) $F_6$/(H/2).

Figures 6, 7 depict the hydrodynamic masses and potential damping coefficients of the hybrid structure. Specifically, the coefficients $A_{11},B_{11}, A_{33},B_{33},A_{55},B_{55},A_{15},B_{15}$ are presented. The depicted results show that the hydrodynamic mass in surge, $A_{11}$, exhibits a peculiar behavior in the neighborhood of $\omega$ ∼2.15 rad/s (see Figure 6A), which corresponds to the pitch resonance of the fluid motion inside the ponds, representing a characteristic feature of bottomless cylindrical bodies (Mavrakos, 1988). A similar behavior is also $A_{55}$ and $A_{15}$ (see Figures 6C,D). Moreover, it is interesting to note that negative values of the added mass coefficients $A_{11},A_{15}$ are obtained in the neighborhood locations. Specifically, near the resonance location, the added mass changes abruptly from a positive value to a negative one in a small frequency range. As far as the added mass in heave is concerned, it attains a smooth variation pattern in the range of [10³, 8 $\times$ 10³] t.

FIGURE 6

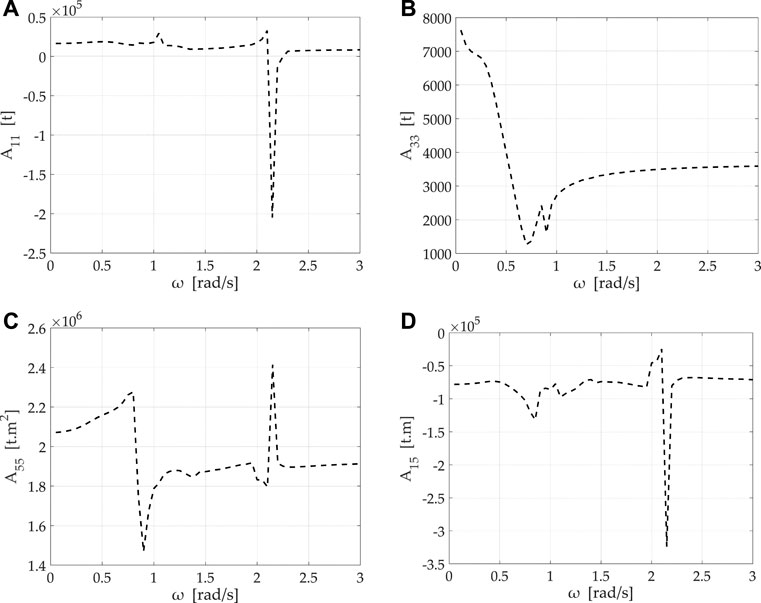
FIGURE 6. Added mass coefficients of the hybrid structure versus wave frequency: (A) $A_{11}$, (B) $A_{33}$, (C) $A_{55}$, (D) $A_{15}$.

FIGURE 7

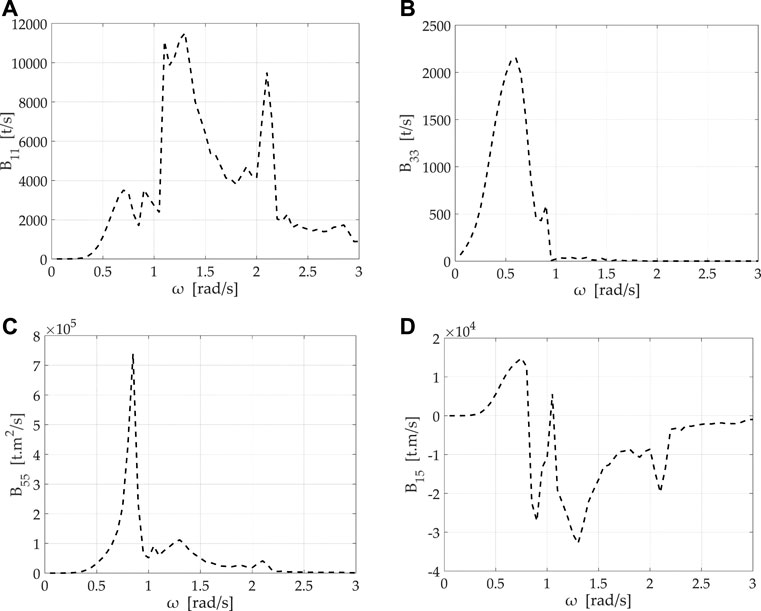
FIGURE 7. Hydrodynamic damping coefficients of the hybrid structure versus wave frequency: (A) $B_{11}$, (B) $B_{33}$, (C) $B_{55}$, (D)$B_{15}$.

Regarding the potential damping coefficients, the values of $B_{11},B_{33},B_{55}$, are always positive, as expected, although they tend to zero within a wide range of $\omega$ (see Figures 7A–C). It should be noted that at the locations where the damping coefficients vanish, the exciting components vanish as well. This can be attributed to Newman-Haskind relations between the damping coefficients and the exciting wave forces (Newman, 1962).

In the following figures the RAOs of the non-dimensional translational, ${\Xi }_{j0}/\left(\frac{H}{2}\right), j=\mathrm{1,3}$ and rotational ${\Xi }_{j0}/\left(k\frac{H}{2}\right), j=5$ motions of the hybrid structure, as being calculated by the coupled hydro-aero-elastic analysis (see Eq. 16) are plotted, in terms of the wave frequency $\omega \in \left[0, 3\right]$, for several examined angles of wave impact, and wind velocities, $U_W$, at the candidate installation locations (i.e., two in the Mediterranean Sea and one in the North Sea). More specifically, in Figure 8 the non-dimensional motions, ${\Xi }_{10}/\left(\frac{H}{2}\right), {\Xi }_{30}/\left(\frac{H}{2}\right), {\Xi }_{50}/\left(k\frac{H}{2}\right),$ of the structure are plotted for angle of wave impact $\beta \in \left[-60, 60\right]$ and $U_W=3 \text{m}/\text{s}$. Starting with the surge motions (see Figures 8A,B) it can be seen that ${\Xi }_{10}/\left(\frac{H}{2}\right)$ variations behave inversely proportionally with $\beta$, regardless the installation location. Specifically, as $\beta$ increases, the surge motions decrease. Concerning the maximization of ${\Xi }_{10}/\left(\frac{H}{2}\right)$ this is due to the mooring restoring stiffness which resonances the surge motion at $\omega \sim 0.1$ rad/s. By comparing the platform’s surge motions at the two installation locations, it can be seen that the pneumatic admittance Λ of the air turbine does not seem to affect the structure’s surge translational motions since the values of ${\Xi }_{10}/\left(\frac{H}{2}\right)$ are similar at both sites. On the other hand, the different air turbine characteristics among the two installation sites affect the structure’s heave motions (see Figures 8C,D). Specifically, at the North Sea location, ${\Xi }_{30}/\left(\frac{H}{2}\right)$ attains higher values than the corresponding ones in the Mediterranean Sea. Nevertheless, due to the selected mooring system and its high axial stiffness, the vertical displacement of the structure can be considered low. As far as the rotational motion of the structure is concerned (see Figures 8E,F, a similar variation pattern with the surge motions is depicted regarding the motion-decrease as $\beta$ increases, as well as the maximization of ${\Xi }_{50}/\left(k\frac{H}{2}\right)$. Furthermore, it can be seen that the characteristics of the air turbine cause an increase in the platform’s rotations in the North Sea compared with the ones in the Mediterranean Sea, which is more pronounced for $\omega \in (0.3, 1)$.

FIGURE 8

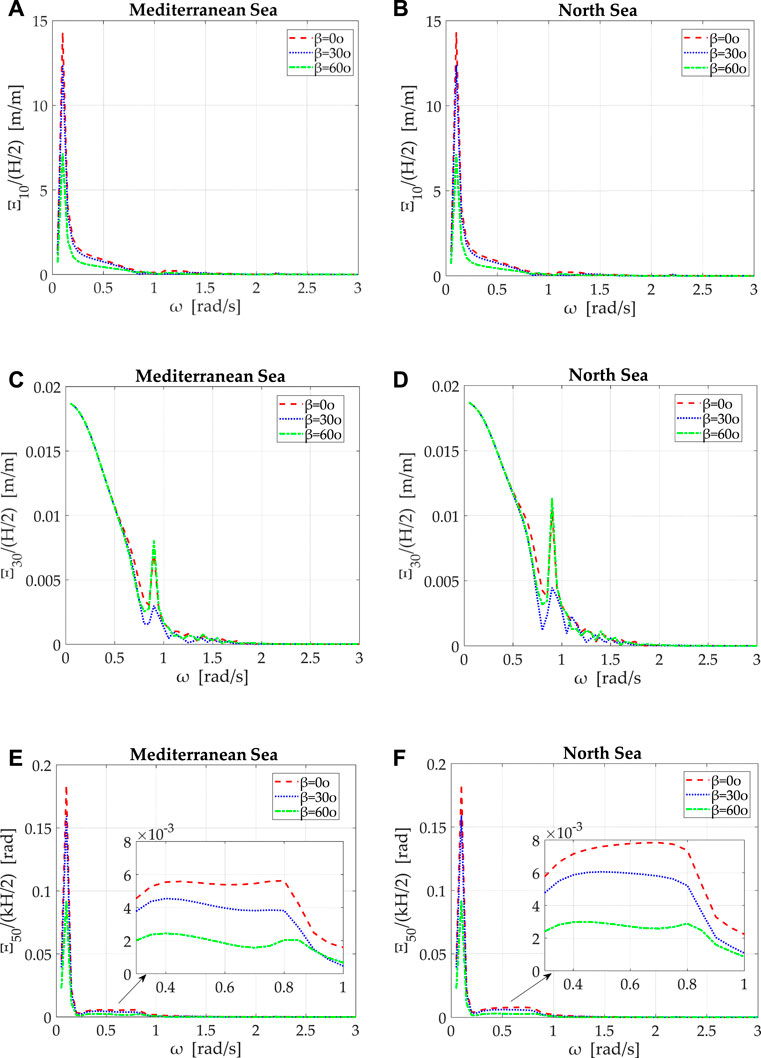
FIGURE 8. Non-dimensional translational and rotational motions of the hybrid structure at candidate installation sites, for wave angles 0, 30, 60° versus wave frequency: (A), (B) ${\Xi }_{10}/\left(\frac{H}{2}\right);$ (C), (D) ${\Xi }_{30}/\left(\frac{H}{2}\right);$ (E), (F) ${\Xi }_{50}/\left(k\frac{H}{2}\right)$. Here the wind velocity equals to $U_W=3 \text{m}/\text{s}$.

Figure 9 depicts the structure’s non-dimensional translational, ${\Xi }_{j0}/\left(\frac{H}{2}\right), j=\mathrm{1,3}$ and rotational ${\Xi }_{j0}/\left(k\frac{H}{2}\right), j=5,$ motions for several examined operating wind velocities, i.e., $U_W=3, 8, 11.4, 15,\text{and }21 \text{m}/\text{s}$, at the North Sea location. Here $\beta =30$ o. This site was indicatively selected since higher motions of the hybrid system are attained, compared to the ones in the Mediterranean Sea (see discussion of Figure 8). The results are also compared with the structure’s motions under extreme environmental conditions, i.e., $U_W=25 \text{m}/\text{s}$. It should be noted that at extreme environmental conditions, the WT and the OWCs devices are not in operation, thus the inner air pressure in each chamber equals the atmospheric pressure. Relieving of the inner air pressure can be achieved by the use of relief valves in each chamber. From the depicted plots, it can be seen that the wind velocity does not seem to affect the translational and rotational motions of the structure. Contrary, when the air pressure inside the OWCs is considered equal to the atmospheric, which corresponds to extreme environmental conditions, the motions of the structure reduce. This is more pronounced in heave motions in which the absence of air pressure oscillation in the chambers decreases the structure’s vertical displacement compared to the operational condition case.

FIGURE 9

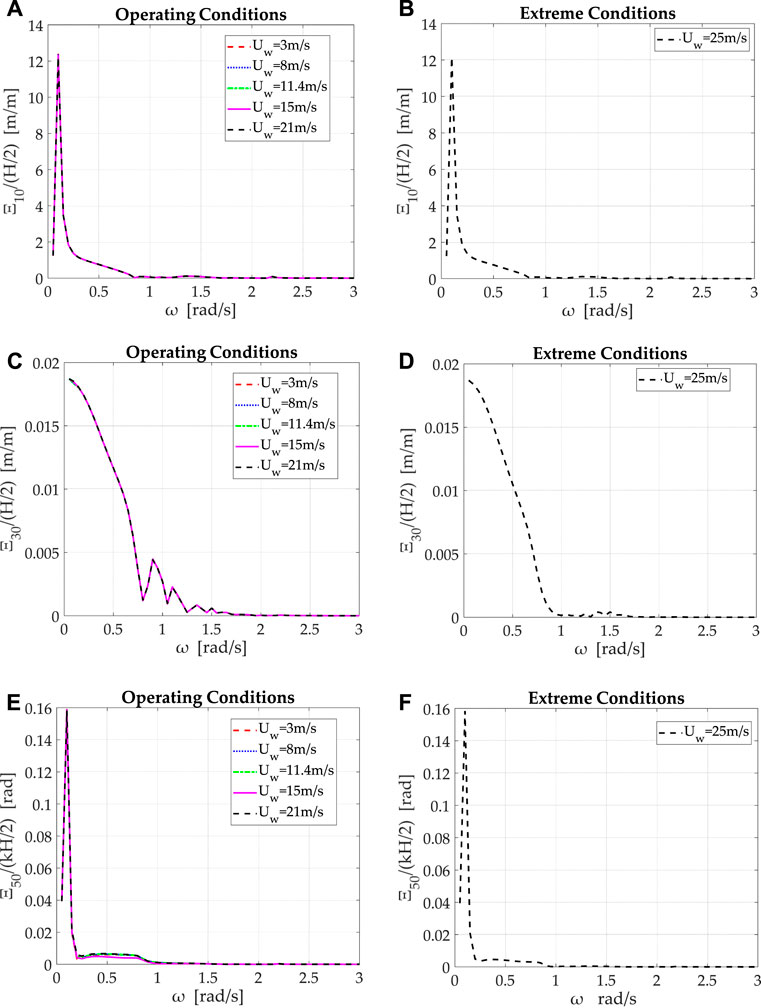
FIGURE 9. Non-dimensional translational and rotational motions of the hybrid structure at the North Sea installation location for operating and extreme environmental conditions: (A), (B) ${\Xi }_{10}/\left(\frac{H}{2}\right);$ (C), (D) ${\Xi }_{30}/\left(\frac{H}{2}\right);$ (E), (F) ${\Xi }_{50}/\left(k\frac{H}{2}\right)$. Here the wave heading angle equals to $\beta =30$ ο.

The decrease in the structure’s motions when the OWCs’ inner air pressure is considered equal to atmospheric, is expected to discharge the mooring system by the additional loads of the air pressure distribution at extreme environmental conditions. This is verified in Figure 10 where the tension forces on the tendons of the structure at the candidate installation locations are plotted for operational- and extreme-environment conditions. Concerning the operational conditions, the examined wind velocity is indicatively considered equal to $U_W=11.4 \text{m}/\text{s}$, whereas $\beta =0$. It can be seen that the dynamic tension exerted on the mooring lines seems dominated by the air pressure oscillation inside the OWCs. Specifically, the inner air pressure causes an increase in the load on the mooring tendon system. The worst installation site seems to be the North Sea location, in which the tension forces are higher than those in the Mediterranean Sea. Comparing the tension loads in the North Sea location for the extreme-environment conditions with those for the operational conditions, it can be concluded that the OWCs increase the tension forces by a mean value of 20%. Nevertheless, this increase is smaller for the Mediterranean Sea site.

FIGURE 10

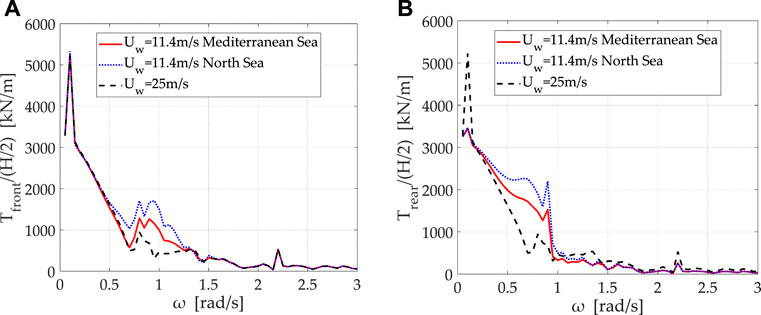
FIGURE 10. Tension forces on the front and rear tendon of the hybrid structure in the Mediterranean- and North-Sea installation locations for operating and extreme environmental conditions: (A) $T_{\text{front}}/\left(\frac{H}{2}\right);$ (B) $T_{\text{rear}}/\left(\frac{H}{2}\right)$. Here the wave heading angle equals to $\beta =0$ ο.

4.2 Time Domain Analysis

The coupled servo-hydro-aero-elasto-dynamic analysis in the time domain, described in Section 3.3, is applied to define the fatigue and the ultimate limit states (FLS, ULS) at several joint-connections (moorings–seabed, moorings–floater, tower–floater, and blades–hub) of the coupled floating system. Table 3 presents the met-ocean data used for the two locations, one in the Mediterranean Sea, L1 (with coordinates 37.30oN, 12.69oE, see Section 2), and the other in the North Sea, L2 (with coordinates 59.42oN, 3.40oE). The table provides the most probable set of wave peak period T_p and significant wave height H_s considered, which corresponds to the normal sea state (NSS) conditions (wind speeds of 5 m/s to 25 m/s) and to the extreme or severe sea state (ESS or SSS) conditions with a 50-year return period (last line of the table). Wind conditions of IEC standard (IEC 61400-1, 2005; IEC 61400-3, 2008) sub-class C have been considered.

TABLE 3

TABLE 3. Met-ocean data at the two installation locations in the Mediterranean Sea and North Sea.

In Table 4, the considered matrix of Design Load Cases (DLCs) based on the IEC standard is shown. DLC1.2 corresponds to the normal operation of the WT in normal turbulence conditions (NTM) and a normal sea state and is used for estimating the FLS. DLCs 1.3, 1.6, and 6.2 correspond to extreme conditions and are performed in order to estimate the ultimate limit state. DLCs 1.3 and 1.6 correspond to normal operation (power production) under either extreme turbulence conditions (ETM) and normal sea state, or normal turbulent conditions and a severe sea state. DLC 6.2 assumes storm conditions under wind and wave conditions with a return period of 50-years. The WT is in idling mode, the blades are pitched to a feather position at 90° and the yaw control is not functional (due to network loss). Thus, three wind misalignment angles have been considered (0°, 30°, and 60°). The OWC is only producing electrical power during the NSS conditions (DLCs 1.2 and 1.3). A 1 h realization has been performed for every case.

TABLE 4

TABLE 4. Definition of DLCs for time domain calculations.

Figure 11 shows the lifetime DELs of the coupled structure for the two locations L1 and L2, calculated assuming a lifetime period of 20 years, a reference number of cycles 10⁷ and a Wohler coefficient m equal to 10 for the blades and to four for the mooring lines and the tower. As expected, higher DELs are estimated for the location L2 in the North Sea. However, the increase in the blade moment is marginal (2% edgewise and 14% flapwise direction). On the contrary, the estimated DELs of the tower and the mooring lines are significantly higher. The DEL of the tower bending moment in the fore-aft direction increases by 50%, whereas the DEL of the mooring line tension at both positions recorded (at the seabed and the connecting point to the floater) increases by 59%.

FIGURE 11

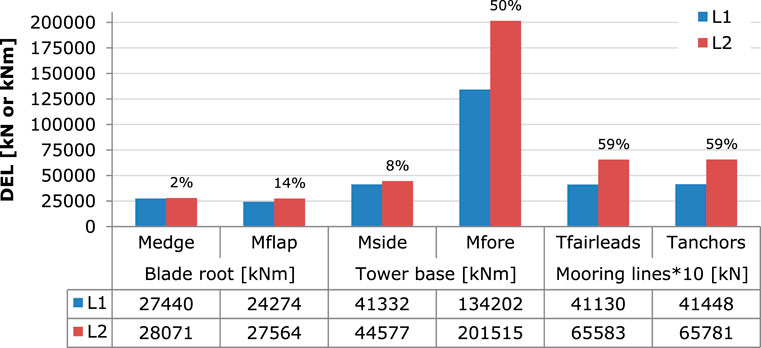
FIGURE 11. Comparison of DELs of blade root edgewise (Medge) and flapwise (Mflap) moments, tower base side-side (Mside) and fore-aft (Mfore) moments, and mooring line tension at fairleads and anchors at L1 and L2 locations based on DLC1-2. The relative percentage difference with respect to L1 is also provided above the bars.

Ultimate analysis results are discussed next. Figure 12 provides the ultimate bending moments at the root of the blade, while Figure 13 shows the ultimate values of the combined moment at the tower base and of the mooring line tension at the fairlead position. It can be seen that DLC 1-6 drives most of the analyzed signals. Further, blade moment in the edgewise direction increases by 16%, while in the flapwise direction by only 5%. The tower base combined moment significantly increases by 41%, whereas mooring lines tension by 15%. The distribution of the combined moment along the tower span at the two considered locations can be seen in Figure 14. At the stress level, the maximum developed stress at the mooring line is 326.4 MPa, which is less than the yield stress of 482.5 MPa of the steel.

FIGURE 12

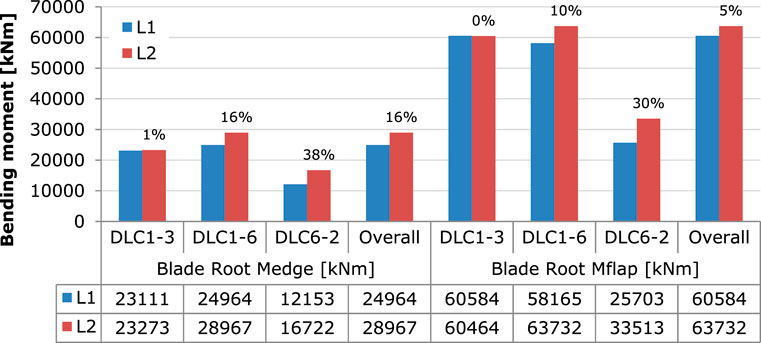
FIGURE 12. Comparison of ultimate blade root edgewise (Medge) and flapwise (Mflap) moments for the DLCs performed at L1 and L2. The relative percentage difference with respect to L1 is also provided above the bars.

FIGURE 13

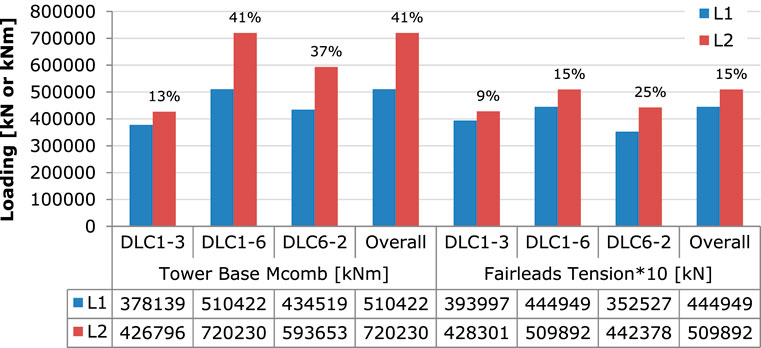
FIGURE 13. Comparison of ultimate tower base combined moment and mooring line tension at fairleads at L1 and L2 locations for the DLCs performed. The relative percentage difference with respect to L1 is also provided above the bars.

FIGURE 14

FIGURE 14. Ultimate combined moment distribution along the tower span at L1 and L2 locations.

Time series of the tension of the first (upwind) mooring line at fairleads position are presented in Figure 15 for the considered DLCs 1-2, 1-3, and 1-6 at 13 m/s, at the location L2 in the North Sea. It can be seen that the mean value of the tension is 23,800 kN, which is higher than its nominal value of 20,650 kN (pretension plus mooring line weight in water). This is attributed to the extra buoyancy applied to the floater due to the surge-heave coupling effect triggered by the thrust of the rotor. This non-linear geometric effect can be accurately accounted for by the dynamic mooring line approach adopted. The figure also demonstrates that the severe sea state conditions (DLC 1-6) drive the ultimate mooring line tension value, as mentioned above. Extreme turbulence conditions (DLC 1-3) have a minor effect on mooring line tension as the fluctuations of the corresponding time series are only slightly higher than those at normal conditions (DLC1-2).

FIGURE 15

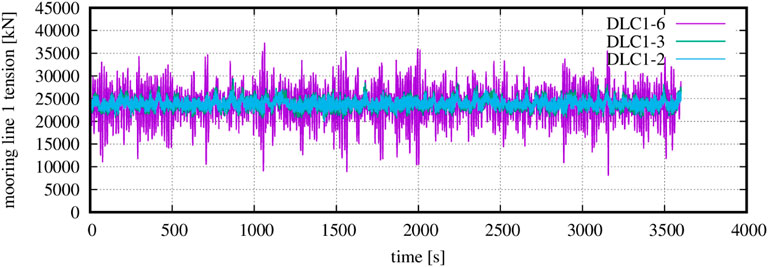
FIGURE 15. Time series of mooring line 1 (upwind) tension [kN] at fairleads position for the considered power production DLCs 1-2, 1-3, and 1-6 at 13 m/s at location L2 in the North Sea.

Finally, the effect of the OWC devices on the ultimate loads of the coupled structure, estimated through DLC 1-3, is assessed in Figure 16. Two sets of numerical simulations are considered, one with the OWC devices producing power (denoted by “with OWC” in the plot) and one considering zero pressure in the OWC chambers so that they do not produce electrical power (denoted by “w/o OWC”). The OWCs operation does not affect the WT components, as the load percentage relative differences are less than 2% for the blade and the tower signals. On the other hand, the OWC devices increase the maximum mooring line tension at fairlead position by 2% at location L1 and by 10% at location L2. Further, the presence of the OWCs reduces the ultimate minimum mooring line tension at fairlead position by 8% at location L1 and by 24% at location L2.

FIGURE 16

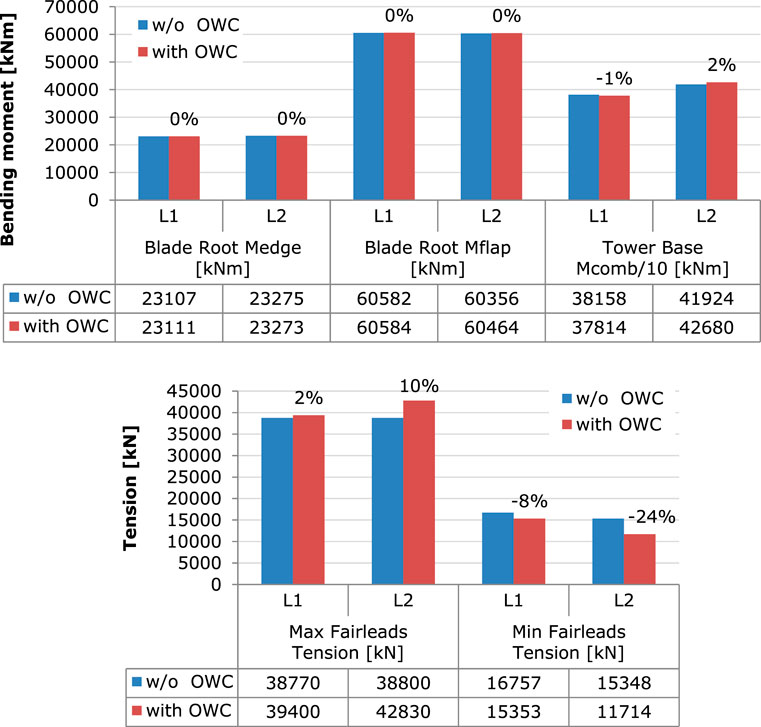
FIGURE 16. Assessment of the OWC effect on loads from DLC1.3. Ultimate blade root edgewise and flapwise moments and tower base combined moment (top) and maximum and minimum ultimate mooring line tension at fairleads (bottom) at L1 and L2, with and without (w/o) the OWC.

5 Conclusion

In the present paper, the coupled dynamic response of an offshore multi-purpose floating structure suitable for wind and wave energy exploitation is examined. The hybrid system consists of a triangular platform supported by three OWC devices at its corners and one cylindrical body in the center supporting the WT. A summary of the main conclusions from the presented analysis in the frequency and time domain is the following:

• The RAOs of the hybrid system have been concluded using a coupled hydro-aero-dynamic formulation in the frequency domain, taking into account the aerodynamic, gravitational, and inertial-gyroscopic linearized loading contributed by the WT.

• Compared to the reverse proportional effect of the incoming wave angle on the structure’s translational and rotational motions, the wind velocity does not seem to affect the responses of the system. On the other hand, the air turbine characteristics dominate the structure’s motions, affecting the heave motions more profoundly.

• The estimated first-order tension forces on the TLP tendons highlight the effect of the inner air pressure oscillation in the OWCs on the increase of the tendon loads. Therefore, the possible installation of relief valves inside each OWC has been foreseen, relieving the inner air pressure in extreme sea conditions.

• From the performed analysis in the time domain, it was found that higher tower (50%) and tendon (59%) DELs are estimated in the North Sea location. The increase in blade moments DEL is slight (2% in edgewise and 14% in flapwise direction).

• Further, DLC1.6 was found to drive the ultimate loading of most of the analyzed signals. The tower base combined moment significantly increased by 41% and the mooring line tension by 15% in the North Sea site, while the blade root flapwise moment decreased by only 5%.

• Finally, the presence of the OWCs under normal sea state conditions increases in absolute value the ultimate minimum and maximum mooring line tension at fairleads position by 24% and 8% respectively, while tower and blade loads remain almost unaffected.

This investigation can be further extended in order to examine the effect of other mooring systems (i.e., taut, catenary mooring lines) on the performance and the dynamic response of the hybrid structure under the action of both regular and irregular wave trains.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.

Author Contributions

DK: conceptualization, investigation, data curation, methodology, writing—original draft. DM: conceptualization, investigation, data curation, methodology, writing—original draft. SV: conceptualization, investigation, writing—review and editing. SM: conceptualization, investigation, supervision, funding acquisition, writing—review and editing.

Funding

This research has been partially financed by the Greek General Secretariat for Research and Innovation, Program Reward 2019, Title: Marine structures, for the exploitation of renewable energy sources and dissemination of results.

Conflict of Interest

Author DM was employed by iWind Renewables Private Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.920151/full#supplementary-material

References

Aubault, A., Alves, M., Sarmento, A., Roddier, D., and Peiffer, A. (2011). “Modeling of an Oscillating Water Column on the Floating Foundation WINDFLOAT,” in 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19-24 June. doi:10.1115/OMAE2011-49014

CrossRef Full Text | Google Scholar

Bachynski, E., and Moan, T. (2013). “Point Absorber Design for a Combined Wind and Wave Energy Converter on a Tension-Leg Support Structure,” in 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9-14 June. doi:10.1115/omae2013-10429

CrossRef Full Text | Google Scholar

Bagherpour, T., Li, X. M., Manolas, D. I., and Riziotis, V. A. (2018). Modeling of Material Bend-Twist Coupling on Wind Turbine Blades. Compos. Struct. 193, 237–246. doi:10.1016/j.compstruct.2018.03.071

CrossRef Full Text | Google Scholar

Bak, C., Zahle, F., Bitsche, R., Kim, T., Yde, A., Henriksen, L. C., et al. (2013). Description of the DTU 10MW Reference Wind Turbine. Wind Energy Report-I-0092. Denmark: DTU.

Google Scholar

Chaviaropoulos, P. K. (1999). Flap/lead-lag Aeroelastic Stability of Wind Turbine Blade Sections. Wind Energy 2, 99–112. doi:10.1002/(sici)1099-1824(199904/06)2:2<99::aid-we21>3.0.co;2-u

CrossRef Full Text | Google Scholar

Cong, P., Teng, B., Bai, W., Ning, D., and Liu, Y. (2021). Wave Power Absorption by an Oscillating Water Column (OWC) Device of Annular Cross-Section in a Combined Wind-Wave Energy System. Appl. Ocean Res. 107, 102499. doi:10.1016/j.apor.2020.102499

CrossRef Full Text | Google Scholar

DualSub (2019). Offshore Wind in Deep Water. Available at: https://www.marinepowersystems.co.uk/dualsub/(Accessed February 8th, 2022).

Google Scholar

Energy (2021). Offshore Wind Market Report: 2021 Edition. Available at: https://www.energy.gov/sites/default/files/2021-08/Offshore%20Wind%20Market%20Report%202021%20Edition_Final.pdf (Accessed February 8th, 2022).

Google Scholar

Falnes, J. (2002). Ocean Waves and Oscillating Systems. Cambridge: Cambridge University Press.

Google Scholar

Floating Power Plant (2021). Join Renewable Energy Pioneer Fpp to Impact Climate Change. Available at: https://www.floatingpowerplant.com/(Accessed February 8th, 2022).

Google Scholar

Gao, Z., Moan, T., Wan, L., and Michailides, C. (2016). Comparative Numerical and Experimental Study of Two Combined Wind and Wave Energy Concepts. J. Ocean Eng. Sci. 1, 36–51. doi:10.1016/j.joes.2015.12.006

CrossRef Full Text | Google Scholar

Hansen, M. H., Gaunaa, M., and Madsen, H. A. (2004). A Beddoes-Leishman Type Dynamic Stall Model in State-Space and Indicial Formulation. Denmark: Forskningscenter Risoe. Risoe Report, Risoe-R-1354(EN).

Google Scholar

IEC 61400-1 (2005). Wind Turbines-Part 1: Design Requirements. Switzerland: International Electrotechnical Commission.

Google Scholar

IEC 61400-3 (2008). Wind Turbines-Part 3: Design Requirements for Offshore Wind Turbines. Switzerland: International Electrotechnical Commission.

Google Scholar

IRENA (2020). Innovation Outlook: Ocean Technologies. Abu Dhabi: International Renewable Energy Agency.

Google Scholar

Karimirad, M., and Koushan, K. (2016). “WindWEC: Combining Wind and Wave Energy Inspired by Hywind and Wavestar,” in 5th International Conference on Renewable Energy Research and Application, Birmingham, UK, 20-23 November.

CrossRef Full Text | Google Scholar

Karimirad, M. (2014). Offshore Energy Structures. Switzerland: Springer International Publishing.

Google Scholar

Konispoliatis, D. N., and Mavrakos, S. A. (2016). Hydrodynamic Analysis of an Array of Interacting Free-Floating Oscillating Water Column (OWC’s) Devices. Ocean. Eng. 111, 179–197. doi:10.1016/j.oceaneng.2015.10.034

CrossRef Full Text | Google Scholar

Konispoliatis, D. N., Mazarakos, T. P., and Mavrakos, S. A. (2016). Hydrodynamic Analysis of Three-Unit Arrays of Floating Annular Oscillating-Water-Column Wave Energy Converters. Appl. Ocean Res. 61, 42–64. doi:10.1016/j.apor.2016.10.003

CrossRef Full Text | Google Scholar

Konispoliatis, D., Mazarakos, T., Katsidoniotaki, E., Vamiadakis, A., Soukissian, T., and Mavrakos, S. (2019). “Efficiency of an Array of OWC Devices Equipped with Air Turbines with Pitch Control,” in 13th European Wave and Tidal Energy Conference, Napoli, Italy, 1–6 September.

Google Scholar

Konispoliatis, D. N., Katsaounis, G. M., Manolas, D. I., Soukissian, T. H., Polyzos, S., Mazarakos, T. P., et al. (2021). REFOS: A Renewable Energy Multi-Purpose Floating Offshore System. Energies 14, 3126. doi:10.3390/en14113126

CrossRef Full Text | Google Scholar

Leishman, J., and Crouse, G. L. (1989). “State-space Model for Unsteady Airfoil Behavior and Dynamic Stall,” in Proceedings of the 30th Structures, Structural Dynamics and Materials Conference, Mobile, AL, USA, 3-5 April. doi:10.2514/6.1989-1319

CrossRef Full Text | Google Scholar

Manolas, D. I., Riziotis, V. A., and Voutsinas, S. G. (2015). Assessing the Importance of Geometric Nonlinear Effects in the Prediction of Wind Turbine Blade Loads. Comput. Nonlinear Dyn. 10, 041008. doi:10.1115/1.4027684

CrossRef Full Text | Google Scholar

Manolas, D. I., Riziotis, V. A., Papadakis, G. P., and Voutsinas, S. G. (2020). Hydro-servo-aero-elastic Analysis of Floating Offshore Wind Turbines. Fluids 5, 200. doi:10.3390/fluids5040200

CrossRef Full Text | Google Scholar

Manolas, D. (2015). Hydro-aero-elastic Analysis of Offshore Wind Turbines. Athens, Greece: NTUA. PhD Thesis.

Google Scholar

Mavrakos, S. Α., and Koumoutsakos, P. (1987). Hydrodynamic Interaction Among Vertical Axisymmetric Bodies Restrained in Waves. Appl. Ocean Res. 9 (3), 128–140. doi:10.1016/0141-1187(87)90017-4

CrossRef Full Text | Google Scholar

Mavrakos, S. A. (1988). Hydrodynamic Coefficients for a Thick-Walled Bottomless Cylindrical Body Floating in Water of Finite Depth. Ocean. Eng. 15 (3), 213–229. doi:10.1016/0029-8018(88)90040-6

CrossRef Full Text | Google Scholar

Mavrakos, S. A. (1991). Hydrodynamic Coefficients for Groups of Interacting Vertical Axisymmetric Bodies. Ocean. Eng. 18 (5), 485–515. doi:10.1016/0029-8018(91)90027-n

CrossRef Full Text | Google Scholar

Mazarakos, T., Konispoliatis, D., Manolas, D., Voutsinas, S., and Mavrakos, S. (2015). “Modelling of an Offshore Multi-Purpose Floating Structure Supporting a Wind Turbine Including Second-Order Wave Loads,” in 11th European Wave and Tidal Energy Conference, Nantes, France, 7 – 10 September.

Google Scholar

Mazarakos, T., Konispoliatis, D., and Mavrakos, S. (2018). “Loads on the Brace System of an Offshore Floating Structure,” in 13th International Marine Design Conference, Helsinki, Finland, 10 – 14 June.

Google Scholar

Mazarakos, T., Konispoliatis, D., Katsaounis, G., Polyzos, S., Manolas, D., Voutsinas, S., et al. (2019a). Numerical and Experimental Studies of a Multi-Purpose Floating TLP Structure for Combined Wind and Wave Energy Exploitation. Medit. Mar. Sci. 20 (4), 745–763. doi:10.12681/mms.19366

CrossRef Full Text | Google Scholar

Mazarakos, T., Konispoliatis, D., Soukissian, T., and Mavrakos, S. (2019b). “Significant Motions of a Multi-Purpose Floating Offshore Structure Due to Environmental Conditions,” in 13th European Wave and Tidal Energy Conference Series (EWTEC), Napoli, Italy, 1 – 6 September.

Google Scholar

Michailides, C., Gao, Z., and Moan, T. (2016a). Experimental Study of the Functionality of a Semisubmersible Wind Turbine Combined with Flap-type Wave Energy Converters. Renew. Energy 93, 675–690. doi:10.1016/j.renene.2016.03.024

CrossRef Full Text | Google Scholar

Michailides, C., Gao, Z., and Moan, T. (2016b). Experimental and Numerical Study of the Response of the Offshore Combined Wind/wave Energy Concept SFC in Extreme Environmental Conditions. Mar. Struct. 50, 35–54. doi:10.1016/j.marstruc.2016.06.005

CrossRef Full Text | Google Scholar

Muliawan, M. J., Karimirad, M., and Moan, T. (2013a). Dynamic Response and Power Performance of a Combined Spar-type Floating Wind Turbine and Coaxial Floating Wave Energy Converter. Renew. Energy 50, 47–57. doi:10.1016/j.renene.2012.05.025

CrossRef Full Text | Google Scholar

Muliawan, M. J., Karimirad, M., Gao, Z., and Moan, T. (2013b). Extreme Responses of a Combined Spar-type Floating Wind Turbine and Floating Wave Energy Converter (STC) System with Survival Modes. Ocean. Eng. 65, 71–82. doi:10.1016/j.oceaneng.2013.03.002

CrossRef Full Text | Google Scholar

Newman, J. N. (1962). The Exciting Forces on Fixed Bodies in Waves. J. Ship Res. 6, 10–17. doi:10.5957/jsr.1962.6.4.10

CrossRef Full Text | Google Scholar

Ocean Energy Europe (2020). 2030 Ocean Energy Vision. Industry Analysis of Future Deployments, Costs and Supply Chains. Available at: https://www.oceanenergy-europe.eu/wp-content/uploads/2020/10/OEE_2030_Ocean_Energy_Vision.pdf (Accessed February 8th, 2022).

Google Scholar

Ocean Energy Ltd (2020). OceanEnergy Flagship Products. Available at: https://oceanenergy.ie/(Accessed February 8th, 2022).

Google Scholar

Pelagic Power AS (2010). Mobilising the Total Offshore Renewable Energy Resource. Available at: https://www.pelagicpower.no (Accessed February 8th, 2022).

Google Scholar

Perez-Collazo, C., Jakobsen, M. M., Buckland, H., and Fernandez-Chozas, J. (2013). “Synergies for a Wave-Wind Energy Concept,” in European Offshore Wind Energy Conference, Frankfurt, Germany.

Google Scholar

Perez-Collazo, C., Greaves, D., and Iglesias, G. (2018). A Novel Hybrid Wind-Wave Energy Converter for Jacket-Frame Substructures. Energies 11 (3), 637. doi:10.3390/en11030637

CrossRef Full Text | Google Scholar

Perez-Collazo, C., Pemberton, R., Greaves, D., and Iglesias, G. (2019). Monopile-mounted Wave Energy Converter for a Hybrid Wind-Wave System. Energy Convers. Manag. 199, 111971. doi:10.1016/j.enconman.2019.111971

CrossRef Full Text | Google Scholar

Petot, D. (1989). Differential Equation Modelling of Dynamic Stall. Recherché Aerosp. 5, 59–72.

Google Scholar

Popko, W., Vorpahl, F., Zuga, A., Kohlmeier, M., Jonkman, J., Robertson, A., et al. (2014). Offshore Code Comparison Collaboration Continuation (OC4), Phase I—Results of Coupled Simulations of an Offshore Wind Turbine with Jacket Support Structure. J. Ocean Wind Energy 1 (1), 1–11.

Google Scholar

REWEC3 (2019). Wave Energy. Available at: https://www.wavenergy.it/portfolio/(Accessed February 8th, 2022).

Google Scholar

Riziotis, V. A., and Voutsinas, S. G. (1997). “GAST: A General Aerodynamic and Structural Prediction Tool for Wind Turbines,” in Proceedings of the EWEC Conference, Dublin Castle, Ireland, 6-9 October 1997, 448–452.

Google Scholar

Riziotis, V. A., Voutsinas, S. G., Politis, E. S., and Chaviaropoulos, P. K. (2004). Aeroelastic Stability of Wind Turbines: the Problem, the Methods and the Issues. Wind Energy 7, 373–392. doi:10.1002/we.133

CrossRef Full Text | Google Scholar

Robertson, A., Jonkman, J., Vorpahl, F., Popko, W., Qvist, J., Frøyd, L., et al. (2014). “Offshore Code Comparison Collaboration Continuation within IEA Wind Task 30: Phase II Results Regarding a Floating Semisubmersible Wind System,” in 33rd International Conference on Ocean, Offshore and Arctic Engineering (OMAE), San Francisco, California, USA, 8-13 June. doi:10.1115/omae2014-24040

CrossRef Full Text | Google Scholar

Sarmiento, J., Iturrioz, A., Ayllón, V., Guanche, R., and Losada, I. J. (2019). Experimental Modelling of a Multi-Use Floating Platform for Wave and Wind Energy Harvesting. Ocean Eng. 173, 761–773.

CrossRef Full Text | Google Scholar

Veigas, M., and Iglesias, G. (2015). A Hybrid Wave-Wind Offshore Farm for an Island. Int. J. Green Energy 12 (6), 570–576. doi:10.1080/15435075.2013.871724

CrossRef Full Text | Google Scholar

Voith Hydro (2009). Voith Wave Power. Available at: https://voith.com/corp-en/index.html (Accessed February 8th, 2022).

Google Scholar

Wang, Y., Zhang, L., Michailides, C., Wan, L., and Shi, W. (2020). Hydrodynamic Response of a Combined Wind-Wave Marine Energy Structure. J. Mar. Sci. Eng. 8 (4), 253. doi:10.3390/jmse8040253

CrossRef Full Text | Google Scholar

Wind Europe (2020). Wind Energy in Europe 2020 Statistics and the Outlook for 2021–2025. Available at: https://windeurope.org/intelligence-platform/product/wind-energy-in-europe-in-2020-trends-and-statistics/(Accessed February 8th, 2022).

Google Scholar

Wind Europe (2021). Offshore Wind Energy: 2021 Mid-year Statistics. Available at: https://windeurope.org/intelligence-platform/product/offshore-wind-energy-2021-mid-year-statistics/(Accessed February 8th, 2022).

Google Scholar

Zhou, Y., Ning, D., Shi, W., Johanning, L., and Liang, D. (2020). Hydrodynamic Investigation on an OWC Wave Energy Converter Integrated into an Offshore Wind Turbine Monopile. Coast. Eng. 162, 103731. doi:10.1016/j.coastaleng.2020.103731

CrossRef Full Text | Google Scholar