Auxiliary Service Market Model Considering the Participation of Pumped-Storage Power Stations in Peak Shaving

In the context of insufficient system operation flexibility and increasing peaking pressure caused by the large-scale integration of renewable energy into the grid, a market model for peaking auxiliary services involving pumped storage power stations is proposed in this study. First, taking the minimum peak shaving cost as the optimization goal, the peak shaving value of the participating peak shaving units is quantified, and the mathematical model of the peak shaving auxiliary service market is established. Then, considering that the pumped-storage power station has both source-load characteristics, the peak-shaving value of the pumped-storage power station is deeply excavated to share the peak-shaving pressure of thermal power units, and a compensation mechanism for peak ancillary service fees is established. Finally, the 11-machine, 14-node system topology is proposed to simulate the peak-shaving auxiliary service market model proposed in this study, and the effectiveness of the proposed method is verified.

Introduction

In recent years, the installed capacity of renewable energy in China has been increasing. By the end of 2021, China’s installed renewable energy capacity reached 3.584 × 108 kW, signifying a year-on-year increase of 23.4% (Lyu et al., 2021). As the proportion of renewable energy connected to the grid continues to increase, the demand for peak shaving capacity of the power grid during the load trough period increases accordingly (Bie et al., 2017; Qi et al., 2019; Li et al., 2019). At the same time, the output of new energy generating units is restricted by primary energy, and they do not have peak shaving capability. The cost of starting and stopping thermal power generating units is high, and they operate in uneconomical areas during deep peak shaving, with insufficient flexibility and poor economy (Shi et al., 2018; Chen et al., 2022; Wang et al., 2020a; Wang et al., 2020b). Pumped-storage power plants have good regulation characteristics and low regulation costs and hence are suitable as the main peak-shaving power sources (Zou et al., 2015; Guo et al., 2018; Wang C. et al., 2020). Therefore, the study of the sharing mechanism of peak shaving auxiliary service cost in the participation of pumped storage power stations is beneficial to improve the flexibility of system operation and the enthusiasm of power generation enterprises to participate in peak shaving.

At present, a large number of research studies have been carried out on the problem of the allocation of peak shaving auxiliary services at home and abroad. Huang, 2020 considered the energy loss and equipment loss factors of thermal power generating units, establishes the peak shaving impact index, and realizes the reasonable allocation of peak shaving costs for thermal power generating units; Ma et al. (2021) studied the allocation and correction mechanism of inter-provincial peak shaving resources to provide theoretical support for cross-provincial scheduling of peak shaving resources; Jian et al. (2018) established an improved peak-shaving auxiliary service fee compensation mechanism model based on Kaldor, which improves the wind power absorption capacity and overall economy of the system; Y. Fu et al. (2019) used the K-means clustering algorithm to classify the peak shaving capacity of units and solved the problem of “dimension disaster” in the calculation process when a large number of units participate in peak shaving; Wang et al. (2019) allocated the compensation fee to the user side in the form of additional electricity charges according to the demand for auxiliary services for peak shaving, which effectively improves the equity of fee allocation.

Most of the abovementioned literatures ensure the basic balance of power supply and demand in the system through the market cost allocation mechanism of the peak-shaving auxiliary services participated by thermal power generating units and users and reduce the number of transactions in the real-time balanced power market. However, the grid connection of large-scale photovoltaic and wind power in the system is not considered, and there is lack of pumped storage power stations to participate in peak regulation. In the case of large-scale, grid-connected renewable energy, the anti–peak shaving characteristics of wind power and photovoltaics lead to an increase in the peak-to-valley difference between loads and an increase in the demand for the peak shaving of the power grid. Moreover, the output of wind power and photovoltaic power generation depends on primary energy and cannot participate in peak shaving. The pumped-storage power station has both source and load characteristics, that is, through the reasonable switching between the pumping mode and the power generation mode, the thermal power generating unit can run in a more reasonable output range. Therefore, it is necessary to introduce pumped storage power stations to participate in the auxiliary service market in order to reduce the cost of system peak shaving and increase the enthusiasm of peak shaving power plants to participate in peak shaving. This study first considers the operating state of the units participating in peak shaving, establishes the minimum objective function of the system peak shaving cost, quantifies the peak shaving value of units participating in peak shaving in thermal power plants and pumped storage power stations, studies the peak shaving value of units participating in peak shaving, and establishes a mathematical model for the peak shaving auxiliary service market. Second, considering the good peak-shaving performance of the pumped-storage power station due to its source-load characteristics, it can relieve the pressure of lifting and lowering loads of thermal power plants for multiple periods of time. Therefore, the pumped storage power station is required to participate in peak shaving and bear the baseload to develop its peak shaving performance. Then, according to the idea of a cooperative game in game theory, the Shapley value method is used to allocate the auxiliary service fee for peak shaving and establish a compensation mechanism for the auxiliary service fee for peak shaving. Finally, the validity of the ancillary service market model proposed in this study is verified by an example.

Peak Shaving Auxiliary Service Market Model

The large-scale integration of wind power into the grid has a great impact on the power system, and it is necessary to rely on auxiliary services to ensure stable operation of the system. In general, the demand for ancillary services is divided into peak-shaving ancillary services, frequency-modulating ancillary services, and spinning reserve ancillary services (Tian et al., 2019). The peak-shaving auxiliary service market guides the participating peak shaving units to make reasonable output adjustments through changes in peak shaving indicators and compensation fees to ensure stable operation of the power grid.

The operating period of the system was set as $T$ and the number of periods is an integer between 1 and 24. The set of thermal power generating units is $I$, where $I=i_1,i_2,\cdots ,i_n$; the set of generating units of pumped storage power stations is $H$, where $H=h_1,h_2,\cdots ,h_n$.

Objective Function

Taking the minimum system peak shaving cost as the optimization goal, the objective function is established as follows:

$\mathit{min}F=C_{\mathrm{PS}}+C_I,(1)$

$C_{\mathrm{PS}}=C_{\mathrm{PS}}^{\mathrm{on}}+C_{\mathrm{PS}}^{\mathrm{off}},(2)$

$C_{\mathrm{PS}}^{\mathrm{on}}={\displaystyle \sum }_{t=1}^{24}{\displaystyle \sum }_{h=1}^H\left[\begin{array}{c}{m}_{h,t}^{\mathrm{ge}}(1-m_{h,t-1}^{\mathrm{ge}})+\\ m_{h,t}^{\mathrm{pw}}(1-m_{h,t-1}^{\mathrm{pw}})\end{array}\right]C_{\mathrm{on}}^H,(3)$

$C_{\mathrm{PS}}^{\mathrm{off}}={\displaystyle \sum }_{t=1}^{24}{\displaystyle \sum }_{h=1}^H\left[\begin{array}{c}(1-m_{h,t}^{\mathrm{ge}})(m_{h,t-1}^{\mathrm{ge}}-m_{h,t}^{\mathrm{ge}})+\\ (1-m_{h,t}^{\mathrm{pw}})(m_{h,t-1}^{\mathrm{pw}}-m_{h,t}^{\mathrm{pw}})\end{array}\right]C_{\mathrm{off}}^H,(4)$

$C_I=C_I^D+C_I^{\mathrm{on}}+C_I^{\mathrm{off}},(5)$

$C_I^D=p_{i}max\left\{0,P_i-P_{D,i,t}\right\},(6)$

$C_I^{\mathrm{on}}={\displaystyle \sum }_{t=1}^{24}{\displaystyle \sum }_{i=1}^I{m}_{i,t}(1-m_{i,t-1})C_{\mathrm{on}}^I,(7)$

$C_I^{\mathrm{off}}={\displaystyle \sum }_{t=1}^{24}{\displaystyle \sum }_{i=1}^I(1-m_{i,t})(m_{i,t-1}-m_{i,t})C_{\mathrm{on}}^I,(8)$

where $F$ is the peak shaving cost of the system; $C_{\text{PS}}$ is the peak shaving cost of the pumped storage unit; $C_{\text{I}}$ represents the peak shaving cost of the thermal power generating unit; $C_{\text{PS}}^{\text{on}}$ and $C_{\text{PS}}^{\text{off}}$ represent the start-up and stop-loss costs of the pumped storage unit, respectively; $m_{h,t}^{\text{ge}}$ and $m_{h,t}^{\text{pw}}$ are 0–1 integer variables, that is, $m_{h,t}^{\text{ge}}=1$ indicates that the pumped-storage unit $h$ is in operation at the pumping condition at time $t$ and $m_{h,t}^{\text{ge}}=0$ means that the pumped-storage unit $h$ is out of service at the pumping condition at time $t$; $m_{h,t}^{\text{pw}}=1$ means that the pumped-storage unit $h$ is in operation at the pumping condition at time $t$ and $m_{h,t}^{\text{pw}}=0$ means that the pumped-storage unit $h$ is out of operation at the pumping condition at time $t$; $C_{\text{on}}^{\text{H}}$ and $C_{\text{off}}^{\text{H}}$ are the single start-up and shutdown loss costs of a single pumped-storage unit, respectively; $C_{\text{I}}^{\text{D}}$, $C_{\text{I}}^{\text{on}}$, and $C_{\text{I}}^{\text{off}}$ are the in-depth peak shaving costs, startup peak shaving costs, and shutdown peak shaving costs, respectively; $p_i$ E is the unit price of thermal power generating unit $i$ for peak shaving in excess of deep peak shaving; $P_i$ is the peak-shaving depth threshold of thermal power generating unit $i$; $P_{D,i,t}$ is the output of thermal power generating unit $i$ at time $t$; $C_{\text{on}}^{\text{I}}$ and $C_{\text{off}}^{\text{I}}$ are the startup and shutdown costs of the thermal power generating unit, respectively; $m_{i,t}=1$ indicates that the thermal power generating unit $i$ is in a startup state at time $t$; $m_{i,t}=0$ indicates that the thermal power generating unit $i$ is in a shutdown operating state at time $t$.

The ancillary service market optimization model proposed in this study considering the participation of pumped-storage power stations in peak shaving is a mixed-integer nonlinear model, which is difficult to solve by conventional optimization algorithms. Therefore, the mixed-integer linear model is established as follows:

$C_{\mathrm{PS},t}\ge C_{\mathrm{on}}^H\left[(1-m_{h,t-1}^{\mathrm{ge}})+(1-m_{h,t-1}^{\mathrm{pw}})\right]+C_{\mathrm{off}}^H\left[(1-m_{h,t}^{\mathrm{ge}})+(1-m_{h,t}^{\mathrm{pw}})\right],(9)$

$C_{I,t}^D\ge p_i(P_i-P_{D,i,t}),(10)$

$C_{I,t}^{\mathrm{on}}\ge C_{\mathrm{on}}^I(1-m_{i,t-1}),(11)$

$C_{I,t}^{\mathrm{off}}\ge C_{\mathrm{on}}^I(1-m_{i,t}),(12)$

$C_{\mathrm{PS},t}\ge 0,C_{I,t}^D\ge 0,C_{I,t}^{\mathrm{on}}\ge 0,C_{I,t}^{\mathrm{off}}\ge 0.(13)$

Restrictions

1) Power balance constraints

${\displaystyle \sum }_{i\in I}{P}_i\left(t\right)+{\displaystyle \sum }_{h\in H}{P}_h\left(t\right)+{\displaystyle \sum }_{w\in W}{P}_w\left(t\right)={\displaystyle \sum }_{j\in J}{L}_j\left(t\right),(14)$

where $P_i$ is the output of the thermal power generating unit $i$; $P_h$ is the output of the pumped-storage generating unit; $P_w$ is the output of the wind power generating unit $w$; $L_j$ is the load demand of the node $j$.

2) Contact line constraints

$S{P}_{\text{G},\mathrm{all}}-S{P}_{\text{L},\mathrm{all}}<P_r,(15)$

where $S$ is the sensitivity matrix of generator set output and branch power flow; $P_{\text{G,all}}$ is the output vector of the whole generator set; $P_{\text{L,all}}$ is the node load vector; $P_r$ is the branch active power flow constraint vector.

3) Spinning spare constraint

${\displaystyle \sum }_{i\in I}{P}_{i,\text{max}}\left(t\right)+{\displaystyle \sum }_{h\in H}{P}_h\left(t\right)+{\displaystyle \sum }_{w\in W}{P}_w\left(t\right)\ge {\displaystyle \sum }_{j\in J}{L}_j\left(t\right)+P_{\text{up}},(16)$

${\displaystyle \sum }_{i\in I}{P}_{i,\text{min}}\left(t\right)+{\displaystyle \sum }_{h\in H}{P}_h\left(t\right)+{\displaystyle \sum }_{w\in W}{P}_w\left(t\right)\le {\displaystyle \sum }_{j\in J}{L}_j\left(t\right)+P_{\text{down}},(17)$

where $P_{i,\max }$ and $P_{i,\min }$, respectively, represent the upper limit and lower limit of the available output of the thermal power generating unit $i$; $P_{\text{up}}$ and $P_{\text{down}}$, respectively, represent the systems upward and downward reserve requirements.

4) State constraints of thermal power generating sets

$P_i\left(t\right)\in \left(P_{\mathrm{up}},P_{\mathrm{down}},P_{i,\text{max}},P_{i,\text{min}},V_i\right),(18)$

where $V_i$ is the maximum ramp rate constraint of the thermal generator set.

5) Wind turbine state constraints

$P_{w,\text{min}}\left(t\right)\le P_w\left(t\right)\le P_{w,\text{max}}\left(t\right),(19)$

where $P_{w,\max }\left(t\right)$ and $P_{w,\min }\left(t\right)$ represent the upper limit and lower limit of the available output of wind turbine $w$, respectively.

6) Pumped-storage power station constraints

$m_{h,t}^{\mathrm{ge}}{P}_{\mathrm{PS},min}^{\mathrm{ge}}\le P_{\mathrm{PS},t}^{\mathrm{ge}}\le m_{h,t}^{\mathrm{ge}}{P}_{\mathrm{PS},ax}^{\mathrm{ge}},(20)$

$m_{h,t}^{\mathrm{pw}}{P}_{\mathrm{PS},min}^{\mathrm{pw}}\le P_{\mathrm{PS},t}^{\mathrm{pw}}\le m_{h,t}^{\mathrm{pw}}{P}_{\mathrm{PS},ax}^{\mathrm{pw}},(21)$

$m_{h,t}^{\mathrm{ge}}+m_{h,t}^{\mathrm{pw}}\le 1,(22)$

where $P_{\text{PS},\max }^{\text{ge}}$ and $P_{\text{PS},\min }^{\text{ge}}$, respectively, represent the upper limit and lower limit of the power generation of the pumped storage power station; $P_{\text{PS},\max }^{\text{pw}}$ and $P_{\text{PS},\min }^{\text{pw}}$, respectively, represent the upper limit and lower limit of the pumping power of the pumped storage power station; $P_{\text{PS},t}^{\text{ge}}$ and $P_{\text{PS},t}^{\text{pw}}$ represent the output in the power generation mode and the output in the pumping mode of the pumped-storage power station at time t, respectively; the sum of $m_{h,t}^{\text{ge}}$ and $m_{h,t}^{\text{pw}}$ is less than or equal to 1, which means that the pumped storage unit can only be in a single working condition in the pumping mode and the power generation mode at the same time. When the pumped-storage power station participates in peak regulation, the adjustment capacity accounts for a small proportion of the overall installed capacity, so the upper reservoir capacity constraint of the pumped-storage power station is not considered.

Compensation Mechanism for Shapley Value Method Peak -Adjusting Assist Service Costs

According to the optimization result of the peak shaving auxiliary service market model aiming at the minimum peak shaving cost, it is determined as the compensation mechanism for the peak shaving auxiliary service fee. When the pumped storage power station does not participate in peak shaving, the conventional thermal power generating unit undertakes all peak shaving tasks, and the peak shaving cost is $F^{\prime }$. When the pumped-storage power station participates in peak shaving and bears the baseload, the peak shaving cost of the whole network is $F$ at this time from the optimization result of the peak shaving auxiliary service market model.

$F_1^{\prime }=C_I^{\text{D},\text{Θ}}+C_I^{\mathrm{on},\text{Θ}}+C_I^{\mathrm{off},\text{Θ}},(23)$

where $C_{\text{I}}^{\text{D,}\Theta }$, $C_{\text{I}}^{\text{on,}\Theta }$, and $C_{\text{I}}^{\text{off,}\Theta }$ are the in-depth peak shaving cost of thermal power generating units, the peak shaving cost of starting thermal power generating units, and the peak shaving cost of thermal power generating units shutting down, respectively. After the pumped storage power station participates in peak shaving and assumes the baseload, the peak shaving price decreases, that is, $F\ge F^{\prime }$. The energy storage characteristics and power characteristics of the pumped storage power station can be reasonably switched between the pumping mode and power generation mode so that the thermal power generating unit can operate in a more reasonable output range. During the operation of the peak shaving auxiliary service market, the peak shaving contribution of the units should be quantified and compensated so as to ensure the enthusiasm for participating in the peak shaving power plant. In order to improve the economy of peak shaving of the system, increase the enthusiasm for participating in the market of peak shaving auxiliary services, and develop the peak shaving capabilities of various power plants, it is determined that the amount of compensation for peak shaving costs obtained by participating peak shaving units is not greater than the profit $F-F^{\prime }$ of the system through this operation mode.

The cost of starting and stopping thermal power generating units is very high, and under low-output operating conditions, it will cause greater wear and tear on the unit, and the loss cost will increase. At the same time, the combustion stability of low-output units is reduced, which may result in combustion-supporting costs such as fuel injection. On the other hand, the pumped storage power station has good regulation ability and low-peak shaving cost because of its combination of source and load characteristics. In order to improve the income and enthusiasm of the power plants participating in peak regulation, this study uses the Shapley value method to allocate compensation fees to deeply explore the peak regulation value of pumped storage power plants.

The traditional peak-shaving auxiliary service market is based on the idea of statistics to allocate compensation fees (Lin et al., 2017). The allocation of compensation fees for power plants participating in the peak-shaving auxiliary service market is a cooperative game problem in game theory (Liu et al., 2018). In order to ensure the equity of the market and the enthusiasm of participating in peak shaving units, considering the synchronism of the unit’s peak shaving value and its compensation, the Shapley value method is used to allocate the compensation fee, and the compensation mechanism for the auxiliary service fee for peak shaving with the participation of multiple power plants based on the cooperative game is used (Nan et al., 2021).

It is assumed that all the units participating in peak shaving belong to the set M, and the number of units is m. The peak shaving costs of the joint peak shaving unit $S\subseteq M$ and the joint peak shaving unit $S$ are as follows:

$F\left(S\right)=F-F_p\left(S\right),(24)$

where $F$ is the grid peak shaving cost when the thermal power generating unit bears the baseload.; $F_p\left(S\right)$ is the unit in the joint peak shaving unit $S$ participating in the grid peak shaving, and the units in the joint peak shaving unit all bear the power grid peak shaving cost when the baseload is used has $PC\left(N\right)=P{C}_1$.

The revenue function of the joint peak shaving unit is as follows:

$R\left(S\right)=F\left(S\right)-{\displaystyle \sum }_{s\in S}F\left(S\right).(25)$

The peak-shaving ancillary service fee allocated based on the Shapley value method can be expressed as follows:

$P_{sha,x}\left(R\right)={\displaystyle \sum }_{s\in S}\frac{(n-\left|S\right|)!(\left|S\right|-1)!}{n!}[R\left(S\right)-R(S-\left\{s\right\})],(26)$

where $x$ is a certain peak shaving cost apportionment unit, $x=\mathrm{1,2},\cdots ,n$; $P_{sha,x}\left(R\right)$ represents the combined peak shaving unit revenue apportioned to the unit; $S$ represents the joint peak shaving unit including unit $x$; $\left|S\right|$ represents the number of units included in the joint peak shaving unit $S$; $n$ represents the number of units providing peak shaving auxiliary services; $n!$ represents the participation sequence of all participants in the peak shaving unit $N$; $S-\left\{s\right\}$ represents the removal of the participant $x$ from the joint peak shaving unit $S$; and $R\left(S\right)-R(S-\left\{s\right\})$ represents the incremental revenue created by unit $S$ for the combined peak shaving unit.

Case Analysis

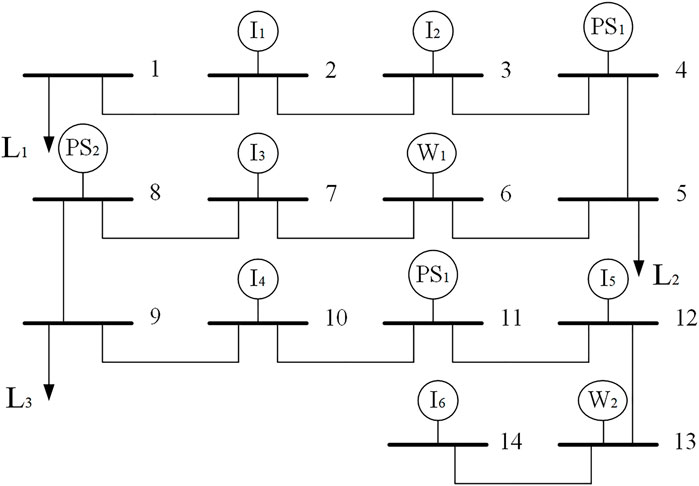
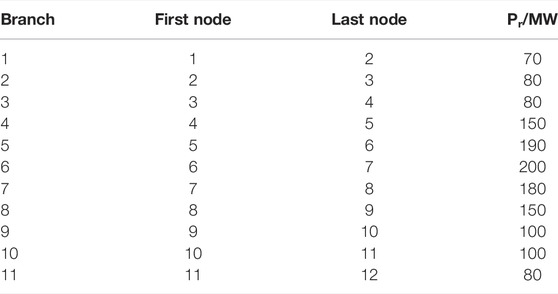
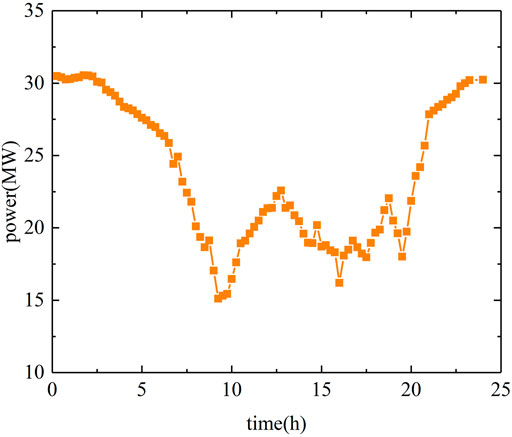
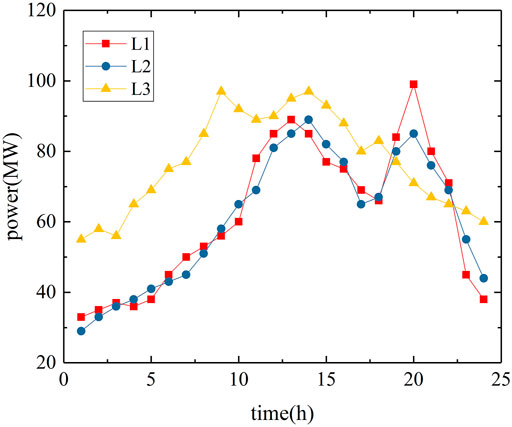
An 11-machine, 14-node system is proposed to simulate and verify the ancillary service market model proposed in this study considering the participation of pumped-storage power stations in peak shaving. The topology of the 11-machine, 14-node system is shown in Figure 1. The system has six thermal power generating units, which are located at nodes 2, 3, 7, 10, 12, and 14. The maximum force of the firepower generator is 550 mW, and the minimum output force is 100 MW. There are three pumped storage units located at nodes 4, 8, and 11. There are two wind turbines located at nodes 6 and 13. The system load is distributed in three load nodes, which are located at nodes 1, 5, and 9. The parameters of each branch of the system are shown in Table 1. A typical daily wind power generation curve is shown in Figure 2. A typical intraday load demand curve is shown in Figure 3.

FIGURE 1

FIGURE 1. Structure of 11-generator 14-node system topology.

TABLE 1

TABLE 1. 11 generator 14 node system branch parameters.

FIGURE 2

FIGURE 2. Typical daily wind power generation curve.

FIGURE 3

FIGURE 3. Typical daily load demand curve of each node.

According to the wind power output and load demand on a typical day, it can be seen that wind power has a strong anti–peak shaving characteristic. When the demand peaks in the 9h–13h and 18h–21h load curves, the wind power output is in a trough period. The peak-shaving demand was caused by the power shortage in the system. In the case of the 22–4 h load curve demand trough, wind power generation is in the peak period, causing trough peak regulation demand.

The simulation environment uses the mixed-integer linear programming operator programming of the GAMS commercial optimization software to solve the auxiliary service market model proposed in this study considering the participation of pumped storage power stations in peak regulation, and the system optimization process can be solved within 23.3 s. The model and method proposed in this study are time-effective and suitable for scheduling intraday power generation and real-time scheduling.

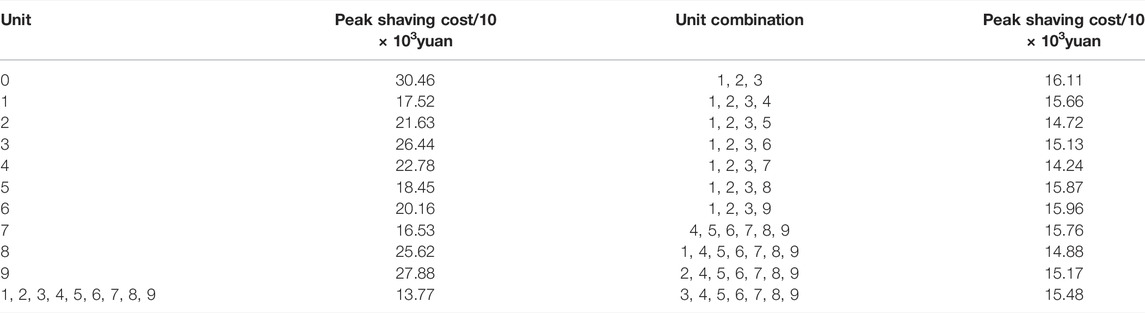
From the perspective of game theory, all the peak shaving units in the system are nine players. According to the income difference obtained from the optimization results, the cooperative game method is applied to apportion the peak-shaving costs of nine units. The set of all players can be expressed as N = {1, 2, 3, 4, 5, 6, 7, 8, and 9}, and typical 21 non-empty subsets in the set are selected to form a joint peak shaving unit. The method proposed in this study is used to calculate the peak shaving cost of each unit in the combined peak shaving unit. The peak shaving cost of each unit in the joint peak shaving unit is shown in Table 2. It can be seen that when only the thermal power generating unit is responsible for peak shaving, the peak shaving cost is the highest. When pumped-storage power stations participate, according to different unit combinations, the peak shaving cost can be reduced by up to 50.61%. Considering that the pumped-storage power station participates in peak shaving, the peak-shaving cost is effectively reduced.

TABLE 2

TABLE 2. Peak shaving cost of each unit in the joint peak shaving unit.

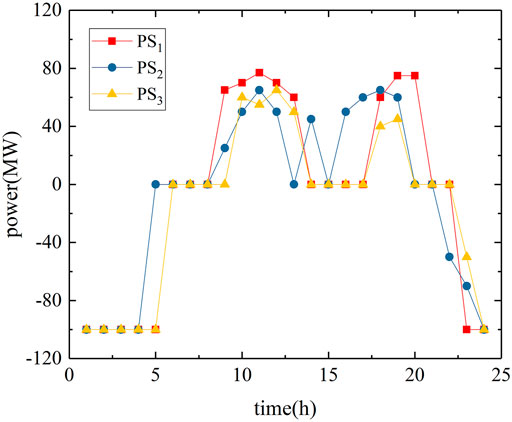
Figure 4 is the output curve of the pumped-storage unit, and the peak-shaving operation status of the pumped-storage unit and the thermal power unit at each moment are shown in Figure 5. It can be seen that under the auxiliary service market established in this study, considering the participation of pumped-storage power stations in peak shaving from 22 –4 h the next day, the pumped-storage power station works in the pumping mode and is mainly responsible for the task of peak shaving in low valleys. At this time, the thermal power plant can work in a more reasonable output range and does not need to significantly reduce the load. In 9–13 h and 18–21 h, there is a large power shortage in the system. The pumped storage power station works in the power generation mode and is mainly responsible for the task of peak regulation during the peak period. At this time, the thermal power generation unit works in the economic zone. Through the coordination of pumped storage power stations and thermal power plants, the cost of peak regulation is reduced.

FIGURE 4

FIGURE 4. Output curve of the pumped storage unit.

FIGURE 5

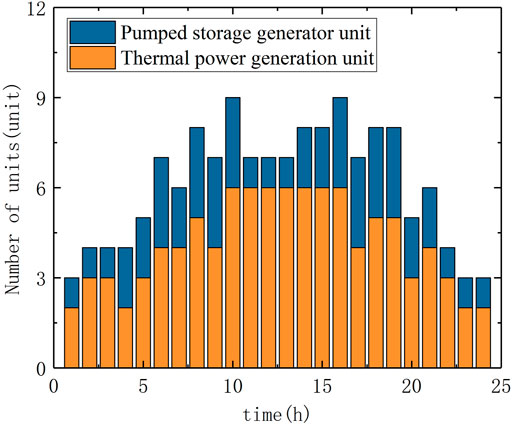
FIGURE 5. Peak shaving operation status of the pumped storage unit and thermal power unit at each moment.

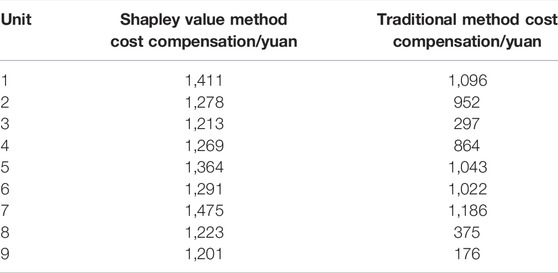
Table 3 shows the unit peak shaving compensation under the two methods of Shapley value and traditional peak shaving auxiliary service fee allocation. It can be seen that the unit with stronger peak shaving capability will receive more compensation for peak shaving costs. At the same time, the amount of peak shaving fee compensation obtained under the Shapley value method is more than that obtained under the traditional peak shaving auxiliary service fee allocation method. The traditional peak-shaving auxiliary service fee allocation method is based on the unit’s peak-shaving value index, and the obtained cost-sharing is proportional to its peak-shaving capacity, which leads to low enthusiasm for units with relatively weak peak-shaving capacity and waste of peak-shaving resources. It also increases the peak load of some units. The Shapley value method is based on the marginal contribution of the unit to the alliance revenue, and the cost compensation per unit of peak shaving capacity must be more.

TABLE 3

TABLE 3. Compensation for unit peak shaving costs under different methods.

Conclusion

In this study, a market model for peak shaving auxiliary services is established based on the background of large-scale grid connection of renewable energy in the power system. First, the pumped storage power station is introduced to participate in peak shaving, the peak shaving value of the units participating in peak shaving is quantified, and the compensation mechanism for peak shaving auxiliary service fees is established. Finally, the model proposed in this study is simulated and verified by an 11-machine, 14-node system. Taking the minimum peak shaving cost as the optimization goal, the peak shaving cost of each unit combination in the combined peak shaving unit is optimized. The results show that the peak shaving cost can be reduced by up to 50.61%. On this basis, the compensation amount of peak shaving costs obtained by the participating peak shaving units is determined according to the difference in peak shaving costs, the Shapley value method is used to allocate peak shaving auxiliary service fees, the enthusiasm of thermal power generating units with weak peak shaving capacity to participate in peak shaving units has been improved, and the peak shaving pressure of thermal power generating units has been eased.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

ZZ and WC are responsible for the modeling work of the study. SL is responsible for the calculation work of the study. CL and SQ are responsible for the simulation work of the study.

Funding

This work is supported by State Grid Xinyuan Holdings Pushihe Company research and application services of key technologies for power station peak regulation assistance and multi-dimensional monitoring based on big data analysis (SGXYPH00YJJS2100149).

Conflict of Interest

Authors ZZ, WC, SL, CL, and SQ were employed by Liaoning Pushihe Pumped Storage Co. Ltd.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bie, Z., Wang, X., and Hu, Y. (2017). Review and Prospect of Planning of Energy Internet[J]. Proc. CSEE 37 (22), 6445. doi:10.13334/j.0258-8013.pcsee.171188

CrossRef Full Text | Google Scholar

Chen, X., Huang, L., Liu, J., Song, D., and Yang, S. (2022). Peak Shaving Benefit Assessment Considering the Joint Operation of Nuclear and Battery Energy Storage Power Stations: Hainan Case Study. Energy 239, 121897. doi:10.1016/j.energy.2021.121897

CrossRef Full Text | Google Scholar

Fu, Y., Chen, H., Jiang, X., and Sun, J. (2019). A Bi-layer Peakregulation Compensation Mechanism for Large-Scale Wind Power Integration[J]. Power Syst. Prot. Control 47 (4), 51. doi:10.7667/PSPC180261

CrossRef Full Text | Google Scholar

Guo, Z., Ye, R., Liu, R., and Ye, J. (2018). Optimal Scheduling Strategy for Renewable Energy System with Pumped Storage Station[J]. Electr. Power Autom. Equip. 38 (3), 7. doi:10.16081/j.issn.1006-6047.2018.03.002

CrossRef Full Text | Google Scholar

Huang, Q. (2020). Stochastic Economic Dispatch and Cost Allocation Considering Peak Regulation Influence Coefficient[J]. Power Syst. Clean Energy 36 (10), 33. doi:10.3969/j.issn.1674-3814.2020.10.006

CrossRef Full Text | Google Scholar

Jian, X., Zhang, L., Yang, L., Han, X., and Wang, M. (2018). Deep-peak Regulation Mechanism Based on Kaldor Improvement under Highpenetration Wind Power[J]. Automation Electr. Power Syst. 42 (8), 110. doi:10.7500/AEPS20170614027

CrossRef Full Text | Google Scholar

Li, Y., Zhang, H., Liang, X., and Huang, B. (2019). Event-triggered Based Distributed Cooperative Energy Management for Multienergy Systems[J]. IEEE Trans. Industrial Inf. 15 (14), 2008–2022. doi:10.1109/tii.2018.2862436

CrossRef Full Text | Google Scholar

Lin, L., Zou, L., and Zhou, P. (2017). Multi-angle Economic Analysis on Deep Peak Regulation of Thermal Power Units with Large-Scale Wind Power Integration[J]. Automation Electr. Power Syst. 41 (7), 21. doi:10.7500/AEPS20160719005

CrossRef Full Text | Google Scholar

Liu, W., Li, Y., and Guo, P. (2018). Stackelberg Game Decision for Lord-Source Associated Day-Ahead Peak Load Regulation[J]. J. Syst. Simul. 30 (8), 3066. doi:10.16182/j.issn1004731x.joss.201808030

CrossRef Full Text | Google Scholar

Lyu, J., Zhang, S., Cheng, H., Li, K., and Yuan, K. (2021). Review and Prospect on Coordinated Planning of Energy Flow and Workload Flow in the Integrated Energy System Containing Data Centers[J]. Proc. CSEE 41 (16), 5500. doi:10.13334/j.0258-8013.pcsee.210326

CrossRef Full Text | Google Scholar

Ma, X., Xue, C., Ren, J., Zhang, X., Meng, X., Yang, Y., et al. (2021). Design and Practice of Inter-provincial Peak Regulation Auxiliary Service Market Mechanism for Northwest China Power Grid[J]. Electr. Power 54 (6), 2. doi:10.11930/j.issn.1004-9649.202005050

CrossRef Full Text | Google Scholar

Nan, J., Wang, P., and Li, D. (2021). A Solution Method for Sharply-Based Equilibrium Strategies of Biform Games[J]. Chin. J. Manag. Sci. 29 (5), 202. doi:10.16381/j.cnki.issn1003-207x.2018.0642

CrossRef Full Text | Google Scholar

Qi, W., Li, J., Liu, Y., and Liu, C. (2019). Planning of Distributed Internet Data Center Microgrids. IEEE Trans. Smart Grid 10 (1), 762–771. doi:10.1109/tsg.2017.2751756

CrossRef Full Text | Google Scholar

Shi, Y., Xu, B., Wang, D., and Zhang, B. (2018). Using Battery Storage for Peak Shaving and Frequency Regulation: Joint Optimization for Superlinear Gains. IEEE Trans. Power Syst. 33 (3), 2882–2894. doi:10.1109/tpwrs.2017.2749512

CrossRef Full Text | Google Scholar

Tian, L., Xie, Y., Zhou, G., and Ge, W. (2019). Deep Peak Regulation Ancillary Service Bidding Strategy for CHP Units Based on Two-Stage Stochastic Programming[J]. Power Syst. Technol. 43 (8), 2789. doi:10.13335/j.1000-3673.pst.2019.0554

CrossRef Full Text | Google Scholar

Wang, C., Qiao, Y., Liu, M., Zhao, Y., and Yan, J. (2020c). Enhancing Peak Shaving Capability by Optimizing Reheat-Steam Temperature Control of a Double-Reheat Boiler. Appl. Energy 260, 114341. doi:10.1016/j.apenergy.2019.114341

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Ma, D., and Hu, X. (2020b). Line Impedance Cooperative Stability Region Identification Method for Grid-Tied Inverters under Weak Grids[J]. IEEE Trans. Smart Grid 11 (4), 2856. doi:10.1109/TSG.2020.2970174

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Zhang, P., Gui, Y., Qin, D., and Wang, P. (2020a). Reduced-Order Transfer Function Model of the Droop-Controlled Inverter via Jordan Continued-Fraction Expansion[J]. IEEE Trans. Energy Convers. 35 (3), 1585. doi:10.1109/TEC.2020.2980033

CrossRef Full Text | Google Scholar

Wang, Y., Liu, L., Li, X., Chen, H., Zhong, J., Shi, K., et al. (2019). Allocation Mechanism of Peak Load Regulation Auxiliary Service Cost[J]. Guangdong Electr. Power 32 (2), 1. doi:10.3969/j.issn.1007-290X.2019.002.001

CrossRef Full Text | Google Scholar

Zou, J., Lai, X., and Wang, N. (2015). Coordinated Operation of Wind Power and Pumped Storage with the Goal of Reducing Wind Abandonment in the Power Grid[J]. Power Syst. Technol. 39 (9), 2472. doi:10.13335/j.1000-3673.pst.2015.09.015

CrossRef Full Text | Google Scholar