Simultaneous Impact of Hollow Droplet and Continuous Dense Droplet on Liquid Film

The Simultaneous impact of a hollow droplet and a continuous dense droplet on a liquid film was investigated using the coupled level set and volume of fluid (CLSVOF) method. Analyses included fluid dynamics and heat transfer characteristics in impact. Results showed that the interfacial phenomena after impact incorporates spreading, central jet between droplets, edge liquid sheet, and counter jet inside the hollow droplet. The pressure gradient is the major cause for the above phenomena. The significant parameter of impact velocity is closely related to the dynamics and heat transfer for droplets impacting on a liquid film. Droplets with higher impact velocity exhibit a greater spreading factor, central jet height, edge jet height, and counter jet height. Besides, wall heat flux increases more notably for droplets with a higher impact velocity. Compared with the continuous droplet, the hollow droplet shows a smaller spreading factor and edge jet height, a higher wall heat flux, but a narrow thermally affected region. This study provides a fundamental understanding for the application of high-pressure spray combustion.

Introduction

Droplet impact on a liquid film has been witnessed in many industrial applications, such as spray cooling, falling-film evaporation, ink jet printing, internal combustion, and plasma spraying (Yarin, 2006; Liu et al., 2013; Liang and Mudawar, 2016; Wang et al., 2017; Wang et al., 2018; Li and Duan, 2019). Recently, a mass of experimental and numerical studies had been conducted on this phenomenon (Li et al., 2017; Liang and Mudawar, 2017a, b; Liang and Mudawar, 2017c; Wang et al., 2018). Compared with investigations on the impact of a single continuous dense droplet, multi-droplet impact received far less attention (Roisman and Tropea, 2002; Sivakumar and Tropea, 2002; Zhang et al., 2016), which, however, is encountered frequently in applications involving droplet impact. On the other hand, microbubbles usually form randomly inside droplets in high-pressure spray combustion (Gulyaev et al., 2009; Kumar et al., 2013; Lu et al., 2015), which indicates that the simultaneous impact of a hollow droplet and a continuous dense droplet is a common occurrence under this context. Also, in a practical condition, a thin liquid film will be builtup on the solid surface upon impact in the initial stage. This implies that the subsequent droplet will interact with the liquid film instead of with the solid surface (Liu et al., 2016). Inspired by the abovementioned information, this study will focus on the dynamics and heat transfer characteristics involved during a hollow droplet and a continuous dense droplet impinging on a liquid film simultaneously.

In recent years, many experimental and numerical efforts have been dedicated to single continuous dense droplet impact (Liang and Mudawar, 2016). From the experimental viewpoint, a high-speed camera was mainly used to investigate the transient dynamic behavior during impact (Oguz and Prosperetti, 1989; Peck and Sigurdson, 1994; Alghoul et al., 2011; Negeed et al., 2013; Negeed et al., 2014; Stevens, 2014). While in numerical studies, typical CFD methods such as marker and cell (MAC) (Harlow and Welch, 1965), level set (Lee et al., 2011), volume of fluid (VOF) (Rocco et al., 2010; Chen et al., 2013; Chen et al., 2015), lattice Boltzmann method (LBM) (Lee and Liu, 2010; Chen and Deng, 2017; Pravinraj and Patrikar, 2017), and coupled level set and volume of fluid (CLSVOF) method (Liang et al., 2014) have been employed. The interfacial phenomena during impact such as spreading, edge liquid sheet, and splashing, with their corresponding underlying mechanisms were comprehensively investigated (Sivakumar and Tropea, 2002; Guo et al., 2010). The effects of impact velocity, droplet initial diameter, impact angle, and the initial thickness of the liquid film were mainly considered. Also, the heat transfer during droplet impact was studied (Liang and Mudawar, 2017c).

When compared with a continuous dense droplet, quite a limited number of studies on hollow droplet impact are found. Due to the effects of cavitation bubbles, hollow droplets have more complex effects on both liquid flow and heat transfer than a continuous dense droplet does alone. Gulyaev and Solonenko (2013) experimentally studied a hollow droplet impact on a flat surface. The central counter jet was analyzed at different operating conditions. Kumar et al. (2012) numerically studied the hollow droplet impact on a flat surface using the VOF method. Hollow droplet impacting was compared with the impact of continuous dense droplets. The influence of the hollow droplet initial impact velocity and shell thickness on the impact dynamics was also analyzed. Li et al. (2018, 2019) used the CLSVOF method to investigate the dynamics and heat transfer associated with a hollow droplet impact on a dry flat surface and a liquid film, respectively. The differences between the hollow droplet impact and continuous dense droplet impact are mainly discussed.

As stated in a previous paragraph, the multi-droplet impact has received far less attention than the single droplet impact. Most of the work is focused on the impact on a solid wall (Park et al., 2012; Qiu et al., 2017). Quite a limited amount of research has focused on multiple droplets’ impact on a liquid film. Cossali et al. (2004) were the first to experimentally investigate multiple droplets’ impact on a liquid film. The effects of impacting velocity and film thickness were mainly analyzed. Soriano et al. (2014) experimentally investigated the hydrodynamics and heat transfer behaviors of multiple droplets' impact on a liquid film. Droplet spacing between adjacent impinging droplets plays an important role in heat transfer behavior. Raman et al. (2015) used the LBM to numerically study the dynamic behavior of two droplets impacting on a liquid film. The results showed that a larger separation gap between the droplets led to a delay in formation of a central jet, while the spread length increased. Liang et al. (2019) numerically investigated multiple droplets successively impacting on a liquid film using the CLSVOF method. It was revealed that successive impacts of multiple droplets increased the splashing thresholds for trailing droplets. Liang et al.(2018) also conducted numerical simulations on multiple droplets simultaneously impacting on the liquid film. A geometric model was established to explain the impact region that contained two semicircular regions and a series of rectangular regions during simultaneous impact. The variations in residual film thickness in each region as well as the total area and average film thickness were analyzed.

However, there are a few studies on the case of the hollow droplet and continuous dense droplets simultaneously impacting on a liquid film. In high-pressure combustion and spay cooling, there are multiple droplets, namely, hollow droplets and continuous dense droplets, impacting on a liquid film. The investigations on a single droplet impacting on a liquid film could not reveal the effects of interaction of the droplets on the hydrodynamics and heat transfer mechanism of the multiple droplets impacting on a liquid film. Thus, it is significantly important and very necessary to deepen the understanding of this case. In this study, a numerical model was developed using the CLSVOF method to simulate droplet dynamics and heat transfer behaviors of a hollow droplet and a continuous dense droplet simultaneously impacting on the liquid film. The interface evolution and associated heat transfer characteristics of the droplets are mainly discussed. The governing mechanisms behind the dynamics and heat transfer behaviors are also analyzed. It is believed that this study will provide a fundamental understanding of high-pressure spray combustion and its associated applications involving hollow droplet impact.

Methodology

Problem Description

Figure 1 shows the geometric model of a hollow droplet and a dense droplet impinging on a liquid film. The two droplets share the same impacting velocity U_p. The initial diameter of the droplets D₀ is 2.091 mm with a dimensionless shell thickness ${\delta }_p^{\ast }$ of 0.25; the latter is defined as ${\delta }_p^{\ast }={\delta }_p/D_p$, where δ_p is the shell thickness. The initial diameter of the continuous dense droplet D₀ is 2 mm, which has the same mass as the hollow droplet to ensure the same initial kinetic energy. The droplets horizontal spacing S is 3.2 mm. The initial thickness of the liquid film h₀ is 0.2091 mm. The droplets' temperature is 323 K, and the temperature of the wall, liquid film, and surrounding air is 300 K. The physical properties and other parameters include liquid density ρ_l = 835 kg m⁻³, air density ρ_g = 1.225 kg m⁻³, surface tension coefficient σ = 0.039 N⋅m⁻¹, liquid viscosity μ_l = 2.745 × 10^–3 Pa s⁻¹, air viscosity μ_g = 1.789 × 10^–5 Pa s⁻¹, equilibrium contact angle θ = 30^o, and gravity = 9.8 m s⁻².

FIGURE 1

FIGURE 1. Computational domain and boundary conditions.

Representative evolution stages prior to and after the droplets' impingement are presented in Figures 2A–C. The spreading diameters of the hollow and continuous dense droplets are D_p,s and D_0,s, respectively. The height of the central jet between the droplets is h_c, and the heights of the edge jet of the hollow droplet and continuous dense droplet are h_p,j and h_0,j, respectively. The height of the counter jet inside the hollow droplet is L_j. For convenience and being consistent with previous works, the spreading factor of a hollow droplet, the spreading factor of a dense droplet, the edge jet height of the hollow droplet, the edge jet height of the dense droplet, and the counter jet height were normalized based on the droplet diameters for analysis, i.e., f_p = D_p,s/D_p, f₀ = D_0,s/D₀, $h_{p,j}^{\ast }=h_{p,j}/D_p$, $h_{0,j}^{\ast }=h_{0,j}/D_0$, and $L_j^{\ast }=L_j/D_p$.

FIGURE 2

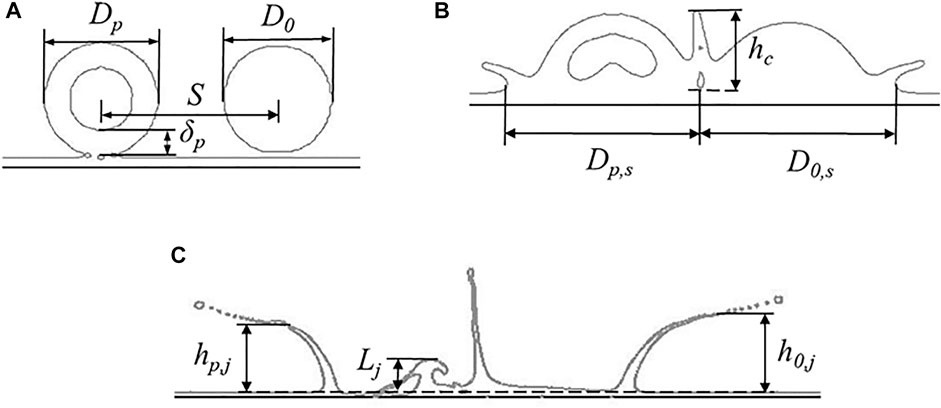
FIGURE 2. Typical evolution stages in the impact of hollow droplet and continuous dense droplet on the liquid film: (A) droplets contact with liquid film, (B) central jet between droplets, and (C) counter jet inside the hollow droplet.

Numerical Method and Mode

In this study, the CLSVOF method (Sussman and Puckett, 2000) is employed to perform the simulations with the aid of the commercial software FLUENT. Continuity, momentum, and energy equations used throughout the domain include

$\mathit{\nabla }\cdot \overrightarrow{V}=0,(1)$

$\frac{\partial }{\partial t}\left(\rho \left(\varphi \right)\overrightarrow{V}\right)+\mathit{\nabla }\cdot \left[\rho \left(\varphi \right)\overrightarrow{V}\overrightarrow{V}\right]=-\mathit{\nabla }p+\mathit{\nabla }\cdot \left[\mu \left(\varphi \right)\left(\mathit{\nabla }\overrightarrow{V}+\mathit{\nabla }{\overrightarrow{V}}^T\right)\right]+\rho \left(\varphi \right)\overrightarrow{g}-\overrightarrow{F},(2)$

$\frac{\partial }{\partial t}\left[\rho \left(\phi \right)c_{p}T\right]+\mathit{\nabla }\cdot \left[\rho \left(\phi \right)c_p\overrightarrow{V}T\right]=\mathit{\nabla }\cdot \left(\lambda \mathit{\nabla }T\right),(3)$

where $\overrightarrow{V}$, $\overrightarrow{g}$, and p represent velocity vector, gravitational acceleration, and pressure, respectively; $\mu \left(\phi \right)$ and $\rho \left(\phi \right)$ signify dynamic viscosity and density, respectively, and $\phi$ is the level set function; c_p, T, and λ are specific heat, temperature, and thermal conductivity, respectively, and $\overrightarrow{F}$ is the surface tension solved by the continuum surface force (CSF) model by Brackbill et al. (1992), expressed as

$\overrightarrow{F}=\sigma \kappa \left(\phi \right)\mathit{\nabla }H\left(\phi \right),(4)$

$H\left(\phi \right)=\{\begin{array}{cc}0& \mathit{\phi }<-{\delta }_{tr}\\ \frac{1}{2}+\frac{\phi }{2a}+\frac{1}{2\pi }\sin \left(\frac{\pi \mathit{\phi }}{a}\right)& \left|\mathit{\phi }\right|\le {\delta }_{tr}\\ 1& \mathit{\phi }>{\delta }_{tr}\end{array}(5)$

where $\kappa \left(\phi \right)$ and $\sigma$ are interface curvature and surface tension coefficient, respectively; ${\delta }_{tr}$ denotes thickness of the transition region at the interface, and ${\delta }_{tr}=1.5a$ is adopted in this study, where a is the minimum size of the computational cell. The smoothed $\rho \left(\phi \right)$ and $\mu \left(\phi \right)$ are respectively expressed as

$\rho \left(\phi \right)={\rho }_g+\left({\rho }_l-{\rho }_g\right)H\left(\phi \right),(6)$

$\mu \left(\phi \right)={\mu }_g+\left({\mu }_l-{\mu }_g\right)H\left(\phi \right),(7)$

where subscripts g and l represent gas and liquid phases, respectively.

Notice that the numerical method above is only briefly introduced, and more details about this method, in particular the solving schemes for the numerical method, can be found in the authors’ previous studies (Li et al., 2018; Li et al., 2019).

In this work, a two-dimensional model that is shown in Figure 1 is used, with a computational domain of 15 × 30 mm. For the purpose of accurately capturing the complex evolution of the central jet between droplets and the counter jet inside droplets, intensified adaptive meshes are used. Numerical results from the structured meshes with total grid numbers of 150,000, 186,000, and 252,000 are compared to check mesh independence. The numerical conditions include D_p = 2.091 mm, ${\delta }_p^{\ast }$ = 0.25, S = 3.2 mm, U_p = 6 m s⁻¹, and h₀ = 0.2091 mm. The spreading factor is set as the comparing criterion, and the results show that the spreading factors with grid numbers of 1,86,000 and 2,52,000 are very close to each other, but the result with the grid number of 1,50,000 has a large difference with the former two. Thus, the grid number of 1,86,000 is used to guarantee the calculation accuracy and also to save the computation resource. It needs to be pointed out that the two-dimensional model in this work has its limitation in simulating the genuine phenomenon of droplets interaction, but it will pave the way for further extension of a three-dimensional model including phase transition.

Model Validation

For the model validation, it will be a good choice to compare the numerical results with closely related experiments. Unfortunately, the experiments of a hollow droplet and a continuous dense droplet simultaneously impacting on a liquid film are not available at present. To warrant the effectiveness of the model, the cases of a hollow droplet impact, and a continuous dense droplet impact are validated, respectively. For the hollow droplet, only experimental results of the hollow droplet impact on a dry substrate are available (Gulyaev and Solonenko, 2013). The conditions are expressed as follows: a glycerin hollow droplet with an initial diameter D_p = 5.25 mm and dimensionless shell thickness ${\delta }_p^{\ast }$ = 0.082 at 5.94 m s⁻¹ velocity impacting on a dry flat surface vertically. The droplet temperature is the same as ambient air. The comparison between the numerical results and experimental data is shown in Figure 3. It is found that they coincide much well with each other, in both the morphology of the impacting droplet and height of the central jet (L_j).

FIGURE 3

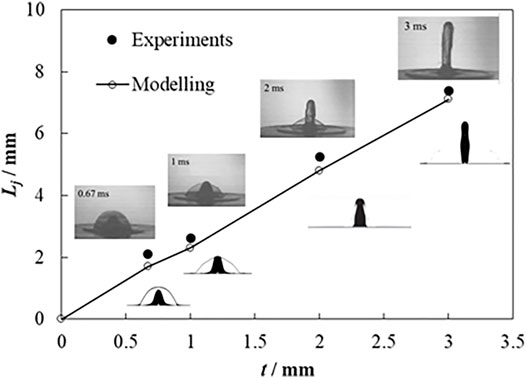
FIGURE 3. Comparison of the experiment (Gulyaev and Solonenko, 2013) and simulation results for hollow droplet impact.

For the dense droplet, experimental observation and measurement from a previous study (Li et al., 2017) are used to validate the numerical result of a continuous dense droplet impact on a liquid film. The conditions are expressed as follows: a continuous dense droplet with an initial diameter D₀ = 2.378 mm at 2.1 m s⁻¹ velocity vertically impacting on a liquid film with an initial thickness of 0.2 mm. The droplet temperature is the same as ambient air. The comparison is exhibited in Figure 4, which shows a very good agreement in droplet qualitative evolution and quantitative spreading factor.

FIGURE 4

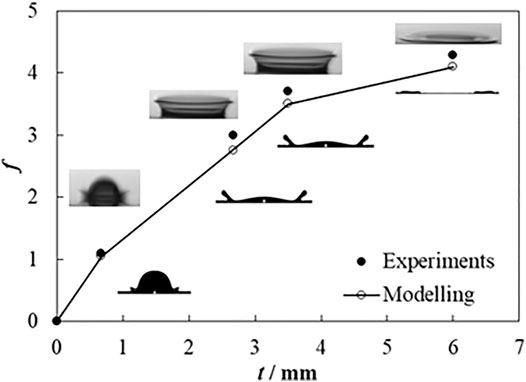
FIGURE 4. Comparison of the experiment (Li et al., 2017) and simulation results for the continuous dense droplet.

Results and Discussions

Morphology of Impacting Droplets

Figure 5 shows the interface evolution of a hollow droplet and a dense droplet simultaneously impacting on a liquid film, with the impact velocity of 6 m s⁻¹. The time when the droplets make contact with the liquid film is set as 0 ms.

FIGURE 5

FIGURE 5. Morphology of droplets impact on liquid film at 6 m s⁻¹.

As can be observed in Figure 5, the droplets spread after making contact with the liquid film. At 0.15 ms, the hollow droplet and continuous dense droplet collide, where the central jet can be found at the colliding point. Also, an entrapped air bubble emerges inside the central jet. At the outside spreading edge, a liquid sheet resulting from the effects of spreading potential, viscous dissipation, and surface tension is observed. At 0.35 ms, the central jet presents an oblique movement toward the hollow droplet. This is mainly due to the effect of the larger spreading potential of the continuous dense droplet, which produces larger colliding energy upon droplets' collision, causing an oblique central jet. Liquid at the top of the central jet ruptures, which produces secondary tiny droplets. Concomitantly, the fluid inside the hollow droplet converges at the impact center, where the counter jet is enveloped. At 0.45 ms, for the hollow droplet impact, the counter jet moves across the liquid shell, resulting in the rupture of the liquid shell. For the continuous dense droplet impact, fluid inside the liquid sheet deforms greatly as a groove, without the counter jet that appears inside the hollow droplet. It is also found that the liquid at the rim of the edge liquid sheet for continuous dense droplet breaks into secondary droplets, which cannot be found for the edge liquid sheet from the hollow droplet. At 1.2 ms, the liquid at the edge liquid sheet shows a more obvious splashing process for both the hollow droplet and the continuous dense droplet. Thus, the obliquely moving central jet and the counter jet are the unique features for the simultaneous impingement of a hollow droplet and a continuous dense droplet.

Fluid Dynamics Analysis

Figure 6 shows pressure and velocity distributions during a hollow droplet and a continuous dense droplet impacting on a liquid film simultaneously, where the conditions are the same to those shown in Figure 5.

FIGURE 6

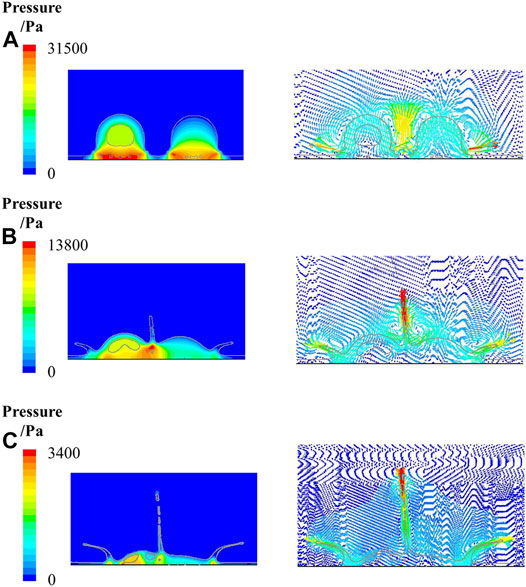
FIGURE 6. Pressure and velocity distribution of droplets impact at different time instants: (A) 0.05 ms, (B) 0.2 ms, and (C) 0.5 ms.

As can be found in Figure 6A, at 0.05 ms, when the droplets make contact with the liquid film, pressures at the spreading edge for both the hollow droplet (31,453 Pa) and continuous dense droplet (29,864 Pa) are greater than the main part of the droplets, which causes the spreading of the droplets. The spreading velocities for the hollow droplet and continuous dense droplet are 13.9 and 14.769 m s⁻¹, respectively.

In Figure 6B at 0.2 ms, the maximum pressure is at the bottom of the central droplets (20,834 Pa). A large pressure gradient can be found within the central jet, which is the main cause for the formation of the central jet. Besides, pressures at the root of the edge liquid sheet for the hollow droplet and the continuous dense droplet are 7,877 and 8,957 Pa, respectively, which are the maximum in the edge liquid sheet area. The pressure gradient causes the formation of an edge jet. Also, the pressure gradient inside the counter jet within a hollow droplet decreases from the bottom (10,264 Pa) to the top (8,839 Pa), which is the main cause for the formation of the counter jet. As can been observed in the velocity distribution, the maximum velocity (14.48 m s⁻¹) of the central jet is at the top, which is larger than the spreading velocities of the hollow droplet (5 m s⁻¹) and continuous dense droplet (5.36 m s⁻¹), as well as the edge jet velocities of the hollow droplet (10 m s⁻¹) and continuous dense droplet (11.43 m s⁻¹). The maximum velocity at the top of the counter jet inside the hollow droplet is 1.525 m s⁻¹.

It can be seen from Figure 6C that at 0.5 ms, the pressure at the bottom of the central jet reduces to 2,173 Pa. The pressure gradient inside the central jet is not sufficient to sustain the development of the central jet. A breakup can be seen at the top of the central liquid jet, where the secondary droplets show significant kinetic splashing under fluid instabilities. Also, the pressures at the spreading edge (2,874 Pa) and the root of the edge jet (1,823 Pa) are larger than those of their surrounding areas, which means that the pressure gradient keeps resulting in spreading and edge jetting. The pressure gradient inside the counter jet within the hollow droplet is also large enough to keep forming the counter jet. As can be found in the velocity distribution at the same instant, the velocity at the top of the central jet reduces to 5.21 m s⁻¹, while the velocity of the secondary droplets is 14.8 m s⁻¹. Also, the spreading velocities of the hollow droplet and continuous dense droplet reduce to 4.5 and 5.2 m s⁻¹, respectively, but the edge jet velocities of the hollow droplet and continuous dense droplet increase to 9.7 and 10.4 m s⁻¹, respectively. The velocities at the bottom of the central jet and counter jet are 0.7 and 0.7439 m s⁻¹, respectively, with an almost existing flow stagnation near this point. Note that it is more difficult to transfer the heat from the droplets to wall surface because of such an existence of flow stagnation.

Effects of Impact Velocity on Flow Characteristics

Figure 7 shows the spreading factor f of two droplets impacting on a liquid film, where S = 3.2 mm and U_p = 6 and 10 m s⁻¹. The spreading factors for the different droplets increase with time. Droplets with a higher impact velocity have larger spreading factors. The maximum spreading factors for the hollow droplet at 6 and 10 m s⁻¹ are 3.17 and 3.7, respectively, while the maximum spreading factors for a continuous dense droplet at 6 and 10 m s⁻¹ are 3.37 and 4.0, respectively. The spreading factor of a continuous dense droplet is always larger than that of a hollow droplet at different impact velocities.

FIGURE 7

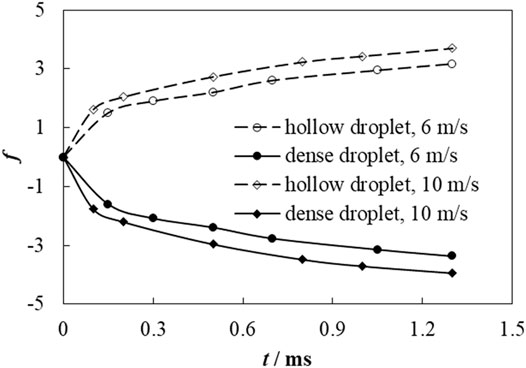
FIGURE 7. Spreading factor of a hollow droplet and continuous dense droplet at impact velocities of 6 and 10 m s⁻¹.

Figure 8 shows the height of the central jet for droplets' impaction at different time instants and impact velocities. Droplets with different impact velocities have the same trend for the height of the central jet. At the initial stage of impact, the height of the central jet increases gently, while after t = 0.1 and 0.15 ms, the increasing trend is accelerated. Also, as can be seen in Figure 6B, an upward-moving flow is observed at the colliding point between the droplets caused by a high pressure at that point, which forms the central jet between the droplets. Due to this, the droplets with a higher impact velocity have greater spreading kinetic energy, which can be converted to a larger pressure at the colliding point between the droplets; consequently, a greater jetting potential can be formed in droplets' colliding. Therefore, the droplets with a higher impact velocity have a larger central jet height.

FIGURE 8

FIGURE 8. Central jet height of droplets at impact velocities of 6 and 10 m s⁻¹.

Figure 9 shows the dimensionless height of the counter jet inside a hollow droplet during droplets' impaction at the different velocities, where t*= tU_p/D_p. As can be seen in Figure 9, the dimensionless height of the counter jet is close to each other at different velocities at the initial stages of its formation. When t* = 0.5, $L_j^{\ast }$ at 6 m s⁻¹ becomes smaller than at 10 m s⁻¹. With increasing time, the gap of $L_j^{\ast }$ between the different velocities is enlarged significantly.

FIGURE 9

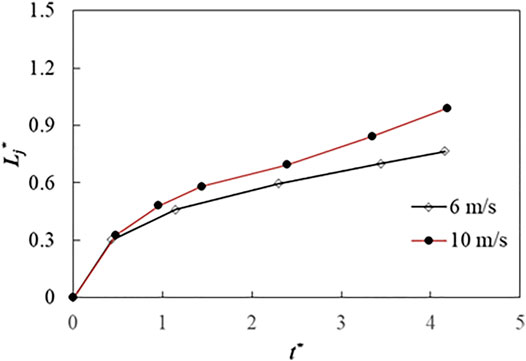
FIGURE 9. Dimensionless counter jet height of hollow droplet at impact velocities of 6 and 10 m s⁻¹.

Figure 10 exhibits the dimensionless height of the edge jet during the droplets' impact on the liquid film at different impact velocities. It is found that the droplets with higher impact velocity have larger dimensionless heights of the edge jet. The dimensionless height of the edge jet for a continuous dense droplet is slightly larger than that for a hollow droplet. This means that the edge jet for a continuous dense droplet is easier to break up due to the effect of hydrodynamic instabilities, which is corresponding to the morphology of droplet impact shown in Figure 5.

FIGURE 10

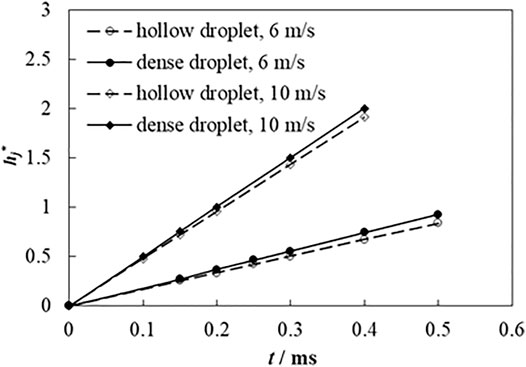
FIGURE 10. Dimensionless edge jet height of hollow droplet and continuous dense droplet at impact velocities of 6 and 10 m s⁻¹.

Effects of Impact Velocity on Heat Transfer Characteristics

Figure 11 shows the distribution of wall heat flux (qw) when a hollow droplet and a continuous dense droplet impinge on a liquid film at several time instants under the impact velocities of 6 and 10 m s⁻¹, in which S = 3.2 mm. The wall heat flux qw can be expressed as

$q_w=h_f\left(T_l-T_w\right),(8)$

where h_f is fluid-side local heat transfer coefficient, determined by

$h_f={-\frac{\lambda }{\Delta T}\frac{\partial T}{\partial y}|}_{y=0},(9)$

where $\lambda$ is the thermal conductivity, $\Delta T$ is the temperature difference, and ${\frac{\partial T}{\partial y}|}_{y=0}$ is the normal ratio of liquid temperature variation at the wall, and T_l and T_w are the local fluid temperature and wall surface temperature, respectively.

FIGURE 11

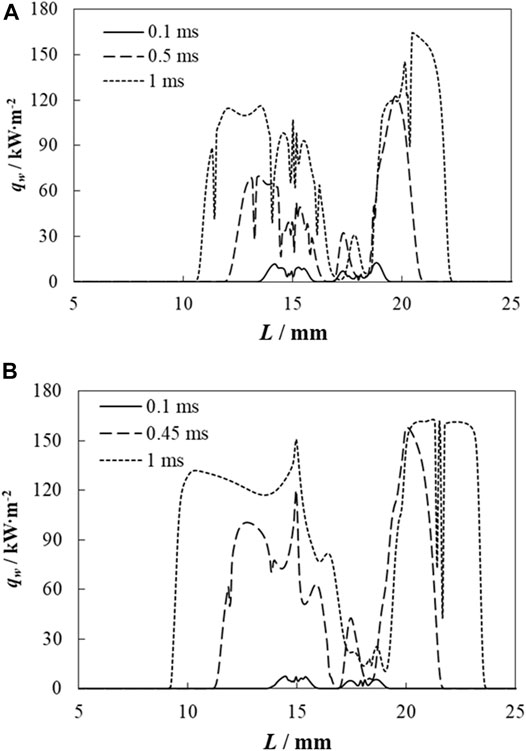
FIGURE 11. Wall heat flux distribution at impact velocities of 6 and 10 m s⁻¹: (A) 6 m s⁻¹ and (B) 10 m s⁻¹.

In Figure 11A at 0.1 ms, the wall heat flux is relatively low because the liquid film prohibits the thermal effect of the impacting droplets on the wall surface. As droplets spread, the interaction between the droplets and wall is enhanced remarkably. At 0.5 ms, the wall heat flux increases sharply, and the maximum wall heat flux reaches 126 kW m⁻². Due to the vortex flow near the wall surface, wall heat flux fluctuates at the droplets' impacting the area. When t = 1 ms, the maximum wall heat flux increases to 165.2 kW m⁻². It needs to be pointed that the wall heat flux at the hollow droplet–impacting area is larger than at the continuous dense droplet–impacting area. This is because the hollow droplet disturbance is more violent than the continuous dense droplets' due to the formation of a counter jet inside the hollow droplet. Also, it can be found that the thermally affected distances of the hollow droplet (r_h,p) are 4.8 and 6 mm at t = 0.5 and 1 ms, respectively, while the thermally affected distances of the continuous dense droplet (r_h,0) are 4.9 and 6.196 mm at t = 0.5 and 1 ms, respectively; the latter of these being slightly larger than those for the hollow droplet. It can be concluded that the dynamics of the impacting droplets affects heat transfer during impaction significantly. It is also found that at instants of 0.5 and 1 ms, when R = 16.5 and 17 mm, respectively, the wall heat flux almost decreases to zero. This is because of flow stagnation (as shown in Figure 6C) at this point due to the formation of the central jet that greatly inhibits heat transfer. This phenomenon should be considered and addressed in particular droplet spray applications.

In Figure 11B, when the impact velocity increases to 10 m s⁻¹, the wall heat flux distribution has almost the same trend as that of impacting at 6 m s⁻¹. At 0.45 ms, the maximum wall heat flux reaches 160.4 kW m⁻², which is very close to that at t = 1 ms for an impact velocity of 6 m s⁻¹. The thermally affected region of the continuous dense droplet is also larger than that of the hollow droplet at 0.45 and 1 ms, where r_h,0 = 5.6452 and 7.6452 mm, and r_h,p = 5.512 and 7.315 mm, respectively. It can also be found that r_h,0 and r_h,p of the droplets impacting at 10 m s⁻¹ are larger than those impacting at 6 m s⁻¹. This means that increasing the impact velocity can enhance heat transfer when the droplets impinge on a liquid film due to the intensified interaction between the droplets and wall surface at higher impact velocities.

Conclusion

With the aid of the CLSVOF method, a hollow droplet and a continuous dense droplet simultaneously impacting on a liquid film are numerically studied in this research. Spreading, central jet between droplets, and edge liquid sheet can be observed after droplets' impingement. Counter jet can be found inside a hollow droplet after impact, which is the main differential feature when compared with a continuous dense droplet. A pressure gradient is the main cause for spreading, central jet, edge liquid sheet, and counter jet formation. The impact velocity is closely related to the dynamics and heat transfer for droplets' impacting on liquid film. Droplets with a higher velocity have a larger spreading factor, central jet height, edge jet height, and counter jet height. The spreading factor and edge jet height for continuous dense droplets are larger than those for hollow droplets. Wall heat flux increases more notably for droplets with a higher impact velocity. A hollow droplet has a larger wall heat flux but a smaller thermally affected region than a continuous droplet. This study could provide guidelines for chip-level electronics cooling, internal combustion design, and surface coating.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

GL and DH contributed to the conception and design of the study, and DL performed the simulations and wrote the first draft of the manuscript. All authors contributed to manuscript revision, and read and approved the submitted version.

Funding

Support of the National Natural Science Foundation of China under Grant No. 51876025 and NSAF Joint Fund under U2030112 is gratefully acknowledged.

Conflict of Interest

The author DL is employed by CNOOC Research Institute Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alghoul, S. K., Eastwick, C. N., and Hann, D. B. (2011). Normal Droplet Impact on Horizontal Moving Films: an Investigation of Impact Behaviour and Regimes. Exp. Fluids 50 (5), 1305–1316. doi:10.1007/s00348-010-0991-0

CrossRef Full Text | Google Scholar

Brackbill, J. U., Kothe, D. B., and Zemach, C. (1992). A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 100 (2), 335–354. doi:10.1016/0021-9991(92)90240-y

CrossRef Full Text | Google Scholar

Chen, Y., and Deng, Z. (2017). Hydrodynamics of a Droplet Passing through a Microfluidic T-junction. J. Fluid Mech. 819, 401–434. doi:10.1017/jfm.2017.181

CrossRef Full Text | Google Scholar

Chen, Y., Liu, X., and Shi, M. (2013). Hydrodynamics of Double Emulsion Droplet in Shear Flow. Appl. Phys. Lett. 102 (5), 051609. doi:10.1063/1.4789865

CrossRef Full Text | Google Scholar

Chen, Y., Wu, L., and Zhang, L. (2015). Dynamic Behaviors of Double Emulsion Formation in a Flow-Focusing Device. Int. J. Heat Mass Transfer 82, 42–50. doi:10.1016/j.ijheatmasstransfer.2014.11.027

CrossRef Full Text | Google Scholar

Cossali, G., Marengo, M., and Santini, M. (2004). “Impact of Single and Multiple Drop Array on a Liquid Film,” in 19th Annual Meeting of ILASS (Nottingham, UK: ILASS Europe), 1–8. 06-08/09/2004.

Google Scholar

Gulyaev, I. P., Solonenko, O. P., Gulyaev, P. Y., and Smirnov, A. V. (2009). Hydrodynamic Features of the Impact of a Hollow Spherical Drop on a Flat Surface. Tech. Phys. Lett. 35 (10), 885–888. doi:10.1134/S1063785009100034

CrossRef Full Text | Google Scholar

Gulyaev, I. P., and Solonenko, O. P. (2013). Hollow Droplets Impacting onto a Solid Surface. Experiments in Fluids 54 (1), 1432. doi:10.1007/s00348-012-1432-z

CrossRef Full Text | Google Scholar

Guo Jia-Hong, J. H., Dai Shi-Qiang, S. Q., and Dai Qin, Q. (2010). Experimental Research on the Droplet Impacting on the Liquid Film. Acta Phys. Sin. 59 (4), 2601–2609. doi:10.7498/aps.59.2601

CrossRef Full Text | Google Scholar

Harlow, F. H., and Welch, J. E. (1965). Numerical Calculation of Time-dependent Viscous Incompressible Flow of Fluid with Free Surface. Phys. Fluids 8 (12), 2182–2189. doi:10.1063/1.1761178

CrossRef Full Text | Google Scholar

Kumar, A., Gu, S., and Kamnis, S. (2012). Simulation of Impact of a Hollow Droplet on a Flat Surface. Appl. Phys. A. 109 (1), 101–109. doi:10.1007/s00339-012-7043-y

CrossRef Full Text | Google Scholar

Kumar, A., Gu, S., Tabbara, H., and Kamnis, S. (2013). Study of Impingement of Hollow ZrO2 Droplets onto a Substrate. Surf. Coat. Technology 220, 164–169. doi:10.1016/j.surfcoat.2012.08.061

CrossRef Full Text | Google Scholar

Lee, S. H., Hur, N., and Kang, S. (2011). A Numerical Analysis of Drop Impact on Liquid Film by Using a Level Set Method. J. Mech. Sci. Technol. 25 (10), 2567–2572. doi:10.1007/s12206-011-0613-7

CrossRef Full Text | Google Scholar

Lee, T., and Liu, L. (2010). Lattice Boltzmann Simulations of Micron-Scale Drop Impact on Dry Surfaces. J. Comput. Phys. 229 (20), 8045–8063. doi:10.1016/j.jcp.2010.07.007

CrossRef Full Text | Google Scholar

Li, D., and Duan, X. (2019). Numerical Analysis of Droplet Impact and Heat Transfer on an Inclined Wet Surface. Int. J. Heat Mass Transfer 128, 459–468. doi:10.1016/j.ijheatmasstransfer.2018.09.025

CrossRef Full Text | Google Scholar

Li, D., Duan, X., Zheng, Z., and Liu, Y. (2018). Dynamics and Heat Transfer of a Hollow Droplet Impact on a Wetted Solid Surface. Int. J. Heat Mass Transfer 122, 1014–1023. doi:10.1016/j.ijheatmasstransfer.2018.02.017

CrossRef Full Text | Google Scholar

Li, D. S., Qiu, X. Q., Zheng, Z. W., and Zhang, D. (2017a). Numerical Analysis of a Coupled Level Set-VOF Method for the Study of Droplet Impact on Wetted Surface. J. Chem. Eng. Chin. Universities 31 (3), 570–578.

Google Scholar

Li, D., Zhang, D., and Zheng, Z. (2019). Numerical Analysis of Hollow Droplet Impacts on a Dry Flat Surface. Int. J. Heat Mass Transfer 129, 753–763. doi:10.1016/j.ijheatmasstransfer.2018.09.063

CrossRef Full Text | Google Scholar

Li, D., Zhang, D., Zheng, Z., and Tian, X. (2017b). Numerical Analysis on Air Entrapment during a Droplet Impacts on a Dry Flat Surface. Int. J. Heat Mass Transfer 115, 186–193. doi:10.1016/j.ijheatmasstransfer.2017.08.023

CrossRef Full Text | Google Scholar

Liang, G., Guo, Y., and Shen, S. (2014). Gas Properties on Crown Behavior and Drop Coalescence. Numer. Heat Transfer, B: Fundamentals 65 (6), 537–553. doi:10.1080/10407790.2014.884834

CrossRef Full Text | Google Scholar

Liang, G., and Mudawar, I. (2017c). Review of Drop Impact on Heated walls. Int. J. Heat Mass Transfer 106, 103–126. doi:10.1016/j.ijheatmasstransfer.2016.10.031

CrossRef Full Text | Google Scholar

Liang, G., and Mudawar, I. (2016). Review of Mass and Momentum Interactions during Drop Impact on a Liquid Film. Int. J. Heat Mass Transfer 101, 577–599. doi:10.1016/j.ijheatmasstransfer.2016.05.062

CrossRef Full Text | Google Scholar

Liang, G., and Mudawar, I. (2017a). Review of spray Cooling - Part 1: Single-phase and Nucleate Boiling Regimes, and Critical Heat Flux. Int. J. Heat Mass Transfer 115, 1174–1205. doi:10.1016/j.ijheatmasstransfer.2017.06.029

CrossRef Full Text | Google Scholar

Liang, G., and Mudawar, I. (2017b). Review of spray Cooling - Part 2: High Temperature Boiling Regimes and Quenching Applications. Int. J. Heat Mass Transfer 115, 1206–1222. doi:10.1016/j.ijheatmasstransfer.2017.06.022

CrossRef Full Text | Google Scholar

Liang, G., Zhang, T., Chen, H., Yu, H., and Shen, S. (2019). Successive Impact of Multiple Droplets on Liquid Film. Eur. J. Mech. - B/Fluids 74, 389–398. doi:10.1016/j.euromechflu.2018.09.011

CrossRef Full Text | Google Scholar

Liang, G., Zhang, T., Yu, H., Chen, H., and Shen, S. (2018). Simultaneous Impact of Multiple Droplets on Liquid Film. J. Ind. Eng. Chem. 65, 51–61. doi:10.1016/j.jiec.2018.04.011

CrossRef Full Text | Google Scholar

Liu, X., Chen, Y., and Shi, M. (2013). Dynamic Performance Analysis on Start-Up of Closed-Loop Pulsating Heat Pipes (CLPHPs). Int. J. Therm. Sci. 65, 224–233. doi:10.1016/j.ijthermalsci.2012.10.012

CrossRef Full Text | Google Scholar

Liu, X., Zhang, C., Yu, W., Deng, Z., and Chen, Y. (2016). Bubble Breakup in a Microfluidic T-junction. Sci. Bull. 61 (10), 811–824. doi:10.1007/s11434-016-1067-1

CrossRef Full Text | Google Scholar

Lü, M., Ning, Z., Yan, K., Fu, J., and Sun, C. (2015). Instability and Breakup of Cavitation Bubbles within Diesel Drops. Chin. J. Chem. Eng. 23 (1), 262–267. doi:10.1016/j.cjche.2014.10.009

CrossRef Full Text | Google Scholar

Negeed, E.-S. R., Albeirutty, M., and Takata, Y. (2014). Dynamic Behavior of Micrometric Single Water Droplets Impacting onto Heated Surfaces with TiO2 Hydrophilic Coating. Int. J. Therm. Sci. 79, 1–17. doi:10.1016/j.ijthermalsci.2013.12.011

CrossRef Full Text | Google Scholar

Negeed, E.-S. R., Hidaka, S., Kohno, M., and Takata, Y. (2013). High Speed Camera Investigation of the Impingement of Single Water Droplets on Oxidized High Temperature Surfaces. Int. J. Therm. Sci. 63, 1–14. doi:10.1016/j.ijthermalsci.2012.07.014

CrossRef Full Text | Google Scholar

Oguz, H. N., and Prosperetti, A. (1989). Surface-tension Effects in the Contact of Liquid Surfaces. J. Fluid Mech. 203, 149–171. doi:10.1017/s0022112089001412

CrossRef Full Text | Google Scholar

Park, J. Y., Min, C. K., Granick, S., and Cahill, D. G. (2012). Residence Time and Heat Transfer when Water Droplets Hit a Scalding Surface. J. Heat Transfer-Transactions Asme 134 (10), 101503. doi:10.1115/1.4006802

CrossRef Full Text | Google Scholar

Peck, B., and Sigurdson, L. (1994). The Three‐dimensional Vortex Structure of an Impacting Water Drop. Phys. Fluids 6 (2), 564–576. doi:10.1063/1.868352

CrossRef Full Text | Google Scholar

Pravinraj, T., and Patrikar, R. (2017). Modelling and Investigation of Partial Wetting Surfaces for Drop Dynamics Using Lattice Boltzmann Method. Appl. Surf. Sci. 409, 214–222. doi:10.1016/j.apsusc.2017.02.242

CrossRef Full Text | Google Scholar

Qiu, L., Dubey, S., Choo, F. H., and Duan, F. (2017). The Statistical Analysis of Droplet Train Splashing after Impinging on a Superheated Surface. J. Heat Transfer-Transactions Asme 139 (5), 052201. doi:10.1115/1.4035661

CrossRef Full Text | Google Scholar

Raman, K. A., Jaiman, R. K., Lee, T. S., and Low, H. T. (2015). On the Dynamics of crown Structure in Simultaneous Two Droplets Impact onto Stationary and Moving Liquid Film. Comput. Fluids 107, 285–300. doi:10.1016/j.compfluid.2014.11.007

CrossRef Full Text | Google Scholar

Rocco, G., Coppola, G., and De Luca, L. (2010). Simulation of Drop Impact on a Thin Liquid Film by Means of the VOF Method. Aerotecnica 89 (1), 25–35.

Google Scholar

Roisman, I. V., and Tropea, C. (2002). Impact of a Drop onto a Wetted wall: Description of crown Formation and Propagation. J. Fluid Mech. 472, 373–397. doi:10.1017/S0022112002002434

CrossRef Full Text | Google Scholar

Sivakumar, D., and Tropea, C. (2002). Splashing Impact of a spray onto a Liquid Film. Phys. Fluids 14 (12), L85–L88. doi:10.1063/1.1521418

CrossRef Full Text | Google Scholar

Soriano, G. E., Zhang, T., and Alvarado, J. L. (2014). Study of the Effects of Single and Multiple Periodic Droplet Impingements on Liquid Film Heat Transfer. Int. J. Heat Mass Transfer 77, 449–463. doi:10.1016/j.ijheatmasstransfer.2014.04.075

CrossRef Full Text | Google Scholar

Stevens, C. S. (2014). Scaling of the Splash Threshold for Low-Viscosity Fluids. Epl 106 (2), 24001. doi:10.1209/0295-5075/106/24001

CrossRef Full Text | Google Scholar

Sussman, M., and Puckett, E. G. (2000). A Coupled Level Set and Volume-Of-Fluid Method for Computing 3D and Axisymmetric Incompressible Two-phase Flows. J. Comput. Phys. 162 (2), 301–337. doi:10.1006/jcph.2000.6537

CrossRef Full Text | Google Scholar

Wang, H., Zhao, Z., Liu, Y., Shao, C., Bian, F., and Zhao, Y. (2018a). Biomimetic Enzyme cascade Reaction System in Microfluidic Electrospray Microcapsules. Sci. Adv. 4 (6). doi:10.1126/sciadv.aat2816

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Gao, W., Zhang, H., Zou, M., Chen, Y., and Zhao, Y. (2018b). Programmable Wettability on Photocontrolled Graphene Film. Sci. Adv. 4 (9), eaat7392. doi:10.1126/sciadv.aat7392

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Sun, L., Zou, M., Gao, W., Liu, C., Shang, L., et al. (2017). Bioinspired Shape-Memory Graphene Film with Tunable Wettability. Sci. Adv. 3 (6), e1700004. doi:10.1126/sciadv.1700004

PubMed Abstract | CrossRef Full Text | Google Scholar

Yarin, A. L. (2006). DROP IMPACT DYNAMICS: Splashing, Spreading, Receding, Bouncing. Annu. Rev. Fluid Mech. 38, 159–192. doi:10.1146/annurev.fluid.38.050304.092144

CrossRef Full Text | Google Scholar

Zhang, T., Muthusamy, J. P., Alvarado, J. L., Kanjirakat, A., and Sadr, R. (2016). Numerical and Experimental Investigations of crown Propagation Dynamics Induced by Droplet Train Impingement. Int. J. Heat Fluid Flow 57, 24–33. doi:10.1016/j.ijheatfluidflow.2015.10.003

CrossRef Full Text | Google Scholar

Nomenclature

a Minimum size of computational cell

c_p Specific heat

D_p Initial diameter of hollow droplet

D_p,s Spreading diameter of hollow droplet

D₀ Initial diameter of continuous dense droplet

D_0,s Spreading diameter of continuous dense droplet

f Spreading factor

$\overrightarrow{F}$ Source term of surface tension

$\overrightarrow{g}$ Gravity vector

h Heat transfer coefficient

h_c Central jet height

h_p,j Edge jet height of hollow droplet

h_0,j Edge jet height of continuous dense droplet

H Heaviside function

L Radius coordinate

L_j Height of counter jet

${\widehat{n}}_w$ Unit vector normal to wall

p Pressure

q_w Wall heat flux

r_h,p Thermally affected distance of hollow droplet

r_h,p Thermally affected distance of hollow droplet

S Droplets horizontal interval

t Time

U_p Impact velocity

$\overrightarrow{V}$ Velocity vector

y Direction normal to wall

Greek symbols

δ_p Shell thickness

θ Equilibrium contact angle

κ (ϕ) Interface curvature

λ Thermal conductivity

μ Viscosity

ρ Density

σ Surface tension coefficient

${\widehat{\tau }}_w$ Unit vector tangential to wall

ϕ Level set function

Superscript

^∗ Dimensionless

Subscripts

g Gas phase

l Liquid phase.