- China Oilfield Services Limited, Tianjin, China
Heavy oil is increasingly becoming an important part of future energy strategy. How to effectively simulate the flow process of steam flooding is the key to develop steam flooding. The purpose of this paper is to establish a mathematical model of steam flooding coupled with permeability and thermal field, and then use the meshless weighted least squares method to solve the mathematical model numerically. The effectiveness of this method is verified by establishing a one-dimensional conceptual model of steam flooding reservoir. It is found that the temperature distribution of the whole reservoir is basically the same except for the gas saturation distribution when calculated at 80, 90 and 100% steam dryness. Sensitivity analysis of porosity of the model is carried out in this paper. It is found that porosity has a direct effect on gas saturation and temperature front distribution. The calculated results are consistent with the perception results of objective facts, which verifies the accuracy and stability of the method.
1 Introduction
At the moment, the globe is rich in Heavy oil resources; Heavy oil, extra heavy oil, bitumen, and oil sands account for around 70% of global oil resources, and its vast resources also dictate its critical function and place in the future energy strategy. Steam flooding is one of the most effective and reliable technologies for Heavy oil development (Maity et al., 2010; Almao, 2012; Guo et al., 2016; Huang et al., 2021). Due to the high cost of steam flooding, it is critical to have a firm grip on the production dynamics and steam leading edge of steam flooding in order to successfully develop steam-flooding oil fields (MurazaGaladima and Galadima, 2015; Sheng et al., 2019).
The steam flooding is primarily accomplished through steam distillation, temperature increase and viscosity decrease, and in situ dissolving (Zhao et al., 2015). Ma calculated the ideal steam injection rate and the link between the injection rate and crude oil production using the steam flooding indoor trials (Ma and MainiOkazawa, 1984). Johnson conducted a laboratory crude oil steam distillation experiment and successfully separated the steam distillation and steam flooding processes (Johnson et al., 1971). Shen conducted an indoor steam flooding experiment using a physical model and found a favorable link between steam dryness and crude oil recovery (Desheng et al., 2013).
The displacement process is simulated numerically, that is, by solving a system of nonlinear partial differential equations (Huang et al., 2019). Partial differential equations provide a cost-effective tool for studying steam flooding operations (Mozaffari et al., 2013). Numerous scholars have focused their attention on multiphase flow computation (Yang et al., 2016). Marx and Langenheim devised a piston steam flooding reservoir model, laying the theoretical groundwork for thermal oil recovery by steam injection MarxLangenheim and Langenheim, (1959). Van Lookeren proposed a leading-edge prediction model for fluidic and radial steam flow that takes gravity overtopping into account and uses the form factor concept to quantify the degree of steam gravity overtopping and optimize the steam injection rate Van Lookeren, (1983). Yueh-Ming Chen created an analytical solution model for steam flooding dynamics prediction based on prior research. The model separates the reservoir into an initial oil-bearing zone, a crude oil-rich zone, a heat flow zone, and a steam zone. At the moment, research into the mechanism and technology of steam flooding replacement is rather thorough, while research into the mathematical model is still in its infancy (Crookston et al., 1979).
Due to the large fluctuation in physical parameters in the steam flooding process, the solution equation may be substantially nonlinear, making numerical solutions challenging to acquire (AtluriShen, 2002; Deng et al., 2022). The frequently used finite-difference or finite-volume methods are based on grids, which are inconvenient to manage before and after the computation, and are not suited for solving complex boundary problems, high-order differential equations, or problems with a large gradient (Guo et al., 2016). The purpose of this study is to present a robust, dependable, and accurate numerical model based on the meshless approach. In comparison to the finite difference, finite element, and finite cell methods, this meshless technique, especially the weighted least squares meshless method (MWLS), has the advantages of avoiding mesh generation (VignjevicCampbell and Campbell, 2009), simplifying data preparation, and allowing for convenient pre-processing and post-processing (Liu et al., 2005). The first meshless approach was Lucy’s smooth mass fluid meshless method, which was successfully applied to astrophysical issues. Atluri presented the meshless local Galerkin method, which eliminates the need for a background mesh during integration. The Galerkin-based method is computationally demanding because it needs the use of higher-order Gaussian integrals. While meshless methods based on the collocation point approach do not require integration, they have low precision and stability, as well as an unbalanced coefficient matrix. The weighted least squares meshless technique removes the control equation’s residuals with high precision and stability at all nodes (including boundary points), and the coefficient matrix is also symmetric (Xu et al., 2022). In comparison to the Galerkin approach, this method is more efficient because it does not require Gaussian integration. Li pioneered the application of the MWLS approach to numerical well testing in complicated fracture block reservoirs, with favorable results in terms of computational accuracy and efficiency. Rao utilized MWLS to the complicated boundary of shale gas, fractured horizontal wells with the two-phase flow of gas and water, and obtained favorable results (Lucy, 1977; AtluriZhu and Zhu, 1998; Rao et al., 2021; Xu et al., 2021).
We adopt a weighted least squares meshless method to numerically model the mass and heat transfer processes, as well as the saturation and temperature distribution fields, in a steam flooding process for the first time in this study. We simulated a one-dimensional homogeneous and inhomogeneous steam flooding process and found that the results are generally consistent with expectations, indicating that the method described in this study is correct.
2 Mathematical Model
2.1 Basic Mathematical Model
Due to the non-volatility of heavy oil, we consider a three-phase condition (oil phase, liquid water phase, and gaseous water phase). When liquid water and gaseous steam are present simultaneously in the three-phase area, the pressure and temperature should obey Dalton’s law of partial pressure. Assumptions include the following: 1) oil, steam, and water are insoluble in each other; 2) flow in the formation follows Darcy’s law; and 3) the effects of capillary forces and gravity are neglected.
The model’s three primary governing equations (mass conservation in the water phase, mass conservation in the oil phase, and energy equation) are as follows (Ping et al., 2021).
Water mass conservation equation:
Oil mass conservation equation:
Energy conservation equation:
Where,
When liquid water and steam are both presented, it should meet:
With the constraint relationship between saturations:
Along with these two relations in addition to the three main governing equations mentioned above, this is a closed mathematical model.
2.2 Meshless Method Solution
The meshless method can be theoretically justified using the weighted residual method. The moving least-squares approach is utilized to construct the approximation function in this article, followed by the least-squares method to discretize the control equations and establish the related meshless method, namely the weighted least squares meshless method (Lin et al., 2020).
Let there be a field function u(x) and a set of randomly distributed discrete nodes xj (j = 1, 2, ..., n) in the solution domain
Where NI is shape function,
The weight function is an important component of the moving least-squares approximation, there are no theoretical specific rules with some arbitrariness, generally satisfying the weight function ω(r) non-negative.
In terms of the variational principle and the weighted residual approach, which is used to build generalized functions and whose weight function or test function is the residual itself, the least-squares method can be used to solve partial differential equations of any type.
The weighted least squares meshless technique is generated by applying the above moving least squares-based approximation function to the specific problem and utilizing the above integral format’s discrete point summation form.
2.3 Weighted Least Squares Gridless Method for Solving the Steam Flooding
The pressure solution equation is first constructed by combining Eqs. 1, 2, disregarding capillary force and differencing the time term, as explained in Ref. (Desheng et al., 2013). After determining the pressure at the subsequent instant, it is replaced into an equation (Guo et al., 2016). The next moment’s saturation of the seepage field is solved and incorporated into the energy conservation equation (Almao, 2012). Assume that the solution domain and boundary include n discrete nodes, such that
The conservation of energy equation can be transformed into:
The residuals of the energy conservation equation are:
Then the MWLS form of its energy conservation equation is:
Where,
Solving Eq. 11 gives the temperature distribution for the next moment.
Successive iterations can be used to overcome the three-phase saturation and temperature problems associated with the steam flooding replacement process.
3 Results and Analysis
3.1 Model Validation
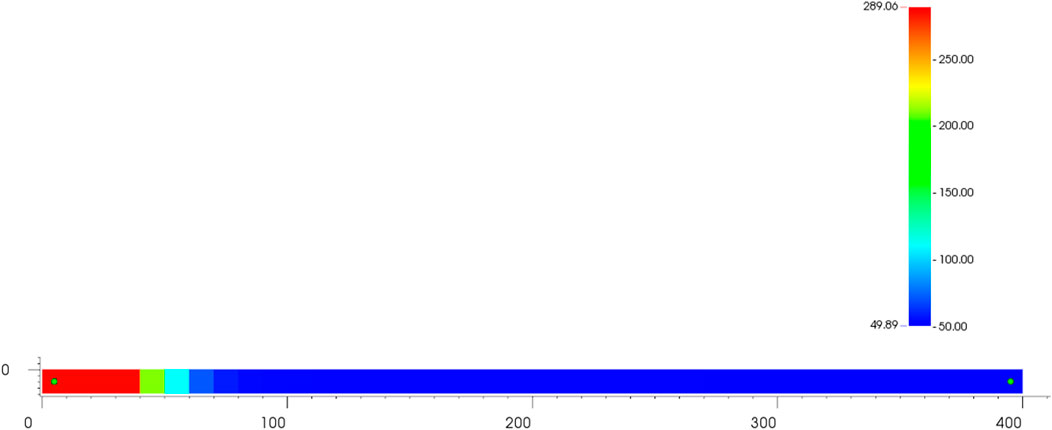
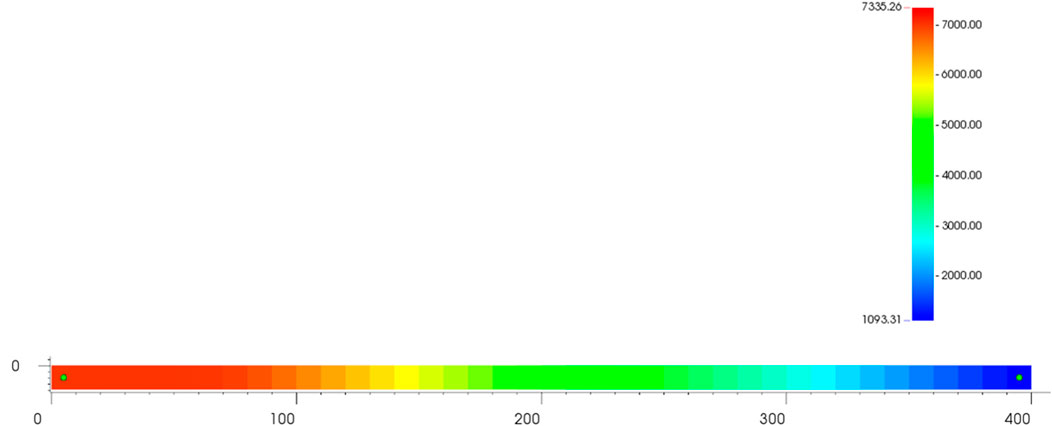
We demonstrate the strategy described in this research by using a one-dimensional steam flooding example. We created a single-injection model with a model size of 400 m*10 m*10 m and a 5 m model distribution interval. At 4,000 mD, the permeability is uniform, the porosity is 0.3, and the first water saturation is 0.15. On the model’s far left side, an injection well with continuous injection of 80 percent wet steam at 7,000 kPa and production well at 300°C are depicted. On the right is a production well capable of continuous output at 1,000 kPa. The reservoir’s initial temperature is 50°C. Calculated over a period of 1,000 days.
From Figures 1– 5, we can see that the temperature and water saturation leading edges are nearly identical. The temperature leading edge is 70°C at 65 m from the injection well site, and the water saturation is 0.175. The steam leading edge is 35 m from the injection well, at a gas saturation of 0.175, a temperature of 285°C, and a pressure of 6,997 kPa, all of which meet the parameters for steam generation and are consistent with objective facts.
It is feasible to divide the reservoir into three regions: steam flooding, hot water flooding, and cold water flooding, which corresponds to prior knowledge of steam flooding calculation and suggests that the method described in this study is reliable and effective.
3.2 Sensitivity Analysis
3.2.1 Effect of Steam Dryness
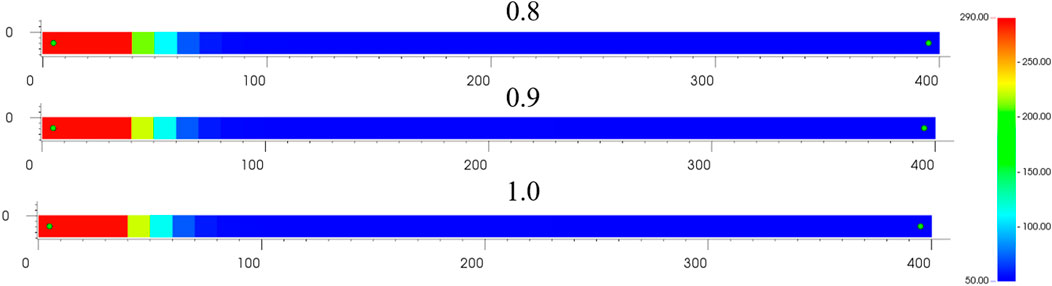
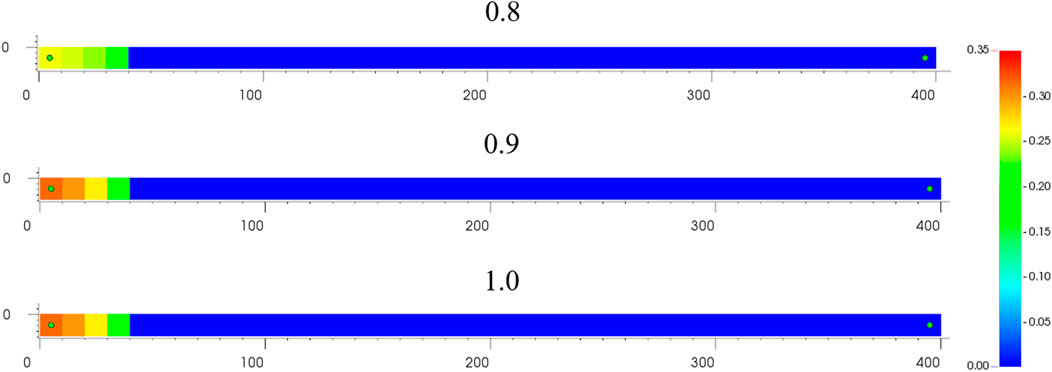
The model mentioned previously was used to adjust the injected steam dryness using steam with a dryness of 80, 90, and 100% and an injection temperature of 270°C. By using the weighted least squares meshless approach, the distribution spacing remains 10 m, and all other parameters stay same from the previous example.
It can be seen from Figure 6 that there is basically no difference in the temperature distribution within the reservoir after 1,000 days of calculations at steam dryness of 80, 90, and 100%, respectively, and the temperature leading edge is still at the location 65 m from the injection well with a temperature of 70.6°C, and the maximum temperature of the reservoir is also both 285°C. From Figure 7, it can be seen that the gas saturation at the location of the injection well is 0.259 and the gas saturation at the leading edge is 0.166 when the dryness of the injection steam is 80%, while when the dryness of the injection steam is 90 and 100%, the gas saturation remains basically the same in both cases. The gas saturation at the injection well is 0.31. The gas saturation at the leading edge is 0.188. The calculation is in line with the objective factual perception and reflects the stability of the calculation method in this paper from the side.
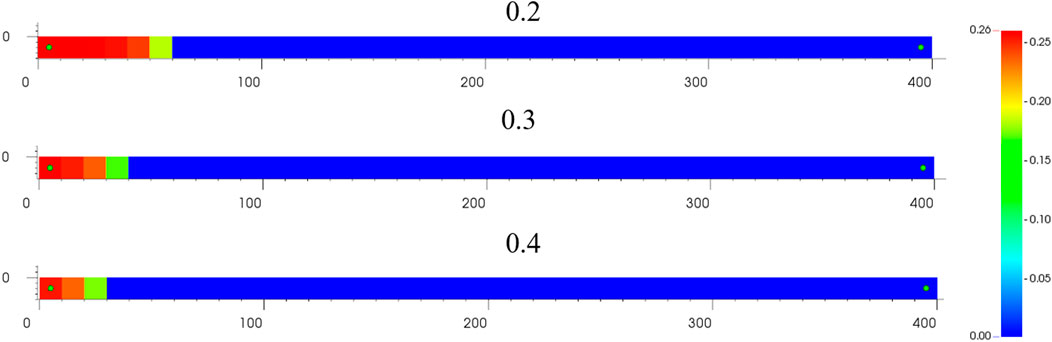
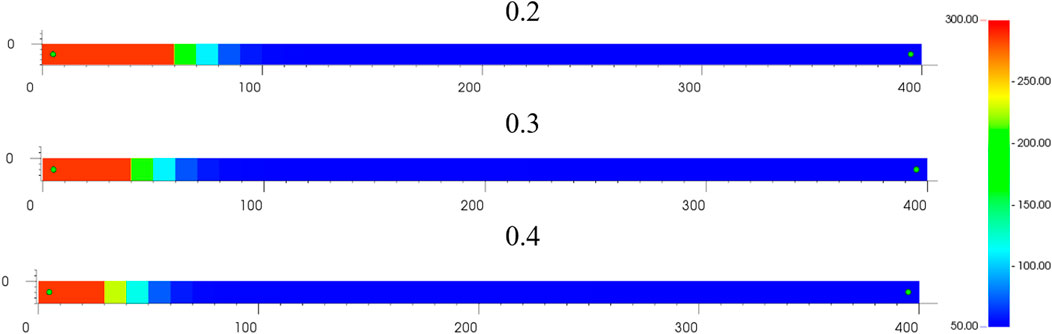
3.2.2 Effect of Porosity
Still using the above model, the initial porosity of the reservoir was varied and calculated using initial porosity of 0.2, 0.3, and 0.4 respectively. The injection temperature is 300°C. Calculated by weighted least squares meshless method. The layout spacing is still 10 m. Other parameters remain the same as above.
As illustrated in Figure 8, there is little difference in the temperature distribution within the reservoir after 1,000 days of calculations at steam dryness values of 80, 90, and 100%, respectively, and the temperature leading edge remains 65 m from the injection well at a temperature of 70.6°C, while the reservoir’s maximum temperature remains the same at 285°C. As illustrated in Figure 9, the gas saturation at the injection well site is 0.259 and the gas saturation at the leading edge is 0.166 when the injection steam is 80 percent dry, whereas the gas saturation remains virtually unchanged when the injection steam is 90 percent or 100 percent dry. The injection well has a gas saturation of 0.31. At the leading edge, the gas saturation is 0.188. The calculation is consistent with objective factual perception and demonstrates the stability of the procedure used in this research.
4 Conclusion
1) A mathematical model of steam flooding reservoir with coupled seepage field and thermal field is established, and the meshless weighted least squares technique is used to solve pressure, saturation and temperature successively. The method has high stability and correctness.
2) A one-dimensional steam flooding model with one injection and one recovery is established and solved by using the method proposed in this paper. The calculated results can be divided into steam flooding area, hot water flooding area and cold water flooding area, which is consistent with the basic knowledge and proves the correctness of the calculation method.
3) The sensitivity of injected steam dryness was analyzed by one-dimensional model. The temperature distribution inside the reservoir changes little at 80 and 80% steam dryness. The maximum gas saturation is 0.31 at 90 and 100%, and 0.259 at 80%, indicating the stability of the method.
4) Sensitivity analysis of model porosity. It is found that porosity directly affects the distribution of gas phase saturation and temperature in the leading edge. When the reservoir porosity is 0.2, 0.3 and 0.4, the gas saturation front is 60, 40 and 30 m, and the temperature front is 90, 70 and 60 m. The calculation is compatible with objective data, and the accuracy of the program used in this paper is proved.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
FW was employed by the company by the China Oilfield Services Limited.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Almao, P. P. (2012). In Situ upgrading of Bitumen and Heavy Oils via Nanocatalysis. Can. J. Chem. Eng. 90 (2), 320–329. doi:10.1002/cjce.21646
AtluriZhu, S. N. T., and Zhu, T. (1998). A New Meshless Local Petrov-Galerkin (MLPG) Approach in Computational Mechanics. Comput. Mech. 22 (2), 117–127. doi:10.1007/s004660050346
Crookston, R. B., CulhamChen, W. E. W. H., and Chen, W. H. (1979). A Numerical Simulation Model for thermal Recovery Processes. Soc. Pet. Eng. J. 19 (01), 37–58. doi:10.2118/6724-pa
Deng, H., Sheng, G., Zhao, H., Meng, F., Zhang, H., Ma, J., et al. (2022). Integrated Optimization of Fracture Parameters for Subdivision Cutting Fractured Horizontal wells in Shale Oil Reservoirs. J. Pet. Sci. Eng. 212, 110205. doi:10.1016/j.petrol.2022.110205
Desheng, M. A., Jia, G., Cheng, Z., Hongzhuang, W., Xiuluan, L., Lin, S. H. I., et al. (2013). Physical Simulation of Improving the Uniformity of Steam Chamber Growth in the Steam Assisted Gravity Drainage. Pet. exploration Dev. 40 (2), 202–207.
Guo, K., Li, H., and Yu, Z. (2016). In-situ Heavy and Extra-heavy Oil Recovery: A Review. Fuel 185, 886–902. doi:10.1016/j.fuel.2016.08.047
Huang, L., Sheng, G., Li, S., Tong, G., and Wang, S. (2021). A Review of Flow Mechanism and Inversion Methods of Fracture Network in Shale Gas Reservoirs. Hindawi: Geofluids, 2021. doi:10.1155/2021/6689698
Huang, S., Chen, X., Liu, H., Xia, Y., Jiang, J., Cao, M., et al. (2019). Experimental and Numerical Study of Steam-Chamber Evolution during Solvent-Enhanced Steam Flooding in Thin Heavy-Oil Reservoirs. J. Pet. Sci. Eng. 172, 776–786. doi:10.1016/j.petrol.2018.08.071
Johnson, F. S., WalkerBayazeed, C. J. A. F., and Bayazeed, A. F. (1971). Oil Vaporization during Steamflooding. J. Pet. Tech. 23 (06), 731–742. doi:10.2118/2977-pa
Lin, C., Jianlong, X., Lixin, H., Feng, H., and Yunfeng, X. (2020). Meshless Method-Based Numerical Simulation of Microbial Flooding. Xinjiang Pet. Geology. 42 (2), 206.
Liu, Y., Zhang, X., Lu, M.-W., and Lu, M.-W. (2005). A Meshless Method Based on Least-Squares Approach for Steady- and Unsteady-State Heat Conduction Problems. Numer. Heat Transfer, B: Fundamentals 47 (3), 257–275. doi:10.1080/10407790590901648
Lucy, L. B. (1977). A Numerical Approach to the Testing of the Fission Hypothesis. astronomical J. 82, 1013–1024. doi:10.1086/112164
Ma, V., and MainiOkazawa, B. T. (1984). Laboratory Simulation of Steam Drive Process. OnePetro: Annual Technical Meeting.
Maity, S. K., AncheytaMarroquín, J. G., and Marroquín, G. (2010). Catalytic Aquathermolysis Used for Viscosity Reduction of Heavy Crude Oils: a Review. Energy Fuels 24 (5), 2809–2816. doi:10.1021/ef100230k
MarxLangenheim, J. W. R., and Langenheim, R. H. (1959). Reservoir Heating by Hot Fluid Injection. Trans. AIME 216 (01), 312–315. doi:10.2118/1266-g
Mozaffari, S., Nikookar, M., Ehsani, M. R., Sahranavard, L., Roayaie, E., and Mohammadi, A. H. (2013). Numerical Modeling of Steam Injection in Heavy Oil Reservoirs. Fuel 112, 185–192. doi:10.1016/j.fuel.2013.04.084
MurazaGaladima, O. A., and Galadima, A. (2015). Aquathermolysis of Heavy Oil: A Review and Perspective on Catalyst Development. Fuel 157, 219–231. doi:10.1016/j.fuel.2015.04.065
Ping, Z., Yue, M., WangWang, M. X., and Wang, X. (2021). Simulation of Steam-Flooding Thermal Heavy Oil Recovery Process with Sequential Implicit Method. IOP Conf. Ser. Earth Environ. Sci. 692, 042027. doi:10.1088/1755-1315/692/4/042027
Rao, X., Zhan, W., Zhao, H., Xu, Y., Liu, D., Dai, W., et al. (2021). Application of the Least-Square Meshless Method to Gas-Water Flow Simulation of Complex-Shape Shale Gas Reservoirs. Eng. Anal. Boundary Elem. 129, 39–54. doi:10.1016/j.enganabound.2021.04.018
Sheng, G., SuWang, Y. W., and Wang, W. (2019). A New Fractal Approach for Describing Induced-Fracture Porosity/permeability/Compressibility in Stimulated Unconventional Reservoirs. J. Pet. Sci. Eng. 179, 855–866. doi:10.1016/j.petrol.2019.04.104
Van Lookeren, J. (1983). Calculation Methods for Linear and Radial Steam Flow in Oil Reservoirs. Soc. Pet. Eng. J. 23 (03), 427–439. doi:10.2118/6788-pa
VignjevicCampbell, R. J., and Campbell, J. (2009). Review of Development of the Smooth Particle Hydrodynamics (SPH) Method, Predictive Modeling of Dynamic Processes. Springer, 367–396. doi:10.1007/978-1-4419-0727-1_20
Xu, Y., Hu, Y., Rao, X., Zhao, H., Zhong, X., Peng, X., et al. (2022). A Fractal Physics-Based Data-Driven Model for Water-Flooding Reservoir (FlowNet-Fractal). J. Pet. Sci. Eng. 210, 109960. doi:10.1016/j.petrol.2021.109960
Xu, Y., Sheng, G., Zhao, H., Hui, Y., Zhou, Y., Ma, J., et al. (2021). A New Approach for Gas-Water Flow Simulation in Multi-Fractured Horizontal wells of Shale Gas Reservoirs. J. Pet. Sci. Eng. 199, 108292. doi:10.1016/j.petrol.2020.108292
Yang, J., Li, X., Chen, Z., Tian, J., Liu, X., and Wu, K. (2016). Combined Steam-Air Flooding Studies: Experiments, Numerical Simulation, and Field Test in the Qi-40 Block. Energy Fuels 30 (3), 2060–2065. doi:10.1021/acs.energyfuels.5b02850
Keywords: steam flooding, fluid dynamics, meshless method, heat transfer, fluid flow
Citation: Wang F (2022) A New Method for Solving the Mass and Heat Transfer Process in Steam Flooding. Front. Energy Res. 10:910829. doi: 10.3389/fenrg.2022.910829
Received: 01 April 2022; Accepted: 12 April 2022;
Published: 12 May 2022.
Edited by:
Xun Zhong, Yangtze University, ChinaCopyright © 2022 Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fei Wang, NzkzNDAwMjVAcXEuY29t
 Fei Wang
Fei Wang