Power Oscillation Analysis of PMSG Wind Power Generation System Considering Power Control Nonlinearity

High proportion of renewable energy generation, especially wind power generation, has changed the dynamic behavior of power systems and leads to emerging stability issues such as oscillation accidents. The commonly used stability analysis methods based on linear system theory cannot tackle the influence of nonlinear elements in the control loop. To fill this gap, the describing function method is used to analyze the stability and power oscillations of a grid-connected permanent magnet synchronous generator (PMSG) wind power generation system in this paper. A complete PMSG system model is taken into consideration, including a wind turbine, a generator, a machine-side converter, a grid-side converter, and a weak grid. Particularly, the nonlinear element introduced by maximum power point tracking control in the power control loop is modeled and analyzed, and the influences of critical system parameters are studied. With the high accuracy of the describing function method, it is revealed that the machine-side converter mainly influences the oscillation amplitude, while the grid-side converter mainly influences the oscillation frequency. Furthermore, the following results can be obtained: 1) High bandwidth of maximum power point tracking control and rotation speed control may enlarge the oscillation amplitude, while a fast current loop of the machine-side converter is beneficial to the stability; 2) Grid-side voltage loop can significantly affect the frequency of the oscillation, and improper high bandwidth of a phase-locked loop (PLL) is harmful to system stability; 3) A stronger grid is not always beneficial to the system stability, and the influence of grid strength should be carefully analyzed and examined when nonlinear elements are considered. All analyses are verified by simulations based on MATLAB/Simulink.

1 Introduction

Converter interfaced power generation technologies for renewable energy integration have significantly changed the dynamic behavior of power systems, leading to new types of stability problems such as power oscillations (Hatziargyriou et al., 2021). High proportion of renewable energy generation has brought a huge risk of power oscillations, and seriously threatens the stability of the power systems (Chi et al., 2019). In recent years, many power oscillation accidents have been reported in, for example, high-voltage direct current (HVDC) systems (Amin et al., 2017), offshore wind farms (Lyu et al., 2018), microgrids (Guo et al., 2017; Wang et al., 2017), and photovoltaic (PV) generators (Xia et al., 2019a; Zhao et al., 2019a). Some of the oscillations that are prone to occur in weak grid-connected wind power systems with the frequency from 2.5 to 50/60 Hz are classified as sub-synchronous oscillations (SSOs), and their harm is tremendous (Bi et al., 2017; Shi et al., 2020). It is reported that some SSO events that happened in Guyuan wind farms even involved more than a thousand wind turbine generators (Shair et al., 2019), and the oscillation frequency characteristics were strongly affected by the converter control parameters (Wang et al., 2015; Xie et al., 2017). Another severe SSO event that happened in Hami wind farms caused widely-propagated oscillations, leading to torsional oscillations of thermal power units 300 km away from the wind farms (Liu et al., 2017). Permanent magnet synchronous generator (PMSG)-based wind turbines were highly involved in these SSO events, and the role of PMSGs in these events is gradually gaining attention. Furthermore, the application of the PMSG-based wind power system is with rapid development due to its tremendous advantages (Mahmoud et al., 2021; Mahmoud et al., 2022), hence power oscillations of the PMSG-based wind power system deserve in-depth study.

Power oscillations generally start from small-signal instability, then rapidly grow due to the lack of damping in the systems, and finally evolve into sustained oscillations that can widely propagate until some of the devices participating in the oscillations are disconnected (Liu et al., 2017; Liu and Xie, 2018; Wu et al., 2021). The characteristics of the oscillations such as amplitude and frequency are strongly related to the control parameters of power converters, and are also influenced by the features of the interface grids, which can be described by grid strength (Wang and Blaabjerg, 2019).

To elaborate the mechanism of the oscillation phenomenon, a variety of linearized models and linear system methods are used for stability analyses. Eigenvalue analysis is a classic stability analysis method, based on which interactions among PMSGs are studied (Huang et al., 2019b; Zhao et al., 2019b). According to the root loci and participation factors of an SSO mode, it is found that a decrease of grid strength may drive the SSO mode towards the unstable region and this mode highly involves the DC capacitor, the AC network and the current control of grid-side converter (GSC) (Huang et al., 2019a). The eigenvalue analysis can be also combined with discrete-time state-space models so that it can be used for complicated high-order systems (Han et al., 2022). Another widely used method is impedance analysis, which has special advantages in “black-box” modeling (Sun, 2009). This method was originally designed for dc-dc converters and then was developed and applied to ac power systems (Liu et al., 2020). For single dc-ac converters, impedance models can be established in dq-domain or sequence-domain (Cespedes and Sun, 2014; Wen et al., 2015), and these two kinds of models are basically equivalent for stability analyses on the condition that there is no significant frequency coupling (Rygg et al., 2017). Based on dq-domain impedance analysis, it is pointed out that the phase-locked loop (PLL) with higher bandwidth may enlarge the frequency range of the negative incremental resistance characteristic introduced by converter controllers, and could make the system unstable (Wen et al., 2016). For wind power systems, impedance models of PMSG considering both machine-side converter (MSC) and GSC are established, and it is proven that the parameters of the MSC controller have a noticeable effect on the impedance characteristic and significantly affect the stability margin (Xue et al., 2020; Liu et al., 2021). Furthermore, impedance analysis is also applied for large-scale power systems with wind farms as a result of being conveniently aggregated (Liu and Xie, 2018).

However, all aforementioned linearized methods are aimed at the small-signal instability stage of power oscillations, but are unsuitable for the stage of sustained oscillations which lasts for much more time with durative harm, since various nonlinear elements are participating in the sustained oscillations. The linearized methods also cannot predict whether the system can reach a new equilibrium point. Although some large-signal modeling and analysis methods such as the equal area method and the phase-plane method are applied to analyze whether new equilibrium points exist after a nonlinear transient process (Hu et al., 2019; Wang et al., 2020), only extremely simplified systems can be analyzed and the oscillation characteristic cannot be reflected in these methods. To study the influence of nonlinear elements on the system stability, describing function (DF) method is introduced. The DF method, also called the harmonic linearization or the harmonic balance method, is a powerful frequency approximate method for nonlinear system analysis and design (Gasparyan, 2008). The main idea of this method is that a time-domain discontinuous nonlinear element can be linearized and replaced by a complex gain in the frequency domain. Hence, the nonlinearity which is commonly ignored by small-signal linearization methods can be analyzed. Furthermore, as a prediction of a limit cycle, or a steady-state periodical process with a certain frequency, the DF method gives a feasible way to calculate the amplitude and frequency of sustained oscillations. This feature can be utilized in the analysis of power oscillations in renewable energy systems, and provide valuable information for the identification and elimination of oscillation events (Xia et al., 2019b).

Power oscillations caused by the grid-connected PV generators are analyzed by the DF method (Wei et al., 2020). It is found that the power control nonlinearity has a significant influence on the system stability, and the improperly fast power control loop will cause sustained power oscillations. In (Xu et al., 2020) and (Wu et al., 2020), power oscillations for wind turbines are also studied based on the DF method. It is reported that the sustained SSO can be estimated more accurately compared with conventional eigenvalue analysis, and the nonlinearity may affect the frequency response of the system at sub-synchronous frequencies, which means the results of conventional small-signal methods should be supplemented and carefully examined. However, the power control nonlinearity has not been considered in these articles, and more importantly, the MSCs and their controllers which have an important effect on system characteristics are omitted. Therefore, power oscillations involving a complete PMSG model with power control nonlinearity still need detailed analysis.

This paper adopts the DF method to analyze the power oscillations that occur in the weak grid-connected PMSG systems with the consideration of a complete PMSG model. First, the model of PMSG including the wind turbine, the generator, the MSC, the GSC, and the weak grid is established. In the model of MSC, the maximum power point tracking controller, i.e. the power control loop of the MSC, applies the perturbation and observation (P&O) algorithm, which is widely used in wind energy systems (Abdullah et al., 2012; Kumar and Chatterjee, 2016). The discontinuous nonlinear element of the P&O algorithm is modeled by a describing function, and other elements that can be linearized are modeled by a transfer function. Then, the stability of the system is analyzed by the DF method. The influence of MSC controller parameters, GSC controller parameters, grid strength, and PLL are studied respectively and the relationship between these parameters and the oscillation characteristics is revealed. The DF method is compared with the conventional linearized stability analysis method to show its advantages, and time-domain simulations are conducted to verify the accuracy of the method. The results show that the nonlinear element has a crucial effect on the system stability, and some of the results obtained by conventional linearized methods are incorrect under certain scenarios. A brief comparison with the existing research is shown in Table 1, and the main contributions of this paper are summarized as follows.

1) This paper adopts the describing function method to tackle the influence of power control nonlinearity, which cannot be tackled by the commonly used stability analysis method based on linear system theory.

2) The describing function-based stability analysis can calculate the amplitude and frequency of power oscillation accurately.

3) Some critical findings can be obtained by analyzing the influences of critical control parameters using describing function method. The different effects of GSC and MSC controllers on oscillation characteristics are distinguished.

TABLE 1

TABLE 1. Comparison with existing stability analysis methods.

The rest of this paper is organized as follows. In Section 2, the basic principles of the DF method are introduced. In Section 3, the complete model of the grid-connected PMSG system is established. In Section 4, stability and oscillations are analyzed by the DF method, and the simulation results are presented. In Section 5, the main conclusions of the analyses are drawn.

2 Brief Introduction to DF Method

Describing function method is a kind of extended frequency response method that can be used to analyze the nonlinear behavior or predict potential limit cycle in nonlinear systems (Nassirharand, 2012). Figure 1 shows a nonlinear Single-Input-Single-Output (SISO) system with a single nonlinear element F(x), and the stability of the system is determined by the distribution of the roots of the closed-loop characteristic equation on the condition that F(x) can be properly linearized. The establishment of the describing function of a nonlinear element is a process of harmonic linearization (Atherton, 1975). Assume that a steady-state periodical process exists, i.e. the input φ(t) = 0 and x(t) = Asin(ωt), then the output y(t) of the nonlinear element is also a periodic function that can be expanded by Fourier series as

$y\left(t\right)=A_0+{\mathrm{\Sigma }}_{k=1}^{\infty }{A}_k\text{sin}\left(k\omega t+{\theta }_k\right)(1)$

FIGURE 1

FIGURE 1. Nonlinear SISO system.

To represent the nonlinear element by a describing function, there are several basic assumptions:

1) The nonlinear element is odd, symmetrical, and memoryless, so that A₀ = 0.

2) Linear part G(s) is low-pass so that higher harmonics (beginning from the second) can be attenuated and neglected.

Based on these assumptions, the describing function is defined as the ratio of the fundamental term of the Fourier series of y(t) to the input signal x(t), i.e.

$N\left(A\right)=\frac{A_1{\mathrm{e}}^{\text{j}{\theta }_1}}{A}=\frac{1}{A}\left(a_1+\text{j}{b}_1\right)(2)$

where $A_1=\sqrt{a_1^2+b_1^2}$, $a_1=\frac{1}{\mathrm{\pi }}\underset{0}{\overset{2\mathrm{\pi }}{{\displaystyle \int }}}F\left(A\sin \psi \right)\sin \psi \mathrm{d}\psi$, $b_1=\frac{1}{\mathrm{\pi }}\underset{0}{\overset{2\mathrm{\pi }}{{\displaystyle \int }}}F\left(A\sin \psi \right)\cos \psi \mathrm{d}\psi$. The describing function N(A) is a complex gain, but in the case of single-value nonlinearities, b₁ = 0, which means the nonlinear element does not cause any phase shift.

The nonlinear element F(x) is replaced by a linear element N(A) which depends on the unknown amplitude A, and the stability of the linearized system can be determined by the position of the roots of the closed-loop characteristic equation

$1+N\left(A\right)G\left(s\right)=0(3)$

If the real part of all the roots is negative, the system will be stable. If the real part of any of the roots is positive, the system will be unstable. If the characteristic equation has a pure imaginary root (or a couple of complex-conjugate pure imaginary roots) and all other roots have negative real parts, the system will be critically stable and a steady oscillation with constant amplitude and frequency may occur. In the last case, the unknown amplitude A and the frequency ω can be calculated through two algebraic equations derived from (3),

$\{\begin{array}{c}\text{Re}\left[N\left(A\right)G\left(\mathrm{j}\omega \right)\right]=-1\\ \text{Im}\left[N\left(A\right)G\left(\mathrm{j}\omega \right)\right]=0\end{array}(4)$

Once the closed-loop characteristic equation is established, the Nyquist criterion can be used, and the corresponding graphical analysis method will avoid repetitive solving of (3). Rewrite (3) as

$G\left(s\right)=-\frac{1}{N\left(A\right)}(5)$

The stability of the whole system can be judged by the relative position of −1/N(A) and G(s) curves in the s plane. As shown in Figure 2, on the condition that G(s) does not have right-plane poles (the open-loop system is stable), the extended Nyquist criterion states that if the −1/N(A) curve is not surrounded by the G(s) curve, the system will be stable, and if −1/N(A) is surrounded by G(s), the system will be unstable. If the two curves intersect, the system will be critically stable, and at least one limit cycle may exist. Furthermore, the stability of the limit cycle depends on whether the system withstands small disturbances at the intersections. For example, provided that the system initially operates at the point P₁ in Figure 2, when it moves to P₁’ due to a small disturbance, the amplitude A will continuously increase along the −1/N(A) curve because the system is unstable at P₁’, until the operating point returns to P₁. In the other direction, at the point P₁″, the amplitude A will decrease because the system is stable, and finally the operating point also returns to P₁. Hence, the intersection P₁ corresponds to a stable limit cycle in the system, and the oscillation information can be derived by (4). Similarly, it can be inferred that P₂ corresponds to an unstable limit cycle, and any slight disturbance will cause the system to deviate from this operating point.

FIGURE 2

FIGURE 2. Stability analysis based on the extended Nyquist criterion.

3 Complete Model of Grid-Connected PMSG System

In this section, a complete model of the grid-connected PMSG is derived considering the wind turbine, the generator, the MSC, the GSC, and the weak grid. Figure 3 shows the structure and the control strategy of the system. The wind turbine with a horizontal axis is directly coupled to the rotor of the PMSG, and the generator is symmetrical and cylindrical. The control methods are selected as voltage-oriented control under unity power coefficient for the grid-side converter, zero d-axis current control for the machine-side converter, and P&O control for the maximum power point tracking. The output current of the generator is i_a,b,cr, the mechanical angular velocity of the generator is ω_g, the electrical angular velocity of the generator is ω_e, and the electrical angle of the generator is θ_e. A shunt capacitor C_dc is connected between the converters, and the capacitor voltage is u_dc. On the DC side, the current flowing out of the MSC is i_dc2, and the current flowing into the GSC is i_dc1. The output current of the GSC is i_a,b,cg filtered by the inductor L_f. The voltage at the point of common coupling (PCC) is u_a,b,cg and the weak grid is represented as a grid inductor L_g in series with an ideal voltage source u_a,b,cs.

FIGURE 3

FIGURE 3. Structure and control strategy of the grid-connected PMSG.

3.1 Model of the Wind Turbine and Drive Train

The wind turbine converts wind energy into mechanical motion and runs the generator. In general, the fraction of power extracted from the wind power is denoted by the power coefficient C_p of the wind turbine, and the actual mechanical power P_m provided by the wind turbine is

$P_{\text{m}}=\frac{1}{2}\text{ρπ}{R}^2{C}_{\mathrm{p}}{v}_{\mathrm{w}}^3(6)$

where ρ denotes the air mass density, R denotes the blade radius, and v_w denotes the wind velocity. C_p is a function of tip velocity ratio λ (λ = ω_gR/v_w) and pitch angle (in degrees) denoted by β,

$C_{\text{p}}=0.22\left(\frac{116}{{\lambda }_i}-0.4\beta -5\right){\mathrm{e}}^{-\frac{12.5}{{\lambda }_i}}(7)$

where

$\frac{1}{{\lambda }_i}=\frac{1}{\lambda +0.08\beta }-\frac{0.035}{{\beta }^3+1}(8)$

Note that (7) and (8) are the mathematical approximation of a real curve of C_p, and they have no physical meaning. When the PMSG works in maximum power point tracking mode, the wind velocity is smaller than the rated value, and hence only the condition that β = 0° is considered.

As the shaft of the wind turbine is directly connected to the rotor of the generator, their rotational speed is the same ω_g. The drive train is modeled by a one-mass model, i.e.

$J\frac{\text{d}{\omega }_{\text{g}}}{\text{d}t}=T_{\text{m}}-T_{\text{e}}(9)$

where T_m=P_m/ω_g is the mechanical torque provided by the wind turbine, T_e is the electrical torque of the generator, and J is the equivalent inertia that contains both the turbine and the generator. Then the small-signal model (after Laplace transform) of the drive train is derived as

$sJ\text{Δ}{\omega }_{\text{g}}=\text{Δ}{T}_{\text{m}}-\text{Δ}{T}_{\text{e}}(10)$

where $\text{Δ}{T}_{\text{m}}=B_{\mathrm{t}}\text{Δ}{\omega }_{\text{g}}$, $B_{\text{t}}={\frac{\text{d}{T}_{\text{m}}}{\text{d}{\omega }_{\text{g}}}|}_{{\omega }_{\text{g}}={\omega }_{\text{g}}^{\ast }}$, ${\omega }_{\text{g}}^{\ast }$ denotes the steady-state value of ω_g at equilibrium points. Besides, the mark Δ denotes small-signal disturbance of the corresponding variables, and capital letters with superscript * denote a steady-state value of the corresponding variables in this paper.

3.2 Model of the PMSG and MSC

Provided that the d-axis is aligned with the magnetic flux linkage of the rotor and the PMSG is a round rotor machine, the small-signal model of PMSG can be expressed as

${\mathit{Z}}_{\mathbf{\text{dqr}}}\cdot \mathbf{\Delta }{\mathit{i}}_{\mathbf{dqr}}=-U_{\text{dc}}^{\text{∗}}\cdot \mathbf{\Delta }{\mathit{d}}_{\mathbf{dqr}}-{\mathit{D}}_{\mathbf{dqr}}^{\text{∗}}\cdot \mathrm{\Delta }{u}_{\text{dc}}+{\mathit{G}}_{\mathbf{\omega e}}\cdot \mathrm{\Delta }{\omega }_{\text{e}}(11)$

$\text{Δ}{T}_{\text{e}}=\frac{3}{2}{n}_{\text{p}}{\psi }_{\text{f}}\text{Δ}{i}_{\text{qr}}(12)$

where ${\mathit{Z}}_{\mathbf{d}\mathbf{q}\mathbf{r}}=\left[\begin{array}{cc}s{L}_{\text{s}}+R_{\text{s}}& -{\omega }_{\text{e}}^{\ast }{L}_{\text{s}}\\ {\omega }_{\text{e}}^{\ast }{L}_{\text{s}}& s{L}_{\text{s}}+R_{\text{s}}\end{array}\right]$, $\mathbf{\Delta }{\mathit{i}}_{\mathbf{dqr}}=\left[\begin{array}{c}\text{Δ}{i}_{\text{dr}}\\ \text{Δ}{i}_{\text{qr}}\end{array}\right]$, $\mathbf{\Delta }{\mathit{d}}_{\mathbf{dqr}}=\left[\begin{array}{c}\text{Δ}{d}_{\text{dr}}\\ \text{Δ}{d}_{\text{qr}}\end{array}\right]$, ${\mathit{D}}_{\mathbf{dqr}}^{\text{*}}=\left[\begin{array}{c}{D}_{\text{dr}}^{\text{*}}\\ D_{\text{qr}}^{\text{*}}\end{array}\right]$, ${\mathit{G}}_{\mathbf{\omega e}}=\left[\begin{array}{c}{L}_{\text{s}}{I}_{\text{qr}}^{\text{*}}\\ {\psi }_{\text{f}}-L_{\text{s}}{I}_{\text{dr}}^{\text{*}}\end{array}\right]$. L_s and R_s denote the armature inductance and stator resistance respectively, i_dr and i_qr denote the dq-axis stator currents respectively, and d_dr and d_qr denote the dq-axis duty ratios of the MSC controller respectively. ψ_f is the permanent magnet flux and n_p is the number of pole pairs. Based on (10) and (12), it is drawn that stator current disturbance can cause mechanical angular velocity disturbance, and their relationship is derived as

$\text{Δ}{\omega }_{\text{g}}=\frac{3n_{\text{p}}{\psi }_{\text{f}}}{2\left(B_{\text{t}}-sJ\right)}\text{Δ}{i}_{\text{qr}}=\left[\begin{array}{cc}0& \frac{3n_{\text{p}}{\psi }_{\text{f}}}{2\left(B_{\text{t}}-sJ\right)}\end{array}\right]\cdot \mathbf{\Delta }{\mathit{i}}_{\mathbf{dqr}}(13)$

Let ${\mathit{G}}_{\mathbf{iq\omega }}=\left[\begin{array}{cc}0& \frac{3n_{\text{p}}{\psi }_{\text{f}}}{2\left(B_{\mathrm{t}}-sJ\right)}\end{array}\right]$, and then $\text{Δ}{\omega }_{\text{g}}={\mathit{G}}_{\mathbf{iq\omega }}\mathbf{\Delta }{\mathit{i}}_{\mathbf{dqr}}$, $\text{Δ}{\omega }_{\text{e}}=n_{\text{p}}{\mathit{G}}_{\mathbf{iq\omega }}\mathbf{\Delta }{\mathit{i}}_{\mathbf{dqr}}$.

In the following, the model of the MSC controller is established. The MSC controller can be found in Figure 3, and it consists of the power control loop based on the P&O algorithm, the rotational speed loop (H_ω), and the current control loop (H_cg). The rotational speed and the current control loops are both based on PI controllers. In Figure 3 MSC controller, P^ref denotes the power reference value, P denotes the actual power output value, I_drref and i_qrref denote the dq-axis current reference value respectively, and ${\omega }_{\text{g}}^{\text{ref}}$ denotes the mechanical angular velocity reference value. Moreover, superscript “c” denotes variables in the controller dq frame, which should be distinguished from the system dq frame because the disturbance of electrical angular velocity can cause electrical angle disturbance, and hence affect the angle used for dq transformation. A typical P&O algorithm is shown in Figure 4, where T_p is the control cycle and ε is the perturbation step. When needed this algorithm can make the PMSG output constant power in the maximum power point tracking mode.

FIGURE 4

FIGURE 4. Flowchart of a typical P&O algorithm.

In fact, by analyzing Figure 4, one can find that the accumulation of ε can be approximated as an integrator on the condition that T_p is small enough. In each control cycle T_p, ${\omega }_{\text{g}}^{\text{ref}}$ increases or decreases by one perturbation step ε, which means the controller is equivalent to an integrator whose integral coefficient is ±ε/T_p, and the direction is determined by the sign of δP∙δω_g and P^ref−P (note that P in Figure 3 has the same meaning as P_n in Figure 4). Therefore, the algorithm shown in Figure 4 can be expressed as

${\omega }_{\text{g}}^{\text{ref}}={\displaystyle \int \frac{\epsilon }{T_{\text{P}}}\text{sgn}\left(P^{\text{ref}}-P\right)\text{sgn}\left(\text{δ}P\cdot \text{δ}{\omega }_g\right)\mathrm{d}t}(14)$

where sgn(x) is a sign function, when x ≥ 0, sgn(x) = 1, and when x < 0, sgn(x) = −1. Furthermore, the basic principle of the P&O algorithm states that the sign of δP∙δω_g reflects whether the system is currently running on the left or the right of the maximum power point, i.e. δP∙δω_g = 1 when ω_g ≤ ω_mpp (left), and δP∙δω_g = −1 when ω_g > ω_mpp (right). ω_mpp denotes the mechanical angular velocity at the maximum power point of a certain wind velocity. If these two cases are discussed separately, (14) can be written as

${\omega }_{\text{g}}^{\text{ref}}=\{\begin{array}{cc}{\displaystyle \int \frac{\epsilon }{T_{\text{P}}}\text{sgn}\left(P^{\text{ref}}-P\right)\text{d}t}& \left({\omega }_{\text{g}}\le {\omega }_{\text{mpp}}\right)\\ -{\displaystyle \int \frac{\epsilon }{T_{\text{P}}}\text{sgn}\left(P^{\text{ref}}-P\right)\text{d}t}& \left({\omega }_{\text{g}}>{\omega }_{\text{mpp}}\right)\end{array}(15)$

Form (15), it is shown that the power control loop contains the linear part and the nonlinear element. The linear part is composed of an integrator with coefficient ε/T_p (or −ε/T_p), and the nonlinear element is the sign function. Based on the definition of the describing function introduced in Section 2, the describing function of the sign function can be derived as

$N\left(A\right)=\frac{4}{\text{π}A}(16)$

Then the approximate small-signal model of the power control loop in the frequency domain is

$\text{Δ}{\omega }_{\text{g}}^{\text{ref}}=\{\begin{array}{cc}\frac{\epsilon }{s{T}_{\text{P}}}N\left(A\right)\cdot \left(-\mathrm{\Delta }P\right)& \left({\omega }_{\text{g}}\le {\omega }_{\text{mpp}}\right)\\ -\frac{\epsilon }{s{T}_{\text{P}}}N\left(A\right)\cdot \left(-\mathrm{\Delta }P\right)& \left({\omega }_{\text{g}}>{\omega }_{\text{mpp}}\right)\end{array}(17)$

The small-signal model of the rotational speed loop and the current control loop of the MSC controller is expressed as

$\mathbf{\Delta }{\mathit{d}}_{\mathbf{dqr}}^{\mathbf{c}}=\frac{1}{U_{\text{dc}}^{\ast }}\left({\mathit{G}}_{\mathbf{cr}}\cdot \mathbf{\Delta }{\mathit{i}}_{\mathbf{dqr}}^{\mathbf{c}}+{\mathit{G}}_{\mathbf{\omega g}}\left({\omega }_{\text{g}}^{\text{ref}}-{\omega }_{\text{g}}\right)+{\mathit{G}}_{\mathbf{\omega e}}\cdot \text{Δ}{\omega }_{\text{e}}\right)(18)$

where ${\mathit{G}}_{\mathbf{cr}}=\left[\begin{array}{cc}{H}_{\text{cr}}& {\omega }_{\text{e}}^{\ast }{L}_{\text{s}}\\ -{\omega }_{\text{e}}^{\ast }{L}_{\text{s}}& H_{\text{cr}}\end{array}\right]$, ${\mathit{G}}_{\mathbf{\omega g}}=\left[\begin{array}{c}0\\ H_{\text{cr}}{H}_{\text{ω}}\end{array}\right]$. H_ω = K_ωp + K_ωi/s, K_ωp and K_ωi are the PI coefficients of the rotational speed loop respectively. H_cr = K_cpr + K_cir/s, K_cpr and K_cir are the PI coefficients of the current control loop of the MSC controller respectively. In the MSC controller, the dq transformation is affected by the electrical angular disturbance, and hence the controller dq frame and the system dq frame should be distinguished. The superscript “c” denotes the variables in the controller dq frame. The same situation also occurs in the GSC model, but the difference is that angular disturbance in the GSC controller is introduced by PLL dynamics, which is widely used in converter modeling and stability analysis field. The small-signal disturbance of the electrical angular is derived as

$\text{Δ}{\mathit{\theta }}_{\text{e}}=\frac{n_{\text{p}}\text{Δ}{\mathit{\omega }}_{\text{g}}}{s}=\frac{3n_{\text{p}}^2{\mathit{\psi }}_{\text{f}}}{2s\left(B_{\mathrm{t}}-sJ\right)}\text{Δ}{i}_{\text{qr}}=H_{\mathrm{\theta }\text{e}}\text{Δ}{i}_{\text{qr}}(19)$

where $H_{\text{θe}}=\frac{3n_{\text{p}}^2{\psi }_{\text{f}}}{2s\left(B_{\mathrm{t}}-sJ\right)}$, and the relationship of variables in the controller dq frame and the system dq frame is directly given as

$\{\begin{array}{c}\mathbf{\Delta }{\mathit{i}}_{\mathbf{dqr}}^{\mathbf{c}}={\mathit{G}}_{\mathbf{\theta e}}^{\mathbf{i}}\cdot \text{Δ}{\mathit{i}}_{\mathbf{dqr}}\\ \mathbf{\Delta }{\mathit{d}}_{\mathbf{dqr}}^{\mathbf{c}}={\mathit{G}}_{\mathbf{\theta e}}^{\mathbf{d}}\cdot \text{Δ}{\mathit{i}}_{\mathbf{dqr}}+\text{Δ}{\mathit{d}}_{\mathbf{dqr}}\end{array}(20)$

where ${\mathit{G}}_{\mathbf{\theta e}}^{\mathbf{i}}=\left[\begin{array}{cc}1& H_{\text{θe}}{I}_{\text{qr}}^{\text{*}}\\ 0& 1-H_{\text{θe}}{I}_{\text{dr}}^{\text{*}}\end{array}\right]$, ${\mathit{G}}_{\mathbf{\theta e}}^{\mathbf{d}}=\left[\begin{array}{cc}0& H_{\text{θe}}{D}_{\text{qr}}^{\text{*}}\\ 0& -H_{\text{θe}}{D}_{\text{dr}}^{\text{*}}\end{array}\right]$.

3.3 Model of the GSC and Weak Grid

The small-signal model of the GSC is expressed as

${\mathit{Z}}_{\mathbf{f}}\mathit{\cdot }\mathbf{\Delta }{\mathit{i}}_{\mathbf{dqg}}=U_{\text{dc}}^{\text{∗}}\cdot \mathbf{\Delta }{\mathit{d}}_{\mathbf{dqg}}+{\mathit{D}}_{\mathbf{dqg}}^{\text{∗}}\cdot \mathbf{\Delta }{u}_{\text{dc}}-\mathbf{\Delta }{\mathit{u}}_{\mathbf{dqg}}(21)$

where ${\mathit{Z}}_{\mathbf{f}}=\left[\begin{array}{cc}s{L}_{\text{f}}& -\omega L_{\text{f}}\\ \omega L_{\text{f}}& s{L}_{\text{f}}\end{array}\right]$, $\mathbf{\Delta }{\mathit{i}}_{\mathbf{dqg}}=\left[\begin{array}{c}\text{Δ}{i}_{\text{dg}}\\ \text{Δ}{i}_{\text{qg}}\end{array}\right]$, $\mathbf{\Delta }{\mathit{d}}_{\mathbf{dqg}}=\left[\begin{array}{c}\text{Δ}{d}_{\text{dg}}\\ \text{Δ}{d}_{\text{qg}}\end{array}\right]$, ${\mathit{D}}_{\mathbf{dqg}}^{\text{*}}=\left[\begin{array}{c}{D}_{\text{dg}}^{\text{*}}\\ D_{\text{qg}}^{\text{*}}\end{array}\right]$, $\mathbf{\Delta }{\mathit{u}}_{\mathbf{dqg}}=\left[\begin{array}{c}\text{Δ}{u}_{\text{dg}}\\ \text{Δ}{u}_{\text{qg}}\end{array}\right]$. L_f denotes the filter inductance and ω is the angular frequency of the power system. i_dg and i_qg denote the dq-axis output current of the GSC respectively, d_dg and d_qg denote the dq-axis duty ratios of the GSC controller respectively, and u_dg and u_qg denote the dq-axis PCC voltage respectively.

The small-signal model of the shunt capacitor is

$s{C}_{\text{dc}}\mathrm{\Delta }{u}_{\text{dc}}=1.5\left({\mathit{D}}_{\mathbf{dqr}}^{\ast T}\cdot \mathbf{\Delta }{\mathit{i}}_{\mathbf{dqr}}+{\mathbf{I}}_{\mathbf{dqr}}^{\ast }\cdot \mathbf{\Delta }{\mathit{d}}_{\mathbf{dqr}}\right)-1.5\left({\mathit{D}}_{\mathbf{dqg}}^{\ast T}\cdot \mathbf{\Delta }{\mathit{i}}_{\mathbf{dqg}}+{\mathit{I}}_{\mathbf{dqg}}^{\ast T}\cdot \mathbf{\Delta }{\mathit{d}}_{\mathbf{dqg}}\right)(22)$

The controller of GSC contains the commonly-used voltage loop and current loop, and the small-signal model is derived as

$\mathbf{\Delta }{\mathit{d}}_{\mathbf{dqg}}^{\mathbf{c}}\cdot U_{\text{dc}}^{\text{∗}}=\mathbf{\Delta }{\mathit{u}}_{\mathbf{dqg}}^{\mathbf{c}}+{\mathit{G}}_{\mathbf{cg}}\mathbf{\Delta }{\mathit{i}}_{\mathbf{dqg}}^{\mathbf{c}}+{\mathit{G}}_{\mathbf{udc}}\text{Δ}{u}_{\text{dc}}(23)$

where ${\mathit{G}}_{\mathbf{cg}}=\left[\begin{array}{cc}-H_{\text{cg}}& -\omega L_{\text{f}}\\ \omega L_{\text{f}}& -H_{\text{cg}}\end{array}\right]$, ${\mathit{G}}_{\mathbf{udc}}=\left[\begin{array}{c}{H}_{\text{cg}}{H}_{\text{v}}\\ 0\end{array}\right]$. H_cg = K_cpg + K_cig/s, K_cpg and K_cig are the PI coefficients of the current control loop of the GSC controller respectively. H_v = K_vp + K_vi/s, K_vp and K_vi are the PI coefficients of the voltage control loop of the GSC controller respectively. U_dcref is the reference value of dc voltage. As mentioned above, the superscript “c” denotes the controller dq frame.

PLL dynamics lead to the angular difference between the controller and the system dq frame and are also significant to the stability of the system. Since the modeling process of PLL is well studied and the existence of angular difference is revealed in many papers (such as (Wen et al., 2016)), the small-signal model of PLL is directly given as (24) and the relationship of variables in the two different dq frames is given as (25).

$\text{Δ}\theta =H_{\text{pll}}\cdot \frac{1}{s}\cdot \text{Δ}{u}_{\text{qg}}^{\text{c}}(24)$

where H_pll = K_ppll + K_ipll/s, K_ppll and K_ipll are the proportional and the integral coefficient of the PI controller of PLL.

$\{\begin{array}{l}\mathbf{\Delta }{\mathit{u}}_{\mathbf{dqg}}^{\mathbf{c}}={\mathit{G}}_{\mathbf{pll}}^{\mathbf{u}}\cdot \mathbf{\Delta }{\mathit{u}}_{\mathbf{dqg}}\hfill \\ \mathbf{\Delta }{\mathit{i}}_{\mathbf{dqg}}^{\mathbf{c}}={\mathit{G}}_{\mathbf{pll}}^{\mathbf{i}}\cdot \mathbf{\Delta }{\mathit{u}}_{\mathbf{dqg}}+\mathbf{\Delta }{\mathit{i}}_{\mathbf{dqg}}\hfill \\ \mathbf{\Delta }{\mathit{d}}_{\mathbf{dqg}}^{\mathbf{c}}={\mathit{G}}_{\mathbf{pll}}^{\mathbf{d}}\cdot \mathbf{\Delta }{\mathit{u}}_{\mathbf{dqg}}+\mathbf{\Delta }{\mathit{d}}_{\mathbf{dqg}}\hfill \end{array}(25)$

where ${\mathit{G}}_{\mathbf{pll}}^{\mathbf{u}}=\left[\begin{array}{cc}1& G_{\text{pll}}{U}_{\text{qg}}^{\text{*}}\\ 0& 1-G_{\text{pll}}{U}_{\text{dg}}^{\text{*}}\end{array}\right]$, ${\mathit{G}}_{\mathbf{pll}}^{\mathbf{i}}=\left[\begin{array}{cc}0& G_{\text{pll}}{I}_{\text{qg}}^{\text{*}}\\ 0& -G_{\text{pll}}{I}_{\text{dg}}^{\text{*}}\end{array}\right]$, ${\mathit{G}}_{\mathbf{pll}}^{\mathbf{d}}=\left[\begin{array}{cc}0& G_{\text{pll}}{D}_{\text{qg}}^{\text{*}}\\ 0& -G_{\text{pll}}{D}_{\text{dg}}^{\text{*}}\end{array}\right]$, $G_{\text{pll}}=\frac{H_{\text{pll}}}{s+U_{\text{dg}}^{\text{*}}{H}_{\text{pll}}}$.

The small-signal model of the weak grid is expressed as

${\mathit{Z}}_{\mathbf{g}}\cdot \mathbf{\Delta }{\mathit{i}}_{\mathbf{dqg}}=\mathbf{\Delta }{\mathit{u}}_{\mathbf{dqg}}(26)$

where ${\mathit{Z}}_{\mathbf{g}}=\left[\begin{array}{cc}s{L}_{\text{g}}& -\omega L_{\text{g}}\\ \omega L_{\text{g}}& s{L}_{\text{g}}\end{array}\right]$.

Moreover, the power output of the PMSG can be linearized as (27), where ${\mathit{U}}_{\mathbf{dqg}}^{\text{*}}=\left[\begin{array}{c}{U}_{\text{dg}}^{\text{*}}\\ U_{\text{qg}}^{\text{*}}\end{array}\right]$.

$\text{Δ}P=1.5\left({\mathit{I}}_{\mathbf{dqg}}^{\text{∗}T}\cdot {\mathit{Z}}_{\mathbf{g}}+{\mathit{U}}_{\mathbf{dqg}}^{\text{∗}\mathit{T}}\right)\cdot \mathbf{\Delta }{\mathit{i}}_{\mathbf{dqg}}.(27)$

3.4 A Complete Model of the Grid-Connected PMSG System

Through the above procedures, the model of each part of the PMSG has been established. It can be found that they are all linear except the model of the power control loop containing a nonlinear element. Combining these models and eliminating intermediate variables, the model of PMSG is reorganized as a typical SISO nonlinear system as shown in Figure 1. Note that ±ε/(sT_p) is the linear part of the power control loop, and G₁(s) expressed in (28) is a linear transfer function, and they form the linear part of the complete model. Finally, the linear model G(s) is expressed as (29).

$\{\begin{array}{l}{G}_1\left(s\right)=\frac{\text{Δ}P}{\text{Δ}{\omega }_{\text{g}}^{\text{ref}}}=1.5\left({\mathit{I}}_{\mathbf{dqg}}^{\ast \mathit{T}}{\mathit{Z}}_{\mathbf{g}}+{\mathit{U}}_{\mathbf{dqg}}^{\ast \mathit{T}}\right){\mathit{M}}_5^{-1}\left({\mathit{D}}_{\mathbf{dqg}}^{\ast }+{\mathit{G}}_{\mathbf{udc}}\right)M_7^{-1}{M}_8\\ {\mathit{M}}_1={\mathit{G}}_{\mathbf{cr}}{\mathit{G}}_{\mathbf{\theta e}}^{\mathbf{i}}-{\mathit{G}}_{\mathbf{\omega g}}{\mathit{G}}_{\mathbf{iq}\mathbf{\omega }}-U_{\text{dc}}^{\ast }{\mathit{G}}_{\mathbf{\theta e}}^{\mathbf{d}}+{\mathit{Z}}_{\mathbf{dqr}}\\ {\mathit{M}}_2={\mathit{G}}_{\mathbf{\omega e}}{\mathit{G}}_{\mathbf{iq\omega }}{n}_{\text{p}}+{\mathit{G}}_{\mathbf{cr}}{\mathit{G}}_{\mathbf{\theta e}}^{\mathbf{i}}-{\mathit{G}}_{\mathbf{\omega g}}{\mathit{G}}_{\mathbf{iq\omega }}-U_{\text{dc}}^{\ast }{\mathit{G}}_{\mathbf{\theta e}}^{\mathbf{d}}\\ {\mathit{M}}_3=\frac{-{\mathit{M}}_2{\mathit{M}}_1^{-1}{\mathit{G}}_{\mathbf{\omega g}}+{\mathit{G}}_{\mathbf{\omega g}}}{U_{\text{dc}}^{\ast }}\\ {\mathit{M}}_4=-\frac{{\mathit{M}}_2{\mathit{M}}_1^{-1}{\mathit{D}}_{\mathbf{dqr}}^{\ast }}{U_{\text{dc}}^{\ast }}\\ {\mathit{M}}_5=-{\mathit{G}}_{\mathbf{cg}}+{\mathit{Z}}_{\mathbf{f}}-\left({\mathit{G}}_{\mathbf{cg}}{\mathit{G}}_{\mathbf{pll}}^{\mathbf{i}}-{\mathit{G}}_{\mathbf{pll}}^{\mathbf{d}}{U}_{\text{dc}}^{\ast }+{\mathit{G}}_{\mathbf{pll}}^{\mathbf{u}}\right){\mathit{Z}}_{\mathbf{g}}+{\mathit{Z}}_{\mathbf{g}}\\ {\mathit{M}}_6=\frac{\begin{array}{l}\left(\left({\mathit{G}}_{\mathbf{cg}}{\mathit{G}}_{\mathbf{pll}}^{\mathbf{i}}-{\mathit{G}}_{\mathbf{pll}}^{\mathbf{d}}{U}_{\text{dc}}^{\ast }+{\mathit{G}}_{\mathbf{pll}}^{\mathbf{u}}\right){\mathit{Z}}_{\mathbf{g}}+{\mathit{G}}_{\mathbf{cg}}\right){\mathit{M}}_5^{-1}\left({\mathit{D}}_{\mathbf{dqg}}^{\ast }+{\mathit{G}}_{\mathbf{udc}}\right)+{\mathit{G}}_{\mathbf{udc}}\end{array}}{U_{\text{dc}}^{\text{*}}}\\ M_7=\left(\frac{2s{C}_{\text{dc}}}{3}+{\mathit{I}}_{\mathbf{dqg}}^{\ast \mathit{T}}{\mathit{M}}_6-{\mathit{I}}_{\mathbf{dqr}}^{\ast \mathit{T}}{\mathit{M}}_4+{\mathit{D}}_{\mathbf{dqg}}^{\ast \mathit{T}}{\mathit{M}}_5^{-1}\left({\mathit{D}}_{\mathbf{dqg}}^{\ast }+{\mathit{G}}_{\mathbf{udc}}\right)+{\mathit{D}}_{\mathbf{dqr}}^{\ast \mathit{T}}{\mathit{M}}_1^{-1}{\mathit{D}}_{\mathbf{dqr}}^{\ast }\right)\\ M_8=-{\mathit{D}}_{\mathit{dqr}}^{\ast \text{T}}\cdot {\mathit{M}}_1^{-1}\cdot {\mathit{G}}_{\mathbf{\omega g}}+{\mathit{I}}_{\mathit{dqr}}^{\ast \text{T}}\cdot {\mathit{M}}_3\end{array}(28)$

$G\left(s\right)=\pm \frac{\epsilon }{T_{\text{P}}s}{G}_1\left(s\right)\cdot \frac{1}{1+T_{\text{f}}s}\cdot \frac{1}{1+1.5T_{\text{P}}s}.(29)$

In (29), 1/(1 + T_fs) is a sampling filter of the power signal, and 1/(1 + 1.5T_ps) is the PWM and controller delay. They are also not negligible for stability analyses.

4 Power Oscillation Analyses Based on the DF Method

In this section, the stability of the grid-connected PMSG system is analyzed. First, by comparing whether to consider the power control loop and its nonlinear element, the necessity and advantage of the DF method are clarified. Then several critical system parameters are chosen to show their influences on the system stability, and the accuracy of the DF method is presented. Finally, the influence of grid strength and PLL is studied. The basic system parameters are listed in Table 2 (Geng et al., 2011), which is used in all cases unless specifically mentioned.

TABLE 2

TABLE 2. System parameters.

4.1 Influence of MSC Controller Parameters

Commonly, the power control loop is ignored in the small-signal analyses as the discontinuous nonlinear element cannot be handled. Then the system is considered linear and G₁ is the closed-loop transfer function of the system whose stability can be judged by the position of the poles of G₁. However, when the power control loop is considered, a latent feedback path formed by the P&O algorithm is introduced, which makes G₁ become a part of the open-loop transfer function of the system whose stability is no longer determined by the poles of G₁. In other words, the power control loop brings a new feedback path with a discontinuous nonlinear element, and the DF method is necessary for stability analyses.

To better explain the necessity of considering the power control loop, stability analyses and simulations when changing the rotational-speed-loop parameters K_ωp and K_ωi are shown in Figure 5. Figure 5A shows the stability analyses base on the DF method. When k changes from 0.5 to 1.5 (K_ωp changes from 6,000 to 18,000, and K_ωi changes from 1750 to 5,250), the intersection of −1/N(A) and G(s) moves in the direction that A increases and all these intersections correspond to stable limit cycles according to the principle introduced in Section 2. Therefore, oscillation occurs in the system, and the amplitude increases when k changes from 0.5 to 1.5. Figure 5B is based on the poles of G₁ which is the closed-loop transfer function when the power control loop is not considered. It is shown that when k changes from 0.5 to 1.5, the dominant pole moves away from the imaginary axis, which means the system should be stable and the stability should be strengthened as k increases. The conclusions of the two methods seem contradictory, however, simulation results presented in Figure 5C prove the correctness of the DF method. P_ac is the output power of the PMSG at the PCC, and the power oscillation occurs. The amplitude expands when K_ωp and K_ωi increase, as predicted by the DF method.

FIGURE 5

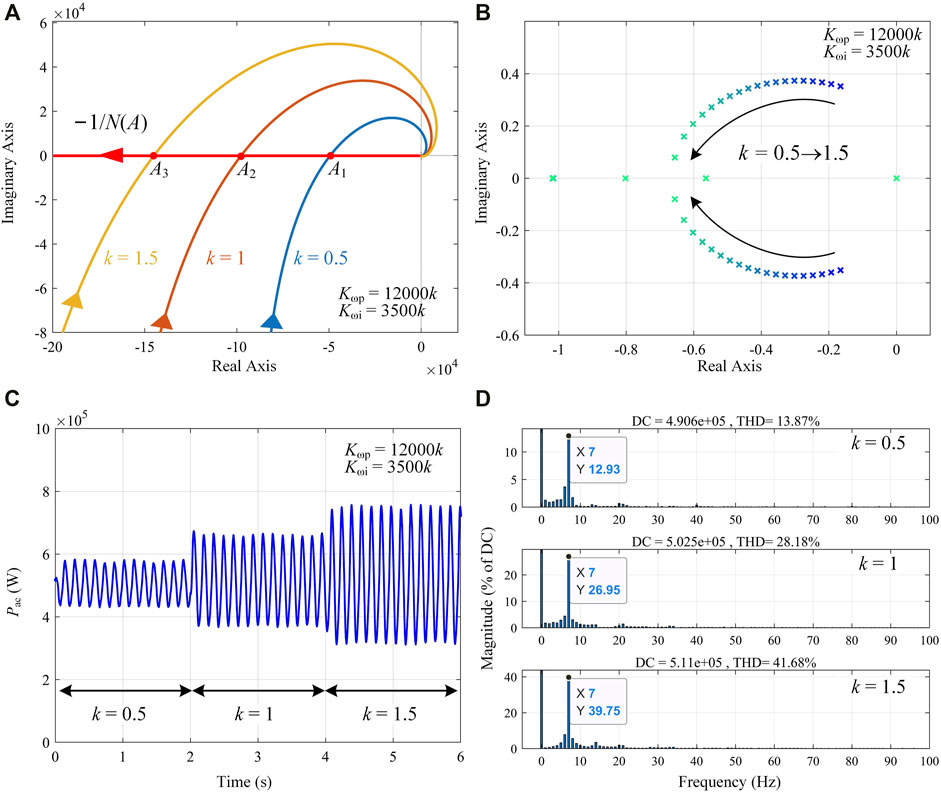
FIGURE 5. Stability analyses and simulations when changing rotational-speed-loop parameters K_ωp and K_ωi. (A) Stability analyses based on the DF method considering the power control loop. (B) Stability analyses based on the poles of G₁ without considering the power control loop. (C) Power output. (D) FFT analyses.

If the intersection of −1/N(A) and G(s) curves corresponds to a stable limit cycle, the frequency and amplitude of the oscillations can be obtained. This information is valuable to the defense and identification of oscillations. It can be calculated that the oscillations at the point A₁, A₂, and A₃ are with the amplitude of 63, 124, and 185 kW respectively, and with the frequency of 7.3, 7.4, and 7.4 Hz respectively. The accuracy of the DF method is verified through FFT analyses, which are shown in Figure 5D. It is shown that the oscillations are with the amplitude of 63, 135, and 203 kW respectively, and with the frequency of 7, 7, and 7 Hz respectively. These results are basically consistent with the theoretical analyses.

Moreover, the traditional method cannot analyze the influence of power control loop parameters on the system stability. Figure 6 shows the stability analyses and simulations when changing the perturbation step ε. The perturbation step is an important parameter because it determines how fast the power control loop can respond, or rather, the equivalent bandwidth of the power control loop. In Figure 6A, the intersection of −1/N(A) and G(s) also moves in the direction that A increases when ε changes from 0.1 × 10⁻⁴ to 1 × 10⁻⁴, which means the increase of ε expands the amplitude of the power oscillation. The simulation result shown in Figure 6B verifies the analyses, and it can be seen that the power oscillation is enlarged as ε increases. The comparison between the analyses and the simulations is listed in Table 3, where FFT analyses are performed for the simulations.

FIGURE 6

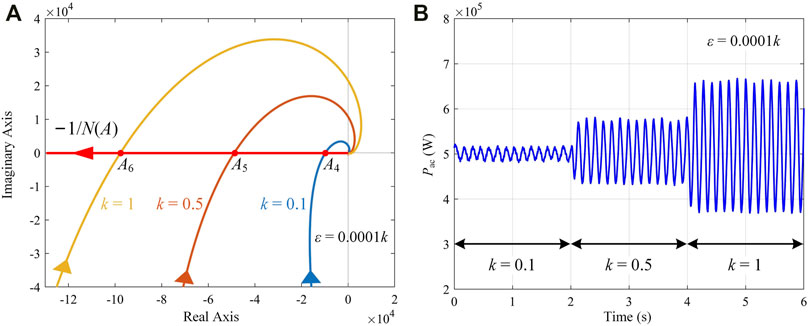
FIGURE 6. Stability analyses and simulations when changing the perturbation step ε. (A) Stability analyses based on the DF method. (B) Power output.

TABLE 3

TABLE 3. Quantitative comparison of MSC controller parameters.

Figure 7 shows the effect of MSC current-loop parameters on the system stability. In Figure 7A, the intersection moves in the direction that A decreases when the bandwidth of the MSC current loop increases. It can be observed in the simulation that the sustained oscillation is suppressed with an incremental k, which is consistent with the analyses. Quantitative comparison results are also listed in Table 3.

FIGURE 7

FIGURE 7. Stability analyses and simulations when changing MSC current-loop parameters K_cpr and K_cir. (A) Stability analyses based on the DF method. (B) Power output.

This part shows the necessity and accuracy of the DF method. On the one hand, the latent feedback path with a nonlinear element can be considered in the stability analyses, which means the accuracy of the results is enhanced. On the other hand, some parameters that the conventional linear system method cannot handle can be analyzed by the DF method, which shows the superiority of the method. The higher bandwidth of the power control loop and rotational speed loop leads to larger oscillation amplitude, which should be avoided in parameter tuning. While higher bandwidth of the MSC current loop is beneficial to suppress the oscillation.

4.2 Influence of GSC Controller Parameters

The DF method can predict oscillation accidents precisely, and the influence of the GSC controller parameters will be analyzed in this part.

Figure 8 shows the stability analyses and the simulations when changing the voltage-loop parameters K_vp and K_vi, and it can be observed that the amplitude is slightly changed but the frequency is significantly changed when K_vp and K_vi increase. According to the intersection information, the amplitude can be calculated as 139, 124, and 103 kW respectively when k is set to 0.2, 1, and 5 (K_vp = 5k and K_vi = 5k), and the frequency can be calculated as 3.9, 7.4, and 10.8 Hz respectively. Simulation results are shown in Figure 8B. The amplitude is 131, 122, and 100 kW respectively, and the frequency is 4, 7, and 9.3 Hz respectively. The simulation results are basically consistent with the analysis results.

FIGURE 8

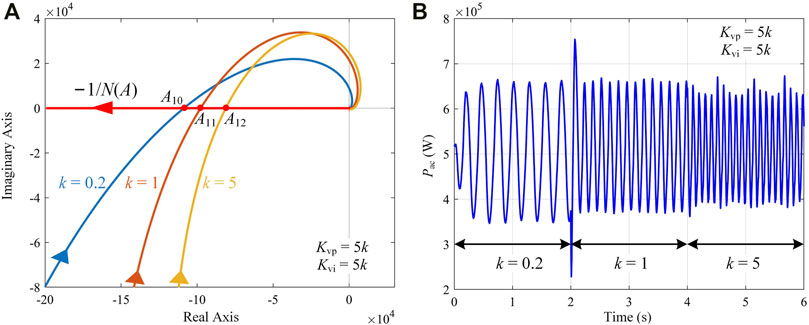
FIGURE 8. Stability analyses and simulations when changing voltage-loop parameters K_vp and K_vi. (A) Stability analyses based on the DF method. (B) Power output.

Figure 9 shows the effect of the GSC current loop. The analyses and the simulations show that the amplitude and the frequency basically remain constant when the bandwidth of the GSC current loop increases, which means the GSC current-loop parameters have almost no effect on the oscillation characteristics. The quantitative comparison between the analyses and the simulations for changing K_vp, K_vi, K_cpg, and K_cig is shown in Table 4.

FIGURE 9

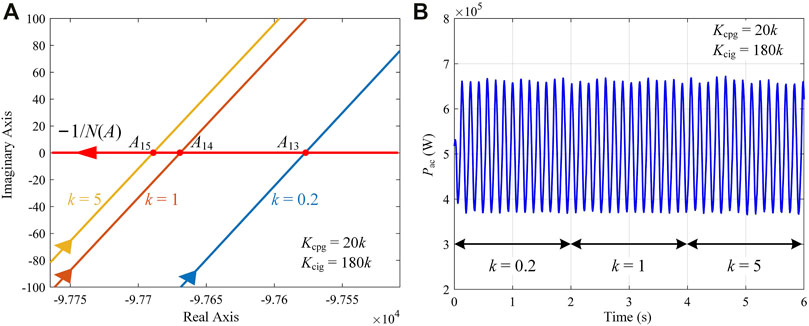
FIGURE 9. Stability analyses and simulations when changing GSC current-loop parameters K_cpg and K_cig. (A) Stability analyses based on the DF method. (B) Power output.

TABLE 4

TABLE 4. Quantitative comparison of GSC controller parameters.

Although the GSC parameters have a smaller influence on the oscillation characteristics, the DF method can distinguish these subtle differences, and accurate information on oscillations can be obtained. Furthermore, the bandwidth of the voltage loop has an evident impact on the oscillation frequency, but a minor impact on oscillation amplitude compared with MSC parameters. The bandwidth of the GSC current loop has almost no effect on the frequency and amplitude of the oscillation.

4.3 Influence of Grid Strength and PLL

Effects of grid strength and PLL on the system stability are strongly coupled, and hence they are discussed together. Grid strength is represented by the grid equivalent inductor L_g, and a larger L_g means a weaker grid strength.

Figure 10 shows the stability analyses when changing L_g and the PLL bandwidth, and Figure 10A is enlarged for better observation. When L_g = 0.1 mH, the incremental bandwidth of PLL has almost no influence on the oscillation. When L_g = 0.6 mH, the incremental bandwidth of PLL has a relatively evident influence on the oscillation. If k is set to 1 (K_ppll = 2k, K_ipll = 35k), the system is stable, but if k is set to 2, the system will be unstable because the open-loop transfer function G(s) has a pair of right-half plane poles, as shown in Figure 10B. Therefore, the excessively high bandwidth of PLL is harmful to the stability of the system, especially when the grid is weak.

FIGURE 10

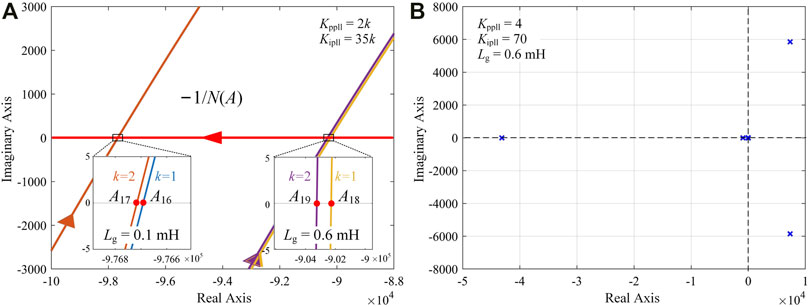
FIGURE 10. Stability analyses when changing L_g and PLL bandwidth (A) Stability analyses based on the DF method. (B) Right-half plane poles when L_g = 0.6 mH and k = 2.

Furthermore, a stronger grid is not always beneficial to keep the system stable, and it would enlarge the amplitude of oscillations under some specific system structure when nonlinear elements are considered. When L_g is increased from 0.1 to 0.6 mH, the amplitude of the oscillation is decreased, in other words, oscillation accidents occurring in the weaker grid have less damage to the power system because the oscillation amplitude is suppressed, and the relationship between stability and the grid strength should be reconsidered and carefully analyzed when nonlinear elements are considered. This conclusion is proved by simulation results shown in Figure 11. When k = 1, the oscillation amplitude is smaller if L_g is larger. The effect of the PLL is also verified in the simulation. When k = 2 and L_g = 0.6 mH, the stable limit cycle vanishes and the system becomes unstable, which is consistent with the analysis results. The quantitative comparison for changing PLL and grid strength parameters is also shown in Table 4.

FIGURE 11

FIGURE 11. Power output when changing L_g and PLL bandwidth.

5 Conclusion

This paper presents the modeling and oscillation analyses of a grid-connected PMSG wind power generation system considering the discontinuous nonlinear element in the power controller. The complete model of the PMSG wind power generation system is established, including the wind turbine, the generator, the MSC, the GSC, and the weak grid. The MSC controller contains a nonlinear maximum power point tracking algorithm. The DF method is adopted to analyze the influence of the MSC controller parameters, the GSC controller parameters, and the grid strength. The analyses and simulations show that the DF method is more functional and accurate than the conventional linearized method. Based on the DF method, several conclusions can be made. 1) Improper high bandwidth of a power control loop and a rotational speed loop is harmful to system stability, and it can enlarge the amplitude of oscillations. While a fast MSC current loop can suppress the oscillation. 2) The machine-side converter mainly influences the oscillation amplitude, while the grid-side converter mainly influences the oscillation frequency. More specifically, a higher bandwidth of a GSC voltage loop may lead to a higher oscillation frequency. 3) The effect of grid strength on stability should receive more attention, as a stronger grid is not always beneficial to stability when nonlinear elements are considered. In addition, PLLs with improper high bandwidth are also detrimental to the stability of the system. The DF method is with high practicability, and it can be further extended in some perspectives: 1) investigate various types of nonlinearity, such as saturation, nonlinear inductor, dead zone, and so on. 2) analyze the nonlinearity considering high-order harmonics. 3) consider multiple nonlinear elements and study their influence on stability.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JL: investigation, modeling, and writing the original draft. MY: methodology, and editing. JZ: validation. YX: conceptualization, and methodology. WW: reviewing and editing.

Funding

This work was supported by the National Natural Science Foundation of China (52077194).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdullah, M. A., Yatim, A. H. M., Tan, C. W., and Saidur, R. (2012). A Review of Maximum Power Point Tracking Algorithms for Wind Energy Systems. Renew. Sustain. Energy Rev. 16, 3220–3227. doi:10.1016/j.rser.2012.02.016

CrossRef Full Text | Google Scholar

Amin, M., Molinas, M., Lyu, J., and Cai, X. (2017). Impact of Power Flow Direction on the Stability of VSC-HVDC Seen from the Impedance Nyquist Plot. IEEE Trans. Power Electron. 32, 8204–8217. doi:10.1109/TPEL.2016.2608278

CrossRef Full Text | Google Scholar

Atherton, D. P. (1975). Nonlinear Control Engineering. New york: Van Nostrand Rheinhold.

Google Scholar

Bi, T., Li, J., Zhang, P., Mitchell-Colgan, E., and Xiao, S. (2017). Study on Response Characteristics of Grid-Side Converter Controller of PMSG to Sub-Synchronous Frequency Component. IET Renew. Power Gener. 11, 966–972. doi:10.1049/iet-rpg.2016.0994

CrossRef Full Text | Google Scholar

Cespedes, M., and Sun, J. (2014). Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 29, 1254–1261. doi:10.1109/TPEL.2013.2262473

CrossRef Full Text | Google Scholar

Chi, Y., Tang, B., Hu, J., Tian, X., Tang, H., Li, Y., et al. (2019). Overview of Mechanism and Mitigation Measures on Multi-Frequency Oscillation Caused by Large-Scale Integration of Wind Power. Csee Jpes 5, 433–443. doi:10.17775/CSEEJPES.2019.01100

CrossRef Full Text | Google Scholar

Gasparyan, O. (2008). Linear and Nonlinear Multivariable Feedback Control: A Classical Approach. New Jersey, US: John Wiley & Sons.

Google Scholar

Geng, H., Yang, G., Xu, D., and Wu, B. (2011). Unified Power Control for PMSG-Based WECS Operating under Different Grid Conditions. IEEE Trans. Energy Convers. 26, 822–830. doi:10.1109/TEC.2011.2127478

CrossRef Full Text | Google Scholar

Guo, L., Zhang, S., Li, X., Li, Y. W., Wang, C., and Feng, Y. (2017). Stability Analysis and Damping Enhancement Based on Frequency-Dependent Virtual Impedance for DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 5, 338–350. doi:10.1109/JESTPE.2016.2598821

CrossRef Full Text | Google Scholar

Han, Y., Sun, H., Huang, B., Qin, S., Mu, Q., and Yu, Y. (2022). Discrete-time State-Space Construction Method for SSO Analysis of Renewable Power Generation Integrated AC/DC Hybrid System. IEEE Trans. Power Syst. 37, 2322–2334. doi:10.1109/TPWRS.2021.3115248

CrossRef Full Text | Google Scholar

Hatziargyriou, N., Milanovic, J., Rahmann, C., Ajjarapu, V., Canizares, C., Erlich, I., et al. (2021). Definition and Classification of Power System Stability - Revisited & Extended. IEEE Trans. Power Syst. 36, 3271–3281. doi:10.1109/TPWRS.2020.3041774

CrossRef Full Text | Google Scholar

Hu, Q., Fu, L., Ma, F., and Ji, F. (2019). Large Signal Synchronizing Instability of PLL-Based VSC Connected to Weak AC Grid. IEEE Trans. Power Syst. 34, 3220–3229. doi:10.1109/TPWRS.2019.2892224

CrossRef Full Text | Google Scholar

Huang, B., Sun, H., Liu, Y., Wang, L., and Chen, Y. (2019a). Study on Subsynchronous Oscillation in D-PMSGs-Based Wind Farm Integrated to Power System. IET Renew. Power Gener. 13, 16–26. doi:10.1049/iet-rpg.2018.5051

CrossRef Full Text | Google Scholar

Huang, B., Sun, H., Wang, L., Chen, Y., and Liu, Y. (2019b). Investigation on SSCI between PMSGs-Based Wind Farm and AC Network. IET Renew. Power Gener. 13, 2958–2965. doi:10.1049/iet-rpg.2019.0362

CrossRef Full Text | Google Scholar

Kumar, D., and Chatterjee, K. (2016). A Review of Conventional and Advanced MPPT Algorithms for Wind Energy Systems. Renew. Sustain. Energy Rev. 55, 957–970. doi:10.1016/j.rser.2015.11.013

CrossRef Full Text | Google Scholar

Liu, H., and Xie, X. (2018). Impedance Network Modeling and Quantitative Stability Analysis of Sub-/super-synchronous Oscillations for Large-Scale Wind Power Systems. IEEE Access 6, 34431–34438. doi:10.1109/ACCESS.2018.2849830

CrossRef Full Text | Google Scholar

Liu, H., Xie, X., He, J., Xu, T., Yu, Z., Wang, C., et al. (2017). Subsynchronous Interaction Between Direct-Drive PMSG Based Wind Farms and Weak AC Networks. IEEE Trans. Power Syst. 32, 4708–4720. doi:10.1109/TPWRS.2017.2682197

CrossRef Full Text | Google Scholar

Liu, J., Tao, X., Yu, M., Xia, Y., and Wei, W. (2020). Impedance Modeling and Analysis of Three-Phase Voltage-Source Converters Viewing from DC Side. IEEE J. Emerg. Sel. Top. Power Electron. 8, 3906–3916. doi:10.1109/JESTPE.2019.2932618

CrossRef Full Text | Google Scholar

Liu, B., Li, Z., Dong, X., Yu, S. S., Chen, X., Oo, A. M. T., et al. (2021). Impedance Modeling and Controllers Shaping Effect Analysis of PMSG Wind Turbines. IEEE J. Emerg. Sel. Top. Power Electron. 9, 1465–1478. doi:10.1109/JESTPE.2020.3014412

CrossRef Full Text | Google Scholar

Lyu, J., Cai, X., Amin, M., and Molinas, M. (2018). Sub-synchronous Oscillation Mechanism and its Suppression in MMC‐based HVDC Connected Wind Farms. IET Gener. Transm. and Distrib. 12, 1021–1029. doi:10.1049/iet-gtd.2017.1066

CrossRef Full Text | Google Scholar

Metwally, M. M., Ratib, M. K., Aly, M. M., and Abdel-Rahim, A. M. (2021). Effect of Grid Faults on Dominant Wind Generators for Electric Power System Integration: A Comparison and Assessment. Energy Syst. Res. 4, 70–78. doi:10.38028/esr.2021.03.0007

CrossRef Full Text | Google Scholar

Mahmoud, M. M., Khalid Ratib, M., Aly, M. M., and Abdel-Rahim, A. M. M. (2022). Wind-Driven Permanent Magnet Synchronous Generators Connected to a Power Grid: Existing Perspective and Future Aspects. Wind Eng. 46, 189–199. doi:10.1177/0309524X211022728

CrossRef Full Text | Google Scholar

Nassirharand, A. (2012). Computer-aided Nonlinear Control System Design: Using Describing Function Models. New york, US: Springer.

Google Scholar

Rygg, A., Molinas, M., Zhang, C., and Cai, X. (2017). On the Equivalence and Impact on Stability of Impedance Modeling of Power Electronic Converters in Different Domains. IEEE J. Emerg. Sel. Top. Power Electron. 5, 1444–1454. doi:10.1109/JESTPE.2017.2744988

CrossRef Full Text | Google Scholar

Shair, J., Xie, X., Wang, L., Liu, W., He, J., and Liu, H. (2019). Overview of Emerging Subsynchronous Oscillations in Practical Wind Power Systems. Renew. Sustain. Energy Rev. 99, 159–168. doi:10.1016/j.rser.2018.09.047

CrossRef Full Text | Google Scholar

Shi, T., Nayanasiri, D., and Li, Y. (2020). Sub-Synchronous Oscillations in Wind Farms - an Overview Study of Mechanisms and Damping Methods. IET Renew. Power Gener. 14, 3974–3988. doi:10.1049/iet-rpg.2020.0479

CrossRef Full Text | Google Scholar

Sun, J. (2009). Small-Signal Methods for AC Distributed Power Systems-A Review. IEEE Trans. Power Electron. 24, 2545–2554. doi:10.1109/TPEL.2009.2029859

CrossRef Full Text | Google Scholar

Wang, X., and Blaabjerg, F. (2019). Harmonic Stability in Power Electronic-Based Power Systems: Concept, Modeling, and Analysis. IEEE Trans. Smart Grid 10, 2858–2870. doi:10.1109/TSG.2018.2812712

CrossRef Full Text | Google Scholar

Wang, L., Xie, X., Jiang, Q., Liu, H., Li, Y., and Liu, H. (2015). Investigation of SSR in Practical DFIG-Based Wind Farms Connected to a Series-Compensated Power System. IEEE Trans. Power Syst. 30, 2772–2779. doi:10.1109/TPWRS.2014.2365197

CrossRef Full Text | Google Scholar

Wang, X., Peng, Y., Zhu, J., Xia, Y., Yu, M., Hu, H., et al. (2017). Decentralized Impedance Specifications for Small-Signal Stability of DC Distributed Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 5, 1578–1588. doi:10.1109/JESTPE.2017.2708141

CrossRef Full Text | Google Scholar

Wang, X., Taul, M. G., Wu, H., Liao, Y., Blaabjerg, F., and Harnefors, L. (2020). Grid-Synchronization Stability of Converter-Based Resources-An Overview. IEEE Open J. Ind. Appl. 1, 115–134. doi:10.1109/OJIA.2020.3020392

CrossRef Full Text | Google Scholar

Wei, W., Xia, Y., and Blaabjerg, F. (2020). Nonlinear Stability Analysis for Three-Phase Grid-Connected PV Generators. IEEE J. Emerg. Sel. Top. Power Electron. 8, 3487–3501. doi:10.1109/JESTPE.2019.2939379

CrossRef Full Text | Google Scholar

Wen, B., Boroyevich, D., Burgos, R., Mattavelli, P., and Shen, Z. (2015). Small-signal Stability Analysis of Three-Phase AC Systems in the Presence of Constant Power Loads Based on Measured D-Q Frame Impedances. IEEE Trans. Power Electron. 30, 5952–5963. doi:10.1109/TPEL.2014.2378731

CrossRef Full Text | Google Scholar

Wen, B., Boroyevich, D., Burgos, R., Mattavelli, P., and Shen, Z. (2016). Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 31, 675–687. doi:10.1109/TPEL.2015.2398192

CrossRef Full Text | Google Scholar

Wu, T., Jiang, Q., Shair, J., Mao, H., and Xie, X. (2021). Inclusion of Current Limiter Nonlinearity in the Characteristic Analysis of Sustained Subsynchronous Oscillations in Grid-Connected PMSGs. IEEE Trans. Energy Convers. 36, 2416–2426. doi:10.1109/TEC.2020.3045296

CrossRef Full Text | Google Scholar

Wu, T., Jiang, Q., Shair, J., Xie, X., Wang, Y., Luo, Y., et al. (2021). Quantitative Analysis of Sustained Oscillation Associated with Saturation Non-linearity in a Grid-connected Voltage Source Converter. IET Renew. Power Gen. 15, 865–876. doi:10.1049/rpg2.12075

CrossRef Full Text | Google Scholar

Xia, Y., Wei, W., Yu, M., and Wang, P. (2019a). Stability Analysis of PV Generators with Consideration of P&O-based Power Control. IEEE Trans. Ind. Electron. 66, 6483–6492. doi:10.1109/TIE.2018.2864695

CrossRef Full Text | Google Scholar

Xia, Y., Yu, M., Wang, X., and Wei, W. (2019b). Describing Function Method Based Power Oscillation Analysis of LCL-Filtered Single-Stage PV Generators Connected to Weak Grid. IEEE Trans. Power Electron. 34, 8724–8738. doi:10.1109/TPEL.2018.2887295

CrossRef Full Text | Google Scholar

Xie, X., Zhang, X., Liu, H., Liu, H., Li, Y., and Zhang, C. (2017). Characteristic Analysis of Subsynchronous Resonance in Practical Wind Farms Connected to Series-Compensated Transmissions. IEEE Trans. Energy Convers. 32, 1117–1126. doi:10.1109/TEC.2017.2676024

CrossRef Full Text | Google Scholar

Xu, Y., Gu, Z., and Sun, K. (2020). Characterization of Subsynchronous Oscillation with Wind Farms Using Describing Function and Generalized Nyquist Criterion. IEEE Trans. Power Syst. 35, 2783–2793. doi:10.1109/TPWRS.2019.2962506

CrossRef Full Text | Google Scholar

Xue, T., Lyu, J., Wang, H., Cai, X., Li, J., and Wang, X. (2020). “A Complete Impedance Model of a PMSG-Based Wind Turbine System Considering Machine-Side Dynamics,” in Proc. 46th Annu. Conf. IEEE Ind. Electron. Soc. (IECON), Singapore, 18-21 October 2020, 3111–3117. doi:10.1109/IECON43393.2020.9254974

CrossRef Full Text | Google Scholar

Zhao, S., Li, R., Gao, B., Wang, N., and Zhang, X. (2019a). Subsynchronous Oscillation of PV Plants Integrated to Weak AC Networks. IET Renew. Power Gener. 13, 409–417. doi:10.1049/iet-rpg.2018.5659

CrossRef Full Text | Google Scholar

Zhao, S., Wang, N., Li, R., Gao, B., Shao, B., and Song, S. (2019b). Sub-Synchronous Control Interaction Between Direct-Drive PMSG-Based Wind Farms and Compensated Grids. Int. J. Electr. Power and Energy Syst. 109, 609–617. doi:10.1016/j.ijepes.2019.02.021

CrossRef Full Text | Google Scholar