Improved Model Predictive Dynamic Voltage Cooperative Control Technology Based on PMU

With the access to a large number of intermittent and fluctuating new energy sources in the low-voltage distribution network, the complex relationship between producers and consumers makes the node voltage stability and other problems in the power system increasingly prominent. Aiming at the voltage stability problem caused by the intermittent and fluctuation of the new power system, based on the high-precision measurement data of PMU, this article used the model predictive control algorithm to realize regional voltage optimization and improve the stability of node voltage. First, the voltage sensitivity matrix is calculated using PMU measurement data and grid structure state information. Second, active power, reactive power, and voltage were taken as the input of the MPC algorithm, and the optimal compensation voltage instruction was obtained by rolling optimization, and the node voltage was compensated by SVG and SVC. Finally, a simulation experiment was carried out on the MATLAB/Simulink simulation platform, and the experimental results verified the correctness and effectiveness of the proposed control method.

Introduction

With the increasing popularity of distributed photovoltaic (PV), the original electricity consumers have been transformed into electricity consumers, which will bring great challenges to the operation of the power grid. In addition, there are a lot of problems such as insufficient use of high-precision measurement data in a distributed generation system. Therefore, it is an urgent problem to improve the adaptability of the distributed generation system by using a large amount of high-precision measurement data. The synchronous phase measurement unit (phase measurement unit, PMU) is based on the precise time provided by the global positioning system (global positioning system, GPS). PMU can collect real-time data from the power system and realize the synchronous measurement of each node. With the development of the distribution network, the application prospect of synchronous PMU in the distribution network has been paid increasing attention. The application of PMU in the distribution network can be mainly divided into diagnostic application and control application, and this article belongs to the application of PMU in the control direction. In this direction, the literature (Yu et al., 2018) proposed a static equivalence method using boundary PMU measurements and established an optimal reactive power tide model based on this method, which has high accuracy for power system tide calculation. The literature (Pham and Erlich, 2014) presents a method for solving optimal reactive power scheduling. This optimization algorithm uses the PMU measurements to estimate the sensitivity, while the LMS is used to maintain the voltage within a limited range for the purpose of minimizing the active power loss.

SVC (static var compensator, SVC) and SVG (static var generator, SVG) are typical reactive power compensation devices; SVC is a means of supplying reactive power different from generators. It mainly includes silicon-controlled rectifiers and electrostatic capacitors. SVC can compensate the consumed reactive power for the load containing capacitor and inductor with unbalanced three phases, which needs a lot of reactive power: adjusting single-phase inductor and capacitor through phase control to achieve three-phase balance of load without changing the active power of grid and load. SVC and SVG have been widely used in the power system for a long time. In the study (Wang et al., 2019), the capacity of the inductor is configured to optimize the FC switching and TCR-triggering angle in the reactive power compensation process, which can effectively resist the risk of subsequent phase change failure and solve the voltage “backstepping” in the SVC compensation process for the common ground fault on the AC side of HVDC transmission. However, the compensation accuracy of this method is relatively weak. In order to improve the voltage compensation accuracy of SVC, in Lei et al. (2013), a second-order nonlinear dynamic model of the SVC system with time-varying parameter uncertainties is developed, and then, the controller of the SVC system is designed on the basis of this model using adaptive control techniques and robust control techniques. In order to consider the access characteristics and operation characteristics of distributed power supply in different reactive power zones, the operating strategies of reactive power compensation devices such as capacitor banks and SVG were proposed in the literature (Lin et al., 2018), and their reactive power values were optimized under various operating conditions. Aiming at the problem of voltage stability caused by unstable output of the new energy power generation system, in Fu and Fan (2015), SVG is used for reactive power control of doubly fed wind turbines, and the control structure model, the selection of capacity, and the determination of main parameters when SVG is grid-connected are discussed. In addition, the hybrid compensation method of SVC and SVG has also been studied in relevant literature studies. In the article (Chen et al., 2016), a low cost–high-capacity SVC is used for initial coarse compensation and a small-capacity SVG for microcompensation, and an improved dynamic PI controller based on an artificial immune algorithm and an inter-module coordination control strategy are used. In order to improve the voltage regulation efficiency of SVG + SVC, in Zhu et al. (2021), the reactive command current is decomposed, and the reactive component with smaller frequency is assigned to SVC for compensation, and the larger frequency is compensated by SVG. The PI parameters of the SVG controller are rectified using an adaptive particle swarm algorithm, and the reactive power is compensated by issuing reactive currents to the SVC and SVG main circuits.

In this article, a SVC + SVG hybrid reactive power rolling optimization compensation-layered control strategy based on PMU measurement data is proposed to solve the problem of voltage stability caused by insufficient use of a large number of PMU measurement data and high proportion of output and consumption. First, the voltage sensitivity matrix is calculated by using the data uploaded by PMU, and the optimal compensation voltage and reactive power are predicted by MPC (model predictive control, MPC) algorithm at the next moment. Second, control instructions are sent to SVG and SVC by the local controller. When the voltage fluctuation frequency is small, reactive power compensation is carried out by SVC; when the voltage fluctuation frequency is large, voltage is dynamically adjusted by SVG. Finally, simulation experiments are carried out on the MATLAB/Simulink simulation platform to verify the effectiveness of the proposed method.

Overview of the Power Grid Structure and Voltage Regulation Device

Overview of the Power Grid Structure

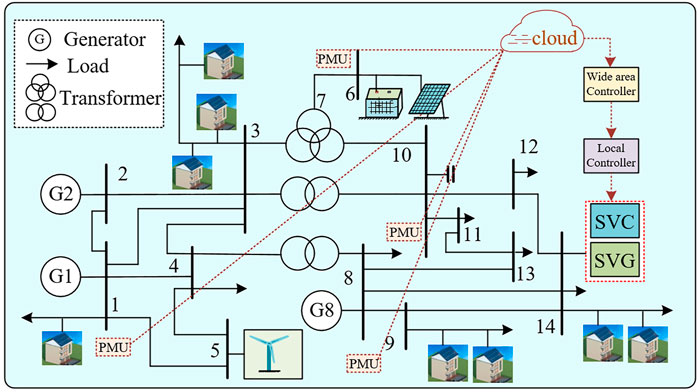
The PV power generation system of the consumer is connected to the low-voltage distribution network to realize grid-connected operation, as shown in Figure 1. The data collected by PMU are transmitted to the wide area controller through communication technology and then sent from the wide area controller to the local controller. The local controller adjusted the voltage of the reactive power compensation device so as to solve the problem of voltage fluctuation caused by the unstable distributed photovoltaic output.

FIGURE 1

FIGURE 1. Schematic diagram of system network structure.

As shown in Figure 1, the photovoltaic power generation system is connected by 14 nodes; node 7 is the neutral point of the three-phase transformer. The configuration of PMU follows IEEEStdC37118.2-2011 standard, installed at nodes 1, 6, 8, and 10, respectively, to fully observe the system; GPS satellite provides accurate synchronization time for PMU to ensure the synchronization of PMU measurement data; the main function of the wide area controller is to be responsible for global regulation. Its output is used as the input of the local controller, which directly controls SVG and SVC.

Overview of SVC and SVG

SVG is usually composed of a three-phase voltage source converter (VSC) based on a gate turnoff thyristor and a DC capacitor, and the response speed of SVG is no more than 5 ms. SVG can be regarded as stepless switching, which can compensate reactive power shortage with a high change frequency and small compensation capacity; SVC is usually composed of a fixed capacitor (FC) and a thyristor-controlled reactor (TCR) in parallel, which controls the conduction angle of thyristor α, and the equivalent reactance of the TCR connected to the circuit is changed, and then the equivalent capacitance of SVC is changed. The response time of SVC is between 20 and 40 ms, which can be regarded as class switching and can compensate the reactive power deficit with low-frequency change and large compensation capacity.

The response speed of SVC is 40 ms and that of SVG is 5 ms. The relationship between frequency F and time T is expressed as follows:

$F=T^{-1}.(1)$

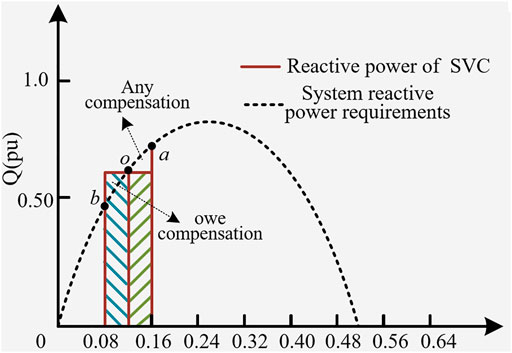
It can be seen from Eq. 1 that SVC can effectively compensate the reactive power whose frequency is less than 25 Hz, and when the reactive power change frequency is higher than 25 Hz, there may be under compensation or over compensation. In order to facilitate the cooperative control of SVC and SVG, the reactive power whose frequency change is less than 25 Hz is defined as low-frequency reactive power, and the reactive power whose frequency change is greater than 25 Hz is defined as high-frequency reactive power. The schematic diagram of over compensation and under compensation is shown in Figure 2. When the reactive power gap required by the system is in the o–a range, and when SVC responds to action once, the reactive power of the system crosses from point b to point o. At this time, the compensation capacity of SVC is less than the reactive power demand required by the system, which will cause under compensation. When SVC responds twice, the reactive power of the system crosses from point b to point a. At this time, the compensation capacity of SVC is greater than the reactive power demand required by the system, which will cause over compensation. Therefore, in order to better dynamically compensate the reactive power of the system, this article adopts SVC and SVG composite reactive power compensation devices. When the reactive power change frequency of the system is greater than 25 Hz, SVC is used to compensate the reactive power of the system; when the reactive power change frequency of the system is less than 25 Hz, then SVG is used to compensate the reactive power of the system.

FIGURE 2

FIGURE 2. Schematic diagram of SVC under compensation and over compensation.

Integrated Model Predictive Controller

Principle of the Model Prediction Algorithm

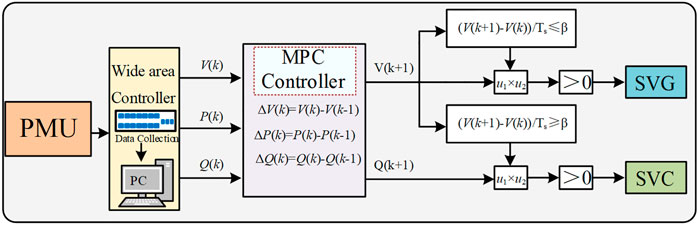
The basic idea of the model prediction algorithm is to first discretize the system, then predict the state of the system in the next N cycles in combination with the current time state and control quantity of the system, and then calculate the optimal control quantity at the current time, according to the expected value. The specific process can be illustrated in Figure 3.

FIGURE 3

FIGURE 3. MPC control algorithm.

In the figure, y(k) represents the output of the system at time k, so the output of the system in the future can be recorded as follows:

${\mathbf{Y}}_{\mathbf{N}}\left(k+1|k\right)=\left[y_{\text{N}}\left(k+1|k\right),y_{\text{N}}\left(k+2|k\right)\cdot \cdot \cdot y_{\text{N}}\left(k+p|k\right)\right].(2)$

In addition, to predict the future output of the system, it is also necessary to predict the control input in the next n-1 cycle. It can be expressed as follows:

${\mathbf{U}}_k=\left[u\left(k|k\right),yu\left(k+1|k\right)\cdot \cdot \cdot u\left(k+\mathbf{N}-1|k\right)\right].(3)$

The control goal of MPC is to make the deviation between the system output, and the reference value tends to 0 and meet the system constraints at the same time. It can be expressed as follows:

$\begin{array}{l}\{\begin{array}{l}{\min }_{U_k}J\left({\mathbf{Y}}_N\left(k+1|k\right),{\mathbf{U}}_k\right)\\ \text{s}\text{.t}\text{. }{u}_{\min }\mathrm{⩽}u\left(k+i|k\right)\mathrm{⩽}{u}_{\max }\left(i=\mathrm{1,2},\cdots ,N\right)\\ y_{\min }\mathrm{⩽}{y}_N(k+i|k)\mathrm{⩽}{y}_{\max }\left(i=\mathrm{0,1},\cdots ,N-1|\right)\end{array}\\ J\left({\mathbf{Y}}_N\left(k+1|k\right),{\mathbf{U}}_k\right)={\displaystyle \sum _{i=k+1}^p{\left(r\left(i\right)-y_N\left(i|k\right)\right)}^2}.\end{array}(4)$

By solving Eq. 4, we obtain the following:

${\mathbf{U}}_k^{\ast }=\left[u^{\ast }\left(k|k\right),u^{\ast }\left(k+1|k\right)\cdot \cdot \cdot u^{\ast }\left(k+p-1|k\right)\right].(5)$

The first component of U $\ast \text{ k}$ is applied to the system. At the time of k+1, the newly obtained measurement y(k+1) is used as the initial condition to solve Eq. 4. Therefore, MPC can be summarized as follows: the optimization problem should be updated with the latest measured values in each sampling period, and the first component of the obtained solution should be allowed to act on the system, continuously circulating. Compared with the traditional PI controller, the model predictive controller does not need the one-to-one correspondence between the input and output loops; it only needs to consider the constraints of input variables, output parameters, and control state. The predictive control quantity is calculated by measuring the deviation value of the control target in real-time, and repeated prediction and optimization are carried out under the given control weight and within the sampling period so as to realize the on-line dynamic tracking control of the system.

Design of the Integrated Model Predictive Controller

Newton–Raphson power flow calculation can be obtained from the power grid state information measured by PMU at time k:

$\left[\begin{array}{l}\text{Δ}P\hfill \\ \text{Δ}Q\hfill \end{array}\right]=-\left[\begin{array}{ll}H\hfill & N\hfill \\ K\hfill & L\hfill \end{array}\right]\left[\begin{array}{c}\text{Δ}\theta \\ V_{\left(\text{k}\right)}^{-1}\cdot △V\end{array}\right].(6)$

Among them, the Jacobian matrix can be expressed as follows: $J=\left[\begin{array}{ll}H\hfill & N\hfill \\ K\hfill & L\hfill \end{array}\right]$

Eq. 6 is multiplied by J⁻¹ at both ends to obtain the following equation.

$\left[\begin{array}{c}\text{Δ}\theta \\ V_{\left(\text{k}\right)}^{-1}\cdot △V\end{array}\right]=-J^{-1}\left[\begin{array}{l}\text{Δ}P\hfill \\ \text{Δ}Q\hfill \end{array}\right]=\left[\begin{array}{ll}A\hfill & B\hfill \\ C\hfill & D\hfill \end{array}\right]\left[\begin{array}{l}\text{Δ}P\hfill \\ \text{Δ}Q\hfill \end{array}\right].(7)$

A, B, C, and D can be calculated by using the Jacobian matrix.

Then, the voltage sensitivity matrix based on the power grid state quantity at time k is as follows:

$\{\begin{array}{l}\frac{\partial \mathbf{V}}{\partial \mathbf{P}}\left(k\right)=V\left(k\right)\times C\hfill \\ \frac{\partial \mathbf{V}}{\partial \mathbf{Q}}\left(k\right)\left(k\right)=V\left(k\right)\times D\hfill \end{array}.(8)$

Therefore, taking the current grid voltage operation state at time k as the initial value and the reactive power plan adjustment of SVC/SVG at time k as the control variable to be optimized, the grid voltage prediction equation at time k+1 is derived as follows:

$\{\begin{array}{l}\mathbf{V}\left(k+1|k\right)=\mathbf{V}\left(k|k\right)+\mathrm{\Delta }\mathbf{V}\left(k|k\right)\hfill \\ \mathrm{\Delta }\mathbf{V}\left(k|k\right)=\frac{\partial \mathbf{V}}{\partial \mathbf{Q}}\left(k\right)\mathrm{\Delta }\mathbf{Q}\left(k|k\right)+\frac{\partial \mathbf{V}}{\partial \mathbf{P}}\left(k\right)\mathrm{\Delta }\mathbf{P}\left(k|k\right)\hfill \end{array}.(9)$

The predicted value of reactive power adjustment value ∆Q is as follows:

$\mathrm{\Delta }Q\left(k|k\right)=\frac{\mathrm{\Delta }V\left(k|k\right)-\frac{\partial V}{\partial P}\left(k\right)\mathrm{\Delta }P\left(k|k\right)\frac{\partial V}{\partial Q}\left(k\right)}{\frac{\partial V}{\partial Q}\left(k\right)}.(10)$

This article calculated the optimal reactive power compensation value and the optimal dynamic voltage compensation size through MPC, so the evaluation function adopted in this article is as follows:

$g=\left|\alpha \left(Q_{ref}-Q\left(k/k+1\right)\right)+\lambda \left(U_{ref}-U\left(k/k+1\right)\right)\right|.(11)$

In Formula (11), α and λ are weight coefficients, and α > λ is more important when the system compensates reactive power. α < λ, when more emphasis is placed on the compensation of reactive power. In this article, α = λ = 0.5.

Since the sampling frequency of the system data is greater than the action frequency of the reactive power compensation device, the value of the next k+1 moment is usually replaced by the value of k moment for model calculation, but this will inevitably bring some errors and reduce the control precision of the system. To compensate, the Lagrange extrapolation method is used to predict the value of K +2 moment. The value at k+2 is applied to the next prediction calculation, and the calculation is carried out in this iterative cycle until the voltage meets the standard requirements. The specific delay link is shown in Formula (12).

$\{\begin{array}{l}V\left(k+2\right)=3V\left(k+1\right)-3V\left(k\right)+V\left(k+3\right)\\ \mathrm{\Delta }Q\left(k+2\right)=3\mathrm{\Delta }Q\left(k+1\right)-3\mathrm{\Delta }Q\left(k\right)+\mathrm{\Delta }Q\left(k+3\right)\end{array}.(12)$

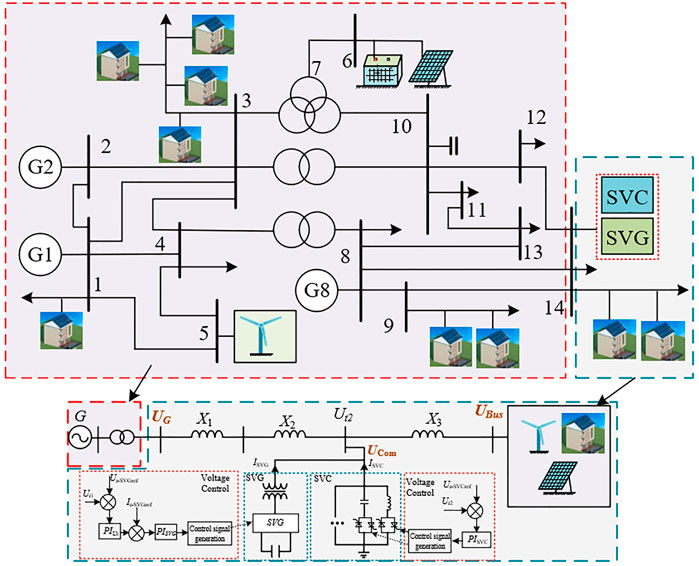
According to the characteristics of SVC and SVG, when the voltage deviation is greater than the trigger threshold β, SVC is used for reactive power compensation to roughly adjust the voltage; when the voltage deviation is small, SVG is used for dynamic adjustment of reactive power. The specific reactive power voltage optimization control structure based on MPC is shown in Figure 4. According to the introduction in Overview of Power Grid Structure section, when the voltage change frequency is higher than 25 Hz, SVC is likely to be overcompensated or undercompensated. In order to improve the voltage compensation effect and consider the 10% compensation margin, β = 22.5 is chosen in this article. Therefore, the voltage change rate dU/dt can be discretized to obtain the following equation:

$\mathrm{d}V\text{/}\mathrm{d}t=\left(V\left(k+1\right)-V\left(k\right)\right)/T_s.(13)$

FIGURE 4

FIGURE 4. Reactive power voltage optimal control structure based on MPC.

Simulation Results and Analysis

In order to verify the effectiveness of the designed local voltage optimization controller, a simulation model is built in the MATLAB/Simulink simulation platform. IEEE14 node is replaced by the generator g with infinite capacity, and photovoltaic/fan and other new energy power generation systems are connected to the system by 14 nodes. The schematic diagram of the simulation system is shown in Figure 5. The parameters of the simulation system are shown in Table 1.

FIGURE 5

FIGURE 5. Schematic diagram of simulation system.

TABLE 1

TABLE 1. Simulation system parameters.

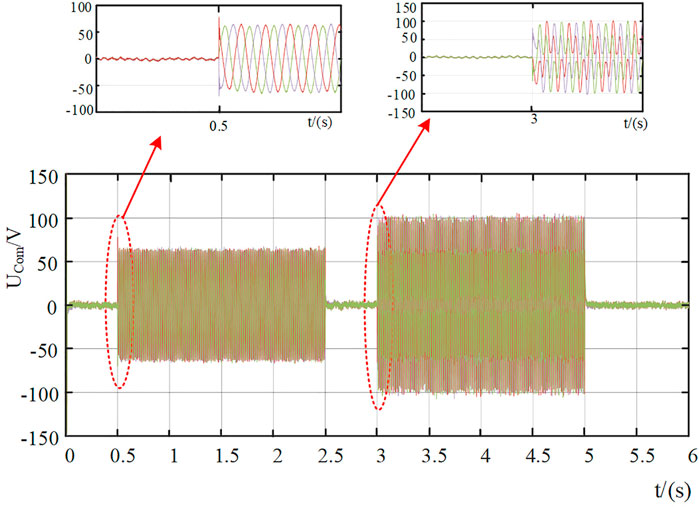
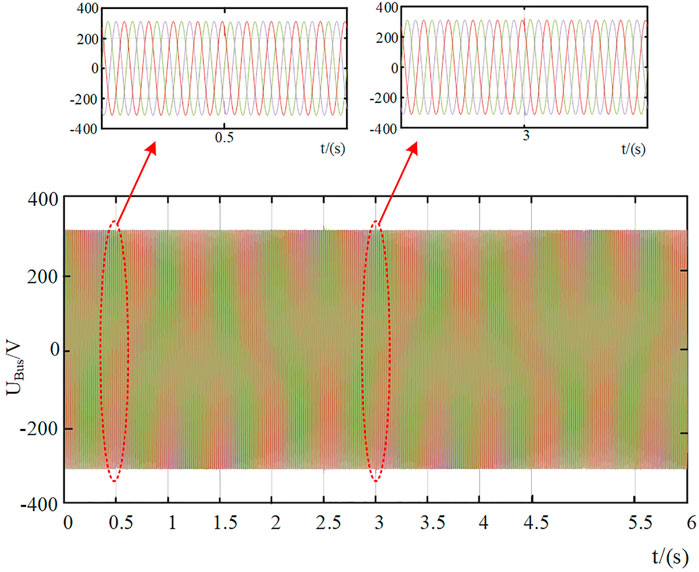
In order to verify the accuracy of the control algorithm proposed in this article, after the system operates stably, the voltage amplitude on the grid side is reduced from 1.0 to 0.8 Pu step by step; after continuous operation for 2s, the grid voltage was restored to the rated voltage for operation. After the system is stabilized again, the grid voltage was set from 1.0 to 1.2pu. After continuous operation for 2s, the grid voltage was restored to the rated voltage for operation. The experimental results are shown in Figures 6–8.

FIGURE 6

FIGURE 6. Grid controlled node voltage.

FIGURE 7

FIGURE 7. Compensation voltage of voltage compensator.

FIGURE 8

FIGURE 8. Compensated node voltage waveform.

The simulation results showed that when the grid voltage is stable, the integrated reactive power compensation device dynamically compensates the interference caused by the fluctuation of new energy power generation by SVG. At this time, the compensation voltage is relatively small, and the bus voltage maintains the rated voltage unchanged; when the grid voltage drops by 0.2 pu at 0.5 s, SVG and SVC act at the same time to compensate the system voltage. The compensation voltage amplitude is 65 V, and the PCC bus voltage continues to maintain the rated voltage. When the grid voltage rises by 0.2 pu compared with the rated value at 3.0 s, SVG and SVC act at the same time to compensate the system voltage. The compensation voltage amplitude is 100 V, and the PCC bus voltage continues to maintain the rated voltage. At the same time, it can be seen from the waveform of the compensation voltage that when the voltage drops, the compensation voltage is in phase with the grid voltage. When the grid voltage rises, the compensation voltage and the grid voltage differ by 180°, and the phase and amplitude of the compensation voltage are controlled so as to achieve the dynamic optimization of the regional voltage.

Conclusion

Aiming at the problem of large regional voltage fluctuation after new energy access, based on the high-precision measurement data on PMU, this article realizes regional voltage optimization using the model predictive control algorithm. The simulation model is built on the MATLAB/Simulink simulation platform, and simulation experiments are carried out to verify the effectiveness of the control strategy proposed in this article. The experimental results showed that:

1) By using SVC + SVG hybrid reactive power compensation, the efficiency of voltage dynamic optimization can be greatly improved. When the voltage change frequency is small, using SVC for voltage adjustment can reduce the capacity configuration of SVG and the investment cost of SVG.

2) The high-precision calculation ability of PMU at the edge of the power grid is fully utilized to realize the optimization of regional voltage. The data acquisition frequency of PMU is high, and the amount of data is large. The local controller used the measured data of PMU for local reactive power compensation, which can reduce the transmission of redundant data and improve the utilization efficiency of data.

3) The model predictive control algorithm used in this article can better optimize the regional voltage. When the voltage on the grid side rises or falls, the MPC controller sends instructions to the reactive power compensation device, and the SVG + SVC hybrid reactive power compensator compensates the reactive power. From the load side voltage, it can be seen that the compensation effect is good, which verifies the effectiveness of the algorithm proposed in this article.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

The author’'s personal contributions are as follows: manuscript writing, SL and ZW; data collection, LZ; and model construction, JZ and LL. All authors have read and agreed to the published version of the manuscript.

Funding

This study received funding from the Science and technology project of State Grid Shanghai Electric Power Company (520940200069).

Conflict of Interest

SL was employed by the company State Grid Shanghai Electric Power Company Electric Power Research Institute, and LZ was employed by the company State Grid Shanghai Electric Power Company Pudong Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor BZ is currently organizing a research topic with the author JZ.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, S., Li, K., Wang, Z., and Yan, W. (2016). A New Hybrid SVC Model and its Control Strategy Based on Artificial Immune Algorithm[J]. Power Autom. Equip. 36 (04), 93–99. doi:10.16081/j.issn.1006-6047.2016.04.015

CrossRef Full Text | Google Scholar

Fu, W., and Fan, C. (2015). Application of SVG in Voltage and Reactive Power Control of Doubly Fed Wind Power Generation System[J]. Power Systerm Prot. Control 43 (03), 61–68. doi:10.16081/j.issn.1006-6047.2016.04.015

CrossRef Full Text | Google Scholar

Guo, L., Jin, N., Gan, C., Xu, L., and Wang, Z., (2019). An Improved Model Predictive Control Strategy to Reduce Common-Mode Voltage for Two-Level Voltage Source Inverters Considering Dead-Time Effects[J]. IEEE Trans. Ind. Electron. 5 (66), 3561–3572. doi:10.1109/tie.2018.2856194

CrossRef Full Text | Google Scholar

Guo, L., Jin, N., Li, Y., and Luo, K., (2021). A Model Predictive Control Method for Grid-Connected Power Converters without AC Voltage Sensors[J]. IEEE Trans. Indust. Electron. 2 (68), 1299–1310. doi:10.1109/tie.2020.2970638

CrossRef Full Text | Google Scholar

Kosen, I., Huang, C., Chen, Z., Zhang, X., Min, L., Zhou, D., et al. (2020). UPS: Unified PMU-Data Storage System to Enhance T+D PMU Data Usability. IEEE Trans. Smart Grid 11 (1), 739–748. doi:10.1109/tsg.2019.2916570

CrossRef Full Text | Google Scholar

Lei, B., Fei, S., Zhai, J., and Dai, S. (2013). A Novel Nonlinear Robust Adaptive Control Design Method for Static Reactive Power Compensator (SVC). J. Chin. Electr. Eng. Sci. 33 (30), 65–70. doi:10.13334/j.0258-8013.pcsee.2013.30.002

CrossRef Full Text | Google Scholar

Lin, S., Wu, J., Mo, C., Wang, Z., and Guo, Q. (2018). Dynamic Reactive Power Partition and Optimization Method of Distribution Network with Distributed Generation Based on Second-Order Cone Programming[J]. Power Syst. Technol. 42 (01), 238–246. doi:10.13335/j.1000-3673.pst.2017.0718

CrossRef Full Text | Google Scholar

Liu, J., Miura, Y., and Ise, T. (2019). Cost-Function-Based Microgrid Decentralized Control of Unbalance and Harmonics for Simultaneous Bus Voltage Compensation and Current Sharing[J]. IEEE Trans. Power Electron. 8 (34), 7397–7410. doi:10.1109/tpel.2018.2879340

CrossRef Full Text | Google Scholar

Luo, R., He, Y., and Liu, J. (2018). Research on the Unbalanced Compensation of Delta-Connected Cascaded H-Bridge Multilevel SVG. IEEE Trans. Ind. Electron. 65 (11), 8667–8676. doi:10.1109/tie.2018.2815952

CrossRef Full Text | Google Scholar

Mi, Y., Ma, C., Fu, Y., Wang, S., and Wang, P., Poh Chiang Loh (2017). The SVC Additional Adaptive Voltage Controller of Isolated Wind-Diesel Power System Based on Double Sliding-Mode Optimal Strategy[J]. IEEE Trans. Sustain. Energy 9 (1), 24–34. doi:10.1109/TSTE.2017.2713700

CrossRef Full Text | Google Scholar

MoraCárdenas-Dobson, A., Cardenas-Dobson, R., Aguilera, R. P., Angulo, A., Donoso, F., and Rodriguez, J. (2019). Computationally Efficient Cascaded Optimal Switching Sequence MPC for Grid-Connected Three-Level NPC Converters. IEEE Trans. Power Electron. 34 (12), 12464–12475. doi:10.1109/tpel.2019.2906805

CrossRef Full Text | Google Scholar

Pereira, R. M. M., Ferreira, C. M. M., and Barbosa, F. P. M. (2014). Comparative Study of STATCOM and SVC Performance on Dynamic Voltage Collapse of an Electric Power System with Wind Generation. IEEE Lat. Am. Trans. 12 (2), 138–145. doi:10.1109/tla.2014.6749530

CrossRef Full Text | Google Scholar

Pham, V. H., and Erlich, I. (2014). “Online Optimal Control of Reactive Power Sources Using Measurement-Based approach[C],” in IEEE PES Innovative Smart Grid Technologies, 1–5.

Google Scholar

Wang, L., Lam, C. S., and Wong, M. C. (2018). Multifunctional Hybrid Structure of SVC and Capacitive Grid-Connected Inverter (SVC//CGCI) for Active Power Injection and Nonactive Power Compensation[J]. IEEE Trans. Ind. Electron. 66 (3), 1660–1670.

Google Scholar

Wang, W., Zhao, M., Tang, X., Lei, J., and Liu, F. (2019). Optimal Design of SVC under Ground Fault and its Control Strategy for Subsequent Phase Change Failure[J]. Autom. Electr. power Syst. 43 (20), 123–129. doi:10.7500/AEPS20190117005

CrossRef Full Text | Google Scholar

Wang, Z. Z., Zhang, B., Mobtahej, M., Baziar, A., and Khan, B. (2021). Advanced Reactive Power Compensation of Wind Power Plant Using PMU Data. IEEE Access 9, 67006–67014. doi:10.1109/access.2021.3075966

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Liu, Y., and Zhou, F., (2020). Modeling and Stability Issues of Voltage-Source Converter Dominated Power Systems: A Review[J]. CSEE J. Power Energy Syst., 1–18. doi:10.17775/CSEEJPES.2020.03590

CrossRef Full Text | Google Scholar

Yu, J., Dai, W., Li, W., Liu, X., and Liu, J. (2018). Optimal Reactive Power Flow of Interconnected Power System Based on Static Equivalent Method Using Border PMU Measurements. IEEE Trans. Power Syst. 33 (1), 421–429. doi:10.1109/tpwrs.2017.2699231

CrossRef Full Text | Google Scholar

Zhu, L., Chen, J., Li, Y., Zheng, K., and Yang, G. (2021). Hierarchical Control Strategy for Hybrid Reactive Power Compensation System[J]. Water Resour. Power 39 (02), 186–189.

Google Scholar