- Department of Electrical and Computer Engineering, King Abdulaziz University, Jeddah, Saudi Arabia
It is necessary to predict solar photovoltaic (PV) output and load profile to guarantee the security, stability, and reliability of hybrid solar power systems. Severe frequency fluctuations in hybrid solar systems are expected due to the intermittent nature of the solar photovoltaic (PV) output and the unexpected variation in load. This paper proposes designing a PID controller along with the integration of a battery energy storage system (BESS) and plug-in hybrid electric vehicle (PHEV) for frequency damping in the hybrid solar power system. The solar PV output is predicted with high accuracy using artificial neural networks (ANN) given that solar irradiance and cell temperature are inputs to the model. The variation in load is also forecasted considering the factors affecting the load using ANN. Optimum values of the PID controller have been found using genetic algorithm, particle swarm optimization, artificial bee colony, and firefly algorithm considering integral absolute error (IAE), integral square error (ISE), and integral time absolute error (ITAE) objective functions. IAE, ISE, ITAE, Rise time, settling time, peak overshoot and maximum frequency deviation have been measured for comparison and effectiveness. The transient behavior has been further improved by utilizing the power from BESS/PHEV to the power system. The results demonstrate the efficacy of the suggested design for frequency control using the genetic algorithm method along with ISE objective function compared with those obtained from the conventional, particle swarm optimization, artificial bee colony, and firefly algorithm techniques.
Introduction
Solar photovoltaic (PV) systems are intermittent in nature. The variation in generated power and load demand is common in solar PV connected power systems. Under normal operating situations, microgrids are powered by the integration of both solar PV systems and the power grid. However, when the output from the solar PV system is lower than expected, and the load demand is high, the power grid may not be able to support enough power because of its slow dynamic response. This will cause the power system to be unstable which leads to severe frequency fluctuations in the system (Sadat, 2012).
Hybrid solar power systems are a source for generating electrical power that use inverters coupled with batteries to store energy later use. In this way, hybrid solar systems will be able to use the stored energy during blackouts and compensate for renewable energy sources output fluctuation (Newkirk, 2015). Integrating microgrids with renewable energy systems is considered an adequate solution to meet the increasing demand of electric power. Such microgrids can utilize plug-in hybrid electric vehicles and battery energy storage systems to maintain the balance between generated power and the load demand. Due to the intermittent nature of renewable energy sources, the change in generation power and load demand would lead the system to instability causing severe frequency fluctuations. Mathematical models were developed to predict the behavior of microgrids in order to dampen frequency fluctuations. Power systems with a high penetration of renewable energy sources were integrated with battery energy storage system (BESS) and plug-in hybrid electric vehicles to maintain the frequency deviations within limits (Akula, 2019).
Mellit (Mellit and Pavan, 2010) uses artificial neural network methods for forecasting the electric power produced by a 20
Hote (2018) studied the PID controller calibrating approaches for load frequency control of Power systems. The prime challenge in LFC was to design a PID controller that could maintain the frequency fluctuations rigorously within the defined limits. Fractional Order PID controller was tuned by Taher (2014) for load frequency control for three area power system with the help of imperialist competitive algorithm (ICA). The response of the interconnected power system towards disruption was smooth and less vibratory as a result of using the proposed controller. Mosaad (Mosaad and Salem., 2014) presented a methodological design for an adaptive PID load frequency using artificial neural networks (ANN) and adaptive Neuro-Fuzzy Inference systems (ANFIS). The PID Controller was able to maintain the effective performance at any load point in the power system with the superiority of ANFIS over ANN with respect to integral absolute error (IAE), integral square of errors. According to Otani (2017), there are possible chances of frequency fluctuations after losing balance between power generated and load demand. Battery storage was incorporated because of its faster response to overcome load frequency deviations using recurrent neural networks.
The desired frequency of the power system deviates due to disturbances in the electric power generation and load fluctuations. Load frequency control has been considered the main issue for power system operation and control for effective and reliable power supply (Sundaram and Jayabarathi, 2011). PI, PID and fuzzy controllers have been used to stabilize the power system when it is integrated with wind power. Kumari et al. (2016) introduce the ANN-based PID controller to sufficiently damp frequency fluctuations produced as a result of load changes. An artificial intelligent controller has been designed using the backpropagation algorithm to reduce the area control error of a two-area hydrothermal power system for automatic generation control purposes in (Rao, 2012).
Meta-heuristic optimization techniques have been employed to get the optimal gains of PID controller for LFC problem. According to (Das et al., 2010), genetic algorithm based PID controller was tuned for autonomous hybrid generation system. Fractional order PID controller was tuned using genetic algorithm for hybrid power system integrated with renewable energy sources (Regad et al., 2019). Multi-objective artificial bee colony technique was adopted to tune the PID controller parameters with the help of integral time multiplied absolute error (ITAE) and integral of time weighted squared error (ITSE) for two area thermal power system (Naidu et al., 2014). Particle swarm optimization has been utilized to tune the fuzzy logic controller for the frequency restoration of multi-area power system (Jaber et al., 2013). PSO is used for obtaining the optimal PID parameters for two area system with integral square error as cost function and showing best convergence profile (Nagarjuna and Shankar, 2015). PID optimal parameters obtained for two and three area power system using firefly algorithm considering the generation rate constraint and governor dead band (Padhan et al., 2014).
Energy storage systems are also used in previous studies for frequency regulation. The role of battery energy storage system has been presented for regulating the frequency in interconnected power system. The results are compared to the conventional PID controller that describe BESS as efficient for LFC purpose (Kalyani et al., 2012). Peak frequency deviation and settling time of two area power system is reduced using the battery energy storage system and choosing the proper integral gain (Aditya and Das, 2001). Plug-in electric vehicles power is utilized for frequency stability of the islanded power system with the help of controllable power rate strategy (Qi et al., 2018). The energy from electric vehicles that are charged during daytime can be utilized in the night-time for small residential power system (Takagi et al., 2009).
The purpose of this study to address the limitations in the previous studies and fulfill the gap. Many load frequency control techniques have been applied to power system for its stability purposes, i.e., robust control, decentralized aspect, linear quadratic, pole shifting, and variable structure. But there have been some drawbacks of these techniques which decrease their execution efficiency. To overcome such problem, artificial intelligence techniques, fuzzy logic (FL) and neural network (NN) have been adopted and applied to solve the non-linear models of the power system. These techniques have proved their effectiveness and efficiency to solve the problem. But they still have some disadvantages. For example, it is hard to train the neural network again and again to set the number of neurons and other parameters to get the best output response. Similarly, fuzzy logic requires hard work to get the influential signal response from the power system (Abd-Elazim and Ali, 2018). Optimization techniques such as genetic algorithm (GA) (Milani and Mozafari, 2009) (Chang et al., 1998; Rerkpreedapong et al., 2003; Das et al., 2010; Das et al., 2012; Mallesham et al., 2012; Konar et al., 2014; Regad et al., 2019; Hemeida et al., 2020; Sidi Brahim et al., 2021), particle swarm optimization (PSO) (Pain and Acharjee, 2014; Abd-Elazim and Ali, 2018) (Gözde et al., 2008; Selvakumaran et al., 2012; Modi et al., 2013; Rao and Rama Krishna Reddy, 2015; Shankar et al., 2015; Hazlee Azil et al., 2016; Jeyalakshmi and Subburaj, 2016; Singh and Ramesh, 2019; Hemeida et al., 2020; Veerasamy et al., 2020; Safari et al., 2021) (Sidi Brahim et al., 2021) (Mallesham et al., 2012)- (Kumari and Jha, 2014), firefly algorithm (FA) (Naidu et al., 2013; Shakarami et al., 2013; Padhan et al., 2014; Chandra Sekhar et al., 2016; Abd-Elazim and Ali, 2018; Boddepalli and Navuri, 2018; Gupta et al., 2021), and artificial bee colony (Ghasemi and Shayeghi, 2011; Rathor et al., 2011; Gozde et al., 2012; Naidu et al., 2014; Elsisi et al., 2015; Kouba et al., 2015; Kumar et al., 2017; Abo-Elyousr, 2018), have been used and found to be effective for load frequency control problem. But proportional, integral and derivative gain range of PID controller during optimization problem has been narrowed. Renewable energy source, photovoltaic and wind turbine, transfer function model has been adopted in the previous studies. In the same way, load frequency control has also been done in previous studies using the energy storage systems but without efficient PID controller that ultimately require large energy storage capacity to damp the frequency (Kalyani et al., 2012)- (Aditya and Das, 2001). Taking into account the mentioned limitations, the current study discusses and solve the problem by taking real-time data to train the network for solar photovoltaic prediction, load deviation forecasting, widening proportional, integral, and derivative controller gain range, and integrating the BESS/PHEV with efficient tuned PID controller.
The major contributions of this paper are threefold and shown below.
1) Solar photovoltaic generated power and load deviation have been forecasted from the affecting factors using artificial neural networks.
2) The forecasted solar photovoltaic power and load deviation have been utilized by the power system model to find the optimal PID controller parameters using genetic algorithm, particle swarm optimization, artificial bee colony and firefly algorithm optimization techniques considering the integral absolute error, integral square error, and integral time absolute error objective functions.
3) BESS/PHEV model, with gain levels 10 and 50 respectively, has been integrated to the power system model to further dampen the frequency deviation.
Power System Model
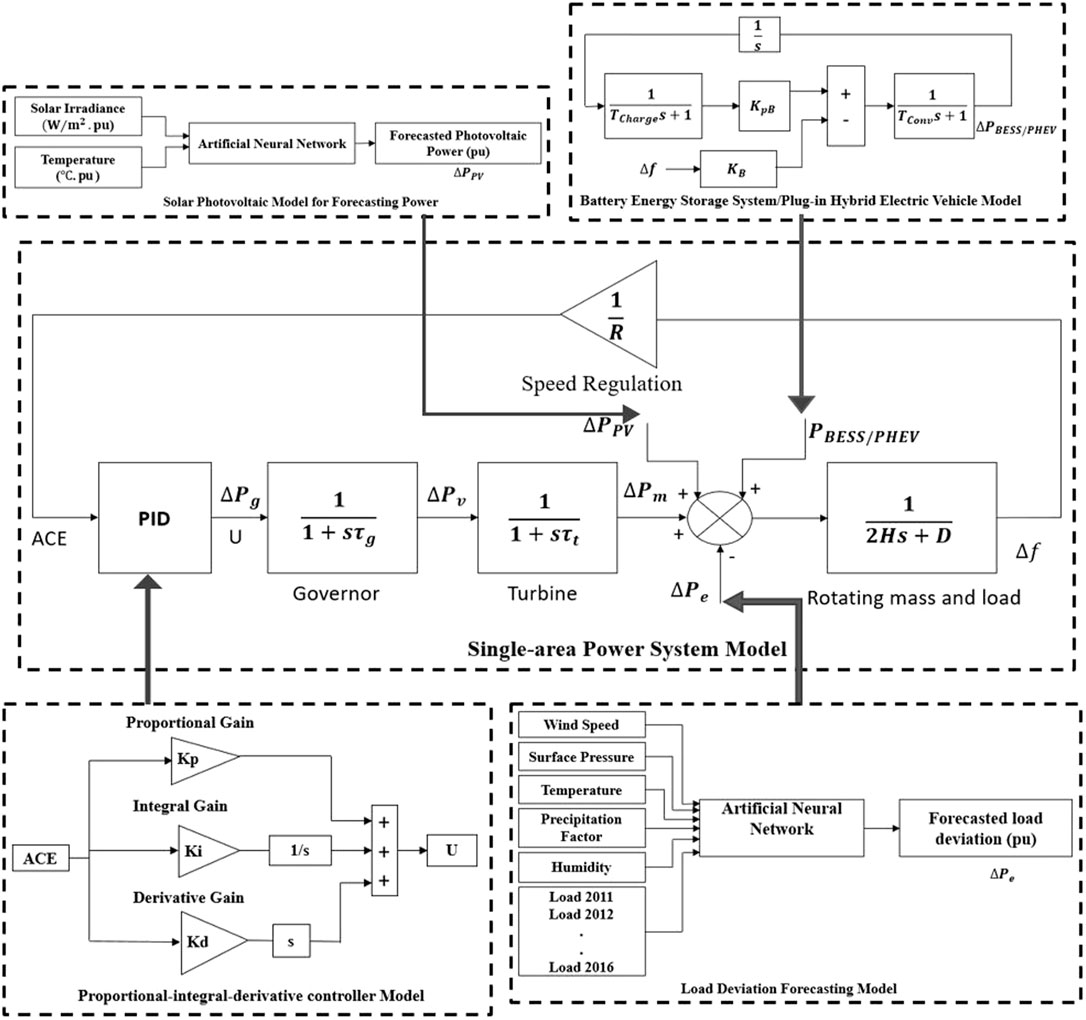
Power system control concentrate on steady state operation. This study presents how to deal with active power to keep the power system in steady state. The major objective of the control strategy is to provide qualitative and reliable power to customers within an interconnected system. Changes in the active power disturb the frequency of the system. Therefore, a control strategy is designed to regulate load frequency control using control loops. Two common approaches, transfer function and state variable, are adopted to transform the power system model into a mathematical model by making some proper assumptions (Prakash and Sinha, 2012; Pain and Acharjee, 2014; Prajapati and Parmar, 2016; Azeer et al., 2017; Lone et al., 2018; Yang-Wu et al., 2019). A single area power system model is shown in Figure 1.
Generator Model
The generator equation has been extracted from the swing equation as shown in Eq. 1.
Load Model
The power system contains resistive and inductive load that is frequency independent and dependent respectively (Sadat, 2012). Therefore, the net change in load power can be described as the combination of frequency sensitive and frequency non-sensitive load changes shown in Eq. 2.
Where
Many factors affect the electric load (Khatoon and Singh, 2014). These factors could be short term, middle term, and long-term influence factors. Some important factors used for load forecasting are categorized as follows.
• Meteorological factors involving temperature, wind speed, humidity, surface pressure, and precipitation factor are responsible for load forecasting.
• Temporal or calendar factors involving hour of the day and day of the week.
• Random factors such as sports activities.
Frequency dependent load change has been observed from the Atlas Power Plant. The Atlas power plant is a coal fired thermal power plant located at the geographic location (Longitude:31.5204, Latitude:74.3587). The historical load demand data has been extracted from the power data reference book produced by the National Transmission and Dispatch Company Limited (NTDCL) (Power Data Reference Book, 2017). Historical daily load data from 2011 to 2016 has been taken as input along with weather and seasonal data. Seasonal and weather data consists of wind speed, surface pressure, temperature, precipitation factor, and humidity. Average load has been calculated for 365 days from load profile data between 2011 and 2016 (Alessandra et al., 2011). Frequency dependent change in load has been extracted from the average load for consecutive 365 days as shown in Figure 2. This change in load power has been taken as an output (Kotur and Žarković, 2016).
The weather data has been first normalized by taking the maximum value as base from each factor affecting the load and dividing the entirety of the weather data with base value within the range (0–1). Similarly, historical data has also been normalized by dividing with the base value 219 MW and converting the load data within the range of (0–1). After normalizing the input and target data, NNTOOL is used to train the network. A multi-layer feed forward neural network was trained using wind speed, surface pressure, temperature, precipitation factor, humidity, and historical load data as input and deviation in load power data as target as shown in Figure 1 of the load deviation model (Srinivasan et al., 1991). The number of neurons has been chosen as 10, Tan sigmoid activation function, and Levenberg Marquardt as learning algorithm as shown in Table 1. The trained model depicts its effectiveness showing the coefficient of regression as 1.0 and mean squared error (MSE) as

TABLE 1. Summary of artificial neural network design and architecture for forecasting load deviation.
Prime Mover Model
It is the origin of mechanical power whose energy is obtained from burning coal or gas, or nuclear fission. The transfer function of the turbine can be represented as the ratio of the change in mechanical output power
Where
Governor Model
The speed governor model can be expressed as Eq. 5.
The speed governor operates as a comparator and its output
Where
Solar Photovoltaic Model
It is fact that photovoltaic output power is intermittent in nature. It depends on two main factors: solar irradiance and temperature (Rodríguez et al., 2018). Solar photovoltaic power is directly proportional to solar irradiance while inversely proportional to temperature (Abd-Elazim and Ali, 2018). Solar photovoltaic model of 5 MW is considered at location (Longitude:31.5204, Latitude:74.3587) near the thermal power plant. Solar PV system is integrated to the thermal power plant. The solar power plant is built by LONGI solar modules of power 540W. LONGI solar module characteristics are shown in Table 2. The solar PV module output (W) was considered at different solar irradiance (ranges 100–1100

TABLE 3. Summary of artificial neural network design and architecture for forecasting solar photovoltaic power.
Battery Energy Storage System/Plug-in Hybrid Electric Vehicle Model
Energy storage systems are a great source of frequency damping in the power system. As discussed in the introduction section, power from battery energy storage systems and plug-in hybrid electric vehicle play an important role for maintaining the frequency. Energy from PHEV can be utilized for small residential systems. The circle of willingness of customers for utilizing PHEV can be enhanced. Figure 1 consists of the control system model for a battery energy storage system or plug-in hybrid electric vehicle integrated to the power system. The term
PID Controller Model for Optimization Problem
The PID Controller model has been adopted in the power system model as shown in Figure 1. The transfer function of the controller is as follows.
The control signal for maintaining the system frequency is given by Eq. 8 (Abd-Elazim and Ali, 2018).
where
Area Control Error (ACE) of studied single-area power system can be written by Eq. 9.
Multi-objective function is used in (Naidu et al., 2014) for load frequency control using the artificial bee colony optimization approach considering ITAE and ITSE. It has been observed the performance of the PID controller can be compromised, i.e., Either frequency deviation or settling time is compromised on the cost of each other. Therefore, it is recommended to use objective functions separately. But, the most suitable objective function should be identified based on the performance indices and convergence profile.
Three objective functions
Where
Frequency deviation permissible limit is calculated using the following steady-state equation (Sadat, 2012).
The maximum steady-state frequency deviation in Hz has found to be −0.7932 Hz for maximum positive load change and 0.5468 Hz for maximum negative load change for studied model. So, the frequency deviation permissible limit range should be (−0.7932, 0.5468) in Hz.
Proposed Approaches for Tuning the PID Controller
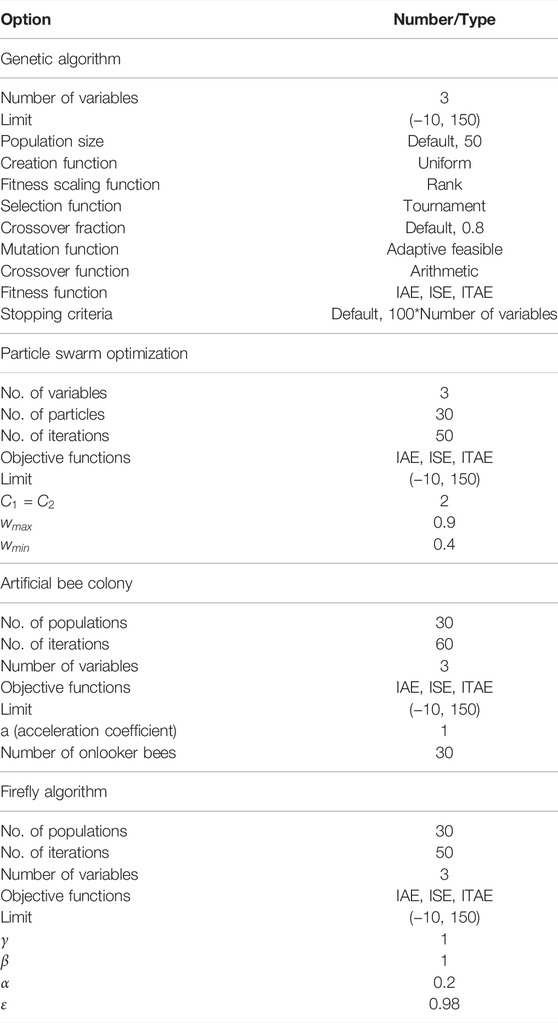
Particle Swarm Optimization
Particle swarm optimization technique was developed by Kennedy and Eberhart in 1995. They used nature inspired optimization algorithms in their technique. In this technique, particles are flown through the search space and update the position of the
This technique is adopted to find the optimal values of the PID controller parameters. Initially, the PID controller proportional gain
Genetic Algorithm
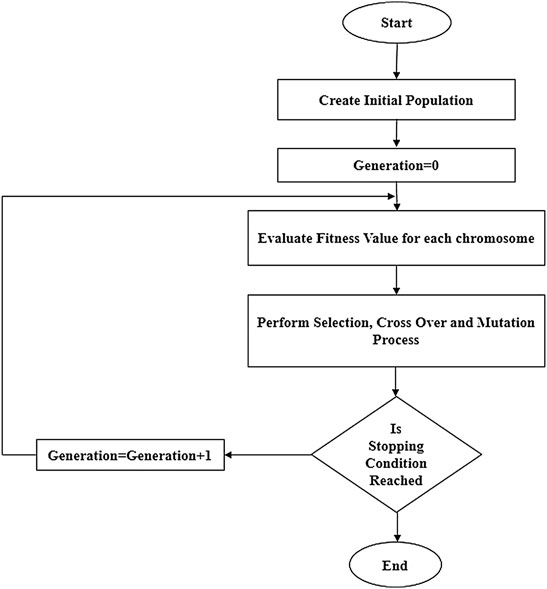
Genetic Algorithm is an optimization technique based on heredity and evolution. This technique was suggested by John Holland in 1960 to search for the best solution of complex problems. It is an iterative process which maintains the constant population size of desired solution. GA initially begins with a randomly selected population of function input that is represented as a bit of strings. The Population is evaluated in each iterative step called generations to give a new population of the desired solution. That means GA uses the current population to produce a new population such that the new population is better on average if compared to the previous population. Best elements are used from the current population to form the best population. The successful process will produce a population better than the old one. Three steps selection, mating, and mutation are used to produce new population from the old population. The basic genetic algorithm cycle is shown in Figure 3. New generations are produced iteratively with the repetition of these three steps. The process continues until the stopping criteria is reached like the maximum number of iterations is achieved or no improvements (Milani and Mozafari, 2009) (Chang et al., 1998; Rerkpreedapong et al., 2003; Das et al., 2010; Das et al., 2012; Mallesham et al., 2012; Konar et al., 2014; Regad et al., 2019; Hemeida et al., 2020; Sidi Brahim et al., 2021).
This technique is adopted to find the optimal values of the PID controller parameters. The PID controller proportional gain
Firefly Algorithm
The flashing light of fireflies is of great importance to study their pattern and rhythmic movement. Studies discussed the main aim of pattern of flashes is either to communicate with the mating partners, to attract the potential prey or to signal other fireflies for potential safety warning. This signal consists of rhythmic flash, rate of flash and amount of flashing. This behavior of flashing light from fireflies can be used to solve many optimization problems. This algorithm has been developed by Xin-She Yang in 2008.
The Euclidian distance
Where
The PID controller proportional gain
Artificial Bee Colony
Artificial bee colony is meta-heuristic optimization algorithm developed by Karaboğa in 2005. Honey bees foraging behavior has been utilized in this technique searching for nectar at different positions. Usually, three kind of honey bees are considered to be responsible for finding nectar positions: employed, onlooker and scouts. This algorithm adopts some variables and steps to proceed for finding optimal solution. The variables of ABC algorithm include population of honey bees (SN), maximum cycle number (MCN), objective functions and some functions to test the probability, fitness and optimization of the objective functions. The steps in the ABC algorithm includes initialization, employed, onlooker and scout bees. The initialization step starts by generating the number of solutions equal to total number of bees (SN). Each solution is obtained within the upper and lower limit of the selected decision variable with the following equation.
Where
Where
Where
Conventional PID Controller
The Simulink model of the single-area power system containing PID controller is tuned using the classical method to enhance the performance and robustness. PID Tuner toolbox is launched from the Simulink model that automatically computes the linear power system model to find gain parameters corresponding to initial controller conditions. The obtained PID controller gains can robustly stabilize the power system. The performance of controller could be checked using frequency deviation performance indicators, i.e., settling time, zero steady state error. If the desired response is not achieved by auto tunning, PID controller gains can be adjusted manually by varying the response time (seconds) and transient behavior. The PID controller gains are updated to the Simulink model after meeting the desired requirement (MathWorks, 2022a)- (MathWorks, 2022b). The compensator formula for PID controller is given as,
In the studied model, best performing PID controller gains have been found to be
Results and Discussion
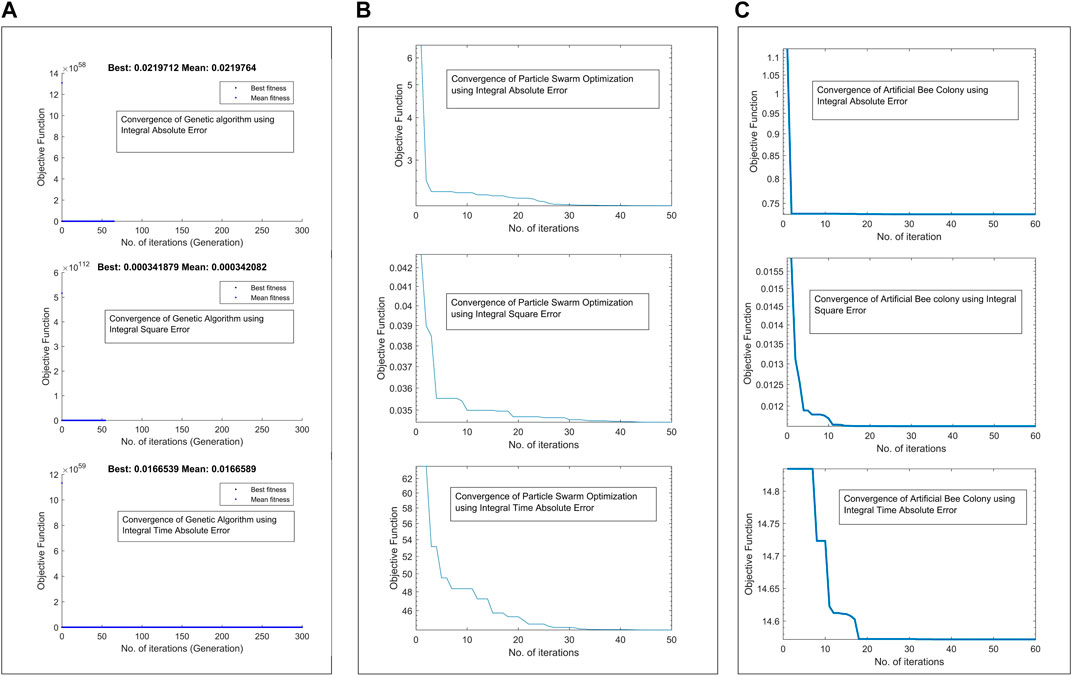
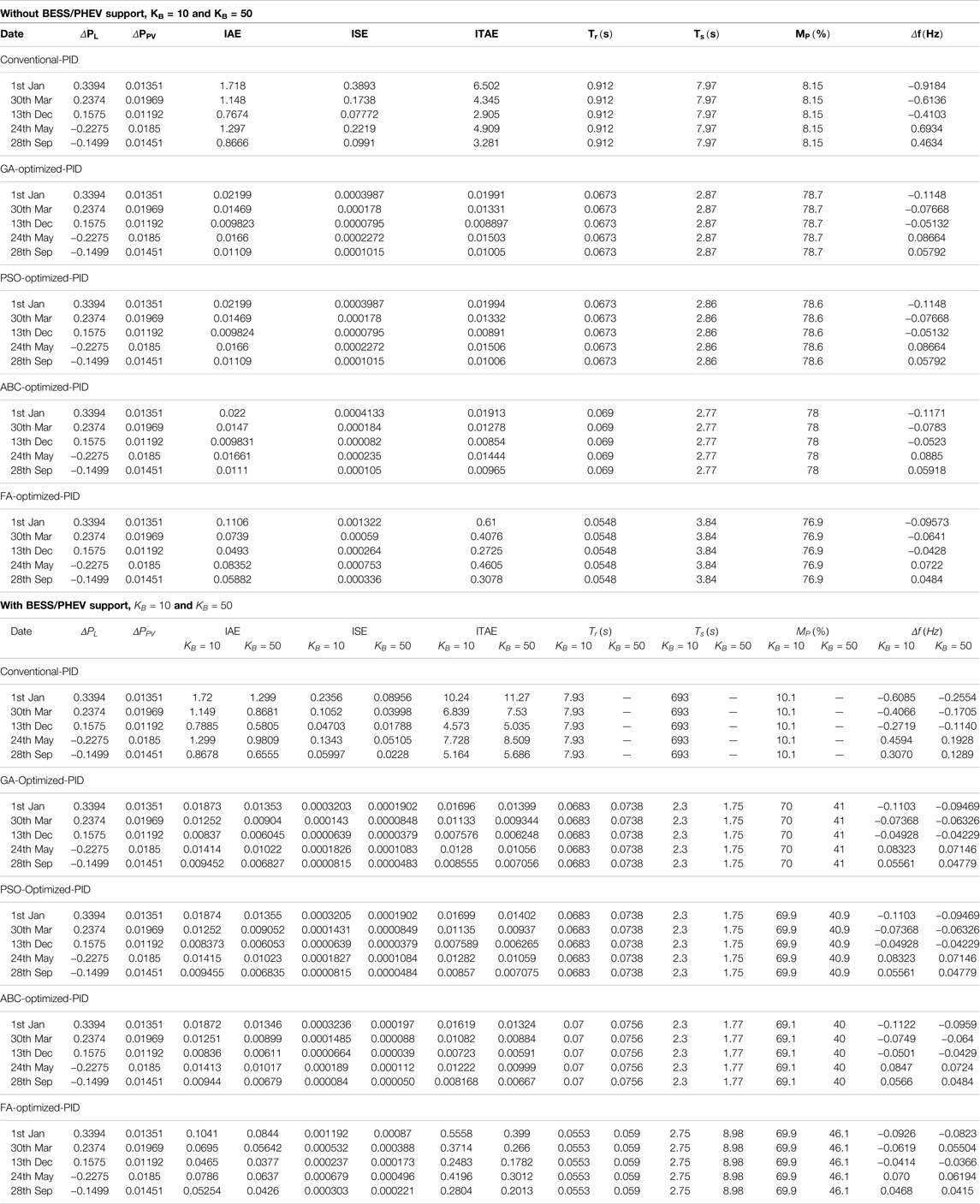
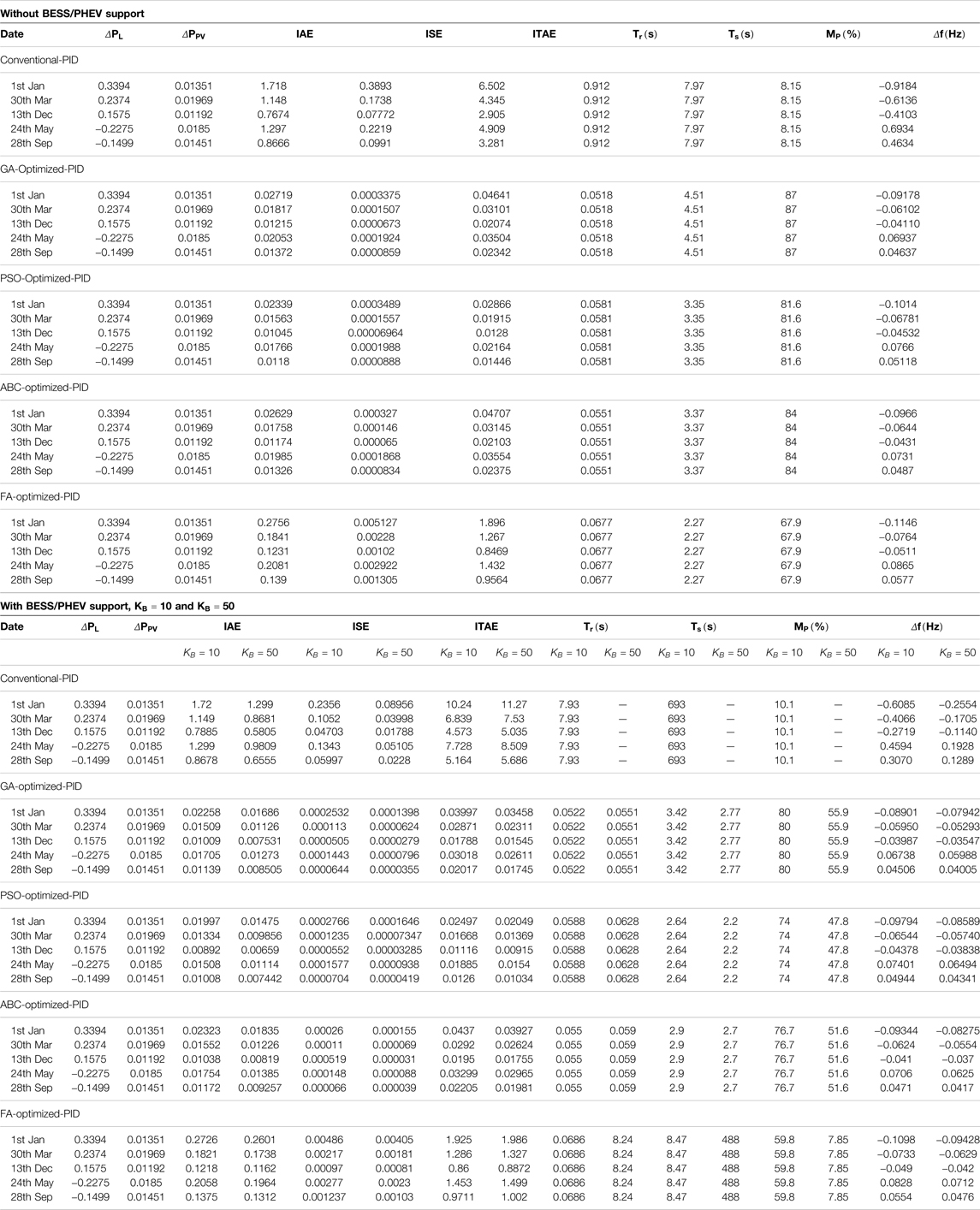
Three objective functions IAE, ISE, and ITAE have been applied to the genetic algorithm, particle swarm optimization, artificial bee colony, and firefly algorithm to find out the optimal proportional gain
The results of the studied model have been categorized into three cases.
• Frequency damping using integral absolute error (IAE) objective function, with and without BESS/PHEV support.
• Frequency damping using integral square error (ISE) objective function, with and without BESS/PHEV support.
• Frequency damping using integral time absolute error (ITAE) objective function, with and without BESS/PHEV support.
Several parameters are used to check the performance indices of hybrid power system for frequency deviation including integral absolute error, integral square error, and integral time absolute error. Rise time
Frequency of the power system deviates either positive or negative depending upon the increase or decrease in load and photovoltaic power. The mismatch between load demand and photovoltaic power give rise to changes in frequency. Five key days, 1st January (
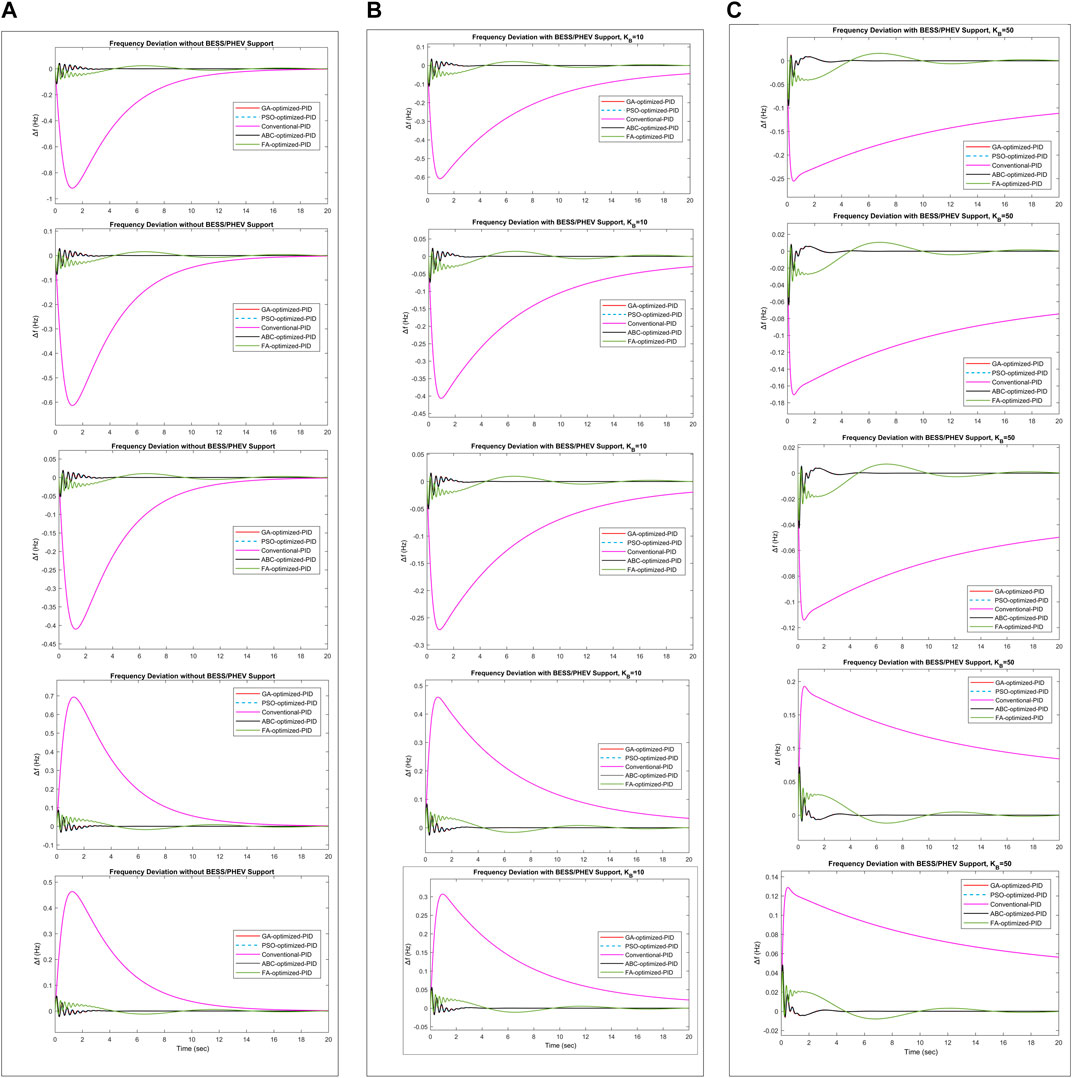
FIGURE 5. Frequency deviation response using integral absolute error (A) without BESS/PHEV support (B) with BESS/PHEV support,
Frequency deviation responses of the GA optimized PID, PSO optimized PID, ABC optimized PID, and FA optimized PID using the IAE objective function is shown in Table 6 and Figure 5. Their performance indices show that GA optimized PID, PSO optimized PID, and ABC optimized PID produce approximately same results as their proportional, integral, and derivative values have been found to be same. IAE, ISE, ITAE and
Considering the effect of BESS/PHEV with its different capacities, BESS/PHEV
Frequency deviation responses of the GA optimized PID, PSO optimized PID, ABC optimized PID, and FA optimized PID using the ISE objective function is shown in Table 7 and Figure 6. Their performance indices show that GA optimized PID, PSO optimized PID, and ABC optimized PID produce efficient and competitive results. IAE, ISE, ITAE and
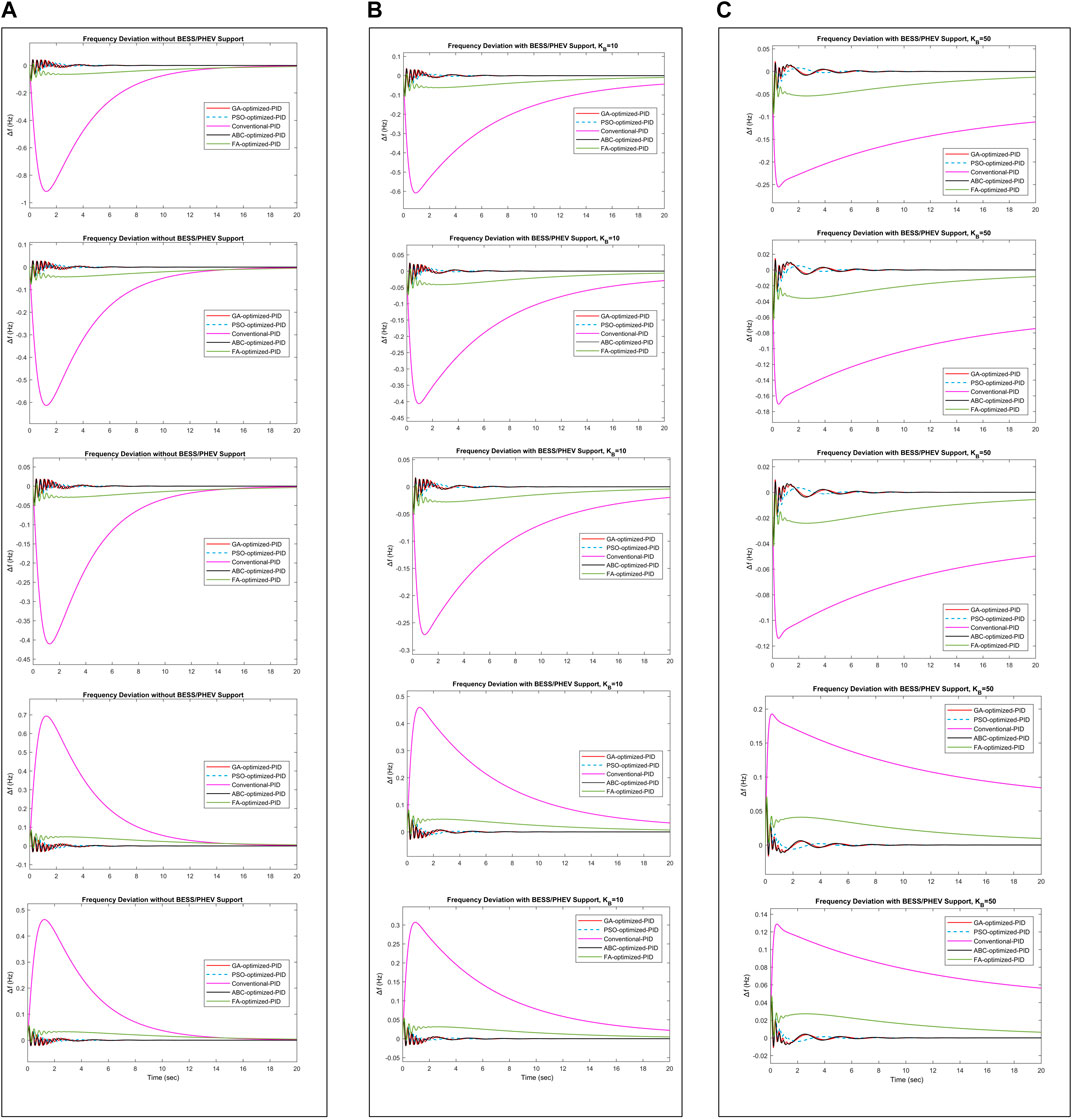
FIGURE 6. Frequency deviation response using integral square error (A) without BESS/PHEV support (B) with BESS/PHEV support,
Considering the effect of BESS/PHEV with its different capacities, gain for
Frequency deviation responses of the GA optimized PID, PSO optimized PID, ABC optimized PID, and FA optimized PID using the ITAE objective function is shown in Table 8 and Figure 7. Their performance indices show that GA optimized PID, PSO optimized PID, and ABC optimized PID produce approximately efficient competitive results. IAE, ISE, ITAE and
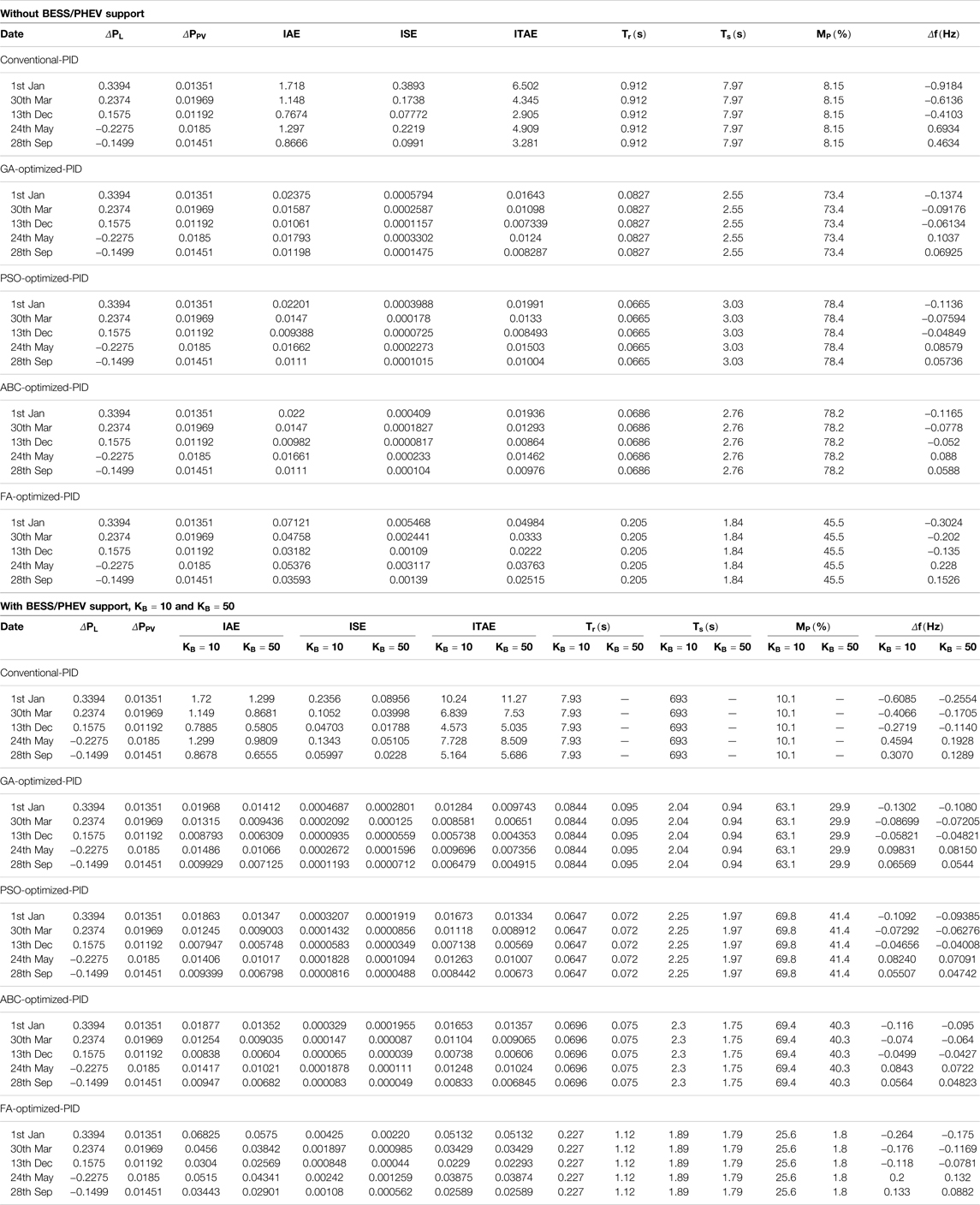
TABLE 8. Frequency deviation parameter indices using integral time absolute error objective function.
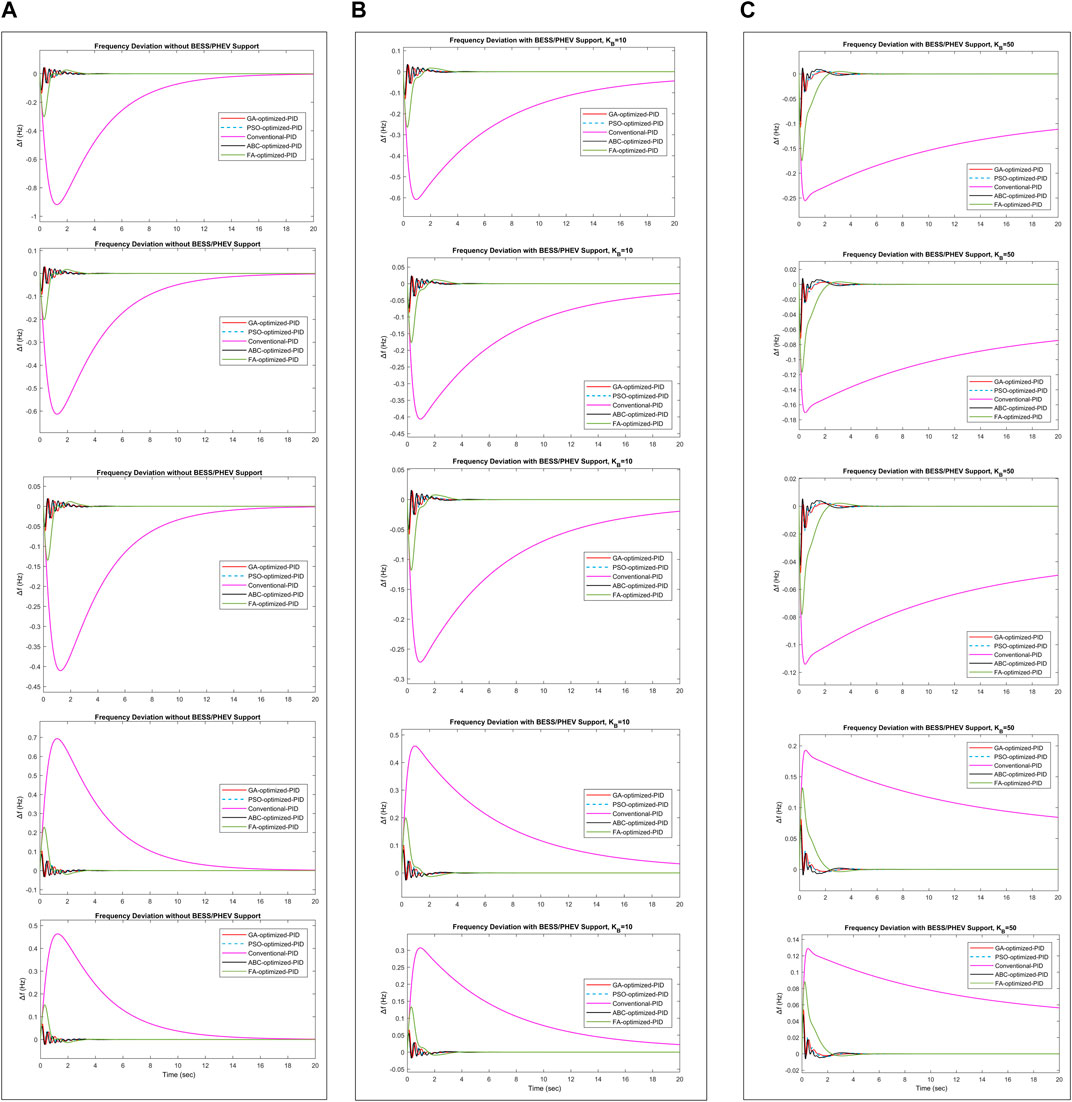
FIGURE 7. Frequency deviation response using integral time absolute error (A) without BESS/PHEV support (B) with BESS/PHEV support,
BESS/PHEV with its different capacities, gain
The conventional PID controller is tuned using the PID tuner toolbox within MATLAB. Tables 6–8 depict that performance indices IAE, ISE, ITAE and
The maximum steady state frequency deviation permissible limit in Hz is found to be in the range (−0.7932, 0.5468) for maximum positive and negative load deviation respectively. It can be seen from Table 6, Table 7 and Table 8 that the frequency deviation in Hz has found to be within permissible range using the GA, PSO, ABC, and FA optimization methods. The frequency deviation has not found to be within steady state limit for Conventional PID controller. The frequency deviation range in Hz is (−0.9184, 0.4634) for Conventional-PID. The frequency deviation is suppressed by adding the BESS/PHEV source. But, the PID controller response becomes unstable if the large capacity of BESS/PHEV source is attached to the power system model. The power delivered to power system by BESS and/or PHEV is 0.025 pu for gain
After comparison between the applied techniques and objective functions, it is concluded that PSO optimized PID controller using the ITAE objective function performs well just to mitigate frequency deviation
Conclusion
The load deviation of single area power system and solar photovoltaic power is forecasted using the state-of-the art artificial neural network. PSO, GA, ABC, and FA metaheuristic techniques have been employed to find out the optimal PID controller gain parameters using the IAE, ISE and ITAE objective functions. Some key days, showing significant load changes, have been chosen to see the performance of the single area hybrid power system. Results indicate the efficiency and competency of GA, PSO, and ABC among each other that sufficiently reduce frequency fluctuations. It has been found that PSO optimized PID along with ITAE cost function can sufficiently minimize the frequency. The performance indices and convergence characteristics show overall better results produced from GA optimized PID than others using ISE objective function. These frequency fluctuations are further improved by integrating power from BESS/PHEV source. Small BESS/PHEV capacity is required to damp the frequency when integrated with GA optimized PID.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://ntdc.gov.pk/services.
Author Contributions
SM and AM conceived the conceptualization and methodology. SM conducted the normal analysis and writing. MR and AM conducted the review and editing. MR managed funding acquisition. All authors have agreed to submitted version of the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IFPIP-1183-135-1442) and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Appendix
The typical values for the hybrid power system are given below
References
Abd-Elazim, S. M., and Ali, E. S. (2018). Load Frequency Controller Design of a Two-Area System Composing of PV Grid and Thermal Generator via Firefly Algorithm. Neural Comput. Applic 30 (2), 607–616. doi:10.1007/s00521-016-2668-y
Abo-Elyousr, F. K. (2018). “Load Frequency Controller with Virtual Inertia Generator for Interconnected Power Systems via Artificial Bee Colony,” in 2018 Twentieth International Middle East Power Systems Conference (MEPCON) (Giza, Egypt: IEEE). doi:10.1109/mepcon.2018.8635143
Aditya, S. K., and Das, D. (2001). Battery Energy Storage for Load Frequency Control of an Interconnected Power System. Electr. power Syst. Res. 58 (3), 179–185. doi:10.1016/s0378-7796(01)00129-8
Akula, S. K. (2019). Frequency Control in Microgrid Communities Using Neural Networks. Wichita, KS, USA: IEEE.
Al-Dahidi, S., Ayadi, O., Alrbai, M., and Adeeb, J. (2019). Ensemble Approach of Optimized Artificial Neural Networks for Solar Photovoltaic Power Prediction. IEEE Access 7, 2923905. doi:10.1109/access.2019.2923905
Alessandra, B. A., Carlos Roberto, M., Mara Lucia, M. L., Fábio Roberto, C., and Nelson Jose, P. (2011). Multinodal Load Forecasting in Power Electric Systems Using a Neural Network with Radial Basis Function. Adv. Mater. Res. 217, 39. doi:10.4028/www.scientific.net/amr.217-218.39
Azeer, S. A., Ramjug-Ballgobin, R., and Sayed Hassen, S. Z. (2017). Intelligent Controllers for Load Frequency Control of Two-Area Power System. IFAC-PapersOnLine 50 (2), 301–306. doi:10.1016/j.ifacol.2017.12.062
Boddepalli, M. K., and Navuri, P. K. (2018). “Design and Analysis of Firefly Algorithm Based PID Controller for Automatic Load Frequency Control Problem,” in 2018 Technologies for Smart-City Energy Security and Power (ICSESP) (Bhubaneswar, India: IEEE).
Chandra Sekhar, G. T., Sahu, R. K., Baliarsingh, A. K., and Panda, S. (2016). Load Frequency Control of Power System under Deregulated Environment Using Optimal Firefly Algorithm. Int. J. Electr. Power & Energy Syst. 74, 195–211. doi:10.1016/j.ijepes.2015.07.025
Chang, C. S., Fu, W., and Wen., F. (1998). Load Frequency Control Using Genetic-Algorithm Based Fuzzy Gain Scheduling of PI Controllers. Electr. Mach. Power Syst. 26 (1), 39–52. doi:10.1080/07313569808955806
Das, D. C., Roy, A. K., and Sinha, N. (2012). GA Based Frequency Controller for Solar Thermal-Diesel-Wind Hybrid Energy Generation/energy Storage System. Int. J. Electr. Power & Energy Syst. 43 (1), 262–279. doi:10.1016/j.ijepes.2012.05.025
Das, D. C., Roy, A. K., and Sinha, N. (2010). “Genetic Algorithm Based PI Controller for Frequency Control of an Autonomous Hybrid Generation System,” in World Congress on Engineering 2012, July 4-6, 2012 (London, UK: International Association of Engineers). Vol. 2189.
Elsisi, M., Soliman, M., Aboelela, M. A. S., and Mansour, W. (2015). ABC Based Design of PID Controller for Two Area Load Frequency Control with Nonlinearities. Telkomnika Indonesian J. Electr. Eng. 16 (1), 58–64. doi:10.11591/tijee.v16i1.1588
Ghasemi, H., and Shayeghi, A. (2011). Market Based LFC Design Using Artificial Bee Colony. Int. J. Tech. Phys. Problems Eng. 3 (6), 1–10.
Gozde, H., Cengiz Taplamacioglu, M., and Kocaarslan, İ. (2012). Comparative Performance Analysis of Artificial Bee Colony Algorithm in Automatic Generation Control for Interconnected Reheat Thermal Power System. Int. J. Electr. Power & Energy Syst. 42 (1), 167–178. doi:10.1016/j.ijepes.2012.03.039
Gözde, H., Taplamacioğlu, M. C., Kocaarslan, İ., and Çam, E. (2008). Particle Swarm Optimization Based Load Frequency Control in a Single Area Power System. Sci. Bull. 2 (8).
Gupta, D. K., Soni, A. K., Jha, A. V., Mishra, S. K., Appasani, B., Srinivasulu, A., et al. (2021). Hybrid Gravitational-Firefly Algorithm-Based Load Frequency Control for Hydrothermal Two-Area System. Mathematics 9 (7), 712. doi:10.3390/math9070712
Hazlee Azil, I., Mohamed Zahari, A. F., and Mokhlis, H. (2016). Optimisation of PID Controller for Load Frequency Control in Two-Area Power System Using Evolutionary Particle Swarm Optimisation. J. Electr. Syst. 12 (2), 315–324.
Hemeida, A., Mohamed, S., and Mahmoud, M. (2020). Load Frequency Control Using Optimized Control Techniques. JES. J. Eng. Sci. 48 (6), 1119–11136. doi:10.21608/jesaun.2020.42349.1011
Hote, Y. V. (2018). PID Controller Design for Load Frequency Control: Past, Present and Future Challenges. IFAC Pap. 51, 608. doi:10.1016/j.ifacol.2018.06.162
Huang, C., Bensoussan, A., Edesess, M., and Tsui, K. L. (2016). Improvement in Artificial Neural Network-Based Estimation of Grid Connected Photovoltaic Power Output. Renew. Energy 97, 838–848. doi:10.1016/j.renene.2016.06.043
Jaber, A. S., Ahmad, A. Z., and Abdalla, A. N. (2013). An Investigation of Scaled-FLC Using PSO for Multi-Area Power System Load Frequency Control. Energy Power Eng. 05 (04), 458–462. doi:10.4236/epe.2013.54b088
Jeyalakshmi, V., and Subburaj, P. (2016). PSO-scaled Fuzzy Logic to Load Frequency Control in Hydrothermal Power System. Soft Comput. 20 (7), 2577–2594. doi:10.1007/s00500-015-1659-8
Kalyani, S., Nagalakshmi, S., and Marisha, R. (2012). “Load Frequency Control Using Battery Energy Storage System in Interconnected Power System,” in 2012 Third International Conference on Computing, Communication and Networking Technologies (ICCCNT'12) (Coimbatore, India: IEEE). doi:10.1109/icccnt.2012.6396052
Khatoon, S., and Singh, A. K. (2014). “Effects of Various Factors on Electric Load Forecasting: An Overview,” in 2014 6th IEEE Power India International Conference (PIICON) (Delhi, India: IEEE). doi:10.1109/poweri.2014.7117763
Konar, G., Mandal, K. K., and Chakraborty, N. (2014). “Two Area Load Frequency Control Using GA Tuned PID Controller in Deregulated Environment,” in Proceedings of the International Multi Conference of Engineers and Computer Scientists, 2.
Kotur, D., and Žarković, M. (2016). “Neural Network Models for Electricity Prices and Loads Short and Long-Term Prediction,” in 2016 4th International Symposium on Environmental Friendly Energies and Applications (EFEA) (Belgrade, Serbia: IEEE). doi:10.1109/efea.2016.7748787
Kouba, N. E. Y., Menaa, M., Hasni, M., and Boudour, M. (2015). “Optimal Load Frequency Control Based on Artificial Bee Colony Optimization Applied to Single, Two and Multi-Area Interconnected Power Systems,” in 2015 3rd International Conference on Control, Engineering & Information Technology (CEIT) (Tlemcen, Algeria: IEEE). doi:10.1109/ceit.2015.7233027
Kumar, D., Mishra, A., and Chatterjee, K. (2017). “Power and Frequency Control of a Wind Energy Power System Using Artificial Bee Colony Algorithm,” in 2017 Third International Conference on Science Technology Engineering & Management (ICONSTEM) (Chennai, India: IEEE). doi:10.1109/iconstem.2017.8261385
Kumari, K., Shankar, G., Kumari, S., and Gupta, S. (2016). “Load Frequency Control Using ANN-PID Controller,” in 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES) (Delhi, India: IEEE). doi:10.1109/icpeices.2016.7853516
Kumari, N., and Jha, A. N. (2014). Frequency Response Enhancement of Hybrid Power System by Using PI Controller Tuned with PSO Technique. Int. J. Adv. Comput. Res. 4 (1), 116.
Liang, L., Jin, Z., and Jiao, Z. (2012). “Frequency Regulation for a Power System with Wind Power and Battery Energy Storage,” in 2012 IEEE International Conference on Power System Technology (POWERCON) (Auckland, New Zealand: IEEE). doi:10.1109/powercon.2012.6401357
Lone, A. H., Yousuf, V., Prakash, S., and bid Bazaz, M. A. (2018). “Load Frequency Control of Two Area Interconnected Power System Using SSSC with PID, Fuzzy and Neural Network Based Controllers,” in 2018 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES) (Delhi, India: IEEE). doi:10.1109/icpeices.2018.8897468
Mallesham, G., Mishra, S., and Jha, A. N. (2012). “Automatic Generation Control of Microgrid Using Artificial Intelligence Techniques,” in 2012 IEEE Power and Energy Society General Meeting (San Diego, CA, USA: IEEE).
MathWorks (2022). PID Controller Tuning in Simulink. Available at: https://www.mathworks.com/help/slcontrol/gs/automated-tuning-of-simulink-pid-controller-block.html.
MathWorks (2022). PID Tuner. Available at: https://www.mathworks.com/help/control/ref/pidtuner-app.html.
Mellit, A., and Pavan, A. M. (2010). Performance Prediction of 20kWp Grid-Connected Photovoltaic Plant at Trieste (Italy) Using Artificial Neural Network. Energy Convers. Manag. 51, 2431–2441. doi:10.1016/j.enconman.2010.05.007
Milani, A. E., and Mozafari, B. (2009). Genetic Algorithm Based Optimal Load Frequency Control in Two‐Area Interconected Power Systems. AIP Conf. Proc. 1159 (1), 43. doi:10.1063/1.3223953
Modi, N., Khare, M., and Chaturvedi, K. (2013). Performance Analysis of Load Frequency Control in Single Area Power System Using GA and PSO Based PID Controller. Int. J. Electr. Electron. Comput. Eng. 2 (1), 108–114.
Mosaad, M. I., and Salem., F. (2014). LFC Based Adaptive PID Controller Using ANN and ANFIS Techniques. J. Electr. Syst. Inf. Technol. 1 (3), 212–222. doi:10.1016/j.jesit.2014.12.004
Nagarjuna, N., and Shankar, G. (2015). “Load Frequency Control of Two Area Power System with AC-DC Tie Line Using PSO Optimized Controller,” in 2015 International Conference on Power and Advanced Control Engineering (ICPACE) (Bengaluru, India: IEEE). doi:10.1109/icpace.2015.7274948
Naidu, K., Mokhlis, H., and Bakar, A. H. A. (2013). “Application of Firefly Algorithm (FA) Based Optimization in Load Frequency Control for Interconnected Reheat Thermal Power System,” in 2013 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT) (Amman, Jordan: IEEE). doi:10.1109/aeect.2013.6716461
Naidu, K., Mokhlis, H., and Bakar, A. H. A. (2014). Multiobjective Optimization Using Weighted Sum Artificial Bee Colony Algorithm for Load Frequency Control. Int. J. Electr. Power & Energy Syst. 55, 657–667. doi:10.1016/j.ijepes.2013.10.022
Ncane, Z. P., and Saha, A. K. (2019). “Forecasting Solar Power Generation Using Fuzzy Logic and Artificial Neural Network,” in 2019 Southern African Universities Power Engineering Conference/Robotics and Mechatronics/Pattern Recognition Association of South Africa (SAUPEC/RobMech/PRASA) (Bloemfontein, South Africa: IEEE). doi:10.1109/robomech.2019.8704737
Newkirk, M. (2015). What Is A Hybrid Solar System? Available at: https://www.cleanenergyreviews.info/blog/2014/8/14/what-is-hybrid-solar.
Otani, T. (2017). “Cooperative Load Frequency Control of Generator and Battery Using a Recurrent Neural Network,” in Proc. of the 2017 IEEE Region 10 Conference (TENCON) (Malaysia: TENCON), 918–923. doi:10.1109/tencon.2017.8227989
Padhan, S., Sahu, R. K., and Panda, S. (2014). Application of Firefly Algorithm for Load Frequency Control of Multi-Area Interconnected Power System. Electr. power components Syst. 42 (13), 1419–1430. doi:10.1080/15325008.2014.933372
Pain, S., and Acharjee, P. (2014). Multiobjective Optimization of Load Frequency Control Using Pso. Int. J. Emerg. Technol. Adv. Eng. 4 (7), 16–22.
Power Data Reference Book (2017). Power Data Reference Book, Vol 2, 2010-11 to 2016-17. Lahore: Planning Power National Transmission and Despatch Company Limited (NTDCL). Available at: https://ntdc.gov.pk/services.
Prajapati, P., and Parmar, A. (2016). “Multi-area Load Frequency Control by Various Conventional Controller Using Battery Energy Storage System,” in 2016 International Conference on Energy Efficient Technologies for Sustainability (ICEETS) (Nagercoil, India: IEEE). doi:10.1109/iceets.2016.7583800
Prakash, S., and Sinha, S. K. (2012). “Four Area Load Frequency Control of Interconnected Hydro-Thermal Power System by Intelligent PID Control Technique,” in 2012 Students Conference on Engineering and Systems (Allahabad, India: IEEE). doi:10.1109/sces.2012.6199090
Qi, X., Bai, Y., Luo, H., Zhang, Y., Zhou, G., and Wei, Z. (2018). Fully-distributed Load Frequency Control Strategy in an Islanded Microgrid Considering Plug-In Electric Vehicles. Energies 11 (6), 1613. doi:10.3390/en11061613
Rao, C. S. (2012). Design of Artificial Intelligent Controller for Automatic Generation Control of Two Area Hydrothermal System. Int. J. Electr. Comput. Eng. 2 (2), 183.
Rao, R. N., and Rama Krishna Reddy, P. (2015). PSO Based Tuning of PID Controller for a Load Frequency Control in Two Area Power System. Int. J. Eng. Res. Appl. 1 (3), 1499–1505.
Rathor, S., Acharya, D. S., Gude, S., and Mishra, P. (2011). “Application of Artificial Bee Colony Optimization for Load Frequency Control,” in 2011 World Congress on Information and Communication Technologies (Mumbai, India: IEEE). doi:10.1109/wict.2011.6141339
Regad, M., Helaimi, M., Taleb, R., Gabbar, H. A., and Othman, A. M. (2019). “Fractional Order PID Control of Hybrid Power System with Renewable Generation Using Genetic Algorithm,” in 2019 IEEE 7th International Conference on Smart Energy Grid Engineering (SEGE) (Oshawa, ON, Canada: IEEE). doi:10.1109/sege.2019.8859970
Rerkpreedapong, D., Hasanovic, A., and Feliachi, A. (2003). Robust Load Frequency Control Using Genetic Algorithms and Linear Matrix Inequalities. IEEE Trans. Power Syst. 18 (2), 855–861. doi:10.1109/tpwrs.2003.811005
Rodríguez, F., Fleetwood, A., Galarza, A., and Fontán, L. (2018). Predicting Solar Energy Generation through Artificial Neural Networks Using Weather Forecasts for Microgrid Control. Renew. energy 126, 855–864. doi:10.1016/j.renene.2018.03.070
Safari, A., Babaei, F., and Farrokhifar, M. (2021). A Load Frequency Control Using a PSO-Based ANN for Micro-grids in the Presence of Electric Vehicles. Int. J. Ambient Energy 42 (6), 688–700. doi:10.1080/01430750.2018.1563811
Sedaghati, F., Nahavandi, A., Ali Badamchizadeh, M., Ghaemi, S., and Abedinpour Fallah, M. (2012). PV Maximum Power-point Tracking by Using Artificial Neural Network. Math. Problems Eng. 2012, 506709. doi:10.1155/2012/506709
Selvakumaran, S., Parthasarathy, S., Karthigaivel, R., and Rajasekaran, V. (2012). Optimal Decentralized Load Frequency Control in a Parallel AC-DC Interconnected Power System through HVDC Link Using PSO Algorithm. Energy Procedia 14, 1849–1854. doi:10.1016/j.egypro.2011.12.1178
Shakarami, M. R., Faraji, I., Asghari, I., and Akbari, M. (2013). “Optimal PID Tuning for Load Frequency Control Using Lévy-Flight Firefly Algorithm,” in 2013 3rd International Conference on Electric Power and Energy Conversion Systems (Istanbul, Turkey: IEEE). doi:10.1109/EPECS.2013.6713008
Shankar, G., Lakshmi, S., and Nagarjuna, N. (2015). “Optimal Load Frequency Control of Hybrid Renewable Energy System Using PSO and LQR,” in 2015 International Conference on Power and Advanced Control Engineering (ICPACE) (Bengaluru, India: IEEE). doi:10.1109/icpace.2015.7274942
Sidi Brahim, R. M., M’hamed, H., Taleb, R., and Lemrabout, A. (2021). Load Frequency Control of Hybrid Power System Using Classical PID Controller. iKSP J. Comput. Sci. Eng. 1 (1).
Singh, R, and Ramesh, L. (2019). Comparison of Automatic Load Frequency Control in Two Area Power Systems Using Pso Algorithm Based Pid Controller and Conventional Pid Controller. J. Phys. Conf. Ser. 1172, 012054. doi:10.1088/1742-6596/1172/1/012054
Srinivasan, D., Liew, A. C., and Chen, J. S. P. (1991). “Short Term Forecasting Using Neural Network Approach,” in Proceedings of the First International Forum on Applications of Neural Networks to Power Systems (Piscataway, NJ, USA: IEEE).
Sundaram, V. S., and Jayabarathi, T. (2011). “Load Frequency Control Using PID Tuned ANN Controller in Power System,” in 2011 1st International Conference on Electrical Energy Systems (Chennai, India: IEEE). doi:10.1109/icees.2011.5725341
Taher, S. A. (2014). Fractional Order PID Controller Design for LFC in Electric Power Systems Using Imperialist Competitive Algorithm. Ain Shams Eng. J. 5, 133–135. doi:10.1016/j.asej.2013.07.006
Takagi, M., Yamamoto, H., Yamaji, K., Okano, K., Hiwatari, R., and Ikeya, T. (2009). Load Frequency Control Method by Charge Control for Plug-In Hybrid Electric Vehicles with LFC Signal. IEEJ Trans. Power Energy 129 (11), 1342–1348. doi:10.1541/ieejpes.129.1342
Uehara, A., Senjyu, T., Yona, A., and Funabashi, T. (2009). “Frequency Control by Coordination Control of WTG and Battery Using Load Estimation,” in 2009 International Conference on Power Electronics and Drive Systems (PEDS) (Taipei, Taiwan: IEEE). doi:10.1109/peds.2009.5385765
Veerasamy, V., Wahab, N. I. A., Ramachandran, R., Othman, M. L., Hizam, H., Irudayaraj, A. X. R., et al. (2020). A Hankel Matrix Based Reduced Order Model for Stability Analysis of Hybrid Power System Using PSO-GSA Optimized Cascade PI-PD Controller for Automatic Load Frequency Control. IEEE Access 8, 71422–71446. doi:10.1109/access.2020.2987387
Yang-Wu, S., Xun, M., Ao, P., Yang-Guang, W., Ting, C., Ding, W., et al. (2019). “Load Frequency Control Strategy for Wind Power Grid-Connected Power Systems Considering Wind Power Forecast,” in 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2) (Changsha, China: IEEE). doi:10.1109/EI247390.2019.9062084
Nomenclature
IAE Integral absolute error
ISE Integral square error
ITAE Integral time absolute error
GA Genetic algorithm
PSO Particle swarm optimization
ABC Artificial bee colony
FA Firefly algorithm
ACE Area control error
Keywords: load frequency control, PID controller design, load deviation forecasting, solar photovoltaic power forecasting, particle swarm optimization, genetic algorithm, artificial bee colony (ABC) algorithm
Citation: Mahboob Ul Hassan S, Ramli MAM and Milyani AH (2022) Robust Load Frequency Control of Hybrid Solar Power Systems Using Optimization Techniques. Front. Energy Res. 10:902776. doi: 10.3389/fenrg.2022.902776
Received: 23 March 2022; Accepted: 04 May 2022;
Published: 14 July 2022.
Edited by:
Chuan-Ke Zhang, China University of Geosciences Wuhan, ChinaReviewed by:
D. Boopathi, Paavai Engineering College, IndiaHazlie Mokhlis, University of Malaya, Malaysia
Copyright © 2022 Mahboob Ul Hassan, Ramli and Milyani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Syed Mahboob Ul Hassan, bWFoYm9vYnVsaGFzc2FuMTQ1QGdtYWlsLmNvbQ==, c3VsaGFzc2FuQHN0dS5rYXUuZWR1LnNh
 Syed Mahboob Ul Hassan
Syed Mahboob Ul Hassan Makbul A. M. Ramli
Makbul A. M. Ramli Ahmad H. Milyani
Ahmad H. Milyani