Reliability Evaluation Method of AC/DC Hybrid Distribution Network Considering Voltage Source Converter Restoration Capability and Network Reconfiguration

In the AC/DC hybrid distribution network, non-faulty areas can maintain uninterrupted power supply by adjusting the control mode of the voltage source converter (VSC) after a fault. In addition, the non-faulty areas can also be restored through network reconfiguration. To account for the impact of these two restoration methods on reliability accurately, this article proposed a reliability evaluation method for the AC/DC hybrid distribution network considering VSC restoration capability and network reconfiguration. First, a restoration optimization model of the AC/DC hybrid distribution network considering network reconfiguration and control modes of VSC is established, which can give full play to these two restoration methods while ensuring the radial constraints of the network. Then, the failure mode and effects analysis (FMEA) method is introduced and combined with the restoration optimization model to analyze the impact caused by faults on the network. Among them, the FMEA method is utilized to determine the network topology after fault isolation, and on this basis, the restoration optimization model is solved to obtain the outage time of loads in the network. Finally, the aforementioned work is combined with the sequential Monte Carlo method to evaluate the reliability of the AC/DC hybrid distribution network to adequately simulate the fluctuation characteristics of distributed generation (DG) and load. The case study shows that the proposed method can accurately evaluate the reliability of the AC/DC hybrid distribution network.

1 Introduction

With the continuous development of the DC distribution technology and the large-scale access to DC equipment such as distributed generation (DG) and electric vehicles, the AC/DC hybrid distribution network has become the development trend of the distribution network in the future (Eajal et al., 2016; Zhang et al., 2019; Xu et al., 2021; Wei et al., 2022). Reliability is the first factor to be considered in power grid construction; therefore, it is of great significance to evaluate the reliability of the AC/DC hybrid distribution network (Zhang et al., 2022).

During reliability evaluation, the restoration capacity of the distribution network needs to be fully considered in order to accurately analyze the outage time of load caused by the fault of components in the network. In the AC/DC hybrid distribution network, due to voltage source converter’s (VSC’s) ability of low voltage ride through (LVRT) and fast control mode switching, the non-fault area can maintain uninterrupted power supply by adjusting the VSC control mode after a fault (Liu et al., 2021). In addition, the AC/DC hybrid distribution network contains a large number of contact lines, so the non-fault area can also be restored through network reconfiguration with the assistance of local resources such as DG. In order to accurately evaluate the reliability of the AC/DC hybrid distribution network, the VSC restoration capability and network reconfiguration need to be fully accounted for.

The current research on the reliability of the AC/DC power grid is mainly focused on transmission networks (Wang et al., 2017; Li et al., 2018; Guo et al., 2020), while less research has been conducted on distribution networks. In Ghadiri et al. (2014), several structures of the AC/DC hybrid distribution network are proposed, and the simulation-based single fault analysis method is used to evaluate their reliabilities. In Zhao et al. (2019), the sequential Monte Carlo method is combined with the minimum path method to evaluate the reliability of the AC/DC hybrid distribution network. However, the aforementioned two references do not take into account the impact of VSC restoration capability on reliability, which will lead to a low-reliability evaluation result of the AC/DC hybrid distribution network.

In response to this problem, some researchers (Cui et al., 2019; Wei et al., 2019; Wu et al., 2020) propose new fault impact analysis methods considering VSC restoration capability and evaluate the reliability of the AC/DC hybrid distribution network based on the Monte Carlo method. In Wu et al. (2020), the minimum path method is combined with power flow verification to analyze the impact of faults on the network. The failure mode and effects analysis (FMEA) method is combined with power flow verification to analyze the impact of faults on the network in Cui et al. (2019). In Wei et al. (2019), VSC control modes are modeled under different faults, and an optimal load shedding model is proposed considering the optimization of VSC parameters to analyze the impact of faults on the network. However, the aforementioned studies do not consider the impact of network reconfiguration on reliability. For the AC/DC hybrid distribution network with contact lines, the reliability results evaluated by the aforementioned methods are lower than the actual value.

In the existing studies, mostly optimization models are adopted to account for the impact of network reconfiguration on the reliability of the distribution network. In Li et al. (2020a), a distribution network reliability evaluation method based on an optimization model is proposed, fully considering detailed placement and actions of circuit breaker (CB) and switch. In Li et al. (2020b), an analytical distribution network reliability evaluation method is proposed which considers the optimal network reconfiguration strategy. An optimization model is proposed to improve the reliability of the distribution network by optimizing feeder reconfiguration and DG placement in Tian et al. (2016). However, the research objects of the aforementioned studies are all AC distribution networks, which means that VSC restoration capability is not taken into account. In Cheng et al. (2016), the restoration capability of multi-terminal DC interconnection (MTDI) is explained, and the FMEA method is combined with the restoration optimization model considering network reconfiguration to evaluate the reliability of the AC distribution network with MTDI. However, it does not consider the operating states and constraints of DC networks. When applied to the AC/DC hybrid distribution network, it not only fails to adequately account for the impact of VSC restoration capability on reliability but also may lead to unsafe operating states of the network, which in turn leads to errors in the results of reliability evaluation.

As mentioned earlier, how to take into account the impact of VSC restoration capability and network reconfiguration on reliability so as to obtain reasonable and accurate reliability evaluation results is a problem to be solved. Aiming at this issue, this article had proposed a reliability evaluation method for the AC/DC hybrid distribution network considering VSC restoration capability and network reconfiguration. The main contributions of this study are summarized as follows:

1) We established a restoration optimization model of the AC/DC hybrid distribution network considering network reconfiguration and control modes of VSC, which can completely utilize the aforementioned two restoration methods while ensuring the radial constraints of the network.

2) A reliability evaluation method combining the FMEA method, restoration optimization model, and sequential Monte Carlo method is proposed. The FMEA method is utilized to determine the network topology after fault isolation, and on this basis, the restoration optimization model is solved to obtain the outage time of loads in the network. The aforementioned work is combined with the sequential Monte Carlo method to evaluate the reliability of the AC/DC hybrid distribution network to adequately simulate the fluctuation characteristics of DG and load.

2 Overall Framework of the Reliability Evaluation Method of AC/DC Hybrid Distribution Network

2.1 Operation Mode and Restoration Method of AC/DC Hybrid Distribution Network

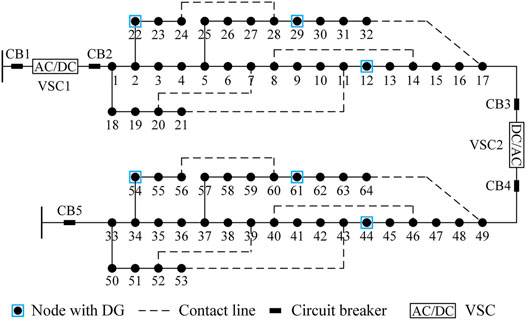
The typical hand-in-hand AC/DC hybrid distribution network is shown in Figure 1, where the DC and AC networks are connected through the VSC. The VSC has two controllable operating parameters. According to the different control parameters, the three most typical control modes of the VSC are as follows (Eajal et al., 2016; Wei et al., 2019):

1) DC voltage and reactive power control (U_dcQ);

2) Active and reactive power control (PQ);

3) AC voltage and phase angle control (U_acθ).

FIGURE 1

FIGURE 1. Topology of AC/DC hybrid distribution network.

Under normal operation, multiple VSCs in the DC network are coordinated by master–slave control. One VSC works in U_dcQ control to provide voltage support for the DC network, while the remaining VSCs work in the PQ control to improve power flow distribution (Wang et al., 2020). After a fault, due to VSC’s ability of LVRT and fast control mode switching, the non-fault area can maintain uninterrupted power supply by adjusting the VSC control mode (Liu et al., 2021). In addition, since the AC/DC hybrid distribution network contains more contact lines and accesses a large number of DGs, the non-fault area can also be restored by network reconfiguration with the assistance of local resources such as DGs.

Therefore, in order to accurately evaluate the reliability of the AC/DC hybrid distribution network, it is necessary to fully take into account the impact of VSC restoration capability and network reconfiguration on reliability. Aiming at this problem, this study proposes a reliability evaluation method for the AC/DC hybrid distribution network combining the FMEA method, restoration optimization model, and sequential Monte Carlo method, which can account for the impact of VSC restoration capability and network reconfiguration on reliability and simulate the fluctuation characteristics of DG and load.

2.2 Overall Framework of the Reliability Evaluation Method

The overall framework of the reliability evaluation method proposed in this study is shown in Figure 2. First, the fault component is sampled using the sequential Monte Carlo method. Then, according to the location of the fault and the placements of protection devices, the FMEA method is used to divide the network into four types of areas with different degrees of impact from the fault, and further obtain the network topology after fault isolation. On the basis, the restoration optimization model with the objective of maximizing restored loads is solved to yield the outage time and outage times of the load in the network. The specific evaluation process is described in Section 5.

FIGURE 2

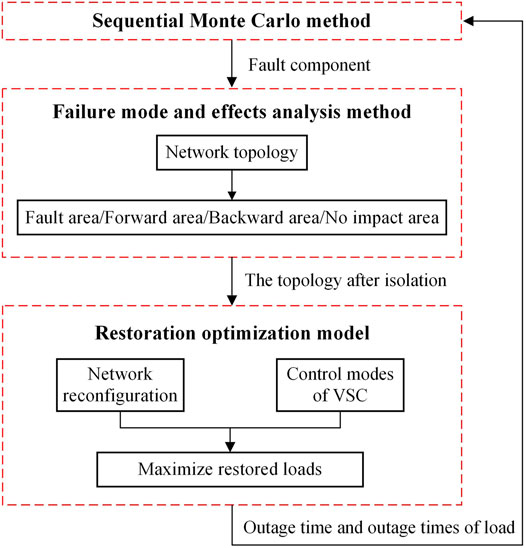
FIGURE 2. Overall framework of the reliability evaluation method of the AC/DC hybrid distribution network.

3 Restoration Optimization Model of AC/DC Hybrid Distribution Network

3.1 Objective

The sub-objective f₁ is to maximize the weighted restored loads in the process of fault repair. The sub-objective f₂ is used to minimize the network losses in the process of fault repair, including the AC and DC network losses, then

$\mathit{max}{\mathit{f}}_1={\displaystyle \sum }_{\forall \mathit{t}}{\displaystyle \sum }_{\forall \mathit{i}\in \mathit{N}}{\mathit{\omega }}_{\mathit{i}}{\mathit{\rho }}_{\mathit{i},\mathit{t}}{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{L}},(1)$

$\mathit{min}{\mathit{f}}_2={\displaystyle \sum }_{\forall \mathit{t}}\left({\displaystyle \sum }_{\forall \mathit{ij}\in {\mathit{B}}^{\mathit{AC}}}{\mathit{I}}_{2,\mathit{ij},\mathit{t}}{\mathit{R}}_{\mathit{ij}}+{\displaystyle \sum }_{\forall \mathit{ij}\in {\mathit{B}}^{\mathit{DC}}}{\mathit{I}}_{2,\mathit{ij},\mathit{t}}{\mathit{R}}_{\mathit{ij}}\right),(2)$

where N is the set of all nodes in the AC/DC hybrid distribution network. B^AC and B^DC are the sets of AC and DC lines in the AC/DC hybrid distribution network, respectively; ω_i is the weight of the load at node i. ρ_i,t indicates whether the load at node i is restored at time t. If the load at node i is restored, ρ_i,t = 1; otherwise, ρ_i,t = 0. $P_{i,t}^L$ is the active power consumed by the load at node i at time t. I_2,ij,t is the squared current from node i to node j at time t. R_ij is the resistance of line ij.

The setting weight method is used to realize the transformation from a multi-objective function to a single-objective function. The objective function can be transformed into

$\mathit{minF}=-{\mathit{\lambda }}_1{\mathit{f}}_1+{\mathit{\lambda }}_2{\mathit{f}}_2,(3)$

where λ₁ and λ₂ are the weight coefficients.

3.2 Topology Constraints of AC/DC Hybrid Distribution Network

The topology constraints are developed to coordinate network reconfiguration and control modes of VSC to ensure the radial constraints of the network during the restoration process, they also include topology constraints of the DC network and AC network.

3.2.1 Topology Constraints of DC Network

${\mathit{\beta }}_{\mathit{ij},\mathit{t}}+{\mathit{\beta }}_{\mathit{ji},\mathit{t}}={\mathit{u}}_{\mathit{ij},\mathit{t}},\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{DC}},(4)$

${\displaystyle \sum _{\mathit{i}\in {\mathit{N}}^{\mathit{D}\mathit{C}}}{\mathit{\beta }}_{\mathit{i}\mathit{j},\mathit{t}}\le 1, \forall \mathit{j}\in {\mathit{N}}^{\mathit{D}\mathit{C}}\backslash \left({\mathit{N}}_{\mathit{m}\mathit{V}\mathit{S}\mathit{C}}^{\mathit{D}\mathit{C}}\cup {\mathit{N}}_{\mathit{s}\mathit{V}\mathit{S}\mathit{C}}^{\mathit{D}\mathit{C}}\cup {\mathit{N}}_{\mathit{D}\mathit{G}}^{\mathit{D}\mathit{C}}\right)},(5)$

${\displaystyle \sum _{\mathit{i}\in {\mathit{N}}^{\mathit{D}\mathit{C}}}{\mathit{\beta }}_{\mathit{i}\mathit{j},\mathit{t}}=\mathbf{0}, \forall \mathit{j}\in {\mathit{N}}_{\mathit{m}\mathit{V}\mathit{S}\mathit{C}}^{\mathit{D}\mathit{C}}},(6)$

${\displaystyle \sum _{\mathit{i}\in {\mathit{N}}^{\mathit{D}\mathit{C}}}{\mathit{\beta }}_{\mathit{i}\mathit{j},\mathit{t}}\le \mathbf{1}, \forall \mathit{j}\in {\mathit{N}}_{\mathit{s}\mathit{V}\mathit{S}\mathit{C}}^{\mathit{D}\mathit{C}}\cup {\mathit{N}}_{\mathit{D}\mathit{G}}^{\mathit{D}\mathit{C}}},(7)$

where B^DC, N^DC, $N_{mVSC}^{DC}$, $N_{sVSC}^{DC}$, and $N_{DG}^{DC}$ are the sets of lines, nodes, master VSC node, slave VSC nodes, and DG nodes in the DC network, respectively. u_ij,t indicates the connection state of line ij at time t. If line ij is connected at time t, u_ij,t = 1; otherwise, u_ij,t = 0. β_ij,t indicates the relationship between nodes i and j at time t. If node i is the parent node of node j at time t, β_ij,t = 1; otherwise, β_ij,t = 0. Constraint (Eq. 4) indicates the relation between u_ij,t and β_ij,t. Constraint (Eq. 5) indicates that the ordinary load node has at most one parent node. Constraint (Eq. 6) indicates that since the master VSC at node j controls the DC voltage, node j has no parent node, that is, ∑β_ij,t = 0. Constraint (Eq. 7) indicates that if the slave VSC or DG at node j controls the DC voltage, node j will have no parent node, that is, ∑β_ij,t = 0; if the slave VSC or DG at node j only controls the active power, node j will have one parent node, that is, ∑β_ij,t = 1.

3.2.2 Topology Constraints of the AC Network

${\mathit{\beta }}_{\mathit{ij},\mathit{t}}+{\mathit{\beta }}_{\mathit{ji},\mathit{t}}={\mathit{u}}_{\mathit{ij},\mathit{t}},\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{AC}},(8)$

${\displaystyle \sum _{\mathit{i}\in {\mathit{N}}^{\mathit{A}\mathit{C}}}{\mathit{\beta }}_{\mathit{i}\mathit{j},\mathit{t}}\le 1, \forall \mathit{j}\in {\mathit{N}}^{\mathit{A}\mathit{C}}\backslash \left({\mathit{N}}_{\mathit{S}\mathit{u}\mathit{b}}^{\mathit{A}\mathit{C}}\cup {\mathit{N}}_{\mathit{V}\mathit{S}\mathit{C}}^{\mathit{A}\mathit{C}}\cup {\mathit{N}}_{\mathit{D}\mathit{G}}^{\mathit{A}\mathit{C}}\right)},(9)$

${\displaystyle \sum _{\mathit{i}\in {\mathit{N}}^{\mathit{AC}}}{\mathit{\beta }}_{\mathit{ij},\mathit{t}}=0,\mathit{ }\forall \mathit{j}\in {\mathit{N}}_{\mathit{Sub}}^{\mathit{AC}}},(10)$

${\displaystyle \sum _{\mathit{i}\in {\mathit{N}}^{\mathit{A}\mathit{C}}}{\mathit{\beta }}_{\mathit{i}\mathit{j},\mathit{t}}\le 1, \forall \mathit{j}\in {\mathit{N}}_{\mathit{V}\mathit{S}\mathit{C}}^{\mathit{A}\mathit{C}}\cup {\mathit{N}}_{\mathit{D}\mathit{G}}^{\mathit{A}\mathit{C}}},(11)$

where B^AC, N^AC, $N_{Sub}^{AC}$, $N_{VSC}^{AC}$, and $N_{DG}^{AC}$ are the sets of lines, nodes, substation node, VSC nodes, and DG nodes in the AC network, respectively. Constraint (Eqs 8, 9) are essentially the same as constraint (Eqs 4, 5), respectively. Constraint (Eq. 10) indicates that since the substation at node j controls the AC voltage, node j has no parent node, that is, ∑β_ij,t = 0. Constraint (Eq. 11) indicates that if the VSC or DG at node j controls the AC voltage, node j will have no parent node, that is, ∑β_ij,t = 0; if the VSC or DG at node j only controls active power, node j will have one parent node, that is, ∑β_ij,t = 1.

3.3 Power Flow Constraints of AC/DC Hybrid Distribution Network

3.3.1 Power Balance and Capacity Constraints of Voltage Source Converters

${\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{VSC}}+{\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{VSC}}=0,\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{VSC}},\mathit{ i}\in {\mathit{N}}^{\mathit{AC}},\mathit{ j}\in {\mathit{N}}^{\mathit{DC}},(12)$

$\sqrt{{\left({\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{VSC}}\right)}^2+{\left({\mathit{Q}}_{\mathit{i},\mathit{t}}^{\mathit{VSC}}\right)}^2}\le {\mathit{u}}_{\mathit{ij},\mathit{t}}{\mathit{S}}_{\mathit{ij}}^{\mathit{VSC}},\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{VSC}},\mathit{ i}\in {\mathit{N}}^{\mathit{AC}},\mathit{ j}\in {\mathit{N}}^{\mathit{DC}},(13)$

where B^VSC is the set of lines with VSC. $P_{i,t}^{VSC}$ and $Q_{i,t}^{VSC}$ are the active power and reactive power injected by the VSC in line ij to AC node i at time t, respectively. $P_{j,t}^{VSC}$ is the active power injected by the VSC in line ij to DC node j at time t. $S_{ij}^{VSC}$ is the capacity of the VSC in line ij.

3.3.2 Power Flow Constraints of the AC Network

$\{\begin{array}{c}{\displaystyle \sum }_{\mathit{ik}\in {\mathit{B}}^{\mathit{AC}}}{\mathit{P}}_{\mathit{ik},\mathit{t}}={\displaystyle \sum }_{\mathit{ji}\in {\mathit{B}}^{\mathit{AC}}}\left({\mathit{P}}_{\mathit{ji},\mathit{t}}-{\mathit{R}}_{\mathit{ji}}{\mathit{I}}_{2,\mathit{ji},\mathit{t}}\right)+{\mathit{P}}_{\mathit{i},\mathit{t}},\\ {\displaystyle \sum }_{\mathit{ik}\in {\mathit{B}}^{\mathit{AC}}}{\mathit{Q}}_{\mathit{ik},\mathit{t}}={\displaystyle \sum }_{\mathit{ji}\in {\mathit{B}}^{\mathit{AC}}}\left({\mathit{Q}}_{\mathit{ji},\mathit{t}}-{\mathit{X}}_{\mathit{ji}}{\mathit{I}}_{2,\mathit{ji},\mathit{t}}\right)+{\mathit{Q}}_{\mathit{i},\mathit{t}},\end{array}\forall \mathit{i}\in {\mathit{N}}^{\mathit{AC}},(14)$

$\{\begin{array}{c}{\mathit{P}}_{\mathit{i},\mathit{t}}={\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{DG}}+{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{VSC}}-{\rho }_{i,t}{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{L}},\\ {\mathit{Q}}_{\mathit{i},\mathit{t}}={\mathit{Q}}_{\mathit{i},\mathit{t}}^{\mathit{DG}}+{\mathit{Q}}_{\mathit{i},\mathit{t}}^{\mathit{VSC}}-{\rho }_{i,t}{\mathit{Q}}_{\mathit{i},\mathit{t}}^{\mathit{L}},\end{array}\forall \mathit{i}\in {\mathit{N}}^{\mathit{AC}},(15)$

$-\mathit{M}\left(1-{\mathit{u}}_{\mathit{ij},\mathit{t}}\right)\le {\mathit{U}}_{2,\mathit{i},\mathit{t}}-{\mathit{U}}_{2,\mathit{j},\mathit{t}}-2\left({\mathit{R}}_{\mathit{ij}}{\mathit{P}}_{\mathit{ij},\mathit{t}}+{\mathit{X}}_{\mathit{ij}}{\mathit{Q}}_{\mathit{ij},\mathit{t}}\right)+\left({\mathit{R}}_{\mathit{ij}}^2+{\mathit{X}}_{\mathit{ij}}^2\right){\mathit{I}}_{2,\mathit{ij},\mathit{t}}\le \mathit{M}\left(1-{\mathit{u}}_{\mathit{ij},\mathit{t}}\right),\forall \mathit{ij}\in {\mathit{B}}^{\mathit{AC}},(16)$

${\mathit{I}}_{2,\mathit{ij},\mathit{t}}=\frac{{\left({\mathit{P}}_{\mathit{ij},\mathit{t}}\right)}^2+{\left({\mathit{Q}}_{\mathit{ij},\mathit{t}}\right)}^2}{{\mathit{U}}_{2,\mathit{i},\mathit{t}}},\forall \mathit{ij}\in {\mathit{B}}^{\mathit{AC}},(17)$

where X_ij is the reactance of line ij. P_ij,t and Q_ij,t are the active power and reactive power from node i to node j at time t, respectively. P_i,t and Q_i,t are the active power and reactive power injected to node i at time t, respectively. $P_{i,t}^{DG}$ and $Q_{i,t}^{DG}$ are the active power and reactive power outputs of the DG at node i at time t, respectively. $Q_{i,t}^L$ is the reactive power consumed by the load at node i at time t, and U_2,i,t is the squared voltage of node i at time t. Constraint (Eq. 16) represent the DistFlow model-based power flow equation for closed lines with u_ij,t = 1, and get relaxed for open lines with u_ij,t = 0. M needs to be big enough, so that for any open line ij, U_2,i,t and U_2,j,t do not directly influence each other. It is adequate to set M = max (U_2,i,t)–min (U_2,j,t).

3.3.3 Power Flow Constraints of DC Network

${\displaystyle \sum _{\mathit{i}\mathit{k}\in {\mathit{B}}^{\mathit{A}\mathit{C}}}{\mathit{P}}_{\mathit{i}\mathit{k},\mathit{t}}}={\displaystyle \sum _{\mathit{j}\mathit{i}\in {\mathit{B}}^{\mathit{A}\mathit{C}}}\left({\mathit{P}}_{\mathit{j}\mathit{i},\mathit{t}}-{\mathit{R}}_{\mathit{j}\mathit{i}}{\mathit{I}}_{\mathbf{2},\mathit{j}\mathit{i},\mathit{t}}\right)+{\mathit{P}}_{\mathit{i},\mathit{t}},\forall \mathit{i}\in {\mathit{N}}^{\mathit{D}\mathit{C}}},(18)$

${\mathit{P}}_{\mathit{i},\mathit{t}}={\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{DG}}+{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{VSC}}-{\rho }_{i,t}{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{L}},\forall \mathit{i}\in {\mathit{N}}^{\mathit{DC}},(19)$

$-\mathit{M}\left(1-{\mathit{u}}_{\mathit{ij},\mathit{t}}\right)\le {\mathit{U}}_{2,\mathit{i},\mathit{t}}-{\mathit{U}}_{2,\mathit{j},\mathit{t}}-2{\mathit{R}}_{\mathit{ij}}{\mathit{P}}_{\mathit{ij},\mathit{t}}+{\mathit{R}}_{\mathit{ij}}^2{\mathit{I}}_{2,\mathit{ij},\mathit{t}}\le \mathit{M}\left(1-{\mathit{u}}_{\mathit{ij},\mathit{t}}\right),\forall \mathit{ij}\in {\mathit{B}}^{\mathit{DC}},(20)$

${\mathit{I}}_{2,\mathit{ij},\mathit{t}}=\frac{{\left({\mathit{P}}_{\mathit{ij},\mathit{t}}\right)}^2}{{\mathit{U}}_{2,\mathit{i},\mathit{t}}},\forall \mathit{ij}\in {\mathit{B}}^{\mathit{AC}}.(21)$

3.3.4 Voltage Constraint

$\{\begin{array}{c}{\left({\mathit{U}}_{\mathit{min}}^{\mathit{AC}}\right)}^2\le {\mathit{U}}_{2,\mathit{i},\mathit{t}}\le {\left({\mathit{U}}_{\mathit{max}}^{\mathit{AC}}\right)}^2,\forall \mathit{i}\in {\mathit{N}}^{\mathit{AC}},\\ {\left({\mathit{U}}_{\mathit{min}}^{\mathit{DC}}\right)}^2\le {\mathit{U}}_{2,\mathit{i},\mathit{t}}\le {\left({\mathit{U}}_{\mathit{max}}^{\mathit{DC}}\right)}^2,\forall \mathit{i}\in {\mathit{N}}^{\mathit{DC}},\end{array}(22)$

where $U_{max}^{AC}$ and $U_{min}^{AC}$ are the maximum and minimum voltage of the AC network, respectively. $U_{max}^{DC}$ and $U_{min}^{DC}$ are the maximum and minimum voltage of the DC network, respectively.

3.3.5 Line Capacity Constraints

$\sqrt{{\left({\mathit{P}}_{\mathit{ij},\mathit{t}}\right)}^2+{\left({\mathit{Q}}_{\mathit{ij},\mathit{t}}\right)}^2}\le {\mathit{u}}_{\mathit{ij},\mathit{t}}{\mathit{S}}_{\mathit{ij}},\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{AC}},(23)$

${\mathit{P}}_{\mathit{ij},\mathit{t}}\le {\mathit{u}}_{\mathit{ij},\mathit{t}}{\mathit{S}}_{\mathit{ij}},\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{DC}},(24)$

where S_ij is the capacity of line ij.

3.4 Second-Order Cone Conversion of the Constraints

Constraints (Eq. 13) and (Eq. 23) are transformed into the standard second-order cone constraints (Eq. 25) and (Eq. 26):

${\Vert \left[\begin{array}{cc}2{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{VSC}}& 2{\mathit{Q}}_{\mathit{i},\mathit{t}}^{\mathit{VSC}}\end{array}\right]}^{\mathit{T}}\Vert \le {\mathit{u}}_{\mathit{ij},\mathit{t}}{\mathit{S}}_{\mathit{ij}}^{\mathit{VSC}},\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{VSC}},\mathit{ i}\in {\mathit{N}}^{\mathit{AC}},\mathit{ j}\in {\mathit{N}}^{\mathit{DC}},(25)$

$\Vert {\left[\begin{array}{cc}2{\mathit{P}}_{\mathit{ij},\mathit{t}}& 2{\mathit{Q}}_{\mathit{ij},\mathit{t}}\end{array}\right]}^{\mathit{T}}\Vert \le {\mathit{u}}_{\mathit{ij},\mathit{t}}{\mathit{S}}_{\mathit{ij}},\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{AC}}.(26)$

Constraints (Eq. 17) and (Eq. 21) are relaxed and then transformed into the standard second-order cone constraints (Eqs 27, 28).

$\Vert {\left[\begin{array}{ccc}2{\mathit{P}}_{\mathit{ij},\mathit{t}}& 2{\mathit{Q}}_{\mathit{ij},\mathit{t}}& {\mathit{I}}_{2,\mathit{ij},\mathit{t}}-{\mathit{U}}_{2,\mathit{i},\mathit{t}}\end{array}\right]}^{\mathit{T}}\Vert \le {\mathit{I}}_{2,\mathit{ij},\mathit{t}}+{\mathit{U}}_{2,\mathit{i},\mathit{t}},\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{AC}},(27)$

$\Vert {\left[\begin{array}{cc}2{\mathit{P}}_{\mathit{ij},\mathit{t}}& {\mathit{I}}_{2,\mathit{ij},\mathit{t}}-{\mathit{U}}_{2,\mathit{i},\mathit{t}}\end{array}\right]}^{\mathit{T}}\Vert \le {\mathit{I}}_{2,\mathit{ij},\mathit{t}}+{\mathit{U}}_{2,\mathit{i},\mathit{t}},\mathit{ }\forall \mathit{ij}\in {\mathit{B}}^{\mathit{DC}}.(28)$

4 Failure Mode and Effect Analysis Method Based on the Segment

This study introduces the FMEA method based on the segment proposed in (Wang, 2012). The segment is a collection of components with the same entry component (Broadwater et al., 1994). The entry component is a switch or protection device, and each segment includes only one switch or protection device (Atwa et al., 2010). The main idea of the method is as follows, and the specific process is described in detail in Wang (2012) and will not be repeated here.

1) First, the switch nodes in the distribution network are encoded by the one-dimensional array. The code represents the location of the switch nodes in the distribution network and the topological relationships between the switch nodes and other switch nodes.

2) Then, the segment to which the switch node belongs and the other nodes in this segment are encoded with the same code as that of the switch node. At this point, all nodes in the distribution network are encoded.

3) Finally, based on the code of the fault component and the code of each segment, the segments in the network are divided into four types of areas with different degrees of impact from fault through the fault impact classification method and code finding technique. Table 1 shows the definition of the four types of areas and the outage time of the loads in them.

TABLE 1

TABLE 1. Definition of the four types of areas.

5 Reliability Evaluation Process Based on the Sequential Monte Carlo Method

The aforementioned work is combined with the sequential Monte Carlo method to evaluate the reliability of the AC/DC hybrid distribution network. The specific evaluation process is as follows (Billinton and Wang, 1999):

1) Read the data and set the simulation period. Initial simulation clock t. Simultaneously, the renewable energy output and load value are sampled.

2) Calculate the time to failure (TTF) of each component according to the fault rate, and TTF_i indicates the TTF of component i.

3) Find the component i with the smallest TTF_i as the fault component, and get the time to repair (TTR) which is the repair time of component i. Increase the simulation clock t by TTF_i.

4) Divide the network into the fault area, backward area, forward area, and no-impact area through the FMEA method. Record the outage time of the loads in the fault area as fault repair time and the outage time of the loads in the forward area as fault isolation time. Construct the network topology after fault isolation based on the forward area, backward area, and no-impact area.

5) Solve the restoration optimization model to yield the restoration scheme of the loads in the backward area in each period of [t, t+TTR]. Considering the power supply continuity of the load, select the restoration scheme of the period with the least restored loads as the restoration scheme during [t, t + TTR]. Record the outage time of the load that can be restored as fault isolation and transfer time, and the outage time of the load that cannot be restored as fault repair time.

6) Increase the simulation clock t by TTR, and calculate the new TTF_i of the component i according to the fault rate.

7) Determine whether t reaches the simulation period. If t reaches, go to step (8); otherwise, return to (3).

8) End the simulation, and calculate the customer interruption frequency (CIF) and customer interruption duration (CID). On this basis, calculate the system average interruption frequency index (SAIFI), system average interruption duration index (SAIDI), average service availability index (ASAI), and expected energy not supplied (EENS) according to Eqs 29–32.

$\mathit{S}\mathit{A}\mathit{I}\mathit{F}\mathit{I}=\frac{{\displaystyle \sum {\mathit{\lambda }}_{\mathit{k}}{\mathit{N}}_{\mathit{k}}}}{{\displaystyle \sum {\mathit{N}}_{\mathit{k}}}},(29)$

$\mathit{S}\mathit{A}\mathit{I}\mathit{D}\mathit{I}=\frac{{\displaystyle \sum {\mathit{t}}_{\mathit{k}}{\mathit{N}}_{\mathit{k}}}}{{\displaystyle \sum {\mathit{N}}_{\mathit{k}}}},(30)$

$\mathit{A}\mathit{S}\mathit{A}\mathit{I}=\frac{{\displaystyle \sum {\mathit{N}}_{\mathit{k}}\times \mathbf{8760}}-{\displaystyle \sum {\mathit{t}}_{\mathit{k}}{\mathit{N}}_{\mathit{k}}}}{{\displaystyle \sum {\mathit{N}}_{\mathit{k}}\times \mathbf{8760}}},(31)$

$\mathit{E}\mathit{E}\mathit{N}\mathit{S}={\displaystyle \sum {\mathit{t}}_{\mathit{k}}{\mathit{P}}_{\mathit{k}}^{\mathit{a}\mathit{v}\mathit{e}\mathit{r}\mathit{a}\mathit{g}\mathit{e}}},(32)$

where λ_k, t_k, N_k, and P^average_k are the CIF, CID, number of customers, and average load value of node k, respectively.

6 Case Study

6.1 Test System Modeling

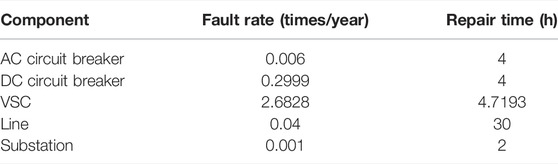
The proposed method is tested on the AC/DC hybrid distribution network in Figure 1, which is composed of two IEEE 33-node distribution networks. The parameters of the network are detailed in Baran and Wu (1989). Circuit breakers are installed at the beginning and end of AC and DC main feeders, and isolation switches are configured on both sides of nodes. The distribution network contains six DGs, which are located at nodes 12, 22, 29, 44, 54, and 61, respectively. The types and parameters of DGs are shown in Table 2. The reliability parameters of the components in the AC/DC hybrid distribution network are drawn from Wu et al. (2020) and Wei et al. (2019), as shown in Table 3. When the network operates normally, VSC 1 works in the U_dcQ control to provide the voltage support for the DC network, and VSC 2 works in the PQ control. Set the switch action time to 0.5 h.

TABLE 2

TABLE 2. Types and parameters of DG.

TABLE 3

TABLE 3. Reliability parameters of components in the AC/DC hybrid distribution network.

6.2 Comparison of Reliability Evaluation Results

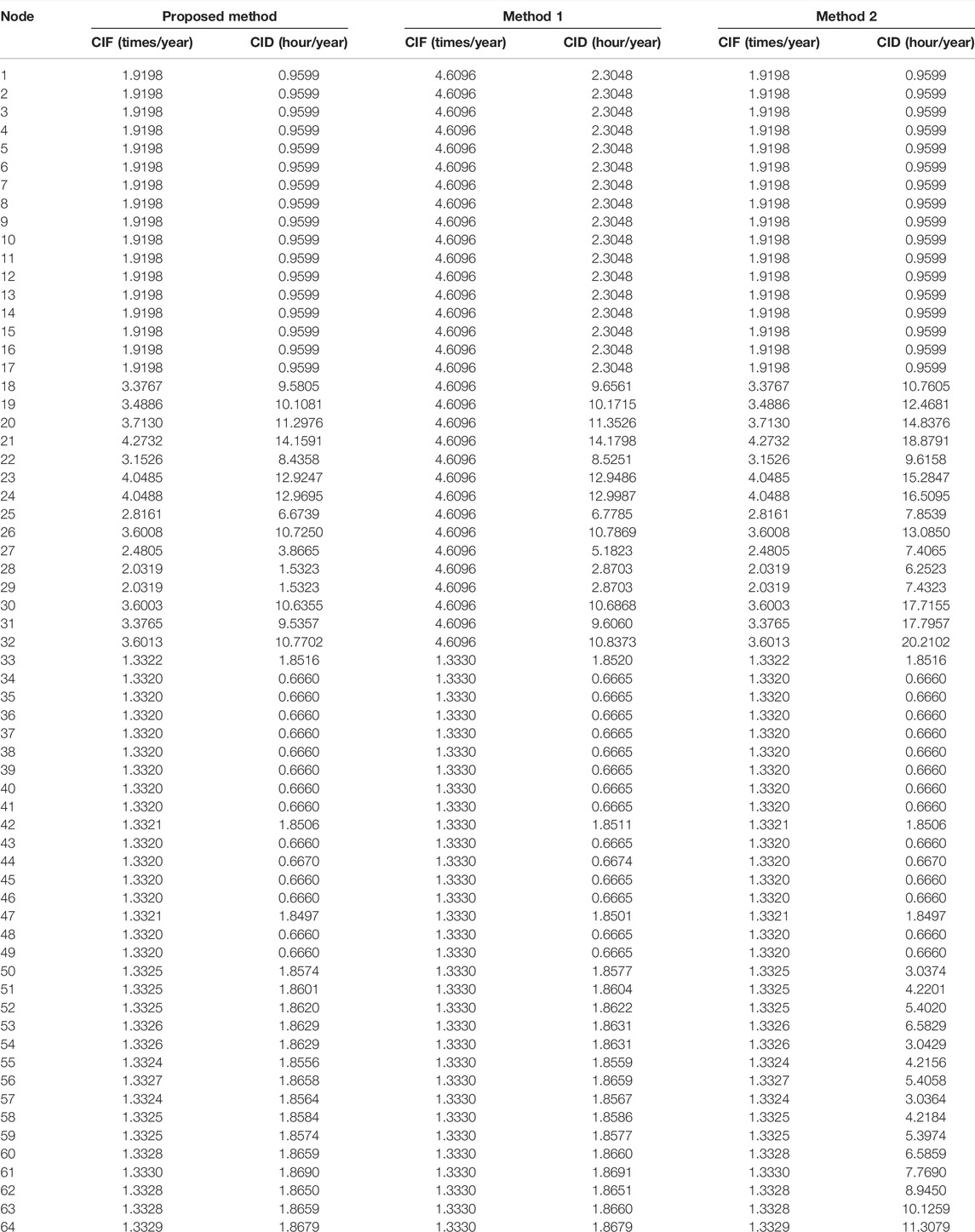
The reliability of the AC/DC hybrid distribution network is evaluated by the proposed method and the two methods defined in Table 4. The nodal CIF and CID of the three methods are shown in Table 5. The SAIFI, SAIDI, ASAI, and EENS of the three methods are shown in Table 6.

TABLE 4

TABLE 4. Definition of the evaluation methods.

TABLE 5

TABLE 5. Nodal CIF and CID of the three methods.

TABLE 6

TABLE 6. System reliability indicators of the three methods.

The comparison in Table 5 shows that:

1) For any nodes 1–64, both the CIF and CID of the proposed method are lower than those of method 1.

2) For any nodes 1–64, the CIF of the proposed method is equal to that of method 2. For any nodes 1–17 and 33–49, the CID of the proposed method is equal to that of method 2, and for any nodes 18–32 and 50–64, the CID of the proposed method is lower than that of method 2.

The comparison in Table 6 shows the following :

1) The SAIFI and SAIDI of the proposed method are 34.3% and 12.5% lower than those of method 1, respectively; the ASAI is 0.0049% higher than that of method 1; and the EENS is 8.4% lower than that of method 1.

2) The SAIFI of the proposed method is equal to that of method 2, the SAIDI is 38.8% lower than that of method 2, the ASAI is 0.0219% higher than that of method 2, and the EENS is 39.2% lower than that of method 2.

6.3 Analysis of Differences in Reliability Evaluation Results

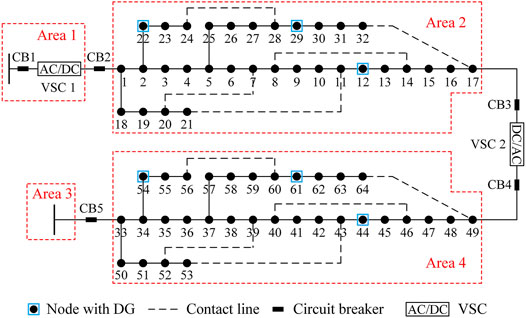
This section analyzes the difference in reliability evaluation results of the three methods from the impact of fault on the network. For the convenience of analysis, four areas are constructed in the AC/DC hybrid distribution network, as shown in Figure 3. The fault of VSC 2 does not need to be analyzed because it has no impact on the network.

FIGURE 3

FIGURE 3. Schematic diagram of area division in the AC/DC hybrid distribution network.

Considering that the fault may occur at any time, nodal customer average outage times (CAOS) and customer average outage time (CAOT) are defined as the average value of outage times and outage time of node when the fault occurs in each period of the day, respectively.

6.3.1 Fault Impact Analysis of CB2 and the Components in Area 1

When one of the components in area 1 fails or CB 2 fails, the nodes 33–64 are not affected. After fault isolation, the main power supply of the DC network fails, then the nodes 1–32 need to be supplied by the AC network. However, due to power flow constraints, only a fraction of the nodes 1–32 can be recovered at times other than low load periods. The recoverable nodes at any time period in these three methods are the same because they all use the restoration optimization model to solve for the recoverable nodes. We analyze the impact of the aforementioned two types of faults on nodes 1–32 separately.

1) When one of the components in area 1 fails, CB 2 disconnects to directly isolate the fault, which means the fault isolation time is 0 h. In the three methods, the outage time of the unrecoverable node is fault repair time, and there are differences in the outage time of the recoverable node. In the proposed method and method 2, VSC 2 is quickly adjusted to the U_dcQ control to provide the voltage support for the DC network, so the recoverable node can maintain uninterrupted power supply during the fault repair, which means the outage time is 0 h. Method 1 does not consider VSC restoration capability, the DC network needs to be powered by the AC network through transfer, so the outage time of the recoverable node is switch action time of 0.5 h. Therefore, when one of the components in area 1 fails, for any nodes 1–32, both the node average outage times of the three methods and the node average outage time of the three methods have the following relationship: proposed method = method 2 < method 1.

2) When CB 2 fails, the fault should be isolated through the isolation switch. In the three methods, the outage time of unrecoverable node is fault repair time, and the analysis process of the outage time of the recoverable node is the same as the aforementioned paragraph, except that the fault isolation time is different. In the proposed method and method 2, the outage time of the recoverable node is switch action time of 0.5 h. In method 1, the outage time of the recoverable node is switch action time of 0.5 h, because this study believes that the isolation switch, contact switch, and transfer switch can operate simultaneously. Therefore, when CB 2 fails, for any nodes 1–32, both the CAOS of the three methods and the CAOT of the three methods have the following relationship: proposed method = method 1 = method 2.

6.3.2 Fault Impact Analysis of the Components in Area 2

When one of the components in area 2 fails, the fault need be isolated through the isolation switch, and the nodes 33–64 are not affected. The faults in area 2 can be divided into the faults of the DC main feeder and the DC branch line, and the impacts of these two types of faults on nodes 1–32 are analyzed separately.

1) When the DC main feeder fails, the nodes upstream of the fault are restored by the main power supply and the outage time of these nodes is switch action time of 0.5 h in the three methods. The outage time of the nodes downstream of the fault is different in the three methods. In the proposed method and method 1, the nodes downstream of the fault are restored by the main power supply through network reconfiguration, and the outage time is switch action time of 0.5 h. Method 2 does not consider network reconfiguration, VSC 2 is adjusted to the U_dcQ control to provide the voltage support for the nodes downstream of the fault, and the outage time is switch action time of 0.5 h. However, if there are many nodes downstream of the fault, limited by the power flow constraints, only a fraction of these nodes can be restored and the nodes on the branch line will be cut off preferentially. The outage time of the nodes that cannot be restored is fault repair time, which is greater than 0.5 h.

2) When the DC branch line fails, except for the nodes downstream of the fault on the branch line, the other nodes are still restored by the main power supply, and the outage time is switch action time of 0.5 h. There are differences in the outage time of the nodes downstream of the fault on the branch line. In the proposed method and method 1, these nodes are still restored by the main power supply through network reconfiguration, and the outage time is switch action time of 0.5 h. Method 2 does not consider network reconfiguration, so these nodes cannot be restored and the outage time is fault repair time.

To sum up, when one of the components in area 2 fails, for any nodes 1–32, the CAOS of the three methods has the following relationship: proposed method = method 1 = method 2; for any nodes on the main feeder, the CAOT of the three methods has the following relationship: proposed method = method 1 = method 2; for any nodes on the branch line, the CAOT of the three methods has the following relationship: proposed method = method 1 < method 2.

6.3.3 Fault Impact Analysis of CB 3

When CB 3 fails, the fault need be isolated through the isolation switch, the nodes 33–64 are not affected and the nodes 1–32 are restored by the main power supply. In the three methods, the outage time of nodes 1–32 is switch action time 0.5 h. Therefore when CB 3 fails, for any nodes 1–32, both the CAOS of the three methods and the CAOT of the three methods have the following relationship: proposed method = method 1 = method 2.

6.3.4 Fault Impact Analysis of CB 4–5 and the Components in Areas 3–4

As can be seen from Figure 3, the topology of the AC network is similar to that of the DC network, so the fault impact analysis of CB 5, CB 4, the components in area 3, and the components in area 4 are the same as that of CB 2, CB 3, the components in area 1, and the components in area 2, respectively. Therefore, under these faults, for any nodes 33–64, the relationship among CAOS/CAOT of the three methods is the same as before.

6.3.5 Summary of Fault Impact Analysis

The relationships among nodal CAOS/CAOT of the three methods under various types of faults are summarized in Table 7. Since the reliability evaluation takes into account, all faults including CB 2–5, VSC 2, and the components in areas 1–4, the relationships among nodal CIF/CID of the three methods can be obtained by superimposing the relationships in Table 7, as shown in Table 8.

TABLE 7

TABLE 7. Relationships among nodal CAOS/CAOT of the three methods under various types of faults.

TABLE 8

TABLE 8. Relationships among nodal CIF/CID of the three methods.

According to the results in Table 8 and Eqs 29–32, the relationship between the system reliability indicators of the three methods can be obtained as follows. The SAIFI, SAIDI, and EENS of the proposed method are lower than those of method 1, and the ASAI of the proposed method is higher than that of method 1. The SAIFI of the proposed method is equal to that of method 2, the SAIDI and EENS of the proposed method are lower than those of method 2, and the ASAI of the proposed method is higher than that of method 2.

From the aforementioned analysis, we can summarize the impact of considering VSC restoration capability and network reconfiguration on the reliability of the AC/DC hybrid distribution network as follows:

1) Since the AC/DC hybrid distribution network contains more contact lines, more nodes can be restored through network reconfiguration after fault isolation. Therefore, considering network reconfiguration cannot reduce the nodal CIF, but can reduce the nodal CID and thus improve the reliability of AC/DC hybrid distribution networks.

2) Due to VSC restoration capability, the nodes in non-faulty areas can maintain uninterrupted power supply by adjusting the VSC control mode when the fault can be quickly isolated by circuit breakers. Therefore, considering VSC restoration capability can reduce both the nodal CIF and CID at the same time, and thus improve the reliability of the AC/DC hybrid distribution network.

Based on the aforementioned results, we can draw the following conclusions: the proposed method fully considers the impact of VSC restoration capability and network reconfiguration on reliability, thus the reliability of the AC/DC hybrid distribution network can be accurately evaluated.

6.4 Analysis of the Impact of Reliability of Key Components on System Reliability

Taking the parameters in Table 3 as the base values, we calculate the system reliability indicators when the fault rates of DC circuit breaker, AC circuit breaker, and VSC are 20%–90% of the base values, respectively, as shown in Figure 4.

FIGURE 4

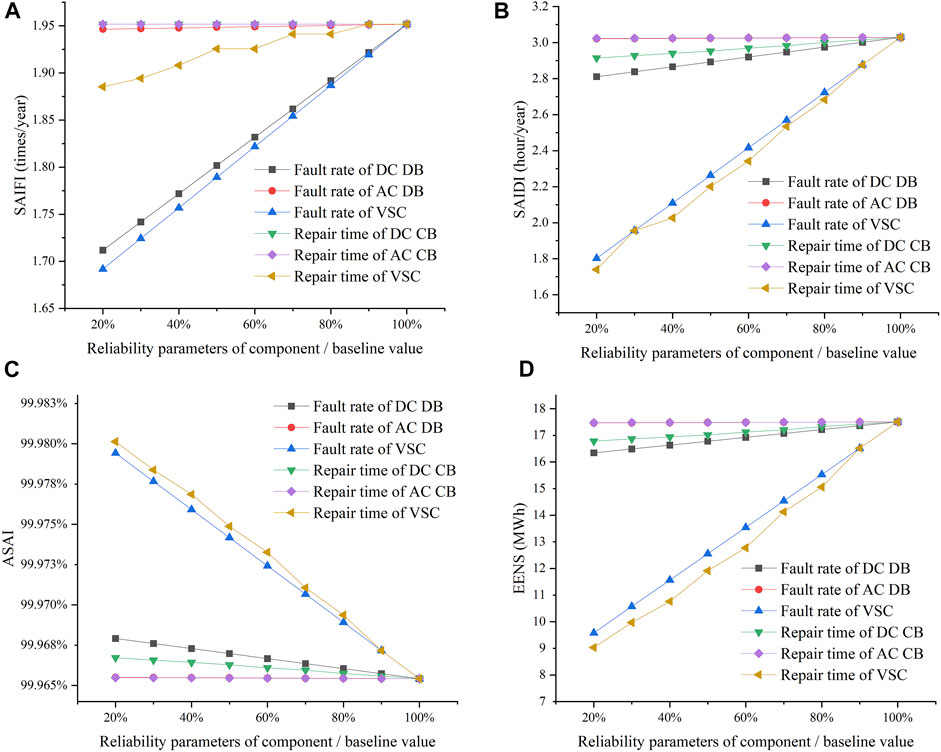
FIGURE 4. Impact of the reliability parameters of components on system reliability indicators. (A) Impact of the reliability parameters of components on SAIFI. (B) Impact of the reliability parameters of components on SAIDI. (C) Impact of the reliability parameters of components on ASAI. (D) Impact of the reliability parameters of components on EENS.

From the comparison in the figure, the following conclusion can be drawn:

1) As the fault rates of the three components decrease, the reliability of the AC/DC hybrid distribution networks increases. Among them, the fault rate of VSC has the most significant impact on SAIFI, SAIDI, EENS, and ASAI, the fault rate of the DC circuit breaker is the second most significant, and the fault rate of the AC circuit breaker has almost no effect. Therefore, priority should be given to improving the reliability of the AC/DC hybrid distribution network by reducing the fault rate of VSC.

2) Similarly, as the repair time of the three components decreases, the reliability of the AC/DC hybrid distribution networks increases. Among them, the repair time of VSC has the most significant impact on SAIFI, SAIDI, EENS, and ASAI, the repair time of the DC circuit breaker is the second most significant, and the repair time of the AC circuit breaker has almost no effect. Therefore, priority should be given to improving the reliability of the AC/DC hybrid distribution network by reducing the repair time of VSC.

6.5 Analysis of the Impact of Voltage Source Converter Capacity on System Reliability

We calculate the system reliability indicators when the capacity of VSC 2 is increased to 1.1–2.0 times of the initial value, respectively, as shown in Figure 5.

FIGURE 5

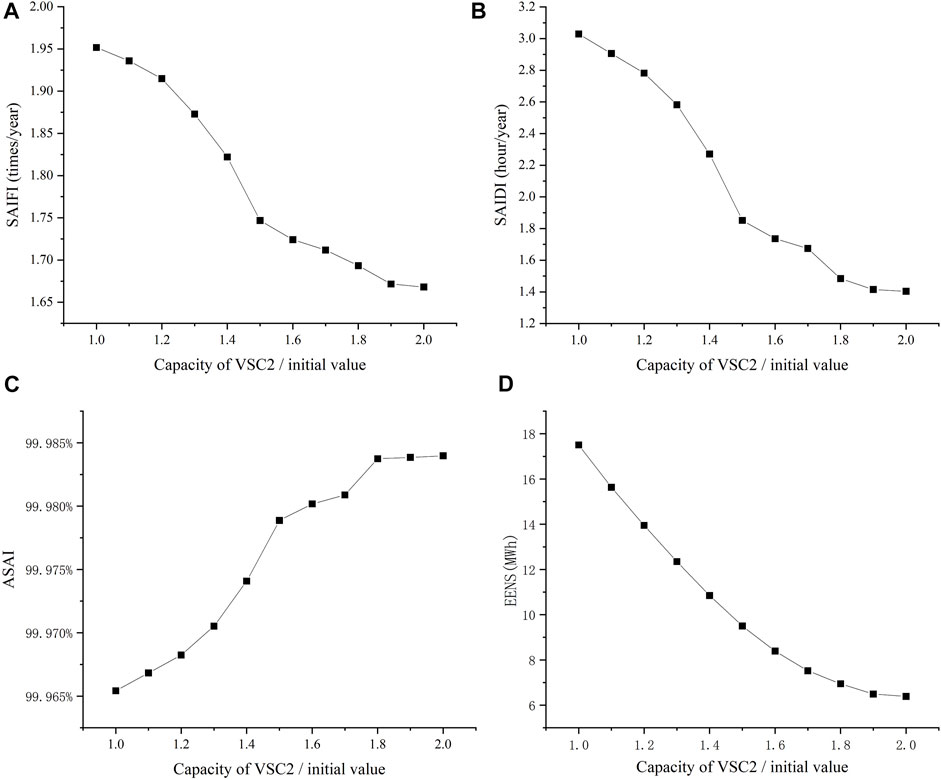
FIGURE 5. Impact of the capacity of VSC 2 on system reliability indicators. (A) Impact of the capacity of VSC 2 on SAIFI. (B) Impact of the capacity of VSC 2 on SAIDI. (C) Impact of the capacity of VSC 2 on ASAI. (D) Impact of the capacity of VSC 2 on EENS.

As seen from the figure, increasing the capacity of the VSC connecting DC network and AC network can improve the reliability of the hybrid AC/DC distribution network. However, when the capacity of VSC is larger enough, the reliability of the hybrid AC/DC distribution network no longer increases with the capacity of VSC. This is because the capacity of the VSC is already larger than the maximum power that can be exchanged between the two networks while satisfying the power flow constraint. Therefore, the capacity of VSC connecting the AC and DC networks can be increased within a certain range to improve the reliability of the AC/DC hybrid distribution network.

7 Conclusion

This study developed a restoration optimization model of the AC/DC hybrid distribution network considering network reconfiguration and control modes of VSC. Based on this, a reliability evaluation method for the AC/DC hybrid distribution network combining the FMEA method, restoration optimization model, and sequential Monte Carlo method was proposed. The following conclusions were drawn from case studies:

1) Considering VSC restoration capability and network reconfiguration can improve the reliability of the AC/DC hybrid distribution network. The proposed method fully accounts for these two restoration methods; thus, the reliability of the AC/DC hybrid distribution network can be accurately evaluated.

2) Among the key components, the reliability of VSC has the most significant impact on the reliability of AC/DC hybrid distribution networks, followed by the reliability of the DC circuit breaker, while the reliability of the AC circuit breaker is the weakest. Reducing the fault rate and repair time of VSC simultaneously is the most effective way to improve the reliability of the AC/DC hybrid distribution network.

3) Increasing the capacity of the VSC connecting AC network and DC network within a certain range can improve the reliability of the AC/DC hybrid distribution network.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LZ developed the research framework and put forward suggestions on the revision and improvement. SY completed the programming work and wrote the manuscript. YC put forward suggestions on the revision and improvement. WT put forward suggestions on the revision and improvement. HC put forward suggestions on the revision and improved the English written of this paper.

Funding

This work was supported by the Funds for International Cooperation and Exchange of the National Natural Science Foundation of China (Grant No. 52061635104).

Conflict of Interest

Author YC is employed by the Electric Power Research Institute of Guizhou Power Grid Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Atwa, Y. M., El-Saadany, E. F., and Guise, A.-C. (2010). Supply Adequacy Assessment of Distribution System Including Wind-Based DG during Different Modes of Operation. IEEE Trans. Power Syst. 25 (1), 78–86. doi:10.1109/TPWRS.2009.2030282

CrossRef Full Text | Google Scholar

Baran, M. E., and Wu, F. F. (1989). Optimal Capacitor Placement on Radial Distribution Systems. IEEE Trans. Power Deliv. 4 (1), 725–734. doi:10.1109/61.19265

CrossRef Full Text | Google Scholar

Billinton, R., and Peng Wang, P. (1999). Teaching Distribution System Reliability Evaluation Using Monte Carlo Simulation. IEEE Trans. Power Syst. 14 (2), 397–403. doi:10.1109/59.761856

CrossRef Full Text | Google Scholar

Broadwater, R. P., Shaalan, H. E., Oka, A., and Lee, R. E. (1994). Distribution System Reliability and Restoration Analysis. Electric Power Syst. Res. 29 (3), 203–211. doi:10.1016/0378-7796(94)90015-9

CrossRef Full Text | Google Scholar

Cheng, L., Wang, X., Chang, Y., Song, F., Gao, Y., Wang, Y., et al. (2016). “Reliability Assessment of AC Distribution Network with Multi-Terminal DC Interconnection,” in 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS) (Beijing, China), 1–6. doi:10.1109/PMAPS.2016.7764162

CrossRef Full Text | Google Scholar

Cui, Y., Wei, T., Su, J., Wang, G., Zhang, L., and Wang, C. (2019). “Reliability Evaluation of Hybrid AC/DC Distribution Network Based on DC Conversion,” in 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), 2849–2854. doi:10.1109/EI247390.2019.9061973

CrossRef Full Text | Google Scholar

Eajal, A. A., Shaaban, M. F., Ponnambalam, K., and El-Saadany, E. F. (2016). Stochastic Centralized Dispatch Scheme for AC/DC Hybrid Smart Distribution Systems. IEEE Trans. Sustain. Energ. 7 (3), 1046–1059. doi:10.1109/TSTE.2016.2516530

CrossRef Full Text | Google Scholar

Ghadiri, A., Mousavizadeh, S., and Haghifam, M. R. (2014). “Reliability Assessment of Possible AC/DC Distribution System Configurations,” in 2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS) (Durham, United Kingdom), 1–6. doi:10.1109/PMAPS.2014.6960668

CrossRef Full Text | Google Scholar

Guo, L., Ding, Y., Bao, M., Shao, C., Wang, P., and Goel, L. (2020). Nodal Reliability Evaluation for a VSC-MTDC-Based Hybrid AC/DC Power System. IEEE Trans. Power Syst. 35 (3), 2300–2312. doi:10.1109/TPWRS.2019.2951711

CrossRef Full Text | Google Scholar

Li, Y., Yuan, S., Liu, W., Zhang, G., Teng, Y., and Chen, X. (2018). A Fast Method for Reliability Evaluation of Ultra High Voltage AC/DC System Based on Hybrid Simulation. IEEE Access 6, 19151–19160. doi:10.1109/ACCESS.2018.2817247

CrossRef Full Text | Google Scholar

Li, Z., Wu, W., Tai, X., and Zhang, B. (2020a). Optimization Model-Based Reliability Assessment for Distribution Networks Considering Detailed Placement of Circuit Breakers and Switches. IEEE Trans. Power Syst. 35 (5), 3991–4004. doi:10.1109/TPWRS.2020.2981508

CrossRef Full Text | Google Scholar

Li, Z., Wu, W., Zhang, B., and Tai, X. (2020b). Analytical Reliability Assessment Method for Complex Distribution Networks Considering Post-Fault Network Reconfiguration. IEEE Trans. Power Syst. 35 (2), 1457–1467. doi:10.1109/TPWRS.2019.2936543

CrossRef Full Text | Google Scholar

Liu, W., Fu, M., Yang, M., Yang, Y., Wang, L., Wang, R., et al. (2021). A Bi-level Interval Robust Optimization Model for Service Restoration in Flexible Distribution Networks. IEEE Trans. Power Syst. 36 (3), 1843–1855. doi:10.1109/TPWRS.2020.3038400

CrossRef Full Text | Google Scholar

Tian, Y., Benidris, M., Sulaeman, S., Elsaiah, S., and Mitra, J. (2016). “Optimal Feeder Reconfiguration and Distributed Generation Placement for Reliability Improvement,” in 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS) (Beijing, China), 1–7. doi:10.1109/PMAPS.2016.7764202

CrossRef Full Text | Google Scholar

Wang, C., Xie, H., Liu, S., and Bie, Z. (2017). “A Novel Reliability Evaluation Method of AC/DC Hybrid Power System with the Injection of Wind Power,” in 2017 IEEE Electrical Power and Energy Conference (Saskatoon, SK, Canada), 1–6. doi:10.1109/EPEC.2017.8286164

CrossRef Full Text | Google Scholar

Wang, H. M. (2012). Reliability Evaluation of Distribution System Including Distributed Generations [D]. Tianjin: Tianjin University.

Google Scholar

Wang, J., Zhou, N., and Wang, Q. (2020). Data-driven Stochastic Service Restoration in Unbalanced Active Distribution Networks with Multi-Terminal Soft Open Points. Int. J. Electr. Power Energ. Syst. 121, 106069. doi:10.1016/j.ijepes.2020.106069

CrossRef Full Text | Google Scholar

Wei, W., Hao, T., and Xu, T. (2022). Day-Ahead Economic Dispatch of AC/DC Hybrid Distribution Network Based on Cell-Distributed Management Mode. Front. Energ. Res. 10. doi:10.3389/fenrg.2022.832243

CrossRef Full Text | Google Scholar

Wei, W., Zhou, Y., Zhu, J., Hou, K., Zhao, H., Li, Z., et al. (2019). Reliability Assessment for AC/DC Hybrid Distribution Network with High Penetration of Renewable Energy. IEEE Access 7, 153141–153150. doi:10.1109/ACCESS.2019.2947707

CrossRef Full Text | Google Scholar

Wu, L., Geng, B., Liu, H., Piao, Z., Wang, H., and Lin, Z. (2020). “Reliability Assessment of AC/DC Hybrid Distribution Network Based on Sequential Monte Carlo Method,” in 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE) (Chnegdu, China), 1096–1100. doi:10.1109/ACPEE48638.2020.9136249

CrossRef Full Text | Google Scholar

Xu, X., Huang, W., Hu, Y., Tai, N., Ji, Y., and Xie, N. (2021). Power Management of AC/DC Hybrid Distribution Network with Multi-Port PET Considering Reliability of Power Supply System. Front. Energ. Res. 9. doi:10.3389/fenrg.2021.721385

CrossRef Full Text | Google Scholar

Zhang, L., Liang, J., Tang, W., Li, G., Cai, Y., and Sheng, W. (2019). Converting AC Distribution Lines to DC to Increase Transfer Capacities and DG Penetration. IEEE Trans. Smart Grid 10 (2), 1477–1487. doi:10.1109/TSG.2017.2768392

CrossRef Full Text | Google Scholar

Zhang, L., Yu, S. J., Wang, C., Tang, W., and Zhang, X. H. (2022). Reliability Evaluation of AC/DC Hybrid Distribution Network Considering VSC Operation Mode and Fault Recovery Optimization. Power Syst. Technol. 46 (1), 292–300. doi:10.13335/j.1000-3673.pst.2021.0169

CrossRef Full Text | Google Scholar

Zhao, H., Hu, E., Zhang, Z., Shen, Z., Fu, M., and Wang, R. (2019). “Reliability Assessment of AC/DC Hybrid Distribution Network Considering Renewable Energy,” in 2019 4th International Conference on Power and Renewable Energy (ICPRE) (Chengdu, China), 46–50. doi:10.1109/ICPRE48497.2019.9034890

CrossRef Full Text | Google Scholar