Effective artificial neural network-based wind power generation and load demand forecasting for optimum energy management

The variability of power production from renewable energy sources (RESs) presents serious challenges in energy management (EM) and power system stability. Power forecasting plays a crucial role in optimal EM and grid security. Then, accurate power forecasting ensures optimum scheduling and EM. Therefore, this study proposes an artificial neural network- (ANN-) based paradigm to predict wind power (WP) generation and load demand, where the meteorological parameters, including wind speed, temperature, and atmospheric pressure, are fed to the model as inputs. The normalized root mean square error (NRMSE) and normalized mean absolute error (NMAE) criteria are used to evaluate the forecasting technique. The performance of ANN was compared to four machine learning methods: LASSO, decision tree (DT), regression vector machines (RVM), and kernel ridge regression (KRR). The obtained results show that ANN provides high effectiveness and accuracy for WP forecasting. Furthermore, ANN has proven to be an interesting tool in ensuring optimum scheduling and EM.

1 Introduction

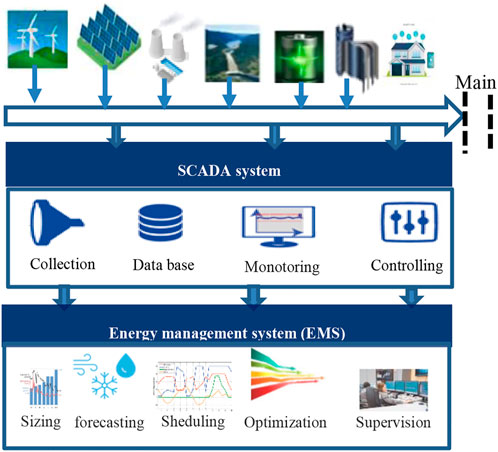
In power systems, the energy balance represents a serious challenge for grid operators to ensure grid stability. Usually, this balance is ensured by continuously adjusting the load demand and controlling the power generation through an energy management system (EMS) (Aoife et al., 2011).

EMSs are automation systems that gather energy data and make it available to users through monitoring tools and energy quality analyzers (Cristian et al., 2014). In addition, supervisory control and data acquisition (SCADA) systems, considered the heart of EMSs, carry out the data acquisition, update the data system through alarm processing, update the user interface, and execute control actions (Gregor et al., 2011). In renewable energy systems, the SCADA system allows access to the online data from sensors installed at the distributed generators and failure detection to improve the overall system reliability (Wenxian et al., 2013). In addition, the introduction of energy storage and EMS, together with the active involvement of users (Zafar et al., 2018) and the “spread” of electricity to cover other energy vectors (the transportation sector), are all considered to be complementary solutions for energy satisfaction. Apparently, the coordination of such smart grids implies high levels of complexity and requires advanced, intelligent EMS that can cope with the intermittency of RES while supporting cost-efficient sizing and operation of all assets and agents while succeeding in satisfying load demand at all times. In this context, a critical attribute for the optimized management of such integrated energy solutions is forecasting extended to capture different variables and microgrid aspects such as RES power generation (mainly wind and solar power), load demand, and electricity prices. Predictions with regard to this information are considered critical for providing meaningful EM services for all agents (operators, producers, and end users) (Tao et al., 2020). Such forecasting models enable uncertainty minimization for both the demand and production sides, along with an optimized operation of the different system components on a day-ahead basis. In other words, renewable energy production can be increased, storage devices can be optimally operated, and EMS strategies become more flexible, ensuring lower power system operation costs.

In this respect, this study focuses on forecasting wind energy production and demand power for optimal EM. Forecasting power models are generally divided into two main groups: physical and statistical models. The statistical approach (Ke et al., 2014; Morgan, 2015) is based on historical data and their statistical relationship with meteorological predictions and measurements from SCADA. In addition, the statistical forecasting approach can be used in numerical weather prediction (NWP) data. NWP models introduce weather forecasts, such as speed, temperature, precipitation, humidity, pressure, and solar irradiation. However, the physical approach presented by Landberg (1999) focuses on integrating physical aspects into the model, such as information about terrain and properties of energy source. Besides, there are different time horizon methods of power forecasting, which are generally classified into three main scales. The very short-term forecasts (up to 9 h) are intended to operate in real time. Statistical methods, such as Kalman filters, autoregressive with exogenous input (ARX), and autoregressive moving average (ARMA), have been used in short-term forecasting (Lei et al., 2009). As these methods are merely based on past production, they are generally not useful for longer horizons. Short-term forecasts (72 h) (Aoife et al., 2011) are useful in power systems for unit commitment and scheduling and for electricity markets where renewable sources and storage systems can be traded and hedged.

In addition, the study presented by Hua and Zhenging (2020) was based on a hybrid short-term wind power (WP) forecasting model that combines data processing, multiple parameters optimization, and multi-intelligent techniques for power forecasting.

Medium-term forecasts and predictions (3–7 days) (Alexandre et al., 2008) are applied to schedule distributed generator maintenance, unit commitment, and maintenance of thermal generators and plan energy storage operations.

Cincotti et al. (2014) proposed different techniques for wind speed forecasting, such as the discrete-time univariate econometric model, support vector machine (SVM), random forest (RF), decision tree (DT), multilayer perceptron (MLP), convolutional neural network (CNN), and long short-term memory (LSTM). The results presented in that paper showed that the SVM methodology gives better forecasting accuracy for price time series. However, the performance of the Wind Net model was higher (lower MAE and RMSE values) compared to that of SVM, RF, DT, MLP, CNN, and LSTM architectures. In addition, Machine learning (ML) methods, including ANN, SVM, nearest neighbor search, and RF, were applied in earlier studies (Chiou and Ping, 2018; Radhia et al., 2019) for fault diagnosis. Jiang et al., 2013 combined SVM and cuckoo search (CS) for short-term wind speed forecasting. In the latter work, CS was used to adjust the parameters of SVM, and the experimental results proved that the performance of CS is higher compared to that of particle swarm optimization. Zhang et al. (2017) integrated three different methods to predict wind speed: the ensemble empirical mode decomposition, adaptive neural network-based fuzzy inference system, and seasonal autoregression integrated moving average (SARIMA). The authors showed that the hybrid wind speed prediction models present an adequate prediction performance.

Moreover, Daniel et al. (2019) developed an advanced forecasting system in the framework of the TILOS project in horizon 2020, where a system that contains a solar source, wind generator, and load has been studied. They proposed a reliable prediction of the power of distributed generators (solar power and WP) and load demand. The ANN and Support Vector Regression (SVR) techniques have been used to predict load demand. The statistical evaluation indices, such as the symmetric mean absolute percentage error and the coefficient of determination (R²), are applied to evaluate the prediction model. The results show that prediction models present remarkable forecasting accuracy with very high scores.

In addition, Amirhossein et al. (2020) addressed the problem of large-scale WP forecasting using ML techniques (DT, boosting, and bagging), where the simulation results showed that the developed learning methods could forecast the WP at different heights of the wind turbine. The simulation results revealed that using longer time intervals and height extrapolation leads to long-term Wind Power Forecasting (WPF) using tree-based learning algorithms considerable accuracy degradation in the forecasted models. Moreover, Zhi et al. (2016) applied an ANN inference system for electricity consumption forecasting to ensure an optimal EM. Dangho (2020) applied an ANN for short-term WP prediction. This study aims to improve the forecasting accuracy of such simple and cost-efficient methods by combining the measurements of a sample building and the approximate energy consumption of a target building. Banafshel (2016) proposed using the ANN-based model in WP forecasting with numerical prediction to exploit the ability of ANN models to find the most effective parameters to forecast generated WP in mountainous regions in Canada. In Banafshel (2016), a comparative study of three forecasting techniques based on NN models was presented, showing that the intelligent mechanism based on NN performs well for WP forecasting.

This study presents short-term and medium-term forecasts of WP generation and power demand (load demand) in grid-connected wind energy systems using an artificial neural network (ANN). A comparison study is developed between ANN and different machine learning techniques. The study is organized as follows: Section 2 presents a brief overview of EMSs; Section 3 presents WP and power demand forecasting techniques based on ANN; Section 4 discusses the obtained results; and Section 5 concludes the paper and presents some future directions.

2 Energy management system

The EMS is performed at the control system level, typically called system control centers, which aims to ensure the security and stability of electric systems. Usually, a SCADA system is installed as an interface between the EMS and the power system, which enables the acquisition and collection of data from each production unit. The EMS is divided into several levels depending on the considered time scale. The first level ensures the sizing of the installation, where the life of the installation is considered as the time scale (Benoit et al., 2013). The second level is devoted to performing the annual planning according to the periods of the year. Thus, the annual production schedule depends on the demand and the maintenance forecast. The third level performs the production planning during a time scale ranging from 1 day to 1 week. This step consists of determining the plant’s production plan based on the data from the forecast and the constraints inherent to the technologies used. Thus, real-time supervision is the last level ensuring the storage power requirement to guarantee the system services (frequency and voltage). Figure 1 illustrates the general structure of an EMS. This study focuses on the third-level operation by presenting the modeling and forecasting of WP generation.

FIGURE 1

FIGURE 1. Structure of an energy management system (EMS).

3 Modeling of the wind turbine

The wind energy conversion system has gained wide attention from the scientific and industrial research community (Abdelmelek et al., 2020). The WP production variability is mainly caused by the meteorological conditions’ changes, such as wind speed, pressure, and temperature. The variation of these parameters presents a significant uncertainty that can provide a rapid fluctuation in WP generation.

The per unit surface power output is modeled as follows (Jannet et al., 2021):

$P_{eol}=0.5\rho C_{p}S{v}^3.(1)$

C_p is the ratio of the power extracted by a wind turbine relative to the energy available in the wind speed (Andreea et al., 2010). C_p is a nonlinear function expressed as follows:

$\begin{array}{l}{C}_p=0.5\left(\frac{151}{{\lambda }_i}-0.58\beta -0.002{\beta }^{2.14}-10\right)e^{-\frac{18.4}{{\lambda }_i}}\\ {\lambda }_i=\frac{1}{\frac{1}{\lambda -0.02\beta }-\frac{0.003}{{\beta }^3+1}}\end{array},(2)$

where ρ is the air density, P_eol is the power extracted from the wind turbine, v is the wind speed in m/s, S is the area swept by the rotor of the wind turbine in m², λ is the speed of the wind turbine, and β is the pitch angle (inclination of the reference axis with respect to the plane of rotation).

The density of dry wind is sensitive to pressure and temperature (Ofualagba and Ubeku, 2008; Marcel et al., 2017; Valdmer et al., 2021):

$\rho \left(P,T\right)=\frac{P}{287.06T},(3)$

$T=273.15+\theta .(4)$

Wind density is expressed as a function of atmospheric pressure, temperature, and relative humidity as follows (Marcel et al., 2017; Oludare et al., 2019):

$\begin{array}{l}\rho (P,T,H_r)=\frac{1}{287.06}(P-230.617H_r*\\ \exp (\frac{17.5043\theta }{\theta +241.2}))\end{array},(5)$

$H_r=\frac{P}{P_{sat}}.100,(6)$

$P_{sat}=6110.213\exp \left(\frac{17.5043\theta }{\theta +241.2}\right),(7)$

where H_r is the relative humidity, P is the pressure, and P_sat is the saturation pressure. Finally, the WP is given by

$\begin{array}{l}{P}_{eol}=0.5\frac{1}{278.06T}(P-230.617H_r*\\ \exp (\frac{17.5043\theta }{\theta +241.2})C_p{v}^3\end{array}.(8)$

4 Power forecasting

As already mentioned, one of the essential features for optimized EM of the power system with high shares of RES is the incorporation of advanced forecasting models. Such models enable uncertainty minimization for both the load demand and the production sides. Furthermore, they can optimize the power scheduling in short-term, intra-day, and day-ahead dispatch scheduling. In this context, production from renewable energy sources (RESs) can be increased, and storage devices can be optimally operated. Power production forecasting is also needed to predict the amount of power to be fed to the grid over the following hours and days.

4.1 Artificial neural network-based forecasting

ANNs are a technology based on studies of the brain and nervous system (Stevan et al., 2003; Khaled et al., 2022). Then, ANN emulates a biological neural network but uses a reduced set of concepts from biological neural systems. Specifically, the ANN models simulate the electrical activity of the brain and nervous system. Typically, the node is arranged in a layer or vector, with the output of one layer serving as the input to the next layer and possibly other layers (Oludare et al., 2019). A node may be connected to all or a subset of the nodes in the subsequent layer. During the learning process, the input values to a node are multiplied by a connection weight w_i,j that simulates the strengthening of neural pathways in the brain. After learning, the ANN performs the validation phase to select the ANN results. Then, it proceeds to the test phase to confirm the performance of the results.

4.2 ANN structure

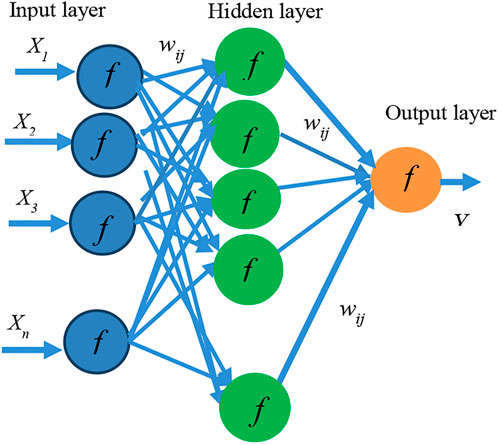
The ANN structure consists of three layers (input, hidden, and output layers), where each layer consists of sets of nodes. The input layer receives network inputs, the hidden layer processes the information, and the output layer provides the network response. The number of neurons in the input layer equals the number of inputs. Similarly, the number of output layer neurons corresponds to the number of outputs of the ANN. However, the number of neurons in the hidden layer is determined experimentally. It consists of several experiments by varying the number of neurons in the hidden layer. According to Hassoum (1995), a simple ANN architecture gives a good prediction compared to a complex ANN structure. Moreover, every two neurons of successive layers are interconnected through a signal of weight w_ij. Each neuron processes the information through an activation function f and sends it to the neurons of the next layer. The sigmoid activation function is the most frequently used, as it is a nonlinear function that can be differentiated (Henrique et al., 2001). This function is a logistic function, it varies from 0 to 1, and its expression is given by

$f=\frac{1}{1+\exp \left(x\right)}.(9)$

The weight equation is expressed as

$w=wij+∆wij.(10)$

The signal weight adjustment equation is written as follows:

$\Delta w_{ij}=\alpha e_i{x}_j.(11)$

The prediction error is expressed as

$e_i=\stackrel{\wedge }{y}\left(t+k\right)-y\left(t+k\right).(12)$

The linear activation function used for the output layer allows a simple summation of the signals received by the output layer to respond to the ANN. The output of the neural network is computed by

$\widehat{y}\left(t+k\right)=f_s\left(\sum w{x}_j\right).(13)$

Figure 2 represents the general structure of an ANN.

FIGURE 2

FIGURE 2. Structure of ANN

4.2.1 Wind energy forecasting with ANN

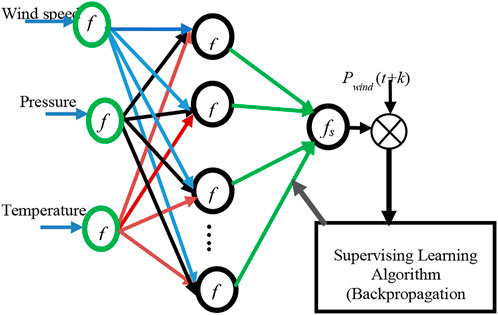
WP forecasting is required to estimate the amount of wind energy that can be extracted from wind farms. It is essential to choose parameters such as network inputs and outputs, the number of hidden layer neurons, activation functions, and learning techniques to implement an ANN. In this study, three layers are used for WP forecasting. The input layer consists of three neurons representing wind speed, temperature, and atmospheric pressure. The output layer comprises a single neuron, represented by the predicted WP. Figure 3 presents the proposed ANN architecture with a three-layered backpropagation model for WP forecasting.

FIGURE 3

FIGURE 3. ANN architecture for WP generation forecasting.

4.2.2 Artificial neural network-based power load demand forecasting

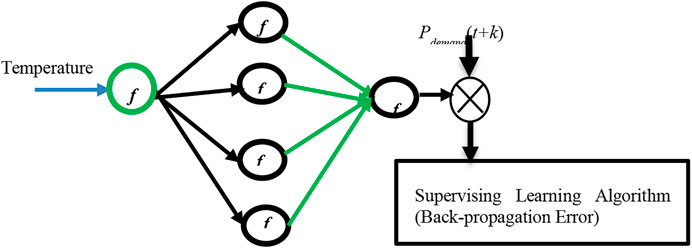
The power demand is also characterized by its high uncertainty. It depends on different factors, such as time, weather, and other random effects. However, for power system planning purposes, the analysis and prediction of power demand variation. For wind production, power demand variations exist in all time scales (short-, medium-, and long-term), and system actions are needed to maintain the generation-demand balance. For power demand forecasts, numerous variables directly or indirectly affect the system’s accuracy. Engene and Dora (2005) introduced several long-term (month or year) load forecasting methods, which are very important for planning and developing future generation, transmission, and distribution systems. Maria et al. (2014) proposed a long-term probabilistic load forecasting method with three modernized elements: predictive modeling, scenario analysis, and weather normalization. Long-term and short-term load forecasts play important roles in formulating secure and reliable operating strategies for the electrical power system. In this study, we develop an ANN model for load power forecasting. The ANN model is composed of one input layer represented by temperature values (obtained from weather forecast), one hidden layer (the number of neurons is determined by a trial-and-error method to minimize the forecast errors from the training set), also the output layer is defined by the load demand prediction. Figure 4 represents the architecture of ANN for forecasting load demand.

FIGURE 4

FIGURE 4. Architecture of ANN for forecasting demand power.

4.2.3 Evaluation of the proposed ANN

Two main criteria are frequently used to evaluate the performance of the proposed ANN algorithm: mean absolute error (MAE) and root mean square error (RMSE) (Demuth et al., 2000). The expression of the error quadratic normalized is defined by

$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left({\stackrel{\wedge }{y}}_k-y_k\right)}^2}.(14)$

The expression of the mean quadratic error normalized is obtained by

$MAE=\frac{1}{n}\sqrt{\left|{\stackrel{\wedge }{y}}_k-y_k\right|},(15)$

where ${\widehat{y}}_k$ and $y_k$ represent the predicted and the measured outputs, respectively, and n defines the number of iterations.

5 Results and discussions

During this study, perceptrons (Abdelhameed et al., 2021) with a single hidden layer of sigmoid units and linear outputs are used. The influence of the number of inputs and the number of hidden nodes in the ANN response is studied to implement the network architecture (Aoife et al., 2011). A set of data inputs (wind speed, temperature, and pressure), randomly chosen, were used during this process. Each data sample of this ensemble was divided into two subsets: one to train the networks and the other to test the generalization ability of the trained networks. Then, 70% of the dataset was employed for training, and the remaining 30% served for validation purposes. The sequence of RMSE minimization tends towards to consistent solution after running it for some iteration; in this paper iterations are performed to get consistent solution to get an optimum output (power forecasting). The forecasting results are obtained through the Neural Network Toolbox of MATLAB.

5.1 Short-term forecasting

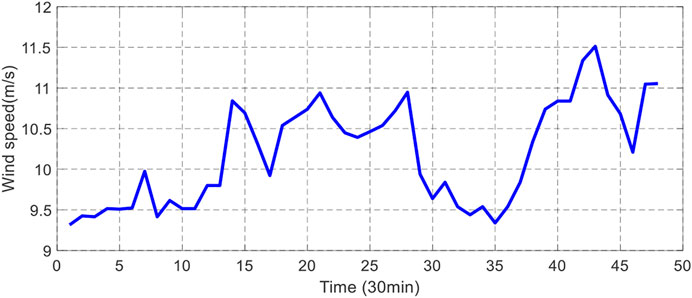
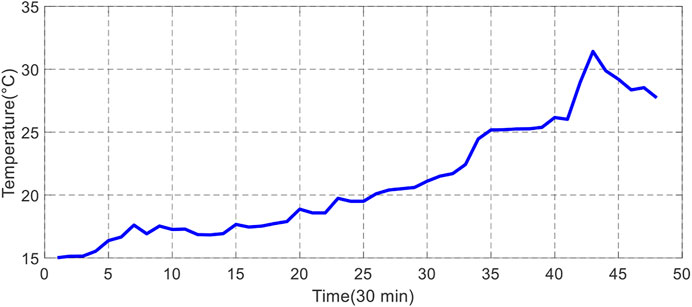
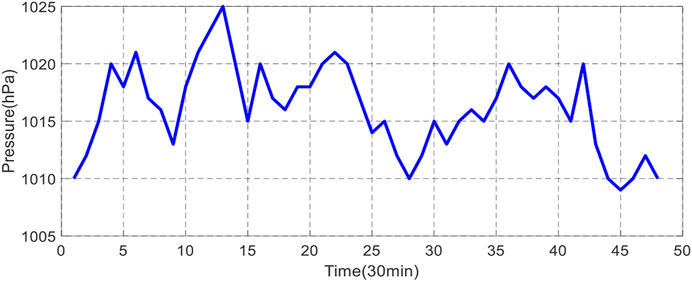
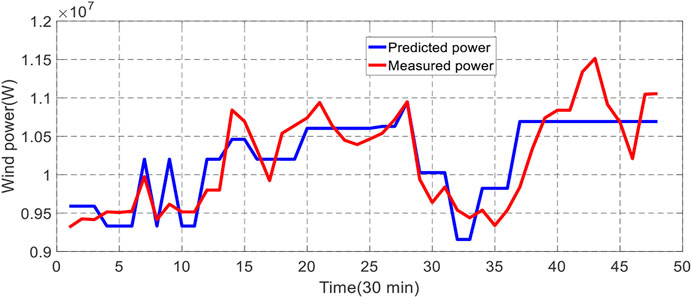
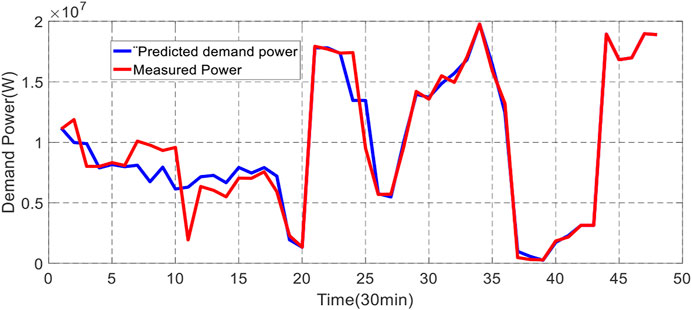
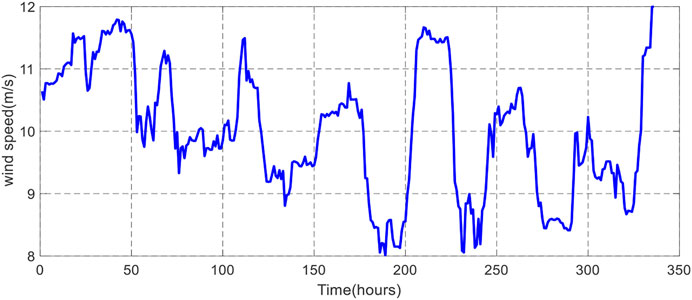
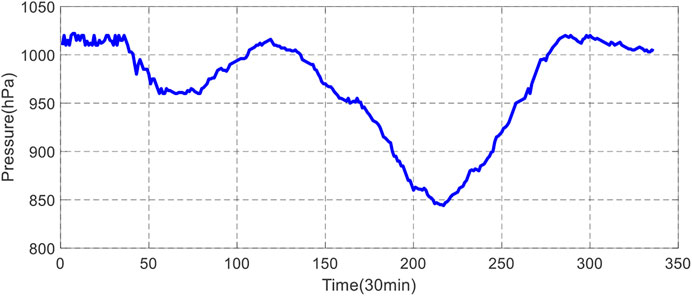
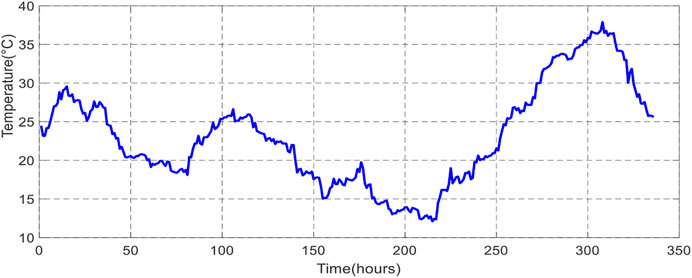
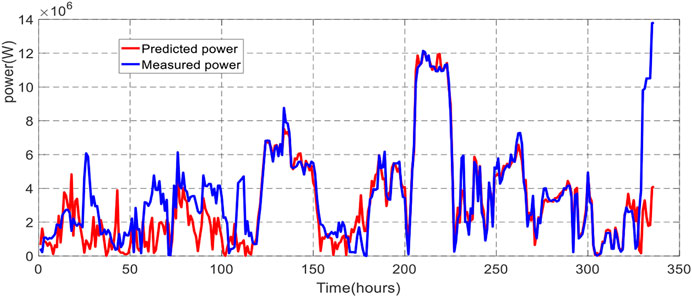
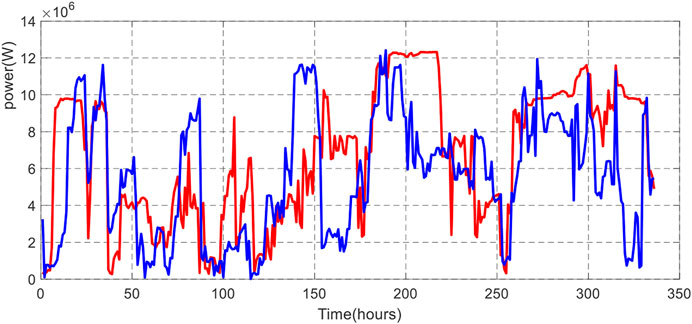
Short-term forecasting was implemented to predict WP generation and power demand (load demand). Forecasting is obtained every 30 min a day ahead (24 h). The plots in Figures 5–7 show the selected inputs (wind speed, temperature, and pressure), whereas the predicted WP generation and load demand are represented in Figures 8, 9.

FIGURE 5

FIGURE 5. Wind speed profile (1 day).

FIGURE 6

FIGURE 6. Temperature profile (1 day).

FIGURE 7

FIGURE 7. Pressure profile (1 day).

FIGURE 8

FIGURE 8. Wind power generation prediction (1 day).

FIGURE 9

FIGURE 9. Load demand prediction (1 day).

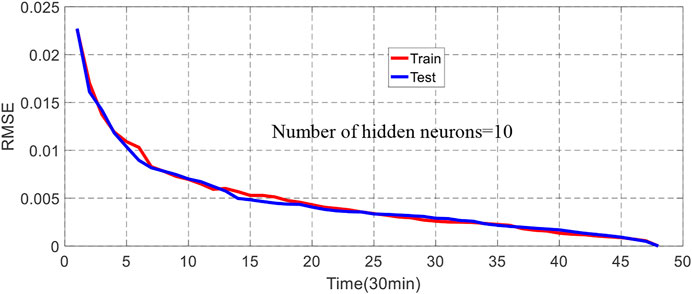
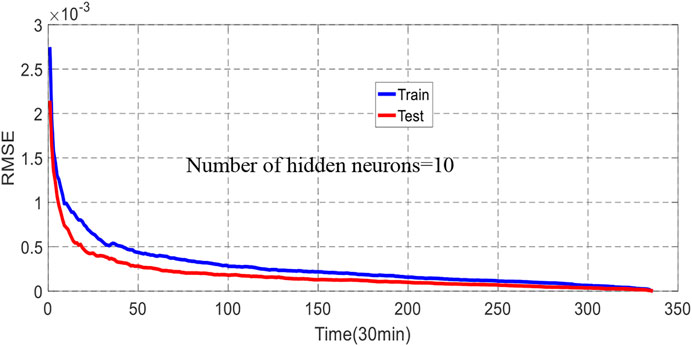
The day-ahead (24 h) RMSE for WP generation and load demand forecasting (10 numbers of hidden nodes) are shown in Figures 10, 11.

FIGURE 10

FIGURE 10. RMSE for wind power forecasting using 10 hidden neurons (1 day).

FIGURE 11

FIGURE 11. RMSE for load demand forecasting using 10 hidden neurons (1 day).

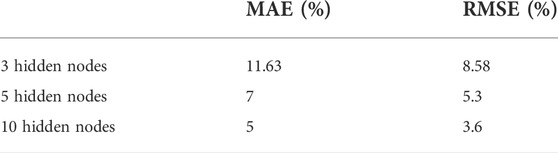
Tables 1, 2 present the evaluation of the performance of WP generation and power demand predictions based on the RMSE and MAE criteria during 24 h.

TABLE 1

TABLE 1. Evaluation of wind power prediction for 1 day.

TABLE 2

TABLE 2. Evaluation of power demand prediction for 1 day.

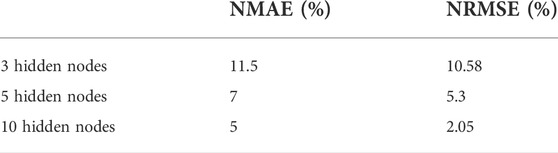
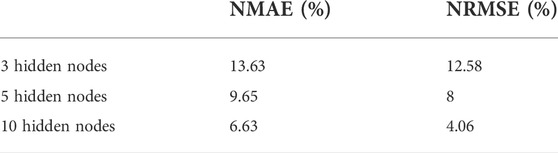
These results show that the short-term forecasting accuracy for WP is better when the number of nodes is higher (10 nodes compared to 3 nodes), the same as obtained for load demand prediction. Notably, the number of hidden units was limited to 10 as no improvements were absorbed with many hidden units. Moreover, the results from the ANN model for WP prediction, which uses three inputs (wind speed, temperature, and pressure), ensure 18% more accurately than the ANN model for demand power predictor with only input (temperature).

5.2 Medium-term forecasting

As seen earlier, medium-term forecasting is used for 1 week up to 1 year and is applied for maintenance scheduling and planning. In this study, the medium-term power prediction scheme was implemented to predict the generated power every 30 min. The plots in Figures 12–14 represent the wind speed variation, temperature, and pressure profiles for a week (inputs), whereas the WP and load demand predictions are represented in Figures 15, 16.

FIGURE 12

FIGURE 12. Wind speed (7 days).

FIGURE 13

FIGURE 13. Pressure profile (7 days).

FIGURE 14

FIGURE 14. Temperature (7 days).

FIGURE 15

FIGURE 15. Wind power forecasting (7 days).

FIGURE 16

FIGURE 16. Load demand prediction (7 days).

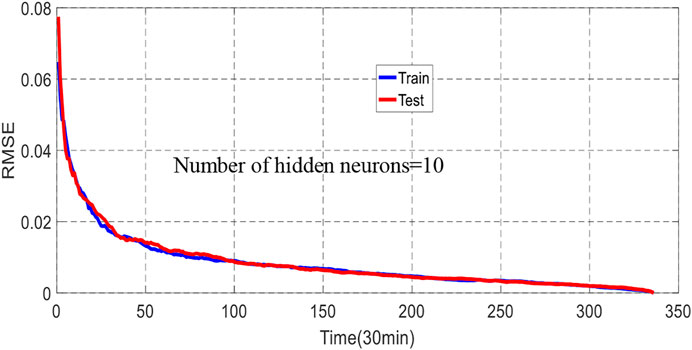
The 7-day RMSE for WP generation and load demand forecasting (with 10 hidden nodes) are shown in Figures 17, 18.

FIGURE 17

FIGURE 17. RMSE for wind power forecasting using 10 hidden neurons (7 days).

FIGURE 18

FIGURE 18. RMSE for load demand forecasting using 10 hidden neurons (7 days).

The RMSE of WP and load demand predictions are significantly reduced compared to the short-term forecasting case due to the effect of the sudden change in wind speed, temperature, or pressure on the ANN accuracy.

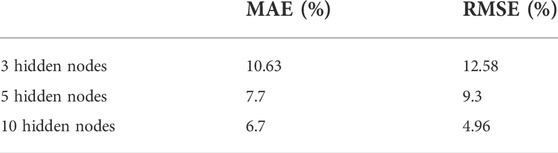
Tables 3, 4 present the evaluation of the performance of WP generation and power demand predictions based on the RMSE and MAE criteria for 7 days.

TABLE 3

TABLE 3. Evaluation of wind power prediction for 7 days.

TABLE 4

TABLE 4. Evaluation of power demand prediction for 7 days.

The number of nodes on the hidden layer of the ANN increased sequentially to reach the optimum number of 10 (Figures 17, 18), resulting in a 53% improvement in the forecast accuracy compared to the basic ANN with three hidden nodes. Moreover, adding more hidden nodes beyond 10 did not improve the results significantly and caused the risk of fitting the noise more than the desired signal. The optimal values are selected as the last 24 h of measured load demand with only input, and RMSE and NMAE are obtained as 4.96% and 6.63%, respectively. Furthermore, the RMSE and MAE in 24 h of WP prediction are 3.06% and 5%, respectively. Besides, the optimal values of RMSE and MAE at 1 week (7 days) are 4.06% and 6.63% for demand power forecasting with temperature as the only input; then, they are equal to 3.55% and 5% for WP prediction. These results show that adding more inputs and utilizing more complex architecture can possibly enhance the performance of ANN.

In addition, the performance of ANN was compared with four machine learning methods: LASSO (Volker, 2004), DT (Kavitha et al., 2016), regression vector machines (RVM) (Achmad and Bo-Suk, 2007), and kernel ridge regression (KRR) (Welling 2013). The performance of these techniques is compared by computing the RMSE and NMAE values. The results are presented in Tables 5, 6.

TABLE 5

TABLE 5. Performance comparison of short-term wind power production and load demand prediction using different ML techniques.

TABLE 6

TABLE 6. Performance comparison of medium-term wind power production and load demand prediction using different ML techniques.

The obtained results show that ANN provides high effectiveness and accuracy for WP forecasting based on the RMSE and NMAE performance criteria. However, ANN is significantly better than LASSO and KRR. In contrast, the differences between ANN and other tested techniques are not statistically significant. The effectiveness of the ANN model could be justified by its robustness and ability to minimize the error in the iterative procedure of parameters optimization, such as learning rate and weight w_i,j, whereas the other techniques have predefined values of some input parameters. However, the main disadvantage of the ANN model over the other four learning methods is its slower learning due to a larger number of iterations needed to reduce the error of forecasting with different activation functions. As a result, the good performance of the ANN model can reduce the fluctuation of wind energy production and load demand. Consequently, the grid operator can ensure better scheduling and optimum EM.

6 Conclusion

This study presented ANN-based forecasting techniques for WP generation and load demand predictions for optimum EM in grid-connected wind energy systems. Firstly, the WP generation model has been described in detail. In addition, for the WP prediction, the effect of wind speed, temperature, and pressure on the generated WP has been discussed. In addition, the performance of the proposed ANN model was compared to four machine learning-based techniques. The results show that all techniques (ANN, LASSO, DT, RVM, and KRR) can generally learn fast and ensure accurate power forecasting. However, the ANN provides the best forecasting accuracy and outperforms the other methods. Moreover, the ANN model for WP (three inputs) performs better than the ANN model for load power forecasting (only input). These results also showed that adding more samples (medium-term forecasting) can enhance the performance of the ANN model compared to the short-term forecasting case. Finally, better forecasting for WP and load demand ensures an optimum EM.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelhameed, I., Syedali, M., Sherif, S. M., Ghoneim, S. S. M., Al-Harthi, M. M., Ibrahim, T. F., et al. (2021). Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm. IEEE Access 10, 125787–125804./ACCESS.3111408. doi:10.1109/access.2021.3111408

CrossRef Full Text | Google Scholar

Abdelmelek, K., Mansour, H., Mohamed, F. H., Majdi, M., Hazem, N., and Mohamed, N. (2020). Hidden Markov model based principal component analysis for intelligent fault diagnosis of wind energy converter systems. Renewable energy, Elsevier. doi:10.1016/j.renene.2020.01.010

CrossRef Full Text | Google Scholar

Achmad, W., and Bo-Suk, Y. (2007). Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal Process. 21, 2560–2574. doi:10.1016/j.ymssp.2006.12.007

CrossRef Full Text | Google Scholar

Alexandre, C., Antonio, C., Jorge, N., Gil, L., Henrik, M., and Everlado, F. (2008). A review on the young history of the wind power short-term prediction. Renew. Sustain. Energy Rev. 12 (6), 1725–1744. ISSN 13640321. doi:10.1016/j.rser.2007.01.015

CrossRef Full Text | Google Scholar

Amirhossein, A., Mojtaba, N., Beham, M., Amani, A. M., and Piran, M. J. (2020). Long term wind power forecasting using tree based learning algorithms. IEEE Access 8, 151511–151522. ACCESS.2020.3017442. doi:10.1109/access.2020.3017442

CrossRef Full Text | Google Scholar

Andreea, P., Dumitru, P., and Pierre, B. (2010). Modeling and control of wind turbines. LSS2010 (12th LSS symposium, Large Scale systems: Theory and Applications).

Google Scholar

Aoife, M. F., Paul, G. L., Antonino, M., and Eamon, J. M. (2011). Current methods and advances in forecasting of wind power generation. Elsevier Renewable Energy. doi:10.1016/j.renene.2011.05.033

CrossRef Full Text | Google Scholar

Banafsheh, B. A. (2016). Wind power forecasting using artificial neural networks with numerical prediction – a case study for mountainous Canada. Master of science. doi:10.14288/1.0308789

CrossRef Full Text | Google Scholar

Benoit, R., Arnaud, D., and Christophe, S. (2013). Methodologies for supervision of hybrid energy sources based on storage systems – a survey. Math. Comput. Simul. 91, 52–71. doi:10.1016/j.matcom.2012.06.014

CrossRef Full Text | Google Scholar

Chiou, J. H., and Ping, H. K. (2018). A short-term wind speed forecasting model by using artificial neural networks with stochastic optimization for renewable energy systems. energies 11, 2777. doi:10.3390/en11102777

CrossRef Full Text | Google Scholar

Cincotti, S., Gallo, G., Ponta, L., and Raberto, M. (2014). Modeling and forecasting of electricity spot-prices: Computational intelligence vs classical econometrics. AI Commun. 27, 301–314. doi:10.3233/aic-140599

CrossRef Full Text | Google Scholar

Cristian-Dragoş, D., and Gligor, A. (2012). SCADA based software for renewable energy management system.Procedia Economics and Finance. Elsevier 3, 262–267. doi:10.1016/S2212-5671(12)00150-5

CrossRef Full Text | Google Scholar

Daniel, H. A., Rafael, N. M., Santiago, D. R., Garcia, S. S., Moustris, K. P., Kavadias, K. K., et al. (2019). An advanced forecasting system for the optimum energy management of island microgrids. Energy Procedia 159, 111–116. doi:10.1016/j.egypro.2018.12.027

CrossRef Full Text | Google Scholar

Dongho, L . (2020). Low-cost and simple short-term load forecasting for energy management systems in small and middle-sized office buildings. Energy Explor. Exploitation 0 (0), 1–20. doi:10.1177/0144598719900964

CrossRef Full Text | Google Scholar

Demuth, H., Beale, M., and Hagan, M. (2000). Neural network toolbox TM 6 user’s guide. MathWorks 9 (4).

Google Scholar

Eugene, A. F., and Dora, G. (2005). “Load forecasting,” in Applied mathematics for restructured electric power systems (Springer), 269–285. doi:10.1007/0-387-23471-3_12

CrossRef Full Text | Google Scholar

Gregor, G., Richard, B., George, K., Michael, D., and Caroline, D. (2011). The state-of-the-art in short-term prediction of wind power: A literature overview. Technical report, ANEMOS.

Google Scholar

Hassoum, M. H. (1995). Fundamentals of artificial networks. MITbook. 9780262082396.

Google Scholar

Henrique, S. H., Carlos, E. P., and Reinaldo, C. S. (2001). Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 16, 44–55. doi:10.1109/59.910780

CrossRef Full Text | Google Scholar

Hua, Y., and Zhenging, P. (2020). A hybrid short-term wind power prediction model combining data processing, multiple parameters optimization and multi-intelligent models apportion strategy. IEEE Access 8, 227126–227140. doi:10.1109/ACCESS.2020.3046001

CrossRef Full Text | Google Scholar

Jannet, J., Dhaker, A., and Mohamed, F. M. (2021). Joint operation between wind power generation and pumped hydro energy storage in the electricity market. Wind Eng. 45 (1), 50–62.

Google Scholar

Jiang, Y., Song, Z., and Kusiak, A. (2013). Very short-term wind speed forecasting with Bayesian structural break model. Renew. Energy 50, 637–647. doi:10.1016/j.renene.2012.07.041

CrossRef Full Text | Google Scholar

Kavitha, S., Varuna, S., and Ramya, R. (2016). “A comparative analysis on linear regression and support vector regression,” in 2016 online international conference on green engineering and technologies (IC-get), 1–5. doi:10.1109/GET.2016.7916627

CrossRef Full Text | Google Scholar

Ke, S. W., Vishal, S. S., and Zhen, Y. Z. (2014). Scada data based condition monitoring of wind turbines. Adv. Manuf. 2 (1), 61–69. doi:10.1007/s40436-014-0067-0

CrossRef Full Text | Google Scholar

Khaled, D., Majdi, M., Kais, B., Hazem, N., and Mohamed, N. (2022). Reduced neural network based ensemble approach for fault detectionand diagnosis of wind energy converter systems. Renewable Energy,Elsevier. doi:10.2139/ssrn.4055327

CrossRef Full Text | Google Scholar

Landberg, L. (1999)., 80. Roskilde, Denmark, 207–220. doi:10.1016/S0167-6105(98)00192-5Short-term prediction of the power production from wind farmsJ. Wind Eng. Industrial Aerodynamics

CrossRef Full Text | Google Scholar

Lei, M., Shiyan, L., Chuanwen, J., Hongling, L., and Yan, Z. (2009)., 13. Shanghai, China, 915–920. doi:10.1016/j.rser.2008.02.002A review on the forecasting of wind speed and generated powerRenew. Sustain. Energy Rev.

CrossRef Full Text | Google Scholar

Marcel, H. S., Sunday, O. O., Sergo, Y. D., and Kofane, T. C. (2017). Assessment of wind energy potential in the Sudanese zone in Chad. Energy Power Eng. 09, 386–402. doi:10.4236/epe.2017.97026

CrossRef Full Text | Google Scholar

Maria, G. G., Congedo, P. M., and Malvoni, M. (2014). Photovoltaic power forecasting using statistical methods: Impact of weather data. IET Sci. Meas. & Technol. 8, 90–97. doi:10.1049/iet-smt.2013.0135smt.2013.0135

CrossRef Full Text | Google Scholar

Maxwell (2013). Kernel Ridge regression. Department of Computer Science University of Toronto.

Google Scholar

Morgan, S. (2015). “Short-term wind power forecasting using artificial neural networks.Degree project,” in Computer science. second level (Stockholm,Sweden.

Google Scholar

Ofualagba, G., and Ubeku, E. U. (2008). “Wind energy conversion System-Wind turbine modeling,” in 2008 IEEE power and energy society general meeting - conversion and delivery of electrical energy in the 21st century, 1–8. doi:10.1109/PES.2008.4596699

CrossRef Full Text | Google Scholar

Oludare, I. A., Aman, J., and Abiodun, E. O. (2019). Comprenhensive Review of artificial neural network applications to pattern recognization. IEEE access 2019, 2945545.

Google Scholar

Radhia, F., Majdi, M., Kamal, A., Mohamed, T., Hazem, N., and Mohamed, N. (2019). “Machine Learning_Based statistical hypothesis testing for fault detection,” in 4th conference on control and fault tolerant systems (Casablanca,Morocco. doi:10.1109/SYSTOL.2019.8864776

CrossRef Full Text | Google Scholar

Tao, H., Y, H., Hamidreza, Z., Weron, R., Yang, D., and Zareipour, H. (2020). Energy forecasting:A review and outlook. IEEE Open J. Power Energy 7, 376–388. doi:10.1109/OAJPE.2020.3029979

CrossRef Full Text | Google Scholar

Valdmer, K., Katrzyna, W., and Henryk, C. (2021). Analysis of the wind turbine selection for the given wind conditions. Energies 2021, 7740. doi:10.3390/en14227740

CrossRef Full Text | Google Scholar

Volker, R. (2004). The generalized lasso. IEEE Trans. Neural Netw. 15, 16–28. doi:10.1109/tnn.2003.809398

PubMed Abstract | CrossRef Full Text | Google Scholar

Wenxian, Y., Richard, C., and Jiesheng, K. (2013). Wind turbine condition monitoring by the approach of scada data analysis. Renew. Energy 53, 365–376. doi:10.1016/j.renene.2012.11.030

CrossRef Full Text | Google Scholar

Zafar, R., Anzar, M, , Sohail, R, , Wamiq, A, , Usman, N, , and Khurram, S, (2018). Prosumer based energy management and sharing in smart grid. Renew. Sustain. Energy Rev. 82, 1675–1684. doi:10.1016/j.rser.2017.07.018

CrossRef Full Text | Google Scholar

Zhang, J., Wei, Y., Tan, Z., Ke, W., and Tian, W. (2017). A hybrid method for short-term wind speed forecasting. Sustainability 9, 596. doi:10.3390/su9040596

CrossRef Full Text | Google Scholar

Zhi, L., Lin, Y., Yongning, Z., Xuri, S., Jingzhu, T., and Jingxin, J. (2016). “Short-term wind power prediction based on extreme learning machine with error correction,” in Protection and control of modern power systems. doi:10.1186/s41601-016-0016-y

CrossRef Full Text | Google Scholar