Semi-Empirical Model of Droplet Size Distribution From the Maximum Entropy Principle in Sodium Spray

When a sodium leakage accident occurs in the sodium-cooled fast reactor, the leaked sodium reacts violently with the air in the form of droplets, resulting in the phenomenon of sodium spray fire. The droplet size distribution formed by liquid sodium injection is the key factor affecting the accident analysis of sodium spray fire. Based on the theory of the maximum entropy principle, a semi-empirical model of sodium spray droplet size distribution is constructed, which is constrained by the mass equation or the momentum equation with viscous resistance, respectively. Based on the existing liquid fuel droplet size distribution experiment results and the sodium spray fire experiment results, the semi-empirical model is verified, which shows that the prediction result with the semi-empirical model constrained by the momentum equation is in good agreement with the experimental result with the error of about 20%. Furthermore, the proposed sodium spray droplet model is compared with other models of the empirical model, the semi-empirical model, and the model based on the maximum entropy principle constrained by the simplified mass equation. The simulation result with the proposed model matches the experimental data better with minor error.

1 Introduction

As a recommended reactor type in the Generation IV advanced nuclear energy system, sodium-cooled fast reactors (SFRs) have attracted worldwide attention due to their mature technology and inherent safety (GIF, 2002). However, sodium shows a high chemical reactivity with oxygen, which entails a fire hazard risk in the case of leaks into the containment, named sodium pool fire and sodium spray fire accident, resulting in equipment damages (Sathiah and Roelofs, 2014). The consequences of spray sodium fire are the most serious, in which the liquid sodium is dispersed into a large number of small droplets in the spray, making a violent sodium burning. According to the research of Sandia National Laboratory (SNL) on sodium spray fire accident phenomenon identification and ranking table, it is found that the prediction of droplet size distribution is very important in sodium spray dynamics (Olivier et al., 2010). However, there is still a lack of relevant physical phenomena, and the empirical model is also lack of experiment verification (Ohno et al., 2012).

The process of sodium spray can be regarded as the breakup process of molten sodium. The distribution of spray diameter determines the heat-transfer interface of sodium droplets, which is related to the subsequent combustion behavior and the aerosol generation and removal behavior (Srinivas et al., 2019). Many experiments and theoretical studies have been carried out. The large-scale sodium spray experiment is conducted on the FAUNA device (Cherdron, 1980; Garcia et al., 2016). It is found that when the initial spray mass is 7, 20, and 40 kg, the average diameter of the sodium droplet is 1.3, 2.15, and 4.8 μm, respectively. The results show that the average diameter of sodium spray droplets is positively correlated with the amount of sodium. However, when the injection mass reaches the maximum value of 60 kg, the pressure also reaches the maximum value of 1.8 bar. The medium-scale sodium spray experiment with an initial spray mass of 0.4–5.25 kg and a pressure of 2.6 bar is conducted (Malet et al., 1982). It is believed that smaller spray size is conducive to pressure propagation. The small-scale sodium spray experiment is carried out on the LISOF device (Torsello et al., 2012; Manzini and Torsello, 2013) using an LDV/PDA system to collect and characterize the sodium spray dynamic parameters. It is found that the droplet number density relative to droplet size is similar to Gaussian distribution. A sodium spray test under a pressure difference of 0.2 MPa is also conducted by Japan Nuclear Cycle Development Institute (JNC) (Nagai et al., 1999) using a laser droplet size analyzer to measure the sodium spray droplet size distribution. The number density distribution with the size of sodium droplets conforms to the Nukiyama–Tanasawa model.

The spray phenomenon widely exists in various fields such as nuclear industries, engine research, and medical treatment. Babinsky and Sojka (2002) of Purdue University in the United States have summarized three basic methods to deal with droplet distribution in the spray process, namely, the empirical correlation method, discrete probability function (DPF) method, and maximum entropy principle. The expression form of the model based on the empirical method is simple and easy to apply. Rosin and Rammler (1933) has developed the Rosin–Rammler empirical relation based on the droplet size distribution in the breakup process of pulverized coal and cement slurry, which can be regarded as a special form of expression of the Nukiyama–Tanasawa model. In addition, the Nukiyama–Tanasawa model, obtained by measuring the droplet size distribution, is adopted in the sodium spray and fire analysis programs of NACOM (Tsai, 1980), CONTAIN-LMR (Murata et al., 1993), and SPHINCS (Yamaguchi and Tajima, 2002). However, the model relies heavily on the determination of the average droplet size. The extension of the pure empirical model under different droplet conditions may be controversial. The DPF method was first applied to modeling drop size distributions in Newtonian sprays by Sovani et al. (1999). A drop size distribution is produced because of the fluctuation of initial conditions. The DPF method requires a set of initial conditions and a model of the breakup mechanism. The DPF has not been validated because of the difficulties involved in obtaining the fluctuating initial conditions (Babinsky and Sojka, 2002). The maximum entropy principle was first proposed by Jaynes (1957), which characterizes the droplet number distribution obtained under a series of physical constraints, and its corresponding system entropy function reaches the maximum value. Cheng et al. (2002) have proposed the droplet size distribution function based on the principle of maximum entropy and established an exponential model that does not change with different test conditions with the constraints of the simplified mass equation. Therefore, Lee et al. (2004); Wu et al. (2020) have used this method to conduct preliminary explorations on fuel combustion in the energy field. Peng et al. (2021) have coupled the continuity and momentum equations to build a droplet size distribution model based on the principle of maximum entropy and have used the present experiment results and current models to validate. However, the model took the basic mass equation and momentum equation as constraints without considering the influence of viscous resistance. Besides, the distribution of the experimental data used for verification is similar, most of which are normally distributed and are not adequate. However, based on the study of the droplet fragmentation mechanism by Zhao et al. (2011) and Cao and Ma (1997), viscous resistance plays an important role. Therefore, it is necessary to develop a maximum entropy droplet size distribution model considering the influence of viscous resistance and to use multiple experimental data types in the form of distribution to validate the model.

Based on the maximum entropy principle, two semi-empirical models of the droplet size distribution, with the main constraint condition of the mass equation and the momentum equation including the viscous resistance term as the main constraint condition, are developed and verified.

2 Establishment of the Droplet Size Distribution Model

2.1 Maximum Entropy Principle With the Mass Equation as the Constraint Condition

The derivation of the sodium droplet size distribution model based on the maximum entropy principle requires the establishment of appropriate physical constraints. Jaynes (1957) applied the maximum entropy principle to physics to obtain the droplet distribution law, shown as Eq. 1.

$S=-T{\displaystyle \sum _k{P}_k\ln P_k}(1)$

where S is the entropy, $T$ is a constant, and $P_k$ is the probability of the number of droplets under a certain volume of the leaked sodium droplet.

When the entropy takes a maximum value, the most probable event occurs, that is, the sodium droplet size distribution function with the largest probability of occurrence is obtained (Cao et al., 2008), shown as Eq 2

${\displaystyle \sum _k{P}_k}\cdot \ln P_k=Max.(2)$

From the mass conservation of sodium droplets in the system (Cheng et al., 2002), Eq. 3 can be obtained

${\displaystyle \sum _k{P}_k}{m}_k{N}_0\left(1+\epsilon \right)=\dot{m}(3)$

where $m_k$ is the ejection mass under the action of the pressure difference when the loop system is broken, $N_0$ is the total number of sodium droplets produced in unit time, $\epsilon$ is the loss of sodium droplets due to chemical reaction or physical actions like pressure difference, and $\dot{m}$ is the mass flow rate of sodium droplets ejected from the break.

Considering that the sodium droplet is an incompressible fluid, Eq. 3 can be transformed into Eq. 4

${\displaystyle \sum _k{P}_k{v}_k{N}_0\left(1+\epsilon \right)}=\dot{V}(4)$

where $v_k$ is the volume of a single sodium droplet and $\dot{V}$ is the total volume flow of sodium droplets ejected from the break.

In various cases, the sum of the number probabilities is 1, shown as Eq. 5

${\displaystyle \sum _k{P}_k}=1(5)$

For the above three basic constraints of Eqs 2, 4, and 5, the Lagrange method is used to obtain the function of $G_{ma}$ as Eqs 6, 7 (Mojaver et al., 2020)

$G_{ma}={\displaystyle \sum _k{P}_k\cdot \ln }{P}_k+\left(\varphi -1\right)\left({\displaystyle \sum _k{P}_k-1}\right)+\omega ({\displaystyle \sum _k{P}_k{v}_k{N}_0(1+\epsilon )}-\dot{V})(6)$

$\frac{d{G}_{\text{ma}}}{d{P}_k}=0(7)$

Then, Eq. 8 can be obtained

$P_k=\exp \left[-\varphi -\omega v_k{N}_0\left(1+\epsilon \right)\right](8)$

where $\varphi$ and $\omega$ are the undetermined Lagrange multipliers.

Eqs 9, 10 can be obtained through inserting Eq. 8 into Eqs 4, 5

${\displaystyle \sum _k\exp \left[-\varphi -\omega v_k{N}_0\left(1+\epsilon \right)\right]}\cdot v_k{N}_0\left(1+\epsilon \right)=\dot{V}(9)$

$\varphi =\ln {\displaystyle \sum _k\exp \left[-\omega v_k{N}_0\left(1+\epsilon \right)\right]}(10)$

Thus, Eq. 11 is obtained

$\dot{V}=\frac{{\displaystyle \sum _k{v}_k{N}_0\left(1+\epsilon \right)\cdot \exp \left[-\omega v_k{N}_0\left(1+\epsilon \right)\right]}}{{\displaystyle \sum _k\exp \left[-\omega v_k{N}_0\left(1+\epsilon \right)\right]}}(11)$

Assuming that the droplet diameter of the particles of atomization sodium droplets ejected from the break of the loop system, denoted as D, conforms to the continuous distribution, Eqs 12, 13 can be obtained

$\varphi =\ln {\displaystyle \underset{D_{\min }}{\overset{D_{\max }}{\int }}\exp \left[-\omega \frac{\pi }{6}{D}^3\cdot N_0\left(1+\epsilon \right)\right]\frac{\pi }{2}{D}^{2}dD}(12)$

$\dot{V}=\frac{{\pi }^2}{12}{N}_0\left(1+\epsilon \right){\displaystyle \underset{D_{\min }}{\overset{D_{\max }}{\int }}{D}^5}\exp \left[-\varphi -\frac{\pi }{6}\omega N_0\left(1+\epsilon \right)D^3\right]dD(13)$

Eq. 14 can be obtained by solving Eq. 12. Insert Eq. 14 into Eq. 13 and integrate it, and Eq. 15 is obtained

$\varphi =\ln \left\{\frac{1}{\omega N_0\left(1+\epsilon \right)}\left\{\exp \left[-\omega N_0\left(1+\epsilon \right)\frac{\pi }{6}{D}_{\min }^3\right]-\exp \left[-\omega N_0\left(1+\epsilon \right)\frac{\pi }{6}{D}_{\max }^3\right]\right\}\right\}(14)$

$\begin{array}{l}\dot{V}=\frac{1}{\omega }\frac{\exp \left[-\frac{\pi }{6}\omega N_0\left(1+\epsilon \right)D_{\max }^3\right]\left[-\frac{\pi \omega N_0\left(1+\epsilon \right)D_{\max }^3}{6}-1\right]}{\left\{\exp \left[-\frac{\pi }{6}\omega N_0\left(1+\epsilon \right)D_{\min }^3\right]-\exp \left[-\frac{\pi }{6}\omega N_0\left(1+\epsilon \right)D_{\max }^3\right]\right\}}\\ -\frac{1}{\omega }\frac{-\exp \left[-\frac{\pi }{6}\omega N_0\left(1+\epsilon \right)D_{\min }^3\right]\left[-\frac{\pi \omega N_0\left(1+\epsilon \right)D_{\min }^3}{6}-1\right]}{\left\{\exp \left[-\frac{\pi }{6}\omega N_0\left(1+\epsilon \right)D_{\min }^3\right]-\exp \left[-\frac{\pi }{6}\omega N_0\left(1+\epsilon \right)D_{\max }^3\right]\right\}}\end{array}(15)$

Finally, Lagrange multipliers $\varphi$ and $\omega$ can be uniquely solved by Eqs 14, 15.

Define $P_{ni}$ as the probability of droplet size distribution, which can be expressed with the integration of $P_k$ in the range of volume intervals $\left[v_i-\frac{\mathrm{\Delta }{v}_i}{2},v_i+\frac{\mathrm{\Delta }{v}_i}{2}\right]$. Eq. 16 can be obtained as follows

$P_{ni}={\displaystyle {\int }_{v_i-\frac{\mathrm{\Delta }{v}_i}{2}}^{v_i+\frac{\mathrm{\Delta }{v}_i}{2}}{P}_{k}dv=}{\displaystyle {\int }_{v_i-\frac{\mathrm{\Delta }{v}_i}{2}}^{v_i+\frac{\mathrm{\Delta }{v}_i}{2}}\exp \left[-\varphi -w{v}_k{N}_0\left(1+\epsilon \right)\right]dv}={\displaystyle {\int }_{D_i-\frac{\mathrm{\Delta }{D}_i}{2}}^{D_i+\frac{\mathrm{\Delta }{D}_i}{2}}\exp \left[-\varphi -w\frac{\pi D^3}{6}{N}_0\left(1+\epsilon \right)\right]\frac{\pi D^2}{2}dD}(16)$

When the droplet diameter size is in the range of $\left[D_i-\frac{\mathrm{\Delta }{D}_i}{2},D_i+\frac{\mathrm{\Delta }{D}_i}{2}\right]$, the probability density function of a sodium droplet of diameter D is defined as dN/dD, and N means the number percentage of sodium droplet diameter. Assuming that the droplet size of the particles of atomization sodium droplets ejected from the break of the loop system conforms to the continuous distribution, the probability of droplet diameter distribution of $P_{ni}$ can be expressed as Eq. 17

$P_{ni}={\displaystyle {\int }_{D_i-\frac{\mathrm{\Delta }{D}_i}{2}}^{D_i+\frac{\mathrm{\Delta }{D}_i}{2}}\frac{dN}{dD}dD}(17)$

The probability density function of a sodium droplet of diameter D can be obtained as Eq. 18

$\frac{dN}{dD}=\frac{\pi }{2}{D}^2\exp \left[-\varphi -\omega \frac{\pi }{6}{D}^3{N}_0\left(1+\epsilon \right)\right](18)$

Consider that there is a pressure differential drive between the sodium circuit system and the external environment where the pipe breaks. Assume that the minimum diameter D_min of the sodium droplet after ejection is 0 and the maximum diameter is D_max, which can also be denoted as D_cr and determined by We_cr (Hinze, 1955)

$D_{cr}=\frac{\sigma W{e}_{cr}}{{\rho }_A{\overline{u}}^2}(19)$

where ${\rho }_A$ is the density of the ambient medium; σ is the surface tension of the sodium droplet; We_cr is the critical value of We; and ${\overline{u}}^2$ is the average value across the whole flow field of the squares of velocity differences over a distance equal to D_cr, which is related to the kinetic energy per unit mass. Therefore, Eq. 20 can be obtained by simplifying Eq. 14

$\varphi =\ln \frac{\left\{1-\exp \left[-\omega N_0\left(1+\epsilon \right)\frac{\pi }{6}{D}_{cr}^3\right]\right\}}{\omega N_0\left(1+\epsilon \right)}(20)$

Insert Eq. 20 into Eq. 18

$\frac{dN}{dD}=\frac{\pi }{2}{D}^2\left\{\frac{\omega N_0\left(1+\epsilon \right)}{1-\exp \left[-\omega N_0\left(1+\epsilon \right)\frac{\pi }{6}{D}_{cr}^3\right]}\right\}\cdot \exp \left[-\omega N_0\left(1+\epsilon \right)\frac{\pi }{6}{D}^3\right](21)$

where $\omega$ can be given by the implicit expression of (1–15). However, for the calculation of the safety analysis of the sodium spray fire accident, it is inconvenient to use the mathematical model of the implicit expression. The semi-empirical relationship based on the constraint of the mass equation will be determined by the method of fitting the experimental data. Eq. 21 can be simplified as Eq. 22

$\frac{dN}{dD}=a{D}^2\cdot \exp \left(b{D}^3\right)(22)$

The mathematical expression form with the maximum entropy principle with the mass equation as the constraint condition can be obtained as Eq. 23

$\ln \left(\frac{dN}{dD}\right)=a+2\ln D+b{D}^3(23)$

where a and b are the coefficients determined by fitting the experimental data.

2.2 Maximum Entropy Principle With the Momentum Equation as the Constraint Condition

The momentum equation considering the viscous resistance term of the sodium droplet is as follows

${\displaystyle \sum _i{P}_i{\nu }_i{N}_0\left[u_0^2+\frac{4{\mu }_l}{{\pi }^2{D}_i^3{\rho }_A}{\left(\frac{\sigma }{D_i{\rho }_l}\right)}^{1/2}\right]}=A{U}_0^3(24)$

where $P_i$ represents the probability of the number of droplets with atomization volume ${\nu }_i$ , $u_0$ is the volume-weighted average velocity, ${\mu }_l$ is the integral of the kinetic viscosity of the sodium droplet for the droplet surface, $D_i$ is the diameter of the sodium droplet, ${\rho }_l$ is the density of the sodium droplet, $A$ is the cross-sectional area of the break, and $U_0$ is the average flow velocity of sodium droplets at the break.

Using the Lagrange method, Eq. 25 is obtained between G_mo and the probability of the number of sodium droplets

$\begin{array}{l}{G}_{mo}={\displaystyle \sum _i{P}_i\ln \left(P_i\right)}+\lambda \left\{{\displaystyle \sum _i{P}_i{\nu }_i{N}_0\left[u_0^2+\frac{4{\mu }_l}{{\pi }^2{D}_i^3{\rho }_A}{\left(\frac{\sigma }{D_i{\rho }_l}\right)}^{1/2}\right]}\right\}\\ -\lambda A{U}_0^3+\left(\beta -1\right)\left({\displaystyle \sum _i{P}_i-1}\right)\end{array}(25)$

The derivation of G_mo with respect to the number probability is 0. Thus, Eqs 26, 27 can be obtained as follows

$\ln P_i+1+\lambda {\nu }_i{N}_0\left[u_0^2+\frac{4{\mu }_l}{{\pi }^2{D}_i^3{\rho }_A}{\left(\frac{\sigma }{D_i{\rho }_l}\right)}^{1/2}\right]+\beta -1=0(26)$

$P_i=\exp \left\{-\beta -\lambda {\nu }_i{N}_0\left[u_0^2+\frac{4{\mu }_l}{{\pi }^2{D}_i^3{\rho }_A}{\left(\frac{\sigma }{D_i{\rho }_l}\right)}^{1/2}\right]\right\}(27)$

where λ and β are the Lagrange multipliers.

The probability of droplet size distribution $P_{ni}$ can be expressed with the integration of $P_i$ in the range of volume intervals $\left[v_i-\frac{\mathrm{\Delta }{v}_i}{2},v_i+\frac{\mathrm{\Delta }{v}_i}{2}\right]$, and Eq. 28 can be obtained

$\begin{array}{c}{P}_{ni}={\displaystyle {\int }_{v_i-\frac{\mathrm{\Delta }{v}_i}{2}}^{v_i+\frac{\mathrm{\Delta }{v}_i}{2}}{P}_{i}dv=}{\displaystyle {\int }_{v_i-\frac{\mathrm{\Delta }{v}_i}{2}}^{v_i+\frac{\mathrm{\Delta }{v}_i}{2}}\exp \left\{-\beta -\lambda {\nu }_i{N}_0\left[u_0^2+\frac{4{\mu }_l}{{\pi }^2{D}_i^3{\rho }_A}{\left(\frac{\sigma }{D_i{\rho }_l}\right)}^{1/2}\right]\right\}dv}={\displaystyle {\int }_{D_i-\frac{\mathrm{\Delta }{D}_i}{2}}^{D_i+\frac{\mathrm{\Delta }{D}_i}{2}}\exp \left\{-\beta -\lambda \frac{\pi D^3}{6}{N}_0\left[u_0^2+\frac{4{\mu }_l}{{\pi }^2{D}^3{\rho }_A}{\left(\frac{\sigma }{D{\rho }_l}\right)}^{1/2}\right]\right\}\frac{\pi D^2}{2}dD}\\ ={\displaystyle {\int }_{D_i-\frac{\mathrm{\Delta }{D}_i}{2}}^{D_i+\frac{\mathrm{\Delta }{D}_i}{2}}\exp \left\{-\beta -\lambda \frac{\pi D^3}{6}{N}_0{u}_0^2-\frac{2}{3}\lambda N_0\frac{{\mu }_l}{\pi {\rho }_A}{\left(\frac{\sigma }{D{\rho }_l}\right)}^{1/2}\right\}\frac{\pi D^2}{2}dD}\end{array}(28)$

Set Eqs 29, 30 as follows. Also, assuming that the droplet size of the sodium droplets ejected from the main system break follows a continuous distribution, Eq. 31 can be obtained from Eq. 28

$\alpha =\frac{\pi }{6}\lambda N_0(29)$

$K=\frac{2}{3}{N}_0\frac{{\mu }_l}{\pi {\rho }_A}{\left(\frac{\sigma }{{\rho }_l}\right)}^{1/2}(30)$

$\frac{dN}{dD}=\exp \left\{-\beta -\alpha u_0^2{D}^3-\lambda K{D}^{-1/2}\right\}\frac{\pi D^2}{2}(31)$

According to Eq. 12, Eq. 32 can be obtained

$\varphi =\ln {\displaystyle \underset{D_{\min }}{\overset{D_{\max }}{\int }}\exp \left\{-\alpha u_0^2{D}^3-\lambda K{D}^{-1/2}\right\}\frac{\pi D^2}{2}dD}(32)$

Insert Eq. 32 into Eq. 31

$\frac{dN}{dD}=\frac{D^2\exp \left(-\alpha D^3{u}_0^2-\lambda K{D}^{-1/2}\right)}{{\displaystyle \underset{D_{\min }}{\overset{D_{\max }}{\int }}{D}^2\exp \left(-\alpha D^3{u}_0^2-\lambda K{D}^{-1/2}\right)dD}}(33)$

Define the coefficient W₁ as follows

$W_1={\displaystyle \underset{D_{\min }}{\overset{D_{\max }}{\int }}{D}^2\exp \left(-\alpha D^3{u}_0^2-\lambda K{D}^{-1/2}\right)dD}(34)$

The mathematical expression form with the maximum entropy principle with the momentum equation as the constraint condition can be obtained as Eq. 35

$\ln \frac{dN}{dD}=-\ln \left(W_1\right)+W_2\ln D-W_3{D}^3-W_4{D}^{-1/2}(35)$

where W₁, W₂, W₃, and W₄ are the coefficients determined by fitting the experimental data.

3 Verification by Comparison With Experiments

3.1 Verification by Liquid Fuel Spray Experiment Results

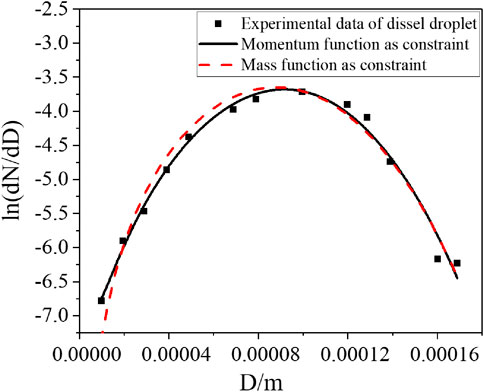
The HAN-based liquid spray experiment (Wang, 2017) is selected, in which the density and viscosity are 1300 kg/m³ and 1.2 × 10⁻³ Pas, respectively, for the simulated working fluid of the HAN-based liquid. The droplet size distribution experiments of spray droplets under the pressure differences of 1.8, 2.2, and 2.6 MPa were carried out, where the droplet size distribution of spray droplets was measured with phase Doppler analysis (PDA). The semi-empirical model with the mass conservation equation as the constraint condition and the momentum conservation equation as the constraint condition was used to simulate the experimental data, and the result is shown in Figures 1–3. Under different pressure differences, the two models can both reflect the spray size distribution of HAN-based liquids. In addition, both models can reflect the trend that the median diameter gradually decreases with the increase of the nozzle pressure difference, which is consistent with the experimental conclusion. The result of the semi-empirical model with the momentum equation as the constraint is in good agreement with the experimental data, with little error, especially for the smaller spray diameter.

FIGURE 1

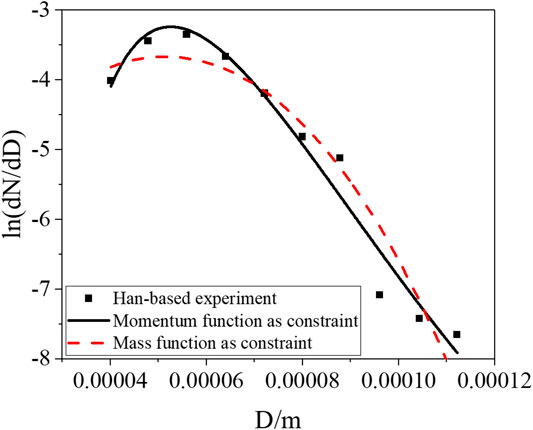
FIGURE 1. Results of droplet size distribution of HAN-based liquid droplets under the pressure difference of 1.8 MPa.

FIGURE 2

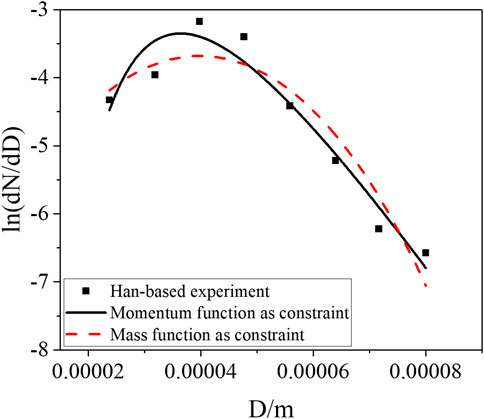
FIGURE 2. Results of droplet size distribution of HAN-based liquid droplets under the pressure difference of 2.2 MPa.

FIGURE 3

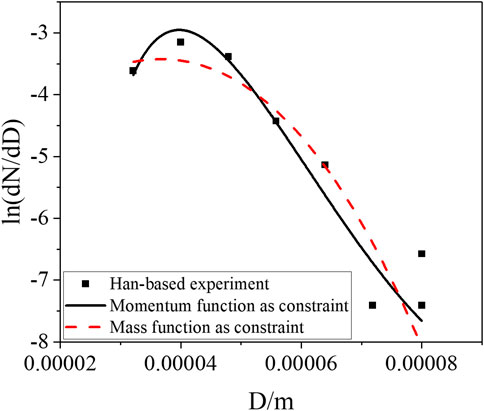
FIGURE 3. Results of droplet size distribution of HAN-based liquid droplets under the pressure difference of 2.6 MPa.

The model is also verified by the spray droplet distribution experiment of injecting diesel into the air combustion chamber (Hiroyasu, 1985) with the pressure differences of 8.8 and 9.8 MPa, respectively. In addition, the sampling time of the experimental data is 4.5 ms after injection. At this time, the atomization state and droplet size are basically stable. The experimental data under the pressure difference of 8.8 MPa show a normal distribution, that is, the distribution of data points near the peak of probability density is nearly symmetrical, shown as Figure 4. However, under the experimental condition of the pressure difference of 9.8 MPa, the overall distribution of the experimental data is asymmetric and is barbed, shown as Figure 5. The results calculated with the both models can reflect the normal distribution very well. However, when the pressure difference reaches 9.8 MPa, the model with the mass equation as the constraint cannot correctly reflect the spray size distribution. The spray size distribution simulated by the semi-empirical model with the momentum equation as the constraint is in good agreement with the experimental data under a higher pressure difference. It is shown that when the peak of the probability density appears at a small diameter under a high pressure difference, the model constrained by the momentum equation also has better applicability due to the influence of viscous force.

FIGURE 4

FIGURE 4. Results of diesel droplet size distribution under the pressure difference of 8.8 MPa.

FIGURE 5

FIGURE 5. Results of diesel droplet size distribution under the pressure difference of 9.8 MPa.

3.2 Verification by Sodium Spray Fire Experiments Results

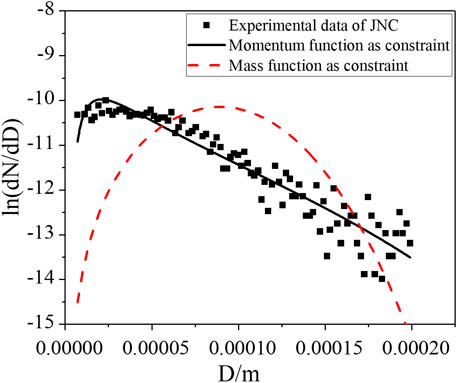
The model is verified by the Italian LISOF sodium spray fire experiment (Torsello et al., 2012) and the sodium spray fire test of JNC (Nagai et al., 1999). The LISOF experiment is carried out for the droplet leakage phenomenon under the small break of the sodium-cooled fast reactor, and it uses sodium with a temperature of 550°C and a 0.2 mm nozzle to simulate the phenomenon of sodium spray under microdefects in a cooling circuit, which is similar to those in SFR. The pressure difference is 0.6 MPa, and the initial mass flow rate is 0.9 g/s. The JNC sodium droplet size distribution experiment is carried out for large-scale sodium spray fire under the pressure nozzle with a pressure difference of 0.2 MPa, an initial mass flow rate of 49.6 g/s, and a sodium temperature of 140°C.

The comparison between the calculation results of the two models and the experimental data of two sodium sprays is shown in Figures 6, 7, which shows similar conclusions with the experimental verification of the liquid fuel spray. In other words, the semi-empirical model with the momentum equation as the constraint can reflect the particle size distribution of sodium spray, whether it is normal distribution or asymmetric distribution, such as barb distribution.

FIGURE 6

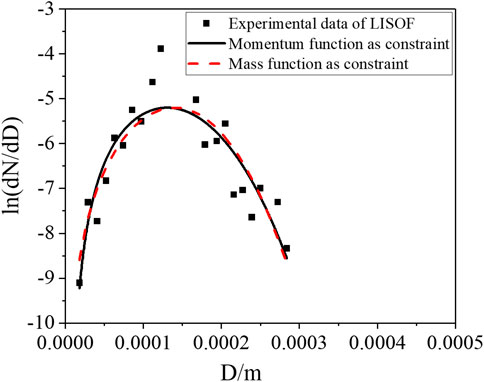
FIGURE 6. Results of LISOF sodium droplet size distribution under the pressure difference of 0.6 MPa.

FIGURE 7

FIGURE 7. Results of JNC sodium droplet size distribution under the pressure difference of 0.2 MPa.

3.3 Comparison of Two Models

The data from the liquid fuel spray experiment and the sodium spray fire experiment are summarized and compared with the both semi-empirical prediction models. The results are shown as Figures 8, 9. The horizontal axis represents the probability density value measured by the four experiments, and the vertical axis represents the predicted value of the model corresponding to the experiments. The error of the semi-empirical model with momentum as a constraint is in the range of 20%. In addition, the error of the semi-empirical model with the mass equation as a constraint is in the range of 30%, except for some data with large deviation.

FIGURE 8

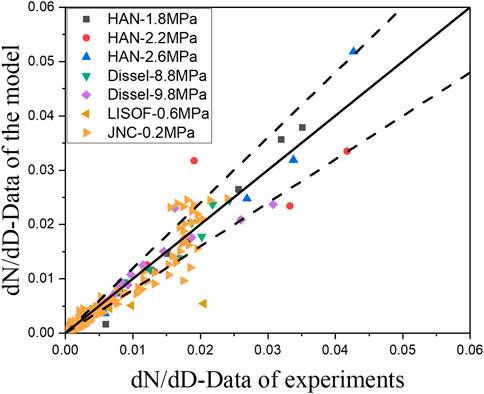
FIGURE 8. Relative error of droplet size number obtained by the model constrained with momentum equation.

FIGURE 9

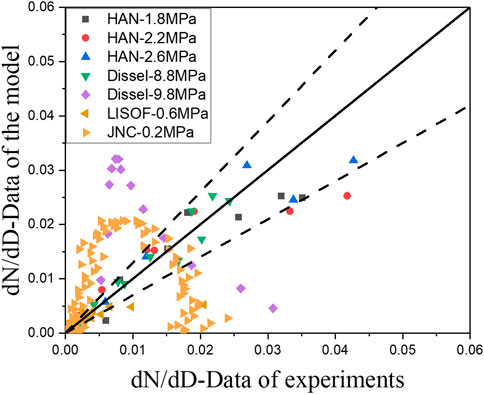
FIGURE 9. Relative error of droplet size number obtained by the model constrained with mass equation.

The semi-empirical model with the mass equation as a constraint does not seem to be able to correctly reflect the slow reduction of the number of large particles with the increase of particle size. This is because after the droplet is ejected, the momentum will decrease due to viscous force and surface tension; as a result, the reduction is not conducive to breaking the droplets into small particles, leading to an increase in the proportion of large droplets. There exists the same problem in the HAN-based liquid experiment, only due to the small amount of data; the fitting results under the two constraints have little difference.

4 Comparison With Current Distribution Models

The existing typical spray droplet size distribution models include the Nukiyama–Tanasawa model (Tsai, 1980), Rosin-Rammler model (Rosin and Rammler, 1933), and Cheng model (Cheng et al., 2002) based on the maximum entropy principle and considering the simplified mass conservation equation, expressed as Eqs 36, 37, 38, where b and q are undetermined coefficients and $\overline{D}$ is the average diameter of droplets. Combined with the proposed sodium spray model constrained with the momentum equation in the paper, the droplet size distribution is compared and verified with the LISOF sodium spray fire experiment and JNC experiment

$\frac{dN}{dD}={\left(\frac{3.915}{\overline{D}}\right)}^6\frac{D^5}{120}\exp \left(-\frac{3.915D}{\overline{D}}\right)(36)$

$\frac{dN}{dD}=bq\cdot D^{q-4}\exp \left(-b{D}^q\right)(37)$

$\frac{dN}{dD}=\frac{\pi }{2}{D}^2\frac{{\rho }_l{N}_0}{\dot{m}}\exp \left(-\frac{\pi }{6}\frac{{\rho }_l{N}_0}{\dot{m}}{D}^3\right)(38)$

The Nukiyama–Tanasawa model with an arithmetic mean diameter of 138.6 μm, a surface area mean diameter of 152.9 μm, a volume mean diameter of 180.7 μm, and a Sauter mean diameter of 252.7 μm is used to compare with LISOF experimental data, shown as Figure 10. The error between the Nukiyama–Tanasawa model with the arithmetic mean diameter (named D₁₀) and experiment data is relatively small.

FIGURE 10

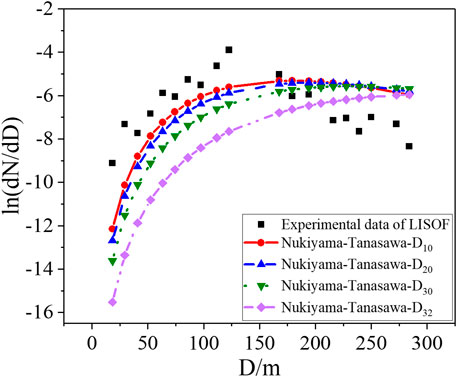
FIGURE 10. Comparison of Nukiyama-Tanasawa model at different mean diameters with LISOF experimental data.

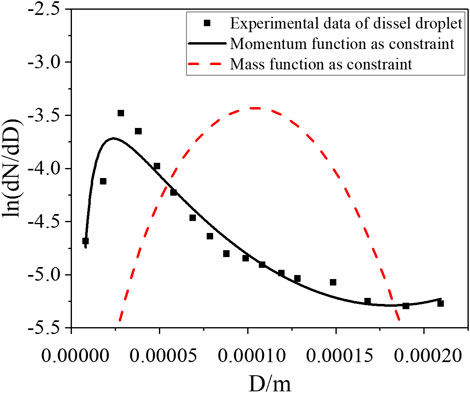
The proposed sodium spray model constrained with the momentum equation, the Nukiyama–Tanasawa model with arithmetic mean diameter D₁₀, the Rosin–Rammler model, and the Cheng model are used to predict LISOF experiment and JNC experiment data, shown as Figures 11, 12. It can be found that the Rosin–Rammler model, the Nukiyama–Tanasawa model with the arithmetic mean diameter, and the Cheng model have serious distortions in the prediction. The proposed sodium spray model constrained with the momentum equation is in good agreement with the experimental data for different distribution forms, which means that it has a wider range of applications.

FIGURE 11

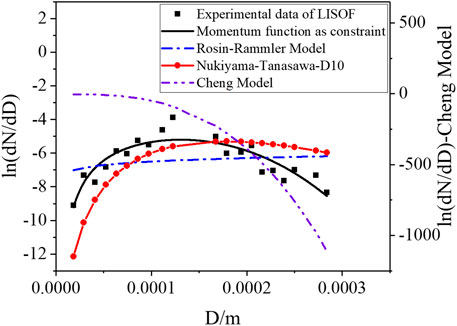
FIGURE 11. Comparison of Nukiyama-Tanasawa model with D10, Cheng model, Rosin-Rammler model and the proposed sodium spray model with LISOF experimental data.

FIGURE 12

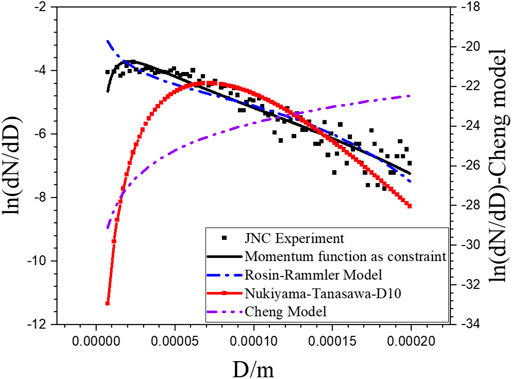
FIGURE 12. Comparison of Nukiyama-Tanasawa model with D10, Cheng model, Rosin-Rammler model and the proposed sodium spray model with JNC experimental data.

5 Conclusion

The semi-empirical model of drop size distribution from the maximum entropy principle is developed and verified with different experimental data. The main conclusions are achieved as follows.

Theoretical analysis is carried out on the size distribution of sodium droplets in sodium spray based on the maximum entropy principle, a semi-empirical model with the mass equation as the main constraint or the semi-empirical model with the momentum equation including the viscous resistance term as the main constraint is developed. Through the comparing with the experimental data of liquid fuel and sodium droplet size distributions, the rationality of the proposed sodium spray model is proved. Regardless of normal distribution or barb distribution, the proposed model is in good agreement with experimental data, with an error of 20%. The proposed model semi-empirical model with the momentum equation constraint considering the influence of viscous force can reflect an increase in the proportion of large droplets due to the decrease in momentum. Compared with other existing models, the proposed sodium spray model constrained with the momentum equation is in better agreement with the experimental data for different distribution forms with minor error.

This study provides a new prediction model for the prediction of the size distribution for the safety analysis of sodium spray fire accidents.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

WZ: model and draft. ZZ: analysis and writing—original. LT: methodology, investigation, and writing—review and editing. CP: analysis.

Funding

This work was financially supported by the National Natural Science Foundation of China (U1967202).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Babinsky, E., and Sojka, P. E. (2002). Modeling Drop Size Distributions. Prog. Energ. Combustion Sci. 28 (4), 303–329. doi:10.1016/s0360-1285(02)00004-7

CrossRef Full Text | Google Scholar

Cao, J. M., He, J., and Li, X. G. (2008). Droplet Size and Velocity Distribution Function in Sprays Based on Maximum Entropy Principle. J. Traffic Transportation Eng. 8 (5), 1–8.

Google Scholar

Cheng, X. B., Huang, R. H., and Zhu, M. L. (2002). Application of Information Entropy to Calculating Drop Size Distribution of spray. J. Huazhong Univ. Sci. Technology 30, 30–32.

Google Scholar

Cherdron, W. (1980). Determination of Sodium Fire Aerosol Process Coefficients from FAUNA-experimentsNUREG/CR-1724.

Google Scholar

Garcia, M., Herranz, L. E., and Kissane, M. P. (2016). Theoretical Assessment of Particle Generation from Sodium Pool Fires. Nucl. Eng. Des. 310, 470–483. doi:10.1016/j.nucengdes.2016.10.024

CrossRef Full Text | Google Scholar

GIF (2002). A Technology Roadmap for Generation IV Nuclear Energy Systems. U.S. DOE Nuclear Energy Research Advisory Committee and the Generation IV International Forum. GIF 002-00.

Google Scholar

Hinze, J. O. (1955). Fundamentals of the Hydrodynamic Mechanism of Splitting in Dispersion Processes. Aiche J. 1 (3), 289–295. doi:10.1002/aic.690010303

CrossRef Full Text | Google Scholar

Hiroyasu, H. (1985). Diesel Engine Combustion and its Modeling. Comodia 85, 53–75.

Google Scholar

Jaynes, E. T. (1957). Information Theory and Statistical Mechanics. Phys. Rev. 106, 620–630. doi:10.1103/PhysRev.106.620

CrossRef Full Text | Google Scholar

Lee, K. H., Lee, C. H., and Lee, C. S. (2004). An Experimental Study on the spray Behavior and Fuel Distribution of GDI Injectors Using the Entropy Analysis and PIV Method. Fuel 83 (7-8), 971–980. doi:10.1016/j.fuel.2003.10.021

CrossRef Full Text | Google Scholar

Malet, J. C., Casselman, C., Duverger de Guy, G., Rzekiecki, R., and Charpenel, J. (1982). Potential Results of spray and Pool Fires. Nucl. Eng. Des. 68 (2), 195–206. doi:10.1016/0029-5493(82)90031-0

CrossRef Full Text | Google Scholar

Manzini, G., and Torsello, G. (2013). “Sodium Safety- spray and Pool Fires ECART Modeling,” in 15th International Topical Meeting on Nuclear Reactor Thermal-hydraulics, Pisa, Italy, May 12-17.

Google Scholar

Mojaver, P., Khalilarya, S., and Chitsaz, A. (2020). Multi-objective Optimization and Decision Analysis of a System Based on Biomass Fueled SOFC Using Couple Method of Entropy/VIKOR. Energ. Convers. Management 203, 112260. doi:10.1016/j.enconman.2019.112260

CrossRef Full Text | Google Scholar

Murata, K. K., Carroll, D. E., Bergeron, K. D., and Valdez, G. D. (1993). CONTAIN LMR/1B-Mod.1, A Computer Code for Containment Analysis of Accidents in Liquid-Metal-Cooled Nuclear Reactors. USA: Sandia National Laboratories. SAND 91-1490.

Google Scholar

Nagai, K., Hirabayashi, M., Onojima, T., Oki, Y., Gunji, M., and Ara, K. (1999). Sodium Leakage and Combustion Tests-Measurement and Distribution of Droplet Size Using Various spray Nozzles. JAPAN: JNC TN. 9400 99-030.

Google Scholar

Ohno, S., Ohshima, H., Tajima, Y., and Ohki, H. (2012). Development of PIRT and Assessment Matrix for Verification and Validation of Sodium Fire Analysis Codes. Jpes 6 (2), 241–254. doi:10.1299/jpes.6.241

CrossRef Full Text | Google Scholar

Olivier, T. J., Blanchat, T. K., Figueroa, V. G., Hewson, J. C., and Nowlen, S. P. (2010). Metal Fires and Their Implications for advance Reactors Part 3: Experimental and Modeling Results. USA: Sandia National Laboratories. SAND 2010-7113, 2010.

Google Scholar

Peng, C., Qiao, D. L., Li, D., and Wu, J. (2021). Liquid spray Modeling under Sodium Fire Accidents. Nucl. Eng. Des. 379, 111260. doi:10.1016/j.nucengdes.2021.111260

CrossRef Full Text | Google Scholar

Rosin, P., and Rammler, E. (1933). The Laws Governing the Fineness of Powdered Coal. J. Inst. Fuel 7, 29–36.

Google Scholar

Sathiah, P., and Roelofs, F. (2014). Numerical Modeling of Sodium Fire-Part I: Spray Combustion. Nucl. Eng. Des. 278, 723–738. doi:10.1016/j.nucengdes.2013.11.081

CrossRef Full Text | Google Scholar

Sovani, S. D., Sojka, P. E., and Sivathanu, Y. R. (1999). Prediction of Drop Size Distributions from First Principles: the Influence of Fluctuations in Relative Velocity and Liquid Physical Properties. Atomization and Sprays 9 (2). doi:10.1615/atomizspr.v9.i2.20

CrossRef Full Text | Google Scholar

Srinivas, C. V., Subramanian, V., Kumar, A., Usha, P., Sujatha, N., Bagavath Singh, A., et al. (2019). Modeling of Atmospheric Dispersion of Sodium Fire Aerosols for Environmental Impact Analysis during Accidental Leaks. J. Aerosol Sci. 137, 105432. doi:10.1016/j.jaerosci.2019.105432

CrossRef Full Text | Google Scholar

Torsello, G., Parozzi, F., Nericcio, L., Araneo, L., Cozzi, F., Carcassi, M., et al. (2012). “Characterization of the Liquid Sodium spray Generated by a Pipework Hole,” in Proceedings of ICAPP ’12, Chicago, USA, June 24-28, 2012. Paper 12152.

Google Scholar

Tsai, S. S. (1980). NACOM Code for Analysis of Postulated Sodium spray Fires in LMFBRS. Upton, NY (USA): Brookhaven National Lab.

Google Scholar

Wang, J. (2017). Experimental and Simulation Studies on the spray Characteristics of Impinging Nozzle. NANJING University of Science and Technology. M.S. Dissertation https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201702&filename=1017053166.nh

Google Scholar

Wu, S., Lao, C. T., Akroyd, J., Mosbach, S., Yang, W., and Kraft, M. (2020). A Joint Moment Projection Method and Maximum Entropy Approach for Simulation of Soot Formation and Oxidation in Diesel Engines. Appl. Energ. 258, 114083. doi:10.1016/j.apenergy.2019.114083

CrossRef Full Text | Google Scholar

Yamaguchi, A., and Tajima, Y. (2002). Validation Study of Computer Code SPHINCS for Sodium Fire Safety Evaluation of Fast Reactor. Nucl. Eng. Des. 219, 19–34.

Google Scholar